SchulLV Logo
Lerninhalte in Mathe
BLF-Aufgaben (MMS)
Digitales Schulbuch
Inhaltsverzeichnis

Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1
\(12\,\%\) von \(650\,\text{m}\) sind:
\(7,8\,\text{m}\)
\(57,2\,\text{m}\)
\(78\,\text{m}\)
\(572\,\text{m}\)
\(728\,\text{m}\)
(1 BE)
2
Die Gleichung \(A_O=\pi \cdot r \cdot(r+s)\) wird nach \(s\) umgestellt. Dann gilt:
\(s=r-\dfrac{A_O}{\pi \cdot r}\)
\(s=\dfrac{A_0-r}{\pi \cdot r}\)
\(s=\dfrac{A_O \cdot \pi}{r}-r\)
\(s=r-\dfrac{\pi \cdot r}{A_O}\)
\(s=\dfrac{A_O}{\pi \cdot r}-r\)
(1 BE)
3
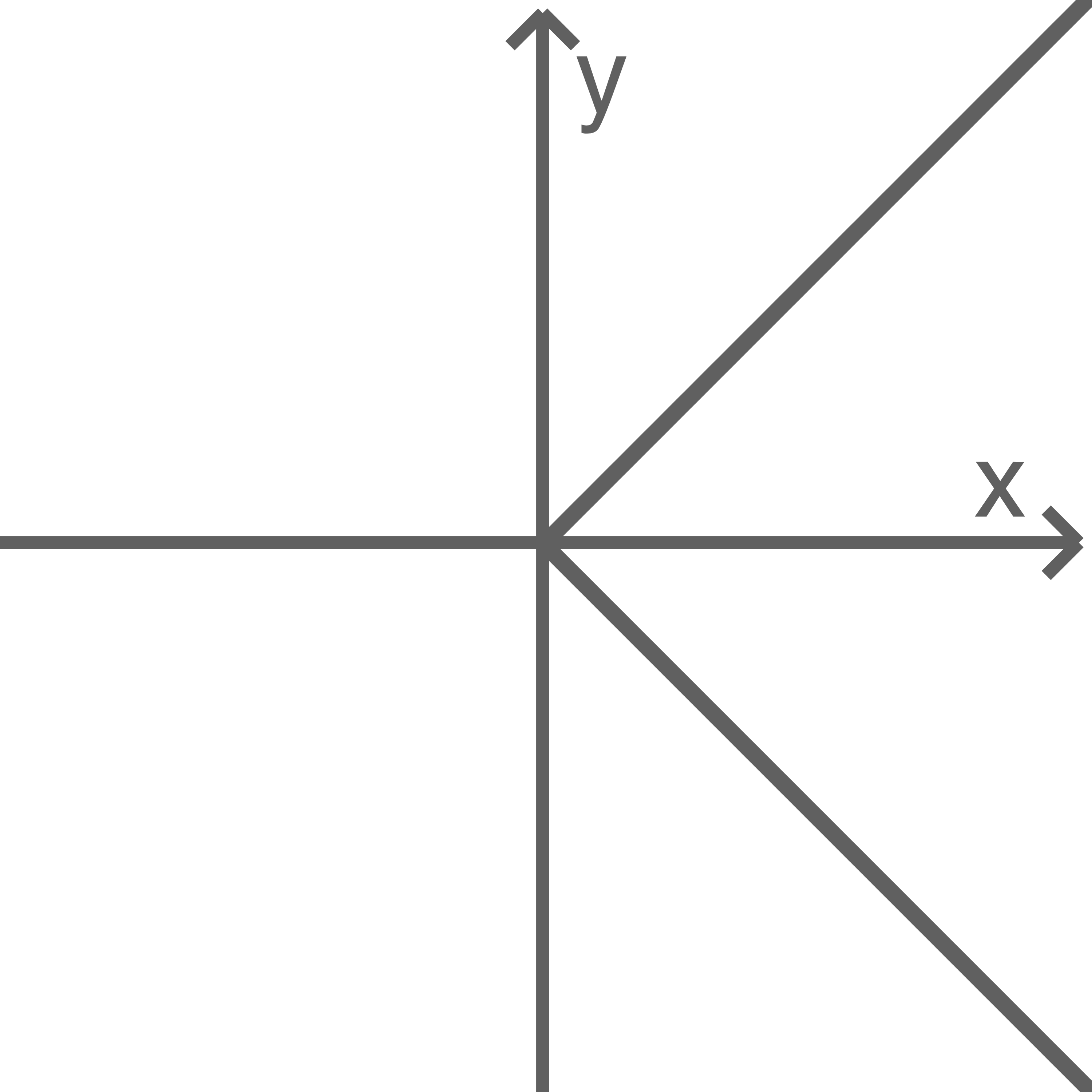
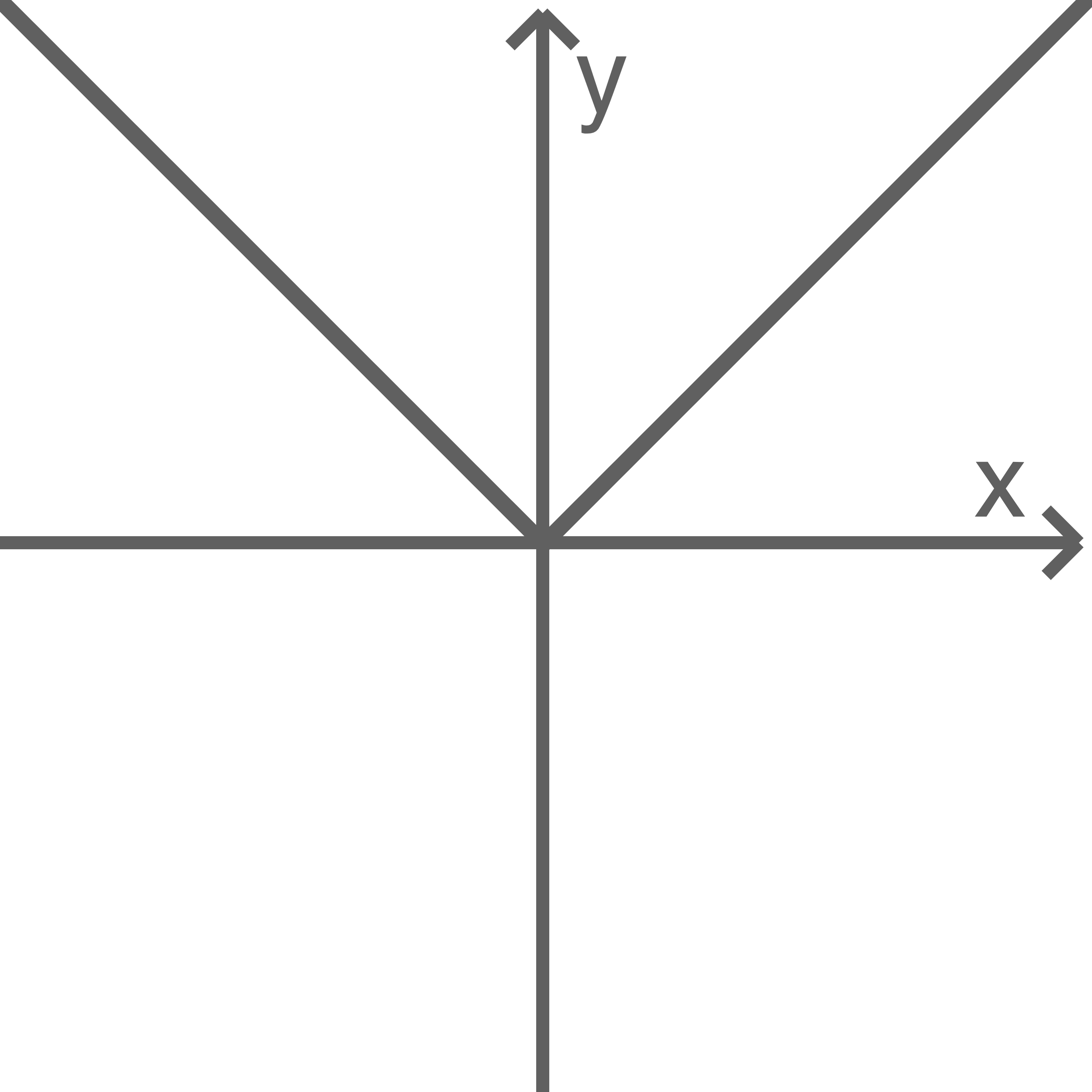
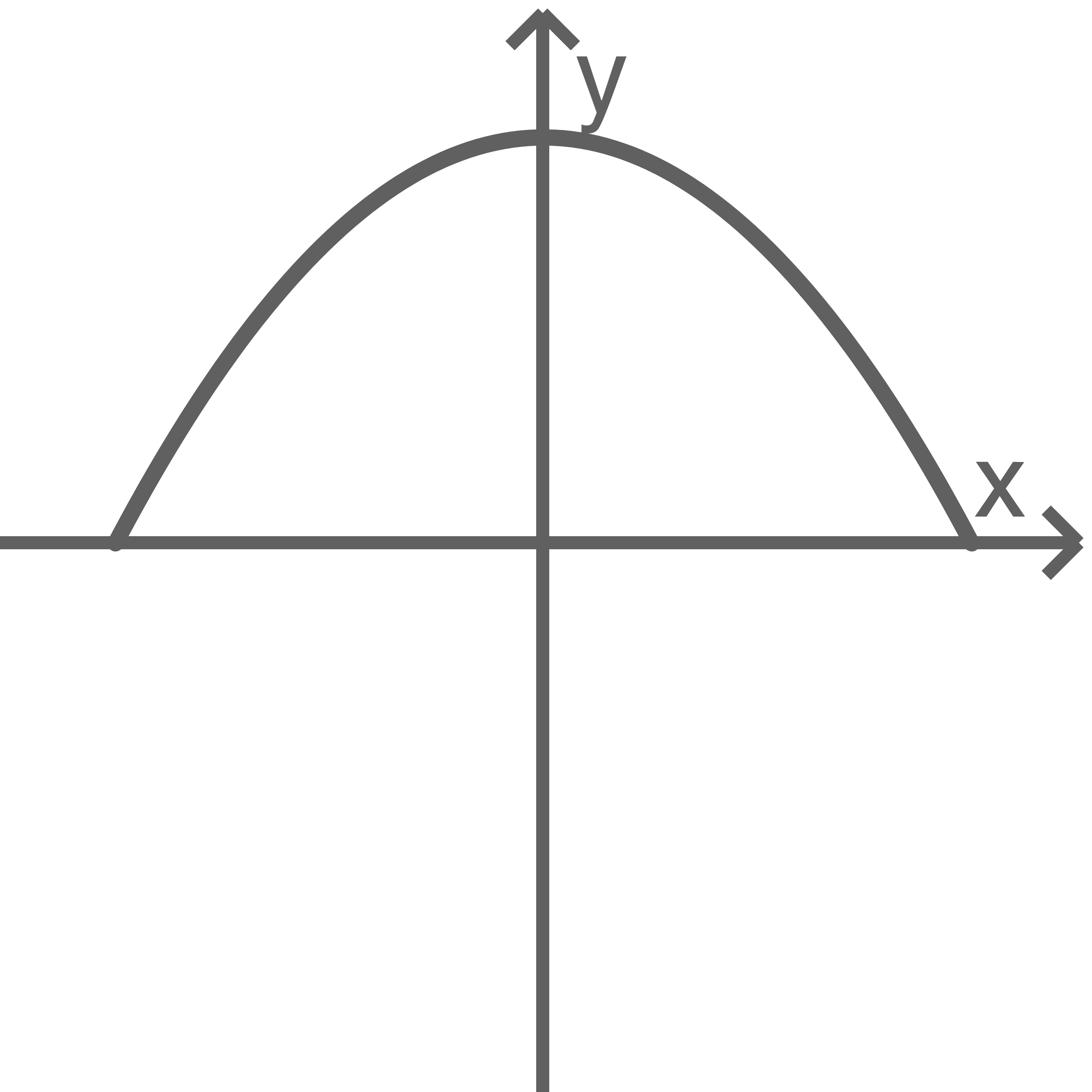
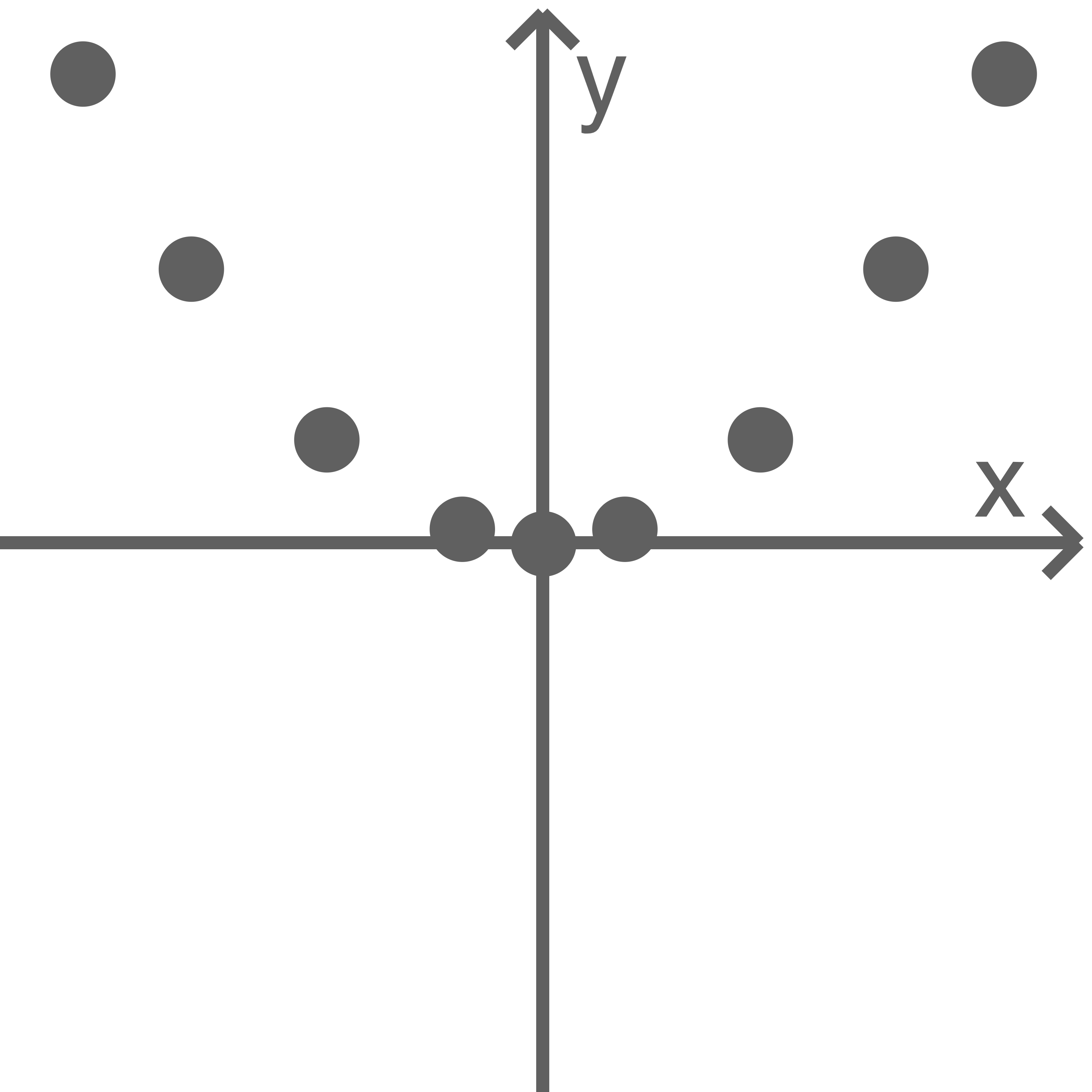
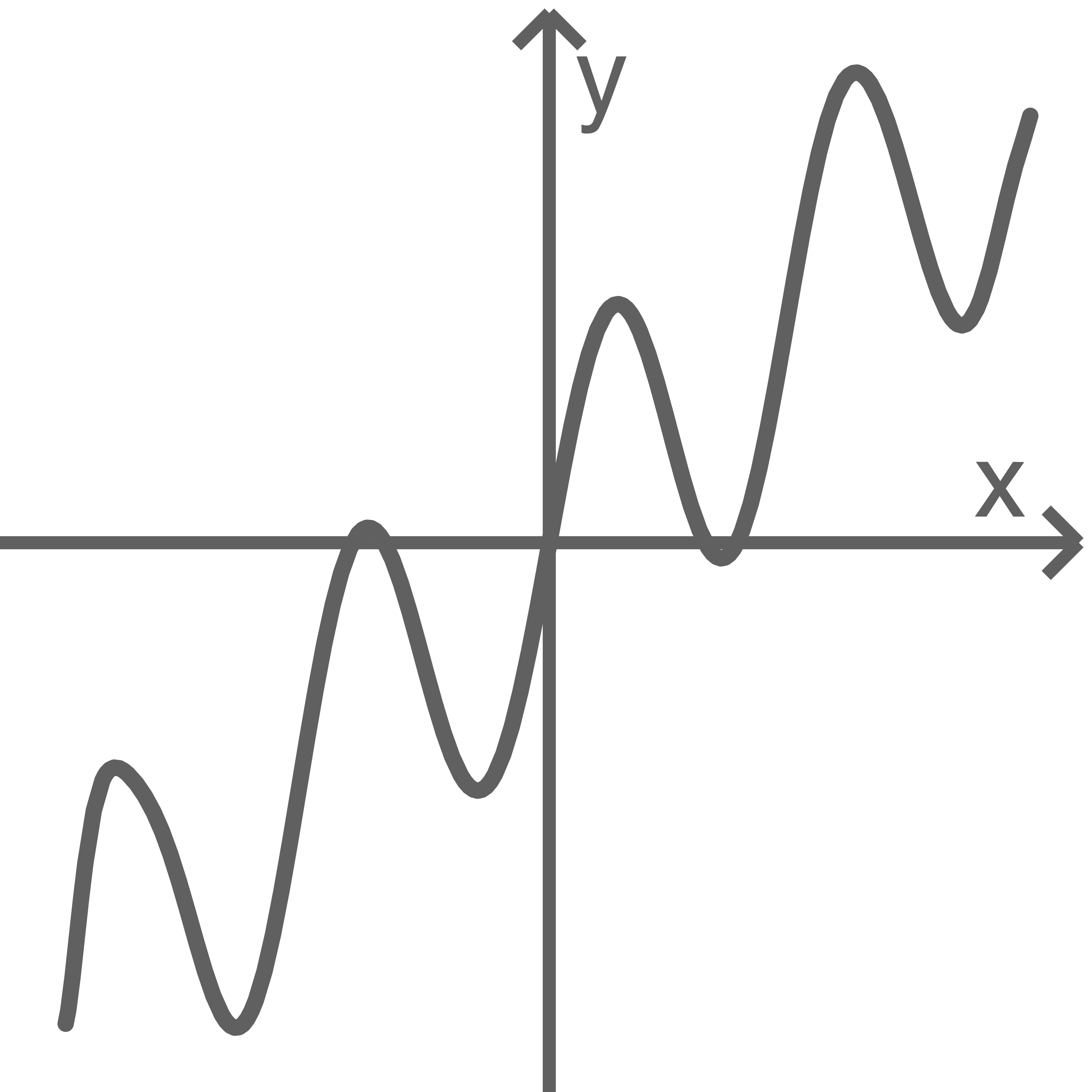
Welche Abbildung stellt nicht den Graphen einer Funktion dar?
sachsen blf 2023 teil a
sachsen blf 2023 teil a
sachsen blf 2023 teil a
sachsen blf 2023 teil a
sachsen blf 2023 teil a
(1 BE)
4
Welche Funktion besitzt für \(x \in \mathbb{R}\) den Wertebereich \(W=\{y \mid y \in \mathbb{R}, y \leq 2\}\) ?
\(y=(x+2)^2-1\)
\(y=(x-2)^2+2\)
\(y=-(x-2)^2+1\)
\(y=-(x-1)^2+2\)
\(y=(x-1)^2-2\)
(1 BE)
5
Der Abstand des Punkts \(A(-3 \mid 4)\) vom Koordinatenursprung beträgt:
\(\sqrt{7}\)
\(\sqrt{12}\)
\(5\)
\(9\)
\(25\)
(1 BE)
6
Welche der folgenden Aussagen ist bezüglich des abgebildeten rechtwinkligen Dreiecks wahr.
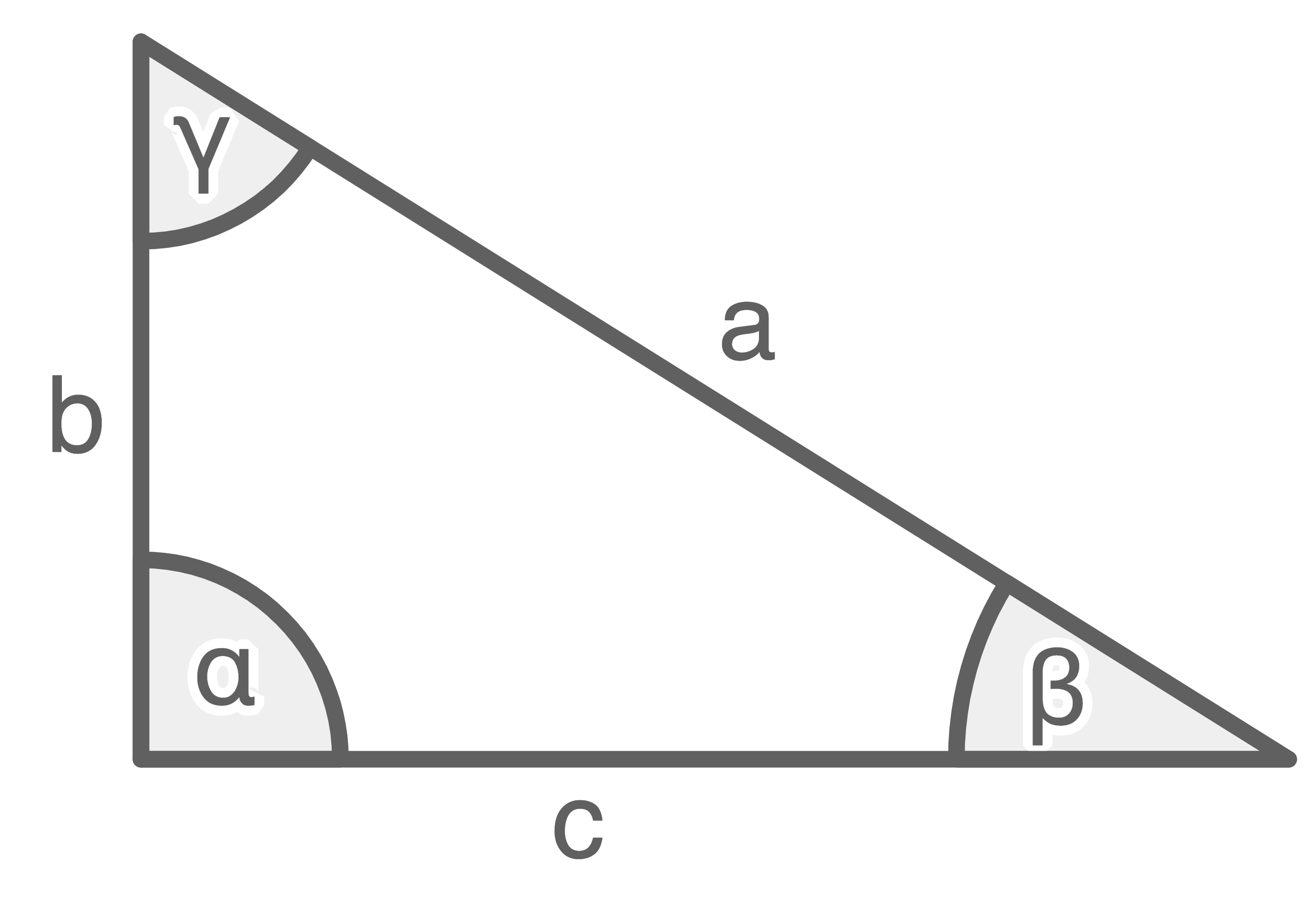
sachsen blf 2023 teil a
\(\sin \alpha=\dfrac{a}{c}\)
\(\sin \beta=\dfrac{c}{a}\)
\(\sin \gamma=\dfrac{c}{a}\)
\(\cos \beta=\dfrac{a}{c}\)
\(\cos \gamma=\dfrac{c}{a}\)
(1 BE)
7
Gegeben ist die Funktion \(g\) mit \(g(x)=\sin (x-1) \quad(x \in \mathbb{R}).\)
7.1
Gib an, wie der Graph von \(g\) aus dem Graphen der Funktion \(f\) mit \(f(x)=\sin x \,(x \in \mathbb{R})\) entsteht.
(1 BE)
7.2
Gib eine Gleichung der Funktion \(h\) an, deren Graph durch Streckung des Graphen von \(g\) mit dem Faktor 2 in \(y\)-Richtung entsteht.
(1 BE)
8
Bestimme \(p \in \mathbb{R}\) so, dass \(x=5\) eine Lösung der quadratischen Gleichung \(x^2+p \cdot x+20=0\) ist.
(2 BE)
9
Betrachtet werden zwei Rechtecke.
9.1
Das erste Rechteck mit den Seiten \(a\) und \(b\) hat einen Umfang von \(44 \mathrm{~cm}\). Die Seite \(a\) ist \(6 \mathrm{~cm}\) länger als die Seite \(b\).
Bestimme die Längen von \(a\) und \(b\).
(3 BE)
9.2
Das zweite Rechteck mit den Seitenlängen \(4 \mathrm{~cm}\) und \(5 \mathrm{~cm}\) rotiert um seine längere Seite. Zeige, dass das Volumen des dabei entstehenden geraden Kreiszylinders \(80 \cdot \pi\, \mathrm{cm}^3\) beträgt.
(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?