SchulLV Logo
  • SchulLV-PLUS
  • Lizenzcode einlösen
  • Testlizenz Lehrer*innen
SachsenGymnasiumKlasse 10
Mathe
Deutsch
Englisch
Mathe / BLF-Aufgaben (MMS)
Zum Inhaltsverzeichnis
Illustration für das Schulfach Mathe
Lerninhalte in Mathe
BLF-Aufgaben (MMS)
Digitales Schulbuch
Inhaltsverzeichnis
Mathe BLF 2025 – Sachsen
BLF 2024
Teil A
Teil B
BLF 2023
Teil A
Teil B
BLF 2022
BLF 2021
BLF 2020
Teil A
Teil B
BLF 2019
Teil A
Teil B
BLF 2018
Teil A
Teil B
BLF 2017
Teil A
Teil B
BLF 2016
Teil A
Teil B

Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1
Welche Umrechnung ist falsch?
 \(5,5\,\text{m}=550\,\text{cm}\)
 \(55\,\text{m}=0,055\,\text{km}\)
 \(5,5\,\text{cm}=0,55\,\text{dm}\)
 \(5,5\,\text{cm}=550\,\text{mm}\)
 \(55\,\text{mm}=0,55\,\text{dm}\)
(1 BE)
2
Welches Viereck muss kein Paar paralleler Seiten besitzen?
 Parallelogramm
 Rechteck
 Drachenviereck
 Trapez
 Quadrat
(1 BE)
3
Ein Preis von \(100 \,€\) wird um \(20 \,\%\) gesenkt. Um wie viel Prozent müsste der neue Preis wieder erhöht werden, damit der ursprüngliche Preis erreicht wird?
 \(20\,\%\)
 \(25\,\%\)
 \(30\,\%\)
 \(120\,\%\)
 \(125\,\%\)
(1 BE)
4
Wie viele verschiedene zweistellige Zahlen können aus den Ziffern 1, 3, 5, 7 und 9 gebildet werden, wenn jede der Ziffern auch doppelt verwendet werden kann?
 5
 7
 10
 20
 25
(1 BE)
5
Welche in \(\mathbb{R}\) definierte Funktion \(f\) hat einen Graphen, der symmetrisch zur \(y\)-Achse ist?
 \(f(x)=x\)
 \(f(x)=(x-1)^2\)
 \(f(x)=x^2-1\)
 \(f(x)=2^{x-1}\)
 \(f(x)=2^x-1\)
(1 BE)
6
Welche in \(\mathbb{R}\) definierte Funktion \(g\) ist im gesamten Definitionsbereich monoton fallend?
 \(g(x)=\dfrac{2}{3}\cdot x-3\)
 \(g(x)=-x^2-3\)
 \(g(x)=3^x\)
 \(g(x)=3^x-2\)
 \(g(x)=3^{-x}\)
(1 BE)
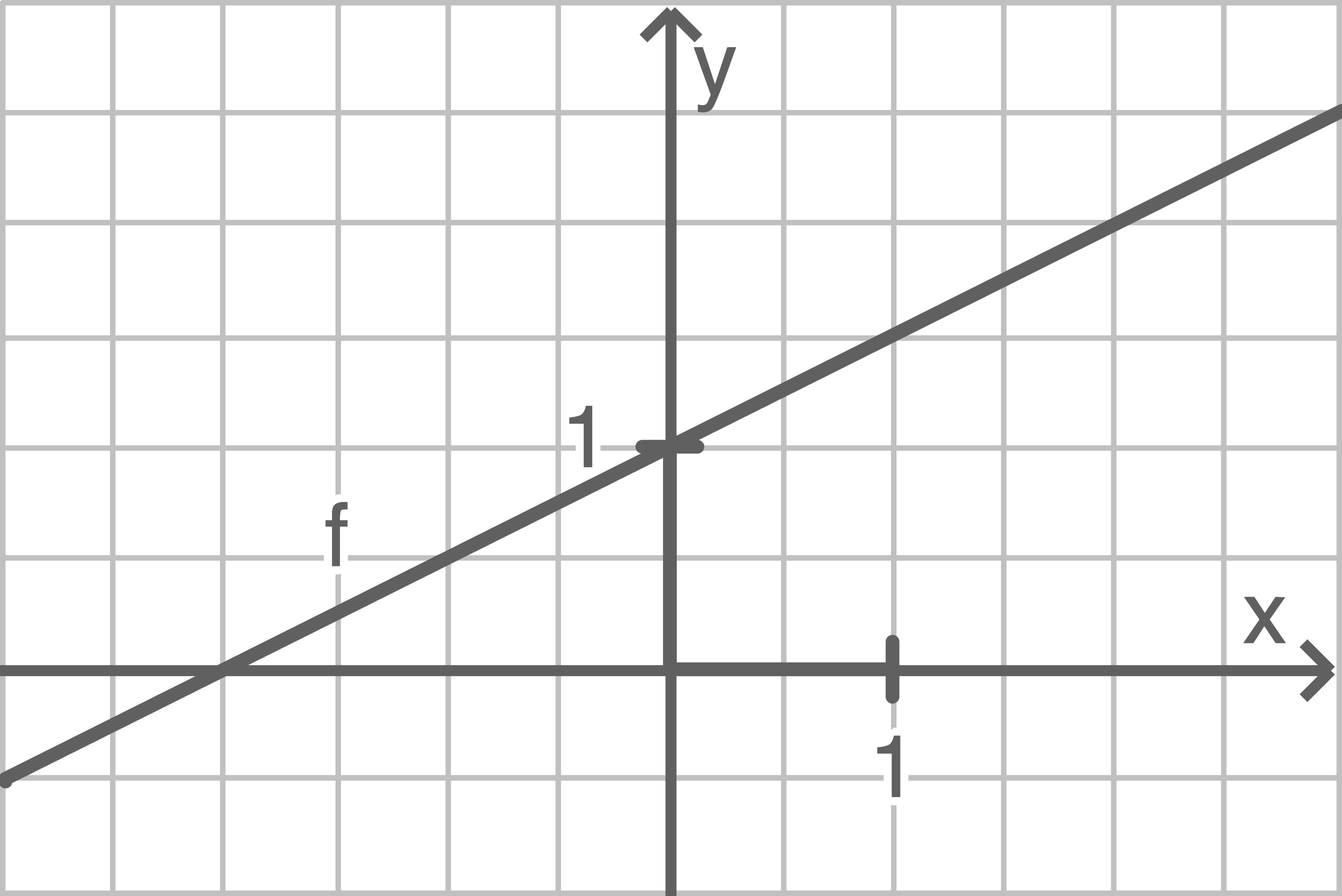
7
In einem Koordinatensystem ist der Graph der in \(\mathbb{R}\) definierten Funktion \(f\) mit \(f(x)=\dfrac{1}{2} \cdot x+1\) dargestellt (siehe Abbildung).
sachsen blf 2024 teil a
7.1
Berechne die Stelle, an welcher der Funktionswert 2024 beträgt.
(2 BE)
7.2
Der Graph der in \(\mathbb{R}\) definierten linearen Funktion \(g\) entsteht durch Spiegelung des Graphen von \(f\) an der \(x\)-Achse.
Gib eine Funktionsgleichung von \(g\) an.
\(\text{_______________________________________}\)
(2 BE)
7.3
Der Graph von \(f\) und die Koordinatenachsen begrenzen ein Dreieck. Dieses Dreieck rotiert um die \(x\)-Achse.
Begründe, dass das Volumen des dabei entstehenden Körpers größer als 2 ist.
(3 BE)
8
Ein Glücksrad besteht aus drei Sektoren, welche rot, blau bzw. gelb gefärbt sind. Beim einmaligen Drehen des Glücksrades wird der rote Sektor mit einer Wahrscheinlichkeit von \(50 \%\) und der blaue Sektor mit einer Wahrscheinlichkeit von \(\dfrac{1}{3}\) erreicht.
8.1
Gib die Wahrscheinlichkeit dafür an, dass beim einmaligen Drehen des Glücksrades der gelbe Sektor erreicht wird.
\(\text{_______________________________________}\)
(1 BE)
8.2
Das Glücksrad wird dreimal gedreht.
Gib ein Ereignis an, dessen Wahrscheinlichkeit durch den Term \(1-\left(\dfrac{1}{3}\right)^3\) berechnet werden kann.
\(\text{_______________________________________}\)
(1 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
\(5,5\,\text{cm}=55\,\text{mm}\neq 550\,\text{mm}\)
2
Bei einem Drachenviereck muss es kein Paar paralleler Seiten geben.
3
\(100\,€\cdot \dfrac{20}{100}=20\,€\)
Gesenkter Preis: \(100\,€-20\,€=80\,€\)
Um den ursprünglichen Wert zu erhalten muss gelten:
\(\begin{array}[t]{rll} p\,\%&=& \dfrac{20\,€}{80\,€}\cdot 100\,\% \\[5pt] &=& 25\,\% \end{array}\)
Der Preis müsste wieder um \(25\,\%\) erhöht werden.
4
Jede der fünf Zahlen kann wiederum mit allen fünf Zahlen kombiniert werden.
Es gibt \(5\cdot 5=25\) Möglichkeiten.
5
Der Graph der Funktion \(f(x)=x^2-1\) ist symmetrisch zur \(y\)-Achse:
\(f(-x)=(-x)^2-1=x^2-1=f(x)\)
6
Der Graph der Funktion \(g(x)=3^{-x}\) ist durch seinen negativen Exponenten im gesamten Definitionsbereich monoton fallend.
7.1
\(\begin{array}[t]{rll} \dfrac{1}{2}\cdot x+1&=& 2024 \quad \scriptsize \mid\; -1 \\[5pt] \dfrac{1}{2}\cdot x&=& 2023 \quad \scriptsize \mid\; \cdot 2 \\[5pt] x&=& 4046 \end{array}\)
An der Stelle \(x=4046\) beträgt der Funktionswert 2024.
7.2
\(g(x)=-f(x)=-\dfrac{1}{2}\cdot x-1\)
7.3
Der entstehende Körper ist ein Kegel mit dem Radius \(r=1\) und der Höhe \(h=2.\) Für das Volumen dieses Kegels gilt:
\(\begin{array}[t]{rll} V&=& \dfrac{1}{3}\cdot \pi\cdot r^2\cdot h \\[5pt] &=& \dfrac{1}{3}\cdot \pi\cdot 1^2\cdot 2\\[5pt] &=& \dfrac{1}{3}\cdot \pi\cdot 2 \end{array}\)
Wegen \(\pi\gt 3\) gilt folglich \(V\gt 2.\)
8.1
\(1-\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{6}{6}-\dfrac{3}{6}-\dfrac{2}{6}=\dfrac{1}{6}\)
8.2
\(E:\) „Bei dreimaligem Drehen wird nicht jedes Mal der blaue Sektor erreicht.“

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
  • Über uns
  • Jobs
  • Kontakt
  • Impressum
  • Datenschutzerklärung
  • Nutzungsbedingungen
  • Link zur App im AppStoreLink zur App im PlayStore

SchulLV

Wir verwenden Cookies 🍪, um das Lern- und Unterrichtserlebnis bei SchulLV zu personalisieren.