Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

In Cunewalde in der Oberlausitz sind originalgetreue Modelle sehenswerter Umgebindehäuser im Maßstab $1 : 5$ zu besichtigen. Das Modell eines Umgebindehauses hat eine Länge von $2,4 \,\text{m}.$ Dieses Umgebindehaus besitzt im Original eine Länge von:

	$5,0\,\text{m}$
	$9,6\,\text{m}$
	$12,0\,\text{m}$
	$14,4\,\text{m}$
	$24,0\,\text{m}$

(1 BE)

Welches Volumen ist am größten?

	$2\,\text{m}^3$
	$20\,\text{dm}^3$
	$20\,\text{Liter}$
	$200\,\text{cm}^3$
	$2\,000\,\text{cm}^3$

(1 BE)

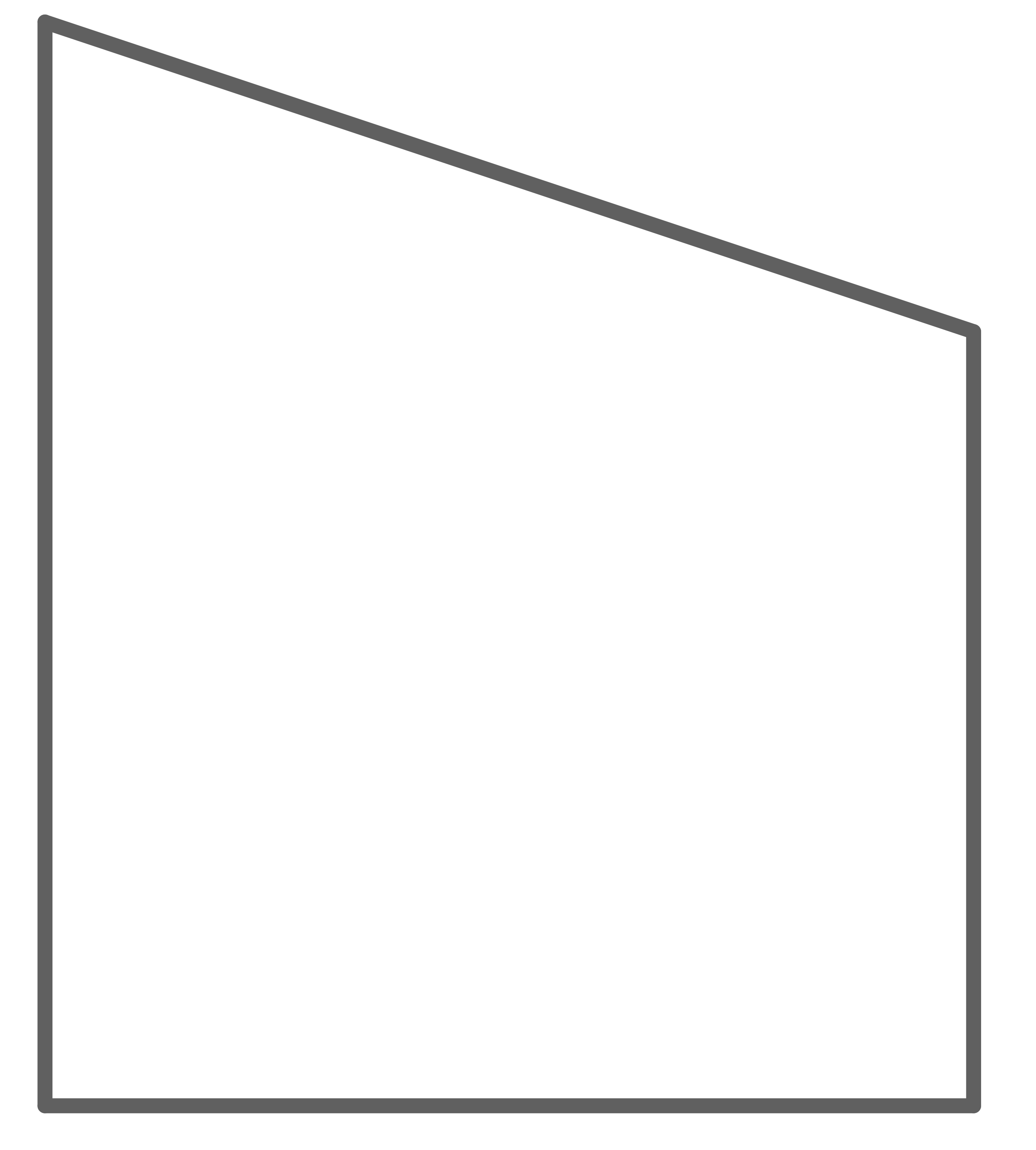
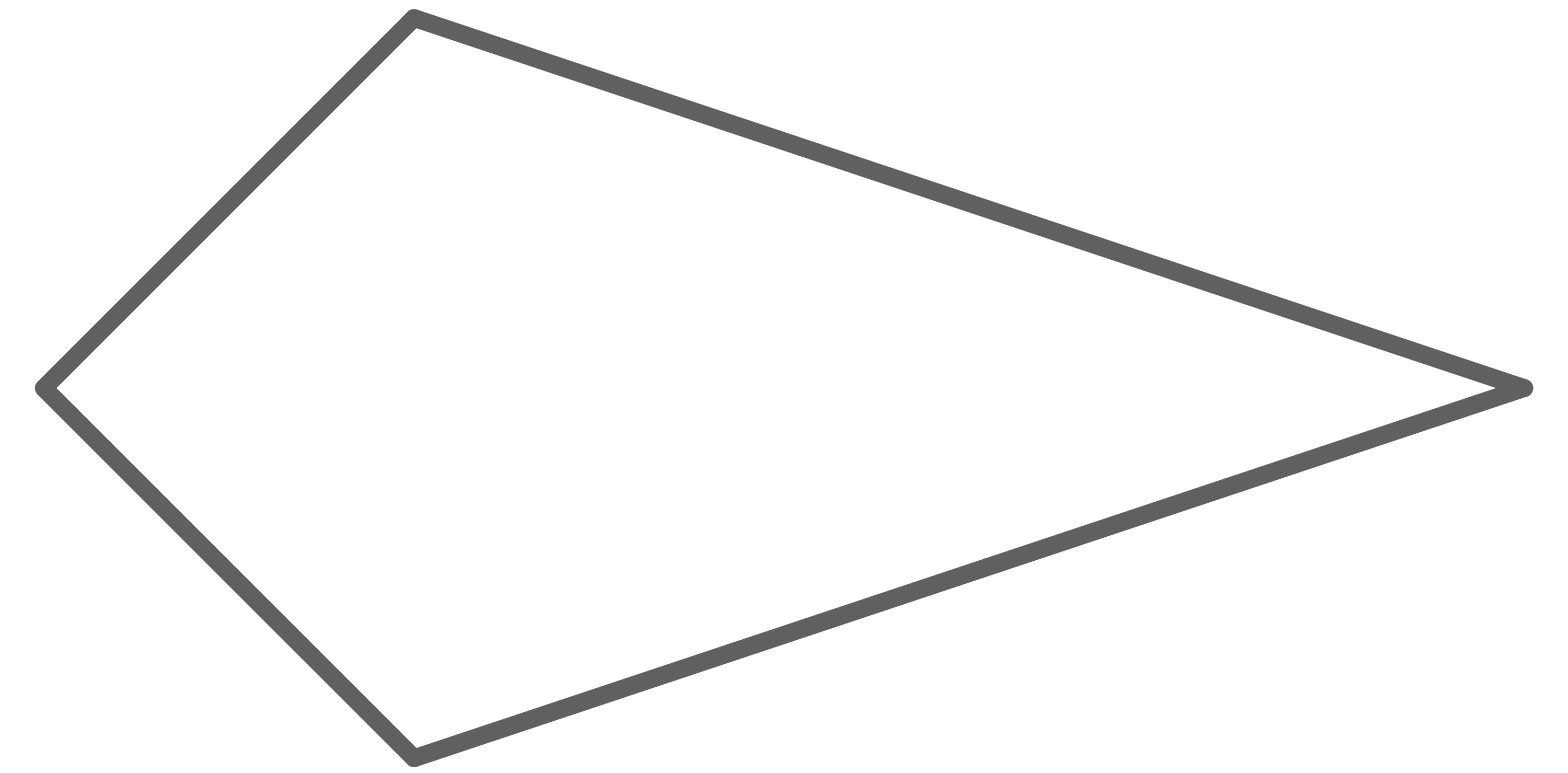
Welche Abbildung stellt kein Trapez dar?







(1 BE)

Welche Gleichung besitzt im Bereich der reellen Zahlen die zwei Lösungen $x_1=-2$ und $x_2=0?$

	$x^2-4=0$
	$x^2+4=0$
	$x\cdot (x-2) = 0$
	$x\cdot (x+2) = 0$
	$x^2-x-2=0$

(1 BE)

Der Graph welcher linearen Funktion schneidet die Koordinatenachsen in den Punkten $A(2\mid 0)$ und $B(0\mid -4)?$

	$y = x-4\quad$ $(x\in \mathbb{R})$
	$y = x-2\quad$ $(x\in \mathbb{R})$
	$y = -2\cdot x-4\quad$ $(x\in \mathbb{R})$
	$y = 2\cdot x-4\quad$ $(x\in \mathbb{R})$
	$y = \dfrac{1}{2}\cdot x+2\quad$ $(x\in \mathbb{R})$

(1 BE)

In welchem Intervall ist die Funktion $f$ mit $y= f(x)=(x-1)^2+2\quad$ $(x\in \mathbb{R})$ monoton steigend?

	$x\leq -2$
	$x\lt -1$
	$x\leq 0$
	$x\lt 1$
	$x \geq 1$

(1 BE)

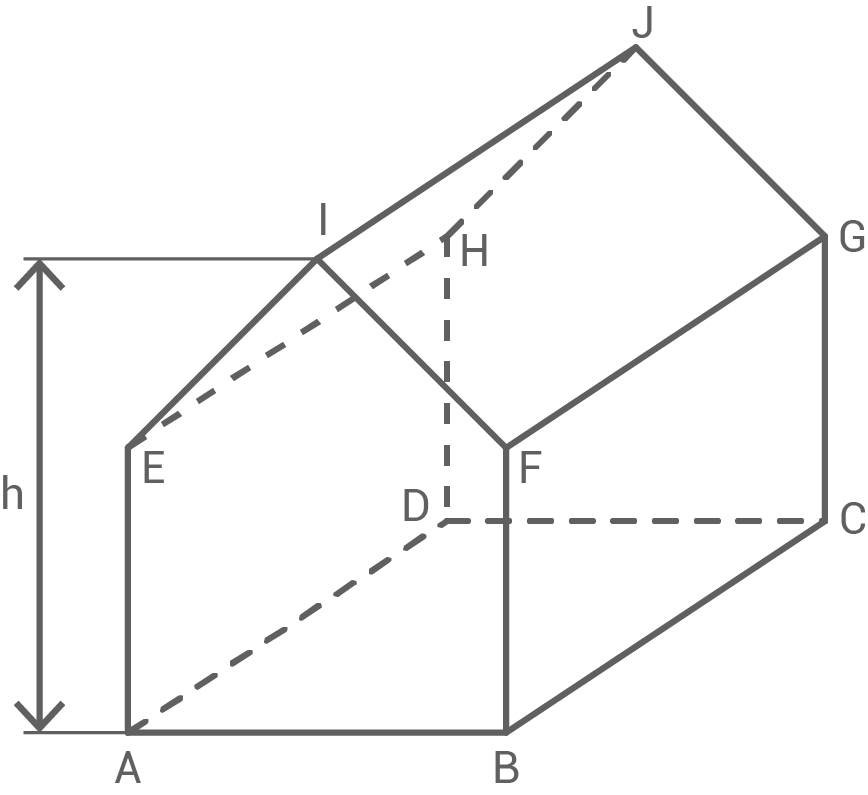
Ein Wohnhaus besitzt die Form eines geraden Prismas (siehe Abbildung).

Abbildung (nicht maßstäblich)

Die Punkte $A,$ $B,$ $C,$ $D,$ $E,$ $F,$ $G$ und $H$ sind Eckpunkte eines Quaders.

Es gilt:

$\overline{AB} = 8 , 0\,\text{m} ,$
$\overline{BC} = \overline{IJ} = 10 , 0\,\text{m} ,$
$\overline{AE} = 3 , 5\,\text{m}$
und $h = 6 , 5\,\text{m} .$

7.1

Gib die Höhe dieses geraden Prismas an.

(1 BE)

7.2

Bestimme das Volumen des durch die Punkte $E,$ $F,$ $G,$ $H,$ $I$ und $J$ begrenzten Dachraumes.

(4 BE)

Ein Schüler kauft für ein Konzert Karten der Preisstufe $\text{I}$ zum Preis von jeweils $20\,$ Euro und Karten der Preisstufe $\text{II}$ zum Preis von jeweils $12\,$ Euro. Er bezahlt für insgesamt $12$ Karten $200\,$ Euro.
Ermittle, wie viele Karten der Schüler von jeder Preisstufe gekauft hat.

(4 BE)

$1\,\text{m}$ im Modell entspricht $5\,\text{m}$ in der Realität:

$2,4\,\text{m}\cdot 5 = 12,0\,\text{m}$

Die dritte Antwortmöglichkeit ist richtig.

$\begin{array}[t]{rll} 2\,\text{m}^3&=& 2\,000\,\text{dm}^3 \\[10pt] 20\,\text{dm}^3&=& 20\,\text{dm}^3 \\[10pt] 20\,\text{Liter}&=& 20\,\text{dm}^3 \\[10pt] 200\,\text{cm}^3&=& 0,2\,\text{dm}^3 \\[10pt] 2\,000\,\text{cm}^3&=& 2\,\text{dm}^3 \\[10pt] \end{array}$

Die erste Antwortmöglichkeit ist richtig.

In einem Trapez muss es zwei gegenüberliegende Seiten geben, die parallel sind. In der letzten Figur ist das nicht der Fall. Hierbei handelt es sich um ein Drachenviereck.

Die letzte Antwortmöglichkeit ist richtig.

Die beiden Lösungen können jeweils in die Gleichungen eingesetzt werden, um zu überprüfen, ob sie die Gleichung erfüllen.

Die vierte Antwortmöglichkeit ist richtig.

Setze die $x$ -Koordinaten der beiden Punkte $A$ und $B$ jeweils in den Funktionsterm ein und überprüfe, ob sich so die richtige $y$ -Koordinate ergibt.

Die vierte Antwortmöglichkeit ist richtig.

Bei dem Graphen von $f$ handelt es sich um eine nach oben geöffnete Parabel mit dem Scheitelpunkt $(1\mid 2).$ $f$ ist also für $x\geq 1$ monoton steigend.

Die letzte Antwortmöglichkeit ist richtig.

7.1

Die Grundfläche des Prismas ist das Fünfeck $ABFIE.$ Da das Prisma gerade ist, entspricht die Höhe des Prismas der Länge der Strecke $\overline{BC}.$

Die Höhe des Prismas beträgt also $10,0\,\text{m}.$

7.2

Der Dachraum besitzt ebenfalls die Form eines Prismas. Die Grundfläche ist das Dreieck $EFI.$

1. Schritt: Grundfläche des Prismas berechnen

Die Grundseite des Dreiecks ist $\overline{EF}.$ Diese ist genauso lang wie $\overline{AB} = 8,0\,\text{m}.$ Die Höhe $h_G$ des Dreiecks lässt sich mithilfe der angegebenen Höhe des Hauses $h= 6,5\,\text{m}$ und der Streckenlänge $\overline{AE} = 3,5\,\text{m}$ berechnen:

$\begin{array}[t]{rll} h_G&=& h -\overline{AE} \\[5pt] &=& 6,5\,\text{m} - 3,5\,\text{m}\\[5pt] &=& 3,0\,\text{m} \end{array}$

Der Flächeninhalt des Dreiecks ist also:

$\begin{array}[t]{rll} G &=& \dfrac{1}{2}\cdot \overline{EF}\cdot h_G \\[5pt] &=& \dfrac{1}{2}\cdot 8,0\,\text{m} \cdot 3,0\,\text{m} \\[5pt] &=& 12,0\,\text{m}^2 \end{array}$

2. Schritt: Volumen berechnen

Die Höhe des Dachraumprismas entspricht der Höhe des gesamten Prismas. Das Volumen ergibt sich also zu:

$\begin{array}[t]{rll} V&=& G\cdot \overline{BC} \\[5pt] &=& 12,0\,\text{m}^2 \cdot 10,0\,\text{m} \\[5pt] &=& 120,0\,\text{m}^3 \end{array}$

Das Volumen des Dachraumes beträgt $120,0\,\text{m}^3.$

Die Anzahl der Karten der Kategorie $\text{I}$ wird mit $x$ und die Anzahl der Karten der Kategorie $\text{II}$ mit $y$ bezeichnet. Damit ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&200 &=& 20\cdot x + 12\cdot y \\ \text{II}\quad&12&=& x +y \\ \end{array}$

Auflösen der zweiten Gleichung nach $x$ liefert:

$\begin{array}[t]{rll} &\text{II} & 12 &=& x+y \quad \scriptsize \mid\;-y \\[5pt] &\text{II}_a & 12-y &=& x \end{array}$

Einsetzen in $\text{I}:$

$\begin{array}[t]{rll} 200&=& 20\cdot (12-y) +12\cdot y \\[5pt] 200&=& 240 -20\cdot y +12\cdot y \\[5pt] 200&=& 240 - 8\cdot y \quad \scriptsize \mid\; -240 \\[5pt] -40 &=& -8\cdot y \quad \scriptsize \mid\; :(-8)\\[5pt] 5&=& y \end{array}$

Einsetzen in $\text{II}_a:$

$x=12-5=7$

Der Schüler hat $7$ Karten der Preisstufe $\text{I}$ und $5$ Karten der Preisstufe $\text{II}$ gekauft.