Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

Die Kantenlängen eines Quaders betragen 10 cm, 20 cm und 50 cm.
Welches Volumen besitzt dieser Quader?

	$1 \,\text{dm}^3$
	$10 \,\text{dm}^3$
	$100 \,\text{dm}^3$
	$1\,000 \,\text{dm}^3$
	$10\,000 \,\text{dm}^3$

(1 BE)

Gegeben ist das lineare Gleichungssystem: $\quad \left| \begin{array}[]{rll} 2\cdot x+y&=& 3 \\[5pt] x-3\cdot y&=&5 \end{array} \right| \quad$

Welche der angegebenen Mengen ist die Lösungsmenge dieses Gleichungssystems?

	$L=\{(1\mid 1)\}$
	$L=\{(1\mid -2)\}$
	$L=\{(1\mid 2)\}$
	$L=\{(2\mid -1)\}$
	$L=\{(2\mid 1)\}$

(1 BE)

Der Term $\sqrt{a^3}$ mit $a\in\mathbb{R}, a\geq 0$ lässt sich auch in folgender Form schreiben:

	$a^{\frac{1}{3}}$
	$a^{\frac{1}{2}}$
	$a^{\frac{2}{3}}$
	$a^{\frac{3}{2}}$
	$a^3$

(1 BE)

Welche der angegebenen Funktionen hat genau zwei Nullstellen?

	$y=x^2+4 \quad x \in \mathbb R$
	$y=x^2-4 \quad x \in \mathbb R$
	$y=-x^2-4 \quad x \in \mathbb R$
	$y=\dfrac{1}{x^2} \quad x \in \mathbb R,\, x\neq 0$
	$y=-\dfrac{1}{x^2} \quad x \in \mathbb R,\, x\neq 0$

(1 BE)

Welche der angegebenen Funktionen hat den Wertebereich $W=\{y\mid\ y\in\mathbb{R};-2\leq y \leq 2\}?$

	$y=\sin(x) \quad x \in \mathbb R$
	$y=4\cdot \sin(x) \quad x \in \mathbb R$
	$y=\sin(2\cdot x) \quad x \in \mathbb R$
	$y=2\cdot \sin(x)+2 \quad x \in \mathbb R$
	$y=2\cdot \sin(x) \quad x \in \mathbb R$

(1 BE)

Beim einmaligen Werfen einer verbogenen Münze fällt „Zahl“ mit der Wahrscheinlichkeit $\dfrac{1}{3}$ und „Wappen" mit der Wahrscheinlichkeit $\dfrac{2}{3}.$ Diese Münze wird genau zweimal geworfen.
Wie groß ist die Wahrscheinlichkeit dafür, dass dabei zweimal „Wappen“ geworfen wird?

	$\dfrac{1}{9}$
	$\dfrac{2}{9}$
	$\dfrac{4}{9}$
	$\dfrac{5}{9}$
	$\dfrac{7}{9}$

(1 BE)

Mithilfe der Gleichung $T_F = \dfrac{9}{5}\cdot T_C + 32$ kann die Temperatur aus der Einheit Grad Celsius $(^°C)$ in die Einheit Grad Fahrenheit $(^°F)$ umgewandelt werden.
Dabei gilt:

$T_C \quad ...$	Temperatur in $^°C$
$T_F \quad ...$	Temperatur in $^°F$

7.1

Eine Temperatur beträgt $30^°C$ . Ermittle diese Temperatur in ${ }^°F.$

(2 BE)

7.2

Stelle die Gleichung $T_F=\dfrac{9}{5}\cdot T_C+32$ nach $T_C$ um.

(2 BE)

Gegeben sind der Kreis $k$ mit dem Mittelpunkt $M(0 \mid 0)$ und dem Radius $r=5$ (siehe Abbildung) sowie die Punkte $A(-5 \mid 0),$ $B(5 \mid 0)$ und $P(-4 \mid 3).$

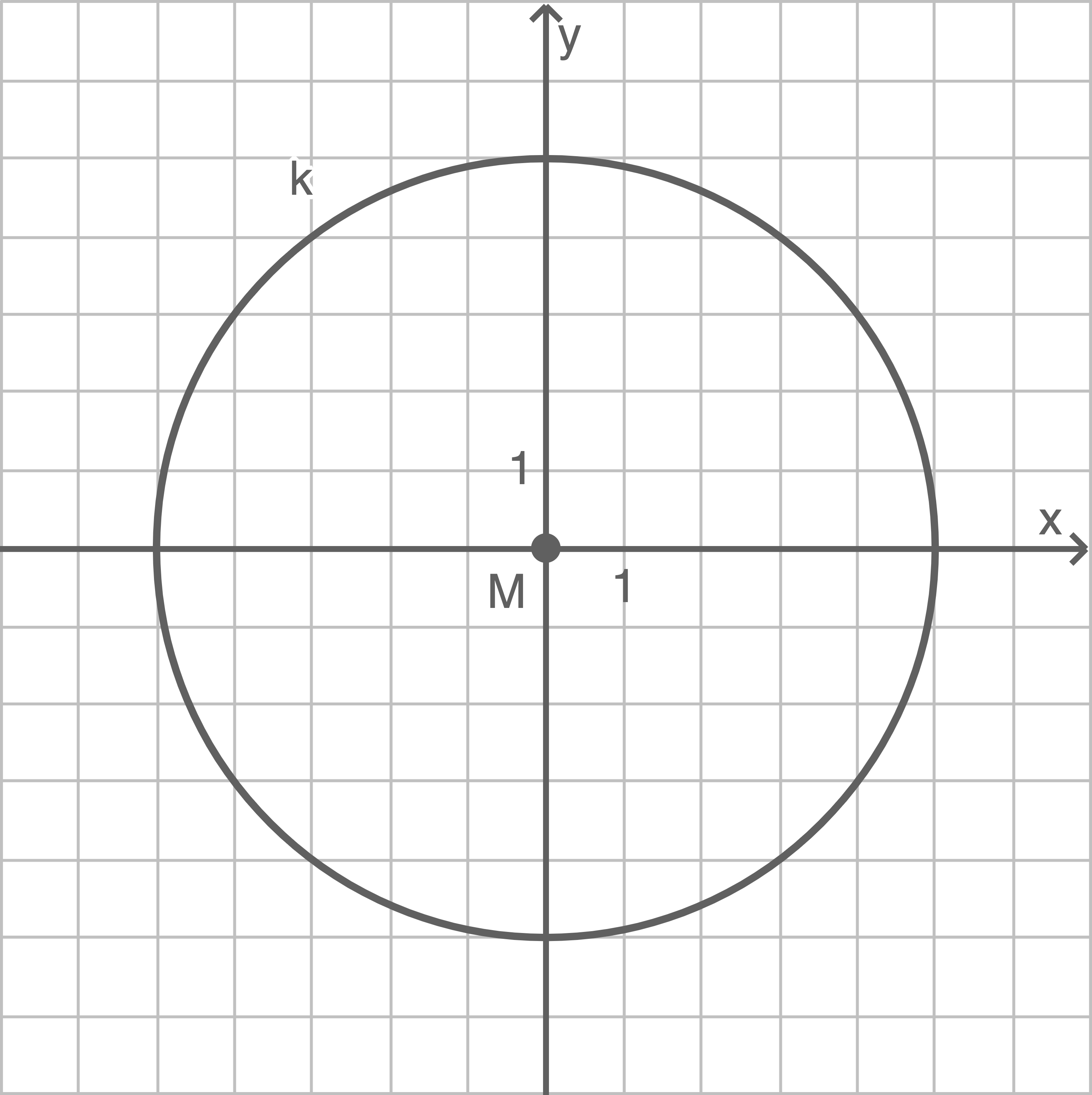
8.1

Durch die Punkte $M$ und $P$ verläuft der Graph der linearen Funktion $f.$
Zeichne den Graphen von $f$ in die Abbildung ein.
Gib eine Gleichung der Funktion $f$ an.

$\text{___________________________}$

(2 BE)

8.2

Zeige rechnerisch, dass der Punkt $P$ auf dem Kreis $k$ liegt.

(2 BE)

8.3

Gib die Größe des Winkels $APB$ an.

$\text{___________________________}$

(1 BE)

$10\,\text{cm}\cdot20\,\text{cm}\cdot50\,\text{cm}=10\,000\,\text{cm}^3=10\,\text{dm}^3$

Das Gleichungssystem kann mithilfe eines geeigneten Verfahrens gelöst werden. Anwendung des Einsetzungsverfahrens:

Umstellen der ersten Gleichung nach $y:$

$\begin{array}[t]{rll} 2x+y&=&3 \quad \scriptsize \mid\; -2x \\[5pt] y&=& 3-2x \end{array}$

$y=3-2x$ in die zweite Gleichung einsetzen:

$\begin{array}[t]{rll} x-3y&=&5 \\[5pt] x-3\cdot(3-2x)&=& 5 \\[5pt] x-9+6x&=& 5 \\[5pt] 7x-9&=& 5 \quad \scriptsize \mid\; +9 \\[5pt] 7x&=& 14 \quad \scriptsize \mid\; :2\\[5pt] x&=& 2 \end{array}$

$x=2$ in die erste Gleichung einsetzen:

$\begin{array}[t]{rll} 2x+y&=& 3 \\[5pt] 2\cdot2+y&=& 3\\[5pt] 4+y&=& 3 \quad \scriptsize \mid\; -4 \\[5pt] y&=& -1 \end{array}$

Folglich ist die Lösung $L=\{2\mid-1\}$ richtig.

Es gilt der Zusammenhang $\sqrt[n]{a^m} = a^\frac{m}{n}.$

Damit folgt $\sqrt{a^3}=a^{\frac{3}{2}}.$

Nullstellen der Funktion $y=x^2-4$ berechnen:

$\begin{array}[t]{rll} x^2-4&=& 0 \\[5pt] x^2&=& 4 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt] x_1&=& -2 \\[5pt] x_2&=& 2 \\[5pt] \end{array}$

Diese Funktion hat genau zwei Nullstellen und ist deshalb die Lösung der Aufgabe.

Eine allgemeine Sinusfunktion hat einen Wertebereich von $-1\leq y\leq1.$ Sie kann in verschiedenen Arten verändert werden.

$y=a\cdot \sin(b\cdot x + c)+d$

Die folgenden Parameter haben Einfluss auf den Wertebereich:

Der $a$ -Wert beschreibt die Streckung beziehungsweise die Stauchung des Graphen der Sinusfunktion.
Der $d$ -Wert beschreibt die Verschiebung des Graphen der Sinusfunktion in $y$ -Richtung.

Für die Wertebereiche folgt:

Die Funktion $y=\sin(x)$ hat den Wertebereich $-1\leq y\leq1$
Die Funktion $y=4\cdot \sin(x)$ hat den Wertebereich $-4\leq y\leq4$
Die Funktion $y=\sin(2\cdot x)$ hat den Wertebereich $-1\leq y\leq1$
Die Funktion $y=2\cdot \sin(x)+2$ hat den Wertebereich $0\leq y\leq4$
Die Funktion $y=2\cdot \sin(x)$ hat den Wertebereich $-2\leq y\leq2$ und ist somit die Lösung für die Aufgabe.

Mit der Produktregel gilt:

$P(WW)=\dfrac{2}{3}\cdot \dfrac{2}{3}=\dfrac{4}{9}$

7.1

$\begin{array}[t]{rll} T_F&=& \dfrac{9}{5}\cdot 30+32 \\[5pt] &=& \dfrac{270}{5}+32 \\[5pt] &=& 54+32 \\[5pt] &=& 86 \end{array}$

Die Temperatur von $30^°C$ beträgt $86^°F.$

7.2

$\begin{array}[t]{rll} T_F&=&\dfrac{9}{5}\cdot T_C+32 \quad \scriptsize \mid\; -32\\[5pt] T_F-32&=&\dfrac{9}{5}\cdot T_C \quad \scriptsize \mid\;\cdot \frac{5}{9} \\[5pt] (T_F-32)\cdot \dfrac{5}{9}&=& T_C \end{array}$

8.1

Graph von $\boldsymbol{f}$ einzeichnen

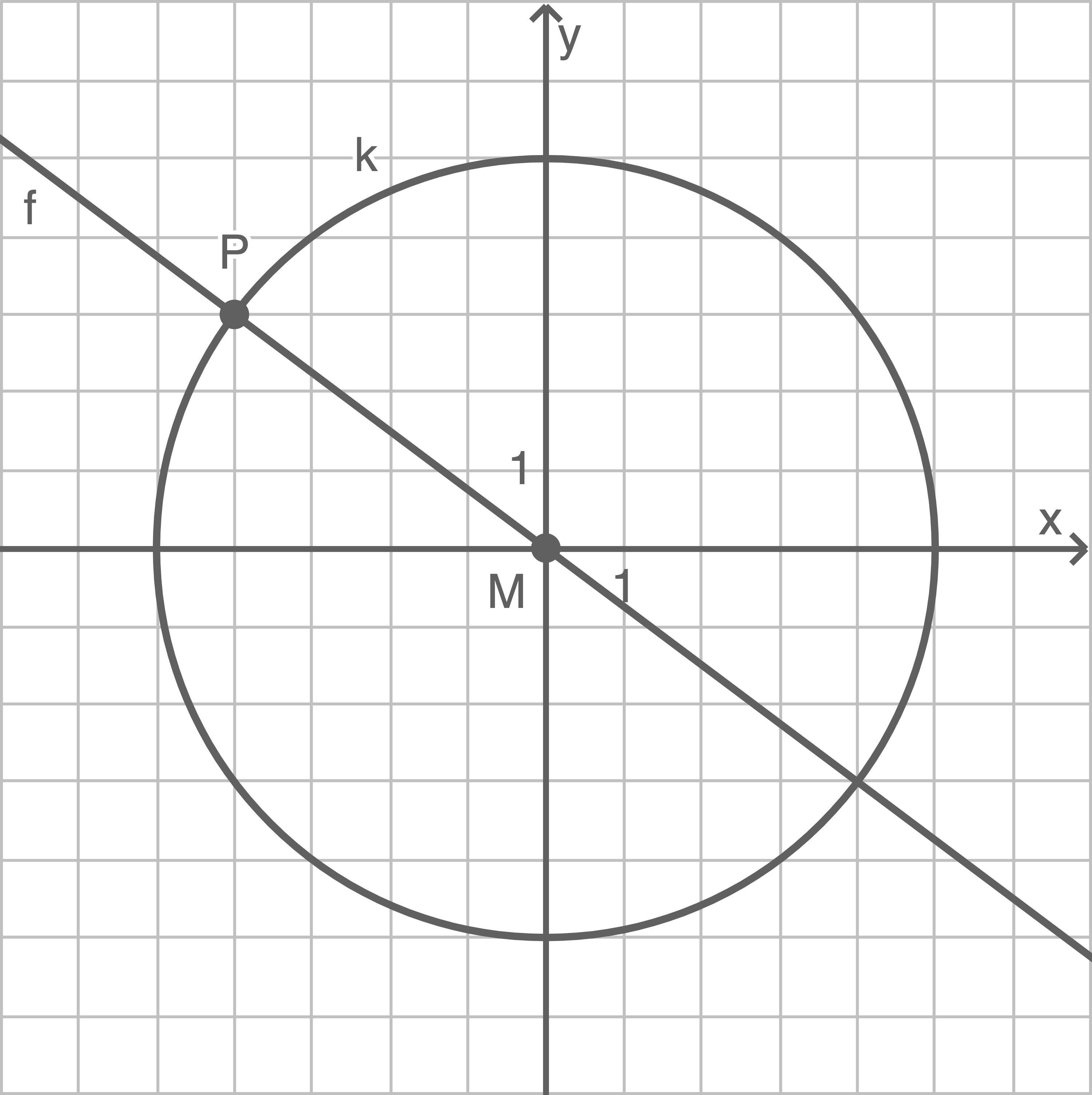Funktionsgleichung von $\boldsymbol{f}$ angeben

Einsetzen der Koordinaten von $P$ in die allgemeine Funktionsgleichung $y=m\cdot x+n$ liefert:

$\begin{array}[t]{rll} y&=& m\cdot x+n \\[5pt] 3&=& -4\cdot m \quad \scriptsize \mid\; :-4\\[5pt] m&=& -\dfrac{3}{4} \end{array}$

Da der Graph von $f$ durch den Koordinatenursprung verläuft, lautet die Funktionsgleichung von $f:$

$f(x)=-\dfrac{3}{4}x$

8.2

Wenn der Punkt $P$ auf dem Kreis liegt, muss er einen Abstand von $5 \,\text{LE}$ vom Mittelpunkt $M$ haben.

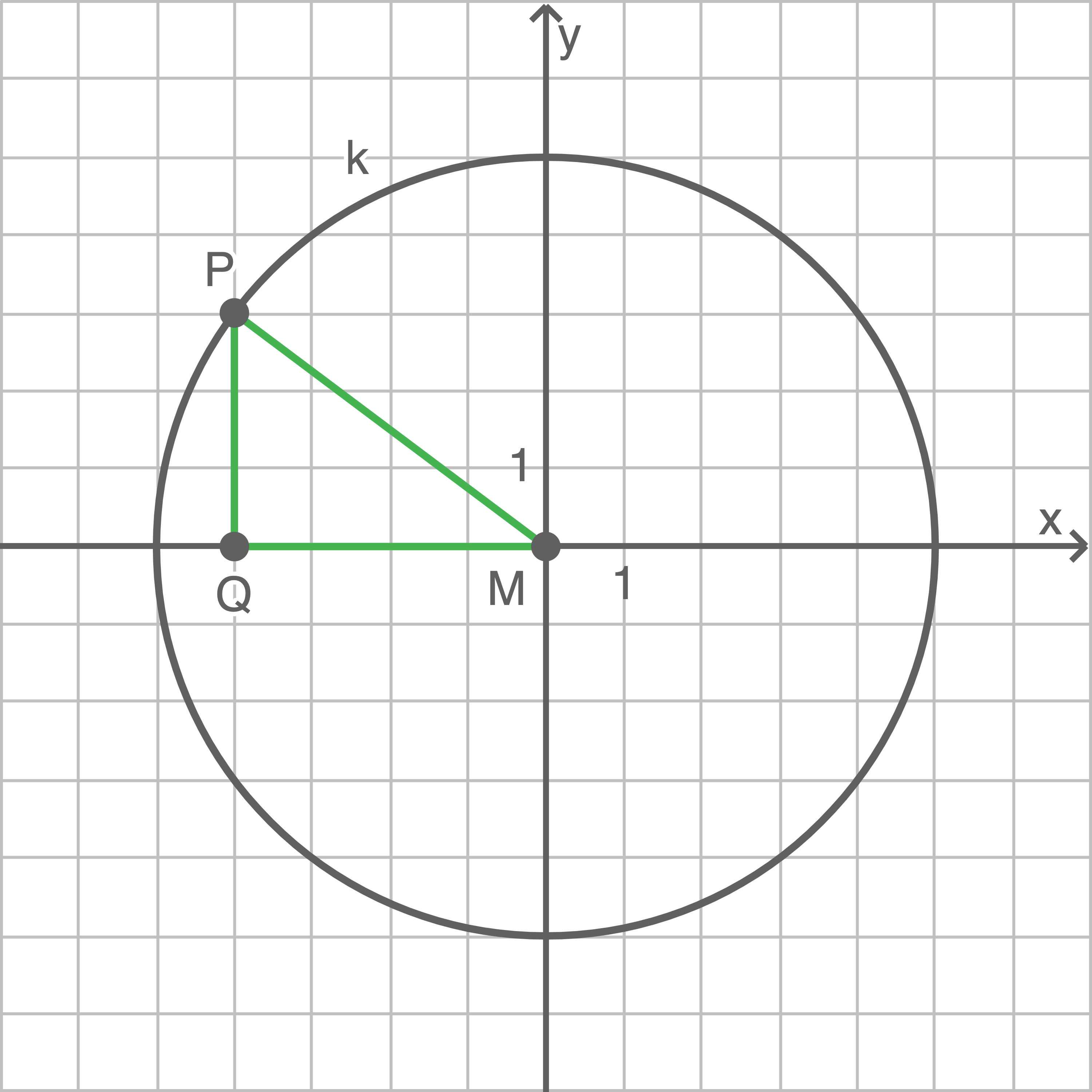Für das eingezeichnete Dreieck gilt:

$\overline{MQ}=4$
$\overline{PQ}=3$

Mit dem Satz des Pythagoras gilt dann für die Länge der Strecke $\overline{MP}:$

$\begin{array}[t]{rll} \overline{MP}^2&=& \overline{MQ}^2+\overline{PQ}^2 \\[5pt] \overline{MP}^2&=& 4^2+3^2 \\[5pt] \overline{MP}^2&=& 25 \quad \scriptsize \mid\;\sqrt{\,}\\[5pt] \overline{MP} &=& 5 \end{array}$

Damit ist bewiesen, dass der Abstand des Punktes $P$ vom Mittelpunkt $5$ beträgt und er damit auf dem Kreis $k$ liegt.

8.3

Nach dem Satz des Thales handelt es sich bei $\sphericalangle APB$ um einen rechten Winkel.

$\sphericalangle APB=90^°$