Teil B

Für $x \in \mathbb{R}$ ist die Funktion $f$ mit $f(x)=\left(\dfrac{6}{5}\right)^x+1$ gegeben. Der Graph der Funktion $g$ entsteht durch Spiegelung des Graphen von $f$ an der $y$ -Achse (siehe Abbildung).

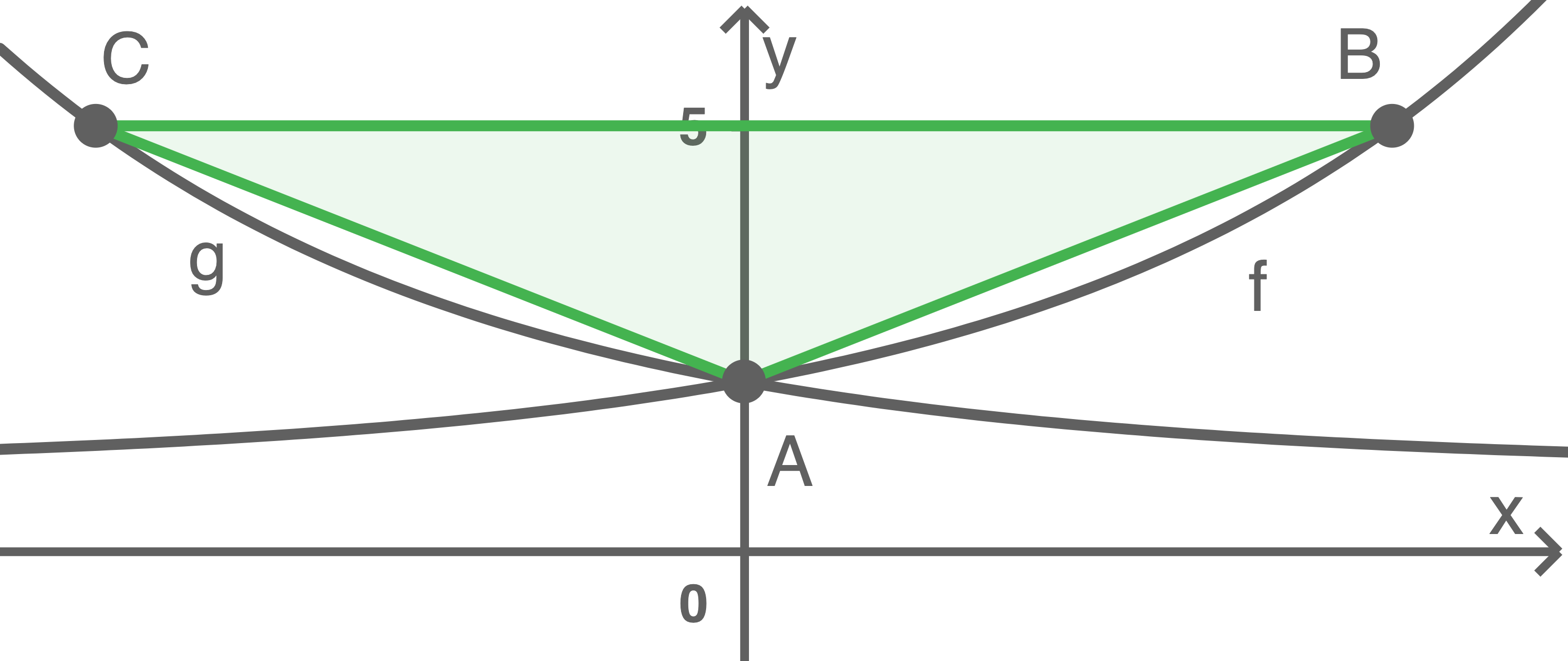
Abbildung (nicht maßstäblich)

1.1

Gib den Wertebereich von $f$ an.

(1 BE)

1.2

Gib eine Gleichung von $g$ an.

(1 BE)

1.3

Der Punkt $A$ ist der Schnittpunkt des Graphen von $f$ mit der Ordinatenachse. Die Punkte $B$ und $C$ liegen auf den Graphen von $f$ bzw. $g.$ Die Strecke $\overline{CB}$ verläuft parallel zur Abszissenachse durch den Punkt $(0 \mid 5)$ (siehe Abbildung).

Ermittle die Koordinaten des Punktes $B.$

Bestimme den Flächeninhalt des Dreiecks $ABC.$

(5 BE)

Die Kantenlänge des Würfels $ABCDEFGH$ beträgt $10 \,\text{cm}.$ Der Punkt $M$ ist Mittelpunkt der Kante $\overline{EH}$ . Dem Würfel ist die Pyramide $ABCDM$ einbeschrieben (siehe Abbildung).

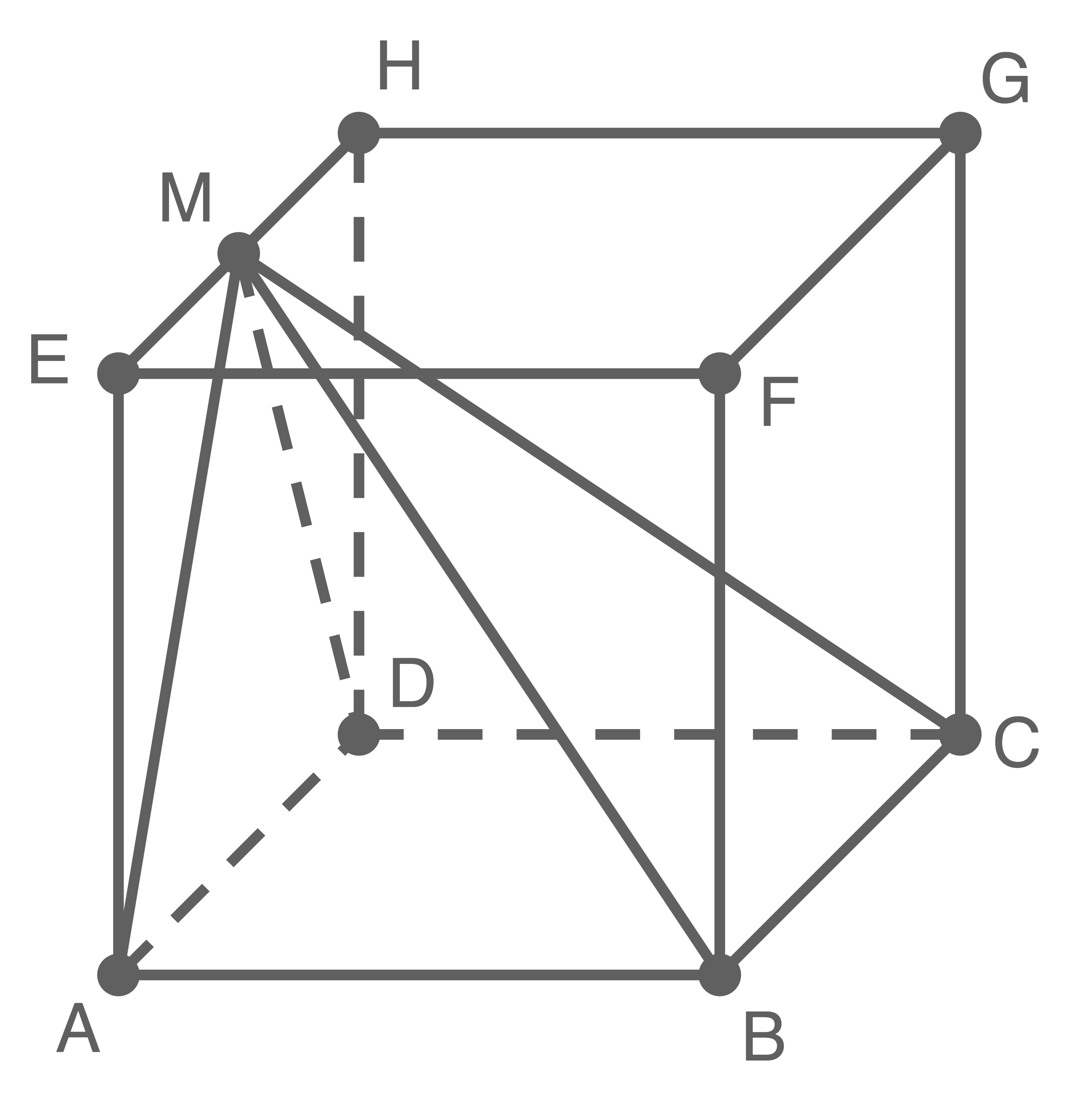
sachsen blf 2020 teil b aufgabe 2 abbildung 2 würfel pyramide

Abbildung (nicht maßstäblich)

2.1

Zeige, dass die Strecke $\overline{BM}$ $15 \,\text{cm}$ lang ist.

(3 BE)

2.2

Berechne die Größe des Winkels $\sphericalangle BMC.$

(3 BE)

2.3

Ermittle das Volumen der Pyramide $ABCDM.$

(2 BE)

Abbildung 1 zeigt den Querschnitt durch eine Talsperre mit Staubecken, Staumauer, Wasserbecken und Ablaufrinne in einem Koordinatensystem (1 Längeneinheit entspricht 1 Meter). Die Ablaufrinne leitet bei zu hohem Wasserspiegel im Wasserbecken das Wasser ab. Die Höhe des Wasserspiegels im Wasserbecken ist $h.$

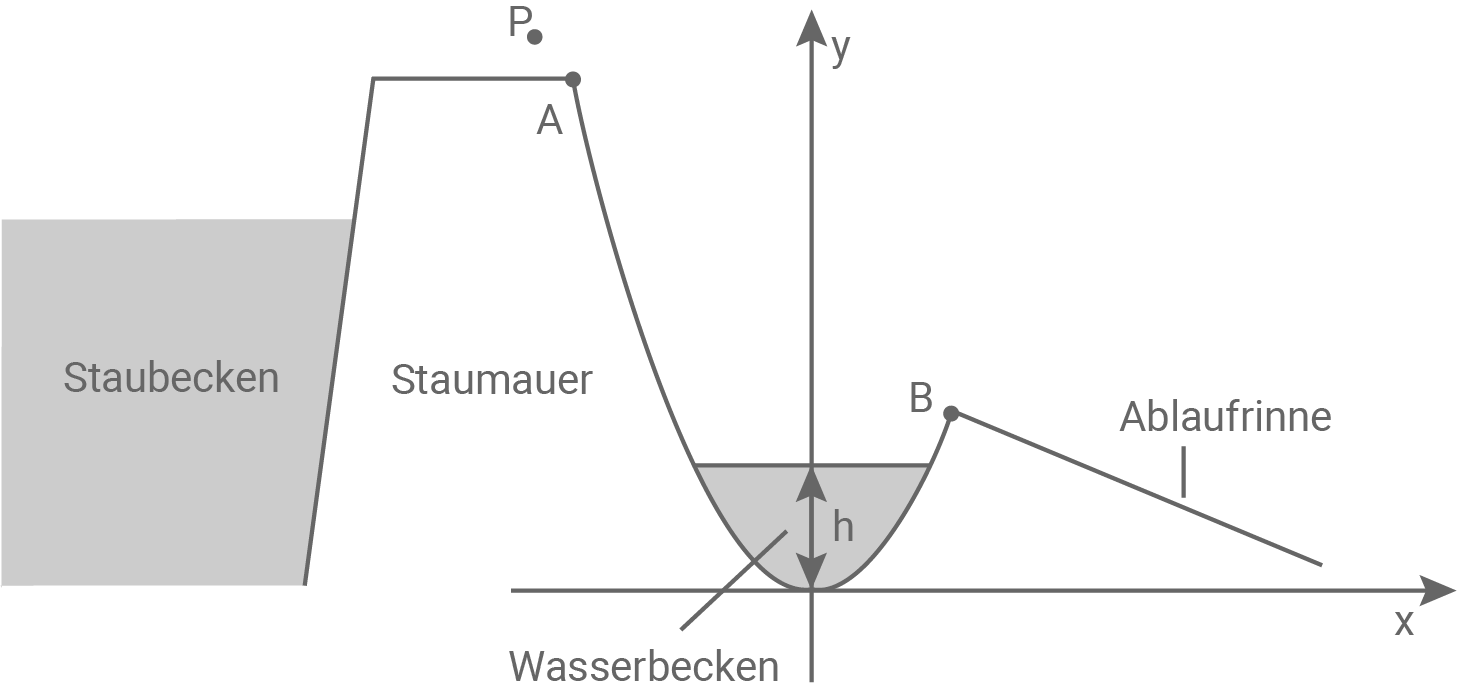
sachsen blf 2020 teil b aufgabe 3 abbildung 3 querschnitt talsperre

Abbildung 1 (nicht maßstäblich)

3.1

Der Parabelabschnitt vom Punkt $A$ zum Punkt $B$ wird durch den Graphen der Funktion $f$ mit

$f(x)=\dfrac{1}{4}\cdot x^2$ $(x \in \mathbb{R};-8 \leq x \leq 4)$

beschrieben. Die Schnittlinie der Ablaufrinne liegt auf dem Graphen der Funktion $g$ mit $g(x)=-\dfrac{3}{50}\cdot x+\dfrac{106}{25}$ $(x \in \mathbb{R}).$

3.1.1

Gib das Gefälle der Ablaufrinne in Prozent an.

(1 BE)

3.1.2

Bestimme die Höhe des Wasserspiegels im Wasserbecken, ab der das Wasser über die Ablaufrinne abgeleitet wird.

(3 BE)

3.1.3

Begründe, dass der Punkt $A$ die Koordinaten $x_A = -8$ und $y_A = 16$ besitzt.

(2 BE)

3.1.4

Ermittle die Höhe des Wasserspiegels im Wasserbecken, ab der das Wasser im Wasserbecken vom Punkt $P(-9 \mid 17,5)$ aus zu sehen ist (siehe Abbildung 1).

(4 BE)

3.2

Das Volumen des Wassers im Wasserbecken verändert sich durch Zufluss vom Staubecken, Ablauf über die Ablaufrinne oder Wasserentnahme. Abbildung 2 stellt für einen ausgewählten Tag den Zusammenhang zwischen dem Volumen des Wassers im Wasserbecken und der Uhrzeit dar.

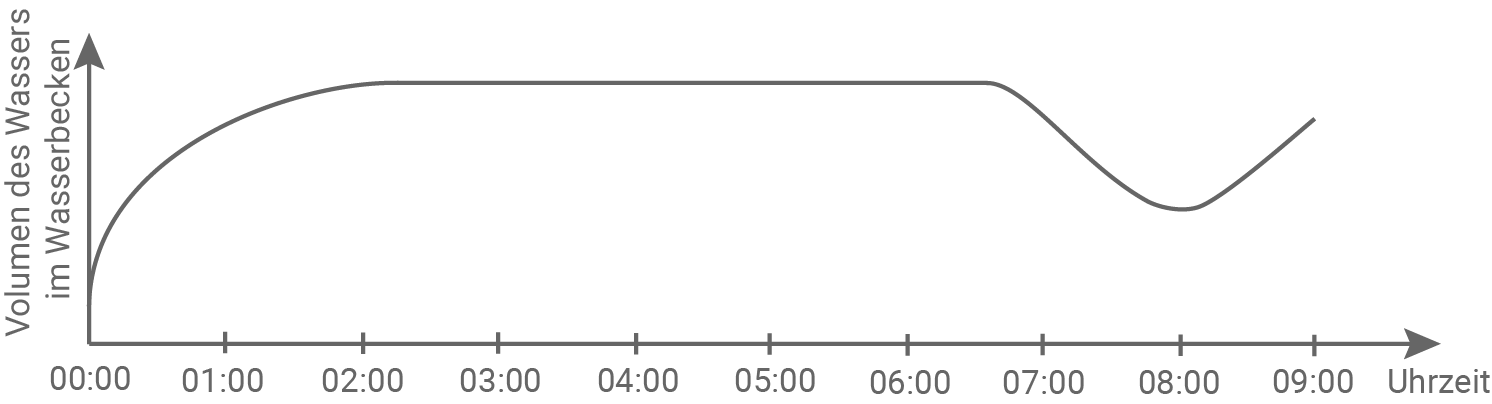sachsen blf 2020 teil b aufgabe 3.2 abbildung 4 volumen des wassers im wasserbecken

Abbildung 2

Betrachtet werden folgende Aussagen für den dargestellten Zeitraum:

Aussage 1: Das Volumen des Wassers im Wasserbecken war mindestens 3 Stunden lang gleich groß.

Aussage 2: Zwischen 07:00 Uhr und 07:15 Uhr verringerte sich das Volumen des Wassers im Wasserbecken.

Aussage 3: Gegen 08:00 Uhr befand sich das kleinste Wasservolumen im Wasserbecken.

Aussage 4: Um 01:00 Uhr änderte sich das Volumen des Wassers im Wasserbecken schneller als um 01:30 Uhr.

3.2.1

Gib jeweils an, ob die Aussagen 1, 2 und 3 wahr oder falsch sind.

(3 BE)

3.2.2

Gib an, ob die Aussage 4 wahr oder falsch ist. Begründe deine Angabe.

(2 BE)

1.1

Der Summand $\left(\dfrac{6}{5}\right)^x$ ist nach Definition immer positiv. Durch die Addition von $1$ ergibt sich der folgende Wertebereich:

$W=\{y \mid y \in \mathbb R;\,y\gt 1\}$

1.2

Da es sich um eine Spiegelung an der $y$ -Achse handelt, muss die Variable $x$ mit $-1$ multipliziert werden.

$\begin{array}[t]{rll} g(x)&=&\left(\dfrac{6}{5}\right)^{-x} +1 \\[5pt] &=&\left(\dfrac{5}{6}\right)^{x} +1 \\[5pt] \end{array}$

1.3

Koordinaten von $\boldsymbol{B}$ ermitteln

Der Punkt $B$ hat den $y$ -Wert $5.$ Gesucht ist also die Lösung der folgenden Gleichung:

$\begin{array}[t]{rll} f(x)&=& 5 \\[5pt] \left(\dfrac{6}{5}\right)^x\,+\,1&=& 5 \end{array}$

Der Taschenrechner liefert die Lösung $x=7,6.$ Der Punkt $B$ liegt also bei $(7,6\mid 5).$

Flächeninhalt des Dreiecks berechnen

Zunächst wird der Schnittpunkt $A$ der beiden Funktionen ermittelt. In der Abbildung ist zu sehen, dass dieser genau dem $y$ -Achsenabschnitt der Funktionen entspricht.

$\begin{array}[t]{rll} f(0)&=& \left( \dfrac {6}{5}\right)^0 \,+\,1 \\[5pt] f(0)&=& 1\,+\,1 \\[5pt] f(0)&=& 2 \\[5pt] \end{array}$

Der Schnittpunkt der beiden Graphen liegt im Punkt $A(0|2).$

Aufgrund der Symmetrie gilt mit dem Punkt $P(0\mid 5)$ die folgende Gleichung für den Flächeninhalt des Dreiecks $ABC:$

$\begin{array}[t]{rll} A_{ABC}&=& \dfrac{1}{2}\cdot \overline{BC}\cdot \overline{PA} \\[5pt] &=& 2\cdot \dfrac{1}{2}\cdot \overline{PB}\cdot \overline{PA} \\[5pt] &=& \overline{PB}\cdot \overline{PA} \end{array}$

Mit $\overline{PA}=5-2=3\,\text{[LE]}$ und $\overline{PB}=7,6-0=7,6\,\text{[LE]}$ folgt:

$\begin{array}[t]{rll} A_{ABC}&=& \overline{PB}\cdot \overline{PA}\\[5pt] &=& 7,6\cdot 3\\[5pt] &=& 22,8\,\text{[FE]} \end{array}$

Der Flächeninhalt des Dreiecks $ABC$ beträgt $22,8\,\text{FE}.$

2.1

Mit dem Satz des Pythagoras gilt:

$\begin{array}[t]{rll} \overline{AM}^2 &=& \overline{AE}^2 + \overline{EM}^2 \\[5pt] \overline{AM}^2 &=& (10\,\text{cm})^2\,+\,(5\,\text{cm})^2 \\[5pt] \overline{AM}^2 &=& 125\,\text{cm}^2 \quad \scriptsize \mid \sqrt{\,}\\[5pt] \overline{AM} &\approx& 11,18\,\text{cm}\\[5pt] \end{array}$

Damit gilt für die Länge der Strecke $\overline{BM}:$

$\begin{array}[t]{rll} \overline{BM}^2&=& \overline{AM}^2\,+\,\overline{AB}^2\\[5pt] \overline{BM}^2&=& (11,18\,\text{cm})^2\,+\,(10\,\text{cm})^2 \\[5pt] \overline{BM}^2&\approx& 225\,\text{cm} \quad \scriptsize \mid\; \sqrt{\,}\\[5pt] \overline{BM}&\approx& 15\,\text{cm} \end{array}$

2.2

Um die Innenwinkel des Dreiecks $BMC$ zu berechnen, wird der Kosinussatz verwendet.

Rechenweg anzeigen

$\cos\,\sphericalangle\,BMC = \dfrac{\overline{BC}^2\,-\,\overline{BM}^2\,-\,\overline{CM}^2}{-\,2\,\cdot\,\overline{BM}\,\cdot\,\overline{CM}}$

Werte einsetzen:

Rechenweg anzeigen

$\sphericalangle\,BMC \approx 38,9^{\circ}$

Der Winkel $\sphericalangle\,BMC$ beträgt $38,9^{\circ}$ .

2.3

Die Höhe $h$ der Pyramide entspricht der Höhe $\overline{AE}$ des Würfels.

$\begin{array}[t]{rll} V &=& \dfrac{1}{3}\,\cdot\,A_G \,\cdot\, h \\[5pt] V &=& \dfrac{1}{3}\,\cdot\, \overline{AB} ^2\, \cdot\, \overline{AE} \\[5pt] V &=& \dfrac{1}{3}\cdot 100\,\text{cm}^2\, \cdot\, 10\,\text{cm} \\[5pt] V &\approx & 333,3 \, \text{cm}^3 \\[5pt] \end{array}$

Das Volumen der Pyramide $ABCDM$ beträgt $333,3\,\text{cm}^3.$

3.1.1

Mit Gefälle ist hier die Steigung der Geraden gemeint. Bei einer Gleichung $f(x)=m\cdot x+n$ stellt $m$ die Steigung und $n$ den $y$ -Achsenabschnitt dar.

$\begin{array}[t]{rll} m&=& -\,\dfrac{3}{50}\\[5pt] m&=& -\,0,06\\[5pt] m&=& -6\,\% \end{array}$

Das Gefälle der Ablaufrinne beträgt $6\,\%.$

3.1.2

Die $x$ -Koordinate des Punktes $B$ wird durch die rechte Intervallgrenze des Definitionsbereichs der Funktion $f$ bestimmt. Es gilt $x_B=4.$

$f(4)=\dfrac{1}{4}\cdot 4^2=4$

Das Wasser tritt also aus, sobald es die Höhe von $4$ Metern erreicht.

3.1.3

Die $x$ -Koordinate des Punktes $A$ wird durch die linke Intervallgrenze des Definitionsbereichs der Funktion $f$ festgelegt. Es gilt $x_A=-8.$

$f(-8)=\dfrac{1}{4}\cdot (-8)^2=16$

Folglich hat der Punkt $A$ die Koordinaten $A(-8\mid 16).$

3.1.4

1. Schritt: Gerade bestimmen, auf der die Punkte $A$ und $P$ liegen

$\begin{array}[t]{rll} m &=& \dfrac {y_P\,-\,y_A}{x_P\,-\,x_A} & \\[5pt] m &=& \dfrac {17,5\,-\,16}{-\,9\,-\, (-\,8)} & \\[5pt] m &=& \dfrac {1,5}{-\,1} &\\[5pt] m &=& - \dfrac {3}{2} &\\[5pt] \end{array}$

Die Steigung und die Koordinaten des Punktes $P$ werden in die allgemeine Funktionsgleichung eingesetzt.

$\begin{array}[t]{rll} y &=& m \,\cdot\,x\,+\,n & \\[5pt] 17,5 &=& -\,\dfrac {3}{2}\,\cdot\,(-\,9)\,+\,n & \\[5pt] \dfrac{35}{2} &=& \dfrac {27}{2}+n \quad \scriptsize \mid\; -\dfrac {27}{2} \\[5pt] \dfrac{8}{2} &=& \, n \\[5pt] 4 &=& n \end{array}$

Die Funktionsgleichung des Graphen, der durch die Punkte $P$ und $A$ verläuft lautet also $h(x) \,=\, -\,\dfrac{3}{2}\,\cdot\,x\,+\,4.$

2. Schritt: Schnittpunkt mit Parabel

Der Schnittpunkt der Graphen von $h$ und $f$ ist der Punkt, an der der Blick auf das Wasser trifft.

$\begin{array}[t]{rll} f(x)&=& h(x)\\[5pt] \dfrac{1}{4}\,x^2 &=& - \dfrac{3}{2}x +4 \end{array}$

Der Taschenrechner liefert die Schnittpunkte $S_1(2 \mid 1)$ und $S_2(-8\mid 16).$

Der gesuchte Schnittpunkt lautet $(2 \mid 1).$ Der zweite Schnittpunkt ist irrelevant, da dieser dem Punkt $A$ entspricht. Die Höhe des Wasserspiegels, ab der man das Wasser sehen kann, beträgt also 1 Meter.

3.2.1

Wahr, denn zwischen ca. 2 Uhr und 6:30 Uhr veränderte sich der Wasserstand nicht.
Wahr, denn der Graph fällt in diesem Zeitraum.
Falsch, denn zu Beginn der Nacht war das Volumen des Wassers noch geringer.

3.2.2

Die Aussage ist wahr, da der Anstieg der Funktion um 01:00 Uhr steiler war als um 01:30 Uhr.