Teil B
1
Für  und
und  ist die Funktion
ist die Funktion  mit
mit  gegeben.
gegeben.
1.1
Gib die Koordinaten eines lokalen Maximumpunktes des Graphen von  im vorgegebenen Definitionsbereich an.
im vorgegebenen Definitionsbereich an.
(2 BE)
1.2
Bestimme den Abstand der beiden lokalen Maximumpunkte des Graphen von  im vorgegebenen Definitionsbereich.
im vorgegebenen Definitionsbereich.
Gib die Bedeutung dieses Abstandes für die Funktion an.
an.
Gib die Bedeutung dieses Abstandes für die Funktion
(3 BE)
1.3
Gib den Wertebereich von  an.
an.
(1 BE)
1.4
Es gibt lineare Funktionen, deren Graph jeweils durch den Punkt  verläuft und mit dem Graphen von
verläuft und mit dem Graphen von  im vorgegebenen Definitionsbereich genau einen Punkt gemeinsam hat.
im vorgegebenen Definitionsbereich genau einen Punkt gemeinsam hat.
Gib eine mögliche Funktionsgleichung einer solchen linearen Funktion an.
Gib eine mögliche Funktionsgleichung einer solchen linearen Funktion an.
(2 BE)
2
Eine gerade Pyramide mit quadratischer Grundfläche besitzt die Höhe  Die Seitenlänge der Grundfläche beträgt
Die Seitenlänge der Grundfläche beträgt 
2.1
Berechne das Volumen dieser Pyramide.
Gib dieses Volumen in Liter an.
Gib dieses Volumen in Liter an.
(3 BE)
2.2
Berechne die Größe der Oberfläche dieser Pyramide.
(4 BE)
3
Ein Künstler stellt im Panometer Leipzig ein  -Panoramabild vom Wrack der Titanic aus. Das Panometer hat die Form eines geraden oben offenen Kreiszylinders mit aufgesetztem Kuppeldach.
-Panoramabild vom Wrack der Titanic aus. Das Panometer hat die Form eines geraden oben offenen Kreiszylinders mit aufgesetztem Kuppeldach.
Abbildung 1 zeigt den zur Grundfläche des Panometers senkrechten Schnitt durch den Mittelpunkt der Grundfläche des Panometers in einem Koordinatensystem (1 Längeneinheit entspricht 1 Meter).
Abbildung 1 zeigt den zur Grundfläche des Panometers senkrechten Schnitt durch den Mittelpunkt der Grundfläche des Panometers in einem Koordinatensystem (1 Längeneinheit entspricht 1 Meter).
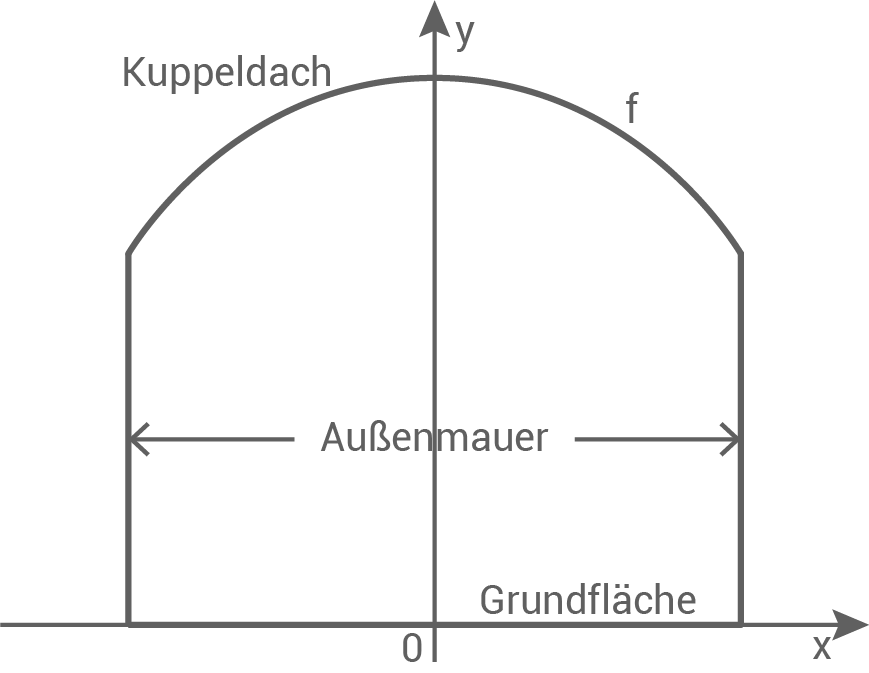
Abbildung 1 (nicht maßstäblich)
Die Schnittlinie des Kuppeldachs kann durch den Graphen der Funktion
3.1
Ermittle die maximale Höhe des Panometers.
(2 BE)
3.2
Die Außenmauer des Panometers ist  hoch.
hoch.
Bestimme den Durchmesser der Grundfläche des Panometers.
Bestimme den Durchmesser der Grundfläche des Panometers.
(3 BE)
Im Inneren des Panometers befindet sich das Panoramabild. Das Panoramabild hat eine Höhe von  und besitzt die Form der Mantelfläche eines geraden Kreiszylinders mit dem Grundkreisradius
und besitzt die Form der Mantelfläche eines geraden Kreiszylinders mit dem Grundkreisradius  . Abbildung 2 zeigt das Panometer mit Panoramabild im senkrechten Schnitt durch den Mittelpunkt der Grundfläche des Panometers und senkrecht von oben betrachtet.
. Abbildung 2 zeigt das Panometer mit Panoramabild im senkrechten Schnitt durch den Mittelpunkt der Grundfläche des Panometers und senkrecht von oben betrachtet.
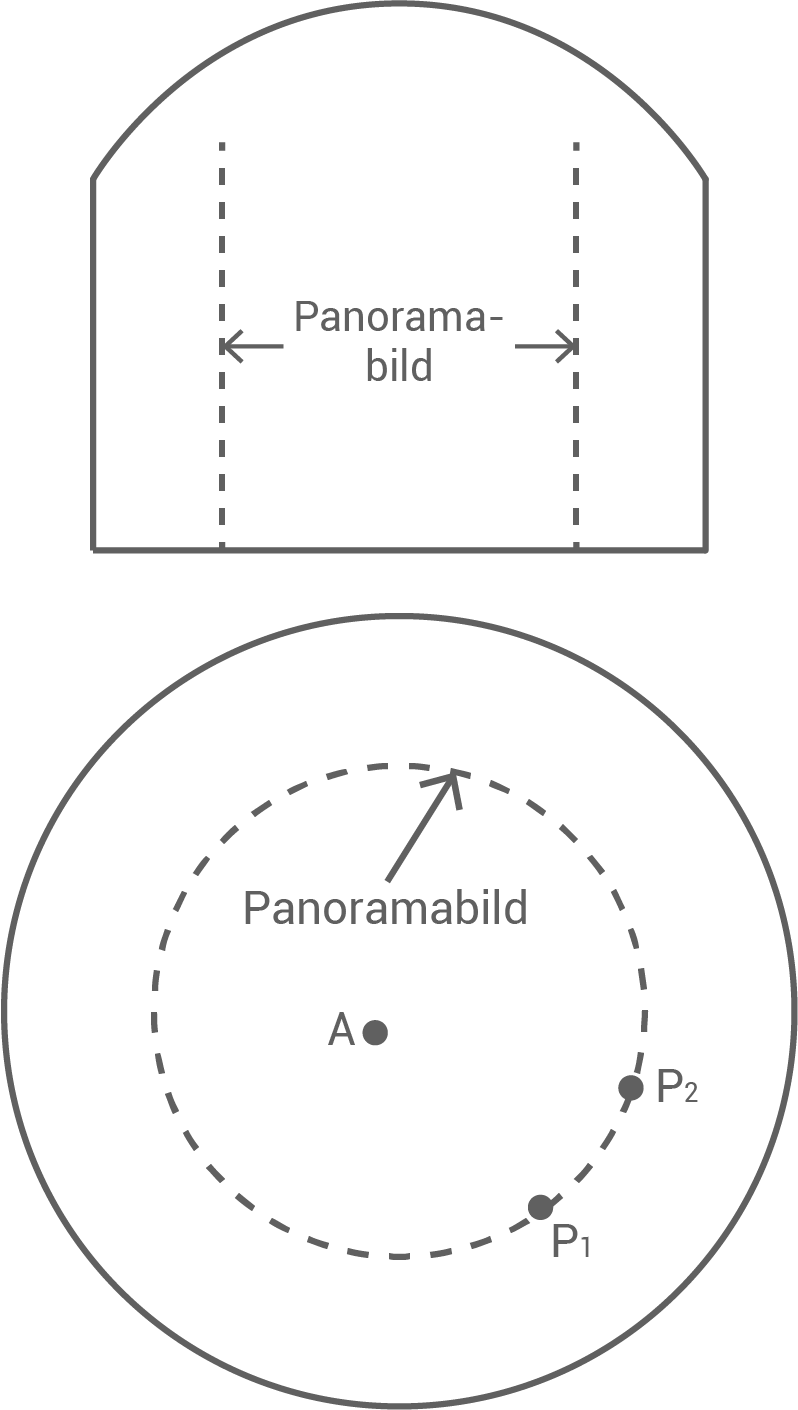

Abbildung 2 (nicht maßstäblich)
3.3
Berechne den Flächeninhalt des Panoramabildes.
(2 BE)
3.4
Im Innenraum des Panoramabildes befindet sich im Punkt  das Objektiv einer Kamera.
das Objektiv einer Kamera.
Die Punkte und
und  befinden sich auf dem Panoramabild und liegen gemeinsam mit dem Punkt
befinden sich auf dem Panoramabild und liegen gemeinsam mit dem Punkt  in gleicher Höhe über der Grundfläche des Panometers.
in gleicher Höhe über der Grundfläche des Panometers.
Es gilt: ,
,  und
und  .
Der Öffnungswinkel des Objektivs der Kamera beträgt
.
Der Öffnungswinkel des Objektivs der Kamera beträgt  .
.
Untersuche, ob das Objektiv der Kamera die Punkte und
und  gleichzeitig erfassen kann.
gleichzeitig erfassen kann.
Die Punkte
Es gilt:
Untersuche, ob das Objektiv der Kamera die Punkte
(4 BE)
3.5
Zum Zeitpunkt des Untergangs der Titanic waren insgesamt  Menschen an Bord. Die Tabelle stellt die Verteilung dieser Menschen auf die einzelnen Personengruppe und den prozentualen Anteil der Geretteten an der jeweiligen Personengruppe dar.
Menschen an Bord. Die Tabelle stellt die Verteilung dieser Menschen auf die einzelnen Personengruppe und den prozentualen Anteil der Geretteten an der jeweiligen Personengruppe dar.
| Personengruppe | Anteil der Personengruppe in Prozent | Gerettete der Personengruppe in Prozent |
|---|---|---|
| Kinder | ||
| Frauen | ||
| Männer |
3.5.1
Ermittle die Anzahl der Kinder an Bord der Titanic zum Zeitpunkt des Untergangs.
(2 BE)
3.5.2
Bestimme die Anzahl der geretteten Frauen beim Untergang der Titanic.
(2 BE)
1.1
Der Graph von  besitzt lokale Maximumpunkte an den Stellen
besitzt lokale Maximumpunkte an den Stellen 

 ... mit der Periode
... mit der Periode  Durch den Faktor
Durch den Faktor  im Funktionsterm
im Funktionsterm  wird der zugehörige Graph entlang der
wird der zugehörige Graph entlang der  -Achse gestaucht und die Periode wird auf
-Achse gestaucht und die Periode wird auf  verkürzt. Der erste lokale Maximumpunkt befindet sich daher schon bei
verkürzt. Der erste lokale Maximumpunkt befindet sich daher schon bei  Bei der Funktion zu
Bei der Funktion zu  beträgt der Funktionswert in jedem Maximumpunkt
beträgt der Funktionswert in jedem Maximumpunkt  Durch den Faktor
Durch den Faktor  im Funktionsterm von
im Funktionsterm von  wird der Graph entlang der
wird der Graph entlang der  -Achse gestreckt. Der Funktionswert im lokalen Maximumpunkt muss also mit
-Achse gestreckt. Der Funktionswert im lokalen Maximumpunkt muss also mit  multipliziert werden und beträgt daher
multipliziert werden und beträgt daher  Die Koordinaten eines lokalen Maximumpunktes im vorgegebenen Definitionsbereich
Die Koordinaten eines lokalen Maximumpunktes im vorgegebenen Definitionsbereich  lauten also
lauten also 
1.2
Die Funktion  ist periodisch und besitzt die Periode
ist periodisch und besitzt die Periode  Der zweite lokale Maximumpunkt im vorgegebenen Definitionsbereich hat daher die Koordinaten
Der zweite lokale Maximumpunkt im vorgegebenen Definitionsbereich hat daher die Koordinaten  Der Abstand der beiden Maximumpunkte beträgt
Der Abstand der beiden Maximumpunkte beträgt  und entspricht der kleinsten Periode der Funktion
und entspricht der kleinsten Periode der Funktion 
1.3
Der Wertebereich der allgemeinen Funktion  mit
mit  ist
ist  Durch den Faktor
Durch den Faktor  im Funktionsterm von
im Funktionsterm von  erhöht sich der kleinstmögliche und der größtmögliche Funktionswert um den Faktor
erhöht sich der kleinstmögliche und der größtmögliche Funktionswert um den Faktor 

1.4
Durch den Punkt  ist der
ist der  -Achsenabschnitt der gesuchten linearen Funktion
-Achsenabschnitt der gesuchten linearen Funktion  vorgegeben:
vorgegeben:
 Die Steigung muss nun so bestimmt werden, dass die Gerade den Graphen von
Die Steigung muss nun so bestimmt werden, dass die Gerade den Graphen von  für
für  genau einmal schneidet. Zur besseren Anschaulichkeit ist es hilfreich, sich den Graphen von
genau einmal schneidet. Zur besseren Anschaulichkeit ist es hilfreich, sich den Graphen von  zu skizzieren.
zu skizzieren.
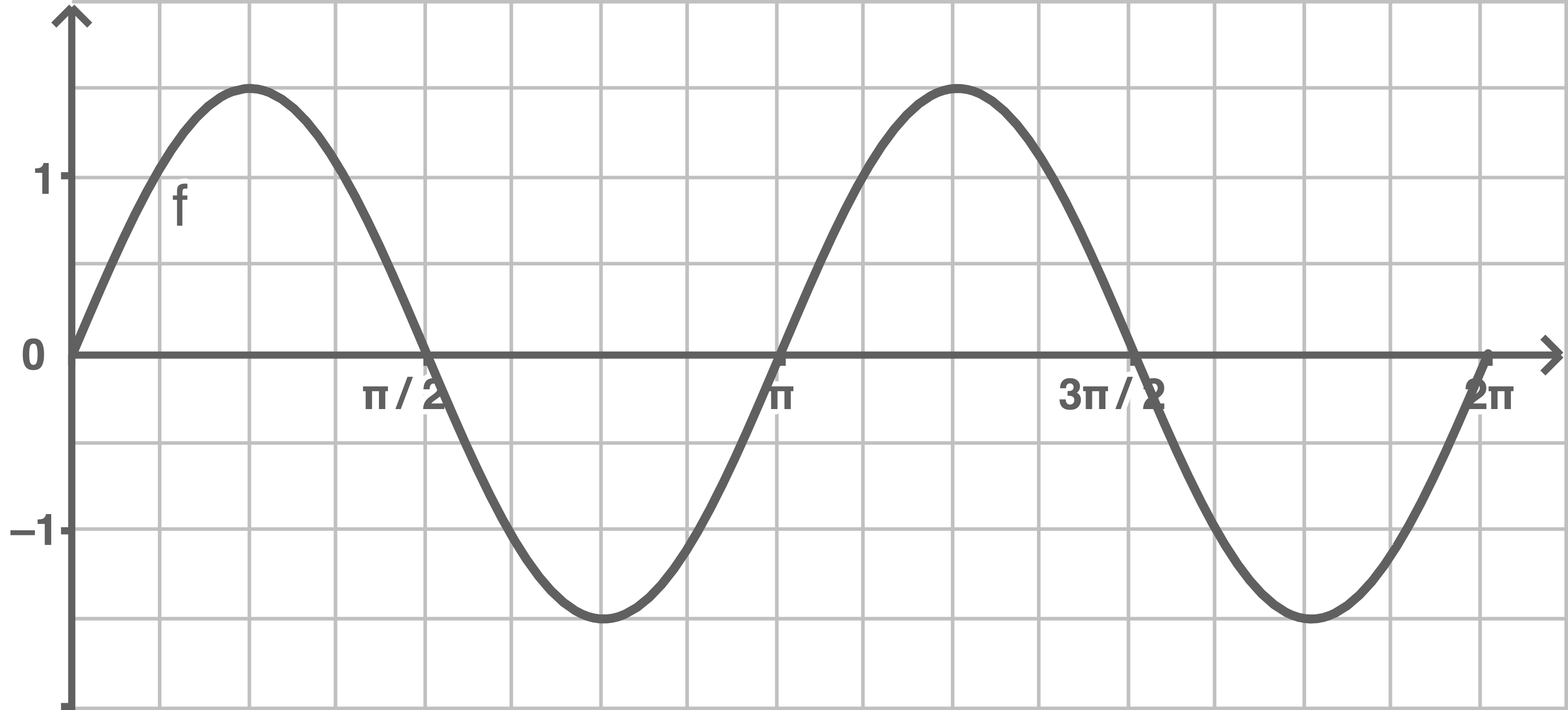 Es kann beispielsweise die Gerade verwendet werden, die durch den Punkt
Es kann beispielsweise die Gerade verwendet werden, die durch den Punkt  verläuft. Damit ergibt sich:
verläuft. Damit ergibt sich:
![\(\begin{array}[t]{rll}
y &=& m\cdot x +\dfrac{3}{2} \quad \scriptsize \mid\; \left(\dfrac{\pi}{4}\mid -\dfrac{3}{2} \right) \\[5pt]
-\dfrac{3}{2} &=& m\cdot \dfrac{\pi}{4} + \dfrac{3}{2} \quad \scriptsize \mid\;- \dfrac{3}{2} \\[5pt]
-3 &=& m\cdot \dfrac{\pi}{4} \quad \scriptsize \mid\;:\dfrac{\pi}{4} \\[5pt]
\dfrac{-12}{\pi} &=& m
\end{array}\)](https://mathjax.schullv.de/9803fd9ba9ca331cac1825d88717dc793f551661bf419f0e7557dbc2965c9bba?color=5a5a5a) Eine mögliche Geradengleichung ist:
Eine mögliche Geradengleichung ist:


2.1
Volumen der Pyramide berechnen
1. Schritt: Größe der Grundfläche berechnen
Die Grundfläche ist quadratisch und besitzt die Seitenlänge  Der Flächeninhalt der Grundfläche ist also:
Der Flächeninhalt der Grundfläche ist also:
 2. Schritt: Volumen berechnen
Die Höhe der Pyramide beträgt
2. Schritt: Volumen berechnen
Die Höhe der Pyramide beträgt  Mit der Formel für das Volumen einer Pyramide folgt:
Mit der Formel für das Volumen einer Pyramide folgt:
![\(\begin{array}[t]{rll}
V &=& \dfrac{1}{3} \cdot G \cdot h \\[5pt]
&=& \dfrac{1}{3}\cdot 2\,500\,\text{cm}^2 \cdot 80\,\text{cm} \\[5pt]
&\approx& 66\,666,67\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/e0c958b5dd94714232d94ab2b28f67c264aa33ca75d6c9893dbd7d81811bcf15?color=5a5a5a) Volumen in Liter angeben
Volumen in Liter angeben
 Liter entspricht
Liter entspricht 
 Die Pyramide hat ein Volumen von ca.
Die Pyramide hat ein Volumen von ca. 
2.2
Die Formel für die Oberfläche einer quadratischen Pyramide lautet:
 1. Schritt: Höhe der Seitenfläche berechnen
1. Schritt: Höhe der Seitenfläche berechnen
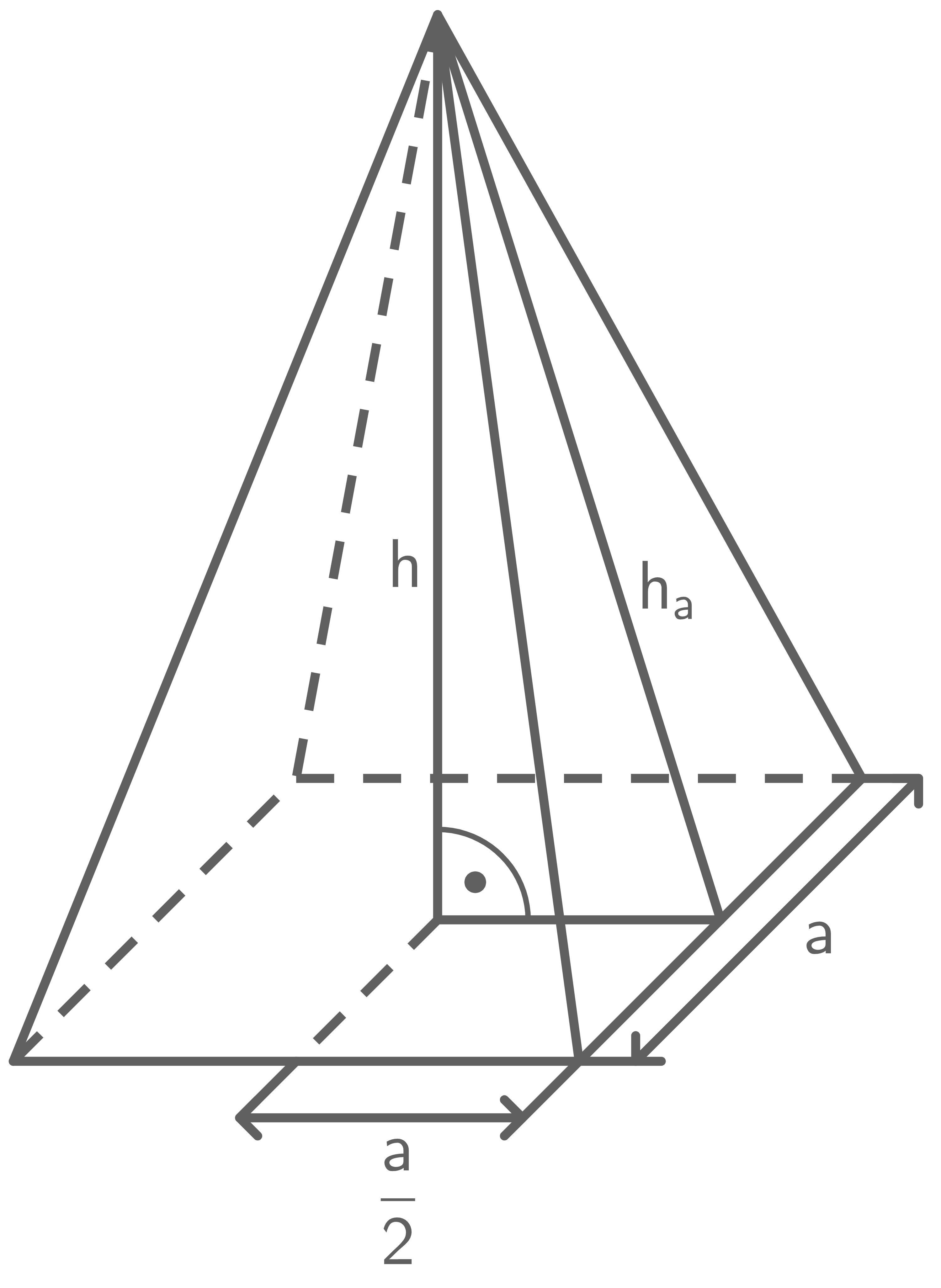 Die Grundseite der dreieckigen Seitenfläche ist
Die Grundseite der dreieckigen Seitenfläche ist  lang. Die zugehörige Höhe
lang. Die zugehörige Höhe  kann mit dem Satz des Pythagoras berechnet werden:
kann mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
h^2 + \left(\dfrac{a}{2} \right)^2 &=& h_a^2 \\[5pt]
\left(80\,\text{cm} \right)^2 + \left( \dfrac{50\,\text{cm}}{2}\right)^2 &=& h_a^2 \\[5pt]
7\,025\,\text{cm}^2&=& h_a^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
83,82\,\text{cm}&\approx& h_a
\end{array}\)](https://mathjax.schullv.de/0eb92b4008ee9776f599238d518693755d9ce756cfa4ac675232429dc537f25d?color=5a5a5a) 2. Schritt: Größe der Oberfläche berechnen
2. Schritt: Größe der Oberfläche berechnen
![\(\begin{array}[t]{rll}
O&=& a^2+2\cdot a\cdot h_a \\[5pt]
&=& (50\,\text{cm})^2 + 2\cdot 50\,\text{cm}\cdot 83,82\,\text{cm} \\[5pt]
&=& 10\,882\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/b9c181606cce9bc80c12a8ac513c42e09d9375f0d98cc05178fa753fc52e6859?color=5a5a5a) Die Oberfläche der Pyramide ist ca.
Die Oberfläche der Pyramide ist ca.  groß.
groß.

Skizze
3.1
Die maximale Höhe des Panometers entspricht dem maximalen Funktionswert von  Der Abbildung kann entnommen werden, dass sich dieser an der Stelle
Der Abbildung kann entnommen werden, dass sich dieser an der Stelle  befindet.
befindet.
![\(\begin{array}[t]{rll}
f(0)&=& -0,0124\cdot 0^2 +40,0 \\[5pt]
&=& 40,0
\end{array}\)](https://mathjax.schullv.de/17692d5e77a99b3bffa69e21a695acfb48ed2383ee2fc1fa192019e8ba72a414?color=5a5a5a) Die maximale Höhe des Panometers beträgt also
Die maximale Höhe des Panometers beträgt also 
3.2
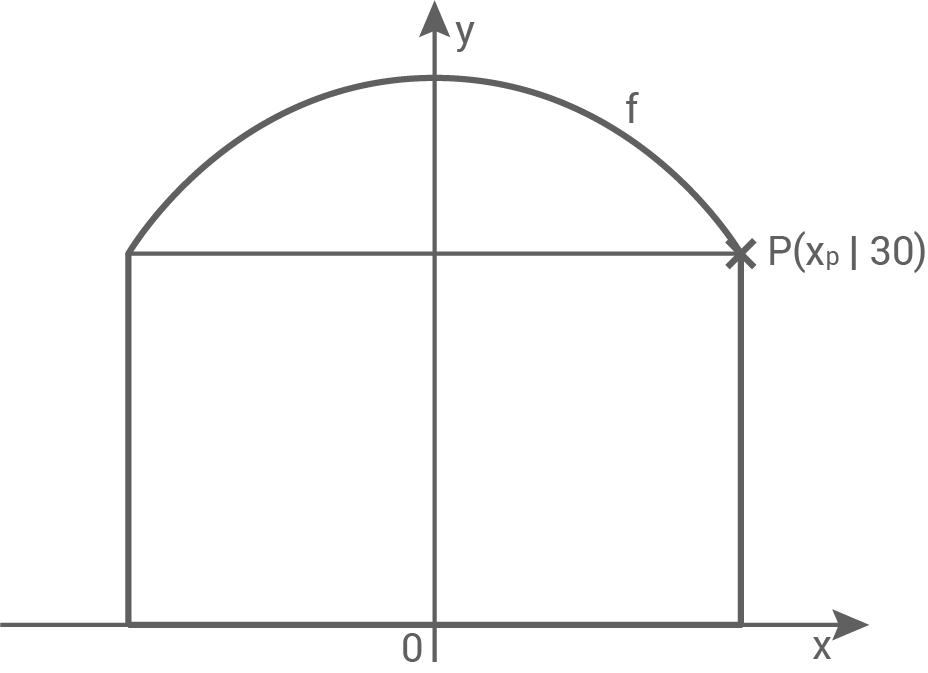
3.3
Das Bild hat die Form der Mantelfläche eines geraden Kreiszylinders mit der Höhe  und dem Grundkreisradius
und dem Grundkreisradius 
Der Flächeninhalt des Bildes lässt sich also über berechnen. Dabei ist
berechnen. Dabei ist  der Umfang des Grundkreises.
der Umfang des Grundkreises.
Mit der Formel für den Umfang eines Kreises ergibt sich:![\(\begin{array}[t]{rll}
U &=& 2\cdot \pi \cdot r \\[5pt]
&=& 2\cdot \pi \cdot 16,7\,\text{m} \\[5pt]
&\approx& 104,93\,\text{m}
\end{array}\)](https://mathjax.schullv.de/8451d3b97898f7a93a399d654357daaf1b12a7c965884cf0fd2802d651132967?color=5a5a5a) Der Flächeninhalt ergibt sich dann zu:
Der Flächeninhalt ergibt sich dann zu:
![\(\begin{array}[t]{rll}
A &=& h\cdot U \\[5pt]
&\approx& 32,0\,\text{m} \cdot 104,93\,\text{m} \\[5pt]
&=& 3\,357,76\,\text{m}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/67aad6d66a84719830744ea7d284007e5bd8ecab19b88e3b630735eb0c8b448b?color=5a5a5a) Der Flächeninhalt des Panoramabildes beträgt ca.
Der Flächeninhalt des Panoramabildes beträgt ca. 
Der Flächeninhalt des Bildes lässt sich also über
Mit der Formel für den Umfang eines Kreises ergibt sich:
3.4
Die drei angegebenen Punkte bilden ein Dreieck. In der Aufgabenstellung sind alle drei Seitenlängen des Dreiecks angegeben:
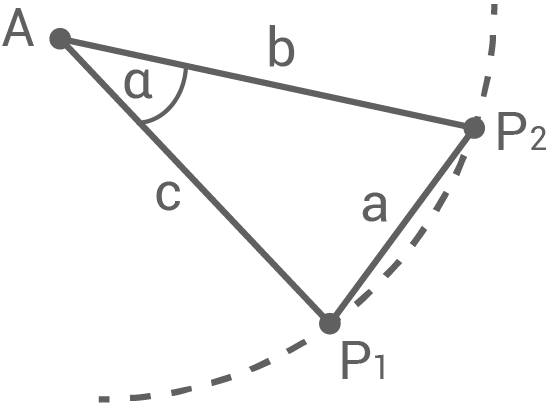 Damit die Kamera beide Punkte
Damit die Kamera beide Punkte  und
und  gleichzeitig erfassen kann, darf der Winkel
gleichzeitig erfassen kann, darf der Winkel  höchstens so groß sein wie der Öffnungswinkel der Kamera, also
höchstens so groß sein wie der Öffnungswinkel der Kamera, also  Mit dem Kosinussatz kann
Mit dem Kosinussatz kann  berechnet werden:
Wegen
berechnet werden:
Wegen  kann die Kamera beide Punkte
kann die Kamera beide Punkte  und
und  gleichzeitig erfassen.
gleichzeitig erfassen.

Skizze Dreieck 
3.5.1
Zum Zeitpunkt des Untergangs waren  Personen an Bord der Titanic. Davon waren laut Tabelle
Personen an Bord der Titanic. Davon waren laut Tabelle  Kinder:
Kinder:
 Zum Zeitpunkt des Untergangs waren ca.
Zum Zeitpunkt des Untergangs waren ca.  Kinder an Bord der Titanic.
Kinder an Bord der Titanic.
3.5.2
1. Schritt: Anzahl der Frauen an Bord berechnen
Von den  Personen an Bord waren
Personen an Bord waren  Frauen:
Frauen:
 An Bord waren
An Bord waren  Frauen.
2. Schritt: Anzahl geretteter Frauen berechnen
Von den
Frauen.
2. Schritt: Anzahl geretteter Frauen berechnen
Von den  Frauen, die an Bord waren, wurden
Frauen, die an Bord waren, wurden  gerettet:
gerettet:
 Beim Untergang der Titanic wurden
Beim Untergang der Titanic wurden  Frauen gerettet.
Frauen gerettet.