SchulLV Logo
Lerninhalte in Mathe
Digitales Schulbuch
Inhaltsverzeichnis

Potenzen mit ganzzahligem Exponent

Definition

Es gilt für jede reelle Zahl \(a:\)
\(a^0=1\)
\(a^1=a\)
\(a^n=\underbrace{a\cdot a\cdot a\cdot a\cdot ...\cdot a}_{\text{n Faktoren}}\quad (n\in \mathbb{N}, n\geq 1)\)
Eine Potenz besteht immer aus einer Basis und einem Exponenten.
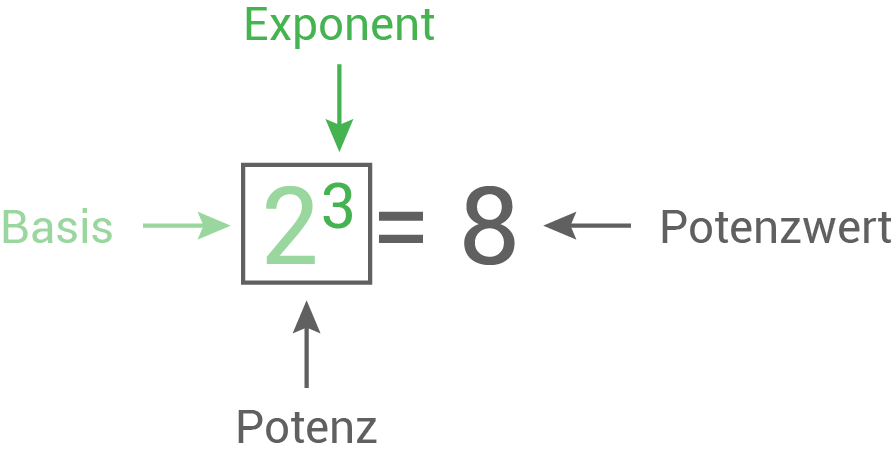
potenzen
Man sagt: „Zwei hoch drei“

Zehnerpotenzen

Die Zahlen 10, 100, 1000 usw. können übersichtlich als Potenz von der Zahl 10 geschrieben werden.
Potenzen anzeigen
Einige Einheitenvorsätze entsprechen Zehnerpotenzen:
Potenz Abkürzung Vorsilbe
\(10^2\) h Hekto
\(10^3\) k Kilo
\(10^6\) M Mega
\(10^9\) G Giga
\(10^{12}\) T Tera
\(10^{15}\) P Peta
\(10^{18}\) E Exa
Große Zahlen können als Produkt einer Zahl zwischen 1 und 10 (wobei die 10 nicht inbegriffen ist) und einer Zehnerpotenz geschrieben werden. Diese Darstellung wird wissenschaftliche Schreibweise genannt.
Beispiel: \(74\,827=7,4827\cdot 10^4\)

Potenzen mit negativem ganzzahligen Exponent

Für alle \(n\in \mathbb N\) und \(a\neq 0\) gilt:
\(a^{-n}=\dfrac{1}{a^n}\)