Wahrscheinlichkeiten
Aufgabe 1
a)
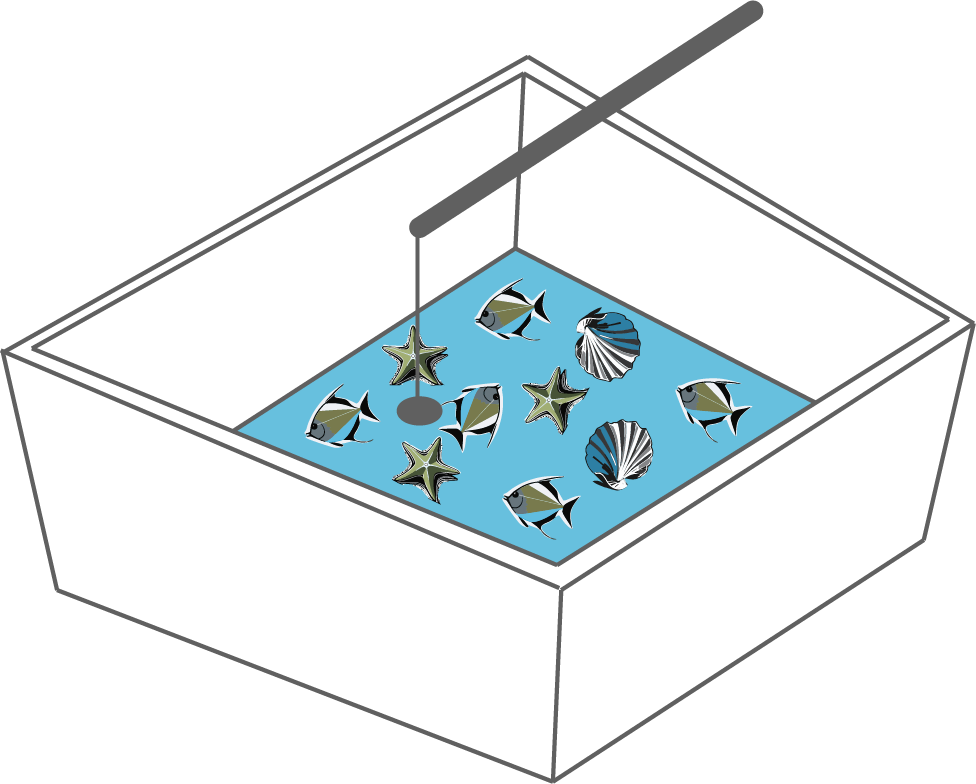
Beim Schulfest bietet die Klasse 10a ein Angelspiel an. Dabei dürfen die Spieler zweimal nacheinander einen Gegenstand aus einem Gefäß angeln. Die Gegenstände werden nicht zurückgelegt. In dem Gefäß liegen fünf Fische, drei Seesterne und zwei Muscheln.
- Berechne die Wahrscheinlichkeit für das Ereignis „zweimal Muschel“.
Für ein Glückspiel wird der gegebene Gewinnplan eingesetzt.
| Ereignis | Gewinn |
| zweimal Muschel | 9,00 € |
| zweimal Seestern | 4,00 € |
| Muschel und Seestern | 2,50 € |
| Einsatz 1,00 € | |
- Berechne den Erwartungswert.
- Wie hoch muss der Gewinn für „zweimal Muschel“ sein?
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2024
Aufgabe 2
a)
Die Klasse 10a verkauft Rubbellose.
Auf jedem Los befinden sich zwei Streifen.
Jeder Streifen enthält die folgenden Ziffern:
 Die Ziffern sind in zufälliger Reihenfolge angeordnet. Der linke Streifen zeigt die Zehnerziffern, der rechte die Einerziffern.
Die Ziffern sind in zufälliger Reihenfolge angeordnet. Der linke Streifen zeigt die Zehnerziffern, der rechte die Einerziffern.
 Auf jedem Streifen wird genau ein Feld freigerubbelt, wodurch eine zweistellige Zahl entsteht.
Auf jedem Streifen wird genau ein Feld freigerubbelt, wodurch eine zweistellige Zahl entsteht.
Die obenstehende Abbildung zeigt die Zahl
 durch eine
durch eine  zu ersetzen.
zu ersetzen.
Auf jedem Los befinden sich zwei Streifen.
Jeder Streifen enthält die folgenden Ziffern:


Die obenstehende Abbildung zeigt die Zahl
- Wie groß ist die Wahrscheinlichkeit, eine Zahl zu erhalten, die größer als
ist?
| Ereignis | Gewinn |
|---|---|
| Zahl größer als |
|
| Zahl |
|
| restliche Möglichkeiten | kein Gewinn |
| Einsatz: |
|
- Berechne den Erwartungswert.
- Erhöht sich dadurch der Gewinn für die Klasse?
Begründe deine Entscheidung durch Rechnung.
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 3
a)
In einem Gefäß liegen acht Kugeln, die rot, blau und grün gefärbt sind.
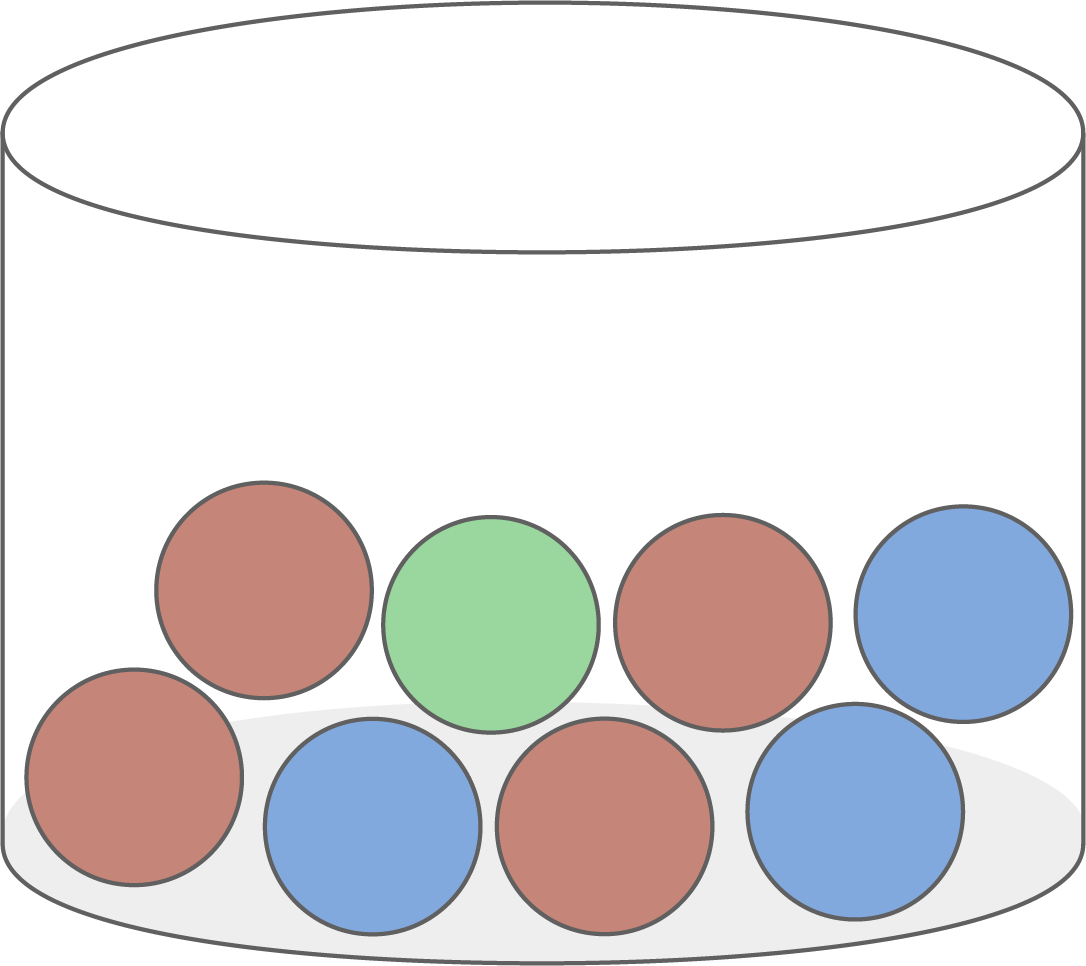 Es werden zwei Kugeln ohne Zurücklegen gezogen.
Es werden zwei Kugeln ohne Zurücklegen gezogen.

- Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Kugeln zu ziehen?
| Ereignis | Gewinn |
|---|---|
| zwei gleichfarbige Kugeln | 4,00 € |
| eine grüne und eine blaue Kugel | 10,00 € |
| Einsatz: 2,50 € pro Spiel | |
- Berechne den Erwartungswert.
- Wie hoch müsste dann der Gewinn für „eine grüne und eine blaue Kugel" sein, wenn alles andere unverändert bleibt?
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 4
a)
Zehn gleich große Karten sind mit vier verschiedenen Symbolen (Handball, Radfahren, Laufen, Fußball) bedruckt.
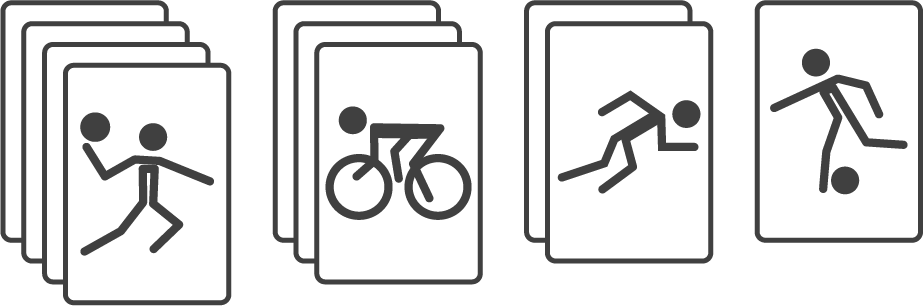 Sie sind nach den vier Symbolen in Stapeln sortiert (siehe Abbildung).
Sie sind nach den vier Symbolen in Stapeln sortiert (siehe Abbildung).
Die Karten werden gemischt und verdeckt auf den Tisch gelegt.
Sie werden für ein Glücksspiel eingesetzt.
Dabei werden zwei Karten gleichzeitig gezogen.
Für das Spiel wird der abgebildete Gewinnplan geprüft.
Berechne den Erwartungswert. Der Veranstalter möchte langfristig pro Spiel einen Erlös von 
 erzielen.
erzielen.

Die Karten werden gemischt und verdeckt auf den Tisch gelegt.
Sie werden für ein Glücksspiel eingesetzt.
Dabei werden zwei Karten gleichzeitig gezogen.
Für das Spiel wird der abgebildete Gewinnplan geprüft.
| Ereignis | Gewinn |
|---|---|
zweimal  |
9,00 € |
 und und  |
6,00 € |
 und und  |
3,00 € |
| andere Ereignisse | kein Gewinn |
| Einsatz pro Spiel: 1,00 € | |
- Wie hoch muss dann der Gewinn für "
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 5
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Ein Glücksrad besteht aus sechs gleich großen Abschnitten. Diese sind beschriftet mit den Buchstaben A, B, B, B, C und C. Das Glücksrad wird zweimal gedreht.
| Ereignis | Gewinn |
|---|---|
| zweimal B | 6,00 € |
| ein A und ein C | 4,50 € |
| Sonstiges | 0 € |
| Einsatz pro Spiel: 3,00 € | |
- Mit welcher Wahrscheinlichkeit erhält man zweimal den Buchstaben C?
- Das Glücksrad soll für ein Glücksspiel verwendet werden. Berechne für den angegebenen Gewinnplan den Erwartungswert.
- Wie groß müsste der Gewinn für "zweimal B" sein, damit das Spiel fair ist, während die anderen Gewinnbeiträge gleich bleiben?
(5 P)
Aufgabe 6
a)
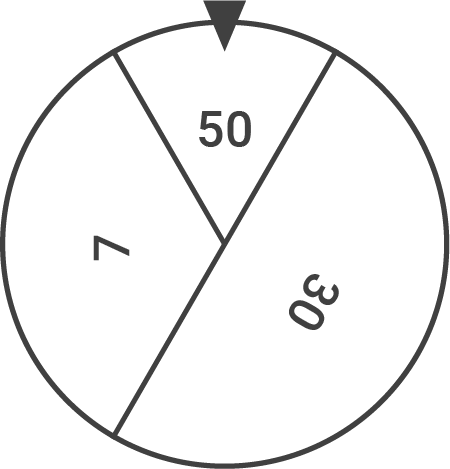
Das abgebildete Glücksrad mit den Mittelpunktswinkeln 60 , 180
, 180 und 120
und 120 ist mit den Zahlen 50, 30 und 7 beschriftet und wird zweimal gedreht.
ist mit den Zahlen 50, 30 und 7 beschriftet und wird zweimal gedreht.
- Mit welcher Wahrscheinlichkeit erhält man Zahlen, die zusammen genau 80 ergeben?
- Wie groß ist die Wahrscheinlichkeit, dass die Summe kleiner als 80 ist?
- Wie groß ist die Wahrscheinlichkeit, dass die Summe größer als 14 ist?
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Aufgabe 7
a)
Die beiden Glücksräder werden gedreht. Nachdem sie stehen bleiben, erkennt man im Sichtfenster eine Kombination zweier Symbole.
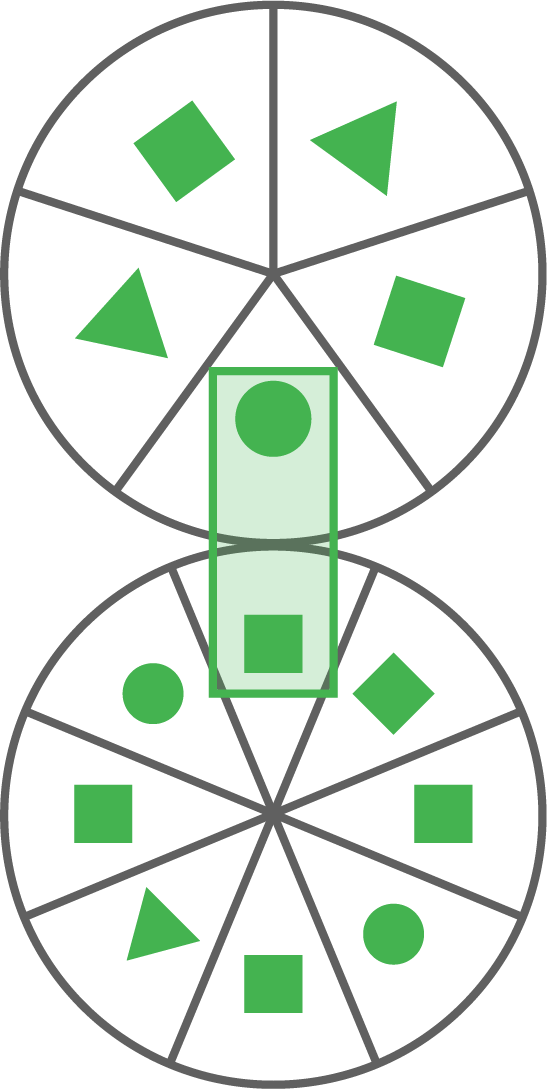 Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole im Sichtfenster zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird der abgebildete Gewinnplan geprüft.
Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole im Sichtfenster zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird der abgebildete Gewinnplan geprüft.
Berechne den Erwartungswert.
Der Gewinnplan soll so verändert werden, dass das Spiel fair wird.
Wie hoch muss dann der Gewinn für das Ereignis „Kreis und Dreieck“ sein, wenn alles andere unverändert bleibt?

| Ereignis | Gewinn |
|---|---|
| gleiche Symbole | |
| Kreis und Dreieck | |
| restliche Möglichkeiten | kein Gewinn |
| Einsatz pro Spiel: |
|
(5,5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 8
a)
Beim Würfelspiel „Augensumme 4 gewinnt“ wird gleichzeitig mit zwei Spielwürfeln geworfen. Die Augenzahlen werden addiert (Augensumme).
Dieses Spiel soll als Glücksspiel eingesetzt werden. Dazu wird nebenstehender Gewinnplan verwendet.
Berechne den Erwartungswert.
Der Betreiber bekommt die Vorgabe, das Glücksspiel zu verändern. Er soll auf einem der beiden Spielwürfel die Vier, die Fünf und die Sechs entweder durch drei Einsen oder durch drei Dreien ersetzen.
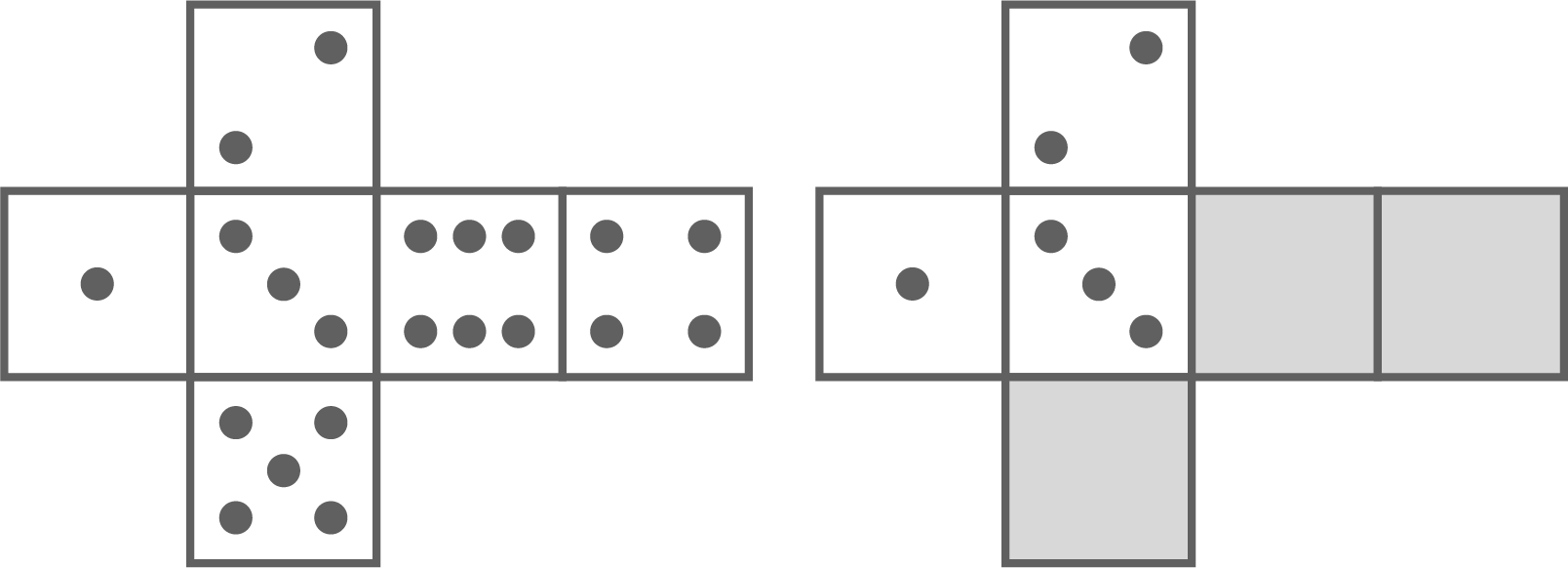 Wofür sollte sich der Betreiber entscheiden?
Wofür sollte sich der Betreiber entscheiden?
Begründe deine Entscheidung durch Rechnung oder Argumentation.
Dieses Spiel soll als Glücksspiel eingesetzt werden. Dazu wird nebenstehender Gewinnplan verwendet.
| Ereignisse | Gewinn |
|---|---|
| „Augensumme gleich 4“ | |
| „Augensumme kleiner 4“ | |
| „Augensumme größer 4“ | kein Gewinn |
| Einsatz pro Spiel: |
|

Begründe deine Entscheidung durch Rechnung oder Argumentation.
(6 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 9
a)
Im Technikunterricht wurde für ein Schulfest ein Zufallsgerät gebaut, bei dem sich zwei Walzen unabhängig voneinander drehen. Die Walzen sind mit Symbolen beklebt. Auf jeder Walze sind vier Zitronen, zwei Glocken und eine Sieben abgebildet.
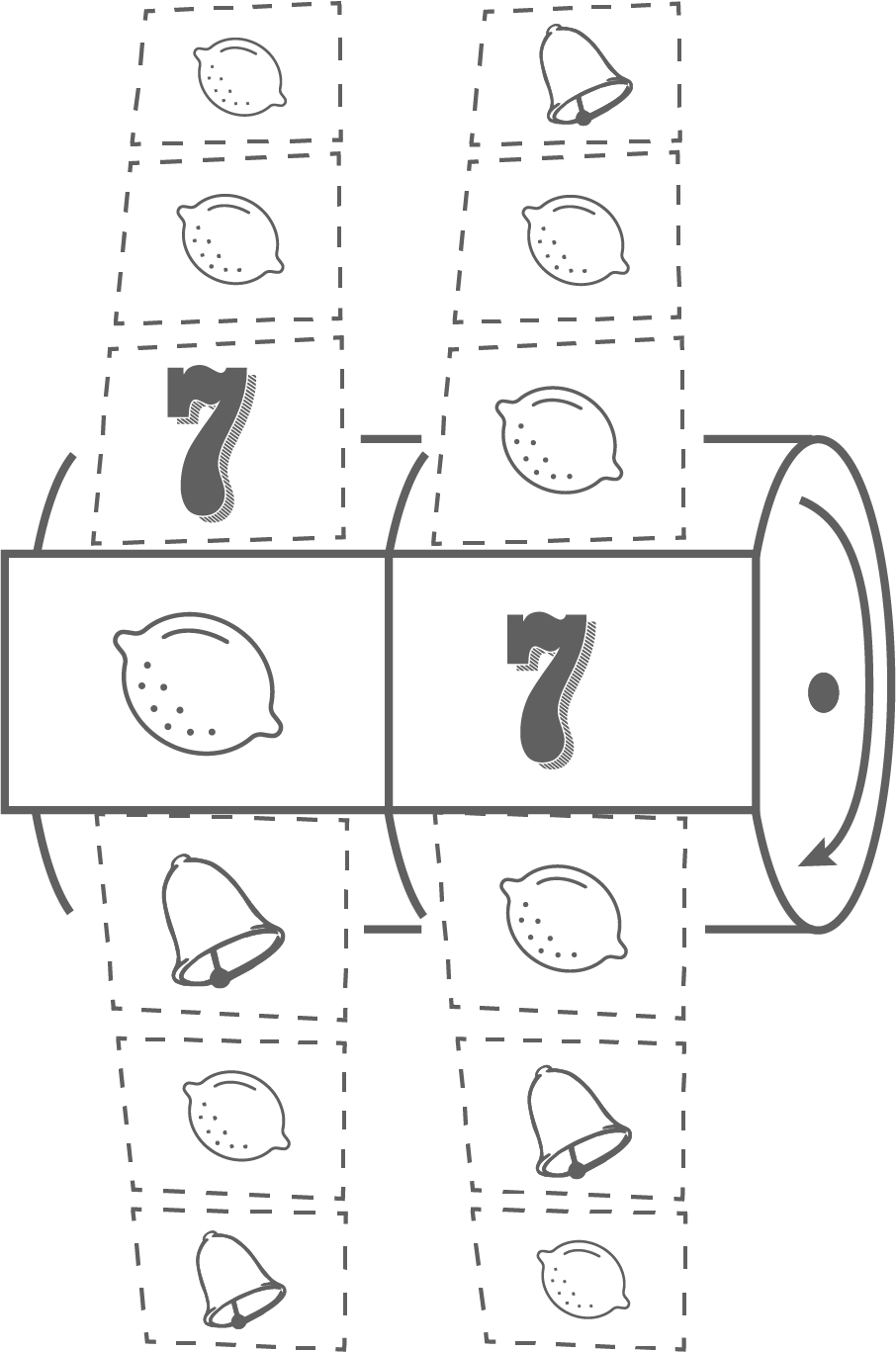 Wenn sie stehen bleiben, erkennt man im Sichtfenster zwei Symbole nebeneinander.
Wie groß ist die Wahrscheinlichkeit für das Ereignis "zweimal Glocke"?
Wenn sie stehen bleiben, erkennt man im Sichtfenster zwei Symbole nebeneinander.
Wie groß ist die Wahrscheinlichkeit für das Ereignis "zweimal Glocke"?
Das Zufallsgerät wird für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
Berechne den Erwartungswert. Was bedeutet das für den Spieler?
Der Einsatz soll auf  erhöht werden. Der Gewinn für "zweimal Glocke" sowie der Erwartungswert bleiben gleich.
Merle behauptet: "Der Gewinn für ‚zweimal Sieben‘ beträgt dann etwa 20€."
Hat Merle recht? Begründe rechnerisch.
erhöht werden. Der Gewinn für "zweimal Glocke" sowie der Erwartungswert bleiben gleich.
Merle behauptet: "Der Gewinn für ‚zweimal Sieben‘ beträgt dann etwa 20€."
Hat Merle recht? Begründe rechnerisch.

| Ereignis | Gewinn |
|---|---|
| zweimal Glocke | |
| zweimal Sieben | |
| sonstige | kein Gewinn |
| Einsatz pro Spiel: |
|
(5,5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 10
a)
Bei einer Wohltätigkeitsveranstaltung wird ein Glücksrad eingesetzt.
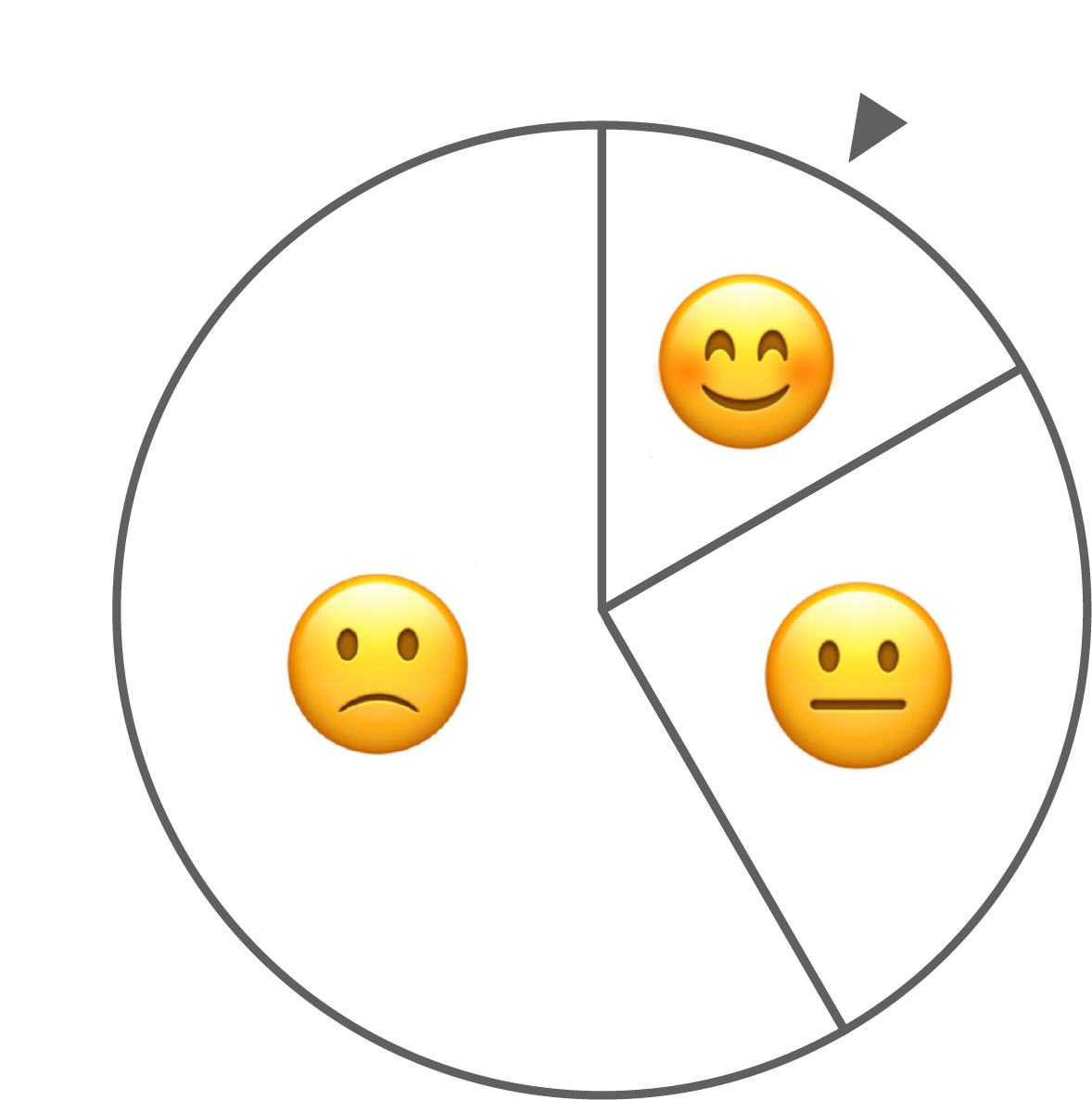 Die Mittelpunktswinkel betragen
Die Mittelpunktswinkel betragen  .
.
Das Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊 ? Das Glücksrad wird für ein Glücksspiel verwendet.
Berechne den Erwartungswert unter Berücksichtigung des untenstehenden Gewinnplans.
Der Gewinnplan soll so verändert werden, dass das Spiel fair wird.
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ sein, wenn alles andere unverändert bleibt?

Das Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊 ? Das Glücksrad wird für ein Glücksspiel verwendet.
Berechne den Erwartungswert unter Berücksichtigung des untenstehenden Gewinnplans.
| Ereignisse | Gewinn |
|---|---|
| zweimal 😊 | 4,00€ |
| zweimal 😐 | 2,00€ |
| sonstige | kein Gewinn |
| Einsatz pro Spiel: 0,50€ |
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ sein, wenn alles andere unverändert bleibt?
(5,5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 11
a)
Bei einer Wohltätigkeitsveranstaltung werden zwei Glücksräder eingesetzt.
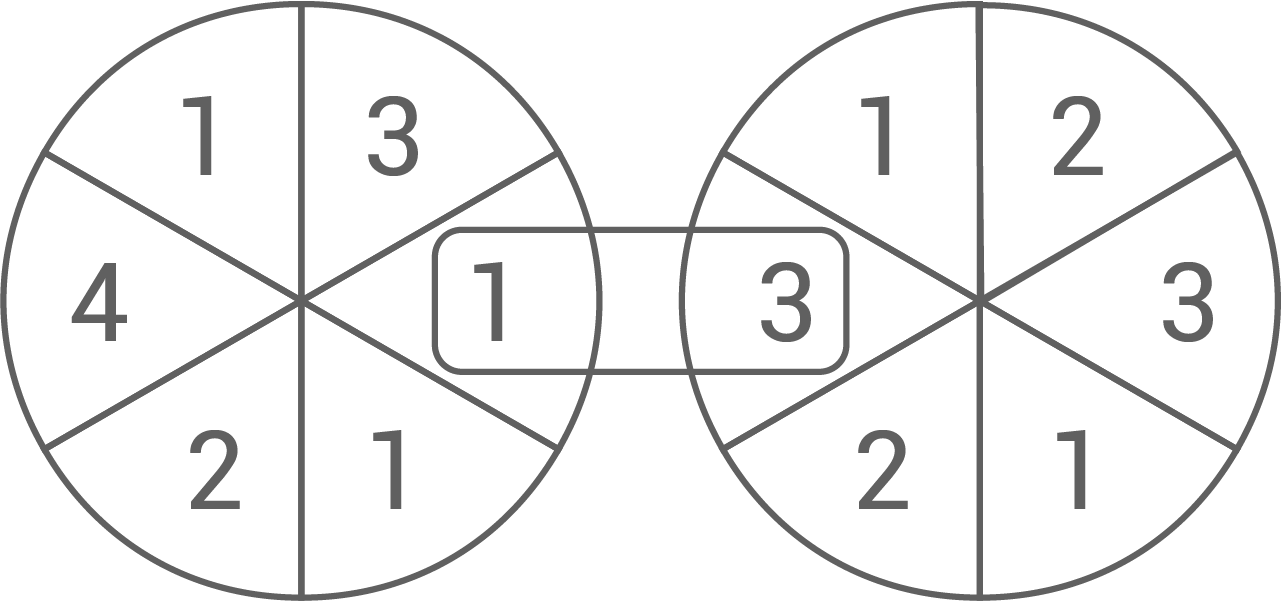 Beide Glücksräder werden gedreht.
Beide Glücksräder werden gedreht.
Wenn sie stehen bleiben, erkennt man im Sichtfenster eine zweistellige Zahl.
Die Abbildung zeigt die Zahl .
Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine Zahl mit zwei gleichen Ziffern zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
.
Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine Zahl mit zwei gleichen Ziffern zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
Berechne den Erwartungswert.
Bei der Wohltätigkeitsveranstaltung soll ein höherer Erlös erzielt werden. Dazu soll beim rechten Glücksrad eine der beiden Dreien durch eine Fünf ersetzt werden.
Der Gewinnplan bleibt gleich. Wäre dies vorteilhaft? Begründe durch Rechnung oder Argumentation.

Wenn sie stehen bleiben, erkennt man im Sichtfenster eine zweistellige Zahl.
Die Abbildung zeigt die Zahl
| Gewinnplan | |
|---|---|
| Ergebnisse | Gewinn |
| zwei gleiche Ziffern | 3,00 € |
| Zahl größer als 40 | 5,00€ |
| restliche Möglichkeiten | kein Gewinn |
| Einsatz 2,00 € | |
Der Gewinnplan bleibt gleich. Wäre dies vorteilhaft? Begründe durch Rechnung oder Argumentation.
(5,5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 12
a)
In einem Kartenstapel liegen zwölf Karten. Die Verteilung ist in der Tabelle dargestellt.
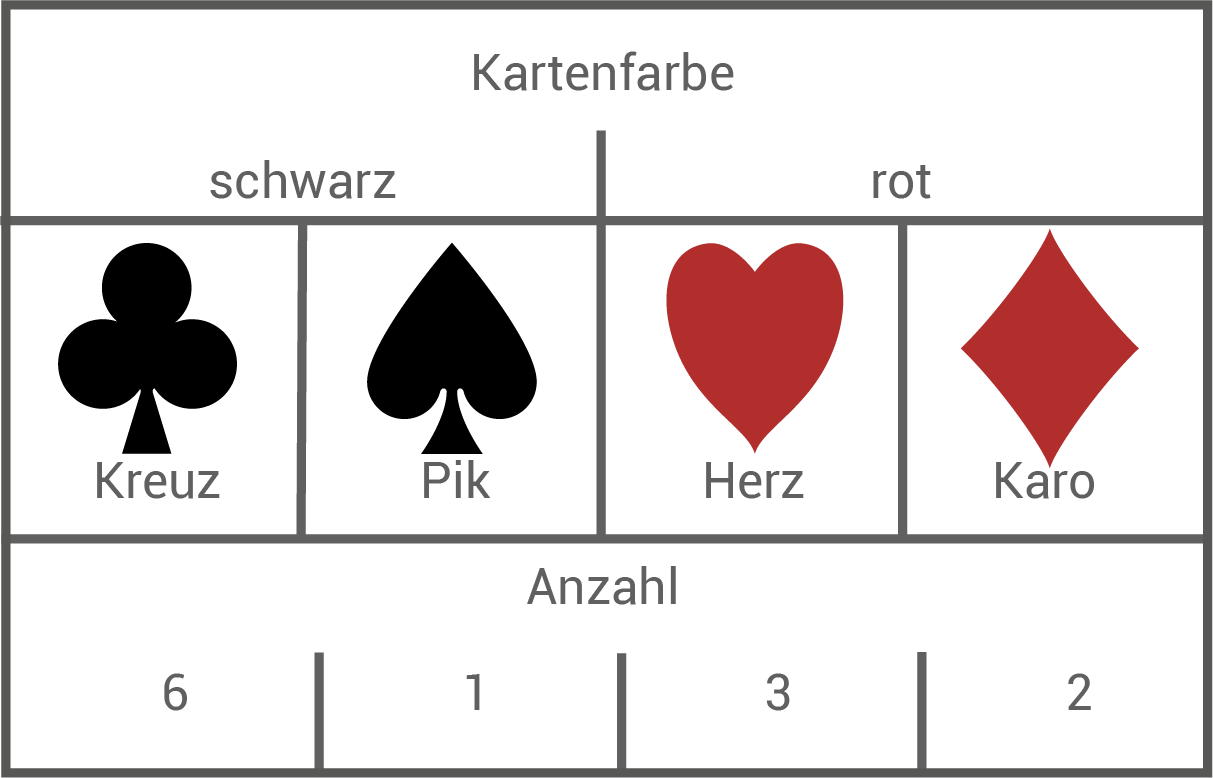 Die Karten werden gemischt und verdeckt auf den Tisch gelegt. Zwei Karten werden gleichzeitig gezogen.
Die Karten werden gemischt und verdeckt auf den Tisch gelegt. Zwei Karten werden gleichzeitig gezogen.
Wie groß ist die Wahrscheinlichkeit, eine rote und eine schwarze Karte zu erhalten? Die zwölf Karten werden für ein Glücksspiel eingesetzt. Es sollen ebenfalls zwei Karten gleichzeitig gezogen werden.
Dazu wird nebenstehender Gewinnplan geprüft.
Berechne den Erwartungswert.
Sophia macht den Vorschlag, den Gewinn für „zweimal Karo“ auf hochzusetzen und alles andere zu belassen.
hochzusetzen und alles andere zu belassen.
Der Betreiber des Glücksspiels protestiert und behauptet, er würde dann Verlust machen.
Hat der Betreiber recht? Begründe durch Rechnung.

Wie groß ist die Wahrscheinlichkeit, eine rote und eine schwarze Karte zu erhalten? Die zwölf Karten werden für ein Glücksspiel eingesetzt. Es sollen ebenfalls zwei Karten gleichzeitig gezogen werden.
Dazu wird nebenstehender Gewinnplan geprüft.
| Ergebnisse | Gewinn |
|---|---|
| zweimal Karo | |
| zweimal Herz | |
| sonstige | kein Gewinn |
| Einsatz pro Spiel: |
|
Sophia macht den Vorschlag, den Gewinn für „zweimal Karo“ auf
Der Betreiber des Glücksspiels protestiert und behauptet, er würde dann Verlust machen.
Hat der Betreiber recht? Begründe durch Rechnung.
(5,5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Wahrscheinlichkeit für Ereignis berechnen
Es sind insgesamt  Gegenstände.
Erwartungswert berechnen
Gegenstände.
Erwartungswert berechnen


 Gewinn für „zweimal Muschel“ berechnen
Neuen Preis
Gewinn für „zweimal Muschel“ berechnen
Neuen Preis  für Gewinn für „zweimal Muschel“ bei fairem Spiel berechnen:
Für ein faires Spiel muss der Gewinn für „zweimal Muschel“
für Gewinn für „zweimal Muschel“ bei fairem Spiel berechnen:
Für ein faires Spiel muss der Gewinn für „zweimal Muschel“  betragen.
betragen.
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2024
Lösung 2
a)
Wahrscheinlichkeit berechnen



 bzw.
bzw.  Erwartungswert berechnen
Erwartungswert berechnen

 Entscheidung treffen und begründen
Ja, der Gewinn erhöht sich dadurch auf lange Sicht.
Entscheidung treffen und begründen
Ja, der Gewinn erhöht sich dadurch auf lange Sicht.


b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Lösung 3
a)
Wahrscheinlichkeit bestimmen




 Erwartungswert berechnen
Erwartungswert berechnen




 Gewinn berechnen
Gewinn berechnen







b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2022
Lösung 4
a)
Erwartungswert berechnen
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?

 und
und 
 und
und 
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Lösung 5
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
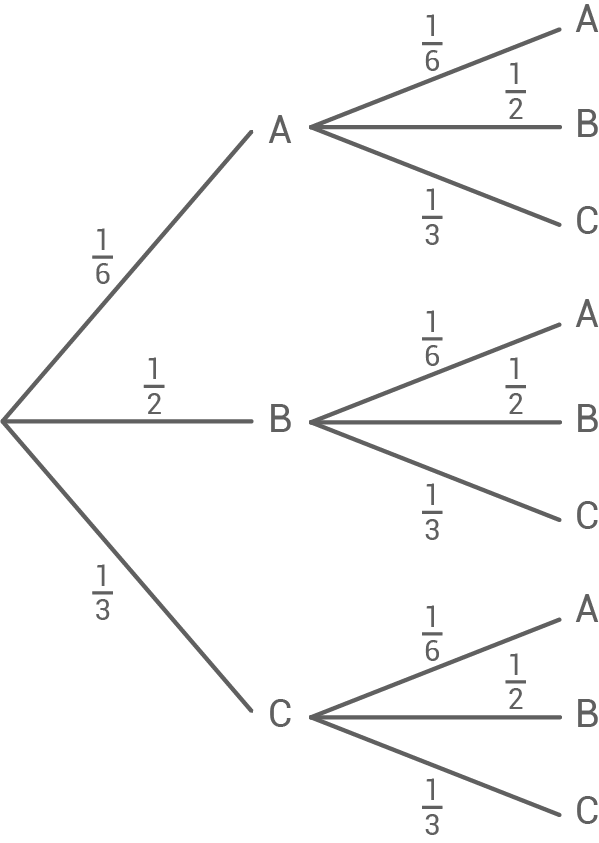
| Ereignis | Gewinn | Wahrscheinlichkeit |
|---|---|---|
| zweimal B | 6,00 € | |
| ein A und ein C | 4,50 € | |
| Sonstiges | 0 € |
Lösung 6
a)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Lösung 7
a)
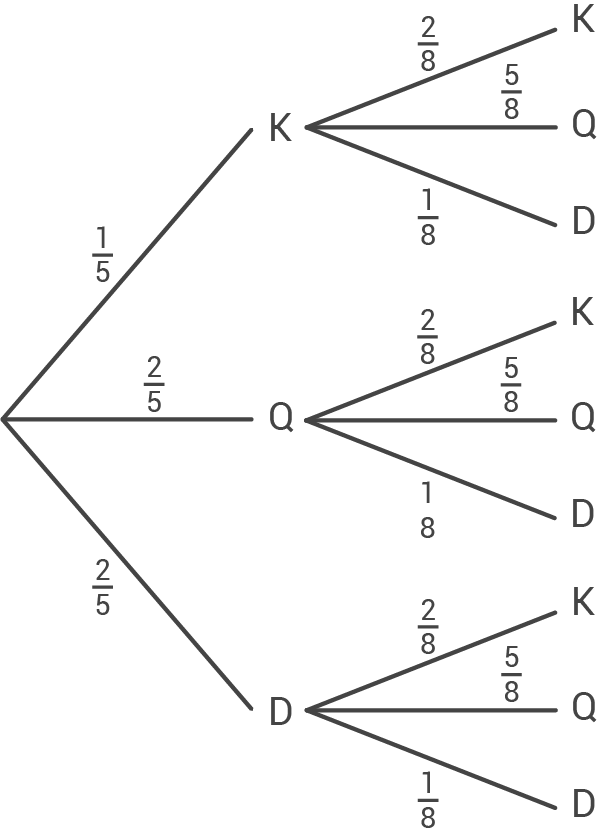
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2020
Lösung 8
a)
Erwartungswert berechnen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{3}{36}+2\,€\cdot \dfrac{3}{36}+0\,€\cdot \dfrac{30}{36}-1\,€\\[5pt]
&=&\dfrac{12}{36}\,€+\dfrac{6}{36}\,€-1\,€\\[5pt]
&=& \dfrac{1}{2}\,€-1\,€\\[5pt]
&=& -\dfrac{1}{2}\,€\\[5pt]
E &=& \underline{\underline{ -0,50\,€}}
\end{array}\)](https://mathjax.schullv.de/1aaebe9aecb5661dee4a64b7a8703ae5c78eaad1924f3ceabaf9526c3963e288?color=5a5a5a) Wofür sollte sich der Betreiber entscheiden?
Version 1: Würfel mit drei Einsen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
Wofür sollte sich der Betreiber entscheiden?
Version 1: Würfel mit drei Einsen
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
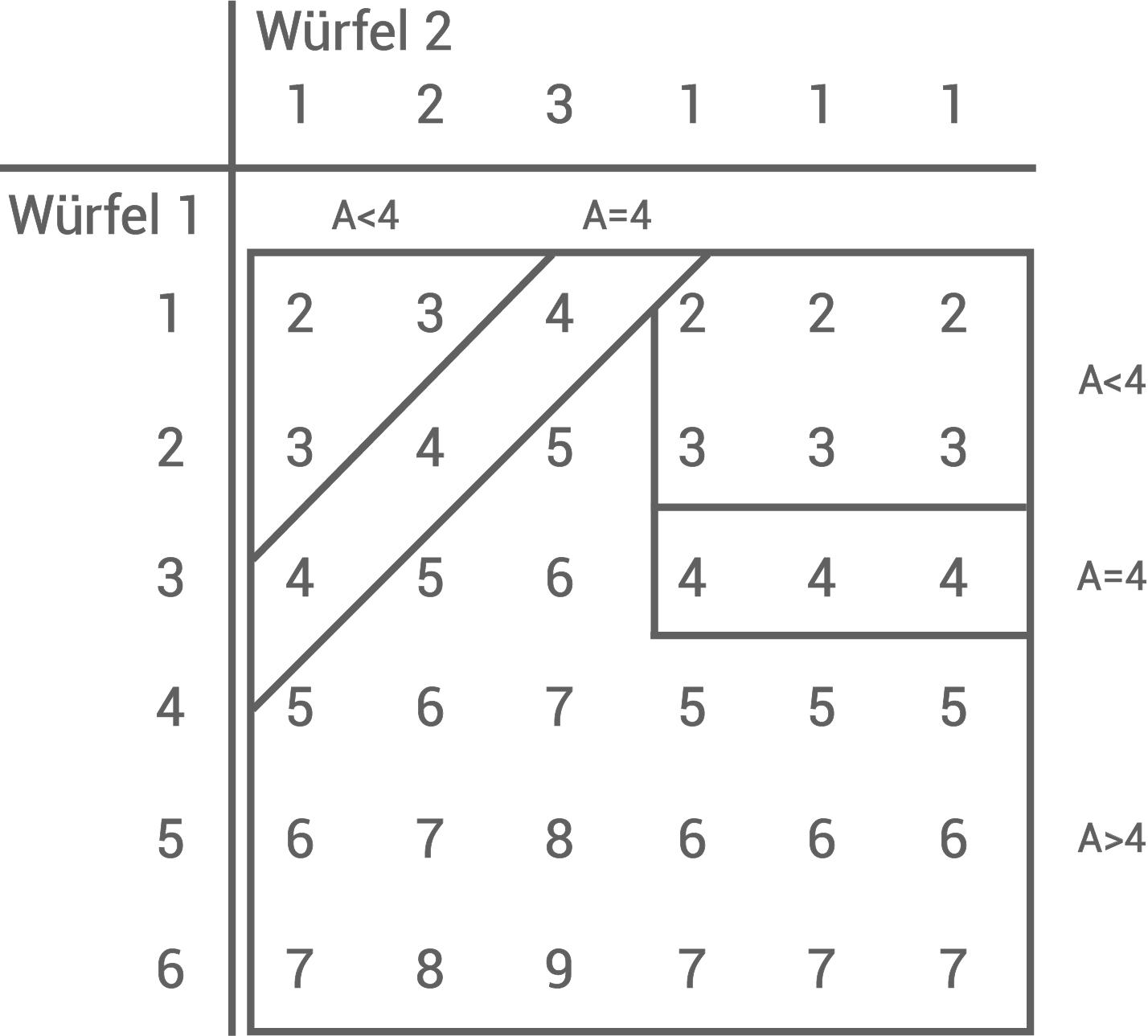 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{6}{36}+2\,€\cdot \dfrac{9}{36}+0\,€\cdot \dfrac{21}{36}-1\,€\\[5pt]
&=&\dfrac{24}{36}\,€+\dfrac{18}{36}\,€-1\,€\\[5pt]
E&=& \underline{ 0,17\,€}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/047a430c022f5a78989ad03777c00d845e607bf25d0c844291d18d1261c66eee?color=5a5a5a) Version 2: Würfel mit drei Dreien
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
Version 2: Würfel mit drei Dreien
1. Schritt: Tabelle mit allen möglichen Augensummen (A) erstellen
 2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
2. Schritt: Wahrscheinlichkeiten mithilfe der Tabelle bestimmen
![\(\begin{array}[t]{rll}
E&=&4\,€\cdot P_1+2\,€\cdot P_2+0\,€\cdot P_3-1\,€ & \\[5pt]
&=&4\,€\cdot \dfrac{6}{36}+2\,€\cdot \dfrac{3}{36}+0\,€\cdot \dfrac{27}{36}-1\,€\\[5pt]
&=&\dfrac{24}{36}\,€+\dfrac{6}{36}\,€-1\,€\\[5pt]
E&=& \underline{ -0,17\,€}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/03d2a7c98049b6add614589853e4a891877fdf37f602fc1d65136f4d0af71654?color=5a5a5a) Da der zu erwartende Gewinn für die Teilnehmer bei Version 2: Würfel mit drei Dreien kleiner als bei Version 1: Würfel mit drei Einsen ist, macht es für den Betreiber mehr Sinn, sich für den Würfel mit drei Dreien zu entscheiden.
Da der zu erwartende Gewinn für die Teilnehmer bei Version 2: Würfel mit drei Dreien kleiner als bei Version 1: Würfel mit drei Einsen ist, macht es für den Betreiber mehr Sinn, sich für den Würfel mit drei Dreien zu entscheiden.
Denn damit kann der Betreiber mit einem durchschnittlichen Gewinn von pro Spiel rechnen.
pro Spiel rechnen.



Denn damit kann der Betreiber mit einem durchschnittlichen Gewinn von
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2019
Lösung 9
a)
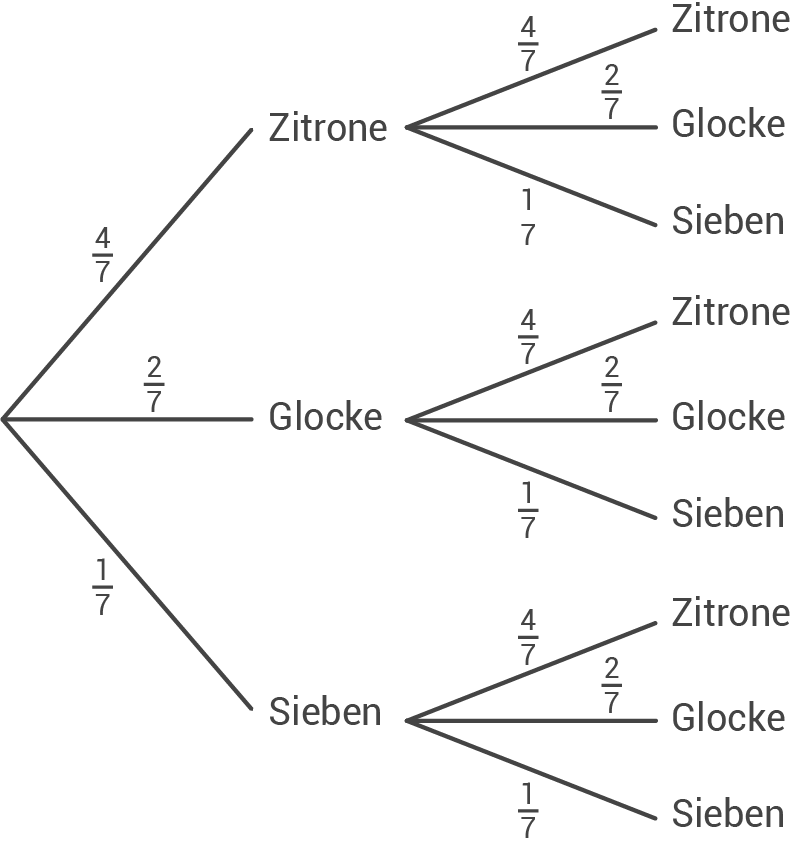
| Ereignis | Gewinn | Wahrscheinlichkeit |
|---|---|---|
| zweimal Glocke | 4 € | |
| zweimal Sieben | 10 € | |
| sonstige | 0 € |
als Erwartungswert
- Gewinn ("zweimal Sieben") als Unbekannte
- Alle anderen Werte bleiben gleich
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2018
Lösung 10
a)
Mit welcher Wahrscheinlichkeit erhält man höchstens einmal das Symbol 😊?
1. Schritt: Anteile der Felder berechnen
😊:  😐:
😐:  🙁:
🙁:  2. Schritt: Wahrscheinlichkeit berechnen
2. Schritt: Wahrscheinlichkeit berechnen
 Berechnung des Erwartungswerts
Berechnung des Erwartungswerts
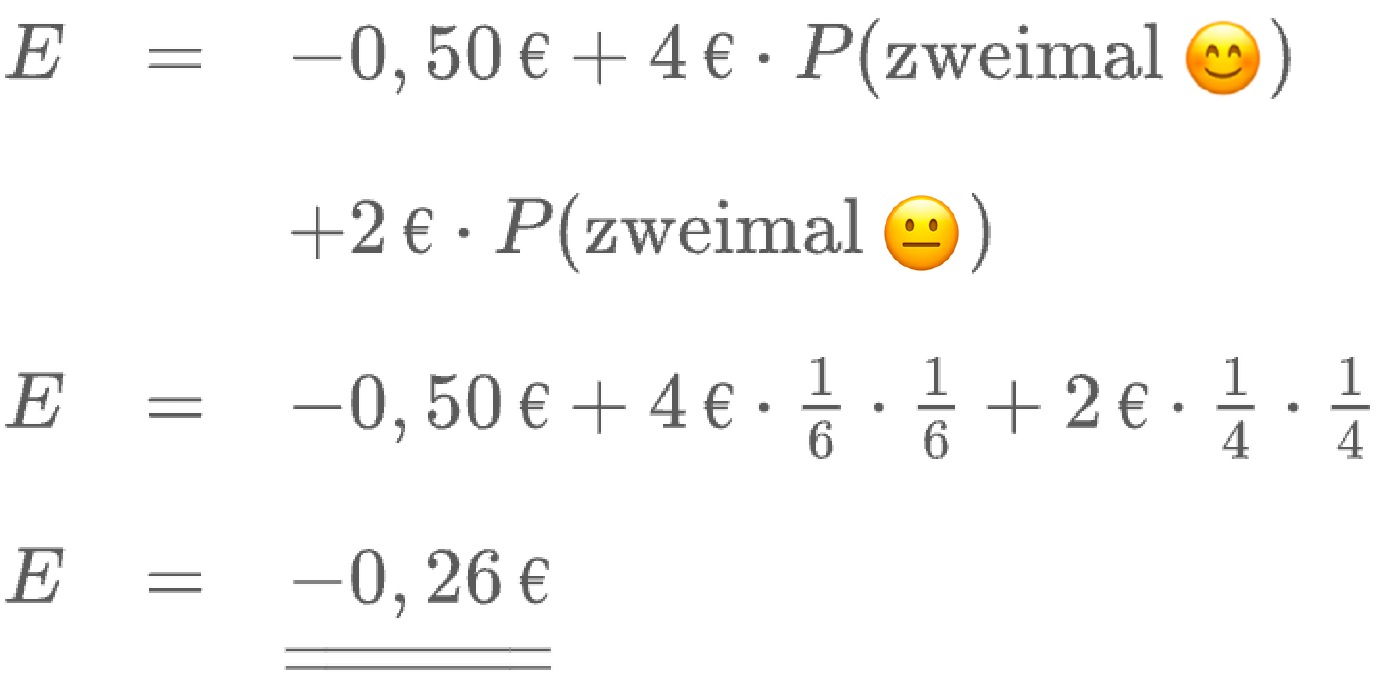 Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ bei einem fairen Spiel sein, wenn alles andere unverändert bleibt?
Wie hoch muss der Gewinn für das Ereignis „ zweimal 😊 “ bei einem fairen Spiel sein, wenn alles andere unverändert bleibt?
 neuer Gewinn bei „ zweimal 😊 “
neuer Gewinn bei „ zweimal 😊 “
 Für ein faires Spiel muss der Gewinn für „ zweimal 😊 “ 13,50 € betragen, wenn alles andere unverändert bleiben soll.
Für ein faires Spiel muss der Gewinn für „ zweimal 😊 “ 13,50 € betragen, wenn alles andere unverändert bleiben soll.

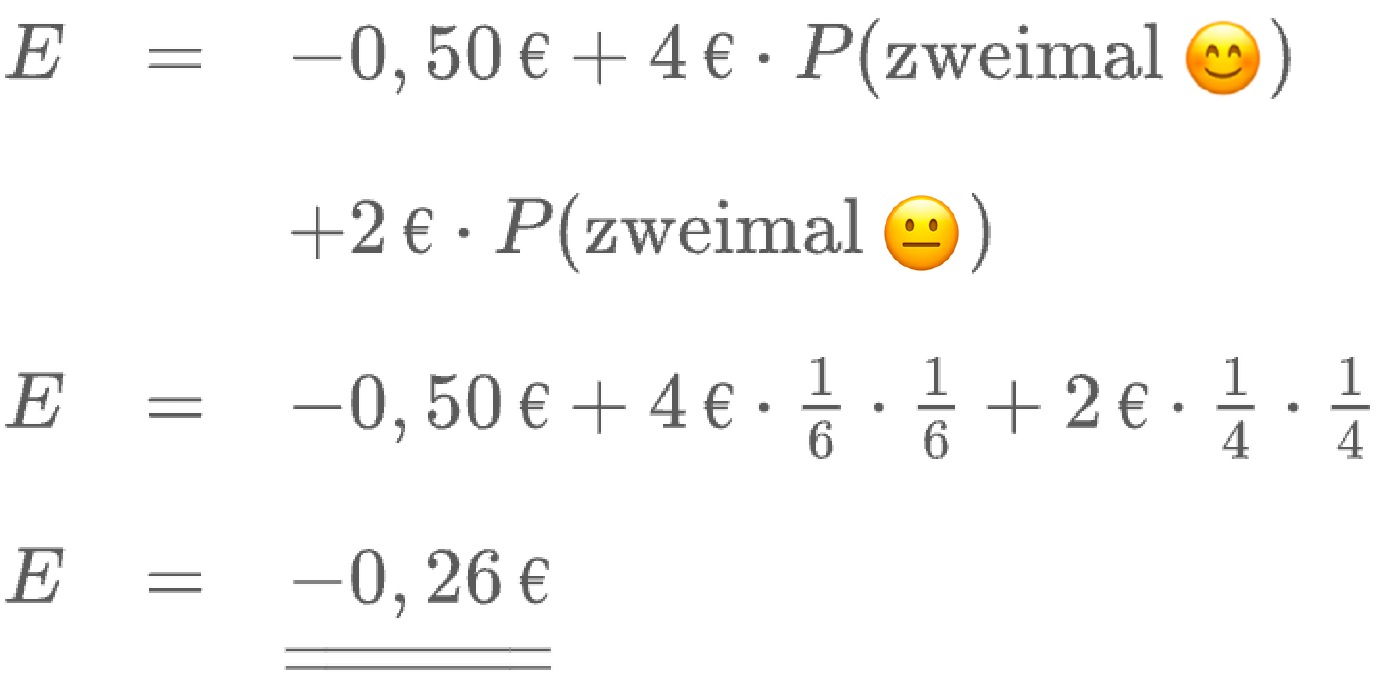

b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2017
Lösung 11
a)
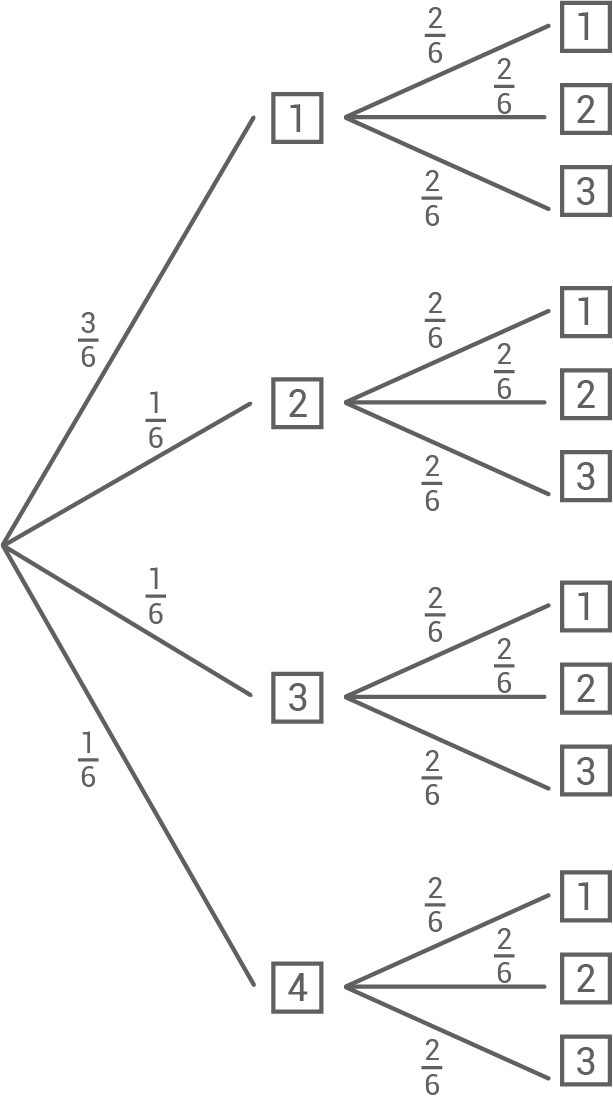
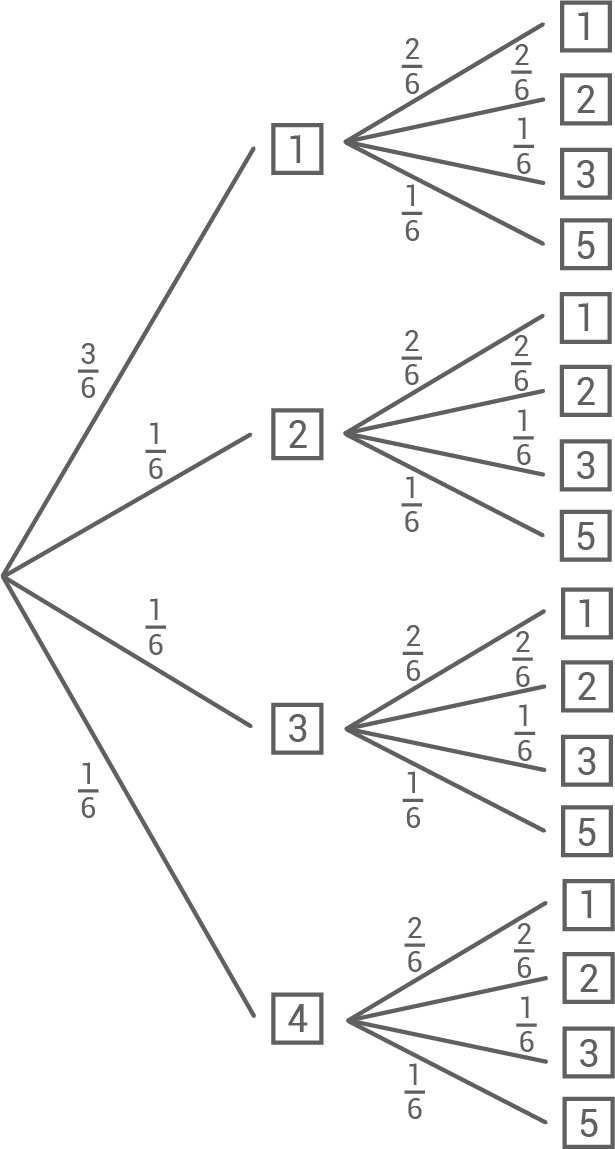
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2016
Lösung 12
a)
Wahrscheinlichkeit berechnen

![\(\begin{array}[t]{rll}
P(s\,\text{und}\; r)&=& \dfrac{7}{12}\cdot \dfrac{5}{11}+\dfrac{5}{12}\cdot \dfrac{7}{11}&\quad \scriptsize \\[5pt]
&=& 0,53 \\[5pt]
P(s\,\text{und}\; r) &=& \underline{\underline{ 53\,\%}}
\end{array}\)](https://mathjax.schullv.de/c5d238522fb2d0a3917e50fc986a33cebebd72adb46eb3a0ffe733b3fafbcc1b?color=5a5a5a) Erwartungswert berechnen
Erwartungswert berechnen
Der Spieler macht auf Dauer also Verlust.
Behauptung prüfen
Der Gewinn von „zweimal Karo“ wird von 10€ auf 20€ erhöht.
Die Behauptung des Betreibers ist nicht richtig. Er macht weiterhin Gewinn aber weniger als zuvor.

| Ergebnisse | Gewinn | Wahrscheinlichkeit |
|---|---|---|
| zweimal Karo | ||
| zweimal Herz | ||
| sonstige | kein Gewinn |
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Abschlussprüfung 2015