Geometrie in der Ebene
Aufgabe 1
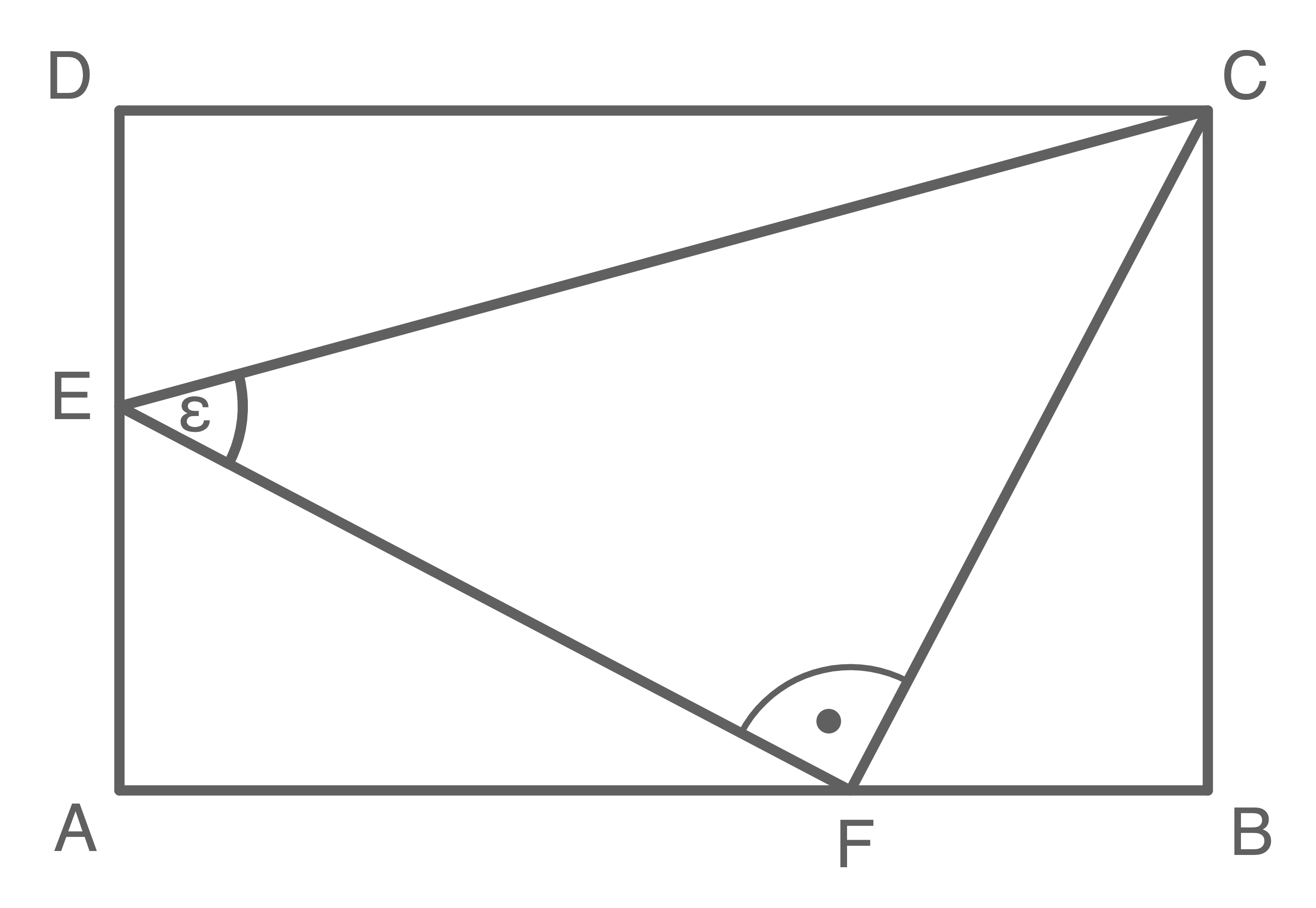
Im Rechteck  gilt:
gilt:
![\(\begin{array}[t]{rll}
\overline{BC} & = &4,6 \mathrm{~cm} \\
\overline{CE} & =& 7,2 \mathrm{~cm} \\
\varepsilon & =& 49,0^{\circ}
\end{array}\)](https://mathjax.schullv.de/3117c39c12d17a41236bdfaa89a700748e37b30da614a999fbea6e61dfeae9ff?color=5a5a5a) Berechne den Umfang des Vierecks
Berechne den Umfang des Vierecks 
(4 P)
Abschlussprüfung 2024
Aufgabe 2
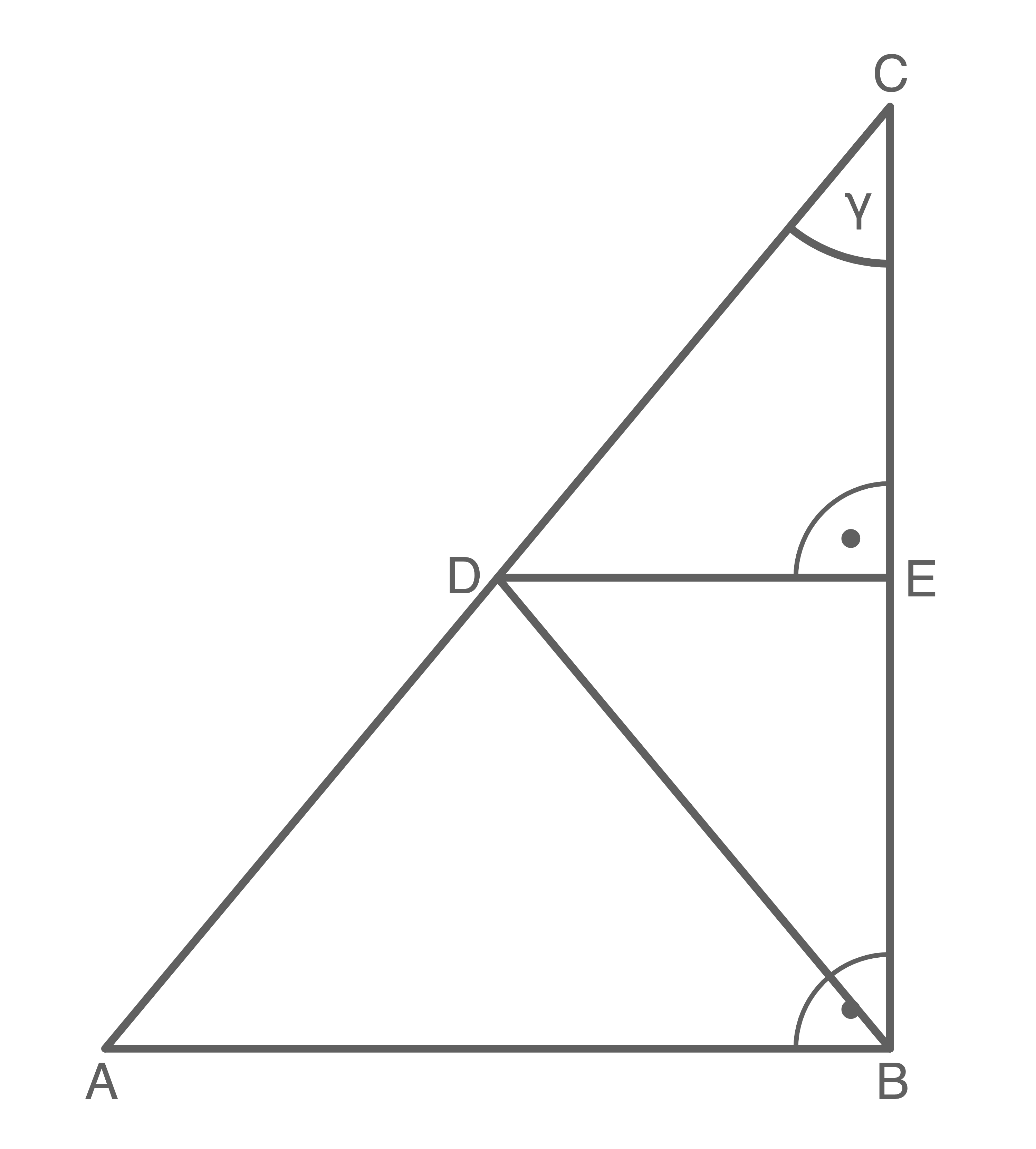
Im rechtwinkligen Dreieck  liegen die beiden gleichschenkligen Dreiecke
liegen die beiden gleichschenkligen Dreiecke  und
und  Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{CD}&=&6,3\,\text{cm}\\
\gamma&=&41,8^{\circ}\\
\overline{AD}&=&\overline{BD}\\
\overline{BD}&=&\overline{CD}
\end{array}\)](https://mathjax.schullv.de/6383417e44b53f6c3d06d255e589378e2cecd17cb9cfecc281b59a30d301ba8a?color=5a5a5a)
- Berechne den Umfang des Dreiecks
- Berechne den Flächeninhalt des Dreiecks
(3,5 P)
Aufgabe 3
Im rechtwinkligen Dreieck  gilt:
gilt:

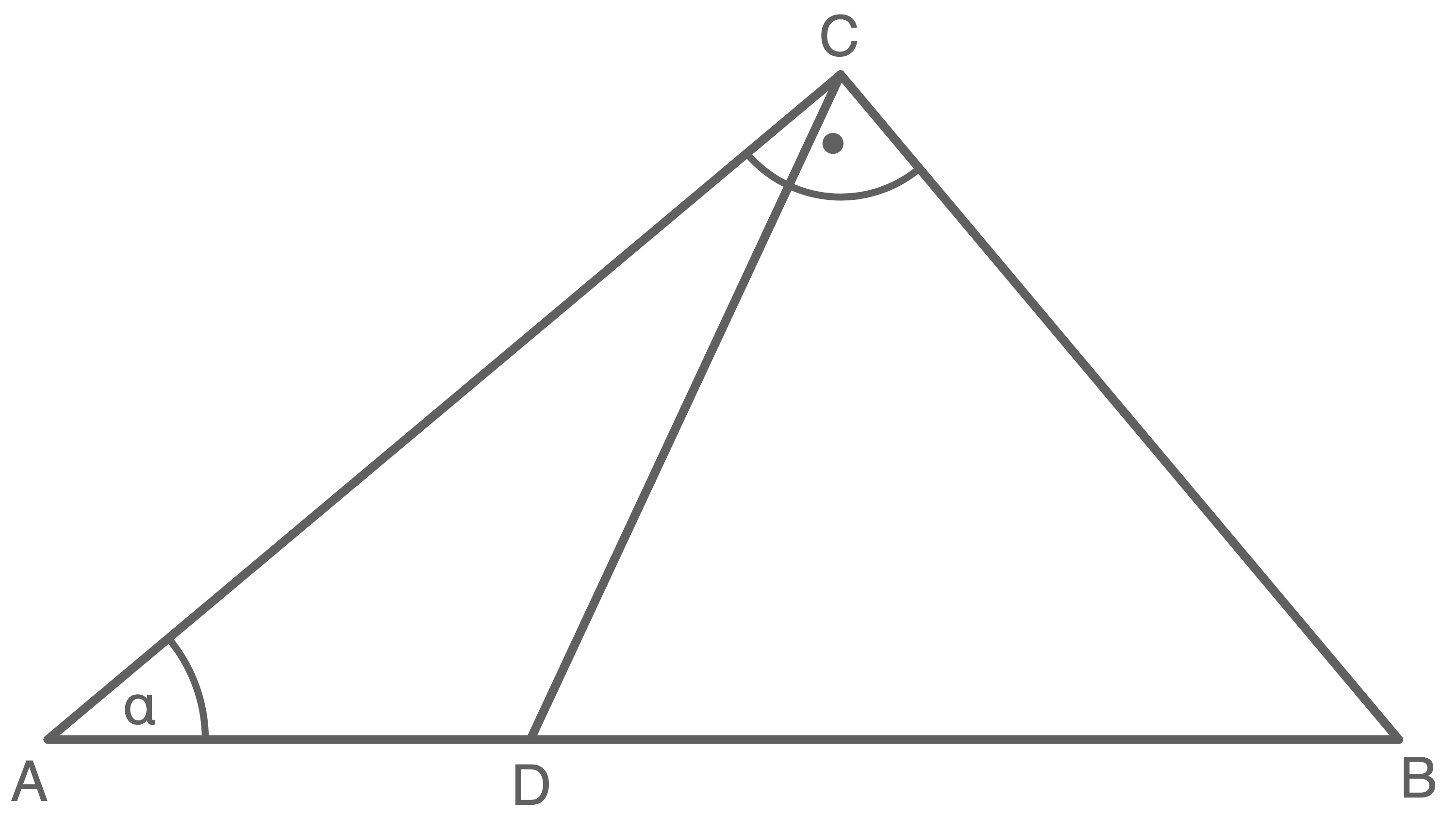 Berechne den Umfang des Dreiecks
Berechne den Umfang des Dreiecks 

(4 P)
Aufgabe 4
Das gleichschenklige Dreieck  und das Quadrat
und das Quadrat  überdecken sich teilweise.
überdecken sich teilweise.
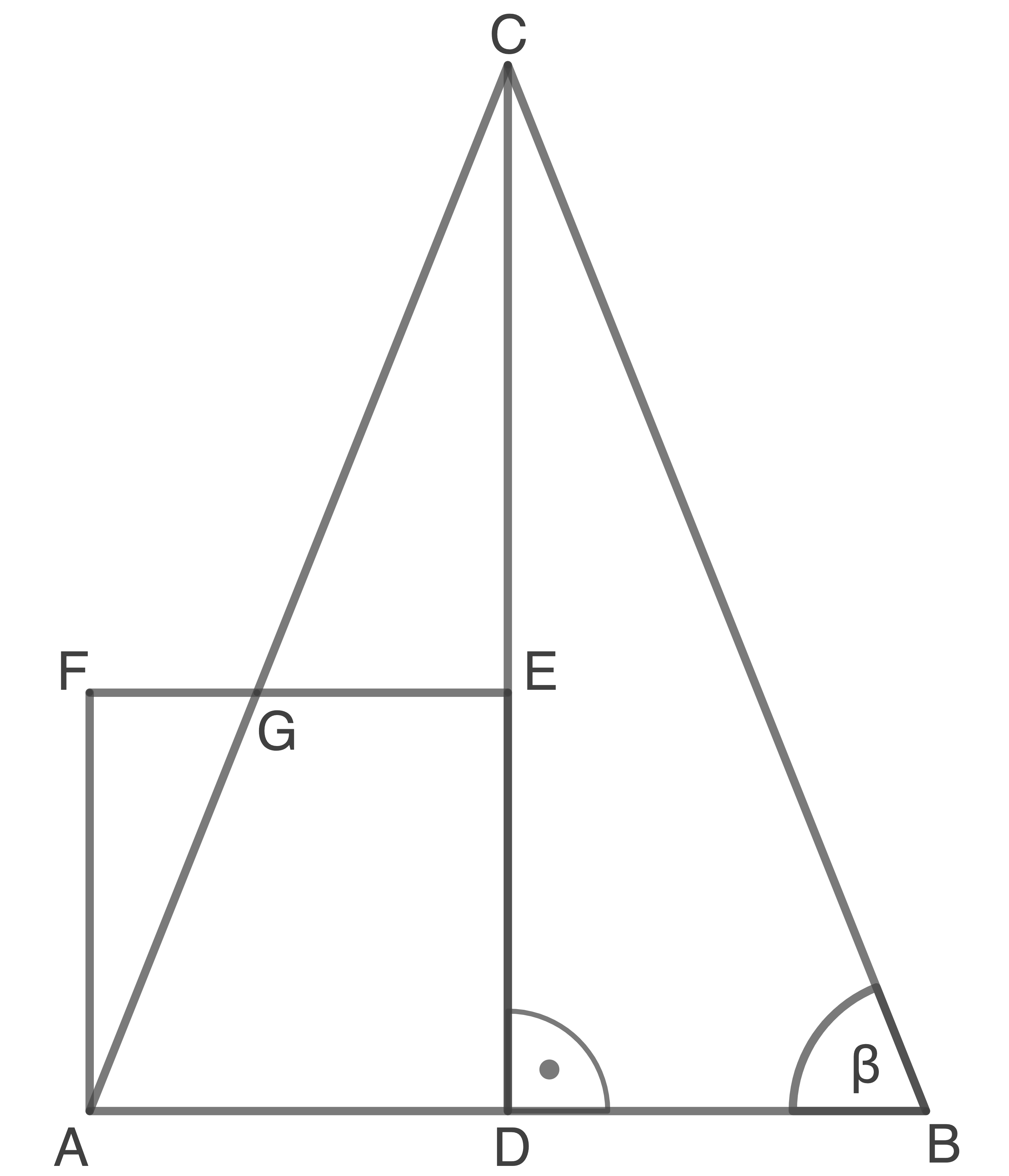 Es gilt:
Es gilt:


 Berechne den Umfang des Dreiecks
Berechne den Umfang des Dreiecks 

(3,5 P)
Aufgabe 5
Die Figur besteht aus den Dreiecken  und
und 
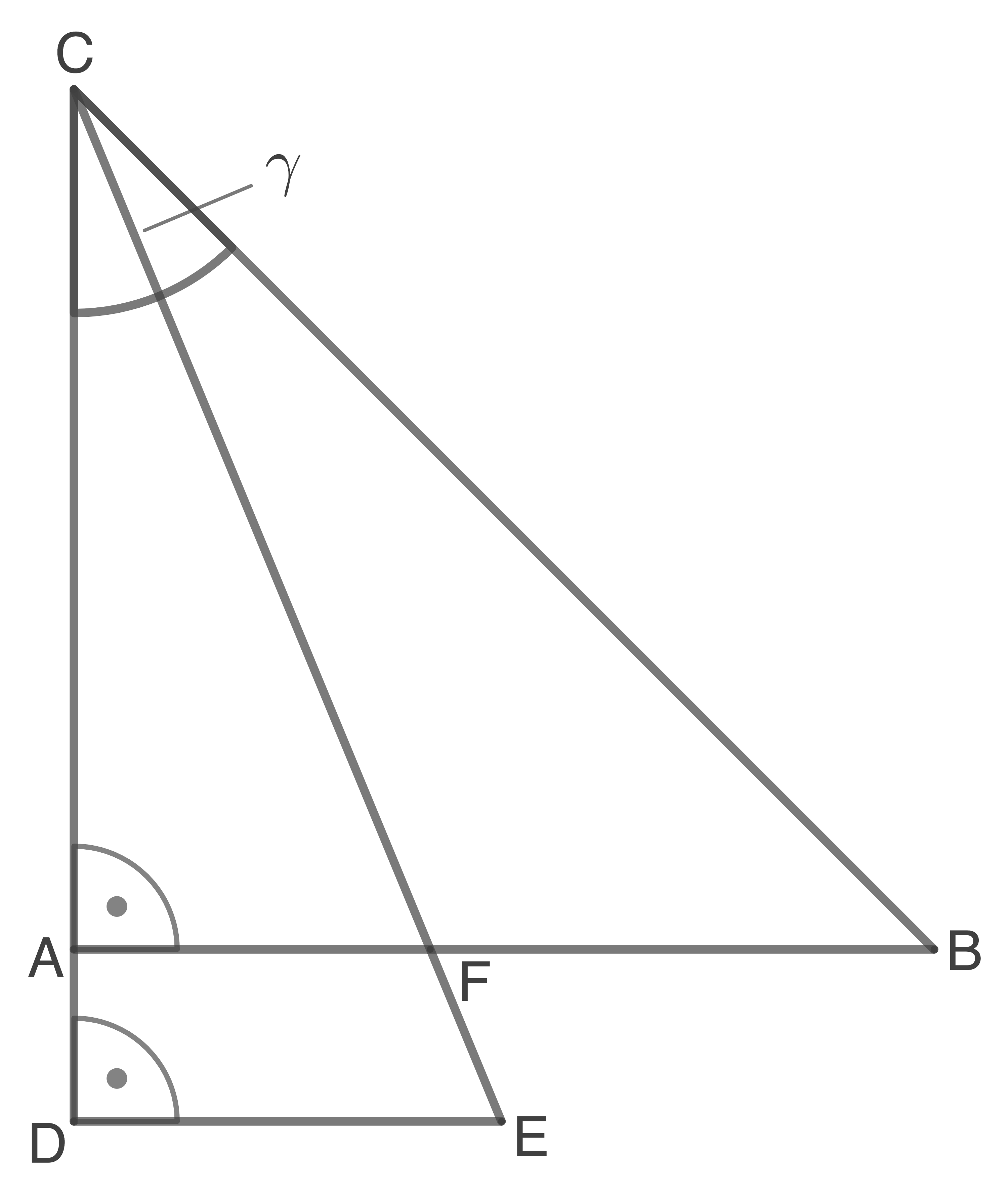 (Skizze nicht maßstäblich)
Davon sind gegeben:
(Skizze nicht maßstäblich)
Davon sind gegeben:



 ist die Winkelhalbierende von
ist die Winkelhalbierende von  Berechne die Streckenlänge
Berechne die Streckenlänge 
 (Skizze nicht maßstäblich)
(Skizze nicht maßstäblich)
(4 P)
Aufgabe 6
Im Viereck  gilt:
gilt:
 und den Flächeninhalt des Dreiecks
und den Flächeninhalt des Dreiecks 
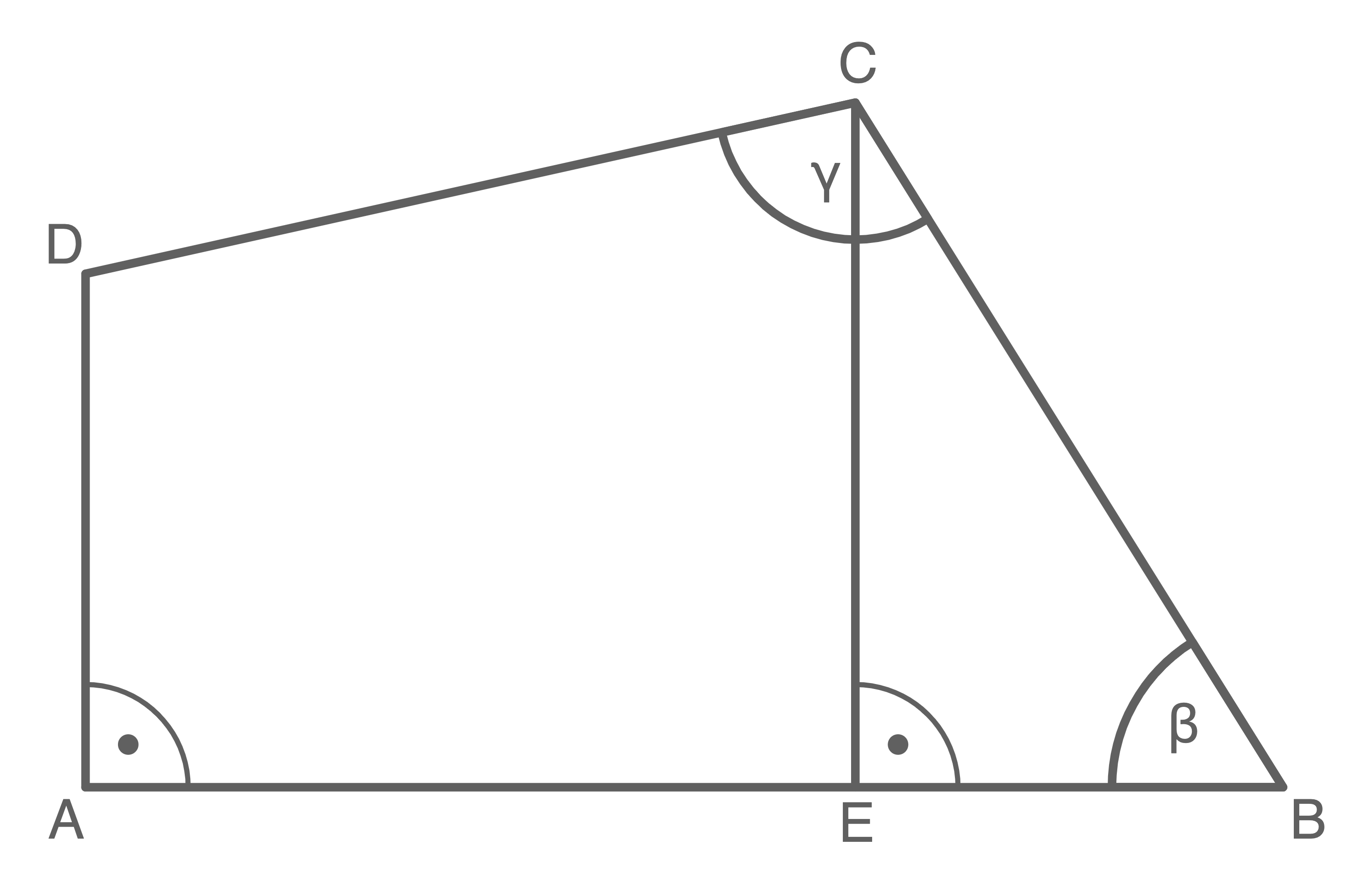
Musterprüfung 2

(Skizze nicht maßstäblich)
(4 P)
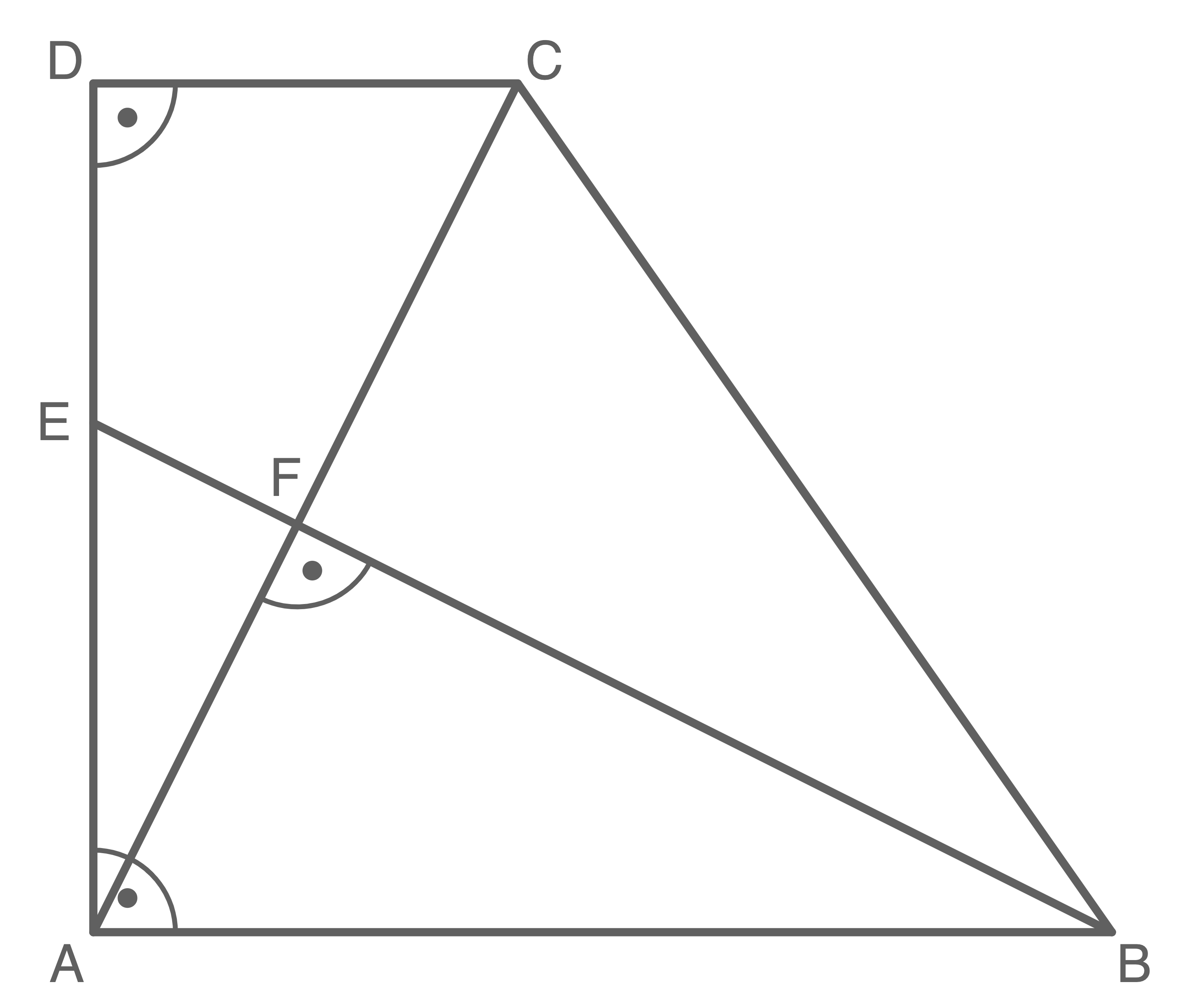
Aufgabe 7
lm Quadrat  Iiegt der Streckenzug
Iiegt der Streckenzug 
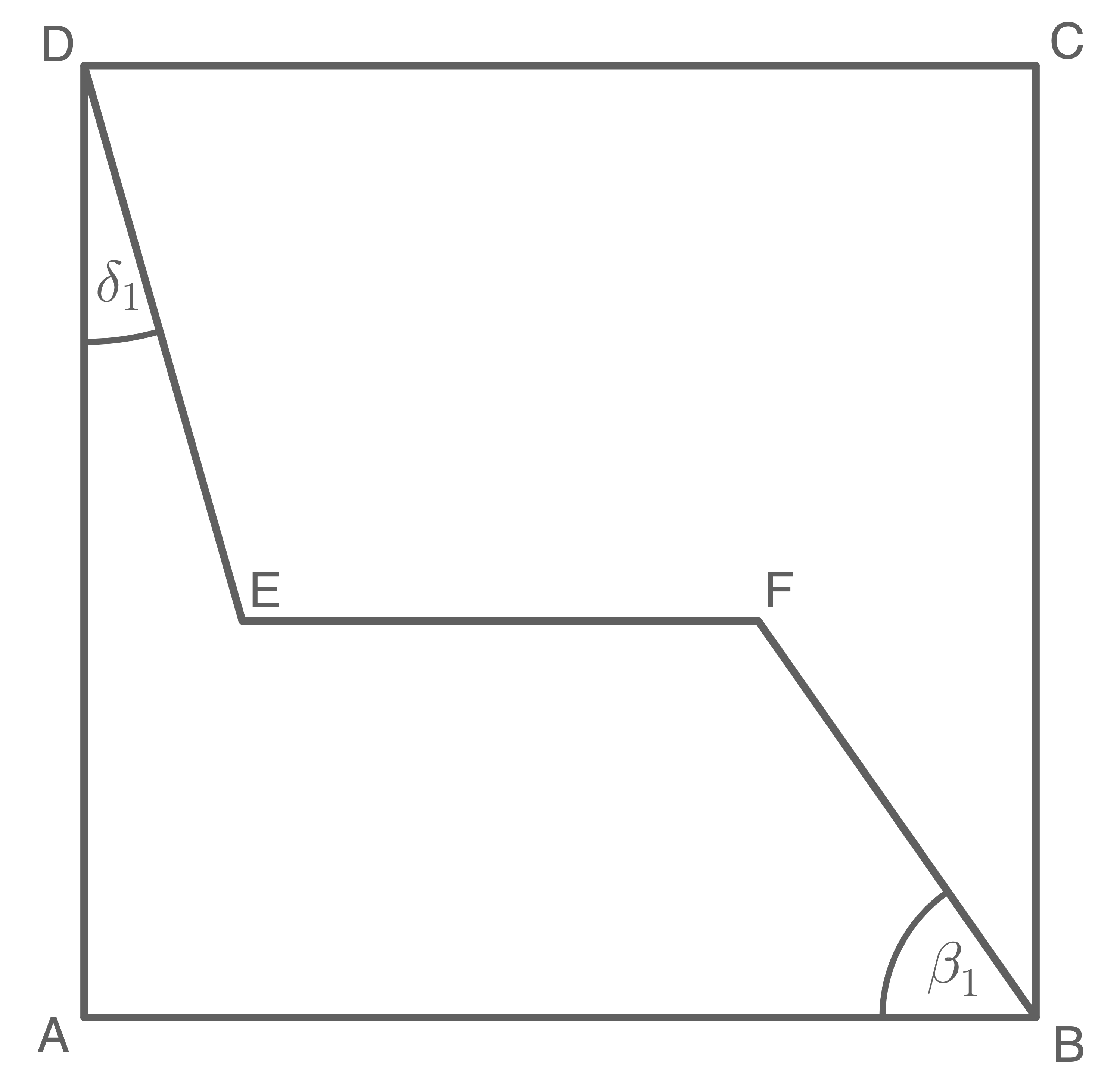 Es gilt:
Es gilt:




 verläuft parallel zu
verläuft parallel zu  Berechne den Winkel
Berechne den Winkel 

(4 P)
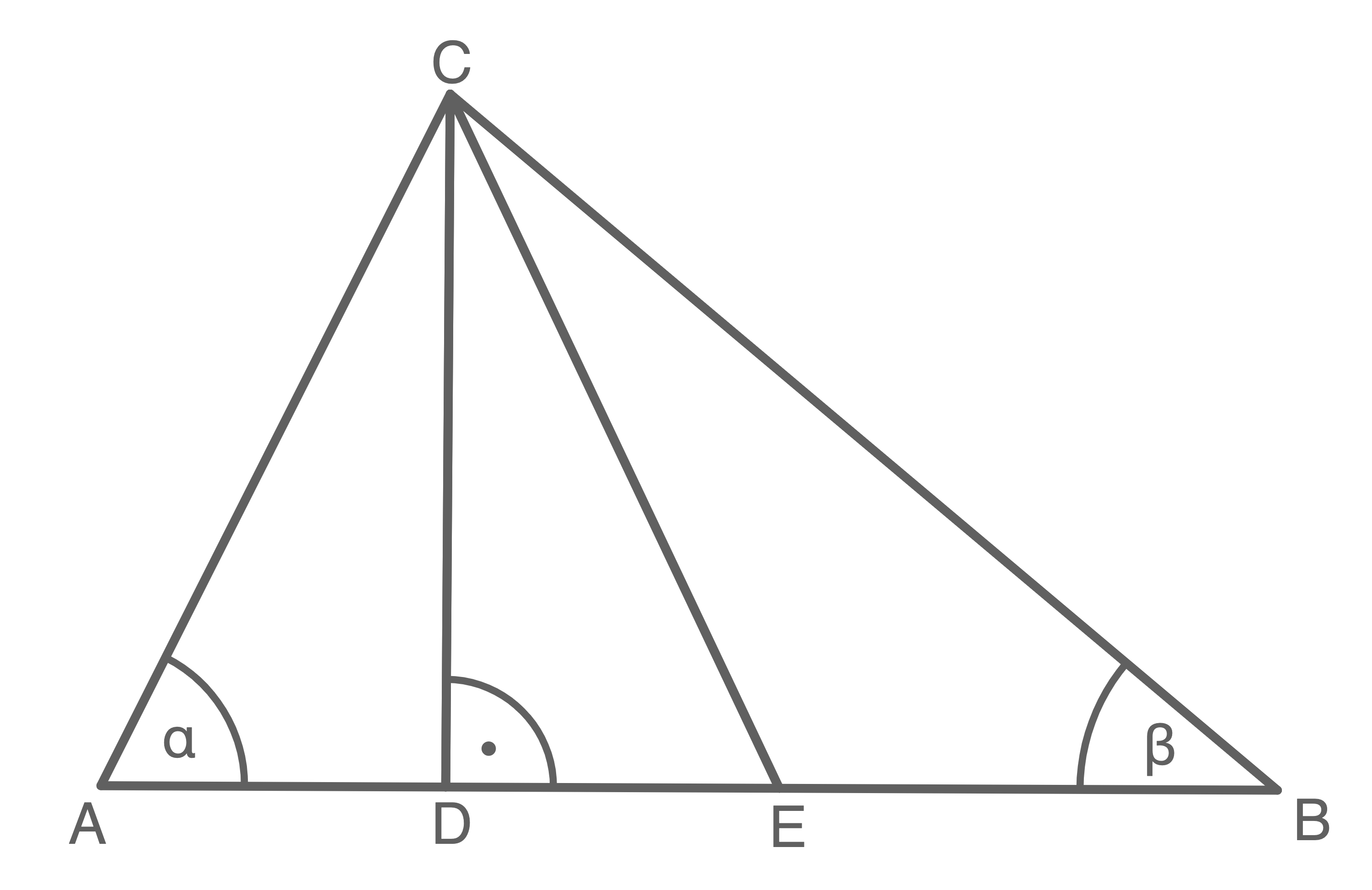
Aufgabe 8
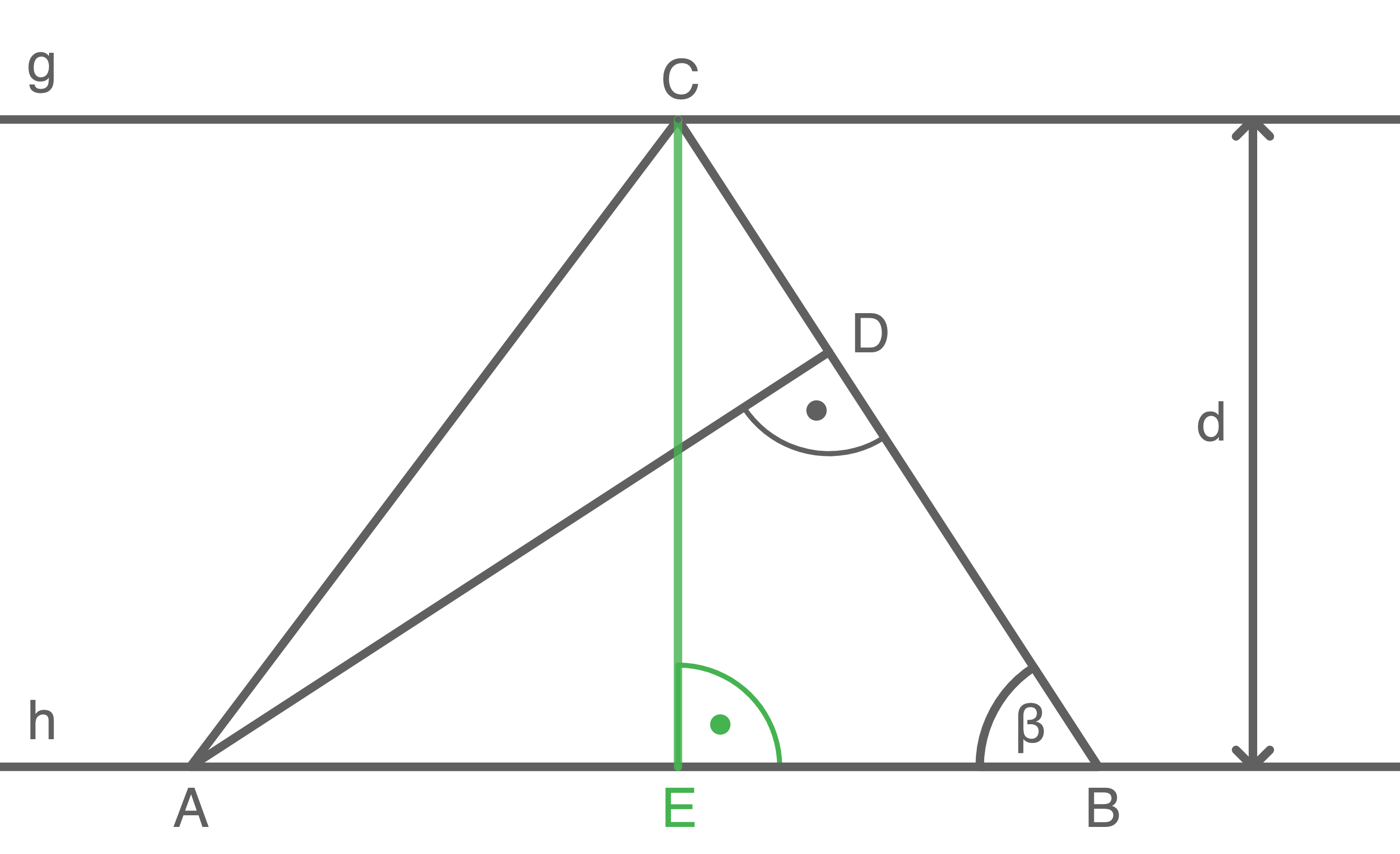
Die Eckpunkte des Dreiecks  liegen auf den Parallelen
liegen auf den Parallelen  und
und 
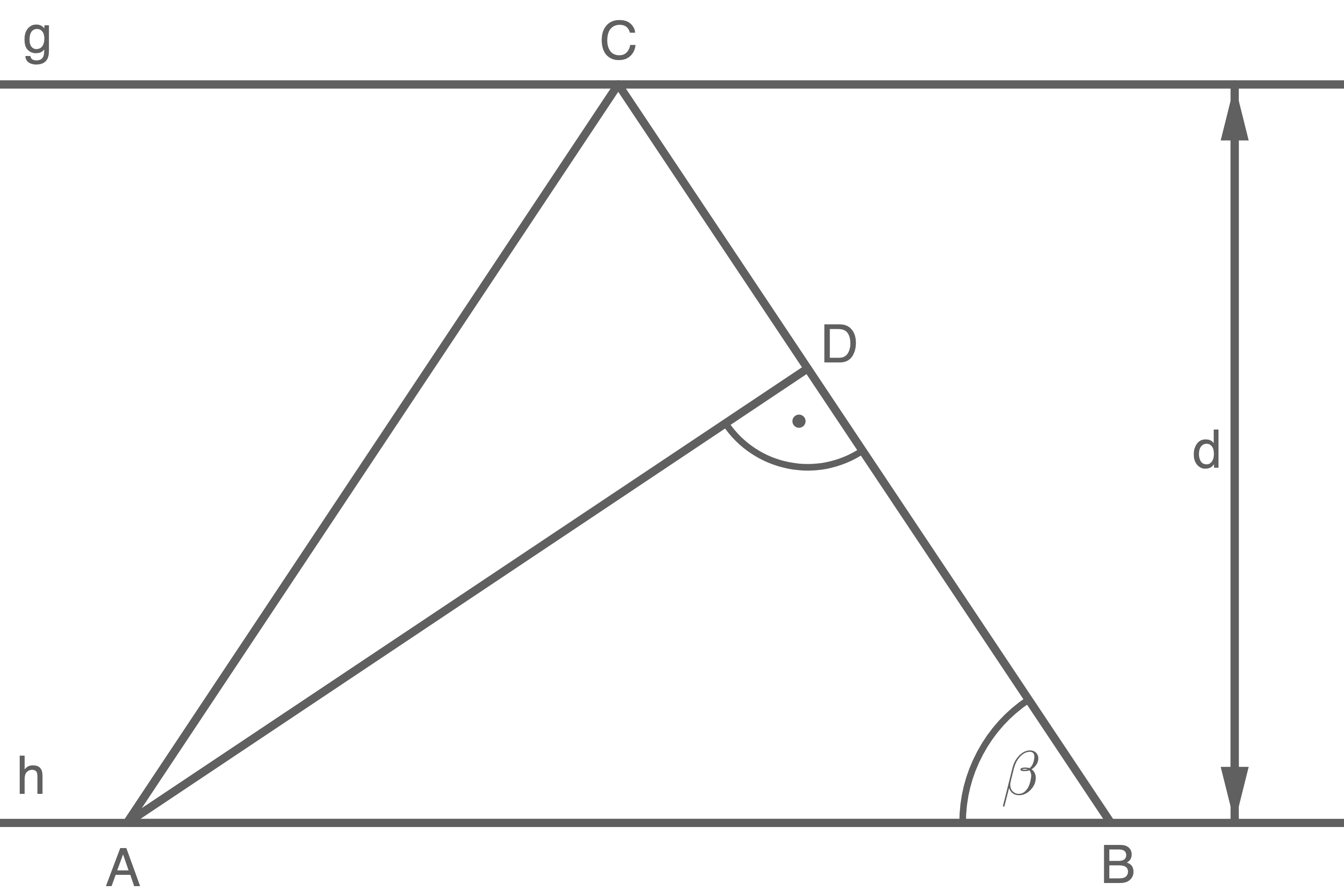 Es gilt:
Es gilt:


 Berechne den Umfang des Dreiecks
Berechne den Umfang des Dreiecks 

(4,5 P)
Aufgabe 9
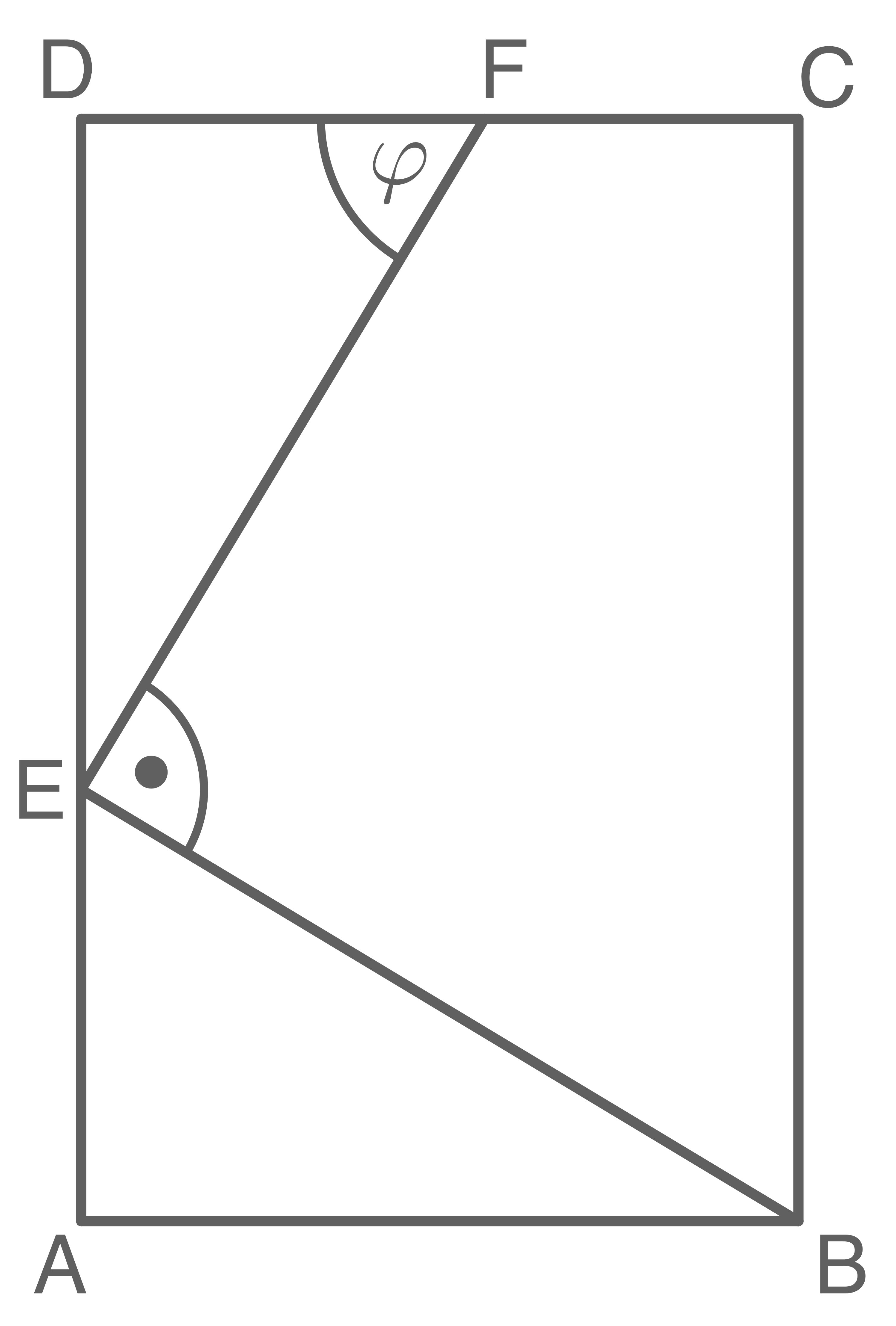
(4,5 P)
Aufgabe 10
Das Dreieck  und das Rechteck
und das Rechteck  überdecken sich teilweise.
überdecken sich teilweise.
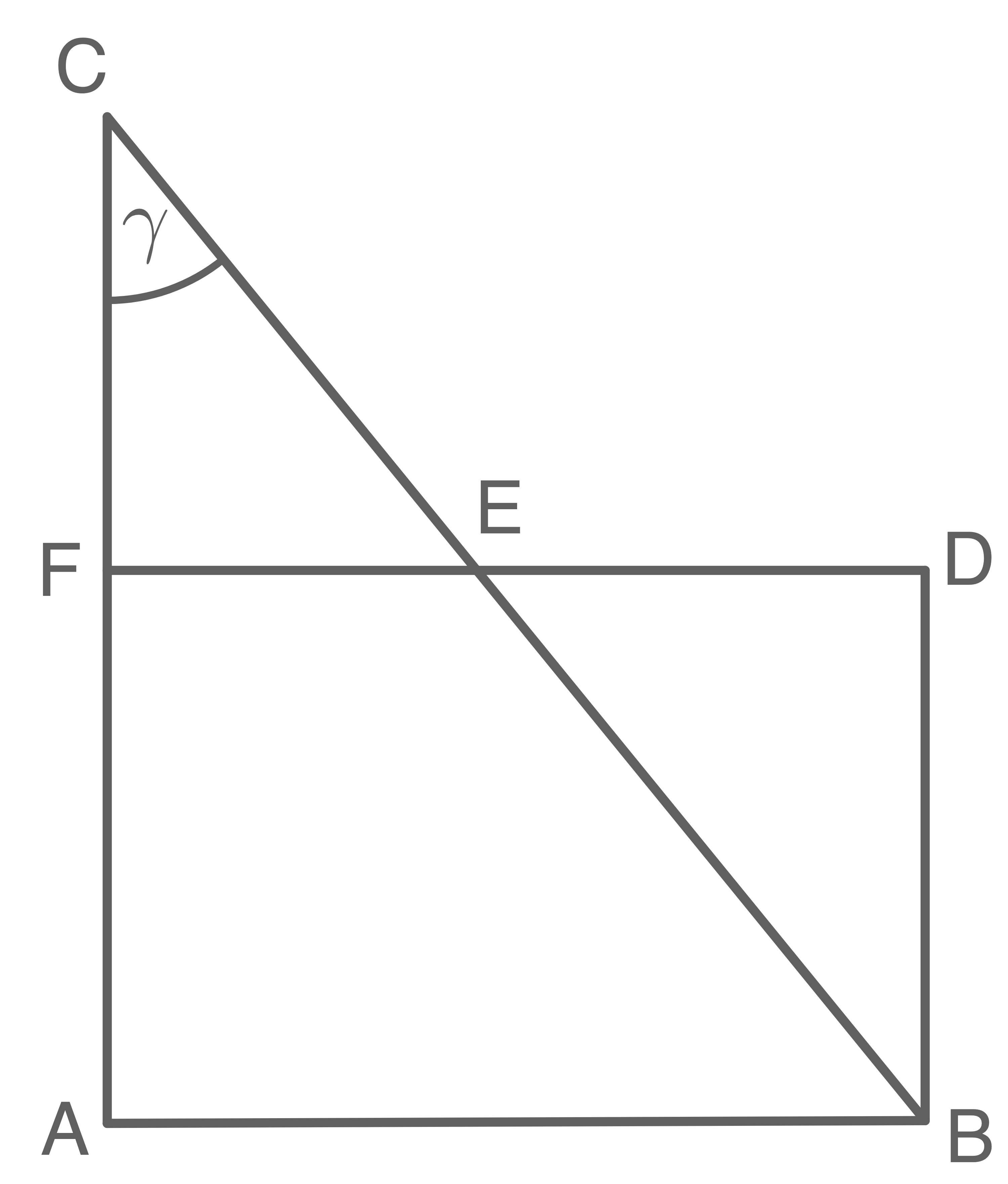 Es gilt:
Es gilt:


(4 P)
Aufgabe 11
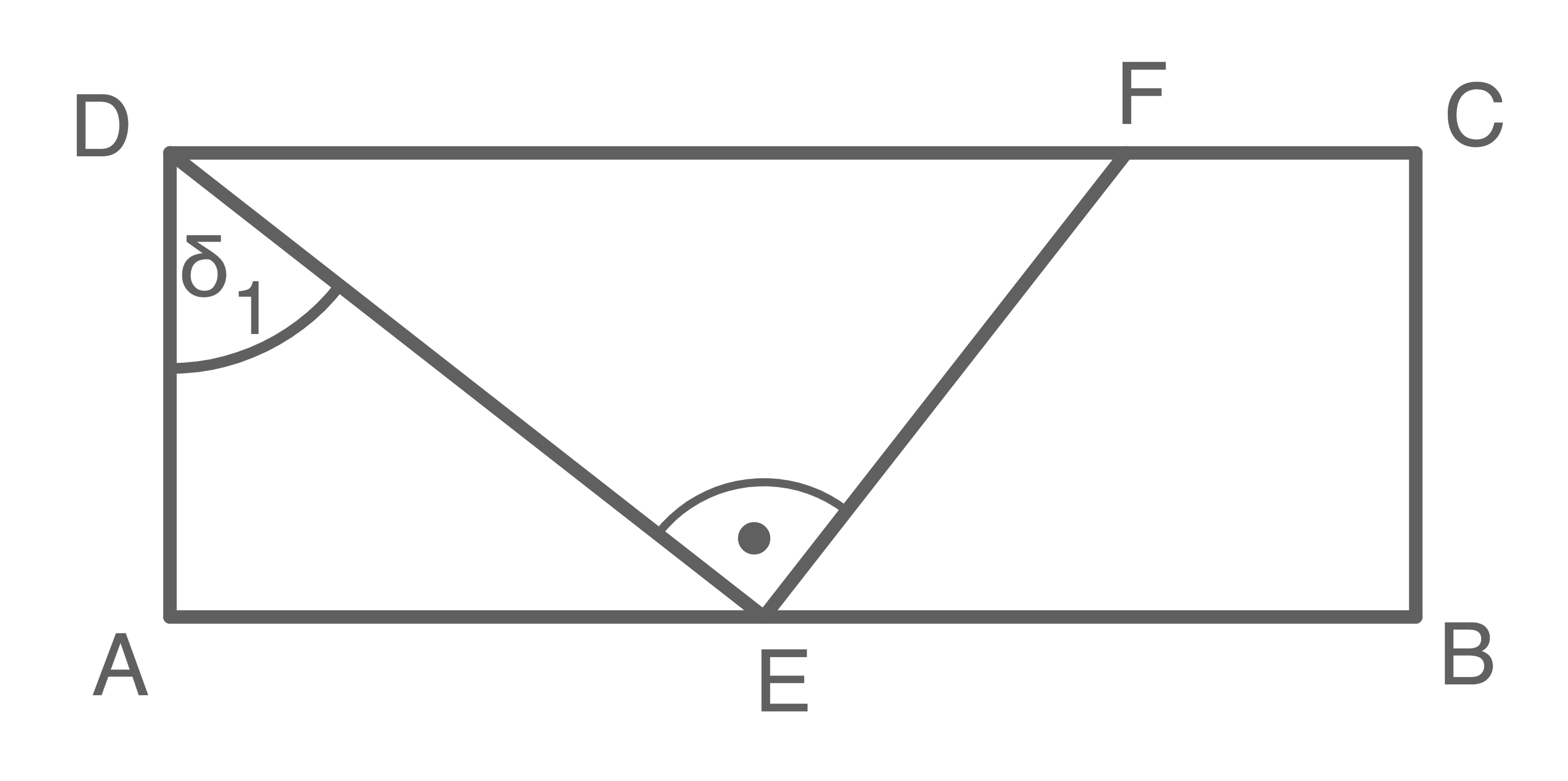
(4 P)
Aufgabe 12
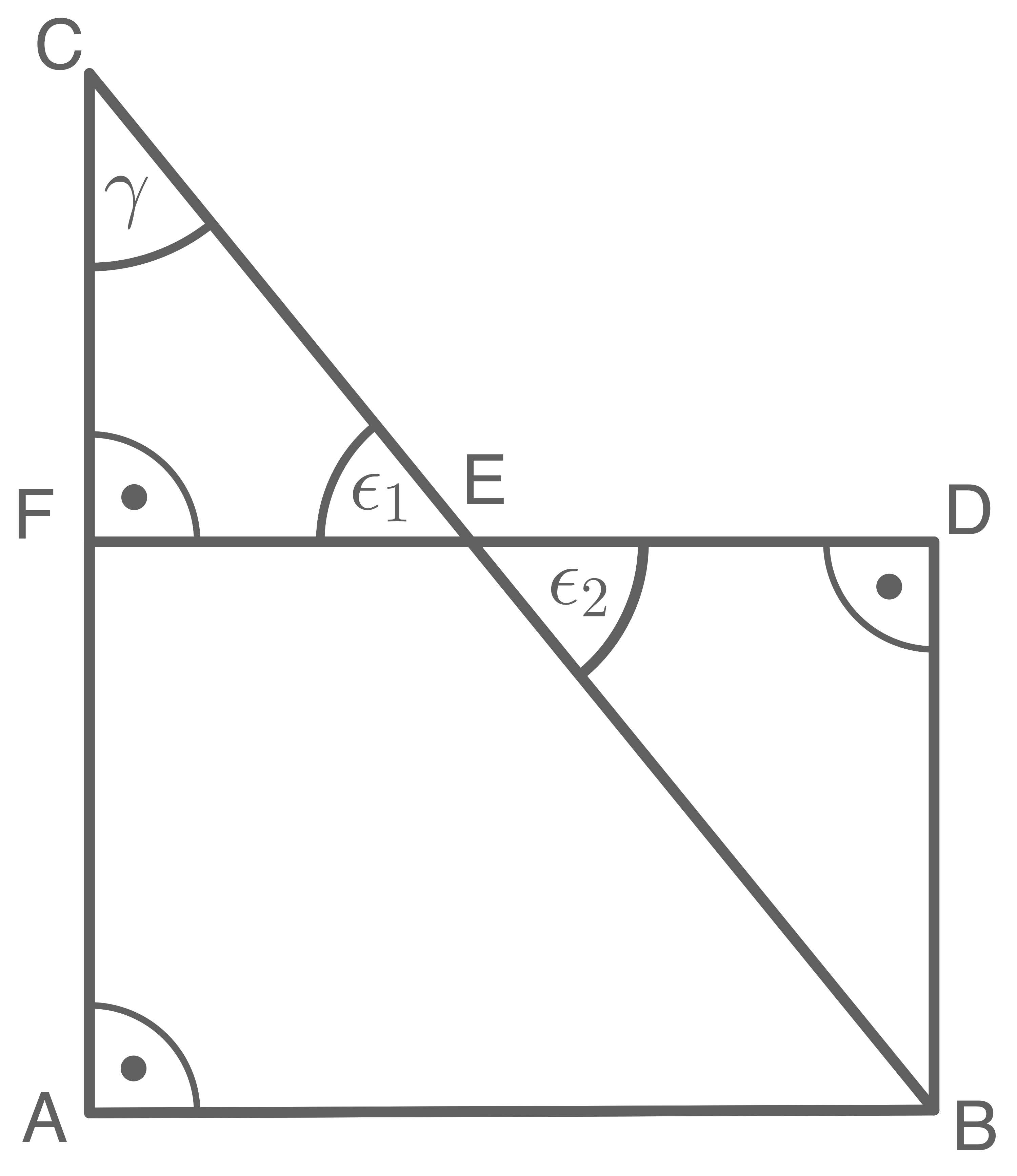
Gegeben sind das gleichschenklige Dreieck  und das rechtwinklige Dreieck
und das rechtwinklige Dreieck 
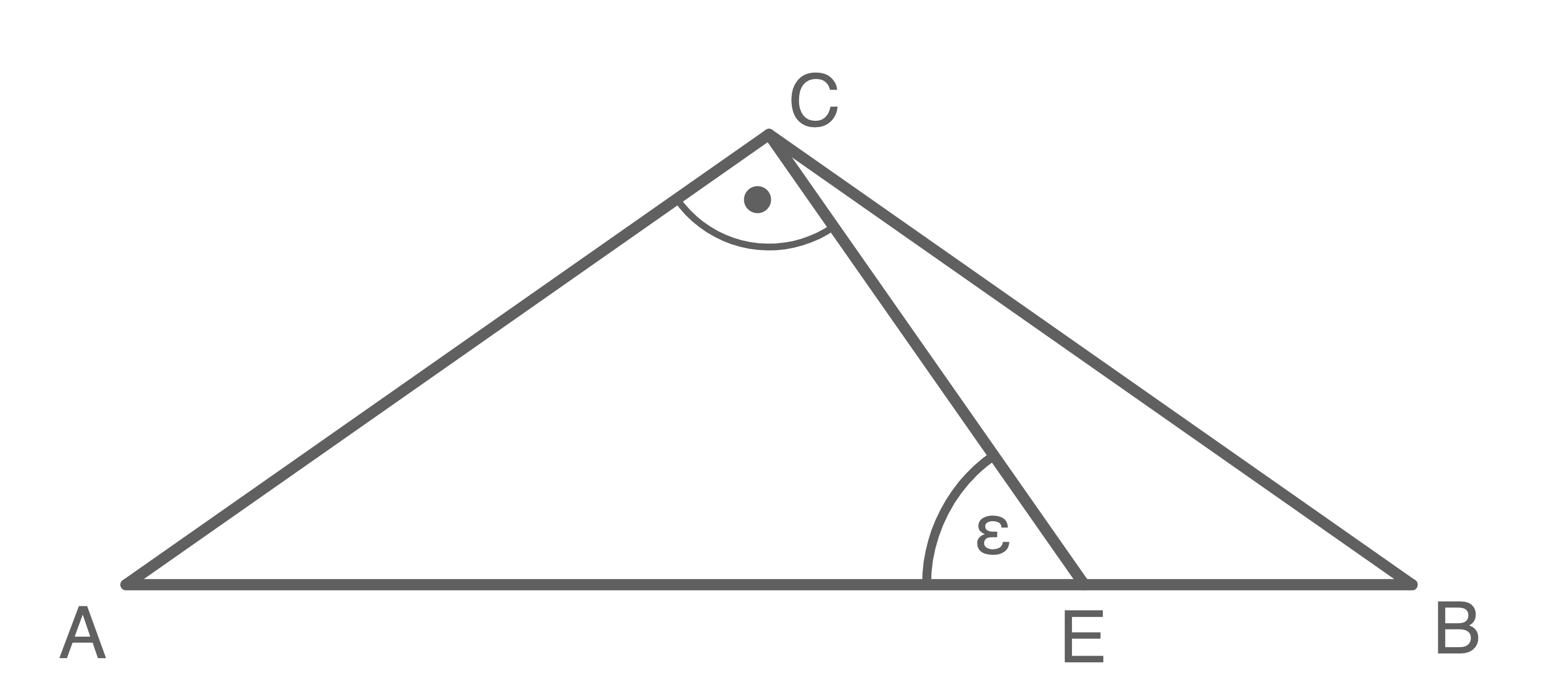
Es gilt:

Es gilt:
(4 P)
Aufgabe 13
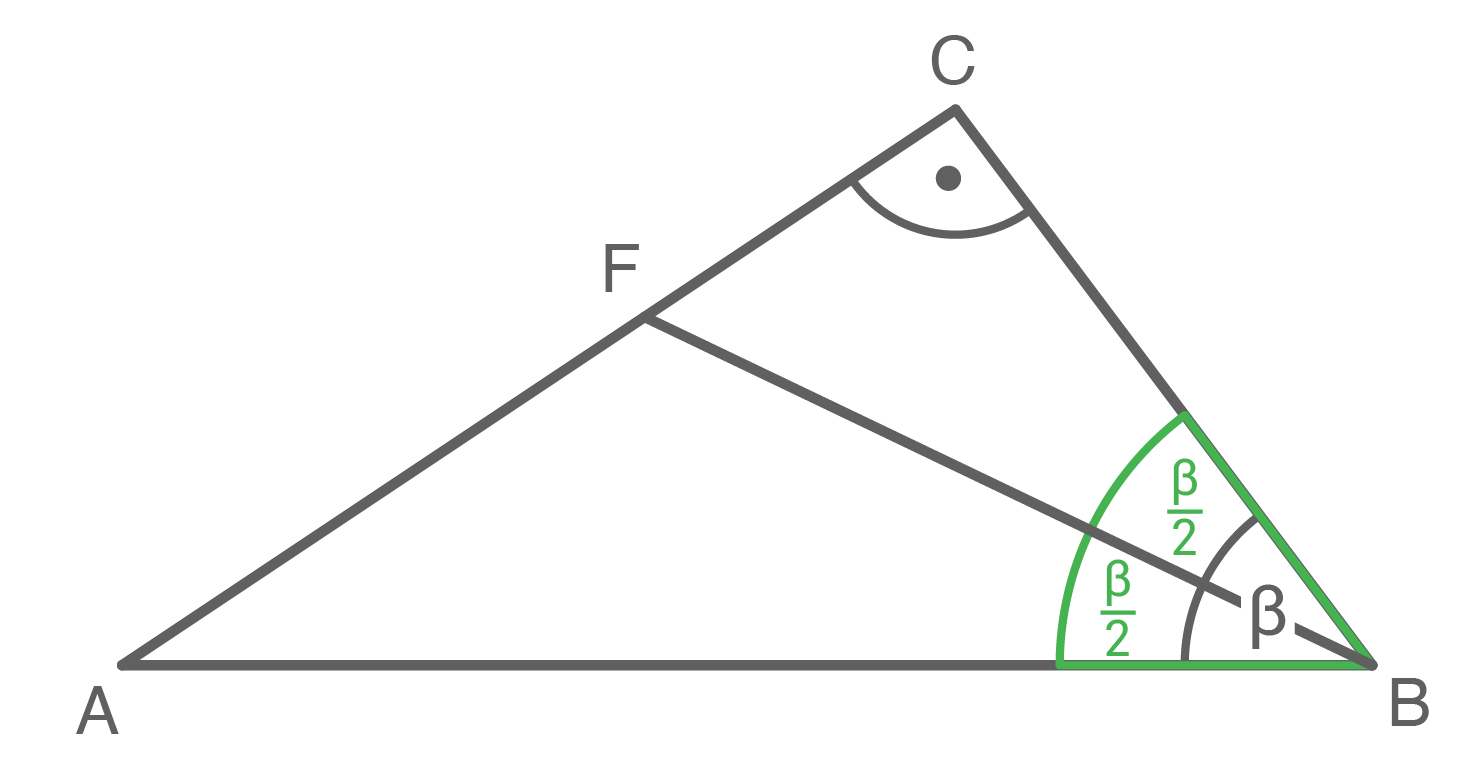
Gegeben ist das rechtwinklige Dreieck  .
.
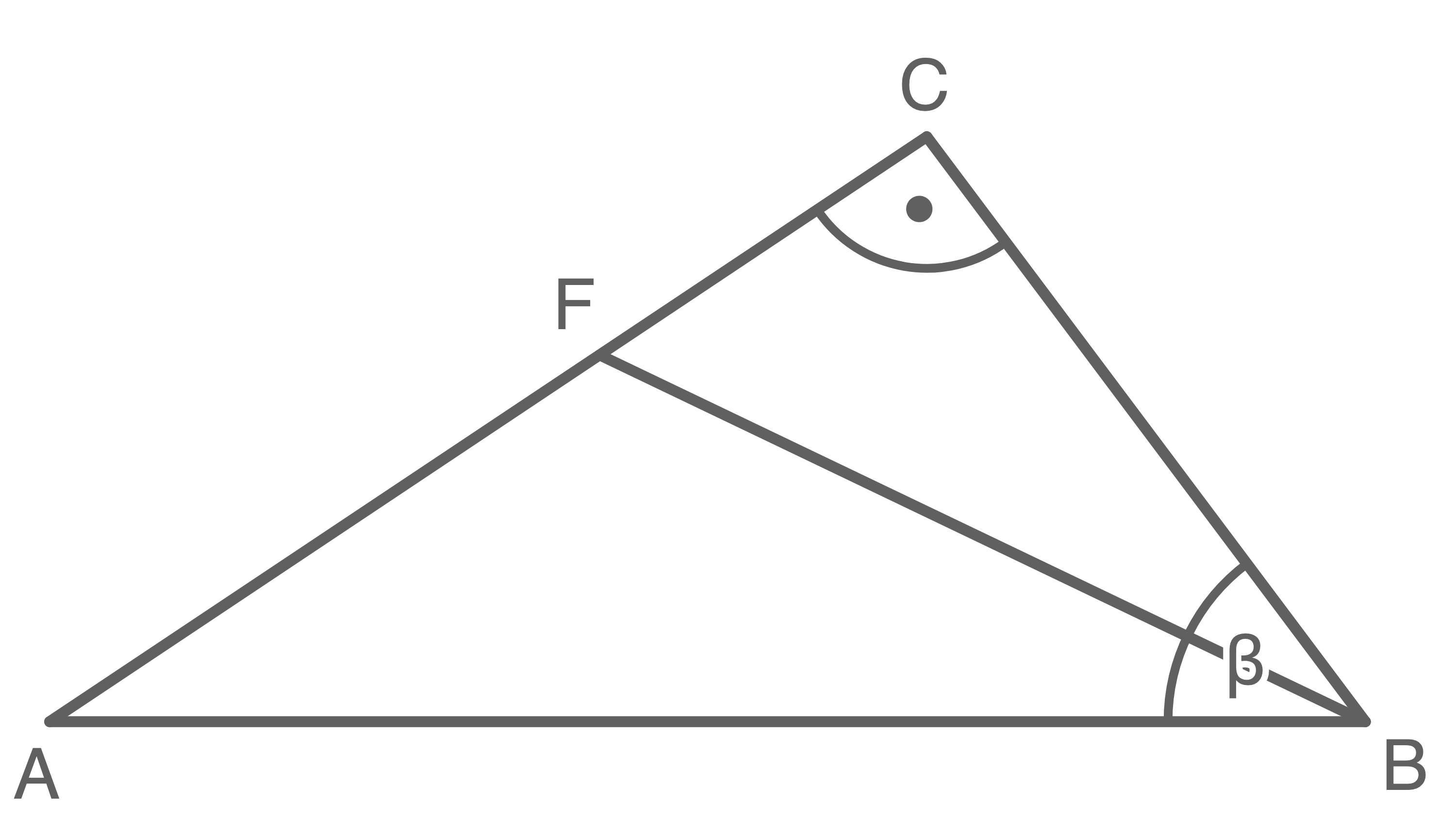 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BC}&=&5,8 \text{ cm} \\[5pt]
\overline{BF}&=&6,6 \text{ cm}
\end{array}\)](https://mathjax.schullv.de/181e185025f6306743357400f5c9ad44494d31bfd247bc58baadfd6e57a2051e?color=5a5a5a)
 halbiert den Winkel
halbiert den Winkel  .
Berechne den Umfang des Dreiecks
.
Berechne den Umfang des Dreiecks  .
.

(4 P)
Aufgabe 14
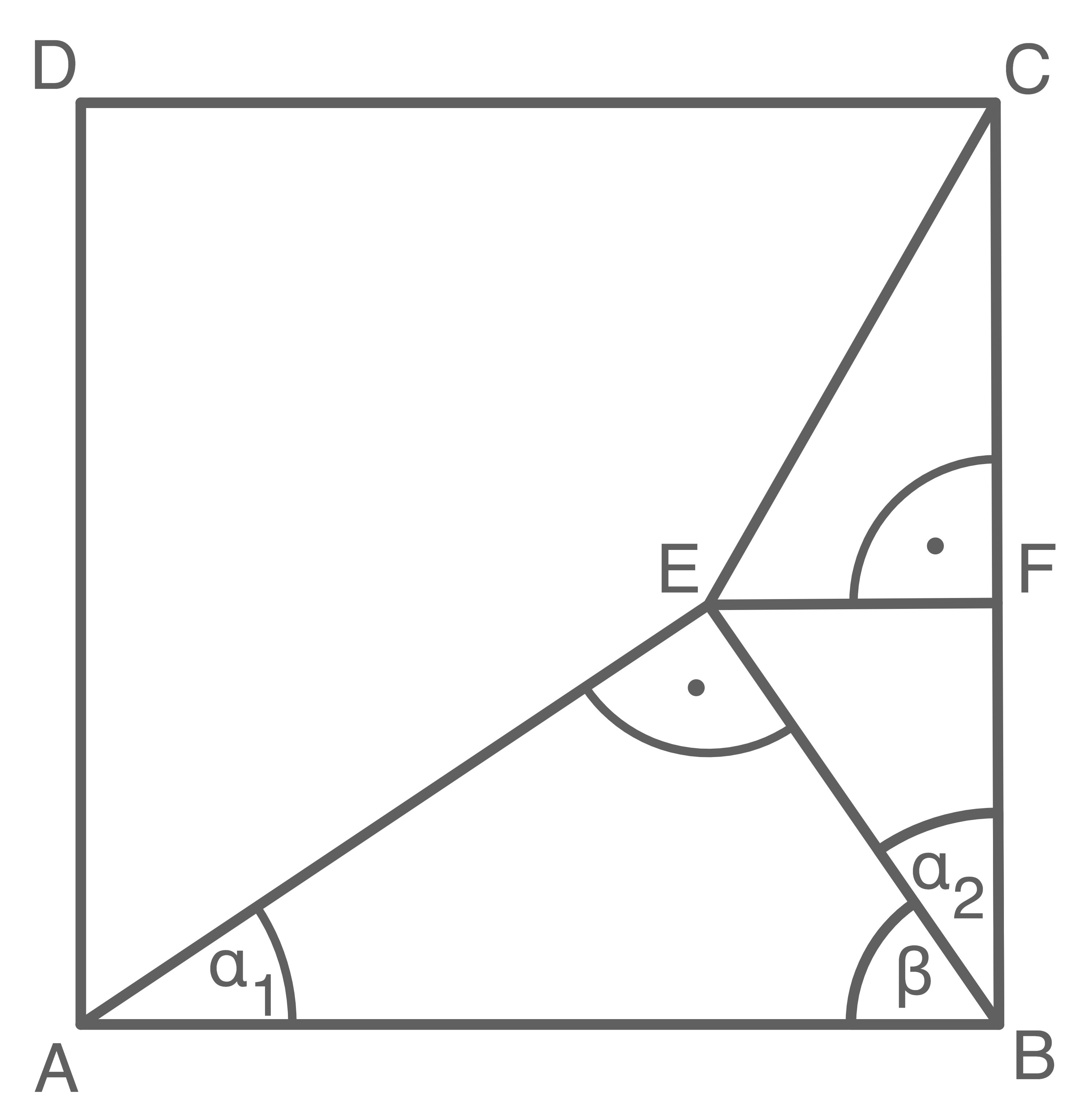
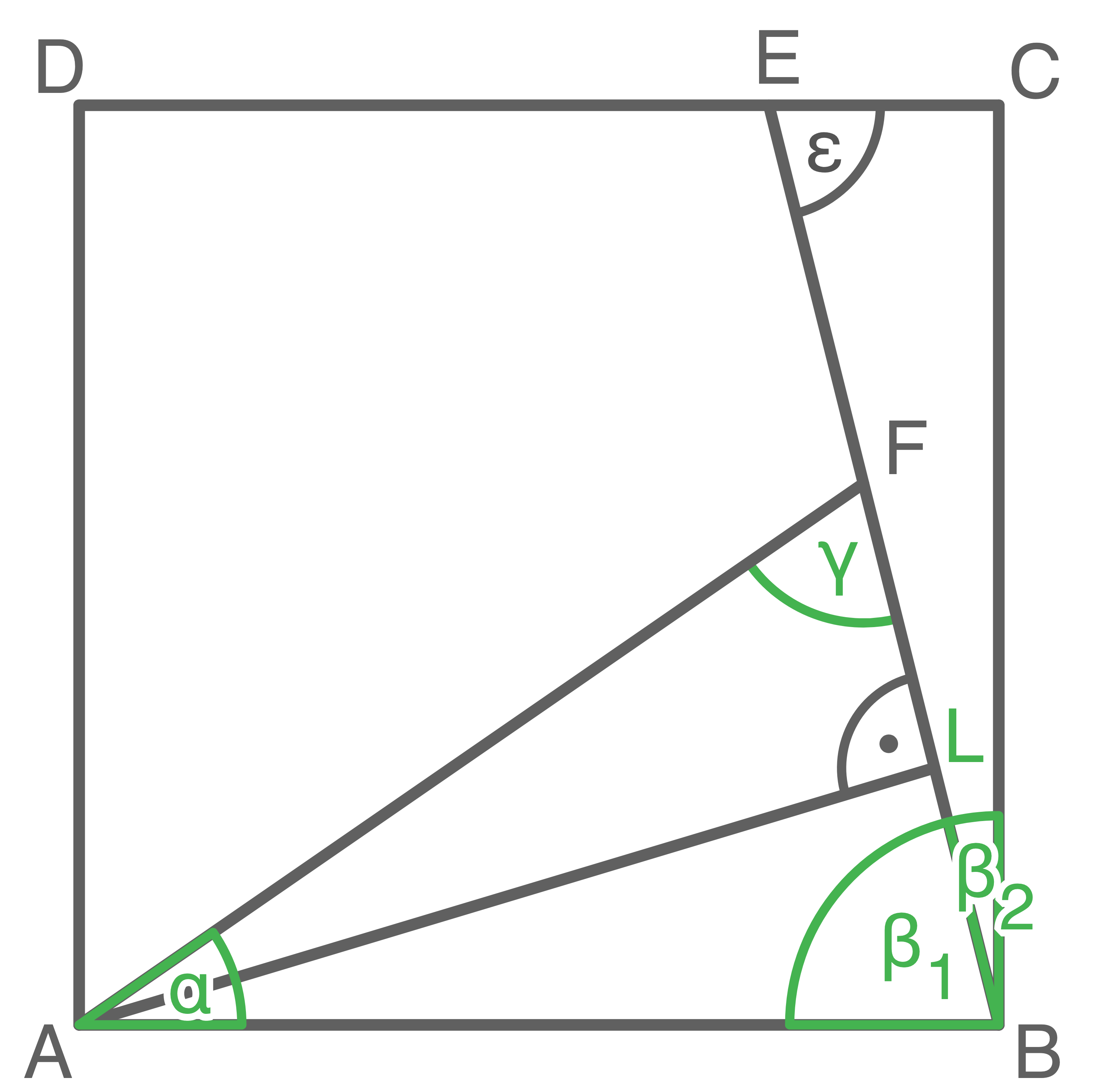
Im Quadrat  liegen das rechtwinklige Dreieck
liegen das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck  .
.
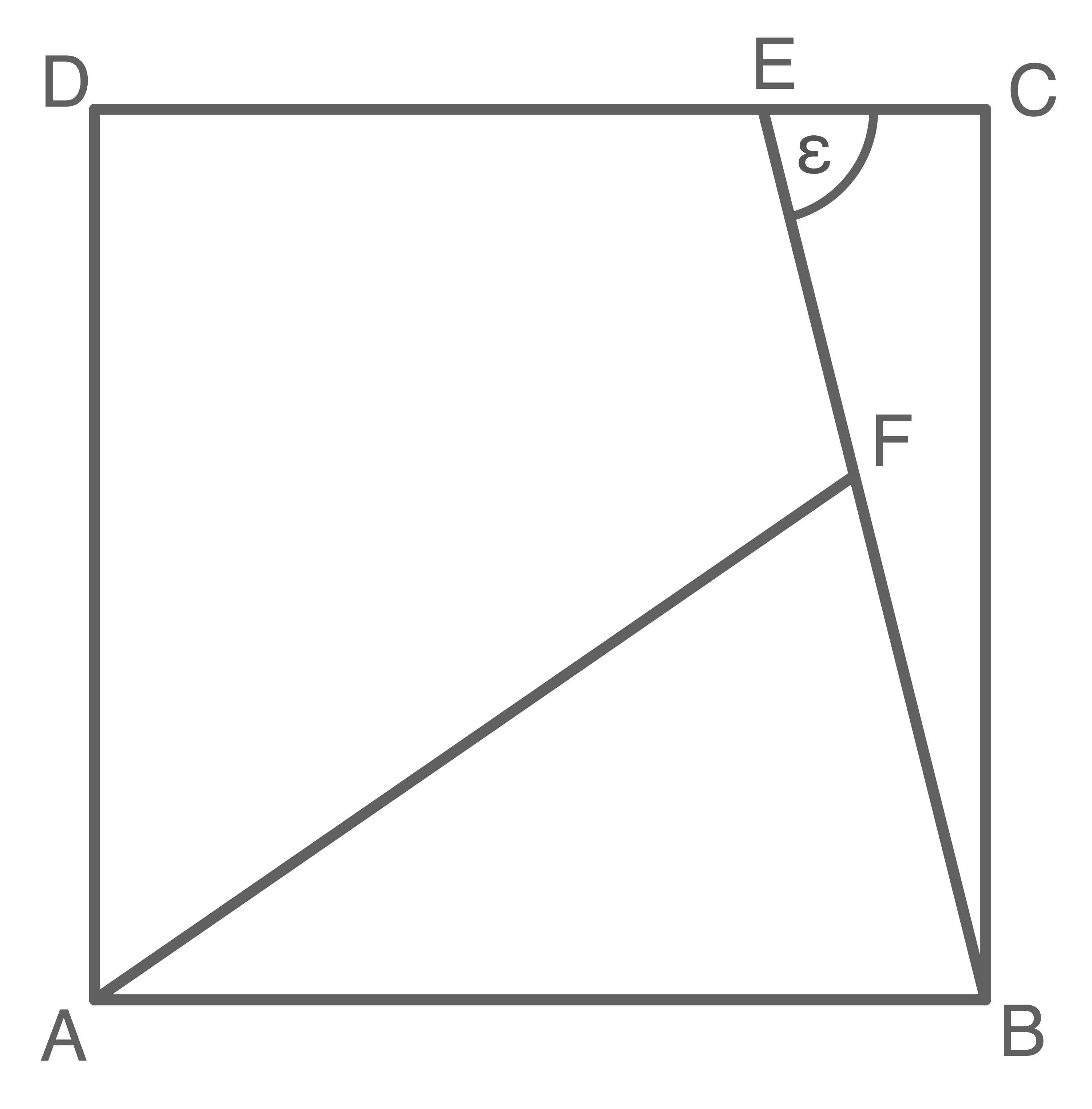 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BC}&=&11,8 \text{ cm} \\[5pt]
\epsilon&=&72,0^{\circ} \\[5pt]
\overline{AB}&=&\overline{AF}
\end{array}\)](https://mathjax.schullv.de/4fee4a09ce7bf03f388ad365b61442726761f45896f07460de56b68168b9c091?color=5a5a5a) Berechne die Länge von
Berechne die Länge von  .
.

(4 P)
Aufgabe 15
Gegeben ist das Dreieck  .
.
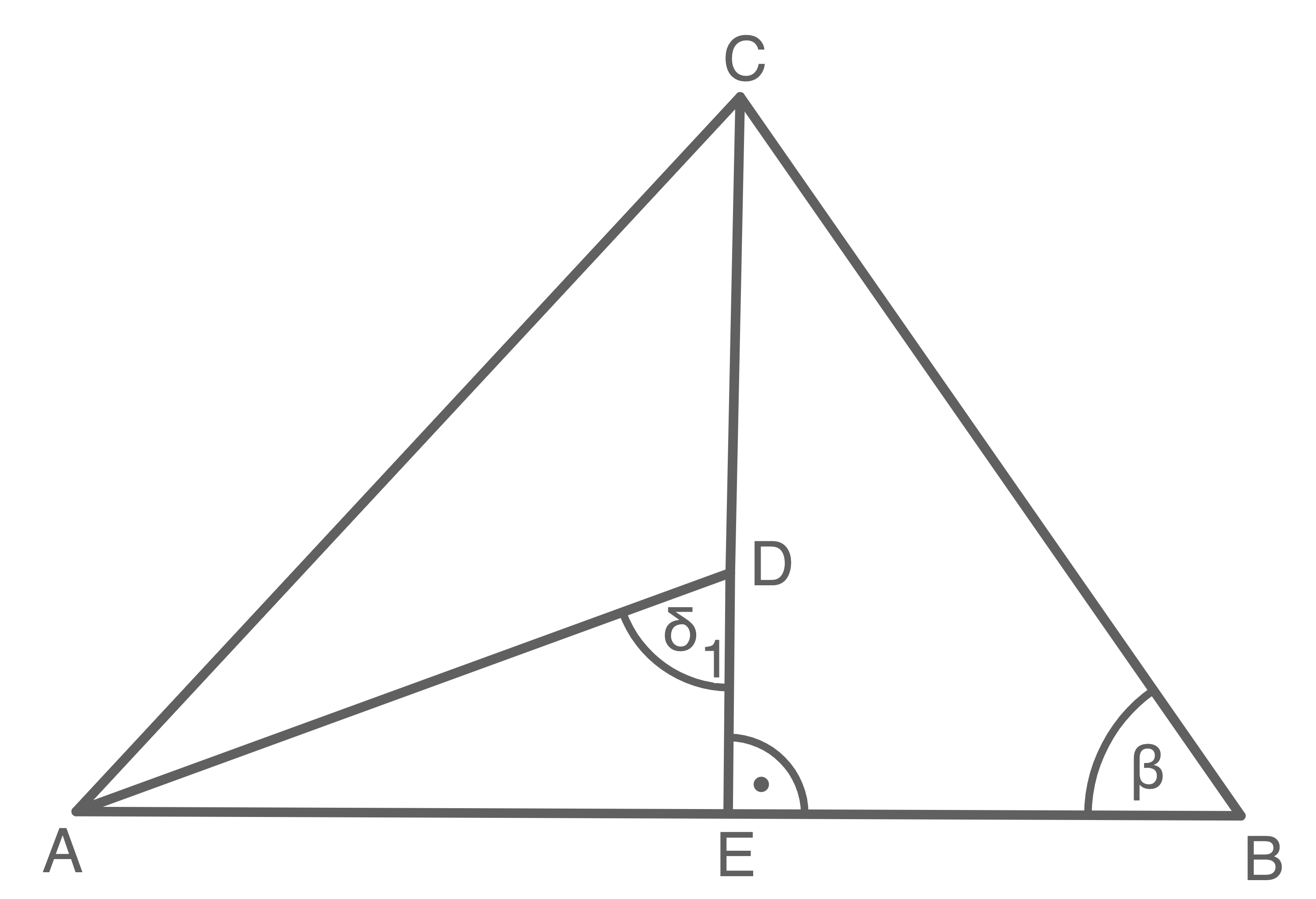 Es gilt:
Es gilt:
![\( \begin{array}[t]{rll}
\overline{BC}&=& 9,0\,\text{cm} \\[5pt]
\overline{AD}&=& 7,3\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/1c547b198142f63ded2730a3f2cde9adb74e4aee8b68a05ef0f3e8708508c607?color=5a5a5a)
![\( \begin{array}[t]{rll}
\beta\hspace{.385cm}&=& 55,0^\circ \\[5pt]
\delta_1\hspace{.385cm}&=& 69,4^\circ
\end{array}\)](https://mathjax.schullv.de/3483a240d077ff877b27eb3f30cb85e103846b60e81ec105280d788fc5000574?color=5a5a5a) Berechne die Länge von
Berechne die Länge von  und den Flächeninhalt des Dreiecks
und den Flächeninhalt des Dreiecks  .
.

(4 P)
Aufgabe 16
(4,5 P)
Aufgabe 17
Berechne den Umfang des Dreiecks
(4 P)
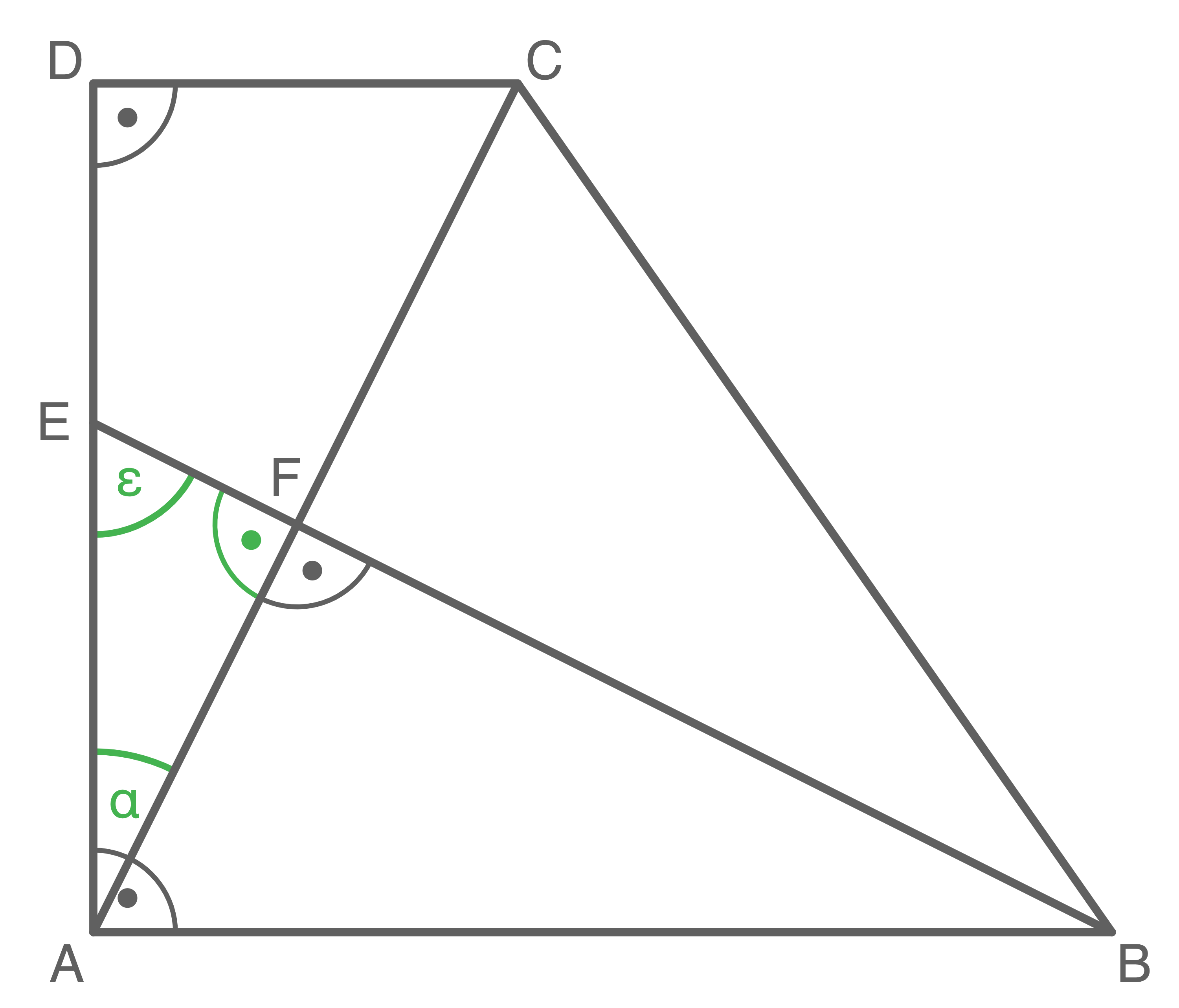
Aufgabe 18
Das Viereck  ist ein Quadrat.
ist ein Quadrat.
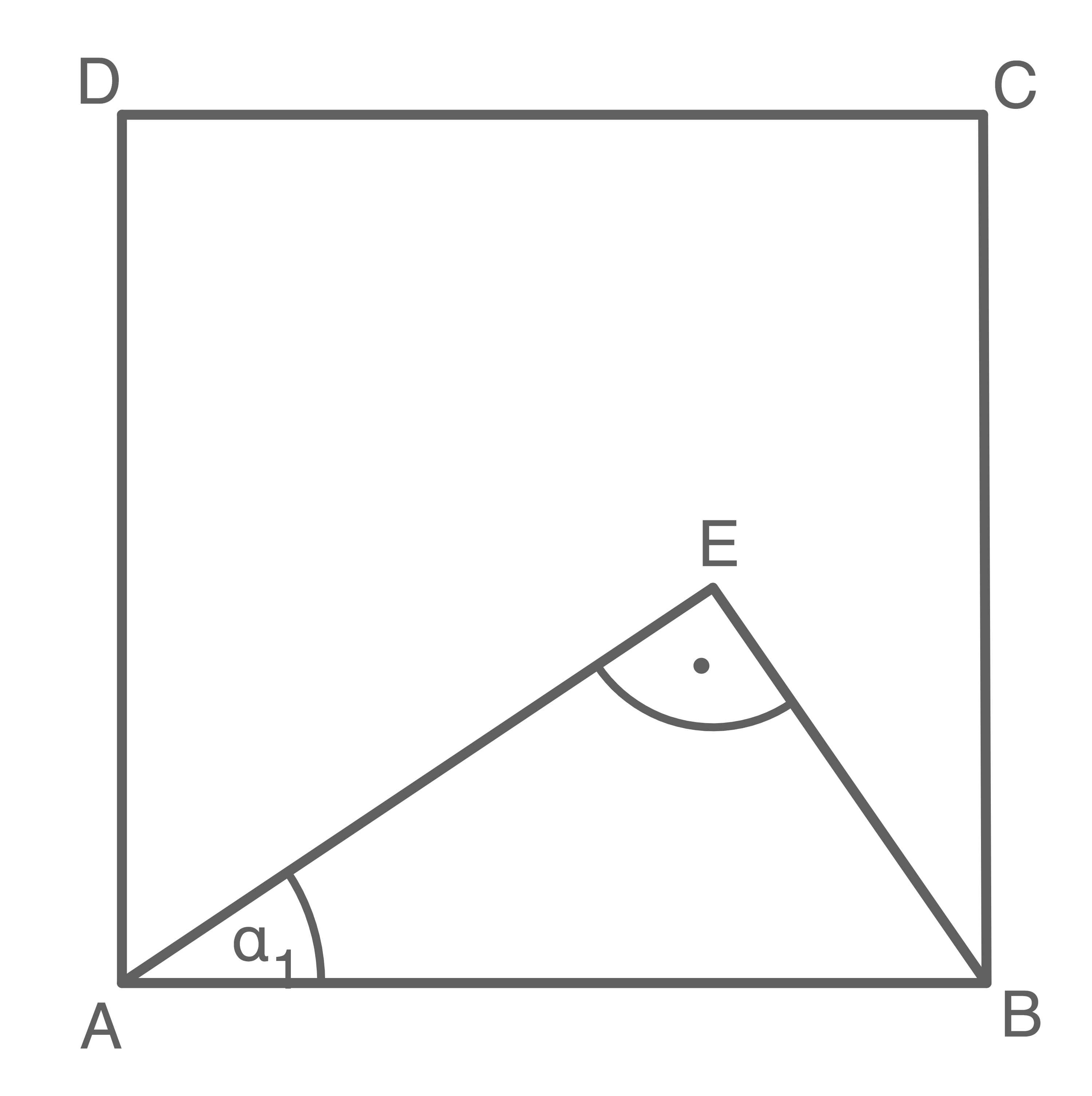 Es gilt:
Es gilt:


Berechne die Länge von .
.
Abschlussprüfung 2015

Berechne die Länge von
(4 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
1. Schritt: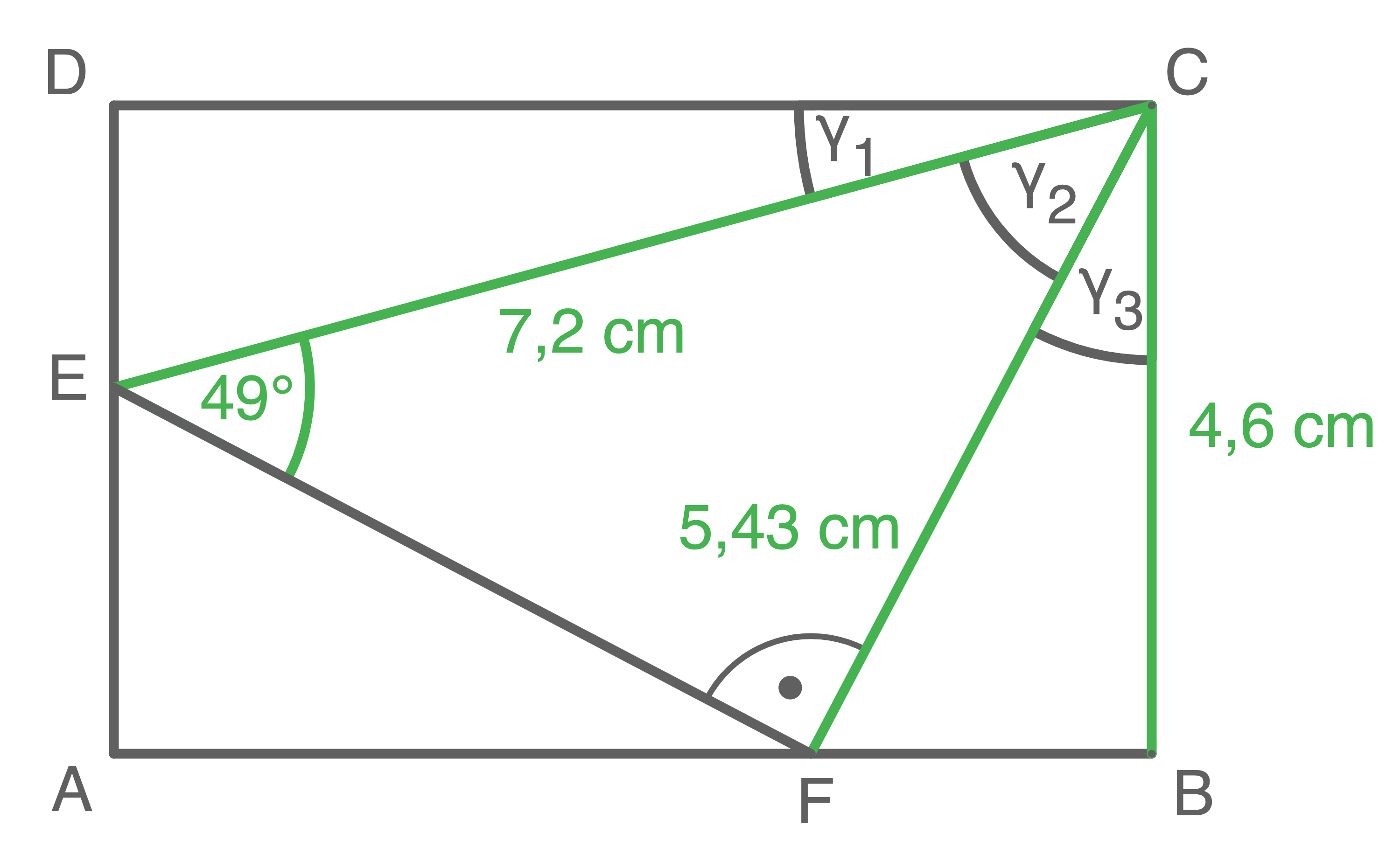
2. Schritt:  berechnen
berechnen
 3. Schritt:
3. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos \gamma_3&=& \dfrac{\overline{BC}}{\overline{CF}} \\[5pt]
\cos \gamma_3&=& \dfrac{4,6\,\text{cm}}{5,43\,\text{cm}} \quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\gamma_3&=& \underline{32,1°}
\end{array}\)](https://mathjax.schullv.de/4e849fd1181b6f8415e1686d5d8d749f7ced4e08e3106eeb8fdaf1bb3cae545b?color=5a5a5a)
4. Schritt: Lösung 2
Umfang Dreieck  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}&=&\overline{AD}+\overline{CD} \quad \scriptsize \overline{AD}=\overline{BD}=\overline{CD} \\[5pt]
&=&\overline{CD}+\overline{CD}\\[5pt]
&=&6,3\,\text{cm}+6,3\,\text{cm}\\[5pt]
\overline{AC}&=&12,6\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/eb0fe0464d021bd16969f5678acf7a6c9bb664bb099f8e304ed8af737009d2db?color=5a5a5a)
![\(\begin{array}[t]{rll}
\sin\gamma&=&\dfrac{\overline{AB}}{\overline{AC}} \quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\sin\gamma\cdot \overline{AC}&=&\overline{AB} \\[5pt]
\overline{AB}&=&\sin\gamma\cdot \overline{AC} \\[5pt]
&=&\sin41,8^\circ\cdot 12,6\,\text{cm}\\[5pt]
\overline{AB}&=&\underline{8,40\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/998292ebfc81ac533e489e917ebaad74bc311cca0f7b0a618c882fda9a525381?color=5a5a5a) 2. Schritt: Umfang berechnen
2. Schritt: Umfang berechnen
![\(\begin{array}[t]{rll}
u_{ABD}&=&\overline{AB}+\overline{BD}+\overline{AD} \\[5pt]
&=&\overline{AB}+\overline{CD}+\overline{CD} \\[5pt]
&=&8,4\,\text{cm}+6,3\,\text{cm}+6,3\,\text{cm}\\[5pt]
u_{ABD}&=&\underline{\underline{21,0\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/27444c4396747d0f84c32b6cbfdea463c4e3d0531c80c620534b81cfbe5cb67b?color=5a5a5a) Flächeninhalt Dreieck
Flächeninhalt Dreieck  berechnen
1. Schritt: Höhe
berechnen
1. Schritt: Höhe  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_\overline{AB}^2&=&\overline{AD}^2-\left(\frac{1}{2}\overline{AB}\right)^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h_\overline{AB}&=&\sqrt{\overline{AD}^2-\left(\frac{1}{2}\overline{AB}\right)^2}\\[5pt]
&=&\sqrt{(6,3\,\text{cm})^2-(4,2\,\text{cm})^2}\\[5pt]
h_\overline{AB}&=&\underline{4,70\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/f40703c4d6b20e5da153516b5dea76d4076eb11bd6f0da5583112ed8ca1e15e0?color=5a5a5a) 2. Schritt: Flächeninhalt berechnen
2. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{ABD}&=&\dfrac{1}{2}\overline{AB}\cdot h_\overline{AB}\\[5pt]
&=&\dfrac{1}{2}\cdot 8,4\,\text{cm}\cdot 4,7\,\text{cm}\\[5pt]
A_{ABD}&=&\underline{\underline{19,7\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/ed03bafcdf59d9bed5ca0827ed192de0874b1015504252dc13bf92526eee3d81?color=5a5a5a)
Abschlussprüfung 2023
Lösung 3
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\text{tan}(\alpha)&=&\dfrac{\overline{BC}}{\overline{AC}} &\quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\overline{BC}&=&\text{tan}(\alpha)\cdot \overline{AC} \\[5pt]
&=&\text{tan}(40^{\circ})\cdot 9,5\,\text{cm} \\[5pt]
\overline{BC}&=&\underline{ 7,97\,\text{cm}}=\overline{BD} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4e046c65cbd1e48f9284d7173a7207f5e6b30f23ca20c8db9a7ff909c92b6dd1?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\text{cos}(\alpha)&=&\dfrac{\overline{AC}}{\overline{AB}} &\quad \scriptsize \mid\;\cdot\overline{AB} \quad\scriptsize \mid\;:\text{cos}(\alpha) \\[5pt]
\overline{AB}&=&\dfrac{\overline{AC}}{\text{cos}(\alpha)} \\[5pt]
&=&\dfrac{9,5\,\text{cm}}{\text{cos}(40^{\circ})} \\[5pt]
\overline{AB}&=& \underline{ 12,40\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/8ee718613ca733ea4aecea9047818401e12c2bf3dc6db376c8213b1640de67a6?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AD}&=&\overline{AB}-\overline{BD} \\[5pt]
&=& 12,40\,\text{cm} -7,97\,\text{cm} \\[5pt]
\overline{AD}&=& \underline{ 4,43\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c86a93c00ce64d5065d67a75b5739348b07047861c247697f4dc9ccb2c58d384?color=5a5a5a) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
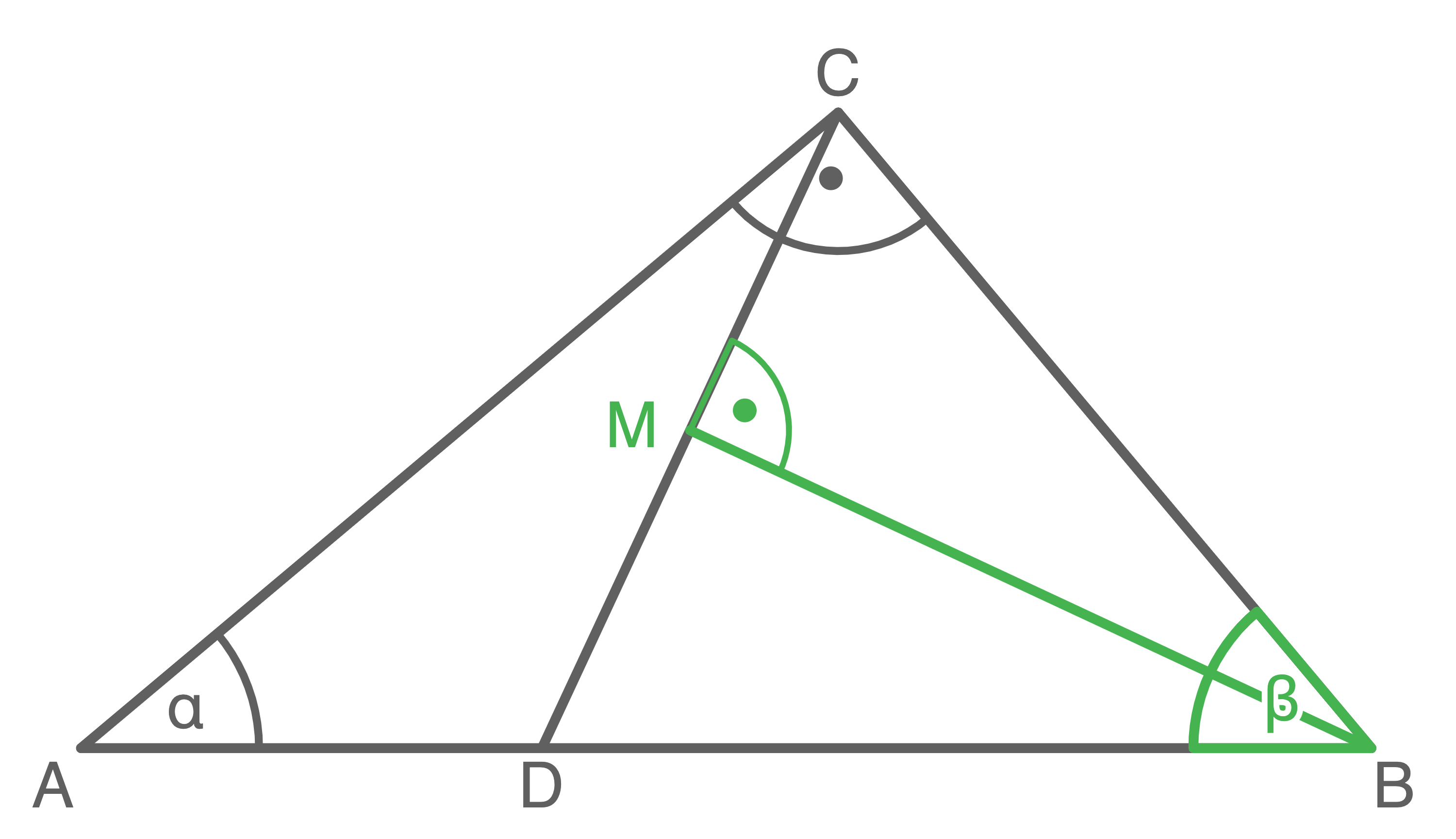
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-90^{\circ}-\alpha \\[5pt]
\beta&=& 180^{\circ}-90^{\circ}-40^{\circ} \\[5pt]
\beta&=& \underline{ 50^{\circ}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/94de9fb3cf959549a6d95dfae46ca8ca0d59445e2dc48b657ce1325d2cd571a0?color=5a5a5a) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\text{sin}\left(\dfrac{\beta}{2}\right)&=& \dfrac{\overline{DM}}{\overline{BD}}\quad \scriptsize \mid\;\cdot \overline{BD} \\[5pt]
\overline{DM}&=&\text{sin}\left(\dfrac{\beta}{2}\right)\cdot \overline{BD} \\[5pt]
&=& \text{sin}(25^{\circ})\cdot 7,97\,\text{cm} \\[5pt]
\overline{DM}&=& \underline{ 3,37\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/0bbc8670266666c2c253404f7247efe3928542f991e5785d8a32457cd9c1f047?color=5a5a5a) Daraus folgt:
Daraus folgt:
 6. Schritt: Umfang berechnen
6. Schritt: Umfang berechnen
![\(\begin{array}[t]{rll}
u&=&\overline{AD}+\overline{CD}+\overline{AC} \\[5pt]
&=& 4,43\,\text{cm} +6,74\,\text{cm} +9,5\,\text{cm} \\[5pt]
&=& 20,67\,\text{cm}\\[5pt]
u&=&\underline{\underline{ 20,7\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/8afd0d9a60eda5b7cfb6bca31757a60c02110c4fa0ec2c87898aca33e41d0aec?color=5a5a5a)
Abschlussprüfung 2022

Lösung 4
1. Schritt: Länge der Strecke  berechnen
Zunächst muss die Länge der Strecke
berechnen
Zunächst muss die Länge der Strecke  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{CD}}{\overline{BD}} \quad \scriptsize \mid\; \cdot\overline{BD}\\[5pt]
\tan(\beta)\cdot \overline{BD} &=&\overline{CD}\\[5pt]
\tan({67^\circ})\cdot 10,0\,\text{cm} &=&\overline{CD}\\[5pt]
23,56\,\text{cm}&=&\overline{CD}\\
\overline{CD}&=&23,56\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/d1e715916704db58601c98eb74d98020fc59fdf7102f5f21a75b9844f0c89885?color=5a5a5a) Als nächstes muss die Länge der Strecke
Als nächstes muss die Länge der Strecke  bestimmt werden. Diese entspricht der Länge der Strecke
bestimmt werden. Diese entspricht der Länge der Strecke  da es sich um ein Quadrat handelt. Das Dreieck
da es sich um ein Quadrat handelt. Das Dreieck  ist gleichschenklig, deshalb sind die Strecken
ist gleichschenklig, deshalb sind die Strecken  und
und  gleich lang.
Also gilt:
gleich lang.
Also gilt:
 Damit folgt für die Länge der Strecke
Damit folgt für die Länge der Strecke 
![\(\begin{array}[t]{rll}
\overline{CE}&=& \overline{CD}-\overline{DE} \\[5pt]
&=& 23,56\,\text{cm}-10,0\,\text{cm} \\[5pt]
&=& \underline{ 13,56\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/74b16a906fb7ffc27961b2924b3670aeddf36a9787d47b515e5ad17a10332c0f?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Anwendung des Zweiten Strahlensatzes:
berechnen
Anwendung des Zweiten Strahlensatzes:
![\(\begin{array}[t]{rll}
\dfrac{\overline{AD}}{\overline{EG}}&=& \dfrac{\overline{CD}}{\overline{CE}} \quad \scriptsize \mid \text{Kehrbruch bilden} \\[5pt]
\dfrac{\overline{EG}}{\overline{AD}}&=&\dfrac{\overline{CE}}{\overline{CD}} \quad \scriptsize \mid\cdot\overline{AD} \\[5pt]
\overline{EG}&=&\dfrac{\overline{CE}}{\overline{CD}}\cdot\overline{AD} \\[5pt]
\overline{EG}&=&\dfrac{13,56\,\text{cm}}{23,56\,\text{cm}}\cdot 10,0\,\text{cm} \\[5pt]
\overline{EG}&=&\underline{ 5,76\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/032c205c61e4602280714d67a294fa59419863a4b58a4b90527f24e0e84f9deb?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
Mit dem Satz des Pythagoras gilt:
berechnen
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rll}
\overline{CG}^2&=&\overline{EG}^2+\overline{CE}^2 \quad \scriptsize \mid \sqrt{.} \\[5pt]
\overline{CG}&=&\sqrt{\overline{EG}^2+\overline{CE}^2 }\\[5pt]
\overline{CG}&=&\sqrt{(5,76\,\text{cm})^2+(13,56\,\text{cm})^2}\\[5pt]
\overline{CG}&=&\underline{ 14,73\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/41ffbba0c72045f01be899de670206a555d1fc167d428a64869d10b6fb0aea4c?color=5a5a5a) 4. Schritt: Umfang berechnen
4. Schritt: Umfang berechnen
![\(\begin{array}[t]{rll}
u&=& \overline{CE}+\overline{EG}+\overline{CG}\\[5pt]
&=& 13,56\,\text{cm}+5,76\,\text{cm}+14,73\,\text{cm}\\[5pt]
&=& 34,05\,\text{cm}\\[5pt]
u&=& \underline{\underline{ 34,1\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/56b768bb51223f886b06472a951db04f920496b354452b47b6132c85af18786c?color=5a5a5a)
Abschlussprüfung 2021
Lösung 5
1. Schritt: Länge der StreckeLösung 6
Länge der Strecke  berechnen
berechnen
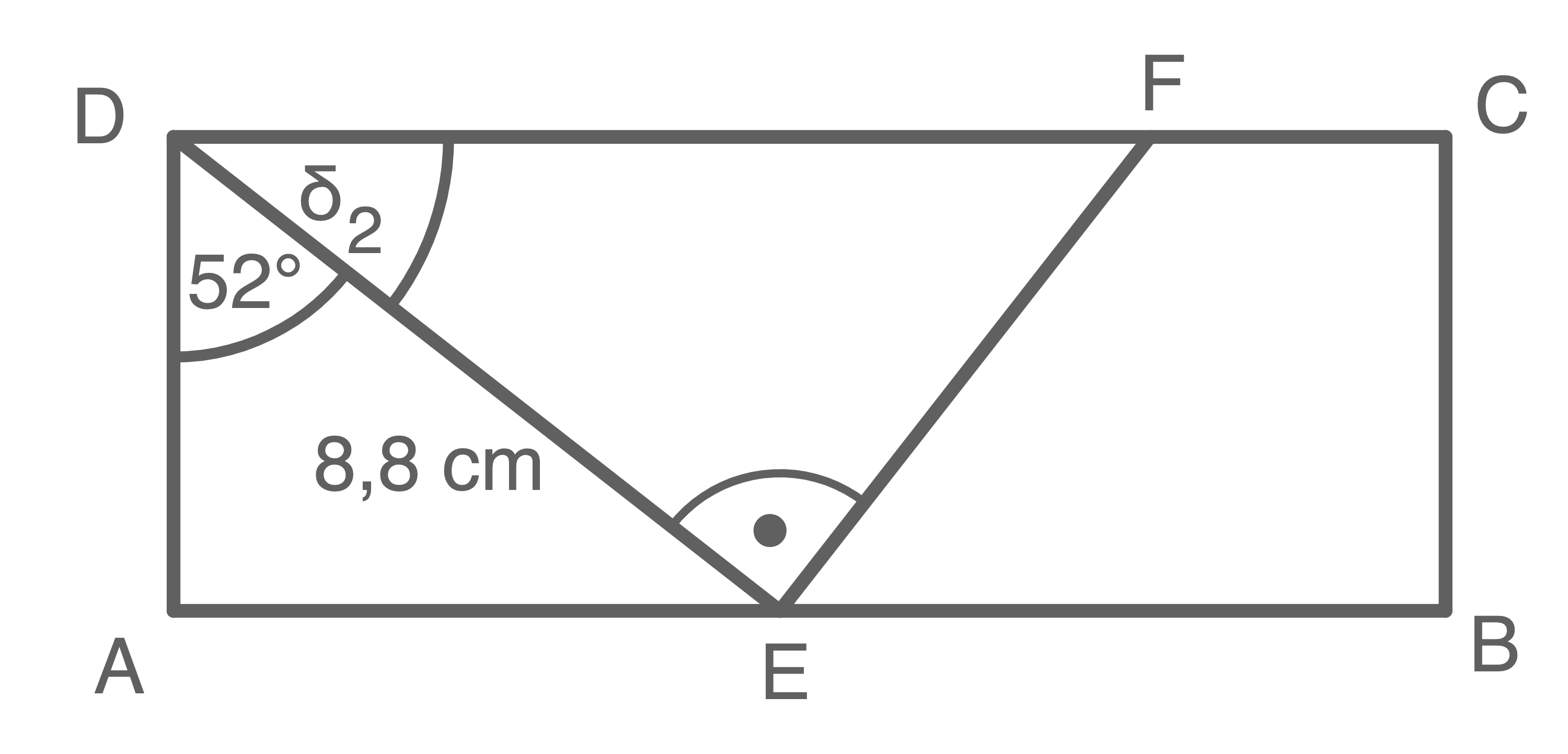
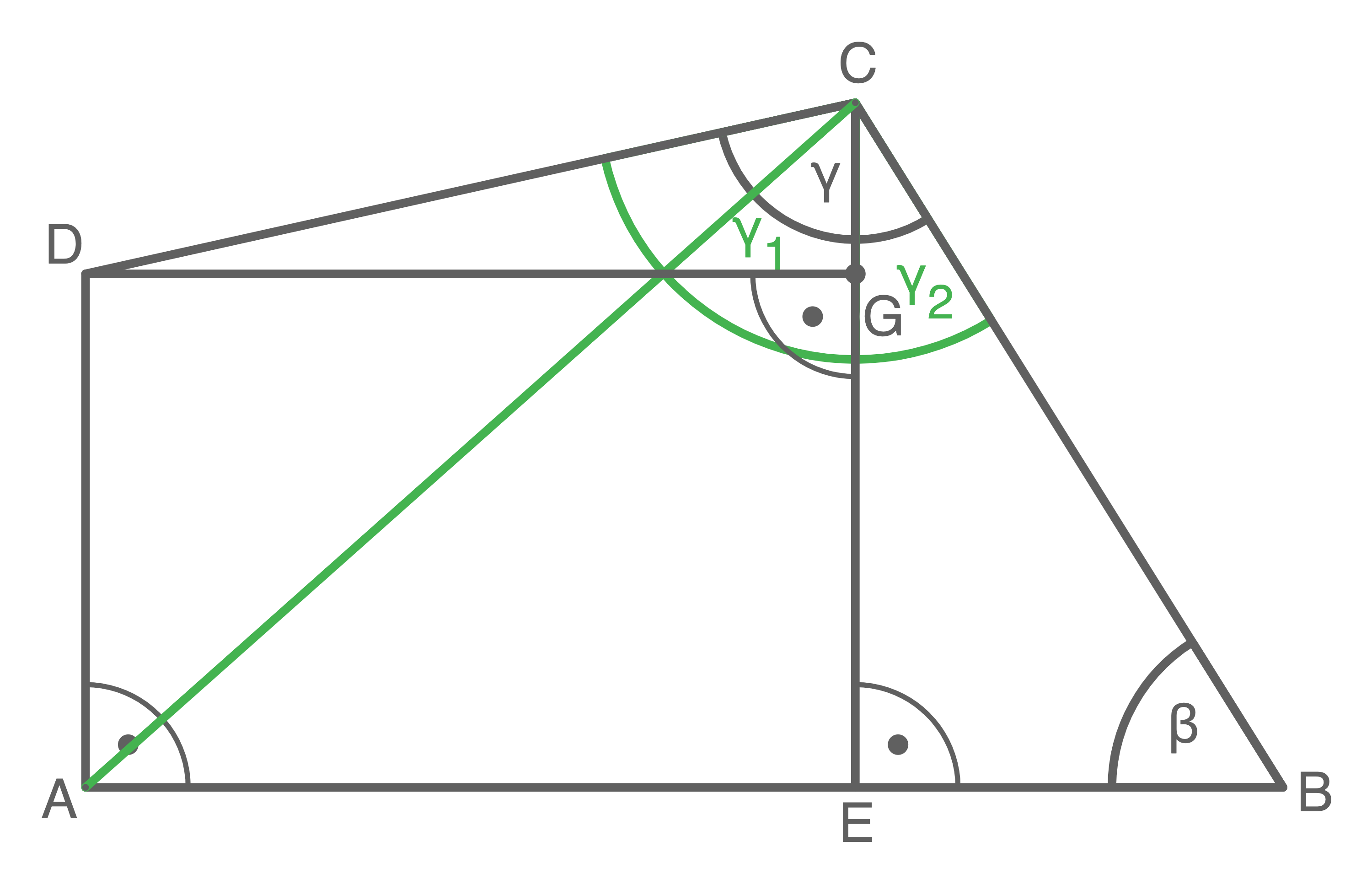 1. Schritt: Winkel
1. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma_2&=&180^{\circ}-\beta-90^{\circ} \\[5pt]
\gamma_2&=&180^{\circ}-52^{\circ}-90^{\circ} \\[5pt]
\gamma_2&=&\underline{ 38^{\circ}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/922bbd42ae91cbdfc8fff5f9b58eec82dceadae0a111ee557deb8b0e90ed996b?color=5a5a5a)
2. Schritt: Winkel berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma_1&=&\gamma-\gamma_2 & \\[5pt]
\gamma_1&=&113^{\circ}-38^{\circ} \\[5pt]
\gamma_1&=&\underline{ 75^{\circ}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/017fe20d5b5b9b2e138b4871c6c885cbe4c44af87a73e9f5844a76278587d1e1?color=5a5a5a)
3. Schritt: Länge der Strecke berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{CE}}{\overline{BE}} \quad \scriptsize \mid\;\cdot \, \overline{BE} \\[5pt]
\overline{CE}&=&\tan(\beta)\cdot \overline{BE} \\[5pt]
&=&\tan(52^{\circ})\cdot 5,9\,\text{cm} \\[5pt]
\overline{CE}&=&\underline{ 7,55\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/898954ca9614b0245cab2f7bca10ec2547cfa92a8825cbf01995411e53ff7290?color=5a5a5a)
4. Schritt: Länge der Strecke berechnen
Es gilt:
berechnen
Es gilt: 
![\(\begin{array}[t]{rll}
\tan(\gamma_1)&=&\dfrac{\overline{DG}}{\overline{CG}} \quad \scriptsize \mid\;\cdot \, \overline{CG} \quad \scriptsize \mid\;:\tan(\gamma_1) \\[5pt]
\overline{CG}&=&\dfrac{\overline{DG}}{\tan(\gamma_1)} \\[5pt]
&=&\dfrac{7,6\,\text{cm}}{\tan(75^{\circ})} \\[5pt]
\overline{CG}&=&\underline{ 2,04\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/40f8acfe53796236a26bdcc21c27a56071b3ff6f16db3b80befd943bceb635ad?color=5a5a5a)
5. Schritt: Länge der Strecke berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{EG}&=&\overline{CE}-\overline{CG} \\[5pt]
&=&7,55\,\text{cm}-2,04\,\text{cm} \\[5pt]
\overline{EG}&=& 5,51\,\text{cm}\\[5pt]
\overline{EG}&=&\underline{\underline{ 5,5\,\text{cm}=\overline{AD}}}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d113acb06d0319a6f5accdbb7ffbe4e1f6a5f86e50ccbe190729d96cfd08d310?color=5a5a5a)
Flächeninhalt des Dreiecks berechnen
berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot \overline{AD}\cdot \overline{DG} \quad \scriptsize\; \overline{DG}=\overline{AE}\\[5pt]
&=&\dfrac{1}{2}\cdot 5,5\,\text{cm} \cdot 7,6\,\text{cm} \\[5pt]
A&=&\underline{\underline{ 20,9\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/cf82d078d2c405c91ff87685ec0046db018952e9a9cc03fb46eca627f6dcabda?color=5a5a5a)
Musterprüfung 2

2. Schritt: Winkel
3. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke
Flächeninhalt des Dreiecks
Lösung 7
Lösung 8
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{\overline{AD}}{\overline{AB}}\quad \scriptsize \\[5pt]
\sin(57^{\circ})&=& \dfrac{\overline{AD}}{9,4\,\text{cm}}\quad \scriptsize \mid\; \cdot\,9,4\,\text{cm} \\[5pt]
\sin(57^{\circ})\cdot\,9,4\,\text{cm} &=& \overline{AD} \\[5pt]
\overline{AD} &=& \sin(57^{\circ})\cdot\,9,4\,\text{cm} \\[5pt]
\overline{AD} &=& \underline{ 7,88\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/a32a7a5edfdf7a32c1036e272a06e23572222de7466dcd7602e4c013d855eaf7?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{\overline{CE}}{\overline{CB}}\\[5pt]
\sin(57^{\circ})&=&\dfrac{6,7\,\text{cm}}{\overline{CB}} \qquad \scriptsize \mid\; \cdot\,\overline{CB} \\[5pt]
\sin(57^{\circ})\cdot \overline{CB}&=&6,7\,\text{cm} \qquad \scriptsize \mid\; : \sin(57^{\circ})\\[5pt]
\overline{CB}&=&\dfrac{6,7\,\text{cm}}{\sin(57^{\circ})} \\[5pt]
\overline{CB}&=&\underline{ 7,99\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/4b9818851f6a3b93e891b6292b1ae5740a78274e6a7fe10a6defeb5c3689a99b?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{DB}}{\overline{AB}} \quad \scriptsize \\[5pt]
\cos(57^{\circ})&=&\dfrac{\overline{DB}}{9,4\,\text{cm}} \quad \scriptsize \mid\;\cdot 9,4\,\text{cm} \\[5pt]
\cos(57^{\circ})\cdot9,4\,\text{cm} &=& \overline{DB} \\[5pt]
\overline{DB} &=& \cos(57^{\circ})\cdot9,4\,\text{cm} \\[5pt]
\overline{DB}&=&\underline{ 5,12\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/28fc0f76fe53acb6782d0e253c1abbbd32a7b1e8ea1913ccf75cb460bab7dfa5?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}&=& \overline{CB}-\overline{DB}&\quad \scriptsize \\[5pt]
&=& 7,99\,\text{cm}-5,12\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 2,87\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/2be525c9026ef2eaab25137ce6addcc5a702f7401e962863b1bc514f36ccc985?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2&=&\overline{AD}^2+\overline{CD}^2 \\[5pt]
\overline{AC}^2&=&(7,88\,\text{cm})^2+(2,87\,\text{cm})^2 \; \scriptsize \mid\;\sqrt{\,} \\[5pt]
\overline{AC}&=&\sqrt{(7,88\,\text{cm})^2+(2,87\,\text{cm})^2} \\[5pt]
\overline{AC}&= & \underline{ 8,39\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/6df06376851b80b16c736121dfa4465506a9f55f858a9a07d2abfe5a8594fa27?color=5a5a5a) Umfang berechnen
Umfang berechnen
![\(\begin{array}[t]{rll}
u&=& \overline{AD}+\overline{CD}+\overline{AC}\\[5pt]
&=&7,88\,\text{cm}\,+2,87\,\text{cm}+8,39\,\text{cm}\\[5pt]
&=&19,14\,\text{cm}\\[5pt]
u&=&\underline{\underline{ 19,1\,\text{cm} }}
\end{array}\)](https://mathjax.schullv.de/ed054cf3b0ea79196db4a53fc23aae7d2774a4a1e9dec6fb054b0145c50c921d?color=5a5a5a)
Abschlussprüfung 2020

Lösung 9
1. Schritt: Länge der Strecke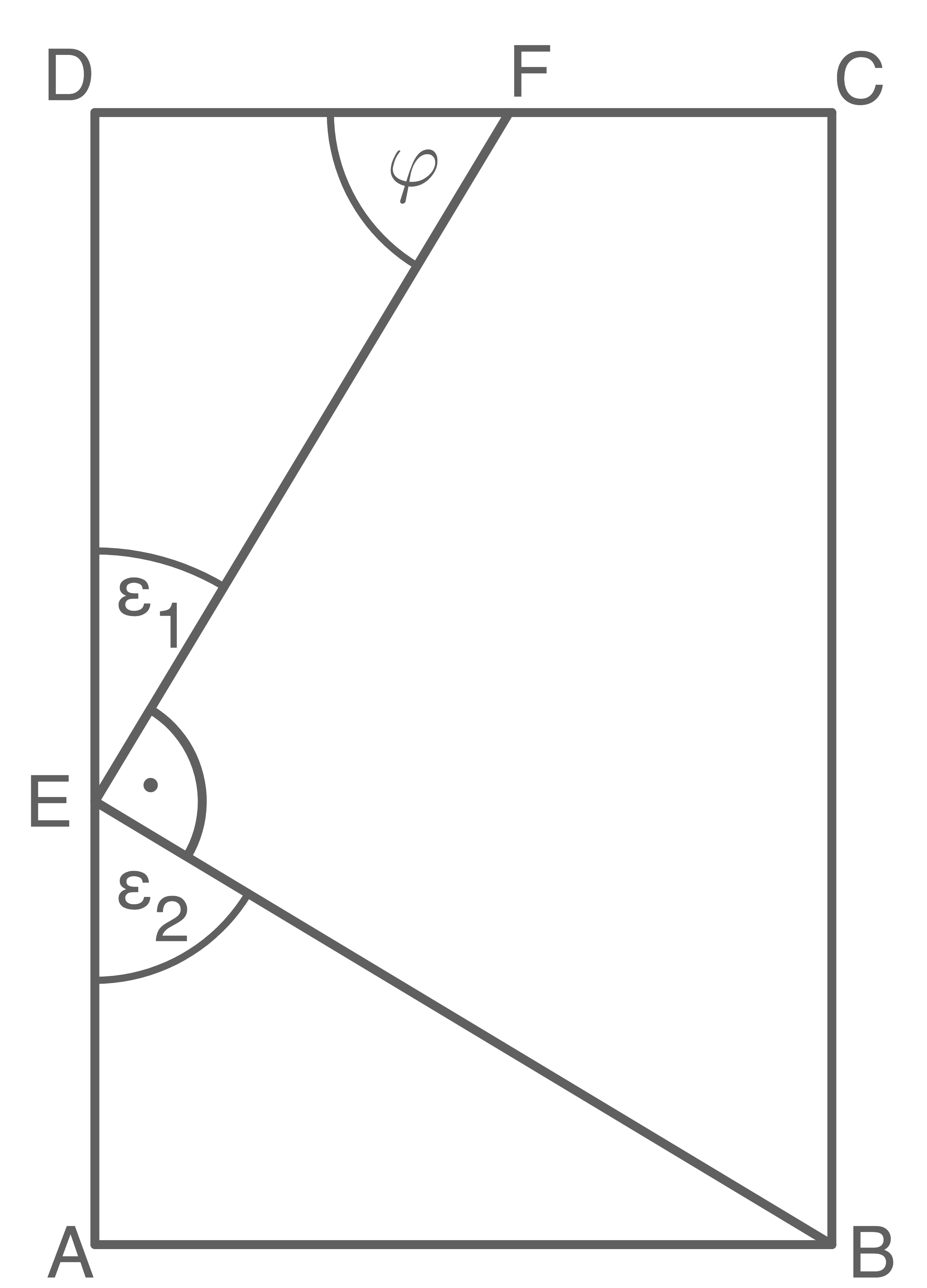
Lösung 10
Lösung 11
Lösung 12
1. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha)&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \\[5pt]
\cos(35^{\circ} ) &=& \dfrac{\overline{AM}}{7,7\,\text{cm}} \quad \scriptsize \mid\; \cdot 7,7\,\text{cm} \\[5pt]
\overline{AM} &=& \underline{ 6,31 \,\text{cm}}= \overline{BM} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b4c2493cb40842b5e578f93928374798a682420a19a8466e1902f18d0b07b884?color=5a5a5a)
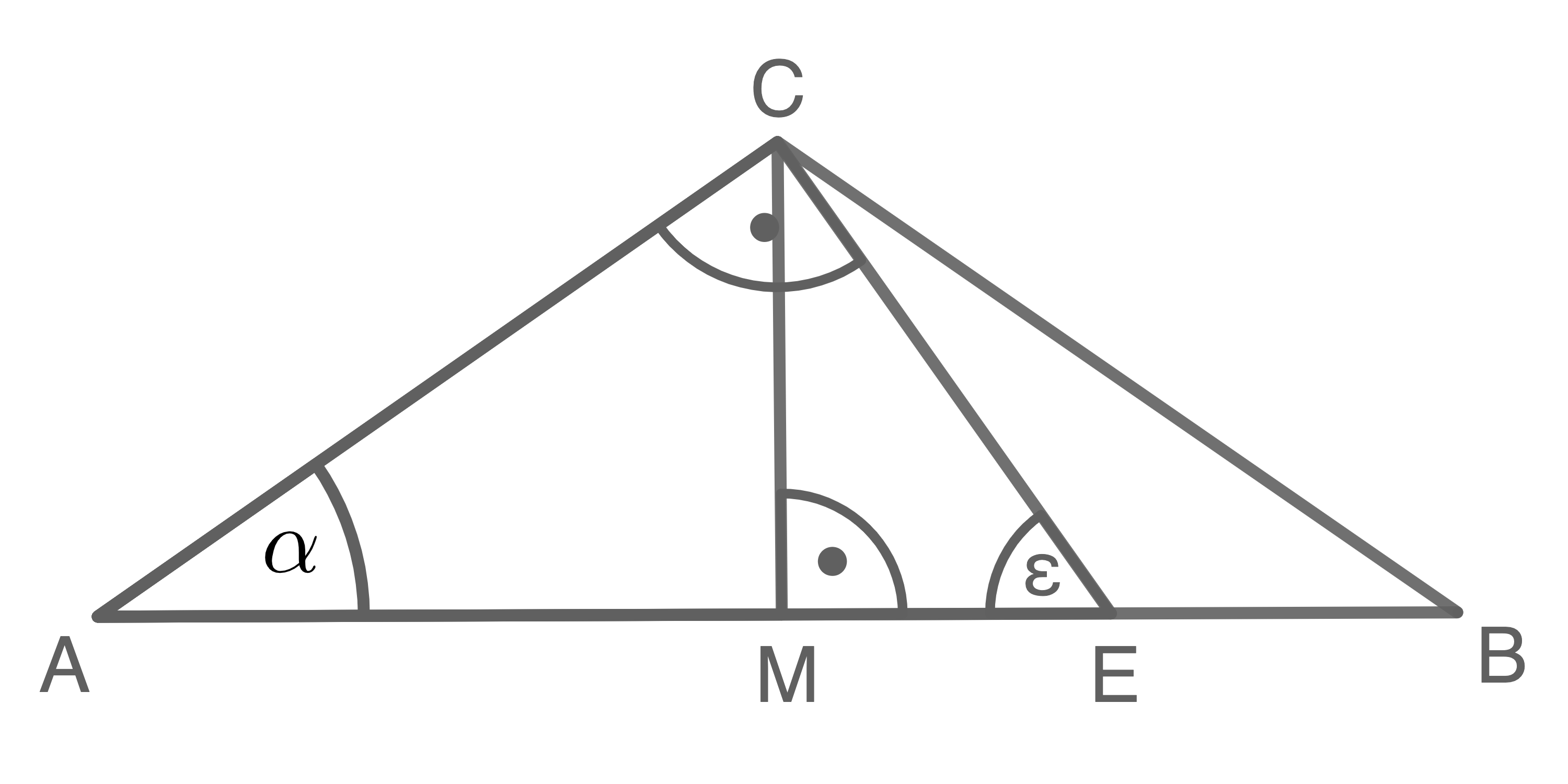
Lösung 13
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\beta}{2}\right)&=& \dfrac{\overline{BC}}{\overline{BF}}\\[5pt]
\cos\left(\dfrac{\beta}{2}\right)&=& \dfrac{5,8\,\text{cm}}{6,6 \,\text{cm}} \quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\dfrac{\beta}{2}&=& 28,50 ^{\circ} \\[5pt]
\beta&=& \underline{57 ^{\circ}}
\end{array}\)](https://mathjax.schullv.de/40e4b220df9404a2d196709f9a113f0feb82b30d9bd0a697ec5ecabb76922e14?color=5a5a5a)
Lösung 14
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\varepsilon)&=&\dfrac{\overline{BC}}{\overline{BE}} \quad \scriptsize \mid\; \cdot \overline{BE} \,\,\, \mid\;:\sin(\varepsilon) \\[5pt]
\overline{BE}&=&\dfrac{\overline{BC}}{\sin(\varepsilon)} \\[5pt]
\overline{BE}&=& \dfrac{11,8 \text{ cm}}{\sin(72^{\circ})} \\[5pt]
\overline{BE}&=& \underline{12,41\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/e4b10ac7abb040d41ac491b077573696ac8741d5b96b5719ccf41103d741d591?color=5a5a5a)
Lösung 15
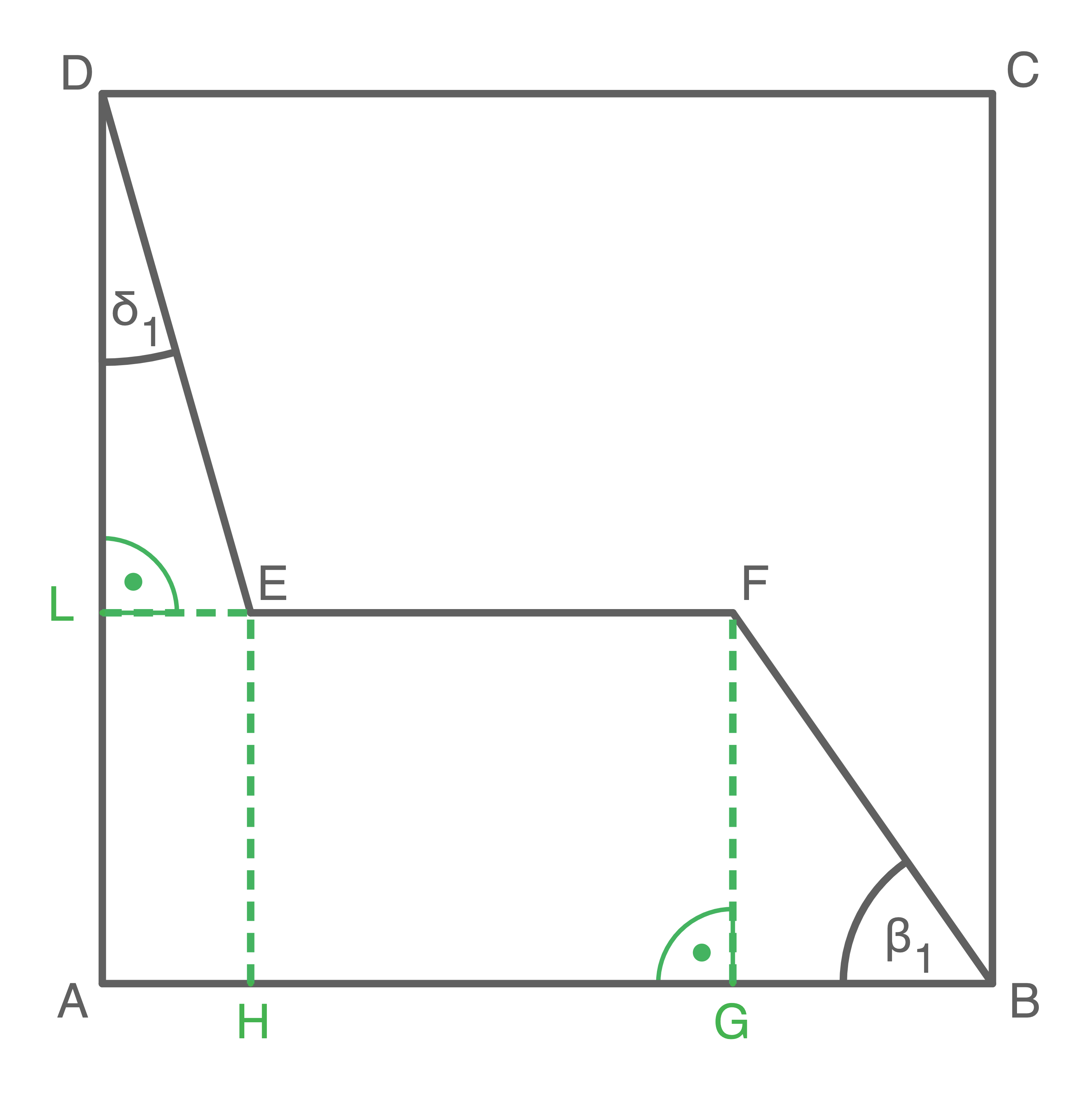
Länge der Strecke  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\delta_1)&=&\dfrac{\overline{DE}}{\overline{AD}} \quad \scriptsize \mid\;\cdot \, \overline{AD} \\[5pt]
\overline{DE}&=&\cos(\delta_1)\cdot \overline{AD} \\[5pt]
\overline{DE}&=&\cos(69,4^{\circ})\cdot 7,3\,\text{cm} \\[5pt]
\overline{DE}&=&\underline{ 2,57\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/778454b600770f22355316af379008c723fa1749cd4994270d87ca8e3a60f810?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{\overline{CE}}{\overline{BC}} \quad \scriptsize \mid\;\cdot \, \overline{BC} \\[5pt]
\overline{CE}&=&\sin(\beta)\cdot \overline{BC} \\[5pt]
\overline{CE}&=&\sin(55^{\circ})\cdot 9,0\,\text{cm} \\[5pt]
\overline{CE}&=&\underline{ 7,37\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/ff2203f0d67ec5ed63484039260e3a4abe72305ffe20251bb92ef7af601702a4?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}&=&\overline{CE}-\overline{DE} & \\[5pt]
&=&7,37\,\text{cm}-2,57\,\text{cm} \\[5pt]
\overline{CD}&=&\underline{\underline{ 4,8\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/c645d13c22da7bcef2ff6a87102d544afc4fd5bd195cef535e0c64059f94be2d?color=5a5a5a) Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}^2+\overline{DE}^2&=&\overline{AD}^2 \quad \scriptsize \mid\;-\,\overline{DE}^2 \\[5pt]
\overline{AE}^2&=&\overline{AD}^2-\overline{DE}^2 \quad \scriptsize \mid\;\,\sqrt{\,\,\,} \\[5pt]
\overline{AE}&=&\sqrt{\overline{AD}^2-\overline{DE}^2} \\[5pt]
\overline{AE}&=&\sqrt{(7,3\,\text{cm})^2-(2,57\,\text{cm})^2} \\[5pt]
\overline{AE}&=&\underline{ 6,83\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/7674a82e7f1990e5bcfeeb81d679e40915532ee62f1fc05e34165dda4c1601a6?color=5a5a5a) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot \overline{CD}\cdot \overline{AE} & \\[5pt]
&=&\dfrac{1}{2}\cdot 4,8\,\text{cm}\cdot 6,83\,\text{cm} \\[5pt]
&=&16,39\,\text{cm}^2 \\[5pt]
A&=& \underline{\underline{ 16,4\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/2822afa3e1e29be4e83aa9a1332fc9c75bbc6893ef335c7d9855304d61a1b708?color=5a5a5a)
Abschlussprüfung 2016
Lösung 16
Lösung 17
1. Schritt: Länge der StreckeLösung 18