Geometrie in der Ebene
Aufgabe 1
a)
Im Rechteck  liegt das Drachenviereck
liegt das Drachenviereck 
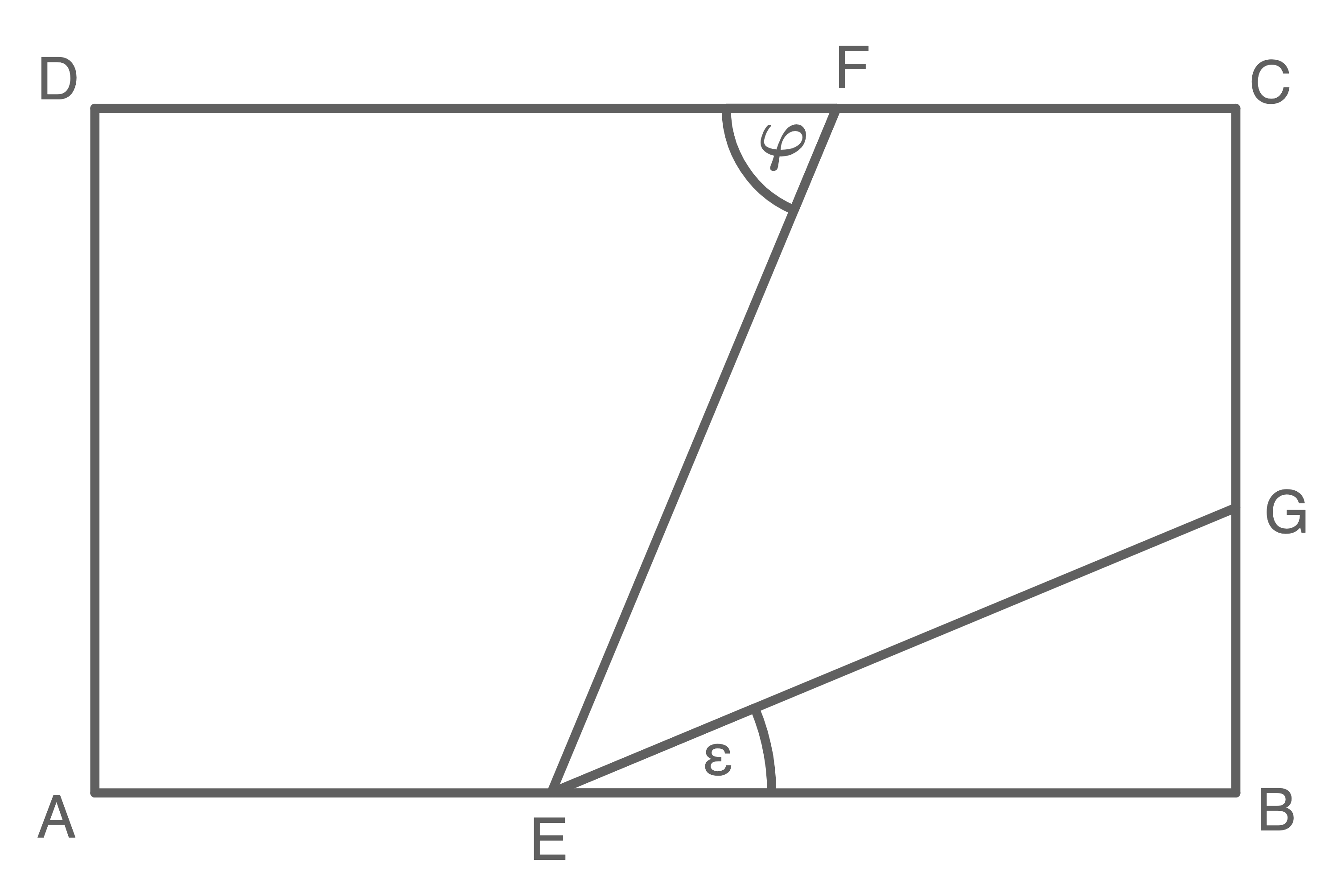
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AB} & =& 9,4 \,\text{cm} \\
\overline{BE} & =& 5,6 \,\text{cm} \\
\varepsilon & =& 20,0^{\circ}
\end{array}\)](https://mathjax.schullv.de/b1d408505da5765fee24f96095443ba459dc32a5c1f0a211452570dafc15ac15?color=5a5a5a)
- Berechne den Winkel
- Berechne den Umfang des Vierecks

(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2024
Aufgabe 2
a)
Das gleichschenklige Dreieck  und das rechtwinklige Trapez
und das rechtwinklige Trapez  überdecken sich teilweise.
überdecken sich teilweise.
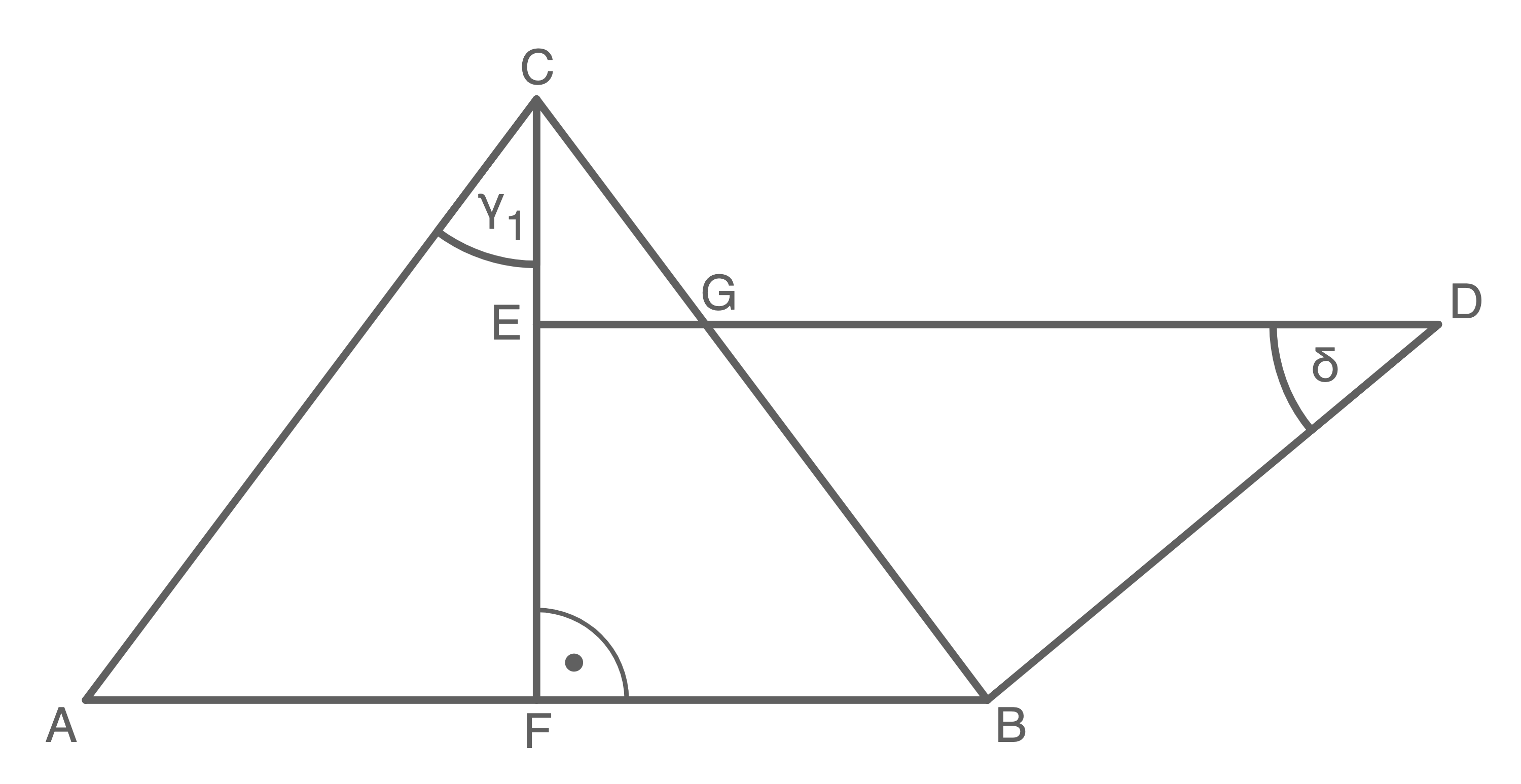 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AC}&=&11,4\,\text{cm}\\
\overline{BD}&=&8,2\,\text{cm}\\
\gamma_1&=&37,6^\circ\\
\delta&=&39,2^\circ\\
\overline{AC}&=&\overline{BC}
\end{array}\)](https://mathjax.schullv.de/39ae3fd492617cfa9f183792abbf261def5e0f40331d608caca90085004f111b?color=5a5a5a) Berechne den Flächeninhalt des Vierecks
Berechne den Flächeninhalt des Vierecks 

(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Aufgabe 3
a)
Im Quadrat  liegen die beiden gleichschenkligen Dreiecke
liegen die beiden gleichschenkligen Dreiecke  und
und 
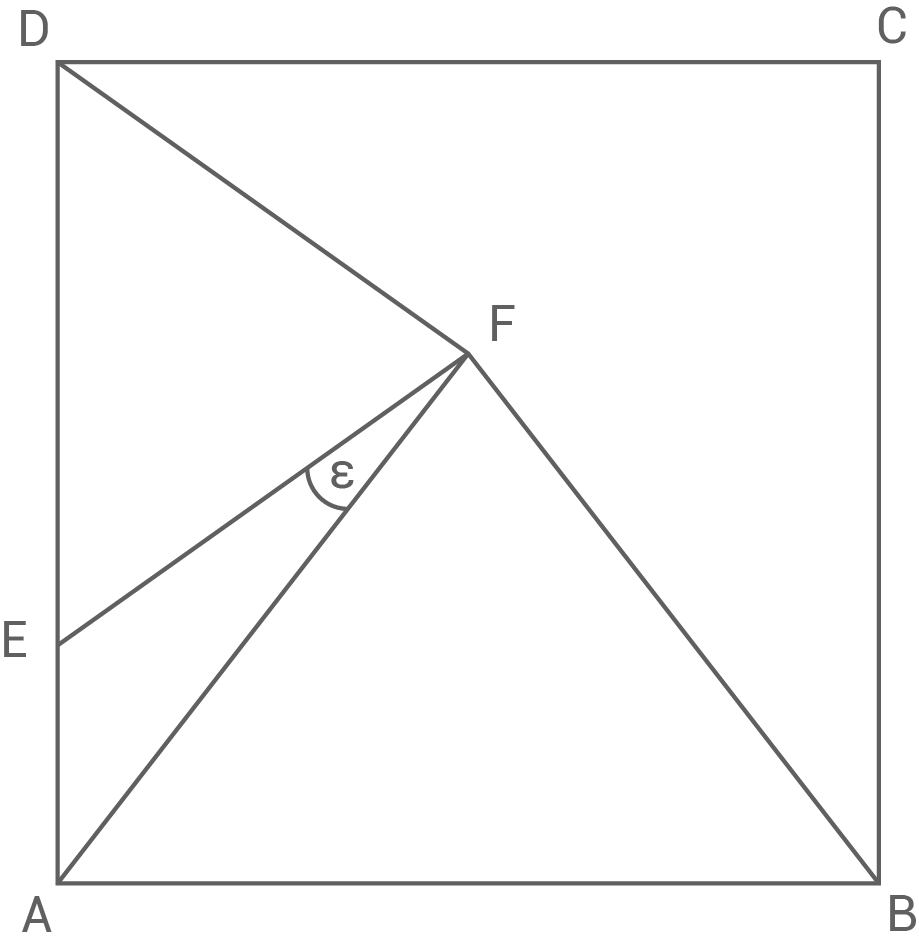 Es gilt:
Es gilt:


- Berechne den Flächeninhalt des Dreiecks
- Berechne den Winkel
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2022
Aufgabe 4
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
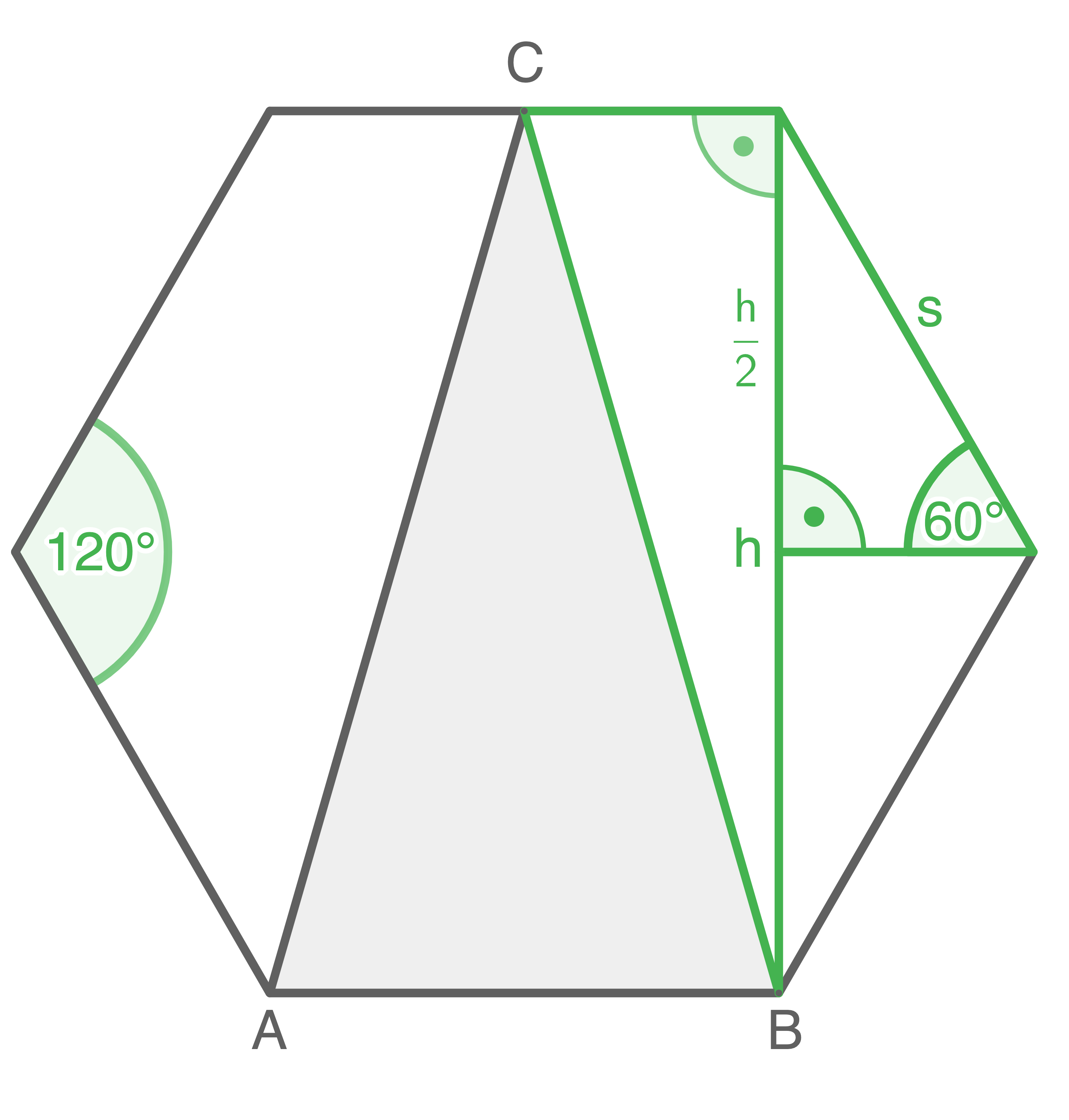
Das regelmäßige Sechseck und das gleichschenklige Dreieck  haben die Seite
haben die Seite  gemeinsam.
Es gilt:
gemeinsam.
Es gilt: 
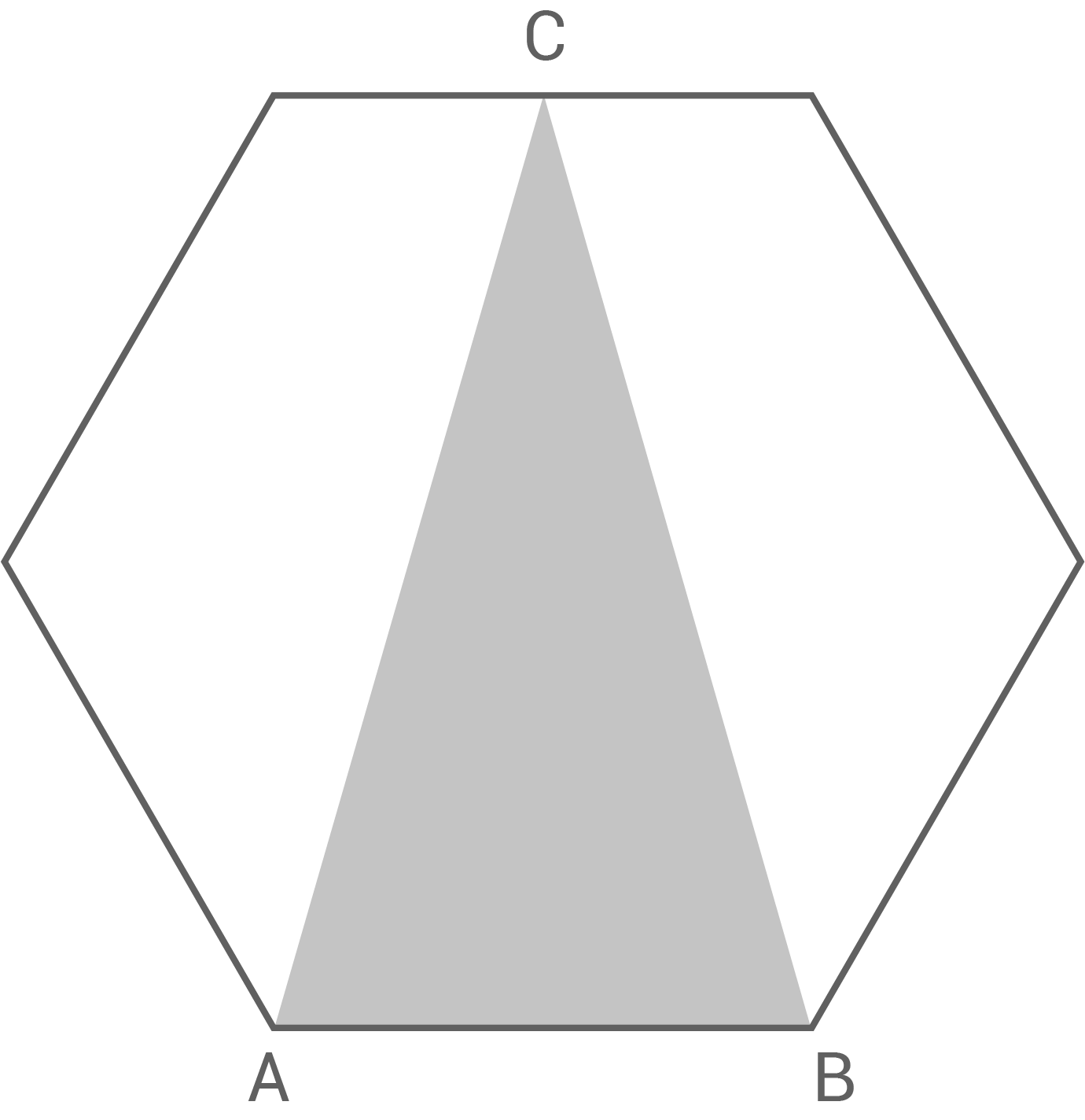 Berechne den Umfang des Dreiecks
Berechne den Umfang des Dreiecks  Tom behauptet: „Der Flächeninhalt des Sechsecks ist dreimal so groß wie der Flächeninhalt des Dreiecks
Tom behauptet: „Der Flächeninhalt des Sechsecks ist dreimal so groß wie der Flächeninhalt des Dreiecks  "
"

- Hat Tom Recht?
Begründe deine Antwort durch Rechnung oder Argumentation.
(5 P)
Aufgabe 5
a)
Gegeben sind das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck 
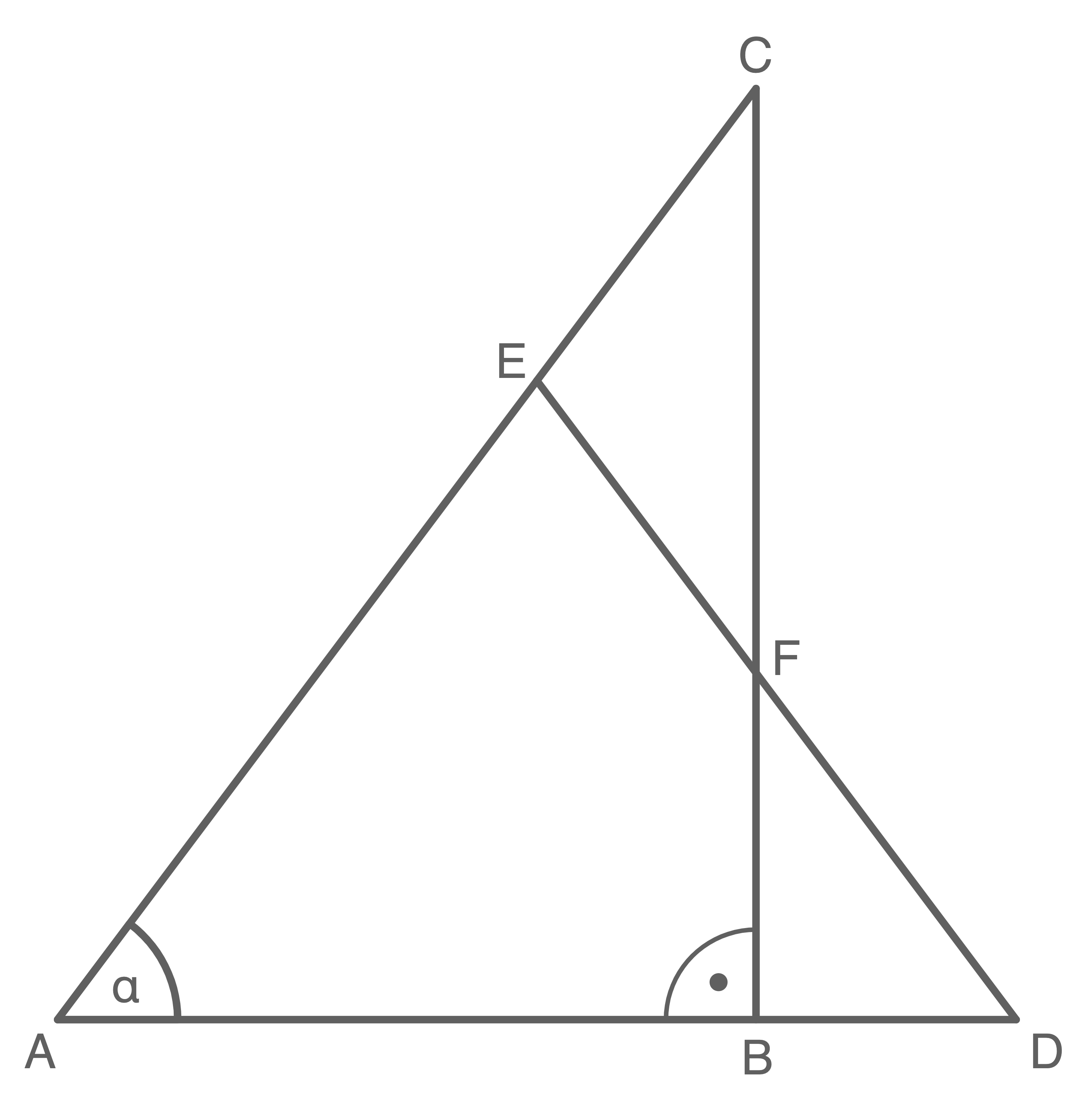 Es gilt:
Es gilt:



 Berechne die Länge von
Berechne die Länge von  Berechne den Umfang des Vierecks
Berechne den Umfang des Vierecks 

(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Aufgabe 6
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
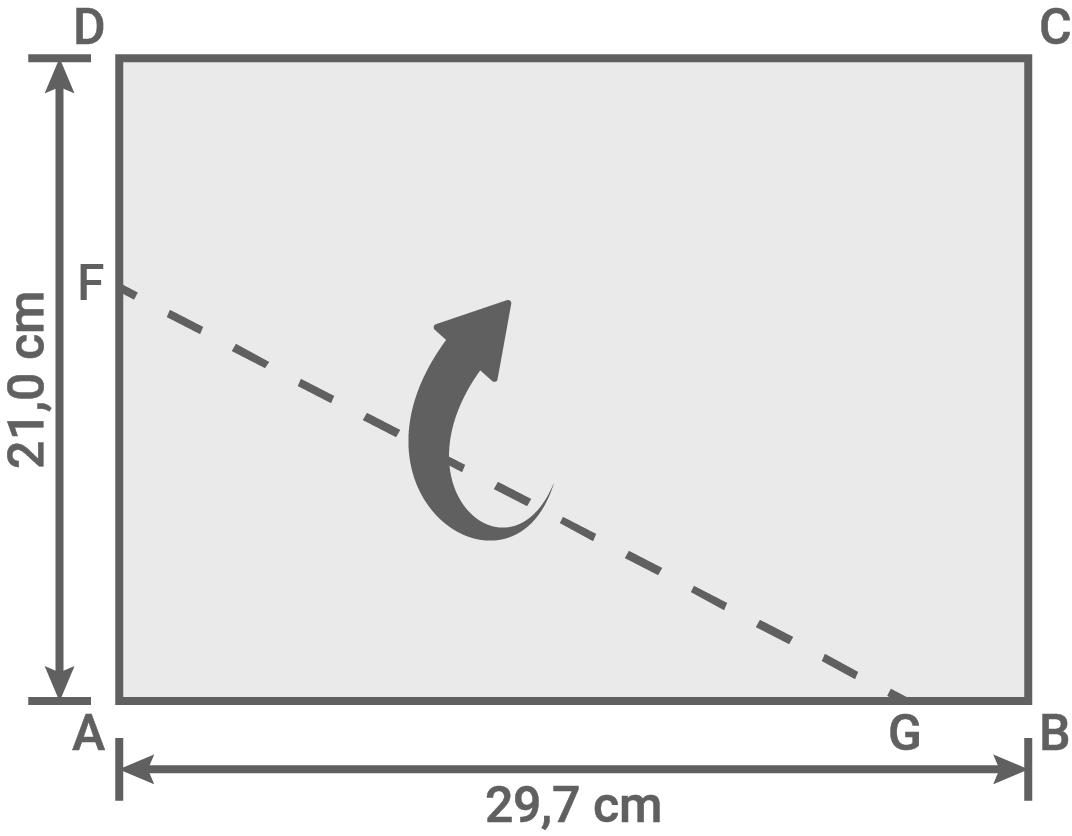
Ein DIN-A4-Blatt hat die Eckpunkte  ,
,  ,
,  und
und 
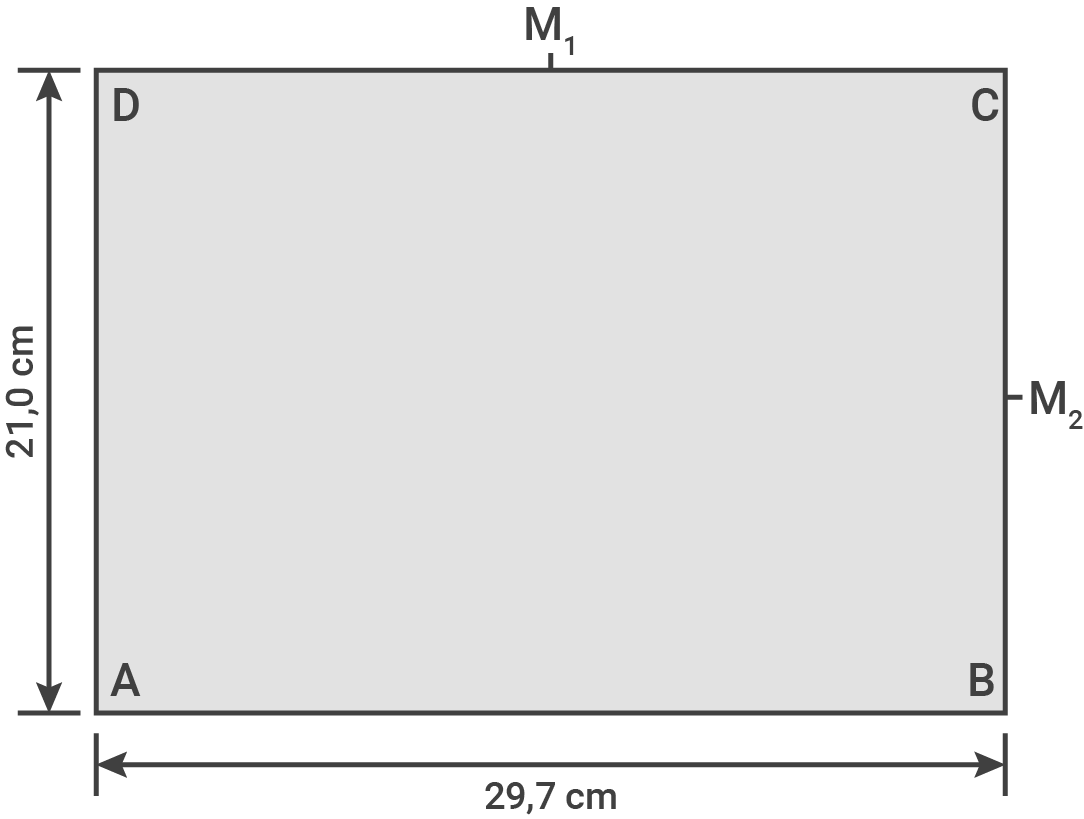
 Die Punkte
Die Punkte  und
und  halbieren die Seitenlängen des DIN-A4-Blatts.
halbieren die Seitenlängen des DIN-A4-Blatts.
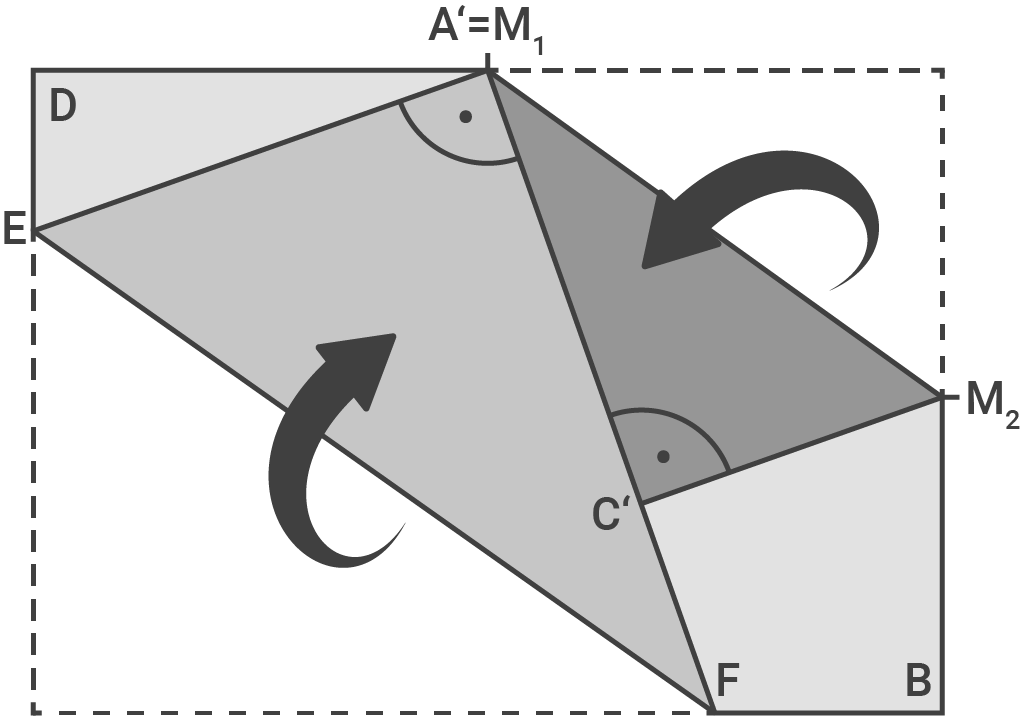
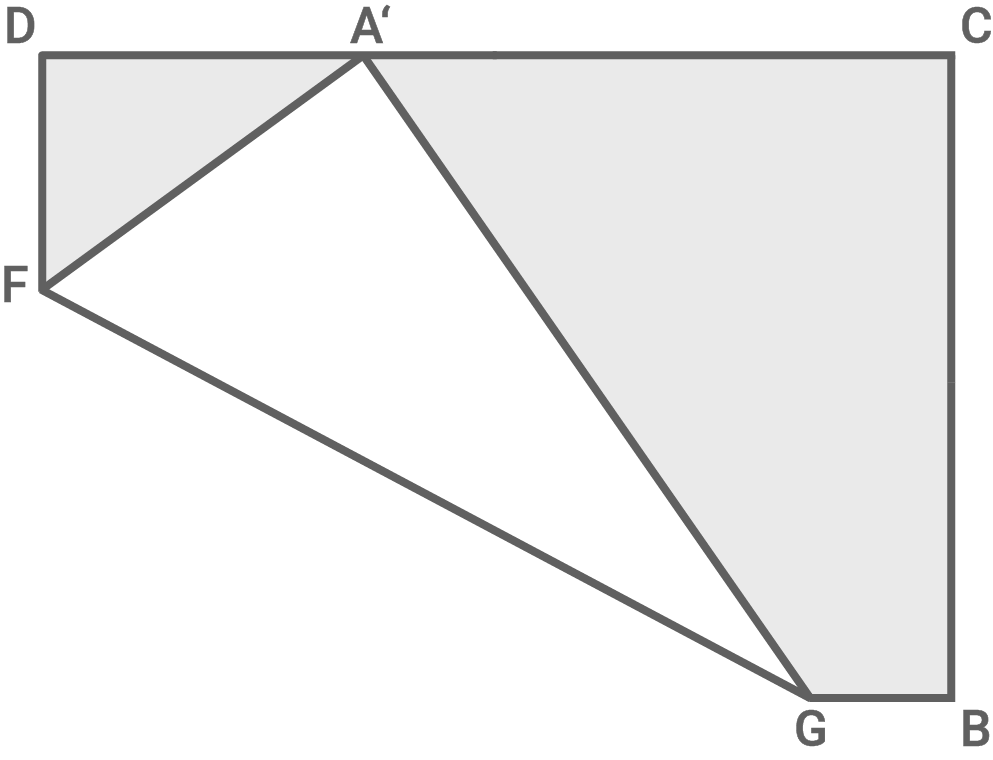
Das DIN-A4-Blatt wird wie abgebildet gefaltet. Der Punkt wird zu
wird zu  und liegt nach dem Falten auf
und liegt nach dem Falten auf 
Der Punkt wird zum Punkt
wird zum Punkt  Die beiden Papierkanten stoßen entlang von
Die beiden Papierkanten stoßen entlang von  aneinander.
Berechne die Flächeninhalte des Dreiecks
aneinander.
Berechne die Flächeninhalte des Dreiecks  und des Vierecks
und des Vierecks  .
.


Das DIN-A4-Blatt wird wie abgebildet gefaltet. Der Punkt
Der Punkt
(5 P)
Aufgabe 7
a)
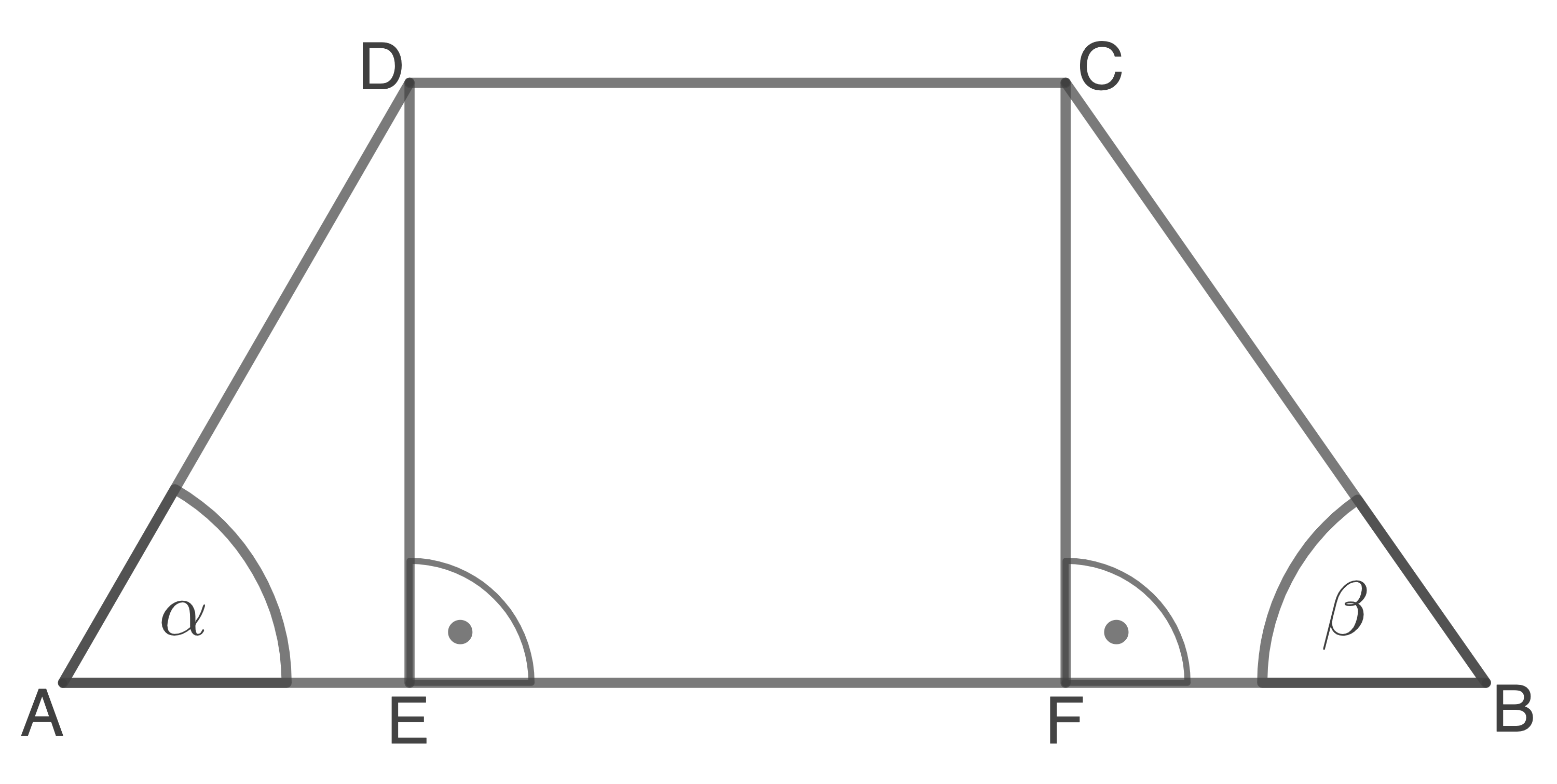
Gegeben ist das Trapez  für das gilt:
für das gilt:
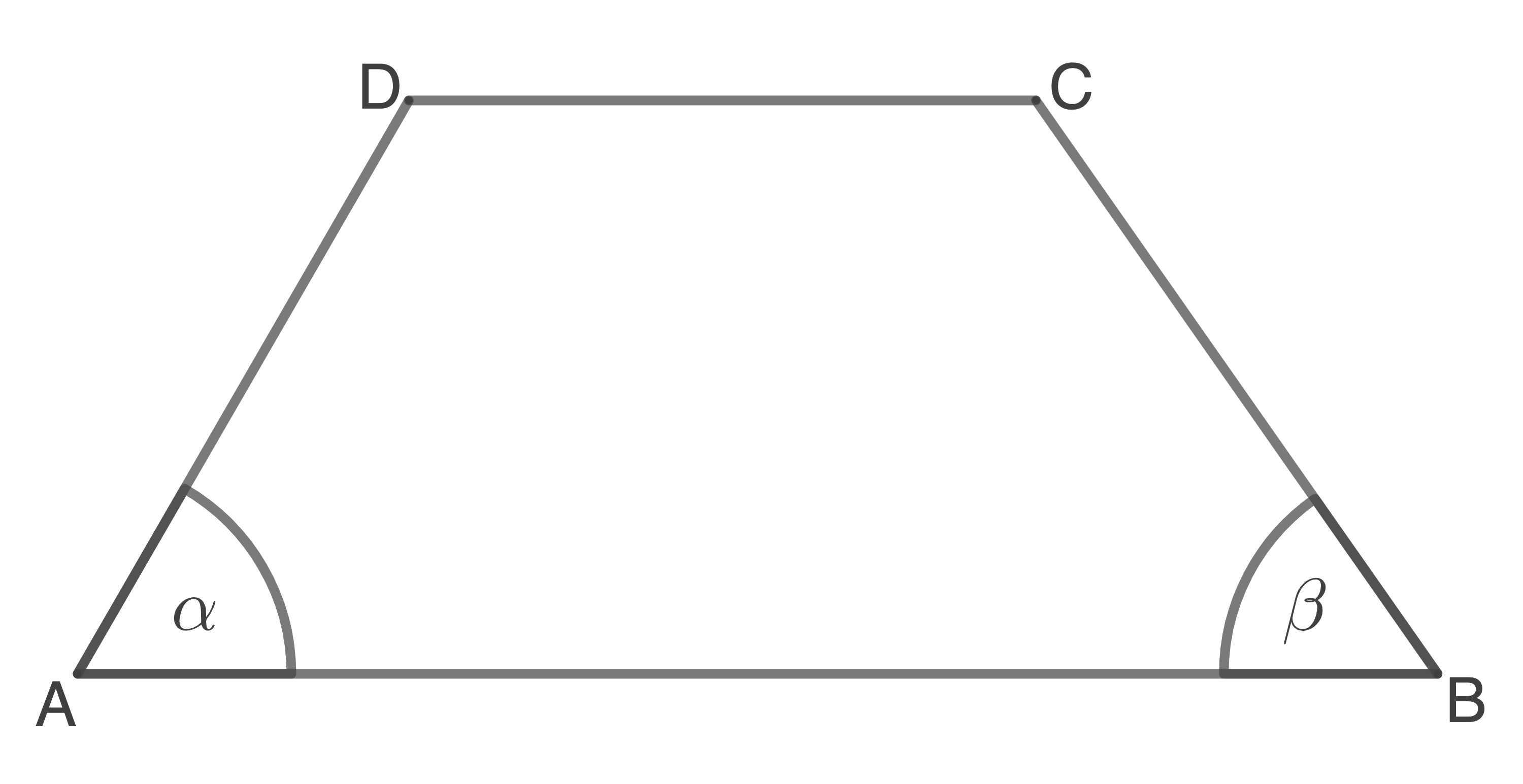



 Berechne die Länge der Strecke
Berechne die Länge der Strecke 

(Skizze nicht maßstäblich)
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Aufgabe 8
a)
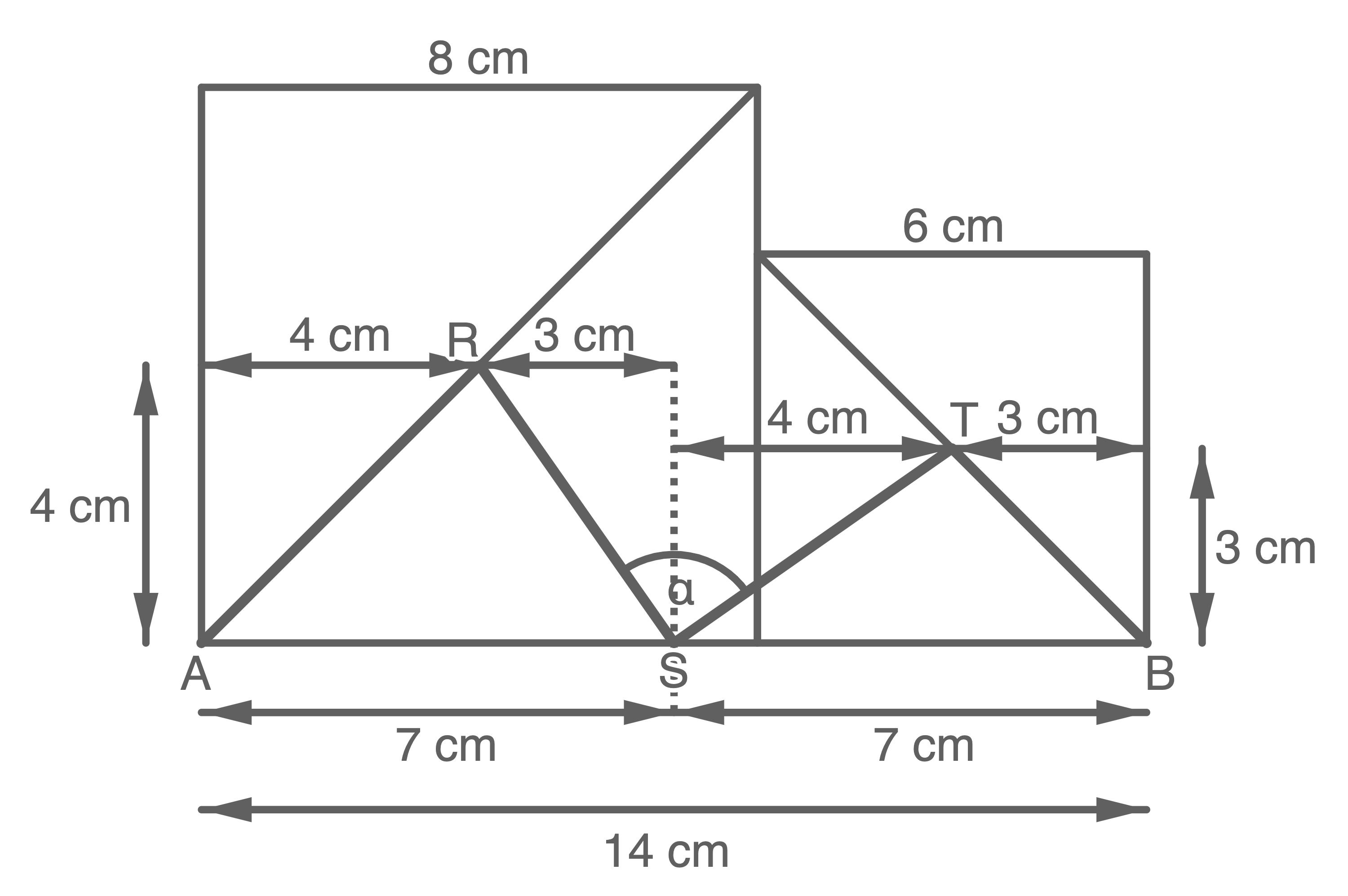
Zwei Quadrate mit den Seitenlängen 8,0 cm und 6,0 cm werden aneinandergelegt.  und
und  sind Mittelpunkte der Diagonalen,
sind Mittelpunkte der Diagonalen,  ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke 
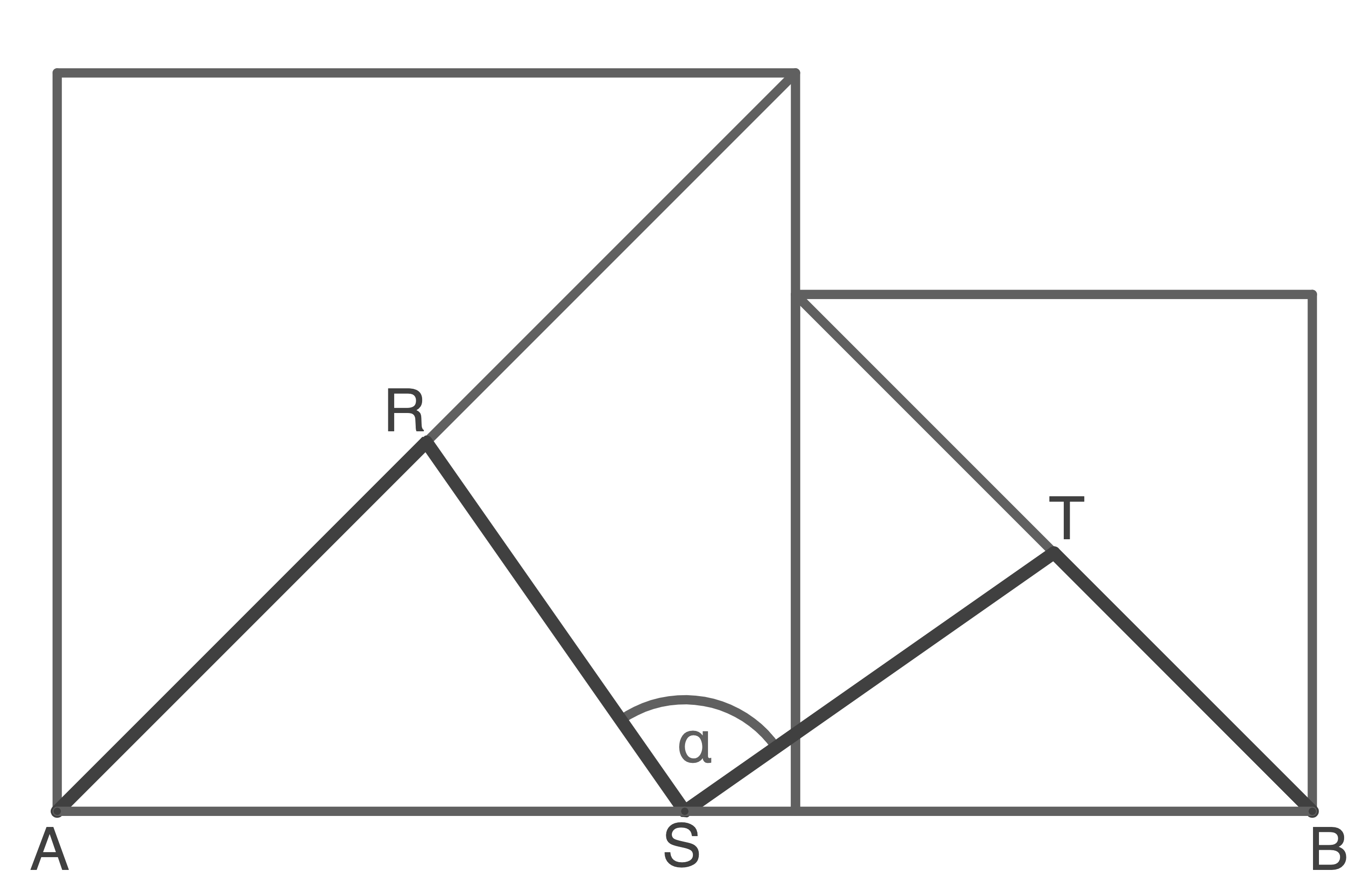 Berechne die Länge des Streckenzuges
Berechne die Länge des Streckenzuges  und die Größe des Winkels
und die Größe des Winkels 

(Skizze nicht maßstäblich)
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Aufgabe 9
a)
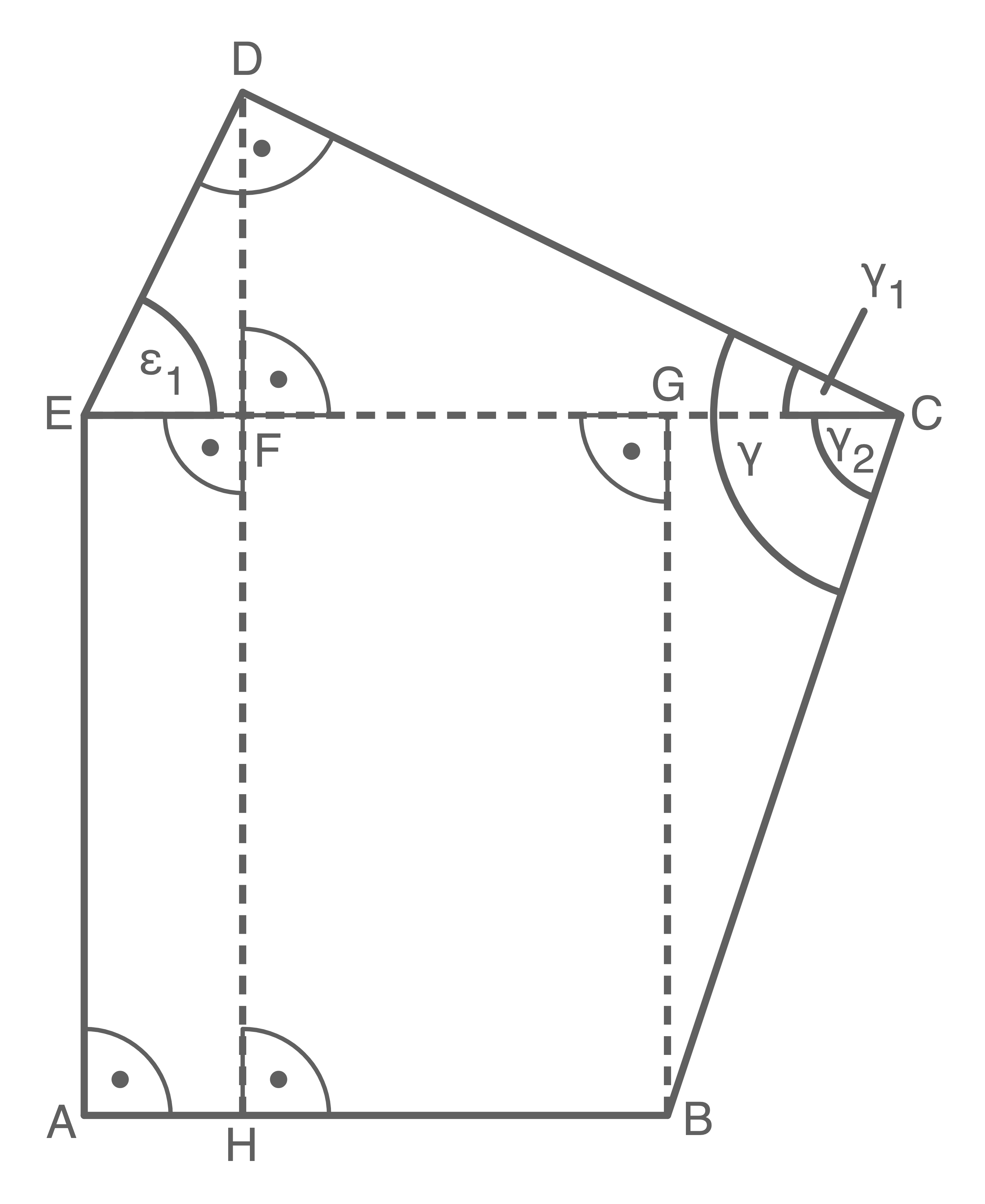
lm Fünfeck  gilt:
gilt:
![\(\begin{array}[t]{rll}
\overline{CD}&=& 9,5\,\text{cm} \\[5pt]
\varepsilon_{1}&=& 64,0^{\circ}\\[5pt]
\gamma&=& 95,0^{\circ}\\[5pt]
\overline{AB} &\parallel& \overline{CE}
\end{array}\)](https://mathjax.schullv.de/e80a6097e479600142b2d03b5cbc3abf220c2c53a7baed4d0511352e2d11da15?color=5a5a5a) Der Abstand des Punktes
Der Abstand des Punktes  zu
zu  beträgt
beträgt  Berechne den Flächeninhalt des Vierecks
Berechne den Flächeninhalt des Vierecks 
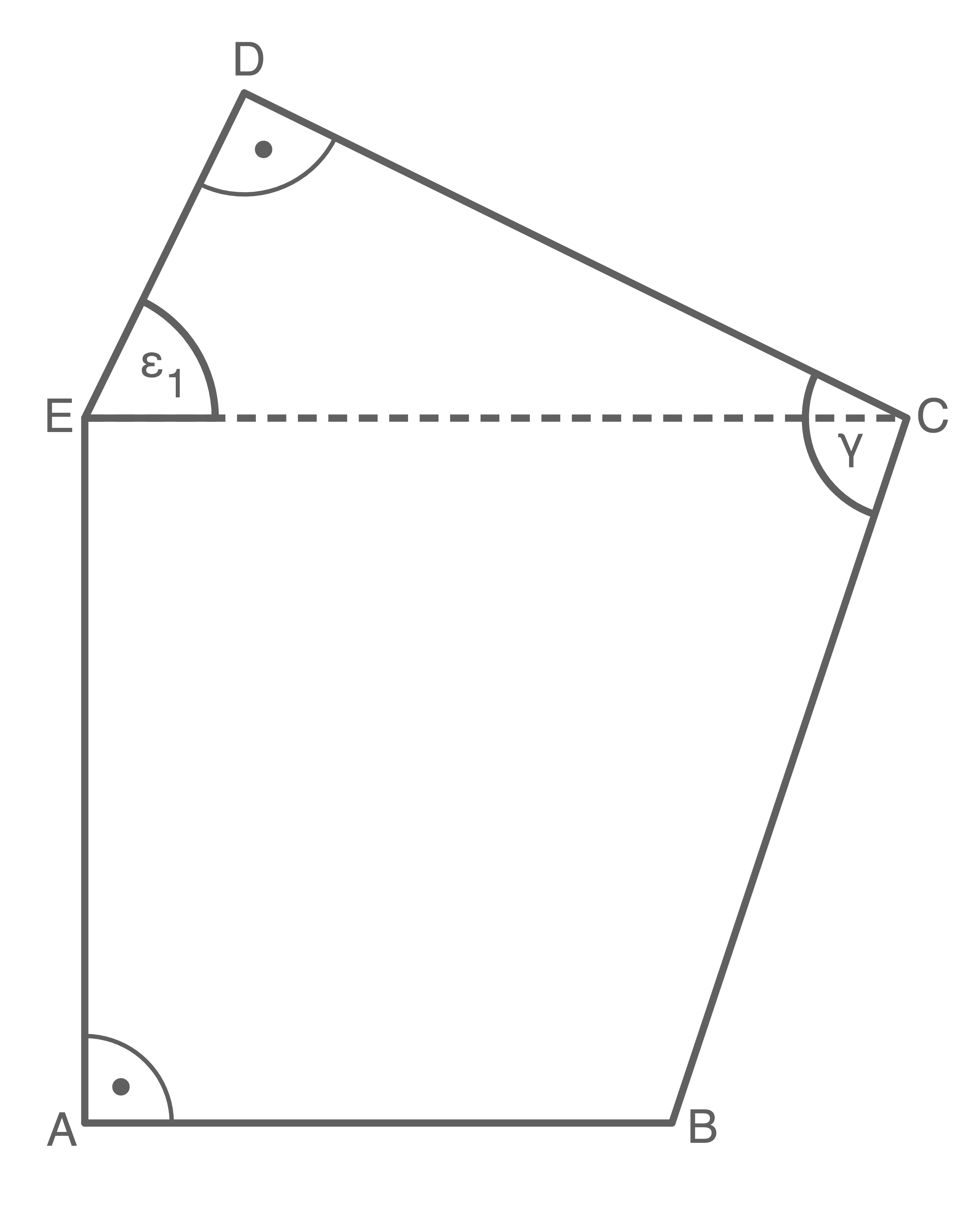
(5,5 P)
b)
lm Rechteck  liegen die gleichseitigen Dreiecke
liegen die gleichseitigen Dreiecke  und
und  Es gilt:
Es gilt:

Weise ohne Verwendung gerundeter Werte nach, dass für den Flächeninhalt des Rechtecks gilt:
gilt:

Weise ohne Verwendung gerundeter Werte nach, dass für den Flächeninhalt des Rechtecks
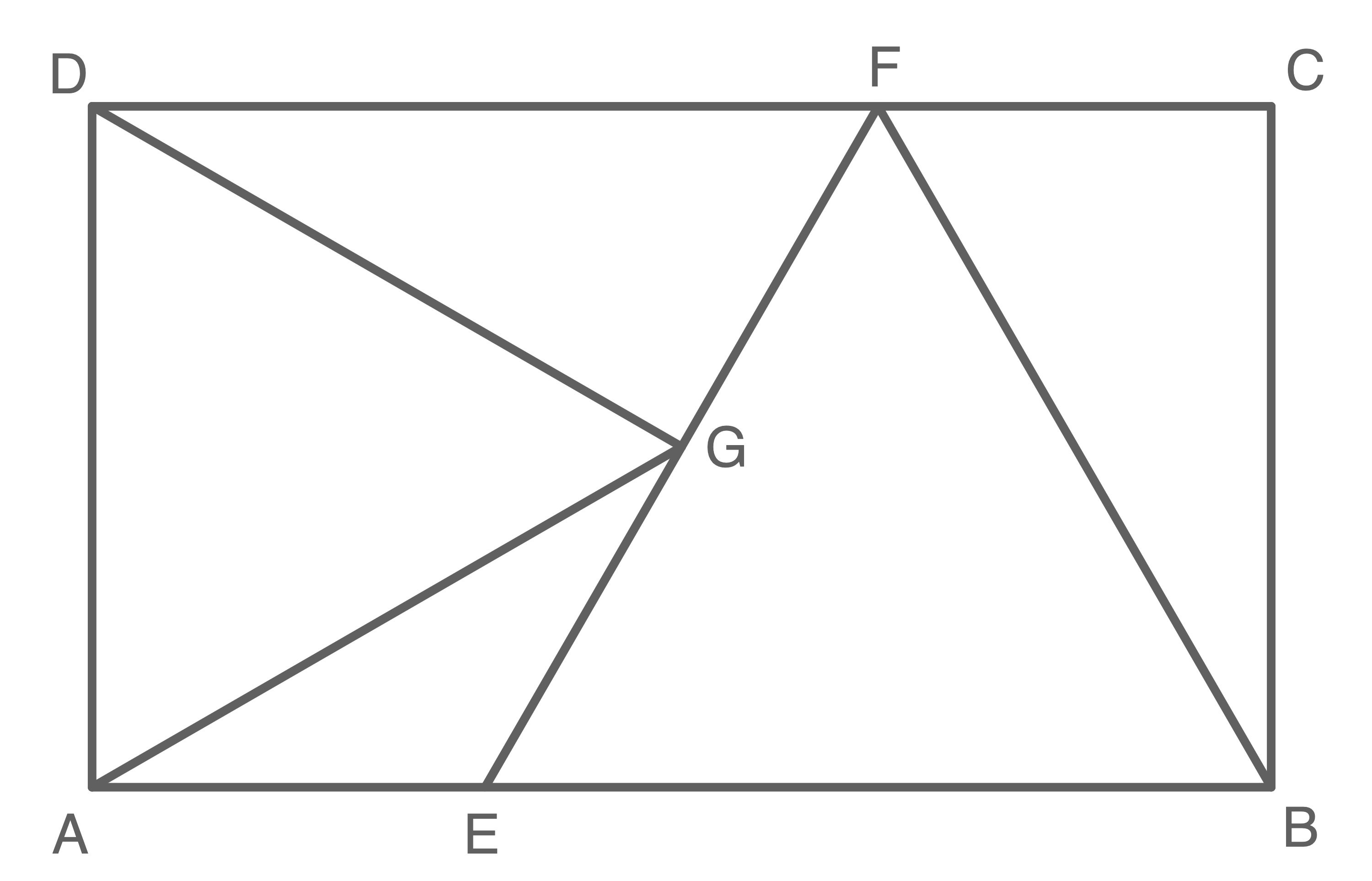
(4,5 P)
Aufgabe 10
a)
Das Fünfeck  besteht aus dem gleichseitigen Dreieck
besteht aus dem gleichseitigen Dreieck  den beiden gleichschenkligen Dreiecken
den beiden gleichschenkligen Dreiecken  und
und  sowie dem Drachenviereck
sowie dem Drachenviereck 
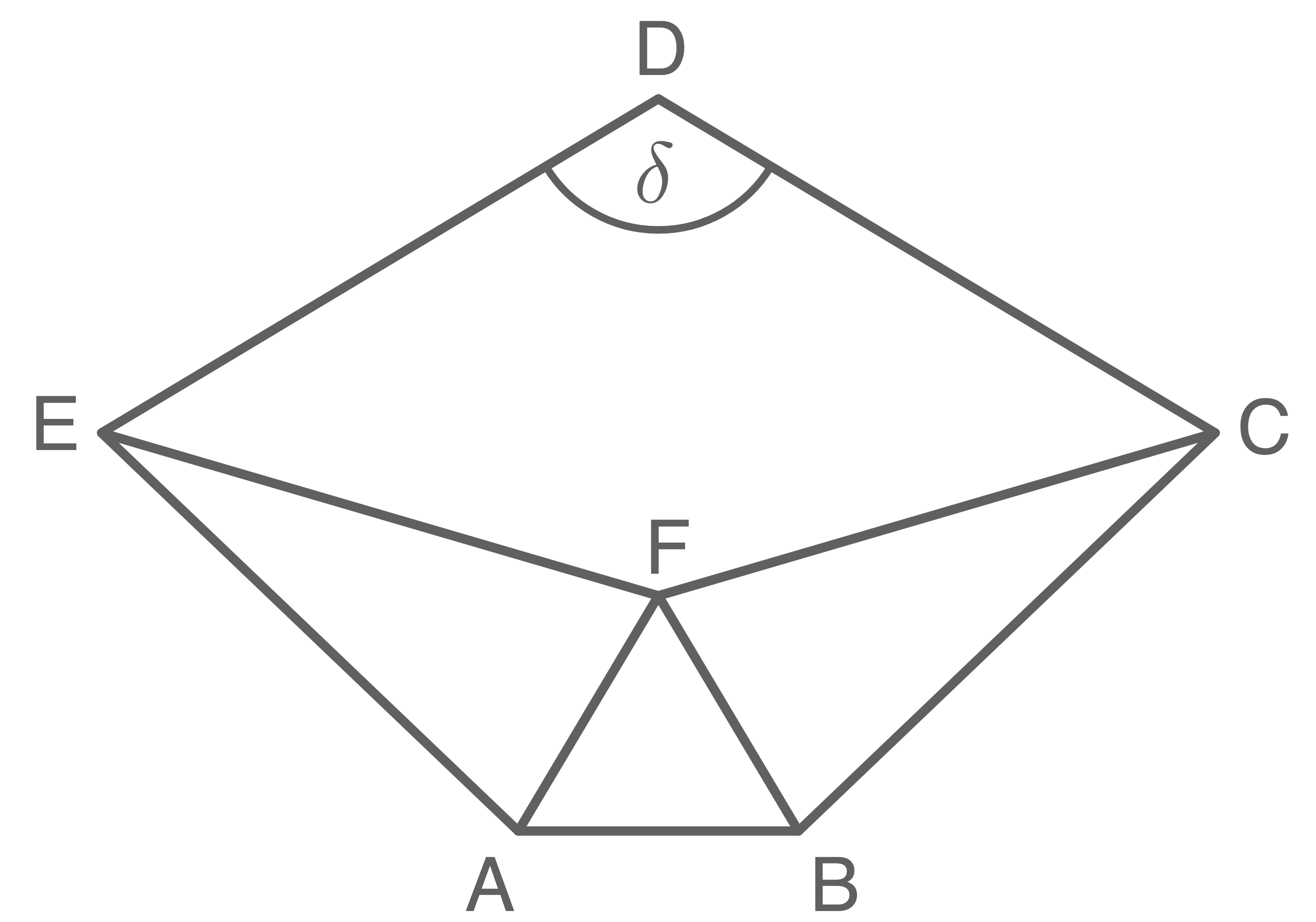 Es gilt:
Es gilt:


 Berechne den Abstand des Punktes
Berechne den Abstand des Punktes  zur Strecke
zur Strecke 

(5,5 P)
b)
Ein DIN-A4-Blatt mit den Eckpunkten  ,
, 
 und
und  wird entlang von
wird entlang von  gefaltet. Dadurch entsteht der Punkt
gefaltet. Dadurch entsteht der Punkt  auf
auf 
 Es gilt:
Es gilt:
 Berechne den Flächeninhalt des Vierecks
Berechne den Flächeninhalt des Vierecks 


(4,5 P)
Aufgabe 11
a)
Gegeben ist das Dreieck 
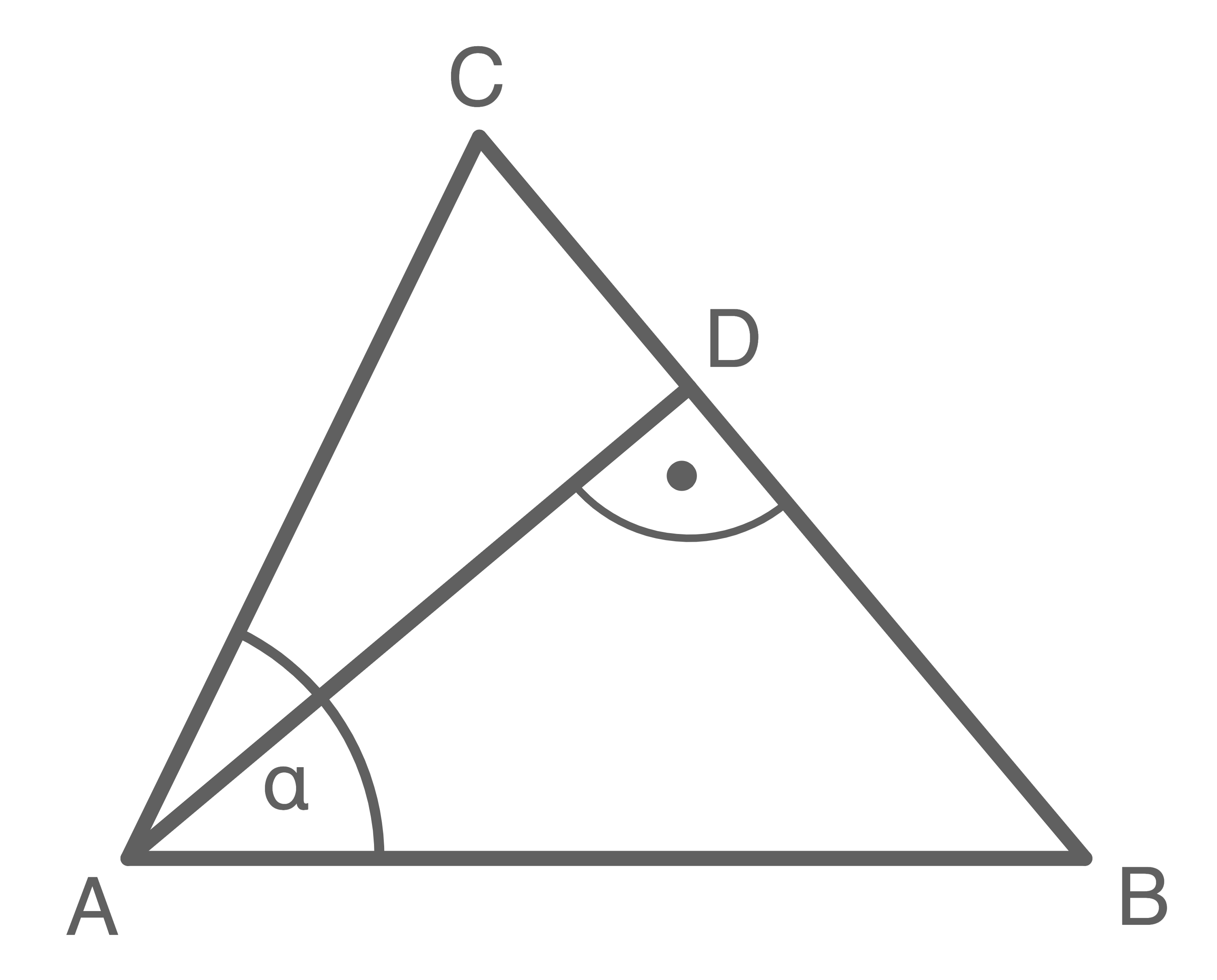 Es gilt:
Es gilt:


 Berechne den Winkel
Berechne den Winkel  sowie den Abstand des Punktes
sowie den Abstand des Punktes  zur Strecke
zur Strecke 

(5,5 P)
b)
Im rechtwinkligen Dreieck  liegt das gleichseitige Dreieck
liegt das gleichseitige Dreieck 
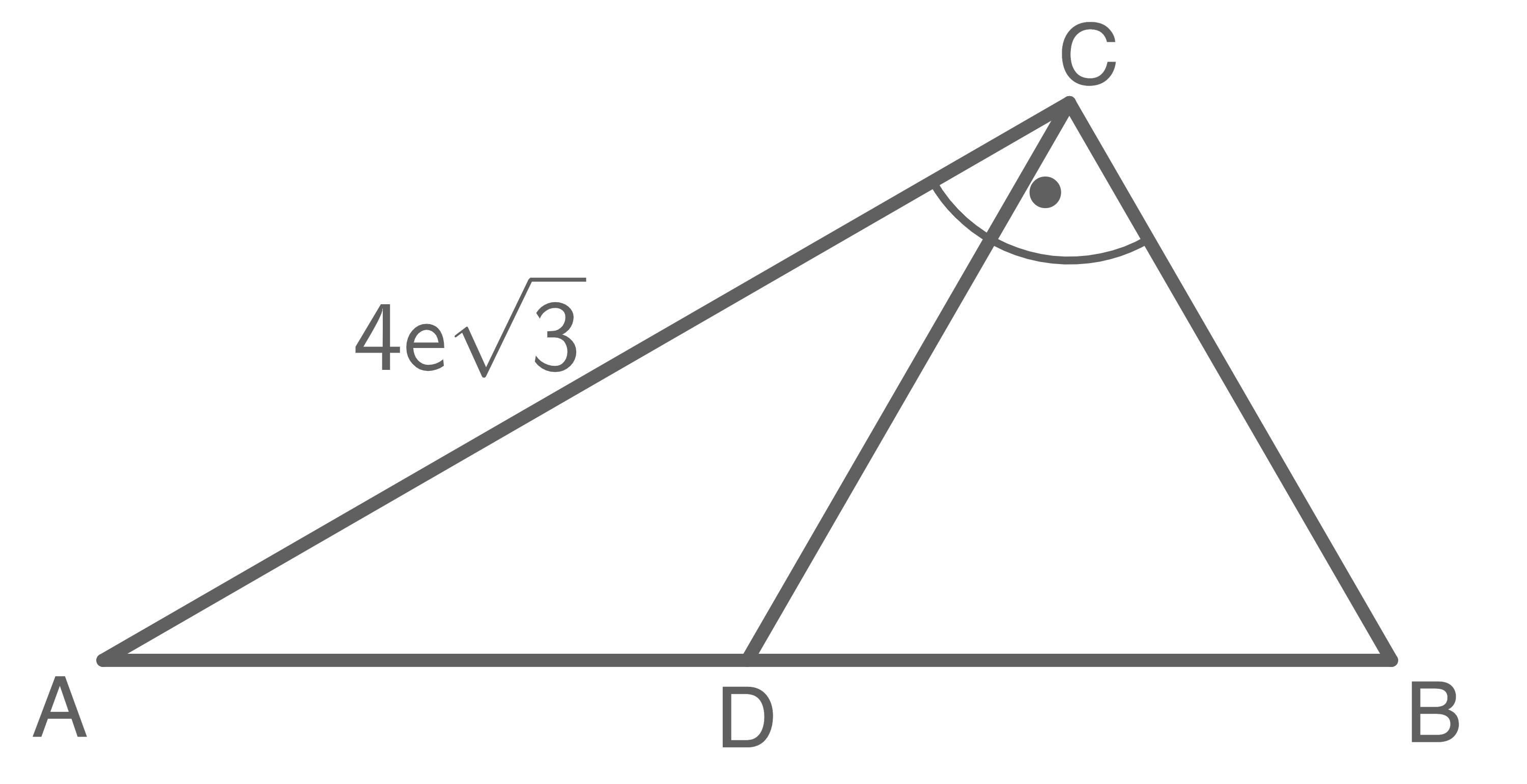
Zeige ohne Verwendung gerundeter Werte, dass die beiden Dreiecke und
und  flächengleich sind.
flächengleich sind.
Der Flächeninhalt des Dreiecks soll
soll  betragen. Für welchen Wert von
betragen. Für welchen Wert von  trifft dies zu?
trifft dies zu?

Zeige ohne Verwendung gerundeter Werte, dass die beiden Dreiecke
Der Flächeninhalt des Dreiecks
(4,5 P)
Aufgabe 12
a)
Das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck  haben die Seite
haben die Seite  gemeinsam.
gemeinsam.
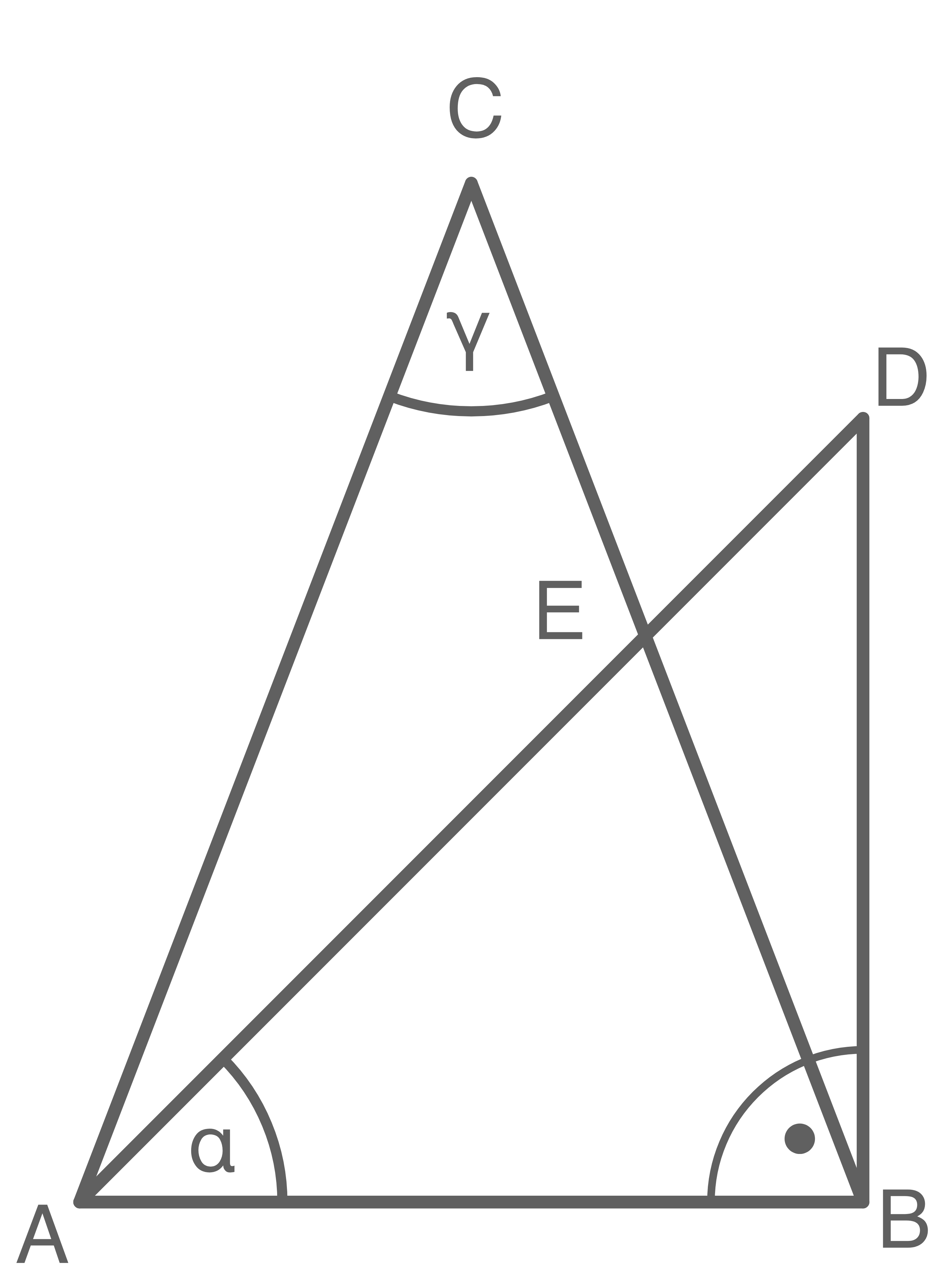 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\overline{BD}&=&7,2 \text{ cm} & \\[5pt]
\overline{DE}&=&3,0 \text{ cm} & \\[5pt]
\alpha&=&42,0^{\circ} & \\[5pt]
\overline{AC}&=&\overline{BC}
\end{array}\)](https://mathjax.schullv.de/173beec24dfb84acf70b77bc0c5969496211bc9cf7a25a3bb4404c07f6ac96fa?color=5a5a5a) Berechne den Abstand des Punktes
Berechne den Abstand des Punktes  von
von  sowie den Winkel
sowie den Winkel  .
.

(5,5 P)
b)
Gegeben sind ein rechtwinkliges Trapez  und ein regelmäßiges Sechseck.
und ein regelmäßiges Sechseck.
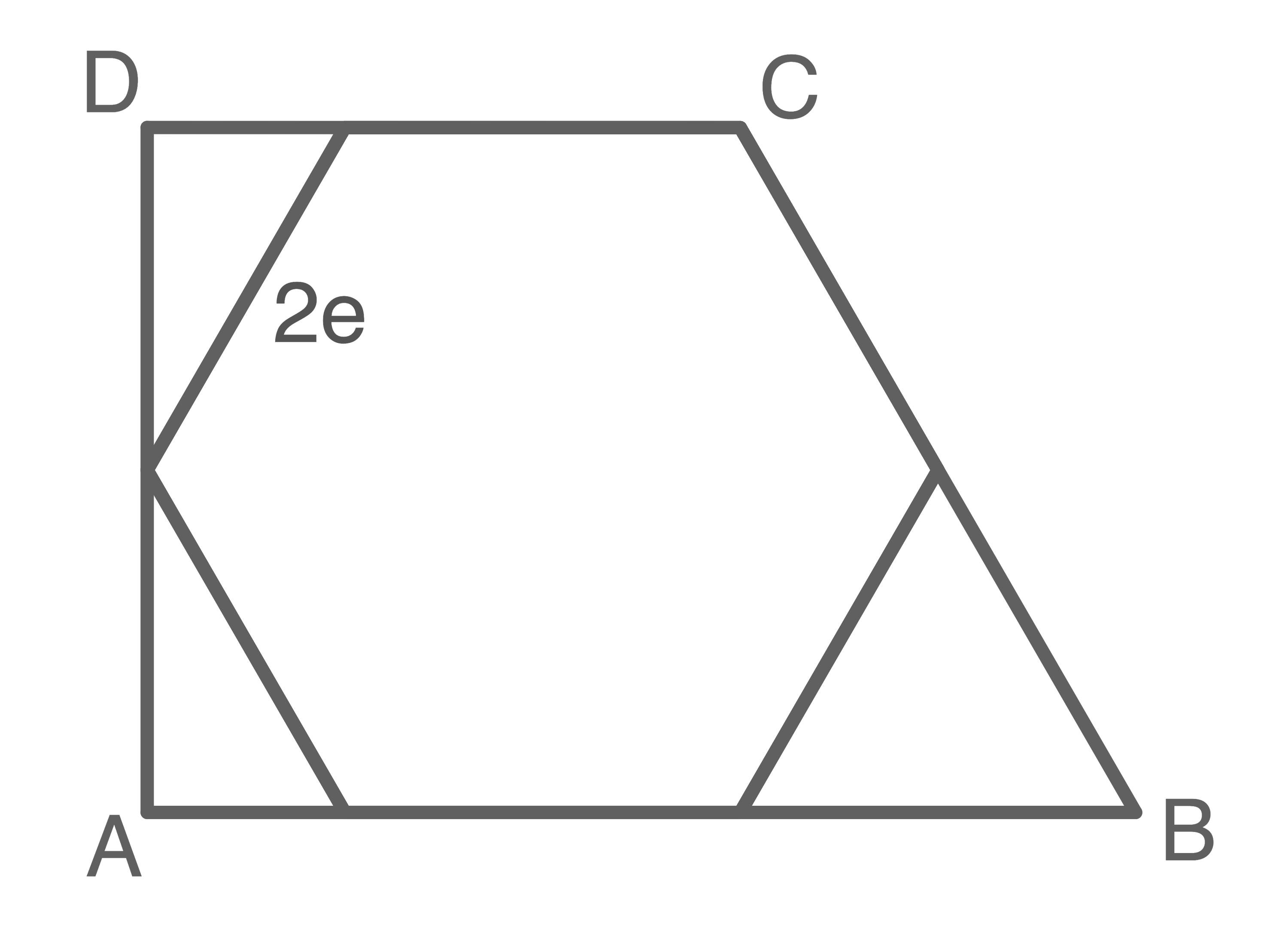 Die Eckpunkte des Sechsecks liegen auf den Seiten des Trapezes.
Zeige ohne Verwendung gerundeter Werte, dass für den Flächeninhalt des Trapezes
Die Eckpunkte des Sechsecks liegen auf den Seiten des Trapezes.
Zeige ohne Verwendung gerundeter Werte, dass für den Flächeninhalt des Trapezes  gilt:
gilt:
 Gib die Länge der Diagonale
Gib die Länge der Diagonale  ohne Verwendung gerundeter Werte an.
ohne Verwendung gerundeter Werte an.

(4,5 P)
Aufgabe 13
a)
Die Eckpunkte des Vierecks  liegen auf den Parallelen
liegen auf den Parallelen  und
und  .
.
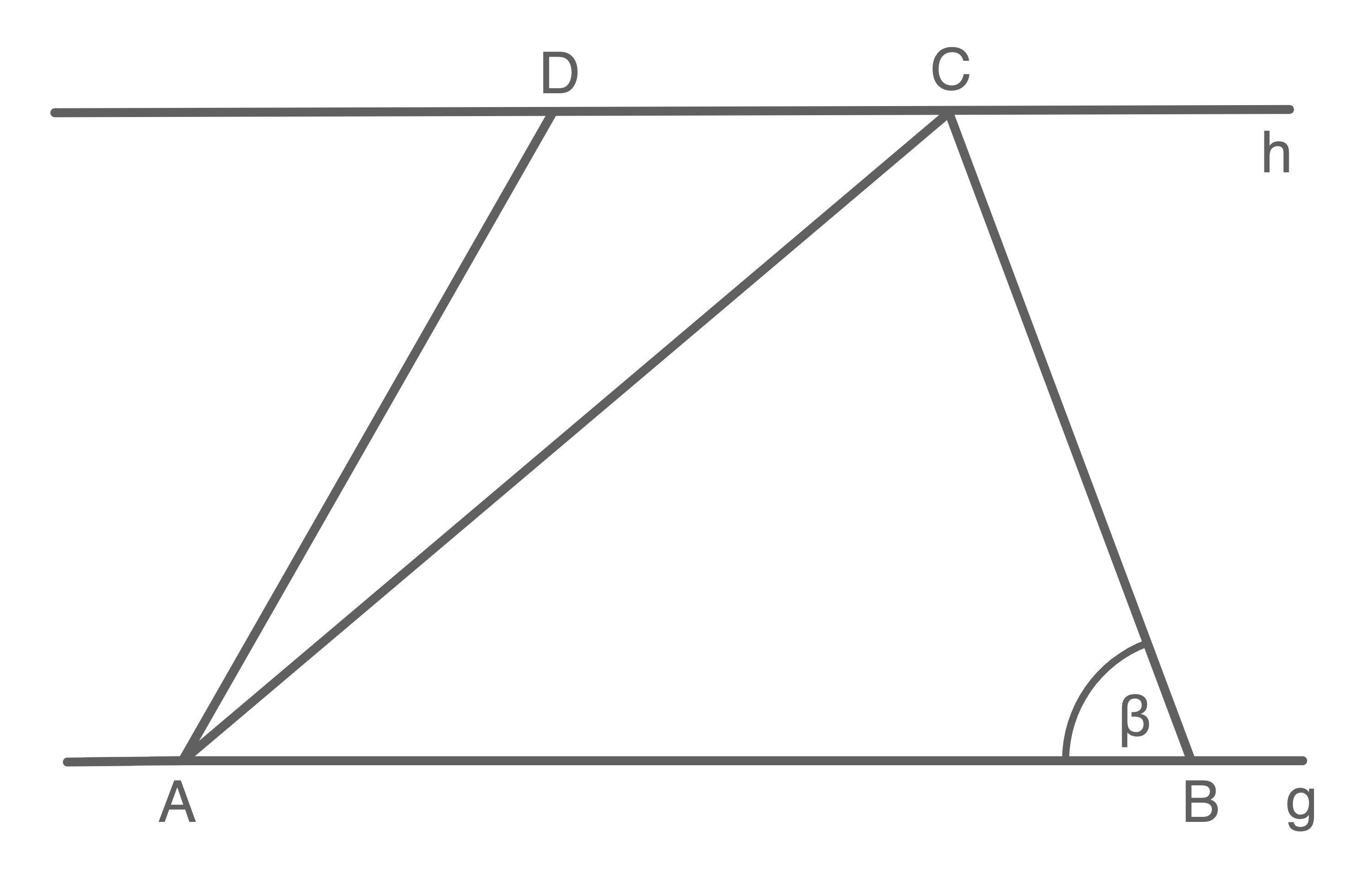 Die Parallelen haben einen Abstand von
Die Parallelen haben einen Abstand von  .
Es gilt:
.
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AD}&=& 10,4\,\text{cm} &\\[5pt]
\beta&=& 70,0^{\circ}&\\[5pt]
\overline{AB}&=&\overline{AC} &\\[5pt]
\end{array}\)](https://mathjax.schullv.de/fbbc62357e70049f6187b49cfcb1b6d2ec2d5f0bbc6316661cd5a46197ccf789?color=5a5a5a) Berechne den Umfang des Vierecks
Berechne den Umfang des Vierecks 

(5,5 P)
b)
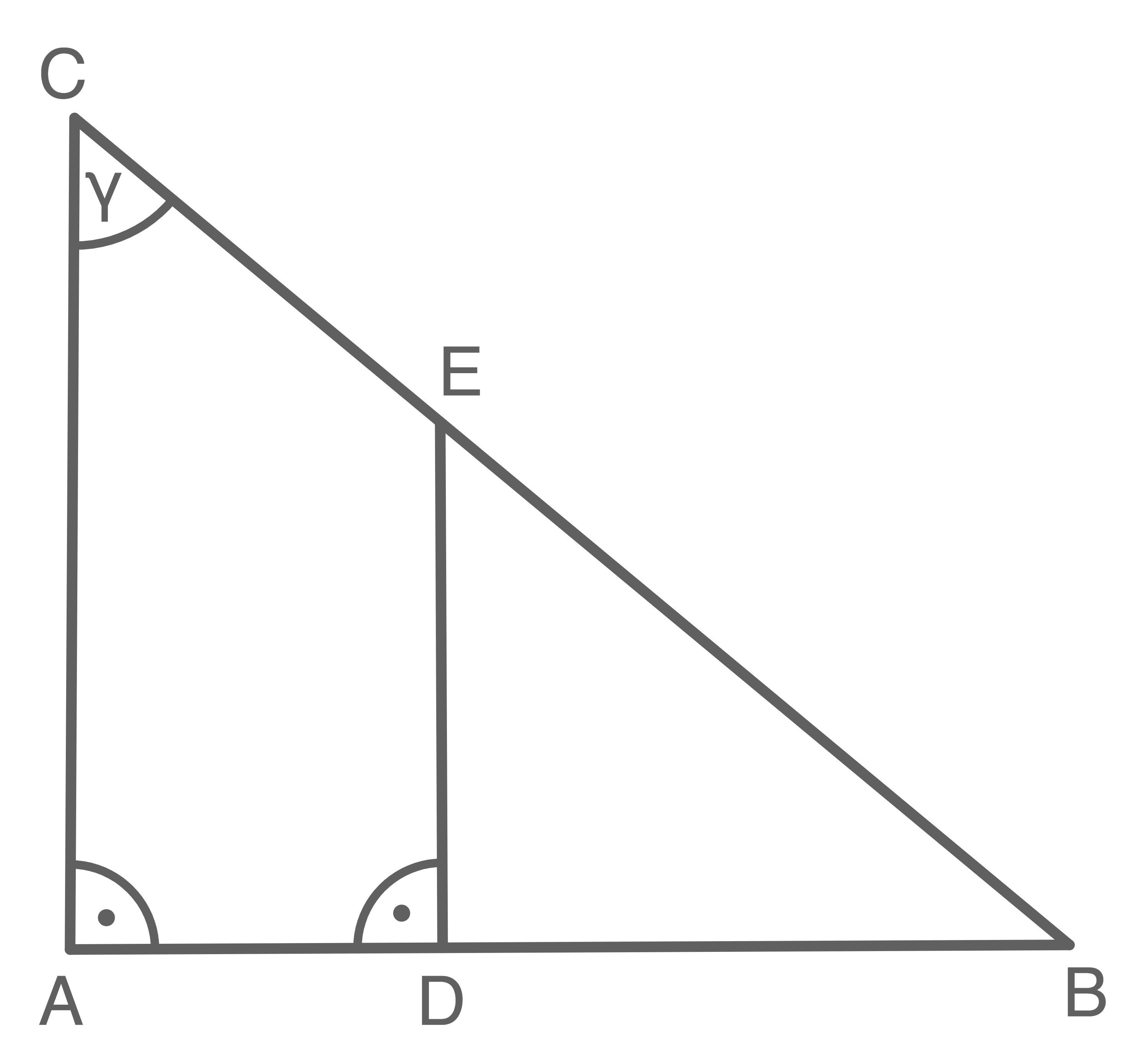
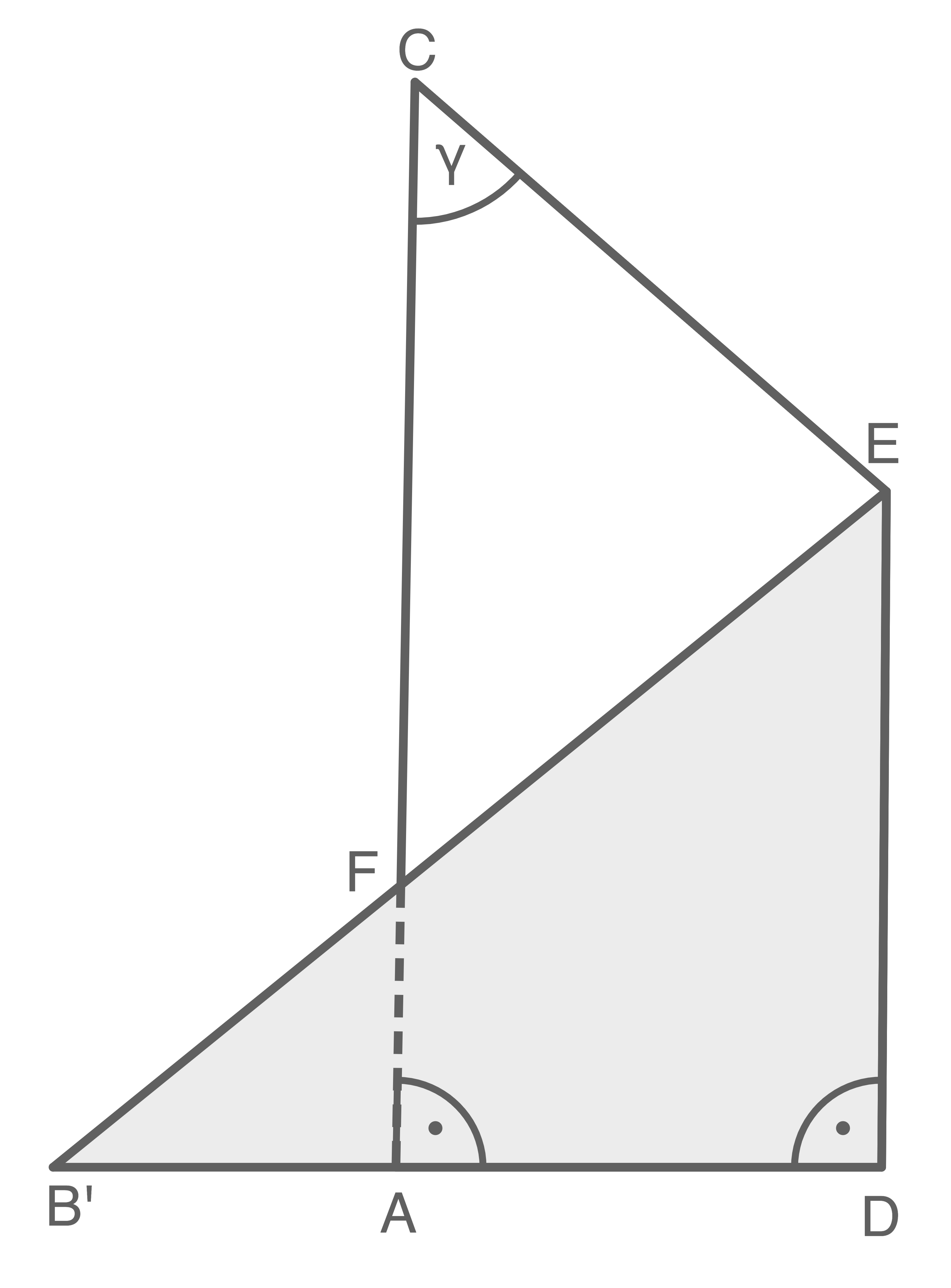
(4,5 P)
Aufgabe 14
a)
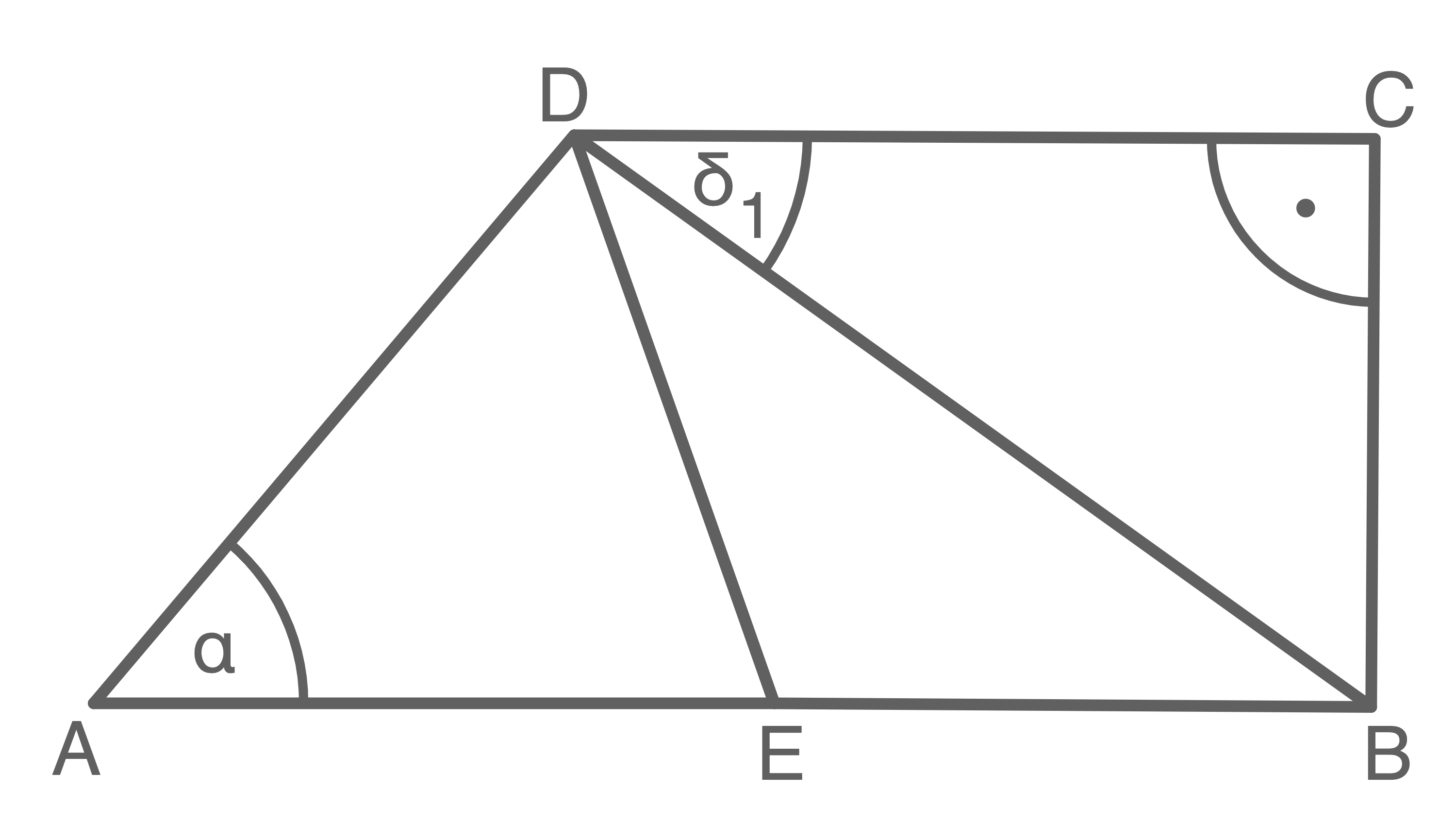
Berechne den Flächeninhalt des Dreiecks
(5,5 P)
b)
Von einem rechteckigen Blatt Papier wird entlang der gestrichelten Linie ein Stück abgeschnitten und an einer anderen Stelle angelegt (siehe Skizze).
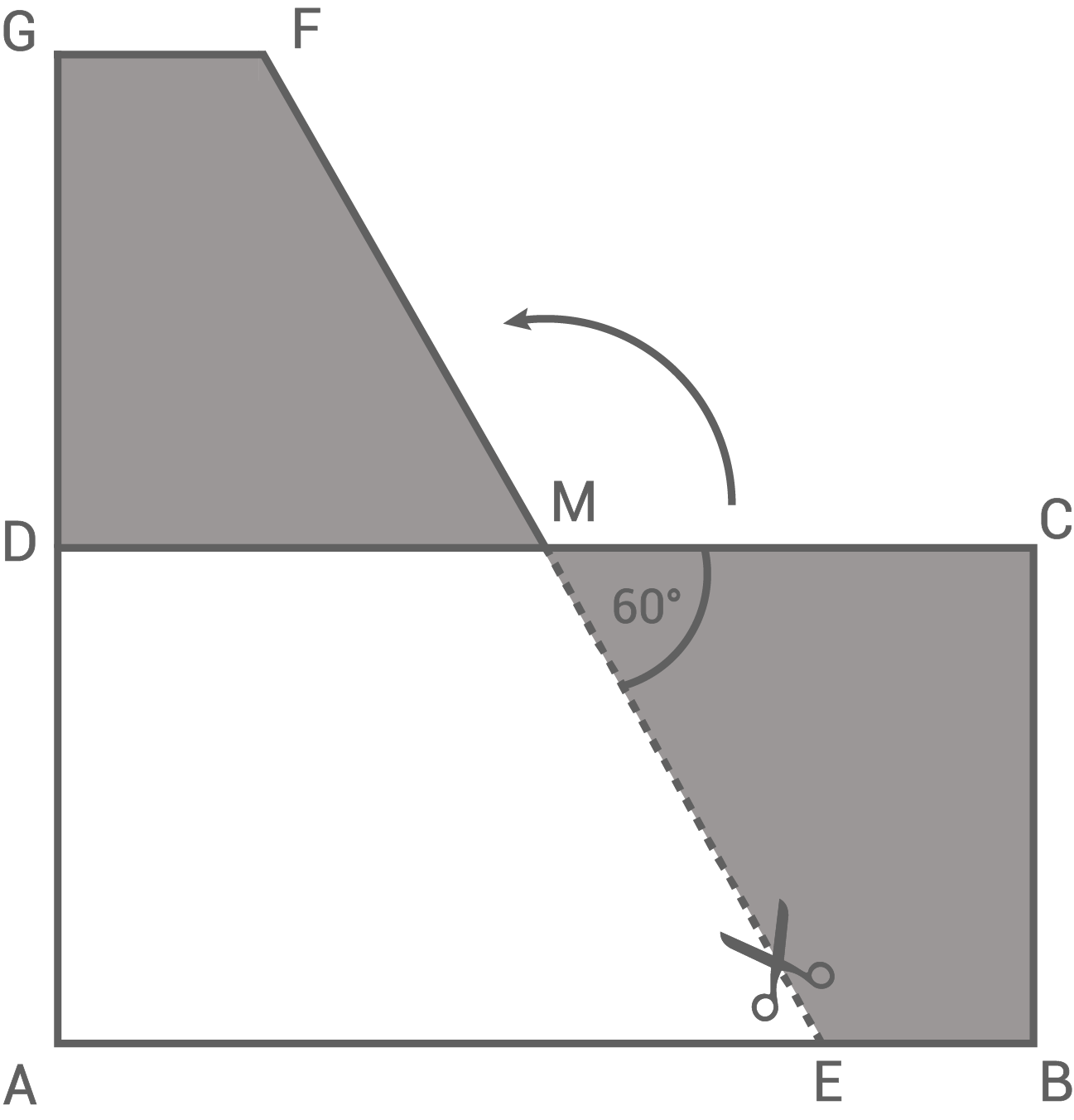 Es gilt:
Es gilt:


 ist Mittelpunkt von
ist Mittelpunkt von  Bea behauptet:
Bea behauptet:
„Das Viereck hat den gleichen Umfang wie das Rechteck
hat den gleichen Umfang wie das Rechteck  “.
“.
Hat Bea recht?
Begründe deine Aussage rechnerisch oder durch Argumentation.

„Das Viereck
Hat Bea recht?
Begründe deine Aussage rechnerisch oder durch Argumentation.
(4,5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Winkel  berechnen
Aufgrund des Symmetrie des Drachenvierecks hat der Winkel
berechnen
Aufgrund des Symmetrie des Drachenvierecks hat der Winkel  die gleiche Größe wie der Winkel
die gleiche Größe wie der Winkel  Daher gilt:
Daher gilt:

 Umfang des Vierecks
Umfang des Vierecks  berechnen
1. Schritt:
berechnen
1. Schritt:  bestimmen
Aufgrund der Symmetrie des Drachenvierecks gilt
bestimmen
Aufgrund der Symmetrie des Drachenvierecks gilt  2. Schritt:
2. Schritt:  berechnen
berechnen

 3. Schritt:
3. Schritt:  berechnen
Aufgrund der Symmetrie des Drachenvierecks gilt
berechnen
Aufgrund der Symmetrie des Drachenvierecks gilt  Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
\cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EG}} \\[5pt]
\cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EF}} \\[5pt]
\cos 20,0°&=& \dfrac{5,6\,\text{cm}}{\overline{EF}} \quad \scriptsize \mid\;\cdot \overline{EF} \\[5pt]
\cos 20,0°\cdot \overline{EF}&=& 5,6\,\text{cm} \quad \scriptsize \mid\; :\cos 20,0°\\[5pt]
\overline{EF}&=& \dfrac{5,6\,\text{cm}}{\cos 20,0°} \\[5pt]
\overline{EF}&=& \underline{5,96\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/f5bf90943ed17cf49fd773e8a5d45637f959f1fefecf98dd2d30a4d7b5640d17?color=5a5a5a) 4. Schritt:
4. Schritt:  berechnen
Zunächst muss die Länge der Strecke
berechnen
Zunächst muss die Länge der Strecke  berechnet werden:
Damit folgt für die Länge der Strecke
berechnet werden:
Damit folgt für die Länge der Strecke 
![\(\begin{array}[t]{rll}
\overline{CF}&=& \overline{CG} \\[5pt]
&=& \overline{AD}-\overline{BG} \\[5pt]
&=& 5,6\,\text{cm}-2,04\,\text{cm} \\[5pt]
&=& 3,56\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/1380d2dd0cbce00401e36a1121ff576556e3424b058a0e6f820a8949b2c6631b?color=5a5a5a) Insgesamt gilt dann für die Strecke
Insgesamt gilt dann für die Strecke 
![\(\begin{array}[t]{rll}
\overline{DF}&=& \overline{AB}-\overline{CF} \\[5pt]
&=& 9,4\,\text{cm}-3,56\,\text{cm} \\[5pt]
&=& \underline{5,84\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/fc8e7cb8d8db7452437839a8528feb58ce874672b173677d4a843e87cad5abd7?color=5a5a5a) 5. Schritt: Umfang berechnen
5. Schritt: Umfang berechnen
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2024
Lösung 2
a)
Hilfsskizze:
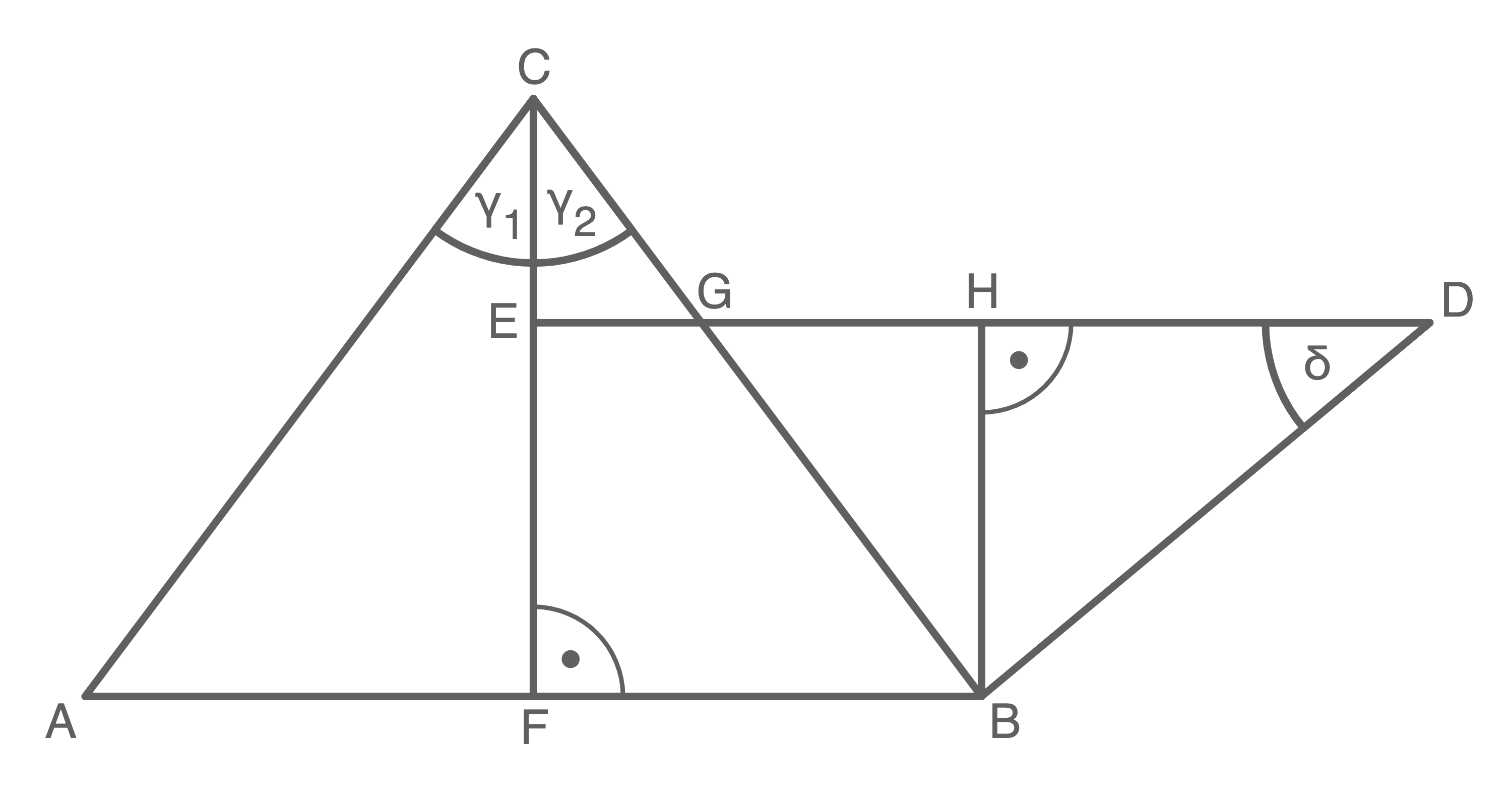 1. Schritt: Länge von
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\gamma_1&=&\dfrac{\overline{AF}}{\overline{AC}} \quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\sin\gamma_1\cdot \overline{AC}&=&\overline{AF}\\[5pt]
\overline{AF}&=&\sin\gamma_1\cdot \overline{AC}\\[5pt]
&=&\sin 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{AF}&=&\underline{6,96\,\text{cm}}=\overline{BF}
\end{array}\)](https://mathjax.schullv.de/dcc53dafe9a49d40e4ab0d2a03e1550f3dd1c585d4161498121ee1d24f6cf467?color=5a5a5a) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\delta&=&\dfrac{\overline{BH}}{\overline{BD}} \quad \scriptsize \mid\;\cdot \overline{BD} \\[5pt]
\sin\delta\cdot \overline{BD}&=&\overline{BH}\\[5pt]
\overline{BH}&=&\sin\delta\cdot \overline{BD}\\[5pt]
&=&\sin 39,2^\circ\cdot 8,2\,\text{cm}\\[5pt]
\overline{BH}&=&\underline{5,18\,\text{cm}}=\overline{EF}
\end{array}\)](https://mathjax.schullv.de/1c6dcf442e1d9de3af8ace8871ace8642933b403aa17ec1e943f7d3049a708f4?color=5a5a5a) 3. Schritt: Länge von
3. Schritt: Länge von  berechnen
3.1. Schritt: Länge von
berechnen
3.1. Schritt: Länge von  berechnen
Es gilt:
berechnen
Es gilt:  und
und 
![\(\begin{array}[t]{rll}
\cos\gamma_2&=&\dfrac{\overline{CF}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt]
\cos\gamma_2\cdot \overline{BC}&=&\overline{CF}\\[5pt]
\overline{CF}&=&\cos\gamma_2\cdot \overline{BC}\\[5pt]
&=&\cos 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{CF}&=&9,03\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/771528dbb41d53ab9d7f9d27d8a9b18dd7bd8a3192f6c9996b8869480c70a644?color=5a5a5a) 3.2. Schritt: Länge von
3.2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CE}&=&\overline{CF}-\overline{EF}\\[5pt]
\overline{CE}&=&9,03\,\text{cm}-5,18\,\text{cm}\\[5pt]
\overline{CE}&=&3,85\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ffafff46286d42bf65ff3f60794966f7fb29fb8f068cbd5203540ea45c50a1a5?color=5a5a5a) 3.3. Schritt: Länge von
3.3. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\gamma_2&=&\dfrac{\overline{EG}}{\overline{CE}} \quad \scriptsize \mid\;\cdot \overline{CE} \\[5pt]
\tan\gamma_2\cdot \overline{CE}&=&\overline{EG}\\[5pt]
\overline{EG}&=&\tan\gamma_2\cdot \overline{CE}\\[5pt]
&=&\tan37,6^\circ\cdot 3,85\,\text{cm}\\[5pt]
\overline{EG}&=&\underline{2,96\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/89d479436556b14e7543658774fdae6307c33e1bd5bb0685e2a22ffc0f3d4c8b?color=5a5a5a) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{\overline{BF}+\overline{EG}}{2}\cdot\overline{EF}\\[5pt]
&=&\dfrac{6,96\,\text{cm}+2,96\,\text{cm}}{2}\cdot 5,18\,\text{cm}\\[5pt]
A&=&\underline{\underline{25,7\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/ebb137dcaeb9d20e4dc05e839fd31af90119e2c7ce6ebecd6a76b801e0459d26?color=5a5a5a)

b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Lösung 3
a)
Flächeninhalt des Dreiecks berechnen
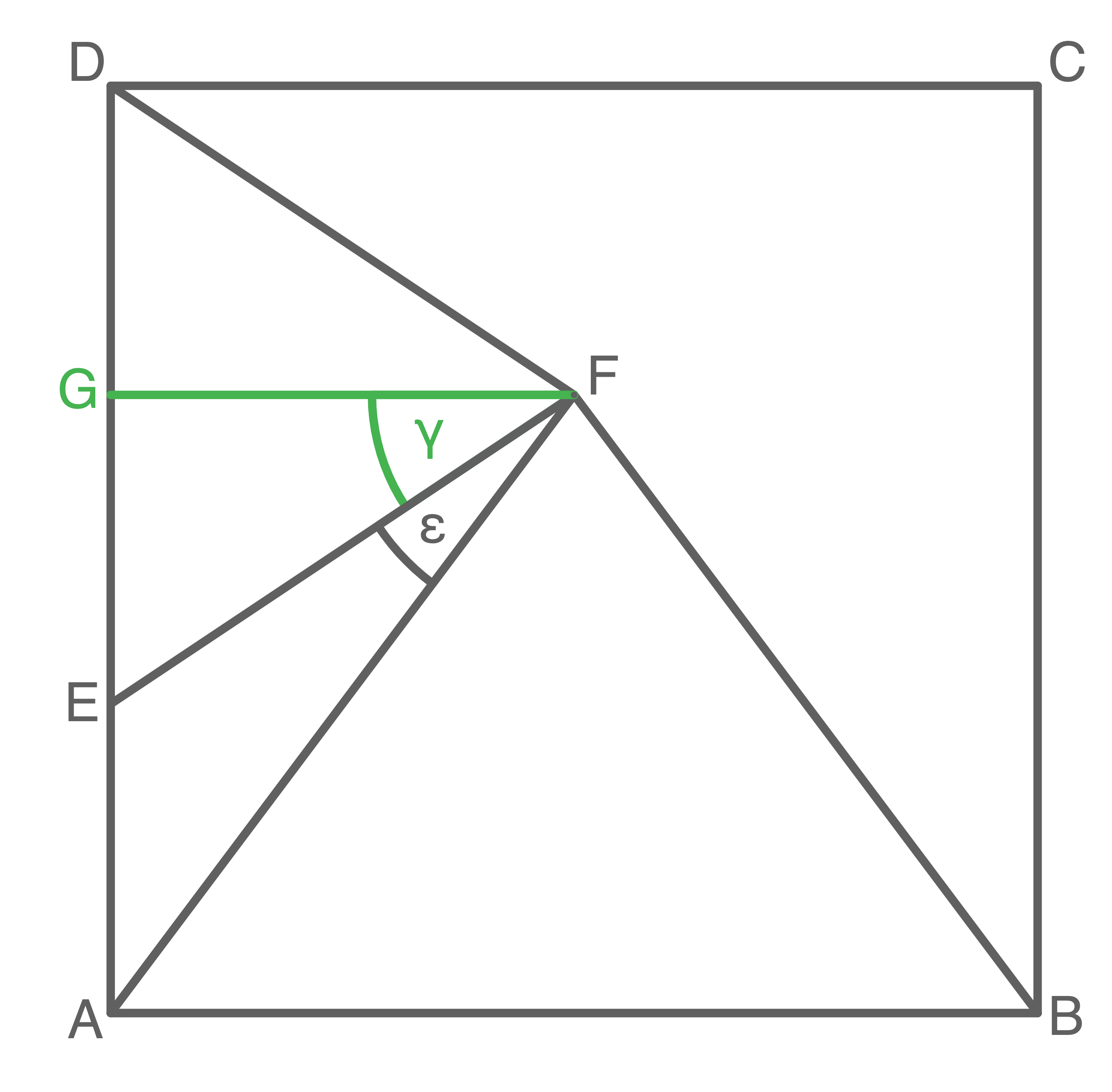 1. Schritt: Länge von
1. Schritt: Länge von  berechnen
berechnen
 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen











 3. Schritt: Flächeninhalt berechnen
3. Schritt: Flächeninhalt berechnen



 Größe des Winkels
Größe des Winkels  berechnen
1. Schritt: Größe des Winkels
berechnen
1. Schritt: Größe des Winkels  berechnen
berechnen


 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
berechnen


 3. Schritt: Größe des Winkels
3. Schritt: Größe des Winkels  berechnen
berechnen




b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2022
Lösung 4
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Lösung 5
a)
Länge der Strecke  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
Dazu wird zunächst die Länge der Strecke
berechnen
Dazu wird zunächst die Länge der Strecke  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overline{AB}}{\overline{AC}} \quad \scriptsize \mid\;\cdot\overline{AC}\;\\[5pt]
\cos(\alpha)\cdot \overline{AC}&=&\overline{AB} \quad \scriptsize \mid\; :\cos(\alpha) \\[5pt]
\overline{AC}&=&\dfrac{\overline{AB}}{\cos(\alpha)}\\[5pt]
\overline{AC} &=&\dfrac{13,2\,\text{cm}}{\cos(55^\circ)}\\[5pt]
\overline{AC} &=& 23,01\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/c3d5204d2ec558c4dcc216970b07a6a102b170f63aede46b10f96486cd75b543?color=5a5a5a) Damit kann nun die Länge der Strecke
Damit kann nun die Länge der Strecke  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AC}-\overline{CE} \\[5pt]
&=& 23,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& \underline{ 15,01\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/23e52ccdfce04b53322bfcdd6d292c12543a8b6a4fbbb6c7cb3f56cf4dc220d3?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Das Dreieck
berechnen
Das Dreieck  ist gleichschenklig.
Begründung:
ist gleichschenklig.
Begründung:
1.

2.
3.
4.
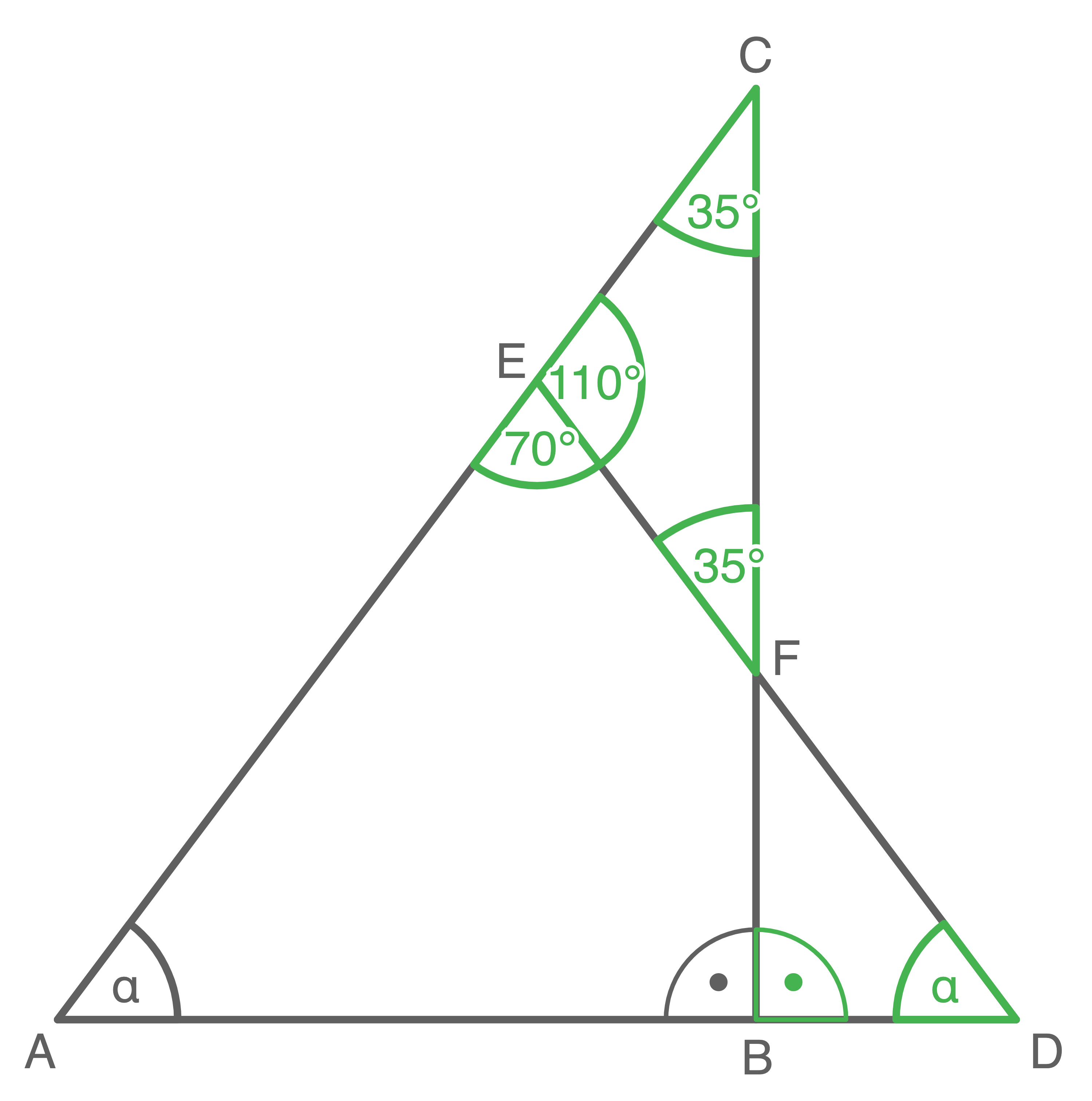 Daraus folgt:
Daraus folgt:  Da das Dreieck
Da das Dreieck  gleichschenklig ist, gilt:
gleichschenklig ist, gilt:  Damit kann nun die Länge der Strecke
Damit kann nun die Länge der Strecke  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\overline{DF}&=& \overline{DE}-\overline{EF} \\[5pt]
&=& \overline{AE}-\overline{EF} \\[5pt]
&=& 15,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& 7,01\,\text{cm}\\[5pt]
&=& \underline{\underline{ 7\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/f442d6c586f7ceed40a2c62e2ed229ff65b9eb637998beee9d8e69756df7832e?color=5a5a5a) Umfang des Vierecks
Umfang des Vierecks  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BF}}{\overline{DF}}\quad \scriptsize \mid\;\cdot \overline{DF} \\[5pt]
\sin(\alpha)\cdot\overline{DF} &=& \overline{BF}\\[5pt]
\sin(55^\circ)\cdot 7\,\text{cm} &=& \overline{BF}\\[5pt]
5,73\,\text{cm} &\approx& \overline{BF}\\
\overline{BF} &\approx&\underline{ 5,73\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/e90a5538e6fb7f872f89722bb621d98782b2bb1b49c43cf408512f2fc3dab053?color=5a5a5a) 2. Schritt: Umfang berechnen
2. Schritt: Umfang berechnen
1.
2.
3.
4.

b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Lösung 6
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Flächeninhalt des Dreicks  berechnen
berechnen
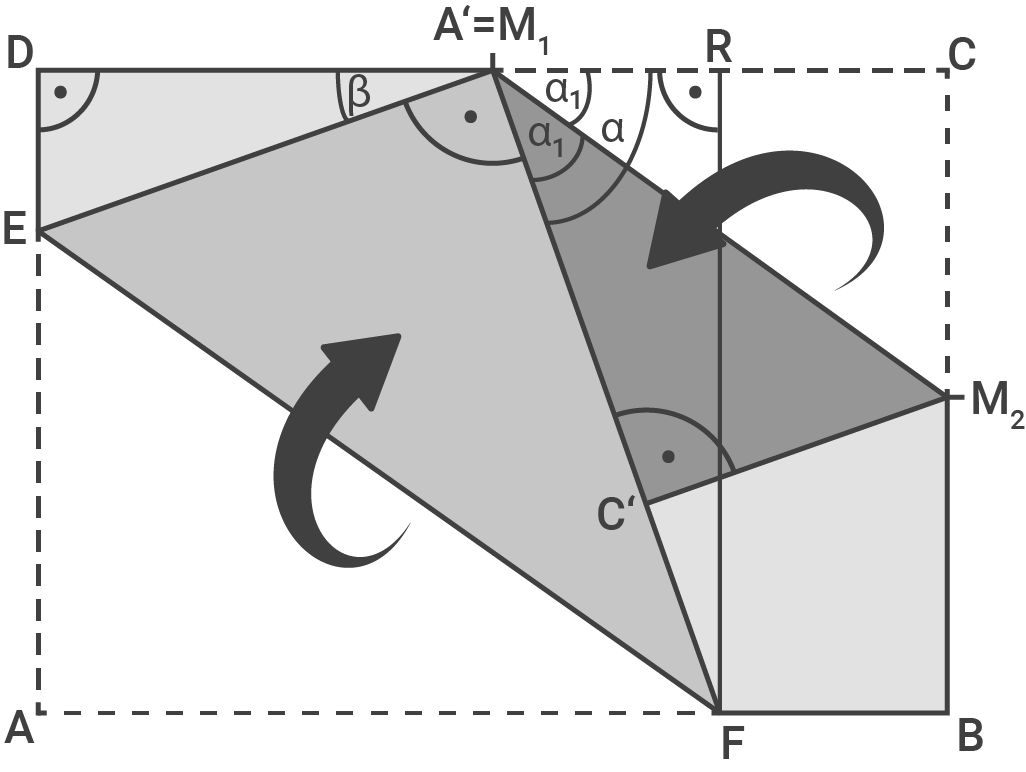 Formel zur Berechnung des Flächeninhalts:
Formel zur Berechnung des Flächeninhalts:  1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{M_1D}&=&\dfrac{1}{2}\cdot \overline{CD} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 29,7\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 14,85\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/3d9fbaffe4dbb5b97f45c2daec732203949a4b902e974d3d8131497ec77dc096?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\overline{M_2C}&=&\dfrac{1}{2}\cdot \overline{BC} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 21\,\text{cm} \\[5pt]
&=& 10,5\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/ac8b25910fe10b53ddf7e0d4c8e1639bf43217eb9189cc4701fc5c7062c62571?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\overline{CM_1}&=& \overline{M_1D}\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/01a42a981c85c5be87fca248b698c30909994a08653cc2d082494b1f7a82b9de?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& \dfrac{\overline{M_2C}}{\overline{CM_1}} \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{\overline{M_2C}}{\overline{CM_1}}\right)&\quad \scriptsize \\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{10,5}{14,85}\right) &\quad \scriptsize \\[5pt]
\alpha_1&=& 35,26^{\circ}
\end{array}\)](https://mathjax.schullv.de/e57eca650d4171d3cf121b42ce2dcf7a812409af71ef5370c51e960524f7d07c?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\alpha&=& 2\cdot \alpha_1 &\quad \scriptsize \\[5pt]
&=& 2\cdot 35,26^{\circ} &\quad \scriptsize \\[5pt]
&=& 70,52^{\circ}
\end{array}\)](https://mathjax.schullv.de/a27c941edeb256924ba0eb0c3d447d3029732e24be5909fafce5b4be9ac8e694?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-90^{\circ}-\alpha &\quad \scriptsize \\[5pt]
&=& 180^{\circ}-90^{\circ}- 70,52^{\circ} &\quad \scriptsize \\[5pt]
&=& 19,48^{\circ}
\end{array}\)](https://mathjax.schullv.de/caad616af3534117695b0c1340653bbb808f338c9f3c635d7f32814198792058?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen:
3. Schritt: Flächeninhalt berechnen
berechnen:
3. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{EM_1D}&=&\dfrac{1}{2}\cdot \overline{M_1D}\cdot \overline{DE} \\[5pt]
&=&\dfrac{1}{2}\cdot 14,85\,\text{cm} \cdot 5,25\,\text{cm} \\[5pt]
&=& 38,98\,\text{cm} ^2
\\[5pt]
&=& \underline{\underline{ 39\,\text{cm} ^2 }}
\end{array}\)](https://mathjax.schullv.de/57fafd6519face23afbb394874d57ca47e348f8853ab5a8cf5081636993452a2?color=5a5a5a) Flächeninhalt des Vierecks
Flächeninhalt des Vierecks  berechnen
Formel zur Berechnung des Flächeninhalts:
berechnen
Formel zur Berechnung des Flächeninhalts:  1. Schritt: Flächeninhalt des Dreiecks
1. Schritt: Flächeninhalt des Dreiecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{M_1M_2C}&=&\dfrac{1}{2}\cdot \overline{M_2C}\cdot \overline{CM_1} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 10,5\,\text{cm} \cdot 14,85\,\text{cm} &\quad \scriptsize \\[5pt]
&= & \underline{ 77,96 \,\text{cm}^2}
\end{array}\)](https://mathjax.schullv.de/acd4772e511e0755038f93e30e6e0b6b7999c7d448c17c8a5695bcb7721e1fce?color=5a5a5a) 2. Schritt: Flächeninhalt des Trapezes
2. Schritt: Flächeninhalt des Trapezes  berechnen
Formel zur Berechnung des Flächeninhalts:
berechnen
Formel zur Berechnung des Flächeninhalts:  Länge der Strecke
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha) &=&\dfrac{\overline{FR}}{\overline{RM_1}} \quad \scriptsize \mid\; \cdot \overline{RM_1} \\[5pt]
\tan(\alpha)\cdot \overline{RM_1} &=& \overline{FR} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{RM_1} &=& \dfrac{\overline{FR} }{\tan(\alpha)} \quad \scriptsize \\[5pt]
\overline{RM_1} &=& \dfrac{21\,\text{cm} }{\tan(70,52^{\circ} )} \quad \scriptsize \\[5pt]
\overline{RM_1}&=& 7,43\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/e4166b73dfb87e198a4a7a2b7f52f6a983305bfb53b9edaaa6aa31663d150b69?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overline{CR}&=&\overline{CM_1}-\overline{RM_1} &\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm} - 7,43\,\text{cm} &\quad \scriptsize \\[5pt]
&=& 7,42\,\text{cm} = \overline{BF}
\end{array}\)](https://mathjax.schullv.de/a21da804fbc58efb640cbefb4de390df5765309fc4615c1172da3d4ea463cd3d?color=5a5a5a) Es gilt also:
Es gilt also:
3. Schritt: Flächeninhalt des Vierecks berechnen
berechnen

3. Schritt: Flächeninhalt des Vierecks
Lösung 7
a)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Musterprüfung 1
Lösung 8
a)
Länge des Streckenzugs  berechnen
berechnen
 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AR}^2&=& (4 \,\text{cm})^2 + (4 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{AR}&=& \sqrt{(4 \,\text{cm})^2 + (4 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5,66 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/3d91f05e3eb2a390c16fc53822bfe7845b24977a6f991ab8af9bdd5a6ec395f4?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{RS}^2&=& (4 \,\text{cm})^2 + (3 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{RS}&=& \sqrt{(4 \,\text{cm})^2 + (3 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/86d2d5582fc35c7bd3e57d19cdf53acf1af2468815a85c148e119eb79939a1c9?color=5a5a5a) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{ST}^2&=& (3 \,\text{cm})^2 + (4 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{ST}&=& \sqrt{(3 \,\text{cm})^2 + (4 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/0d90a298cd72fea58048cab28787e96f956bb672be94aaf40224e76f24d3aaf0?color=5a5a5a) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{TB}^2&=& (3 \,\text{cm})^2 + (3 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{TB}&=& \sqrt{(3 \,\text{cm})^2 + (3 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 4,24 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/e978fd5bb7e59149842b6930b9f7ccdc8e50b43016db63e7b6f1caf0a91cc1f7?color=5a5a5a) 6. Schritt: Gesamten Streckenzug
6. Schritt: Gesamten Streckenzug  berechnen
Größe des Winkels
berechnen
Größe des Winkels  berechnen
berechnen
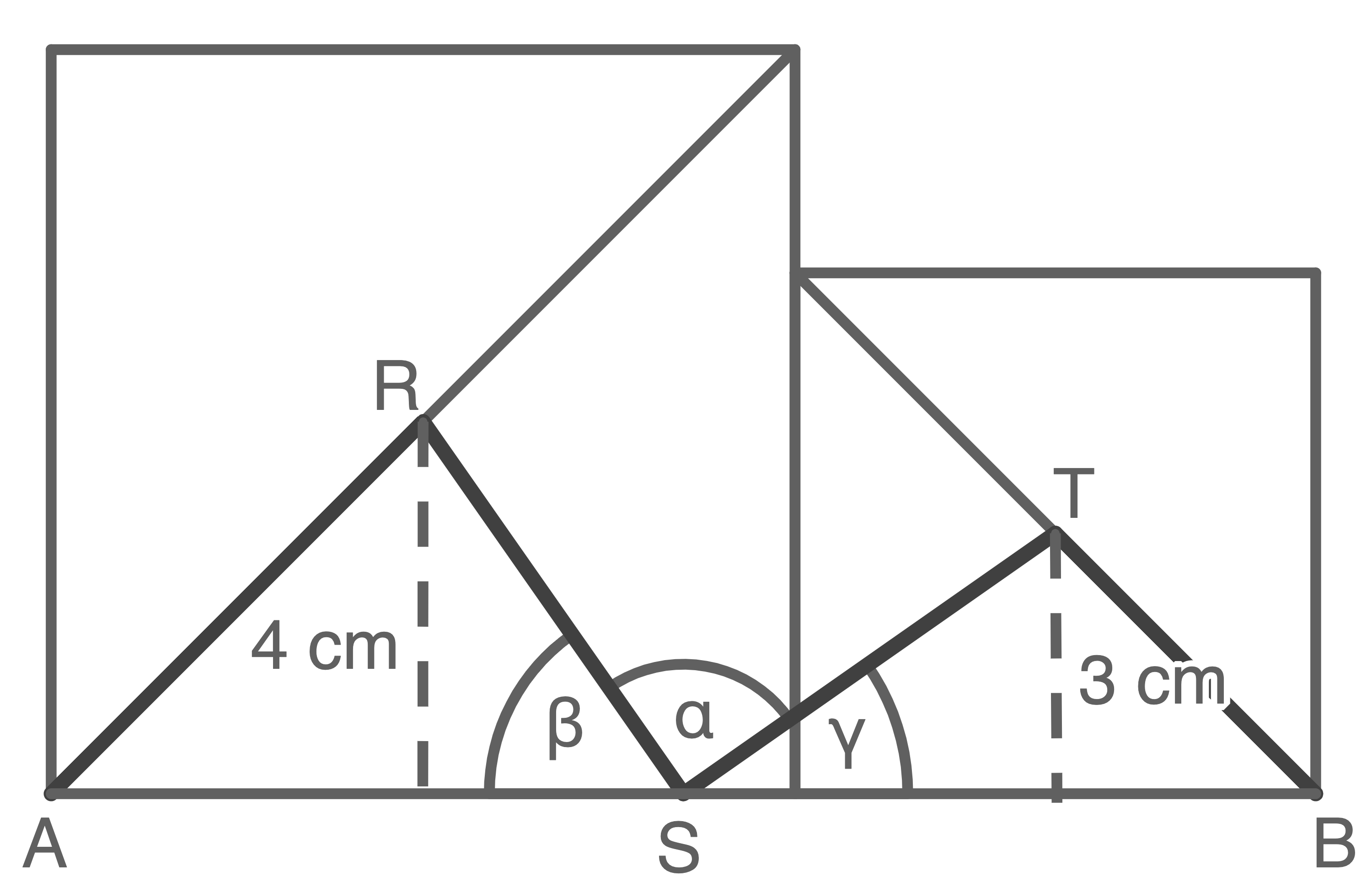 1. Schritt: Größe des Winkels
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma)&=& \dfrac{3\,\text{cm}}{5\,\text{cm}}\\[5pt]
\gamma&=& \underline{ 36,9^{\circ}}
\end{array}\)](https://mathjax.schullv.de/2926921ed8b80f4345a8c9c2ea42d5596f2b950b76b0c94f986a67530c130285?color=5a5a5a) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{4\,\text{cm}}{5\,\text{cm}}\\[5pt]
\beta&=& \underline{ 53,1^{\circ}}
\end{array}\)](https://mathjax.schullv.de/969d64a85239e24a78e5e5a455b01e4b7c8642db3c62175eee971448e0f8c289?color=5a5a5a) 3. Schritt: Größe des Winkels
3. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\alpha&=& 180^{\circ} -\gamma - \beta &\quad \scriptsize \\[5pt]
\alpha&=& 180^{\circ} -36,9^{\circ} - 53,1^{\circ} &\quad \scriptsize \\[5pt]
&=& \underline{\underline{ 90^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/7302220aa949451a69385c89e22949801dba914f32af7f84c951076db900a633?color=5a5a5a)


b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Lösung 9
a)
b)
Formel zur Berechnung des Flächeninhalts:  In einem gleichseitigen Dreieck sind alle Winkel
In einem gleichseitigen Dreieck sind alle Winkel  groß:
groß:
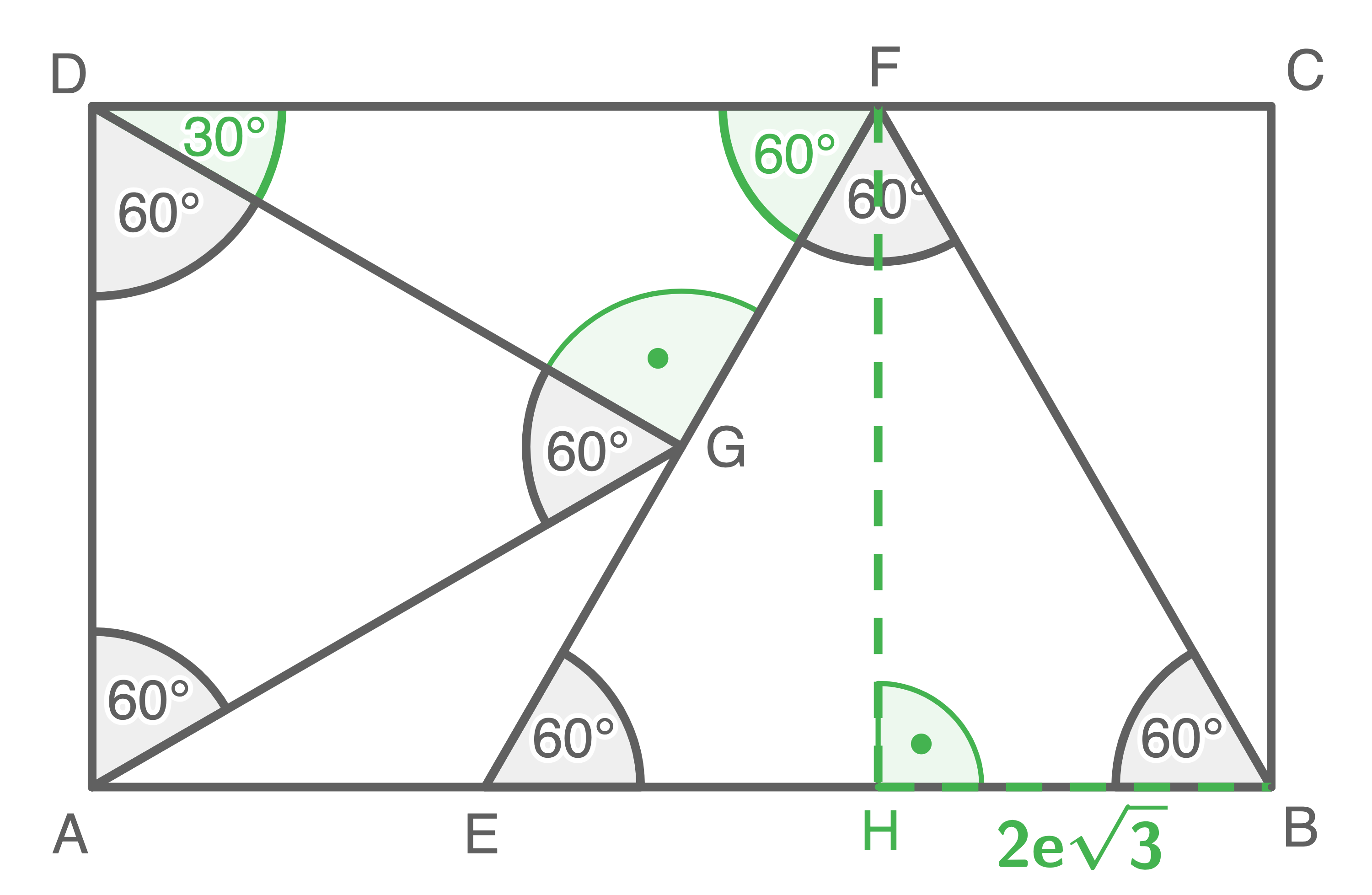 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\tan(60^{\circ})&=&\dfrac{\overline{HF}}{2\mathrm{e}\sqrt{3}} \quad \scriptsize \mid\; \cdot 2 \mathrm{e}\sqrt{3} \\[5pt]
\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3} &=& \overline{HF}\\[5pt]
\overline{HF} &=&\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3}\\[5pt]
\overline{HF}&=&\underline{ 6\mathrm{e}} \quad = \overline{AD} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f997c82a1f730ef4e12dee8337ab28128c28652c047b585890ecd112753a6279?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Da in einem gleichseitigen Dreieck alle Seiten gleich lang sind, gilt
berechnen
Da in einem gleichseitigen Dreieck alle Seiten gleich lang sind, gilt 
![\(\begin{array}[t]{rll}
\cos(30^{\circ}) &=& \dfrac{\overline{DG}}{\overline{DF}} \\[5pt]
\cos(30^{\circ}) &=& \dfrac{6\mathrm{e}}{\overline{DF}}\quad \scriptsize \mid\; \cdot \overline{DF}\\[5pt]
\cos(30^{\circ}) \cdot \overline{DF} &=& 6\mathrm{e} \quad \scriptsize \mid\; :\cos(30^{\circ}) \\[5pt]
\overline{DF} &=& \dfrac{6\mathrm{e}}{\cos(30^{\circ})} \\[5pt]
\overline{DF} &=& \underline{ 4 \mathrm{e}\sqrt{3}}
\end{array}\)](https://mathjax.schullv.de/c64f3b29f550f2f74e9d1070e1478d57d94cb82bbafb8c3c587fdf9963cc7a35?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\overline{DC}&=& \overline{DF} + \overline{FC}\\[5pt]
&=& 4 \mathrm{e}\sqrt{3} + 2 \mathrm{e}\sqrt{3}\\[5pt]
&=& \underline{ 6\mathrm{e}\sqrt{3}}
\end{array}\)](https://mathjax.schullv.de/85682e3d34adf3dc1aac7a56ea4696dcabf3cc01033157731b0d2c346ec6588a?color=5a5a5a) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& \overline{AD} \cdot \overline{DC} \\[5pt]
&=& 6\mathrm{e} \cdot 6\mathrm{e}\sqrt{3} \\[5pt]
&=& \underline{\underline{ 36\mathrm{e}^2\sqrt{3}}}
\end{array}\)](https://mathjax.schullv.de/f157043d0028e83389606a3be4906c36a67460f457fb334132e65f48ac7c30d4?color=5a5a5a) Damit ist die Aussage bewiesen.
Damit ist die Aussage bewiesen.
Abschlussprüfung 2020

Lösung 10
a)
1. Schritt: Länge der Strecke  berechnen
berechnen
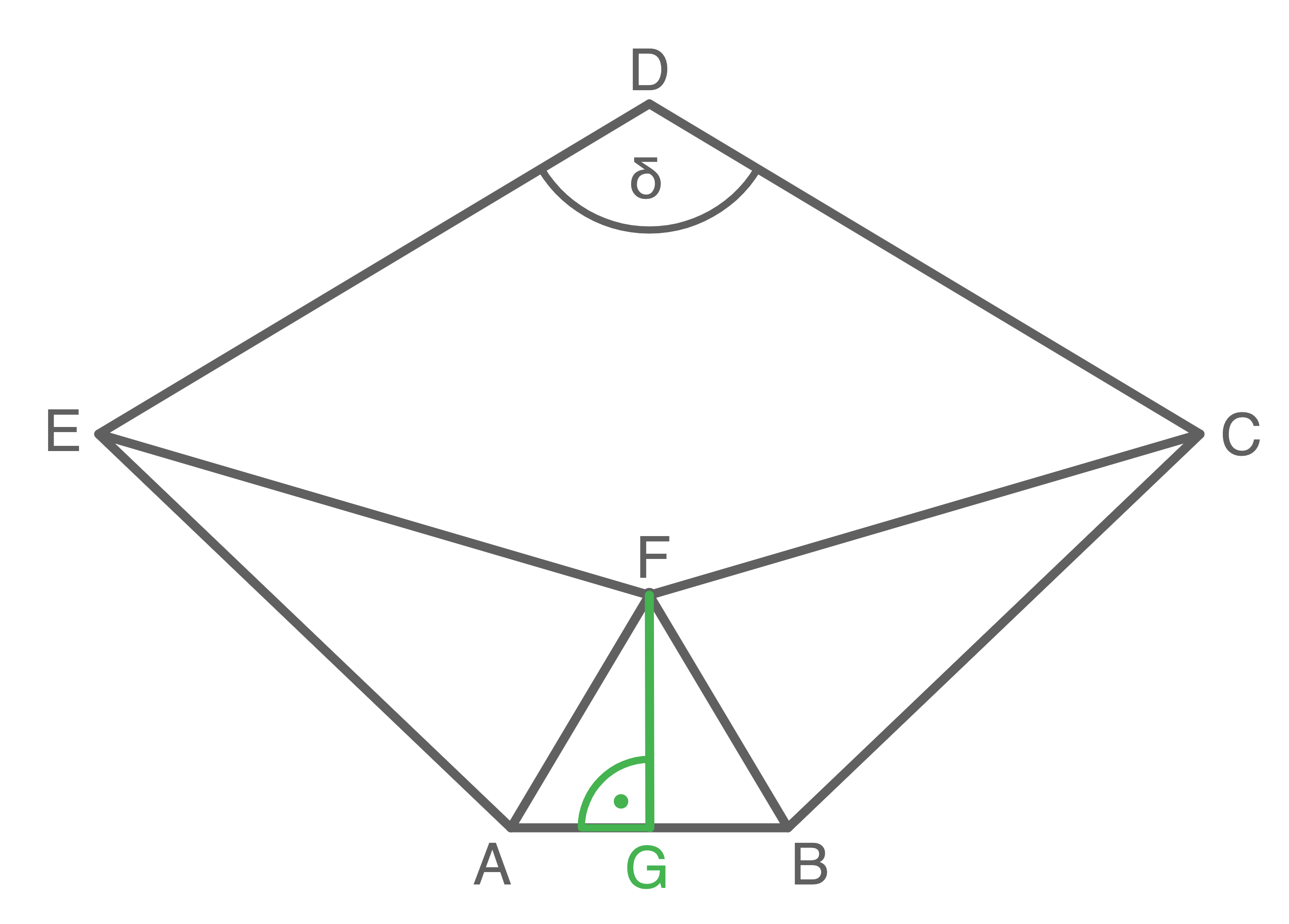 Satz des Pythagoras anwenden
Satz des Pythagoras anwenden
![\(\begin{array}[t]{rll}
\overline{AF}^2&=& \overline{AG}^2+\overline{FG}^2\quad \scriptsize \mid\;-\overline{AG}^2 \\[5pt]
\overline{FG}^2&=&\overline{AF}^2-\overline{AG}^2\\[5pt]
\overline{FG}^2&=&(3,4\,\text{cm})^2-(1,7\,\text{cm})^2\quad \scriptsize \mid\; \sqrt{\,\,\,} \\[5pt]
\overline{FG}&=& \sqrt{(3,4\,\text{cm})^2-(1,7\,\text{cm})^2}\\[5pt]
\overline{FG}&=& \underline{ 2,94\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/87e6120b7190b1b40d9577506acfdd47e32b2508a324fca0cfa76ce3443ccf56?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
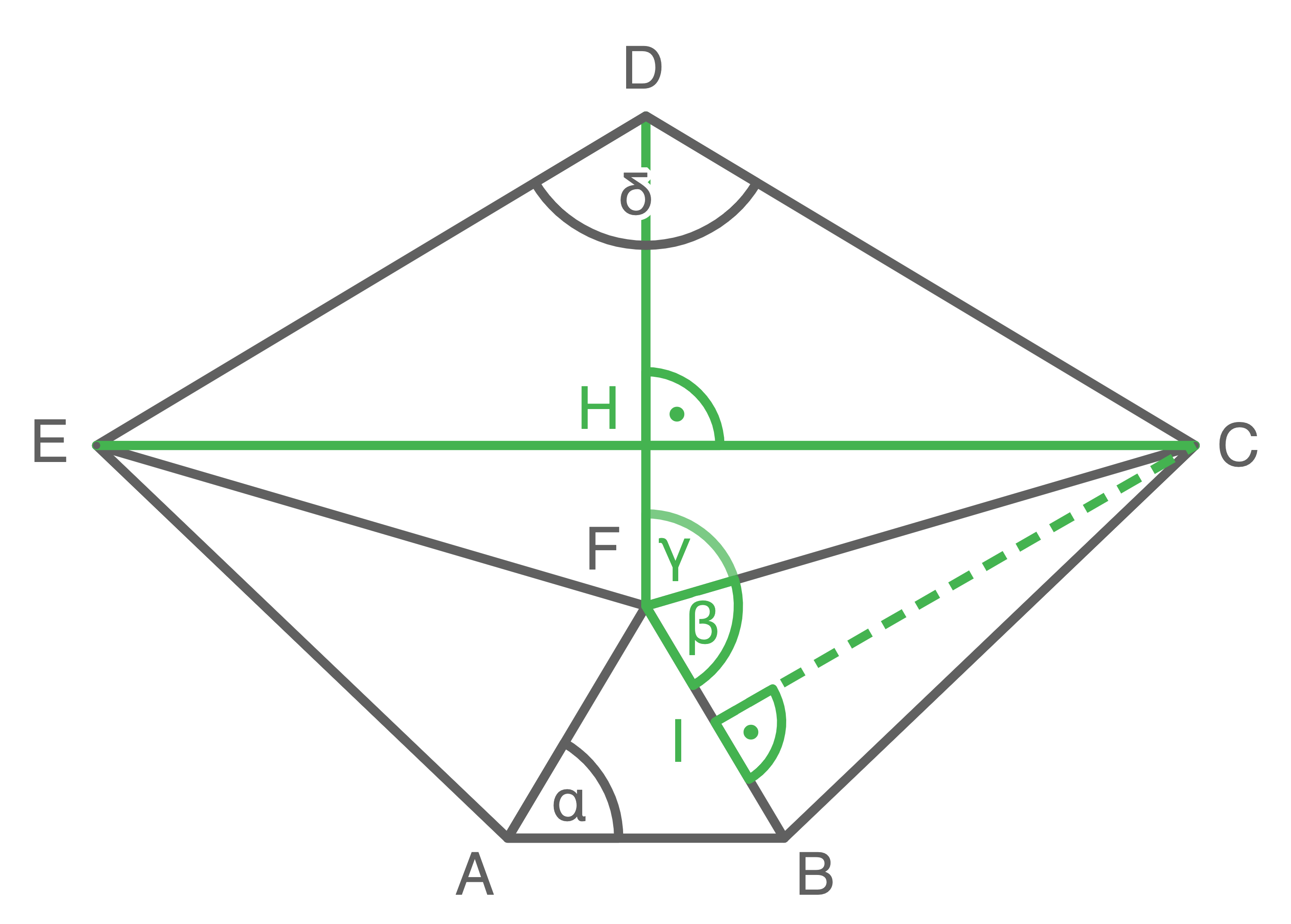 Größe des Winkels
Größe des Winkels  berechnen
Da das Dreieck
berechnen
Da das Dreieck  gleichschenklig ist, gilt
gleichschenklig ist, gilt 
![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{FI}}{\overline{CF}} &\quad \\[5pt]
\cos(\beta)&=&\dfrac{1,7\,\text{cm} }{7,0\,\text{cm} } \\[5pt]
\beta&=&\underline{ 75,94^{\circ}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/de67ce1b76d4327f746a41d0dd29517648895853a9bfafd0ae963ee1a5c0d3fa?color=5a5a5a) Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=&180^{\circ}-\beta-\dfrac{\alpha}{2} \\[5pt]
\gamma&=&180^{\circ}-75,94^{\circ}-\dfrac{60^{\circ}}{2} \\[5pt]
\gamma&=&\underline{ 74,06^{\circ}}
\end{array}\)](https://mathjax.schullv.de/4181315cf5edbbdfd4956520a4f5ab002b5f475c97559859aa9f2826478ace31?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\gamma)&=&\dfrac{\overline{HF}}{\overline{CF}} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{HF}&=&\overline{CF}\cdot \cos(\gamma) \\[5pt]
\overline{HF}&=&7,0\,\text{cm}\cdot \cos(74,06^{\circ}) \\[5pt]
\overline{HF}&=&\underline{ 1,92\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/8db02f0d87cd45c689719dc60f3a8be45e4b6870b6d44bece549ea30b24d0b8d?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma)&=&\dfrac{\overline{CH}}{CF} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{CH}&=&\overline{CF}\cdot \sin(\gamma) \\[5pt]
\overline{CH}&=&7,0\,\text{cm}\cdot \sin(74,06^{\circ}) \\[5pt]
\overline{CH}&=&\underline{ 6,73\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7b9a3cddf7b716c276bb1781c596c67b2ec89b456ba6bfe64a1e87792f354721?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\delta}{2}\right)&=&\dfrac{\overline{CH}}{\overline{DH}} &\quad \scriptsize \mid\;\cdot \overline{DH} \\[5pt]
\overline{DH}\cdot \tan\left(\dfrac{\delta}{2}\right) &=& \overline{CH}&\quad\scriptsize \mid\;:\tan\left(\dfrac{\delta}{2}\right) \\[5pt]
\overline{DH}&=&\dfrac{\overline{CH}}{\tan\left(\dfrac{\delta}{2}\right)} \\[5pt]
\overline{DH}&=&\dfrac{6,73\,\text{cm}}{\tan(59^{\circ})} \\[5pt]
\overline{DH}&=&\underline{ 4,04\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/c49c22667f04cca3450464288390dd93e849472a19b22adcfaa5678bc82fcea3?color=5a5a5a) 3. Schritt: Abstand des Punktes
3. Schritt: Abstand des Punktes  zur Strecke
zur Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DG}&=&\overline{DH}+\overline{HF}+\overline{FG} & \\[5pt]
\overline{DG}&=&4,04\,\text{cm}+1,92\,\text{cm}+2,94\,\text{cm} \\[5pt]
\overline{DG}&=&\underline{\underline{ 8,9\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/249199456a9a8cc30ec1111d7ee985dccd0a5037a45caef03fe4f3392c347bca?color=5a5a5a)


b)
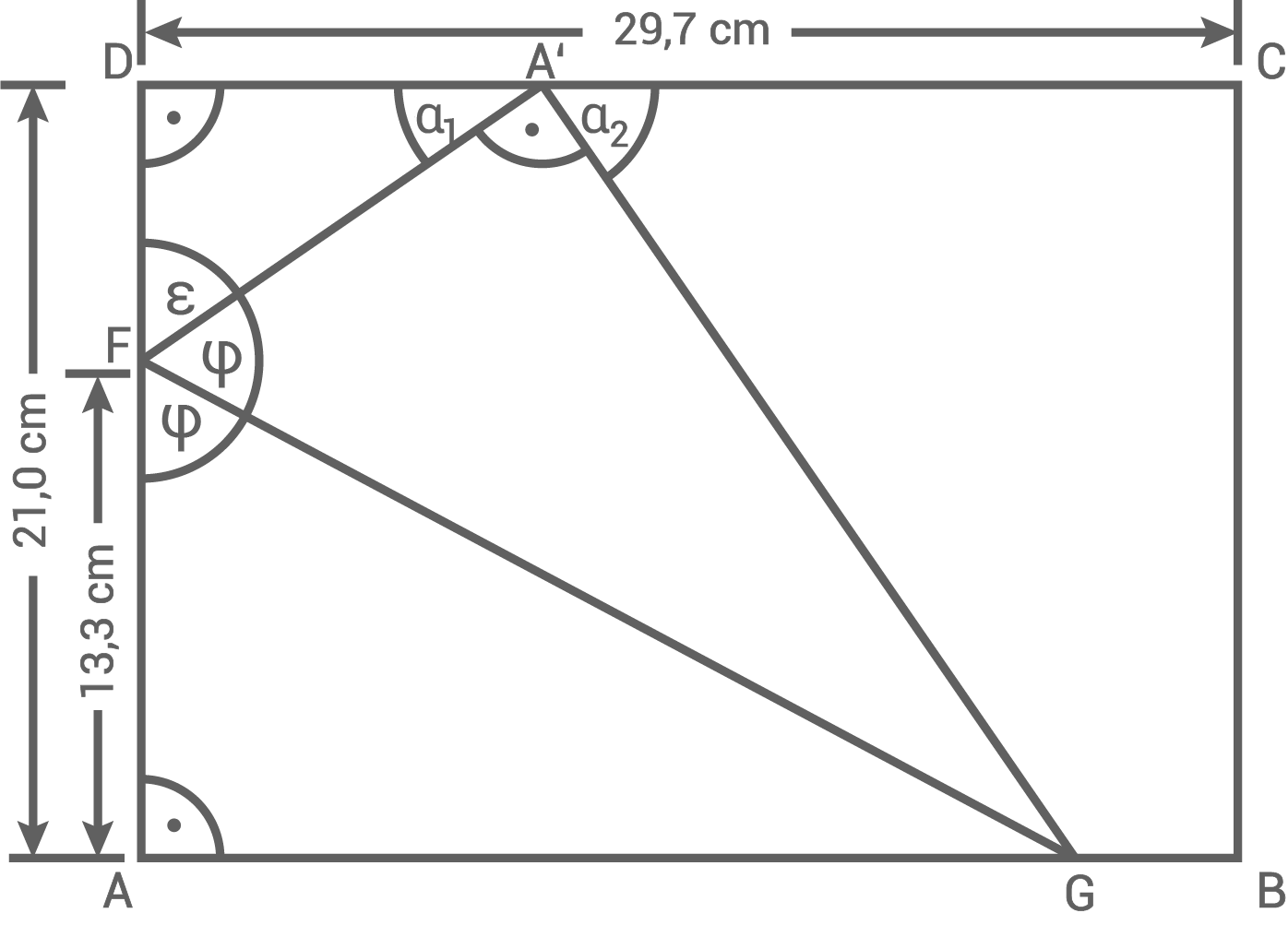
Lösung 11
a)
Hilfsskizze
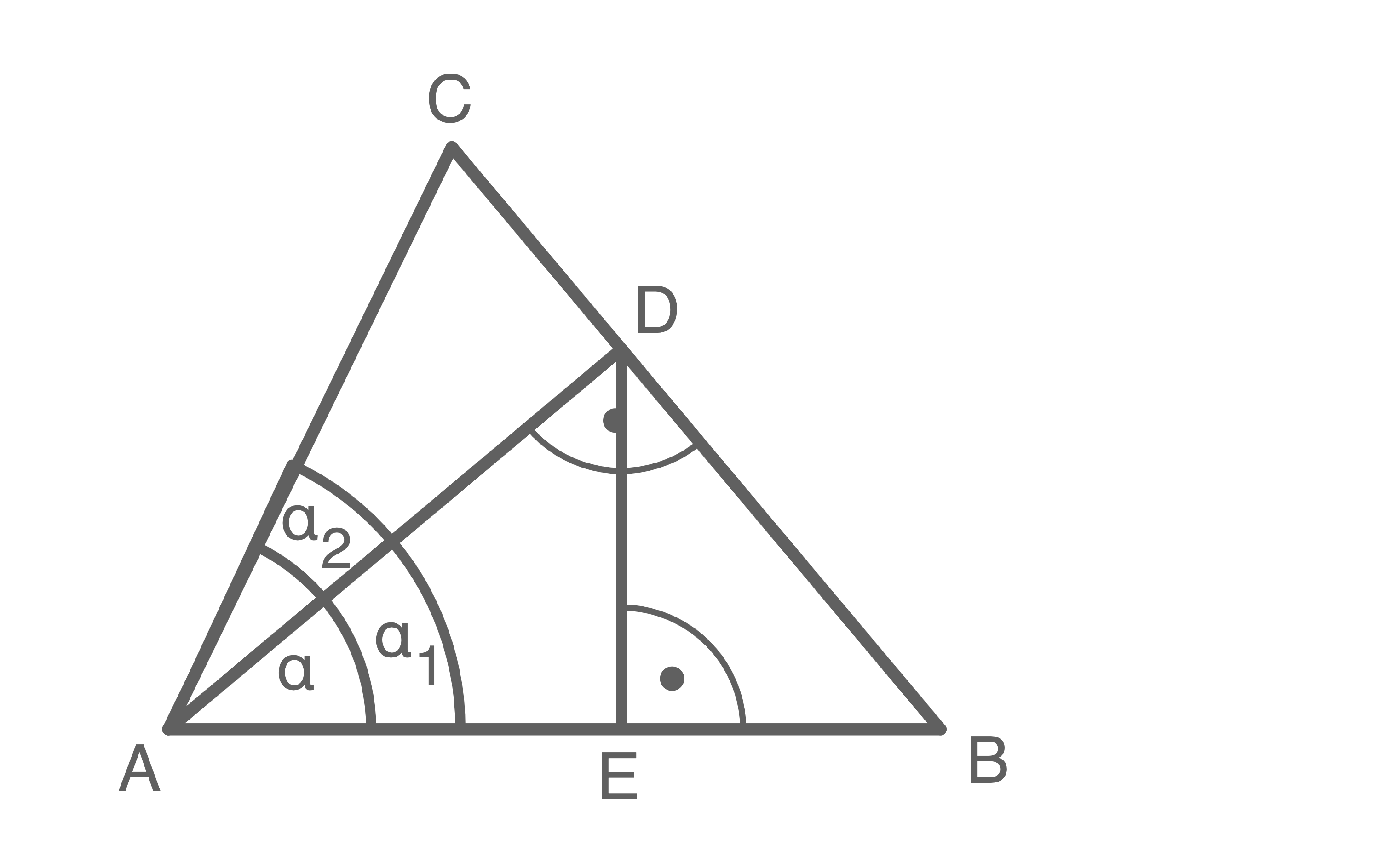 Winkel
Winkel  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
Die Strecke
berechnen
Die Strecke  ist die Höhe des Dreiecks
ist die Höhe des Dreiecks  zur Grundseite
zur Grundseite 
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2} \cdot g \cdot h \\[5pt]
A_{ABC}&=& \dfrac{1}{2} \cdot \overline{BC} \cdot \overline{AD}\\[5pt]
54\,\text{cm}^2 &=& \dfrac{1}{2} \cdot 11,6\,\text{cm} \cdot \overline{AD} \\[5pt]
54\,\text{cm}^2 &=& 5,8\,\text{cm} \cdot \overline{AD} \quad\scriptsize \mid\; :5,8\,\text{cm} \\[5pt]
\overline{AD} &=& \underline{ 9,31 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9c13d390c7990b1faedb2cdb0e1a15c24682261ebd7563ba88291b4beaf4edb8?color=5a5a5a) 2. Schritt: Winkel
2. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha_1)&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} &\quad \scriptsize \\[5pt]
\cos(\alpha_1) &=& \dfrac{\overline{AD}}{\overline{AB}} &\quad \scriptsize \\[5pt]
\cos(\alpha_1) &=& \dfrac{9,31\,\text{cm}}{12,0\,\text{cm}} \quad \scriptsize \mid\;\cos^{-1} \\[5pt]
\alpha_1&=& \underline{ 39,12^{\circ}}
\end{array}\)](https://mathjax.schullv.de/cb6353147fe759d8943abe2694e2caf437eb8906beb380feddc965196a736e27?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
4. Schritt: Länge der Strecke
berechnen
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD} &=& \overline{BC} - \overline{BD} &\quad \scriptsize \\[5pt]
&=& 11,6 \,\text{cm} - 7,57 \,\text{cm} &\quad \scriptsize \\[5pt]
\overline{CD} &=& \underline{ 4,03 \,\text{cm}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8edf5feb45b81cbd478d1a45be43dd2983e0ded51f2cfd05b9f8c3d498ade66a?color=5a5a5a) 5. Schritt: Winkel
5. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha_2)&=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} &\quad \scriptsize \\[5pt]
\tan(\alpha_2) &=& \dfrac{\overline{CD}}{\overline{AD}} &\quad \scriptsize \\[5pt]
\tan(\alpha_2) &=& \dfrac{4,03\,\text{cm}}{9,31\,\text{cm}} \quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\alpha_2&=& \underline{ 23,41^{\circ}}
\end{array}\)](https://mathjax.schullv.de/c18002303fbf07c784f58ed3b56a3af2194a108a1414c12102bbdc3dc81326ae?color=5a5a5a) 6. Schritt: Winkel
6. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\alpha &=& \alpha_1 + \alpha_2 &\quad \scriptsize \\[5pt]
&=& 39,12^{\circ} + 23,41^{\circ} &\quad \scriptsize \\[5pt]
&=& 62,53^{\circ} \\[5pt]
\alpha&=&\underline{\underline{ 62,5^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/1ccc48655f1edc54b9a46470edaf7cb1a0d767d3c2fe9b96d6a5c7bbec4dd0a8?color=5a5a5a) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} &=& \sin(\alpha_1)&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9b90173eaaf7cf48022ec7f5e1c5a6c665b75f99168ae73edf5bb63a7ae6e2e4?color=5a5a5a)
![\(\begin{array}[t]{rll}
\dfrac{\overline{DE}}{\overline{AD}} &=& \sin(\alpha_1)\quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt]
\overline{DE} &=& \sin(\alpha_1)\cdot \overline{AD} &\quad \scriptsize\\[5pt]
&=& \sin(39,12^{\circ}) \cdot 9,31\,\text{cm} &\quad \scriptsize \\[5pt]
&=& 5,87\,\text{cm} \\[5pt]
\overline{DE} &=& \underline{\underline{ 5,9\,\text{cm}}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/998efb823012a8cf6cb9e331ac729162f7d8f0c1c4161a0f8bc9c92e54855a7f?color=5a5a5a)

b)
Nachweis, dass die Dreiecke flächengleich sind
1. Schritt: Flächeninhalt des Dreiecks  berechnen
Länge von
berechnen
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{AC}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt]
\tan(\beta)\cdot \overline{BC}&=&\overline{AC}\quad \scriptsize \mid\;:\tan(\beta)\\[5pt]
\overline{BC}&=&\dfrac{\overline{AC}}{\tan(\beta)}\quad \scriptsize \mid\;:\tan(\beta)
\end{array}\)](https://mathjax.schullv.de/e0fcd5458086987a4ae23edbfd37b0f66dc0ce55a48b0ca0e474cae918e52690?color=5a5a5a) Da das Dreieck
Da das Dreieck  gleichseitig ist, gilt:
gleichseitig ist, gilt: 

 Flächeninhalt
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{DBC}&=&\dfrac{\overline{BC}^2}{4}\sqrt{3}\\[5pt]
&=&\dfrac{(4e)^2}{4}\sqrt{3}\\[5pt]
&=&\dfrac{16e^2}{4}\sqrt{3}\\[5pt]
A_{DBC}&=&\underline{ 4e^2\sqrt{3}}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/e2718206818bd34e364d88a7931ef6118356b99dcefc8665e61826f6faa3c030?color=5a5a5a) 2. Schritt: Flächeninhalt des Dreiecks
2. Schritt: Flächeninhalt des Dreiecks  berechnen
Flächeninhalt
berechnen
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{ABC}&=&\dfrac{1}{2}\cdot\overline{BC}\cdot \overline{AC}\\[5pt]
&=&\dfrac{1}{2}\cdot4e\cdot 4e\sqrt{3}\\[5pt]
A_{ABC}&=&8e^2\sqrt{3}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bfd666e47c97ea8e94118b11b21c29a0b7f0948657754f3eb00bc48ea6f836bb?color=5a5a5a) Flächeninhalt
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{ADC}&=&A_{ABC}-A_{DBC}\\[5pt]
&=&8e^2\sqrt{3}-4e^2\sqrt{3}\\[5pt]
A_{ADC}&=&\underline{ 4e^2\sqrt{3}}
\end{array}\)](https://mathjax.schullv.de/4c284bd918de7055289ee210d1ccb862fa7c8b924badd7e89955d76180ceb059?color=5a5a5a) Damit ist gezeigt, dass beide Dreiecke flächengleich sind.
Wert von
Damit ist gezeigt, dass beide Dreiecke flächengleich sind.
Wert von  berechnen
Der Flächeninhalt des Dreiecks
berechnen
Der Flächeninhalt des Dreiecks  lautet (s.o.)
lautet (s.o.) 
![\(\begin{array}[t]{rll}
A_{ABC}&=& 200 \\[5pt]
8e^2\sqrt{3}&=& 200 \quad \scriptsize \mid\;:(8\sqrt{3}) \\[5pt]
e^2&=&\dfrac{25}{\sqrt{3}}\\[5pt]
&=&\dfrac{25\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}}\\[5pt]
e^2&=&\dfrac{25\cdot \sqrt{3}}{3}\\[5pt]
e_1&=&5\sqrt{\dfrac{\sqrt{3}}{3}}
\\[5pt]
e_2&=&-5\sqrt{\dfrac{\sqrt{3}}{3}}
\end{array}\)](https://mathjax.schullv.de/c11d56834c3ddd899ab02b523bef3b024630f4185a4245153c62a6b6d641e443?color=5a5a5a)
 ist negativ und scheidet somit als Ergebnis aus.
Für
ist negativ und scheidet somit als Ergebnis aus.
Für  beträgt der Flächeninhalt
beträgt der Flächeninhalt 
Abschlussprüfung 2018
Lösung 12
a)
Abstand von  zu
zu  berechnen
berechnen
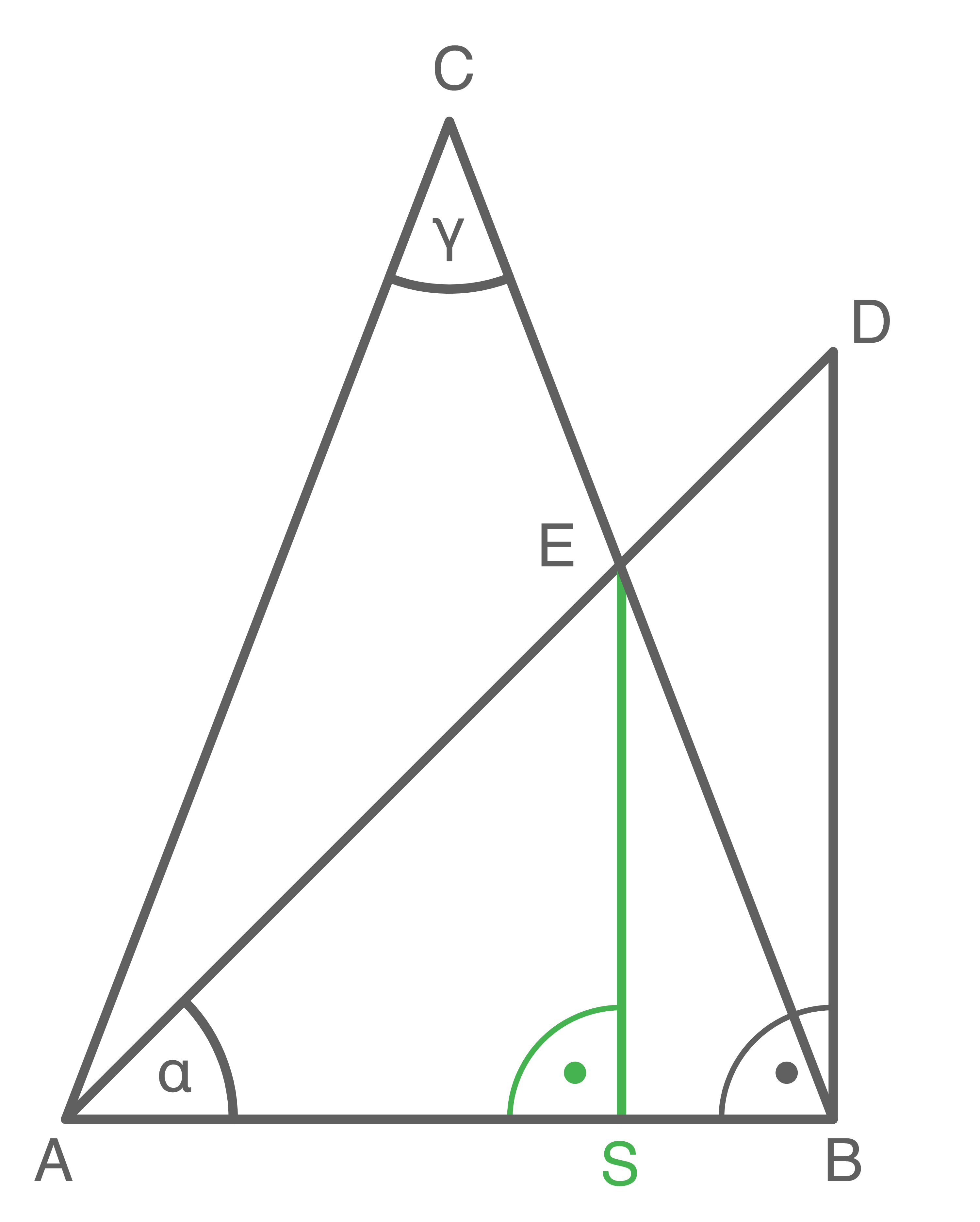 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BD}}{\overline{AD}} \\[5pt]
\sin(42,0^{\circ})&=& \dfrac{7,2 \,\text{cm}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt]
\sin(42,0^{\circ})\cdot \overline{AD}&=& 7,2 \,\text{cm} \quad \scriptsize \mid\; : \sin(42,0^{\circ}) \\[5pt]
\overline{AD}&=& \dfrac{7,2 \,\text{cm}}{\sin(42,0^{\circ})} \\[5pt]
\overline{AD}&=& \underline{10, 76 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/661948f8774e92cf4bf7fa2b32eead09ad2937ccd27d3bcea1c342fecc87dd6e?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AD}-\overline{DE} \\[5pt]
&=& 10,76 \,\text{cm} - 3,0 \,\text{cm} \\[5pt]
&=& \underline{7,76 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/dce5af3145091ba9b110ed52ba11d265f8d161c87bb3e22724a7eb26eeac5d80?color=5a5a5a) 3. Schritt: Abstand bestimmen
Größe des Winkels
3. Schritt: Abstand bestimmen
Größe des Winkels  berechnen
berechnen
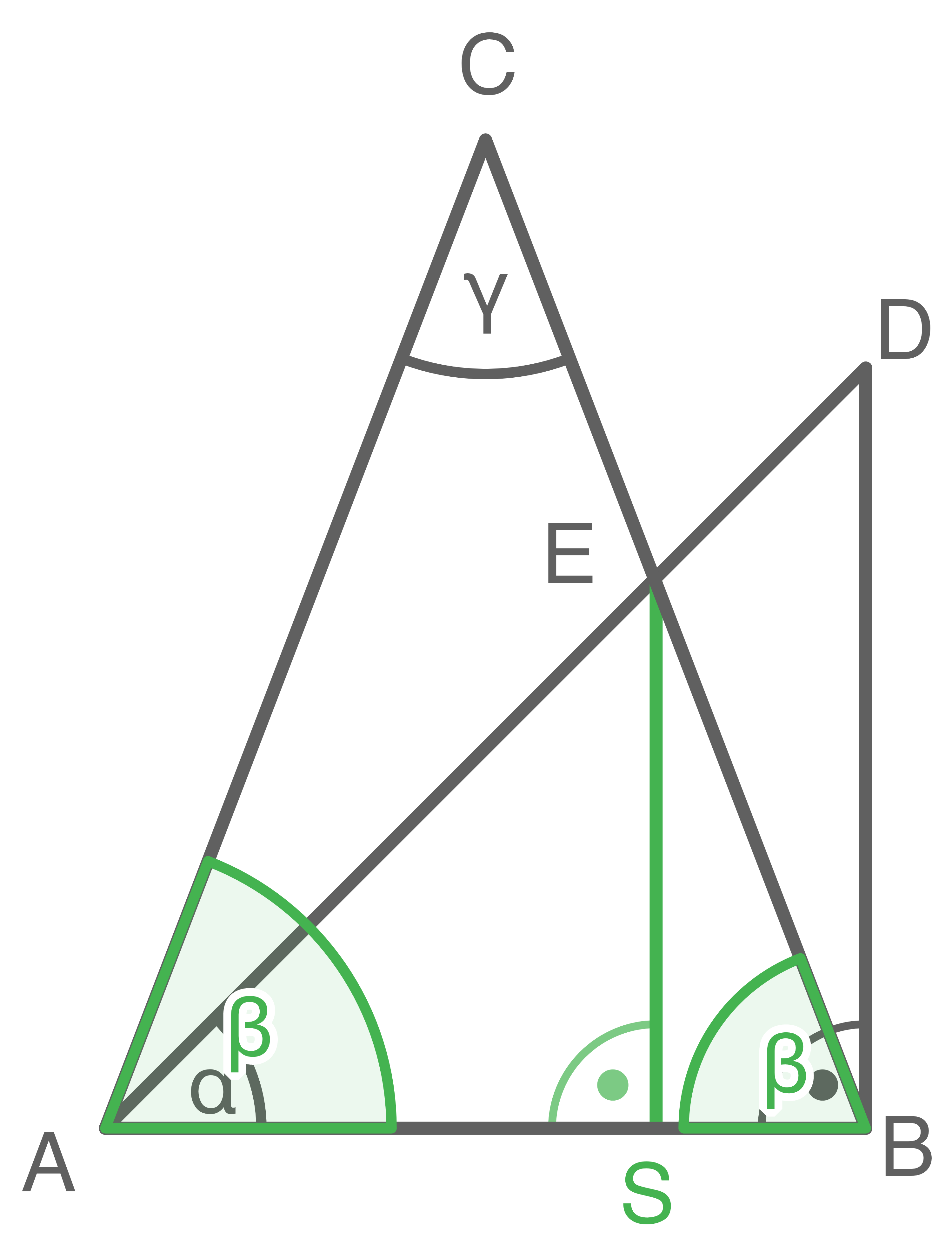 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{\overline{BD}}{\overline{AB}} \\[5pt]
\tan(42,0^{\circ})&=& \dfrac{7,2\,\text{cm}}{\overline{AB}} \quad \scriptsize \mid\; \cdot \overline{AB} \\[5pt]
\tan(42,0^{\circ})\cdot \overline{AB} &=& 7,2\,\text{cm} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{AB}&=& \dfrac{7,2 \,\text{cm}}{\tan(42,0^{\circ})} \\[5pt]
\overline{AB}&=& 8,00 \,\text{cm} \\[5pt]
\overline{AB}&=& \underline{8\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/69c4174b0183bca04e80f7edf6ed62c17f5de24899fdd748e851f35fa055e3e8?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
3. Schritt: Länge der Strecke
bestimmen
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BS}&=& \overline{AB} - \overline{AS} \\[5pt]
&=& 8 \,\text{cm} - 5,77 \,\text{cm} \\[5pt]
&=& \underline{2,23 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/d5b351aff2815f26b297353b725af0c828da674f5a530b53160679cabcac8a6a?color=5a5a5a) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan (\beta)&=&\dfrac{\overline{ES}}{\overline{BS}} \\[5pt]
\tan (\beta)&=&\dfrac{5,19\text{ cm}}{2,23 \,\text{cm} } &\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\beta&=& \underline{66,75^{\circ}}
\end{array}\)](https://mathjax.schullv.de/8d3fa08a5b7a68213960f2756ffe16afcbb4f3b10d7f87998424472a1db4b2ba?color=5a5a5a) 5. Schritt: Größe des Winkels
5. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=& 180^{\circ}-2\cdot \beta \\[5pt]
&=& 180^{\circ}-2\cdot 66,75^{\circ} \\[5pt]
&=& \underline{\underline{ 46,5^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/5c2cb8e02eebe1ead9b561d8cef36348a09f9266065da608338c902833945696?color=5a5a5a)


b)
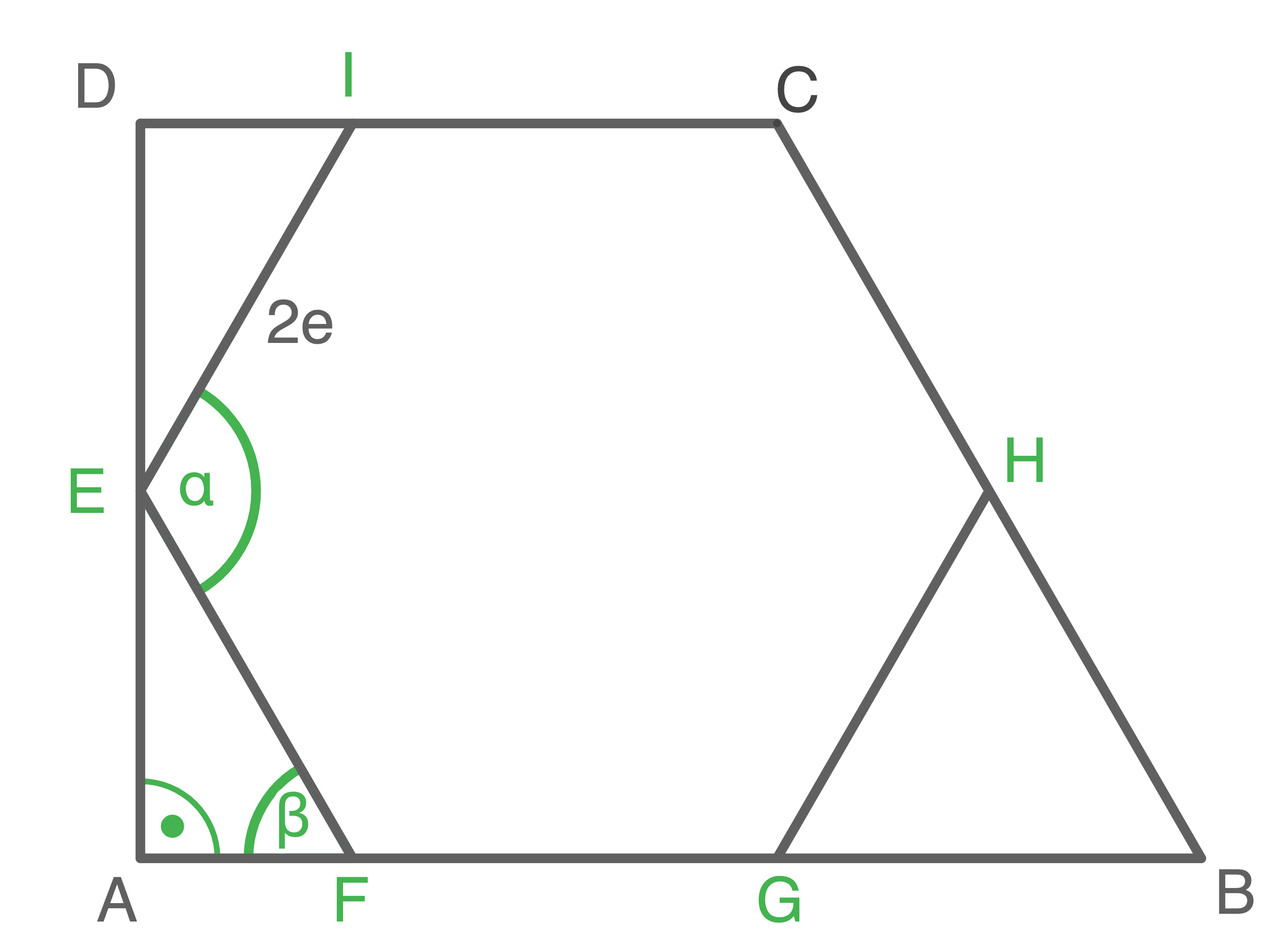
Somit sind alle Innenwinkel von
Lösung 13
a)
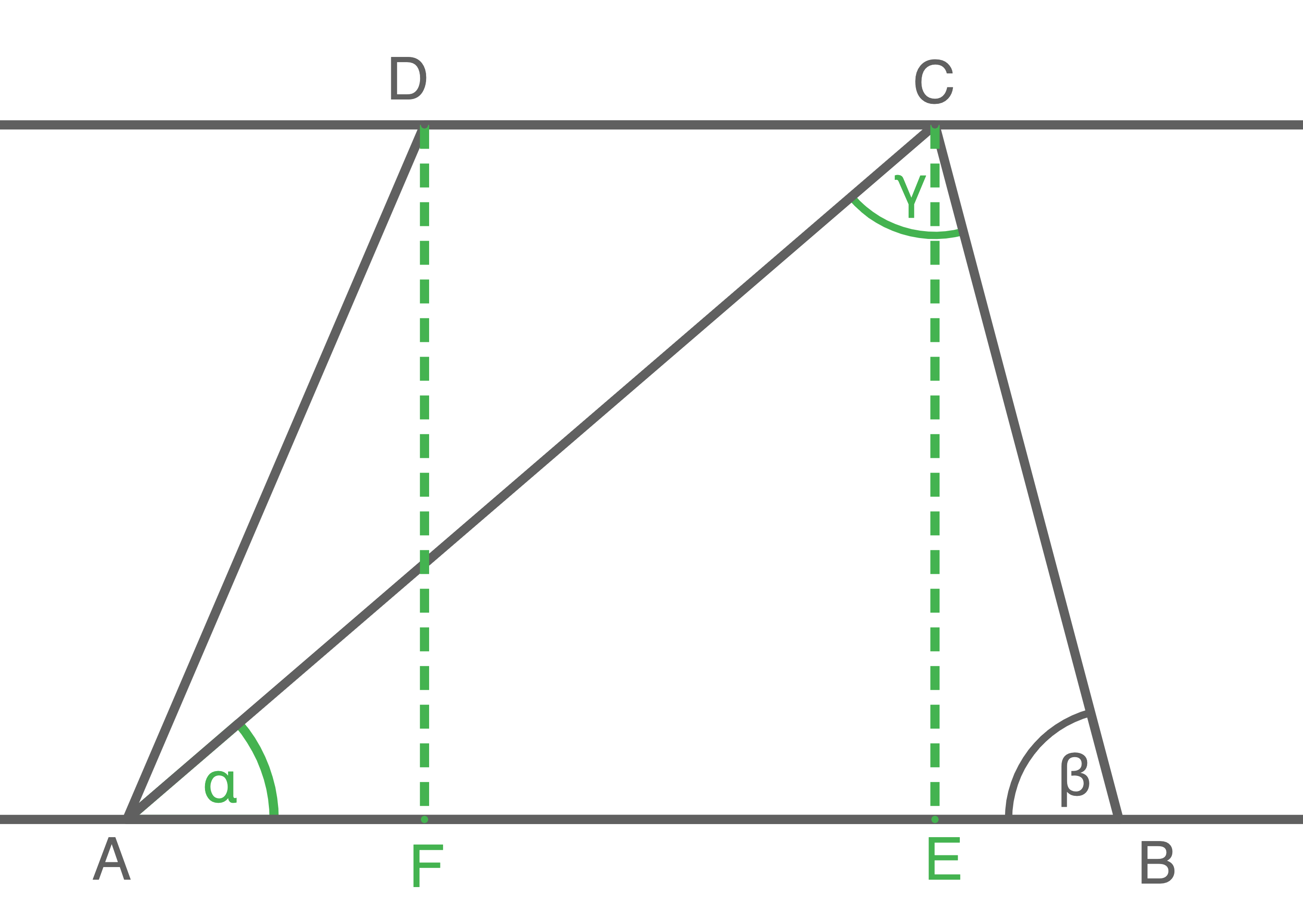
b)
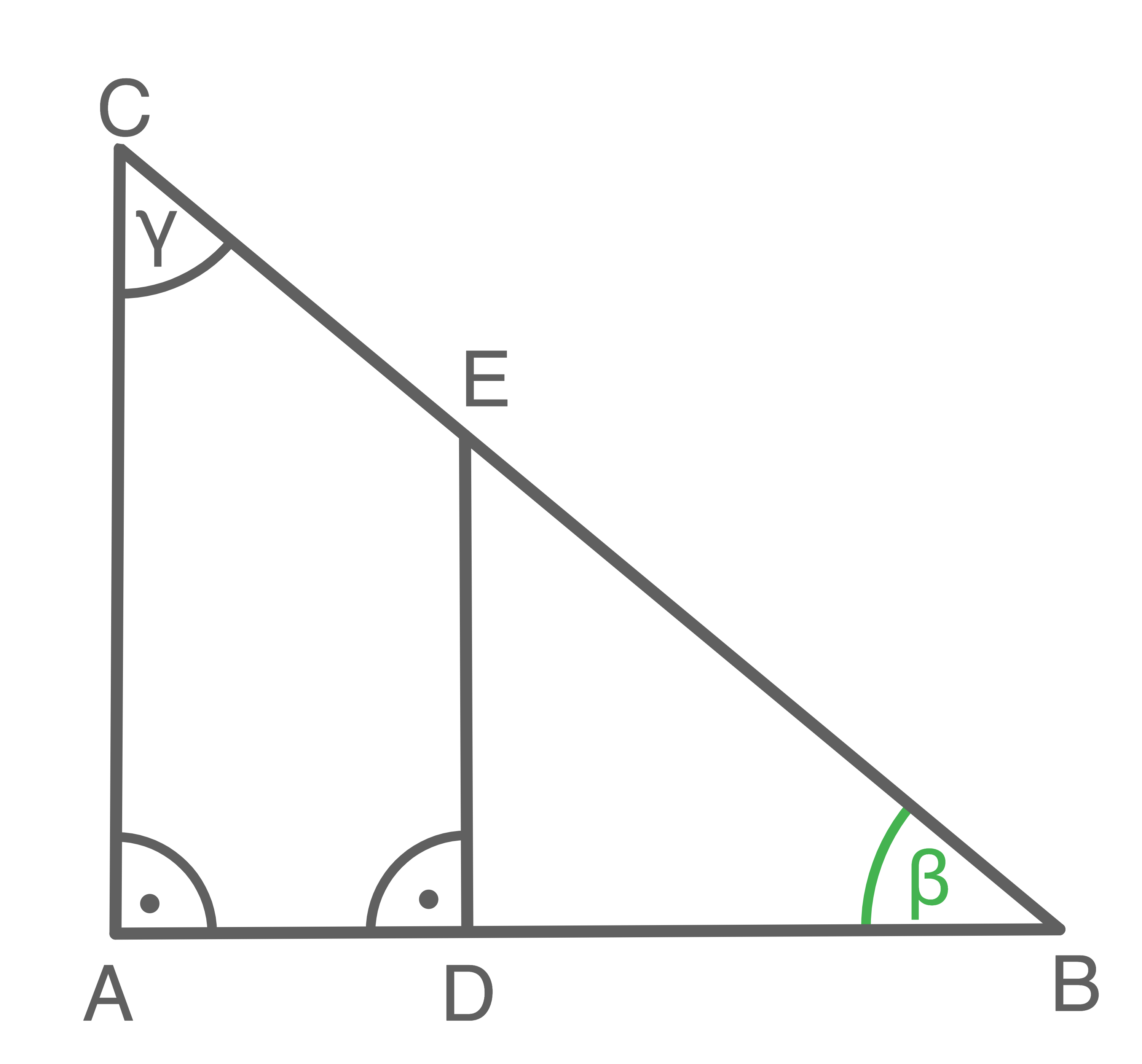
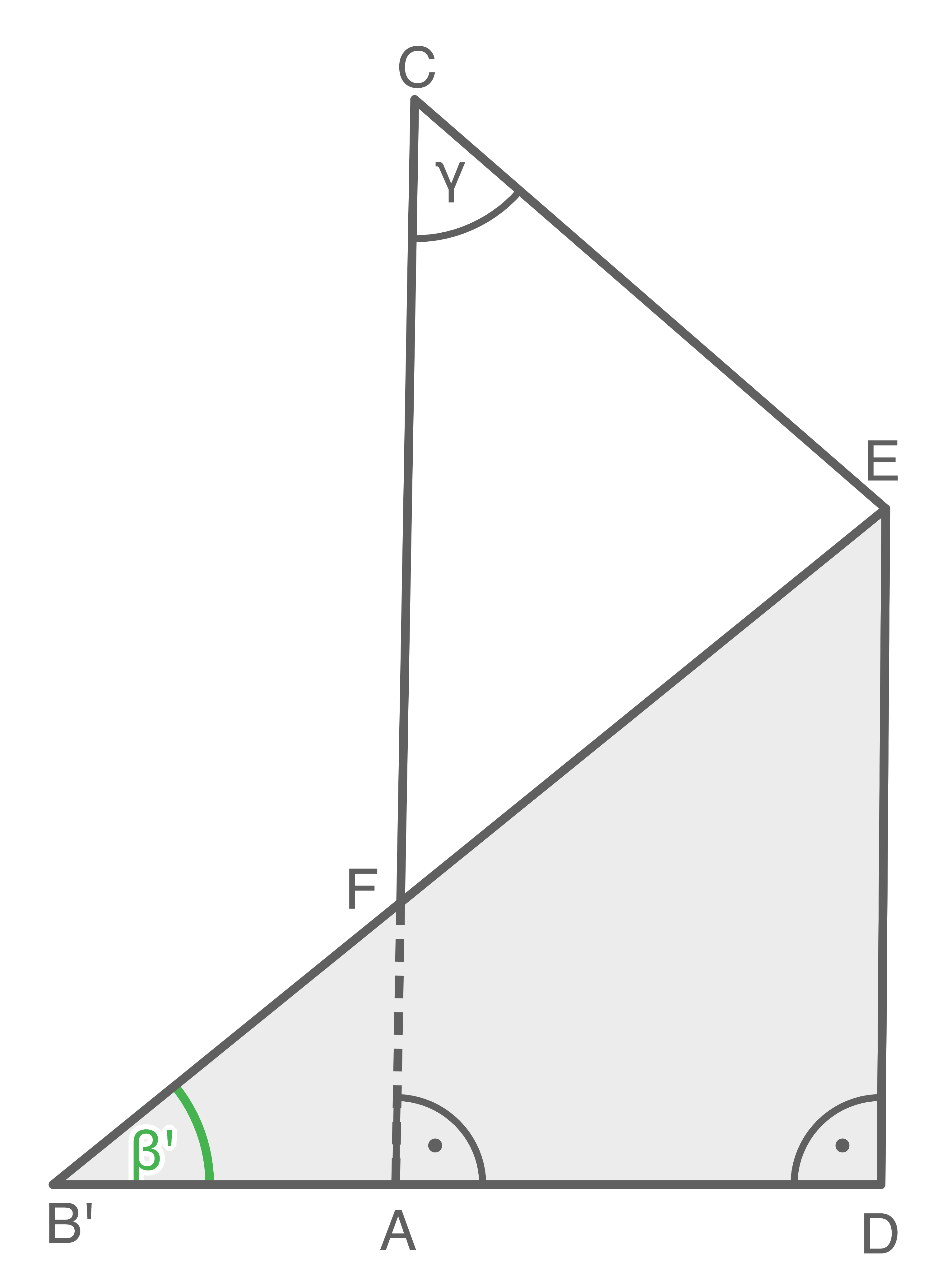
Lösung 14
a)
Größe des Winkels  berechnen
berechnen
 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{\overline{DR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt]
\overline{DR} &=& \sin(\alpha)\cdot \overline{AD} &\quad \scriptsize \\[5pt]
\overline{DR} &=& \sin(50^{\circ}) \cdot 8,4 \,\text{cm} &\quad \scriptsize \\[5pt]
\overline{DR} &=& \underline{ 6,43 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/aa6523540a5bc3c3ef414c0f22be1c36a3ac09705a45608661b070320657d7e4?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overline{AR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt]
\overline{AR} &=& \cos(\alpha) \cdot \overline{AD} &\quad \scriptsize \\[5pt]
\overline{AR} &=& \cos(50^{\circ}) \cdot 8,4\,\text{cm} &\quad \scriptsize \\[5pt]
\overline{AR} &= & \underline{ 5,40\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/307265a519579dbba0a3d28876c02a2ff72851b99fe560a90ad88caa1b7c8aae?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{ER}&=&\overline{AE}-\overline{AR} &\quad \scriptsize \\[5pt]
\overline{ER}&=& 7,8\,\text{cm}- 5,40\,\text{cm} &\quad \scriptsize \\[5pt]
\overline{ER}&=& \underline{ 2,40 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/25aee4942ee517e987edce4eafe87a0e06daf396f64bfd624268cbb8529c4a2e?color=5a5a5a) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\beta)&=&\dfrac{2,4\,\text{cm}}{6,43\,\text{cm} } \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\beta&=& \underline{ 20,5^{\circ}}
\end{array}\)](https://mathjax.schullv.de/066a151ee10fcc145a21d53d3f92ef7df99aa5e229bec9062c02f26f2cbe1965?color=5a5a5a) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{\overline{ER}}{\overline{DE}}\quad \scriptsize \mid\; \cdot \overline{DE} \\[5pt]
\sin(\beta)\cdot \overline{DE}&=& \overline{ER}\quad \scriptsize \mid\; : \sin(\beta) \\[5pt]
\overline{DE}&=&\dfrac{\overline{ER}}{\sin(\beta)} &\quad \scriptsize \\[5pt]
\overline{DE}&=&\dfrac{2,4\,\text{cm}}{\sin(20,5^{\circ} )} &\quad \scriptsize \\[5pt]
\overline{DE}&=& \underline{ 6,85\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/e05e815a54f76c38ffa5b7fa7cc893918a693d642f9147bb41490157ddceb7bf?color=5a5a5a) 6. Schritt: Größe des Winkels
6. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\delta_2)&=&\dfrac{\overline{BR}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\delta_2)&=&\dfrac{\overline{BE}+\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\delta_2)&=& \dfrac{6,85\,\text{cm}+2,4\,\text{cm}}{6,43\,\text{cm}}\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\delta_2&=& \underline{ 55,2^{\circ}}
\end{array}\)](https://mathjax.schullv.de/2dcc32584362c889cc625c2fa92ce948c9a9e213388398bf808d15ddbcf32212?color=5a5a5a) 7. Schritt: Größe des Winkels
7. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\delta_1&=&90^{\circ}-\delta_2 &\quad \scriptsize \\[5pt]
&=&90^{\circ}- 55,2^{\circ} &\quad \scriptsize \\[5pt]
\delta_1 &=& \underline{\underline{ 34,8^{\circ}}}
\end{array}\)](https://mathjax.schullv.de/3b84ddb85a3189c34e49e079a6e69f802fd351915c0394fb09be4ac6adbac20f?color=5a5a5a) Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  berechnen
berechnen

![\(\begin{array}[t]{rll}
A_{\,\text{EBD}}&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot \overline{EB}\cdot \overline{DR} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 6,86 \,\text{cm}\cdot 6,43 \,\text{cm} &\quad \scriptsize \\[5pt]
A_{EBD}&=& \underline{\underline{ 22,1 \,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/6a59600199706b503fb41a8c81013a24bd6148a315214e59b2519b8ffb8f53c5?color=5a5a5a)


b)
Beas Aussage prüfen
![\(\begin{array}[t]{rll}
u_{\,\text{Rechteck}}&=& 2\cdot 6e+2\cdot 3e &\quad \scriptsize \\[5pt]
u_{\,\text{Rechteck}}&=& 18e
\end{array}\)](https://mathjax.schullv.de/3a3ac8364af46e50d843c59a2ea7f779ae4fc9dfca9f4cb0b74bb6afab4fcfb5?color=5a5a5a)

 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AG}&=& 2\cdot \overline{BC}&\quad \scriptsize \\[5pt]
&=& 2\cdot 3e &\quad \scriptsize \\[5pt]
\overline{AG}&=& \underline{ 6e}
\end{array}\)](https://mathjax.schullv.de/0ecc31be9970e0f703d9a148660950c7f3f7d27897a97383b10eaa0be76428a1?color=5a5a5a) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BE}&=&\dfrac{\overline{CM}}{2} &\quad \scriptsize \\[5pt]
&=&\dfrac{3e}{2} &\quad \scriptsize \\[5pt]
\overline{BE}&=& \underline{ 1,5e }=\overline{FG}
\end{array}\)](https://mathjax.schullv.de/9495dd904e19b08b6ab6f9b715d19630ad92dbfdeef27768bda16fd5fad0fd30?color=5a5a5a) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}&=&\overline{AB}-\overline{BE} &\quad \scriptsize \\[5pt]
&=& 6e-1,5e &\quad \scriptsize \\[5pt]
\overline{AE}&=&\underline{ 4,5e}
\end{array}\)](https://mathjax.schullv.de/274866a6cc0fb3d6e20118115bf173e4d2ffc4f9509d58e0f80fddc80ec85eed?color=5a5a5a) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(30^{\circ})&=&\dfrac{\overline{MR}}{\overline{EM}} \quad \scriptsize \mid\; \cdot \overline{EM} \\[5pt]
\cos(30^{\circ}) \cdot \overline{EM}&=& \overline{MR}\quad \scriptsize \mid\; :\cos(30^{\circ})\\[5pt]
\overline{EM}&=&\dfrac{\overline{MR}}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt]
\overline{EM}&=&\dfrac{3e}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt]
\overline{EM}&=& 2\cdot \sqrt{3}e
\end{array}\)](https://mathjax.schullv.de/d96d9f1dba9d1dbc8dce83211f11e3163d9ee797d4de6bee4c9875f02b36cf22?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overline{EF}&=& 2 \cdot \overline{EM} &\quad \scriptsize \\[5pt]
&=& 2 \cdot 2\cdot \sqrt{3}e &\quad \scriptsize \\[5pt]
\overline{EF}&=& \underline{ 4\sqrt{3}e}
\end{array}\)](https://mathjax.schullv.de/1d501292f2075b3e28b775eeca18115a9ed9a3ad0c121a70968fad3b26adb752?color=5a5a5a) 5. Schritt: Umfang des Vierecks
5. Schritt: Umfang des Vierecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
u_{AEFG}&=& \overline{AG}+\overline{FG}+\overline{AE}+\overline{EF} \quad \scriptsize \\[5pt]
&=& 6e+1,5e+4,5e+4\cdot \sqrt{3}e \\[5pt]
u_{AEFG}&=& \underline{ 18,93e}
\end{array}\)](https://mathjax.schullv.de/e3d328620594eb2654ea1fd047a88fd8bef4eedcc50fe04e69ab35f8e70e5dad?color=5a5a5a) Beas Aussage ist nicht richtig, da
Beas Aussage ist nicht richtig, da  gilt.
gilt.
Abschlussprüfung 2015
