Wahrscheinlichkeiten

Aufgabe 1

Melina und Paul besitzen Fußball-Sammelbilder. In Pauls Schuhkarton liegen 20 Sammelbilder von Nationalspielern.
Die Tabelle zeigt deren Verteilung auf drei Nationalmannschaften.

Nationalmannschaft	Anzahl der Sammelbilder
Frankreich	9
Deutschland	6
Portugal	5

Melina zieht zwei Sammelbilder gleichzeitig.

Wie groß ist die Wahrscheinlichkeit, dass auf den beiden gezogenen Sammelbildern

portugiesische Spieler abgebildet sind?
höchstens ein deutscher Spieler abgebildet ist?
kein französischer Spieler abgebildet ist?

(3 P)

Abschlussprüfung 2024

Aufgabe 2

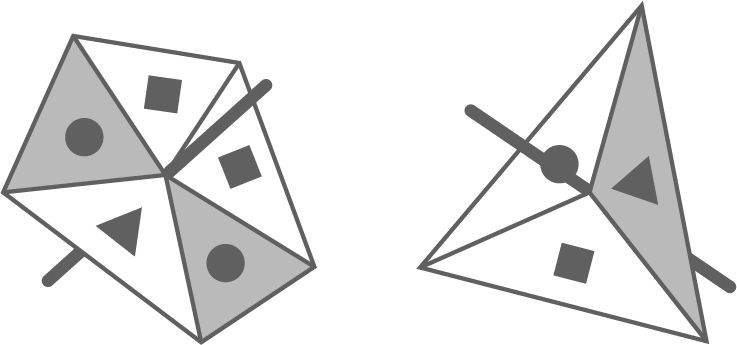
Auf zwei Kreiseln befinden sich die Symbole ●,▲ und ◼︎.
Die Felder eines Kreisels sind jeweils gleich groß.
Sie sind grau bzw. weiß gefärbt.
Die beiden Kreisel werden gedreht und bleiben auf einer Kante liegen.

Berechne die Wahrscheinlichkeit für folgende Ereignisse:

zwei gleiche Symbole
Kreis und Dreieck
höchstens ein graues Feld

(3 P)

Abschlussprüfung 2023

Aufgabe 3

Die Klasse 5c verkauft Lose beim Schulfest.
Es gibt folgende Gewinne: 12 Fußbälle und 8 Basketbälle.
Die restlichen 80 Lose sind Nieten.

Francesca möchte zwei Lose ziehen.

Wie groß ist die Wahrscheinlichkeit, dass sie

zwei Nieten zieht?
einen Fußball und einen Basketball gewinnt?

(3 P)

Abschlussprüfung 2022

Aufgabe 4

Die beiden Glücksräder werden gedreht.
Wenn sie stehen bleiben, erkennt man im Sichtfenster eine zweistellige Zahl.
Die Abbildung zeigt die Zahl 43.

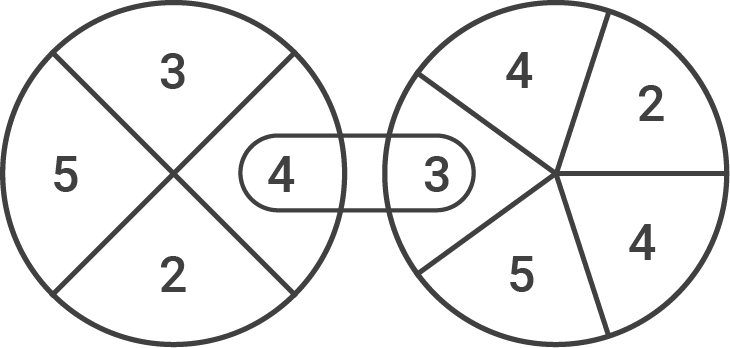Zwei Kreise mit Zahlen und Verbindungen zwischen ihnen, die verschiedene Segmente darstellen.

Mit welcher Wahrscheinlichkeit ist im Sichtfenster

eine Zahl mit zwei gleichen Ziffern zu sehen?
eine durch 12 teilbare Zahl zu sehen?
höchstens einmal die Ziffer 4 zu sehen?

(3,5 P)

Abschlussprüfung 2021

Aufgabe 5

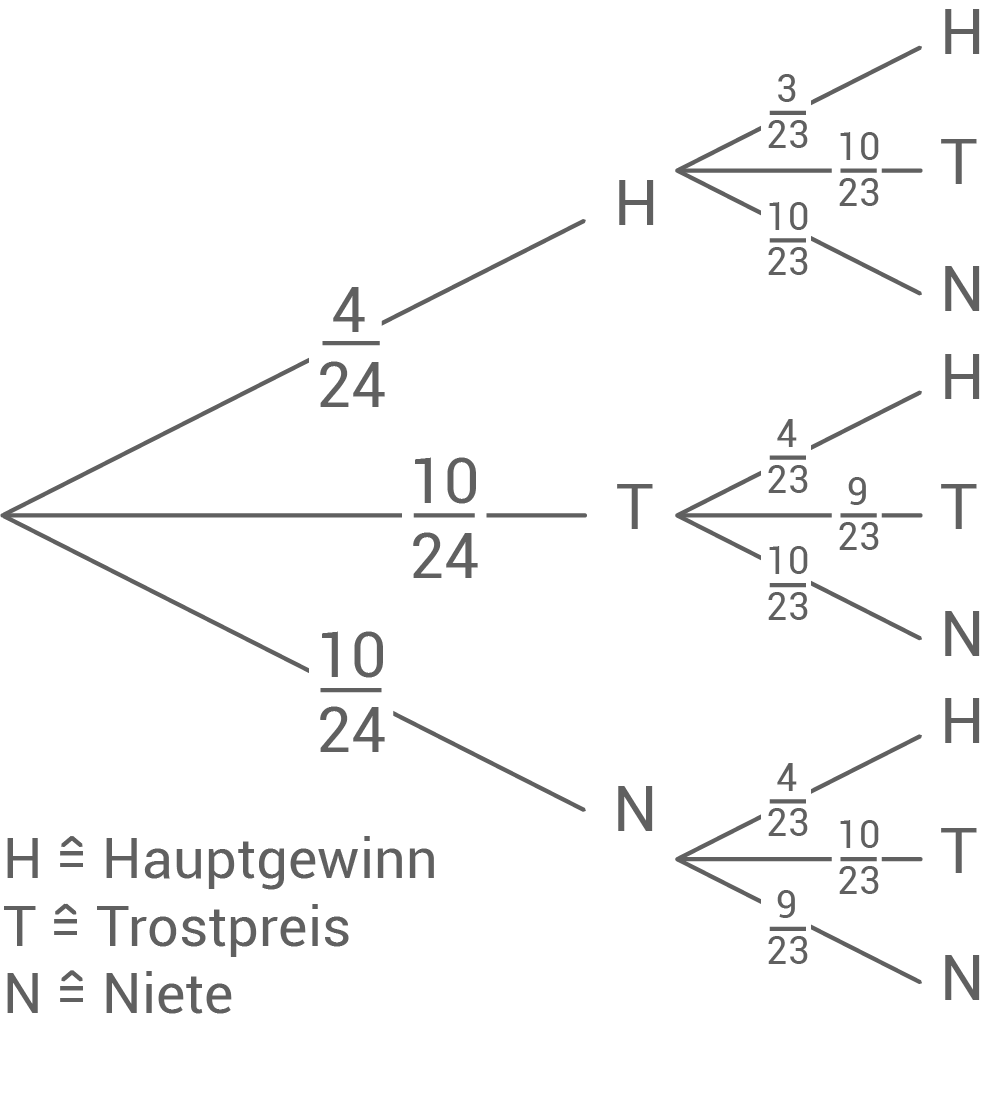
Auf einem Jahrmarkt gibt es eine Lostrommel. In dieser befinden sich 4 Lose für die Hauptgewinne, 10 Lose für Trostpreise und 10 Nieten. Mia zieht ohne hinzuschauen zwei Lose.

Mit welcher Wahrscheinlichkeit zieht sie genau zwei Hauptgewinne?

Mit welcher Wahrscheinlichkeit erhält sie mindestens einen Hauptgewinn?

(3 P)

Musterprüfung 1

Aufgabe 6

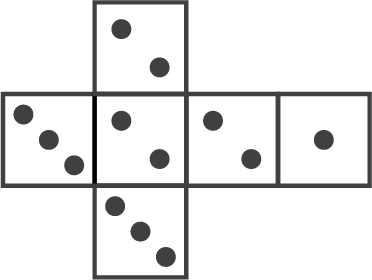
Ein nicht idealer Würfel wird zweimal geworfen. Die Abbildung zeigt diesen Würfel.

Schwarze Dominosteine auf einem weißen Hintergrund in einer Kreuzform angeordnet.

Bestimme die Wahrscheinlichkeit dafür, dass ein Pasch (zwei gleiche Augenzahlen) gewürfelt wird.
Wie lautet die Wahrscheinlichkeit dafür, dass die Augensumme der beiden Würfe 5 beträgt?
Würde man eine Augenzahl 2 durch eine 3 ersetzen, ändert sich dann die Wahrscheinlichkeit? Begründe deine Entscheidung.

(3 P)

Musterprüfung 2

Aufgabe 7

Ben, Laura und Emma besitzen jeweils ein Rubbel-Los. Auf jedem Los befinden sich 16 gleich große Felder.

Raster mit grünen Feldern und zwei Zahlen: 0 € und 10 € in weißen Feldern.

Nur zwei der 16 Felder werden freigerubbelt. Die beiden Beträge, die dadurch sichtbar werden, werden addiert und ergeben den Gewinn. Auf acht Feldern steht der Betrag $0 \,€,$ auf sechs Feldern steht der Betrag $1 \,€$ und auf zwei Feldern der Betrag $10 \,€.$

Ben hat auf seinem Los zwei Felder freigerubbelt (siehe Abbildung).
Berechne die Wahrscheinlichkeit für das Ereignis "Gewinn $10 \,€$ ".
Laura überlegt sich, wie groß die Wahrscheinlichkeit ist, den Hauptgewinn von $20 \,€$ zu erhalten.
Berechne die Wahrscheinlichkeit.
Emma möchte mehr als $10 \,€$ gewinnen.
Berechne diese Wahrscheinlichkeit.

(4 P)

Abschlussprüfung 2020

Aufgabe 8

In einem Kaugummiautomaten befinden sich 10 rote, 9 weiße und 6 grüne Kaugummis.
Betätigt man den Drehgriff, erhält man einen Kaugummi. Luisa dreht zweimal.

Mit welcher Wahrscheinlichkeit erhält sie

zuerst einen roten, dann einen weißen Kaugummi?
keinen grünen Kaugummi?

Von den 25 Kaugummis sind die Hälfte der roten und die Hälfte der grünen Kaugummis mit Brause gefüllt.

Mit welcher Wahrscheinlichkeit erhält Luisa zwei mit Brause gefüllte Kaugummis?

(3,5 P)

Abschlussprüfung 2019

Aufgabe 9

In einer Schale liegen rote, grüne und weiße Gummibärchen. Insgesamt sind es 12 Stück. Sofia nimmt, ohne hinzusehen, gleichzeitig zwei Gummibärchen aus der Schale.

Die Grafik zeigt ein unvollständiges Baumdiagramm dieses Zufallsversuchs.

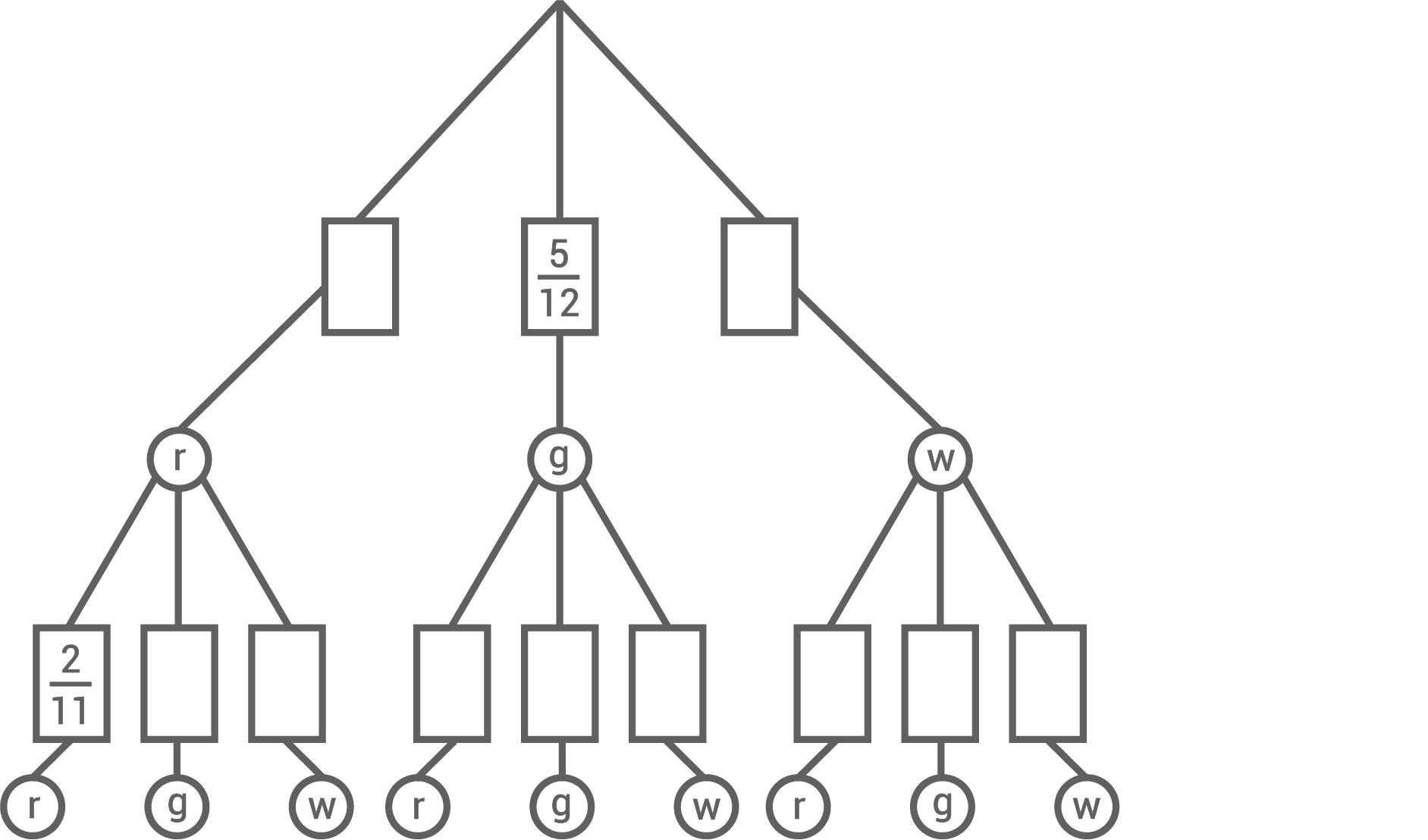Diagramm eines Entscheidungsbaums mit verschiedenen Ästen und Wahrscheinlichkeiten.

Vervollständige dieses Baumdiagramm.

Mit welcher Wahrscheinlichkeit zieht Antonetta bei diesem Zufallsversuch

genau ein rotes Gummibärchen?
höchstens ein weißes Gummibärchen?

(3,5 P)

Abschlussprüfung 2018

Aufgabe 10

Max und Nele spielen ein Würfelspiel.
Zwei Würfel werden gleichzeitig geworfen.
Die beiden Augenzahlen werden addiert (Augensumme).
Gewonnen hat der Spieler mit der größeren Augensumme.

Überprüfe die Aussage:
„Die Wahrscheinlichkeit für Augensumme 6 ist größer als die Wahrscheinlichkeit für Augensumme 9.“
Begründe deine Antwort durch eine Rechnung oder Argumentation.

Max hat eine 5 und eine 3 geworfen.
Wie groß ist die Wahrscheinlichkeit, dass Nele mit dem nächsten Wurf das Spiel gewinnt?

(3,5 P)

Abschlussprüfung 2017

Aufgabe 11

Hannah legt Buchstabenkärtchen.

Auf dem Tisch liegen bereits folgende vier Buchstabenkärtchen.

In einem Beutel befinden sich die abgebildeten zehn Buchstabenkärtchen.

Daraus zieht Hannah zwei Buchstabenkärtchen gleichzeitig.

Bilder mit Buchstaben in verschiedenen Kästchen, die ein kreatives Layout bilden.

Wie groß ist die Wahrscheinlichkeit, mit den beiden gezogenen Buchstaben

Zwei Wortspiele mit den Buchstaben S, C, H, A, L, T, Z zur Bildung von Wörtern.

(3,5 P)

Abschlussprüfung 2016

Aufgabe 12

In einem Behälter liegen 20 Kugeln. Sie sind rot, blau und grün gefärbt.
Es werden zwei Kugeln gleichzeitig gezogen.

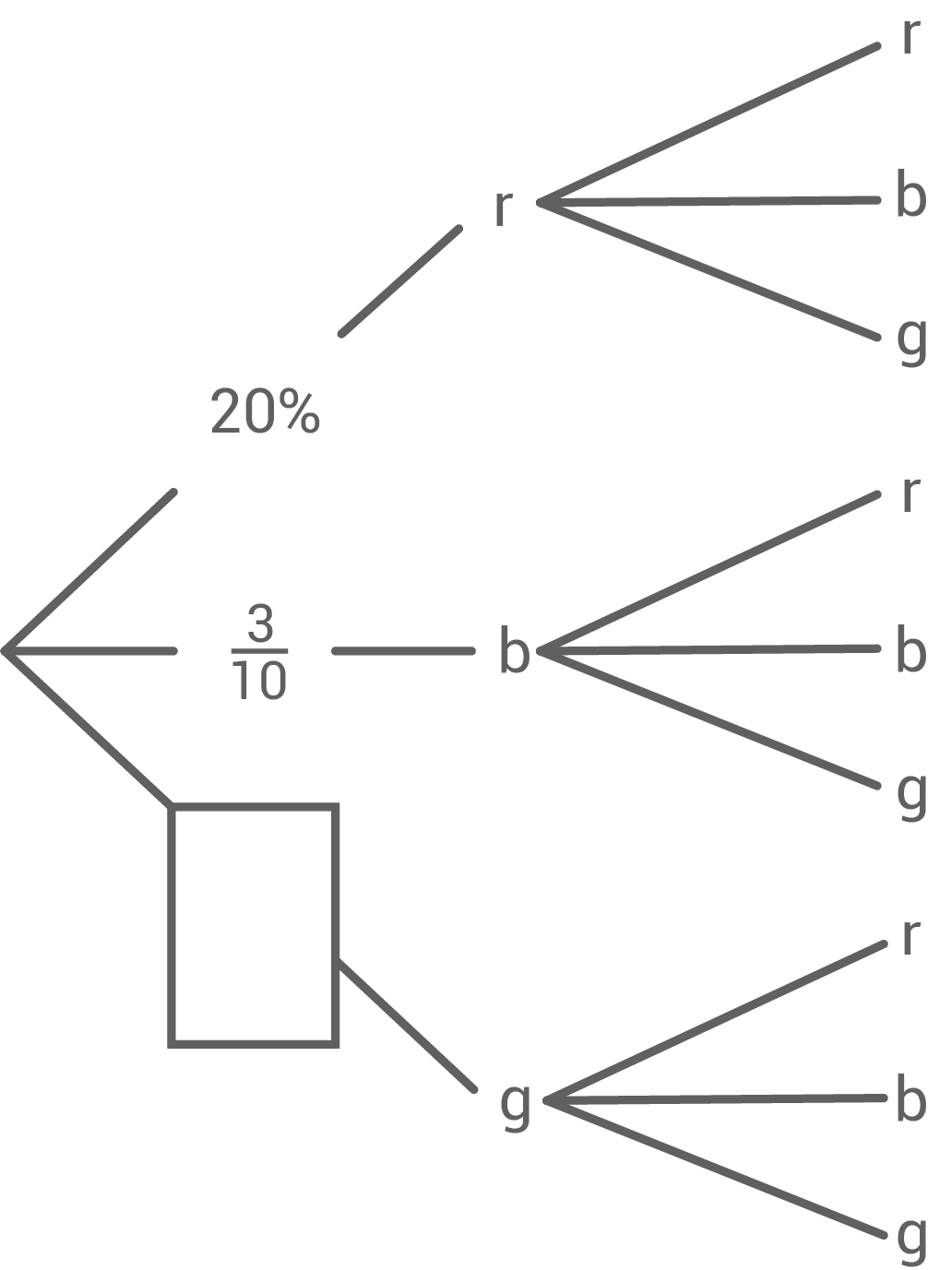Diagramm zur Darstellung von Wahrscheinlichkeiten mit Farben und Wahrscheinlichkeitswerten.

Im Baumdiagramm fehlt eine Wahrscheinlichkeitsangabe.
Ergänze diese.

Wie groß ist die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen?

In einem anderen Behälter liegen von jeder Farbe doppelt so viele Kugeln, also insgesamt 40 Kugeln.
Es werden ebenfalls zwei Kugeln gleichzeitig gezogen.

Uli sagt: „Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, ist gleich.“

Hat Uli recht?
Begründe durch Rechnung.

(4 P)

Abschlussprüfung 2015

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\begin{array}[t]{rll} & P(\text{zwei portugiesische Spieler}) \\[5pt] =& \dfrac{5}{20}\cdot \dfrac{4}{19} \\[5pt] =& \underline{\underline{\dfrac{1}{19}=5,3\,\%}} \end{array}$

$\begin{array}[t]{rll} & P(\text{höchstens ein deutscher Spieler}) \\[5pt] =& 1-P(\text{zwei deutsche Spieler}) \\[5pt] =& 1-\dfrac{6}{20}\cdot \dfrac{5}{19} \\[5pt] =& \underline{\underline{\dfrac{35}{38}=92,1\,\%}} \end{array}$

$\begin{array}[t]{rll} & P(\text{kein französischer Spieler}) \\[5pt] =& \dfrac{5+6}{20}\cdot \dfrac{5+6-1}{19} \\[5pt] =& \underline{\underline{\dfrac{11}{38}=28,9\,\%}} \end{array}$

Abschlussprüfung 2024

Lösung 2

$P(\text{zwei gleiche Symbole})$ $=\dfrac{2}{5}\cdot\dfrac{1}{3}+\dfrac{1}{5}\cdot\dfrac{1}{3}+\dfrac{2}{5}\cdot\dfrac{1}{3}$ $=\dfrac{2}{15}+\dfrac{1}{15}+\dfrac{2}{15}$ $=\dfrac{5}{15}=\underline{\underline{\dfrac{1}{3}}}$ bzw. $33,3\,\%$

$P(\text{● und ▲})$ $=\dfrac{2}{5}\cdot\dfrac{1}{3}+\dfrac{1}{5}\cdot\dfrac{1}{3}$ $=\dfrac{2}{15}+\dfrac{1}{15}$ $=\dfrac{3}{15}=\underline{\underline{\dfrac{1}{5}}}$ bzw. $20\,\%$

$P(\text{höchstens ein graues Feld})$ $=1-\dfrac{2}{5}\cdot\dfrac{1}{3}=\dfrac{15}{15}-\dfrac{2}{15}$ $=\underline{\underline{\dfrac{13}{15}}}$ bzw. $86,7\,\%$

Abschlussprüfung 2023

Lösung 3

Es gilt:

$P(\,\text{Fußball})=\dfrac{12}{100}$
$P(\,\text{Basketball})=\dfrac{8}{100}$
$P(\,\text{Niete})=\dfrac{80}{100}$

Daraus folgt:

$\begin{array}[t]{rll} P(\,\text{zwei Nieten})&=&\dfrac{80}{100}\cdot \dfrac{79}{99} \\[5pt] &=& 0,638 \end{array}$

Die Wahrscheinlichkeit, zwei Nieten zu ziehen, liegt also bei $\underline{\underline{ 63,8\,\%}}$ .

$\quad P(\,\text{Fußball, Basketball})$

$\begin{array}[t]{rll} &=&\dfrac{12}{100}\cdot \dfrac{8}{99}+\dfrac{8}{100}\cdot \dfrac{12}{99} \\[5pt] &= & 0,019 \end{array}$

Die Wahrscheinlichkeit, einen Fußball und einen Basketball zu gewinnen, liegt also bei $\underline{\underline{ 1,9\,\%}}$ .

Abschlussprüfung 2022

Lösung 4

Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine Zahl mit zwei gleichen Ziffern zu sehen?

$\begin{array}[t]{rll} &P(\text{zwei gleiche Ziffern}) \\[5pt] &= P(2;2)+P(3;3)+P(4;4)+P(5;5) \\[5pt] &= \dfrac{1}{4} \cdot \dfrac{1}{5}+\dfrac{1}{4} \cdot \dfrac{1}{5}+\dfrac{1}{4} \cdot \dfrac{2}{5}+\dfrac{1}{4} \cdot \dfrac{1}{5} \\[5pt] &= \dfrac{5}{20}\\[5pt] &= \dfrac{1}{4} \end{array}$

Die Wahrscheinlichkeit beträgt also $\underline{\underline{ 25\,\%}}.$

Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine durch 12 teilbare Zahl zu sehen?

Die einzige Zahl, die durch 12 teilbar ist und im Sichtfenster zu sehen sein kann, ist 24.

$\begin{array}[t]{rll} &P(\text{durch 12 teilbar}) \\[5pt] &=\dfrac{1}{4} \cdot \dfrac{2}{5} \\[5pt] &=\dfrac{2}{20}= \dfrac{1}{10} \end{array}$

Die Wahrscheinlichkeit beträgt also $\underline{\underline{ 10\, \%}}.$

Mit welcher Wahrscheinlichkeit ist im Sichtfenster höchstens einmal die Ziffer 4 zu sehen?

$\begin{array}[t]{rll} &P(\text{höchstens eine 4}) \\[5pt] &= 1-P(\text{zweimal vier}) \\[5pt] &= 1-\dfrac{1}{4} \cdot \dfrac{2}{5} \\[5pt] &= 1-\dfrac{1}{10} \\[5pt] &=\dfrac{9}{10} \end{array}$

Die Wahrscheinlichkeit beträgt also $\underline{\underline{ 90 \,\%}}.$

Abschlussprüfung 2021

Lösung 5

realschulprüfung musterprüfung baden-württemberg

$\begin{array}[t]{rll} P(\text{H};\text{H})&=&\dfrac{4}{24}\cdot \dfrac{3}{23} \\[5pt] &=& 0,0217 \\[5pt] &=& 2,17\,\% \\[5pt] \end{array}$

Das Gegenereignis von „mindestens ein Hauptgewinn“ ist „kein Hauptgewinn“:

$\begin{array}[t]{rll} P(\text{mind. 1x H})&=& 1-P(\text{kein H}) \\[5pt] &=& 1-\dfrac{20}{24}\cdot \dfrac{19}{23}&\quad \scriptsize \\[5pt] &=& 0,3116\\[5pt] &=& \underline{\underline{ 31,16\,\%}} \end{array}$

Musterprüfung 1

Lösung 6

Wahlbereich Baumdiagramm Stochastik Wahrscheinlichkeit Würfel

Wahrscheinlichkeit für einen Pasch bestimmen

$\begin{array}[t]{rll} P(\,\text{Pasch})&=&\dfrac{1}{6}\cdot \dfrac{1}{6}+\dfrac{3}{6}\cdot \dfrac{3}{6}+\dfrac{2}{6}\cdot \dfrac{2}{6} \\[5pt] &=&\dfrac{1}{36}+\dfrac{9}{36}+\dfrac{4}{36} \\[5pt] &=&\dfrac{14}{36}=\dfrac{7}{18} \\[5pt] &=&0,389=\underline{\underline{ 38,9\,\%}} \end{array}$

Wahrscheinlichkeit für die Augensumme 5 berechnen

$\begin{array}[t]{rll} P(\,\text{Augensumme 5})&=&\dfrac{3}{6} \cdot \dfrac{2}{6}+\dfrac{2}{6} \cdot \dfrac{3}{6} & \\[5pt] &=&\dfrac{6}{36}+\dfrac{6}{36} \\[5pt] &=&\dfrac{12}{36} \\[5pt] &=&\dfrac{1}{3}= \underline{\underline{ 33,3\,\%}} \end{array}$

Würde man eine Augenzahl 2 durch eine 3 ersetzen, ändert sich dann die Wahrscheinlichkeit?

Nein, sie verändert sich nicht, da die Augenzahl 2 und die Augenzahl 3 nur ihre Wahrscheinlichkeiten tauschen.
Dabei wird die Wahrscheinlichkeit einen Pasch oder die Augensumme 5 zu würfeln, nicht verändert.

Musterprüfung 2

Lösung 7

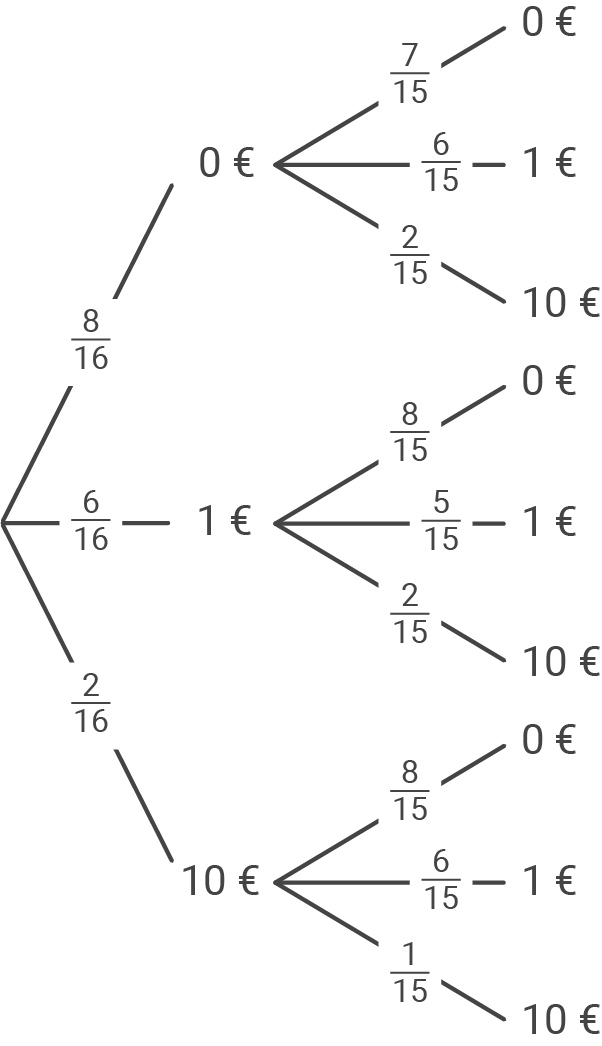
Diagramm mit Entscheidungsbaum und verschiedenen Geldbeträgen.

Wahrscheinlichkeit für das Ereignis „Gewinn 10 €“ berechnen

Rechenweg anzeigen

$P(\text{Gewinn }10\,€) = \underline{\underline{ 13,3 \,\%}}$

Wahrscheinlichkeit für den Hauptgewinn berechnen

Rechenweg anzeigen

$P(\text{Gewinn }20\,€) = \underline{\underline{ 0,8\,\%}}$

Wahrscheinlichkeit berechnen, mehr als 10 € zu gewinnen

Rechenweg anzeigen

$P(\text{Gewinn}\gt10\,€) = \underline{\underline{ 10,8\,\% }}$

Abschlussprüfung 2020

Lösung 8

Mit welcher Wahrscheinlichkeit erhält sie zuerst einen roten, dann einen weißen Kaugummi?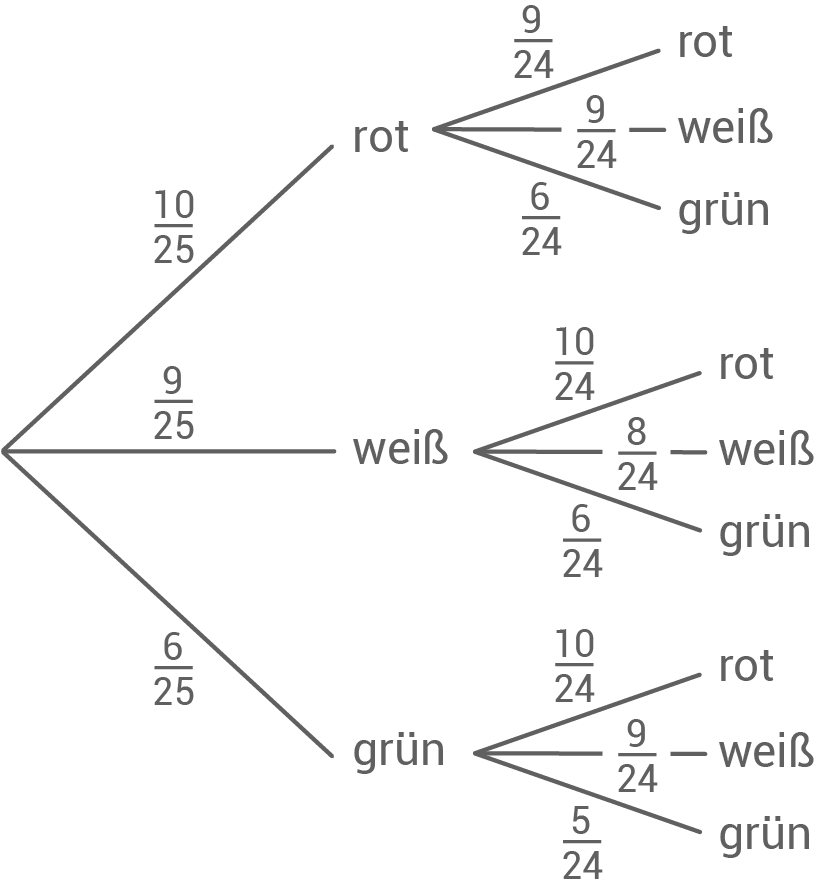

Diagramm mit Wahrscheinlichkeiten für die Farben rot, weiß und grün in verschiedenen Verzweigungen.

$\begin{array}[t]{rll} P(\,\text{rot, dann weiß})&=& \dfrac{10}{25} \cdot \dfrac{9}{24}\\[5pt] &=& \dfrac{3}{20} = 0,15 \\[5pt] \end{array}$

Die Wahrscheinlichkeit liegt bei $\underline{\underline{ 15 \,\%}}.$

Mit welcher Wahrscheinlichkeit erhält sie keinen grünen Kaugummi?

$\begin{array}[t]{rll} &&P(\,\text{keinen grünen Kaugummi}) \\[5pt] &=& \dfrac{10}{25} \cdot \dfrac{9}{24}+\dfrac{10}{25} \cdot \dfrac{9}{24}+\dfrac{9}{25} \cdot \dfrac{10}{24}+\dfrac{9}{25} \cdot \dfrac{8}{24} \\[5pt] &=& \dfrac{57}{100} = 0,57\\[5pt] \end{array}$

Die Wahrscheinlichkeit liegt bei $\underline{\underline{ 57 \,\%}}.$

Mit welcher Wahrscheinlichkeit erhält Luisa zwei mit Brause gefüllte Kaugummis?

Anzahl der Kaugummis mit Brause:
$10 :2 + 6:2=8$

$\begin{array}[t]{rll} P(\,\text{zweimal Brause}) &=& \dfrac{8}{25} \cdot\dfrac{7}{24} \\[5pt] &=& \dfrac{7}{75}\\[5pt] &=& 0,093 \end{array}$

Die Wahrscheinlichkeit liegt bei $\underline{\underline{ 9,3 \,\%}}.$

Abschlussprüfung 2019

Lösung 9

Baumdiagramm vervollständigen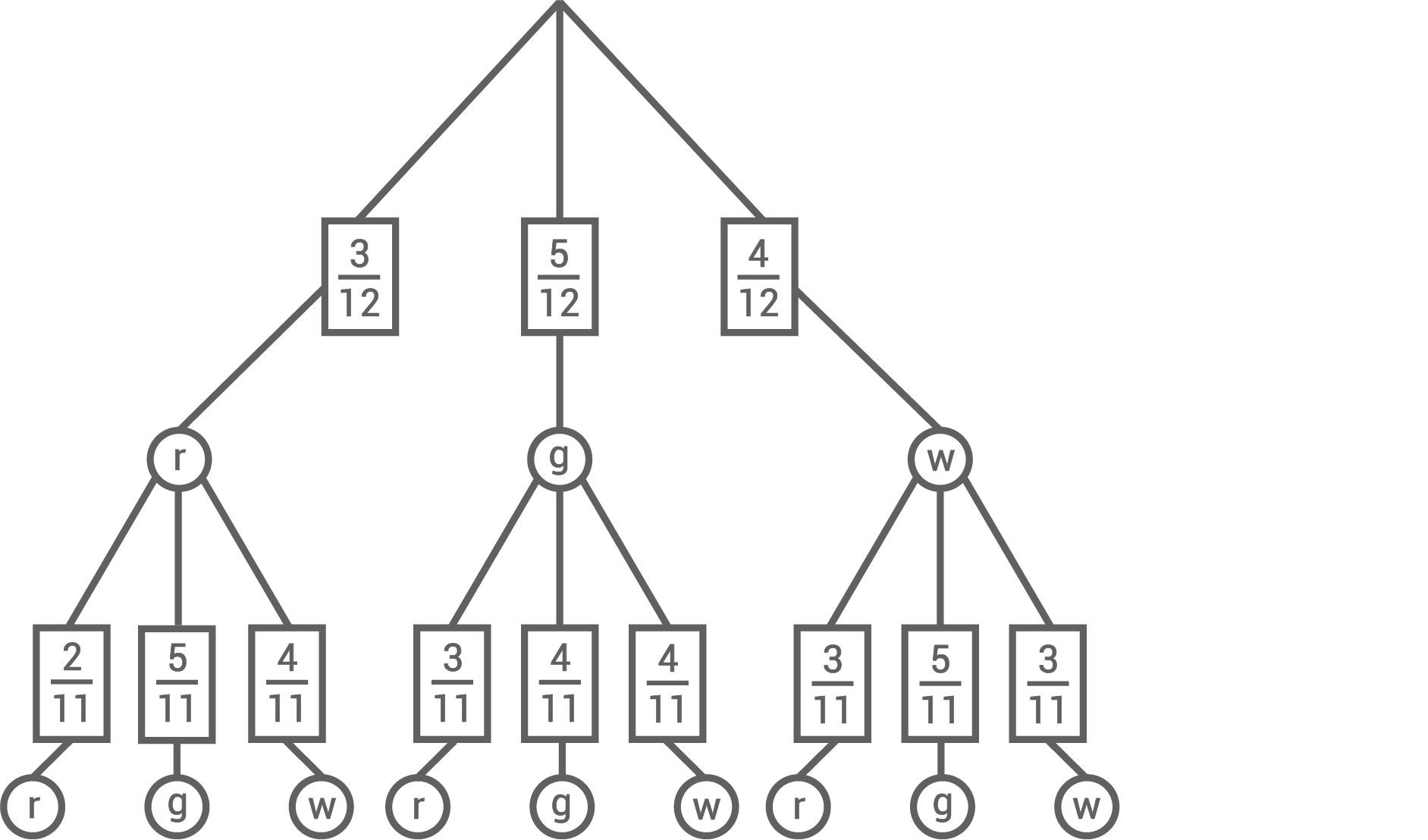

Wahrscheinlichkeiten berechnen

Mit der Produkt- und Summenregel ergibt sich:

Rechenweg anzeigen

$\,\text{P (genau ein rotes Gb)} = \dfrac{9}{22}= 41\%$

Mit einer Wahrscheinlichkeit von $41\%$ zieht Sofia genau ein rotes Gummibärchen.

Dass Sofia höchstens ein weißes Gummibärchen zieht, ist das Gegenereignis dazu, dass sie genau zwei weiße Gummibärchen zieht.

$\begin{array}[t]{rll} \,\text{P (zwei weiße Gb)} &=& P(\,\text{w};\,\text{w}) \\[5pt] &=& \dfrac{4}{12}\cdot \dfrac{3}{11} \\[5pt] &=& \dfrac{1}{11}\\[5pt] \end{array}$

$\,\text{P (höchstens ein weißes Gb)}$ $= 1- \dfrac{1}{11} = \dfrac{10}{11}=\underline{\underline{ 91\,\%}}$

Mit einer Wahrscheinlichkeit von $91\%$ zieht Sofia höchstens ein weißes Gummibärchen.

Abschlussprüfung 2018

Lösung 10

Begründung durch Rechnung

Wahrscheinlichkeit für die Augensumme 6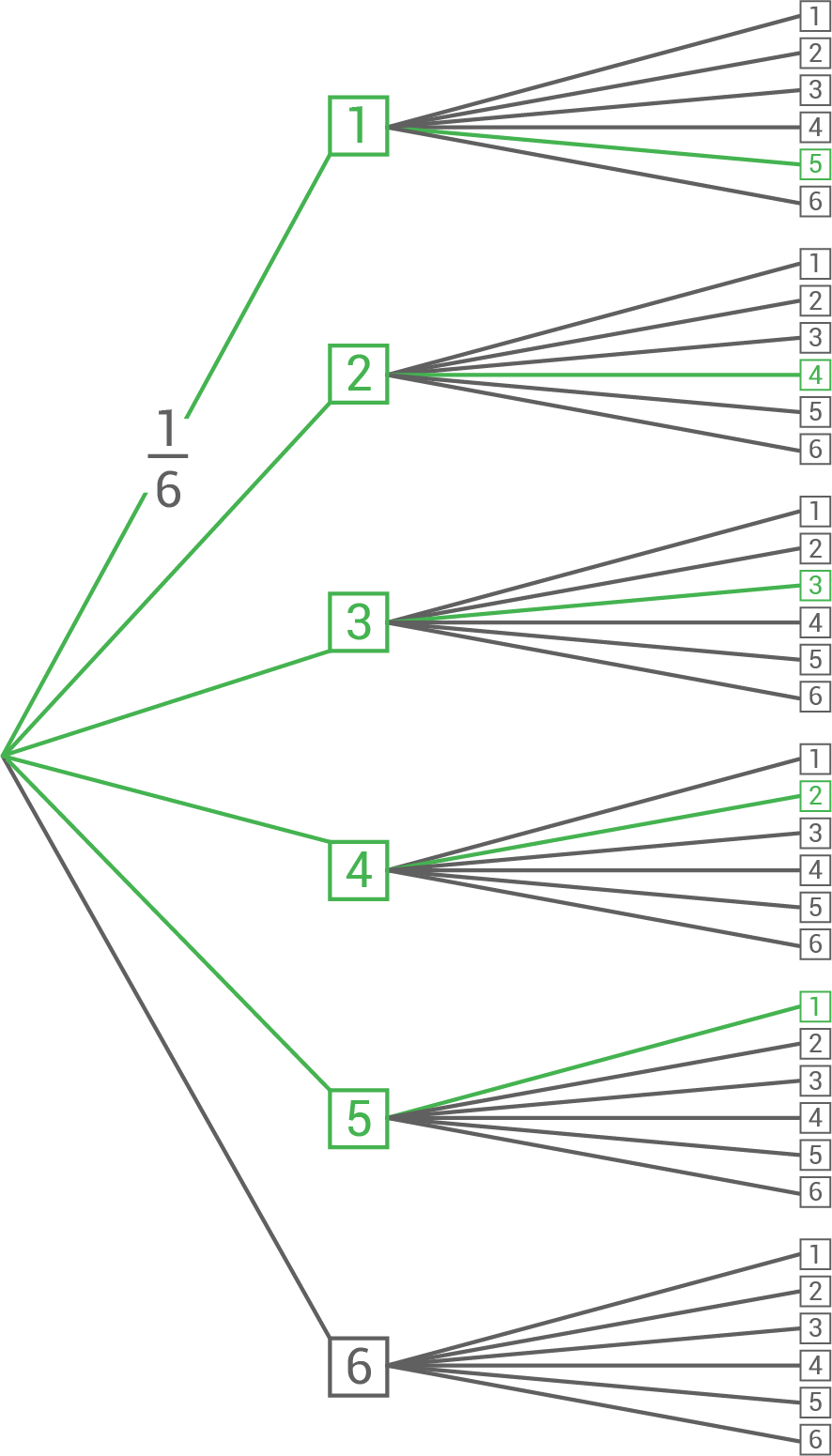

Diagramm mit Verzweigungen und Zahlen, das eine Struktur oder Beziehung darstellt.

Die Wahrscheinlichkeit jedes Pfades beträgt $\dfrac{1}{6}\cdot \dfrac{1}{6} = \dfrac{1}{36}.$ Damit folgt:

$\begin{array}[t]{rll} &P(\text{Augensumme 6})&=& \left(\dfrac{1}{6}\cdot \dfrac{1}{6}\right) \cdot 5 \\[5pt] &&=& \dfrac{5}{36} \\[5pt] &&\approx& 0,1389 \end{array}$

Die Wahrscheinlichkeit, die Augensumme 6 zu würfeln, beträgt also $\underline{13,89 \%.}$

Wahrscheinlichkeit für die Augensumme 9

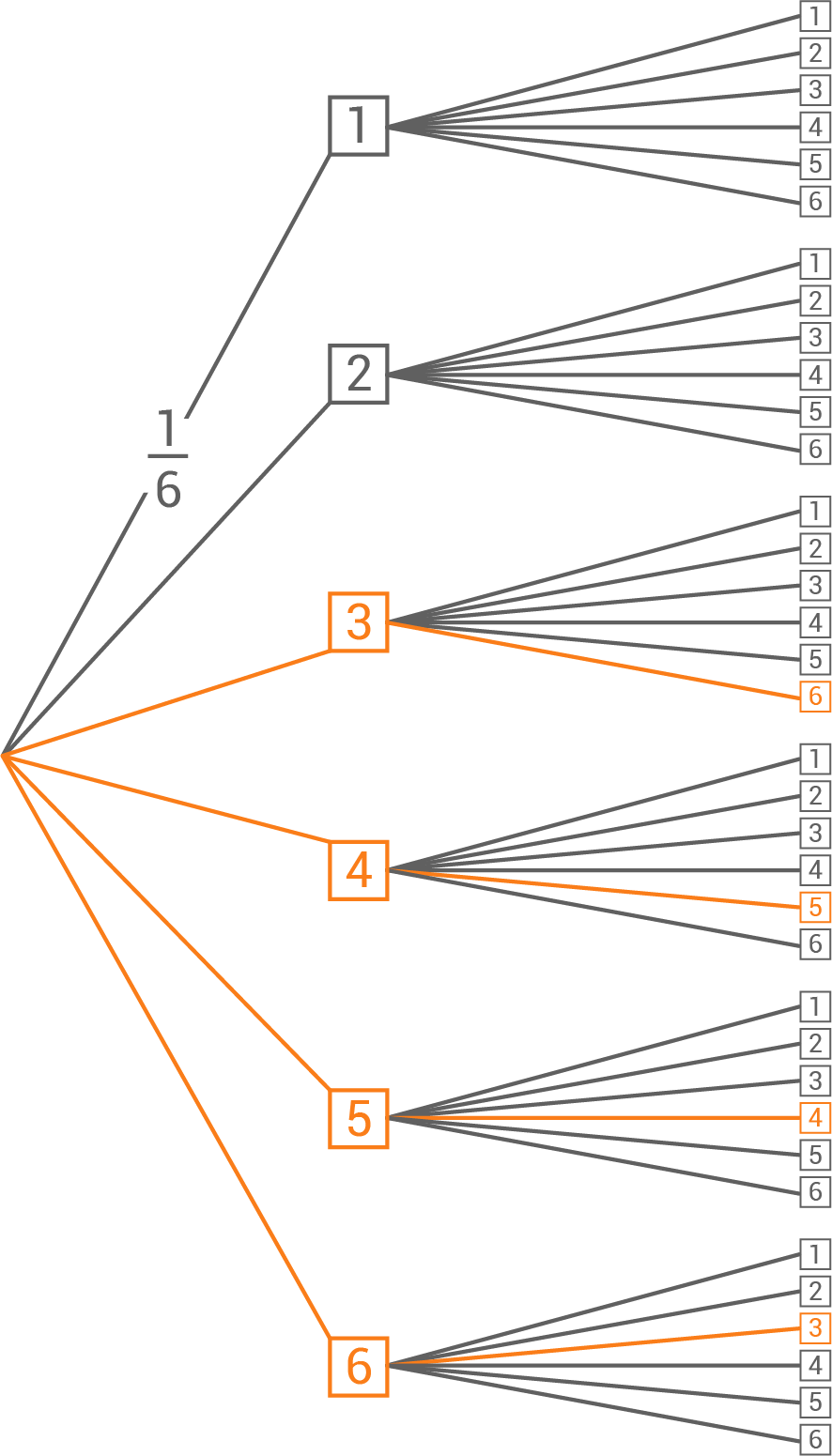
Diagramm mit Verzweigungen und Zahlen zur Darstellung von Beziehungen oder Wahrscheinlichkeiten.

Die Wahrscheinlichkeit jedes Pfades beträgt $\dfrac{1}{6}\cdot \dfrac{1}{6} = \dfrac{1}{36}.$ Damit folgt:

$\begin{array}[t]{rll} &P(\text{Augensumme 9})&=& \left(\dfrac{1}{6}\cdot \dfrac{1}{6}\right) \cdot 4 \\[5pt] &&=& \dfrac{4}{36} \\[5pt] &&\approx& 0,1111 \end{array}$

Die Wahrscheinlichkeit, die Augensumme 9 zu würfeln, beträgt also $\underline{11,11\,\%.}$

Somit stimmt die Aussage.

Begründung durch Argumentation

Wahrscheinlichkeit für die Augensumme 6

Es gibt insgesamt fünf Möglichkeiten, die Augensumme 6 zu würfeln:

1 und 5
2 und 4
3 und 3
4 und 2
5 und 1

Wahrscheinlichkeit für die Augensumme 9

Um die Augensumme 9 zu würfeln, gibt es allerdings nur vier Möglichkeiten:

3 und 6
4 und 5
5 und 4
6 und 3

Für jede dieser Möglichkeiten ist die Wahrscheinlichkeit gleich. Somit reicht es, die Anzahl der Möglichkeiten zu vergleichen, um die Aussage zu bewerten. Für die Augensumme 6 gibt es mehr Möglichkeiten, also stimmt die Aussage.

Wie groß ist die Wahrscheinlichkeit, dass Nele mit dem nächsten Wurf das Spiel gewinnt?

Nele gewinnt dann das Spiel, wenn sie eine größere Augenzahl als 8 würfelt.
Dafür gibt es insgesamt zehn Möglichkeiten:

3 und 6
4 und 5
4 und 6
5 und 4
5 und 5

5 und 6
6 und 3
6 und 4
6 und 5
6 und 6

$\begin{array}[t]{rll} P(\,\text{Augenzahl > 8})&=& \left(\dfrac{1}{6} \cdot\dfrac{1}{6}\right) \cdot 10 \\[5pt] &=& \dfrac{5}{18} \\[5pt] &=& 0,278 \\[5pt] &=& \underline{\underline{27,8\,\%}} \\[5pt] \end{array}$

Abschlussprüfung 2017

Lösung 11

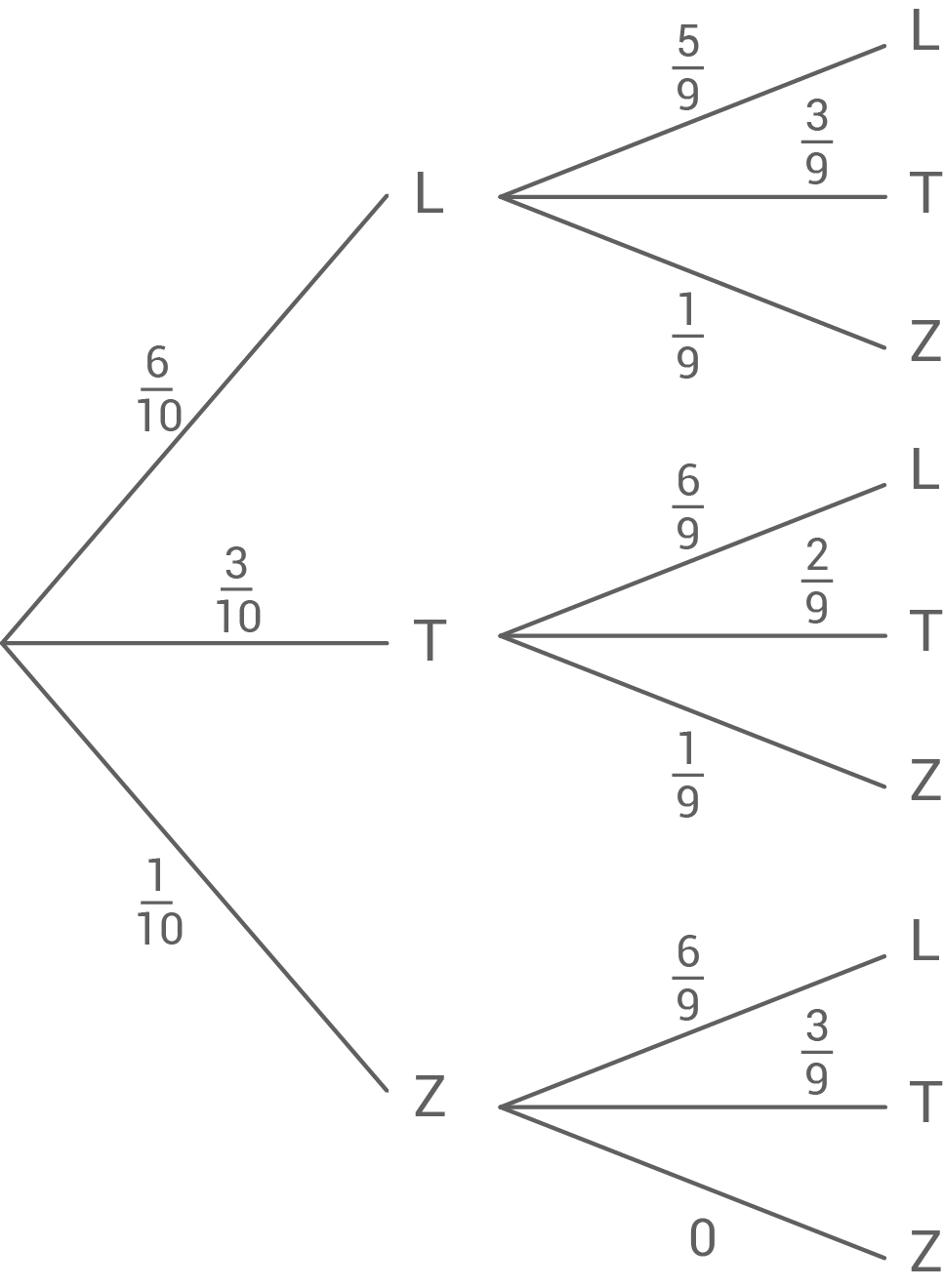
Pflichtbereich Baumdiagramm Stochastik Buchstaben

Wie groß ist die Wahrscheinlichkeit, das Wort „SCHALL“ legen zu können?

$\begin{array}[t]{rll} P(\text{SCHALL})&=& \dfrac{6}{10}\,\cdot\,\dfrac{5}{9}&\quad \scriptsize \\[5pt] &=& \dfrac{1}{3} \\[5pt] P(\text{SCHALL})&=&\underline{\underline{ 33,3\%}} \end{array}$

Die Wahrscheinlichkeit mit den beiden gezogenen Buchstaben das Wort „SCHALL“ zu legen, liegt bei $33,3\,\%$ .

Wie groß ist die Wahrscheinlichkeit, das Wort „SCHATZ“ legen zu können?

$\begin{array}[t]{rll} P(\text{SCHATZ})&=& \dfrac{3}{10}\,\cdot\,\dfrac{1}{9} + \dfrac{1}{10}\,\cdot\,\dfrac{3}{9} &\quad \scriptsize \\[5pt] &=& \dfrac{1}{15} \\[5pt] P(\text{SCHATZ})&=& \underline{\underline{ 6,7\,\% }} \end{array}$

Die Wahrscheinlichkeit mit den beiden gezogenen Buchstaben das Wort „SCHATZ“ zu legen, liegt bei $6,7\,\%$ .

Abschlussprüfung 2016

Lösung 12

Fehlende Angabe ergänzen

1. Schritt: Anzahl rote und blaue Kugeln berechnen

$\begin{array}[t]{rll} P(r)&=& 20\,\% \cdot 20 &\quad \scriptsize \\[5pt] P(r)&=& 4 \end{array}$

Es sind also vier rote Kugeln.

$\dfrac{3}{10}\cdot 20=6$

Es sind demnach sechs blaue Kugeln.

2. Schritt: Wahrscheinlichkeit für grün im ersten Zug berechnen

$\begin{array}[t]{rll} P(g)&=& \dfrac{20}{20}-\dfrac{4}{20}-\dfrac{6}{20} &\quad \scriptsize \\[5pt] &=&\dfrac{10}{20}\\[5pt] P(g)&=&\underline{ \dfrac{1}{2}} \end{array}$

Die fehlende Wahrscheinlichkeitsangabe entspricht also $\dfrac{1}{2}.$

Wie groß ist die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen?

Die Wahrscheinlichkeit von höchstens einer grünen Kugel kann über das Gegenereignis von genau zwei grünen Kugeln berechnet werden.
Es gilt also:

Formel anzeigen

Da nach der Ziehung der ersten grünen Kugel nur noch 19 Kugeln im Behälter sind, liegt die Wahrscheinlichkeit für die zweite grüne Kugel bei $\dfrac{9}{19}.$

Daraus folgt:

$\begin{array}[t]{rll} P(\,\text{2 grüne Kugeln})&=& \dfrac{1}{2}\cdot \dfrac{9}{19}&\quad \scriptsize \\[5pt] &=& 0,237 \end{array}$

Für die schlussendliche Wahrscheinlichkeit gilt also:

Rechenweg anzeigen

$\underline{\underline{ P=76,3\,\%}}$

Ulis Aussage überprüfen

Die neue Wahrscheinlichkeit kann wie in der letzten Aufgabe über das Gegenereignis berechnet werden.
Die Wahrscheinlichkeit für die erste grüne Kugel liegt noch immer bei $\dfrac{20}{40}=\dfrac{1}{2},$ jedoch liegt die Wahrscheinlichkeit für die zweite grüne Kugel bei $\dfrac{19}{39}.$

Rechenweg anzeigen

$\underline{\underline{ P=75,6\,\% }}$

Da die Ergebnisse unterschiedlich sind, ist Ulis Aussage falsch.

Abschlussprüfung 2015

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?