Funktionen und Gleichungen
Aufgabe 1
Gegeben sind drei Funktionsgleichungen und drei Graphen.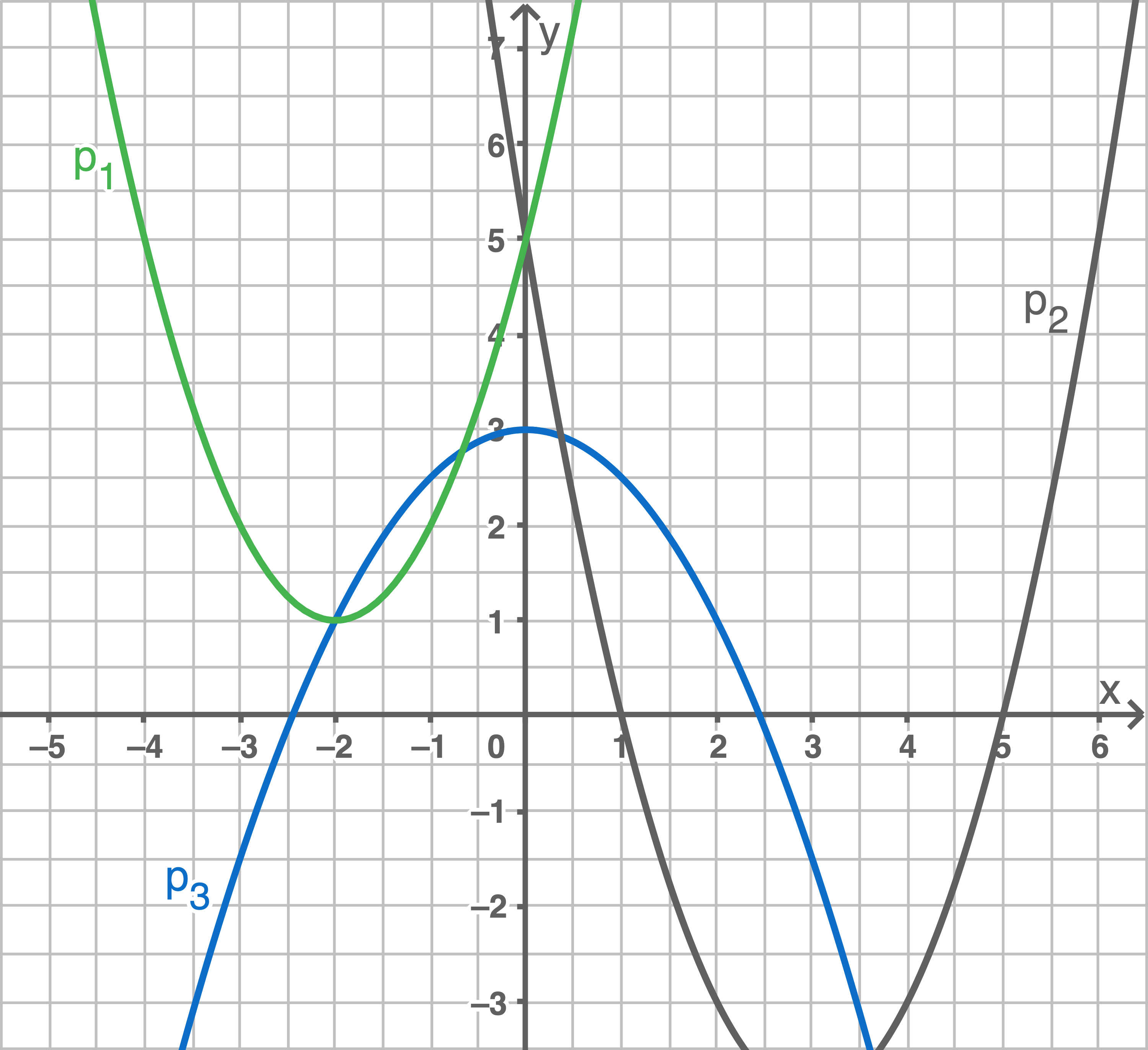
- Welcher Graph gehört zu welcher Funktionsgleichung?
Begründe deine Entscheidung. - Bestimme den Wert für
mithilfe des Schaubildes.
- Bestimme die Funktionsgleichung der Geraden
(3,5 P)
Abschlussprüfung 2024
Aufgabe 2
Löse die Gleichung.
(3 P)
Abschlussprüfung 2024
Aufgabe 3
Löse das Gleichungssystem.

Abschlussprüfung 2023
(3 P)
Aufgabe 4
Die Abbildung zeigt den Ausschnitt einer verschobenen nach oben geöffneten Normalparabel 
 schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  und hat die Steigung
und hat die Steigung  .
.
- Bestimme die Funktionsgleichung der Parabel
Entnimm dazu geeignete Werte aus der Zeichnung.
- Berechne die Koordinaten der Schnittpunkte
und
der Parabel und der Geraden.
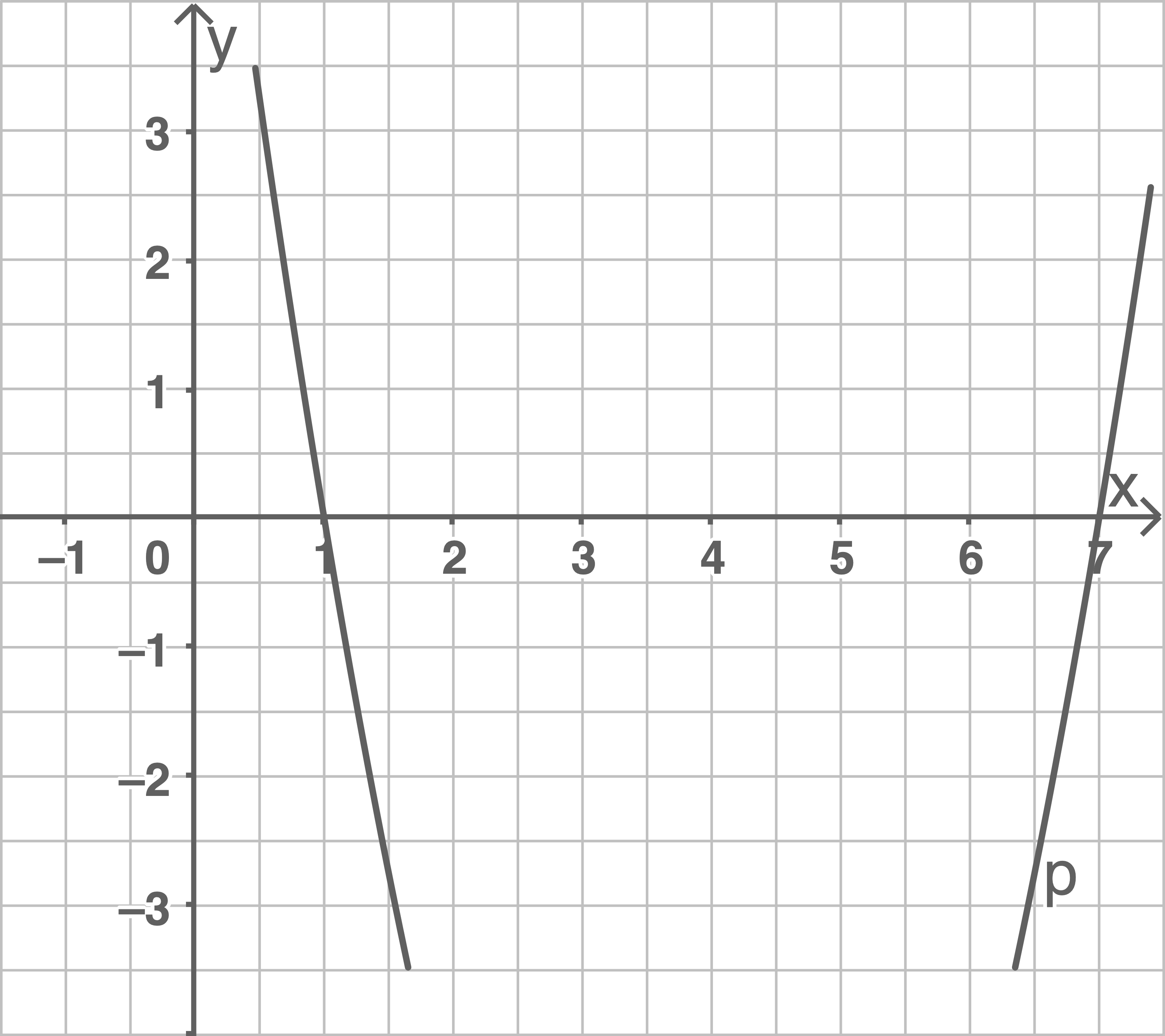
(3 P)
Aufgabe 5
Löse die Gleichung.

Abschlussprüfung 2022
(3 P)
Aufgabe 6
Das Schaubild zeigt den Ausschnitt einer verschobenen Normalparabel 
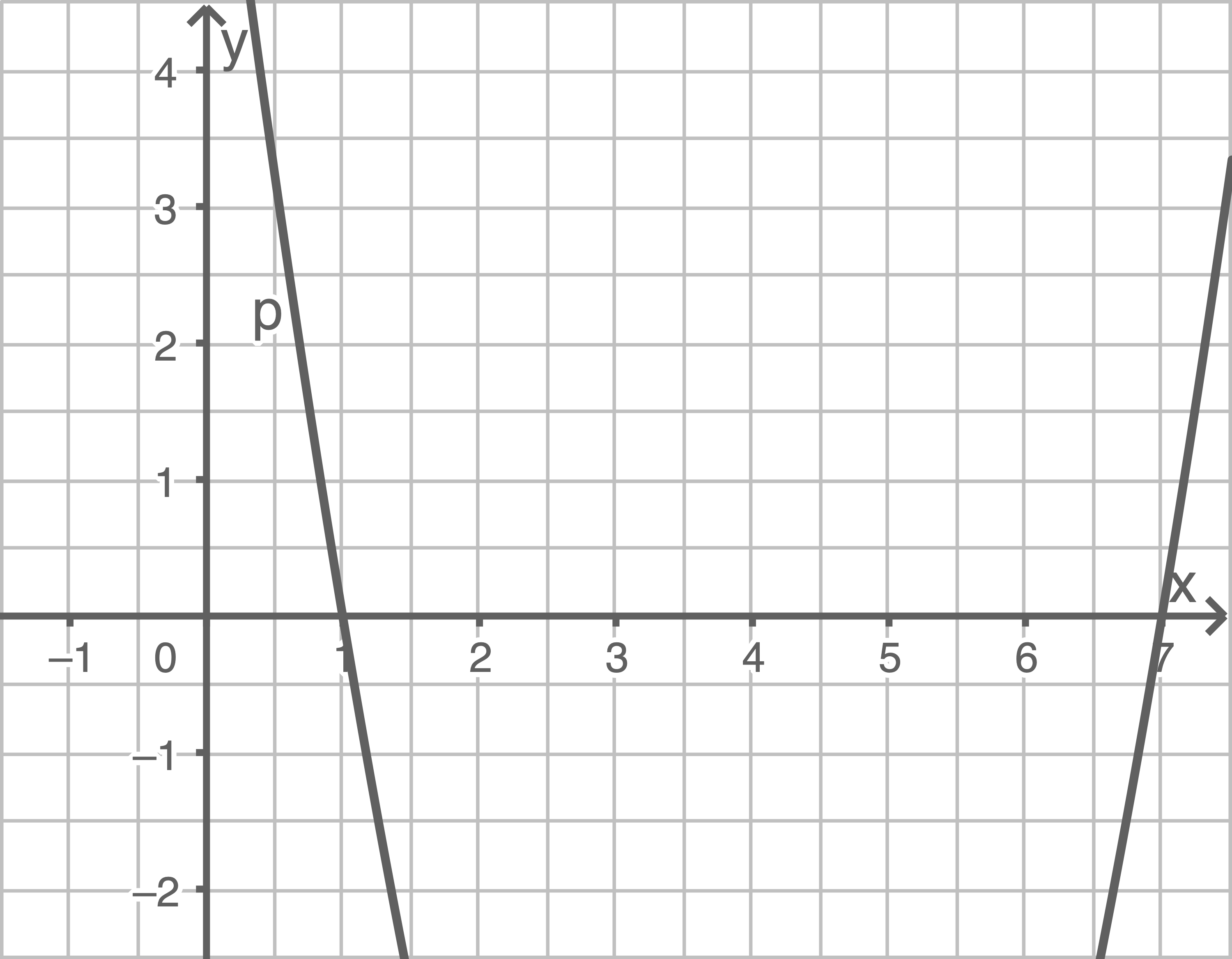

 mit der Funktionsgleichung
mit der Funktionsgleichung  schneidet die Parabel
schneidet die Parabel  in den Punkten
in den Punkten  und
und 
Abschlussprüfung 2022

- Bestimme die Funktionsgleichung von
| -3 | -2 | -1 | 0 | |
- Ergänze die fehlenden
-Werte in der Wertetabelle.
- Berechne die Koordinaten der Schnittpunkte
und
(3,5 P)
Aufgabe 7
Die Parabel  hat die Funktionsgleichung
hat die Funktionsgleichung 
Eine Gerade besitzt die Steigung
besitzt die Steigung 
Sie geht durch den Scheitelpunkt der Parabel
der Parabel 
 verläuft senkrecht zur Geraden
verläuft senkrecht zur Geraden  und geht durch den Punkt
und geht durch den Punkt 
Abschlussprüfung 2021
Eine Gerade
Sie geht durch den Scheitelpunkt
- Berechne die Koordinaten des zweiten Schnittpunkts
der Parabel
mit der Geraden
- Berechne die Funktionsgleichung der Geraden
(3 P)
Aufgabe 8
Eine Parabel  ist mit der Funktionsgleichung
ist mit der Funktionsgleichung  gegeben.
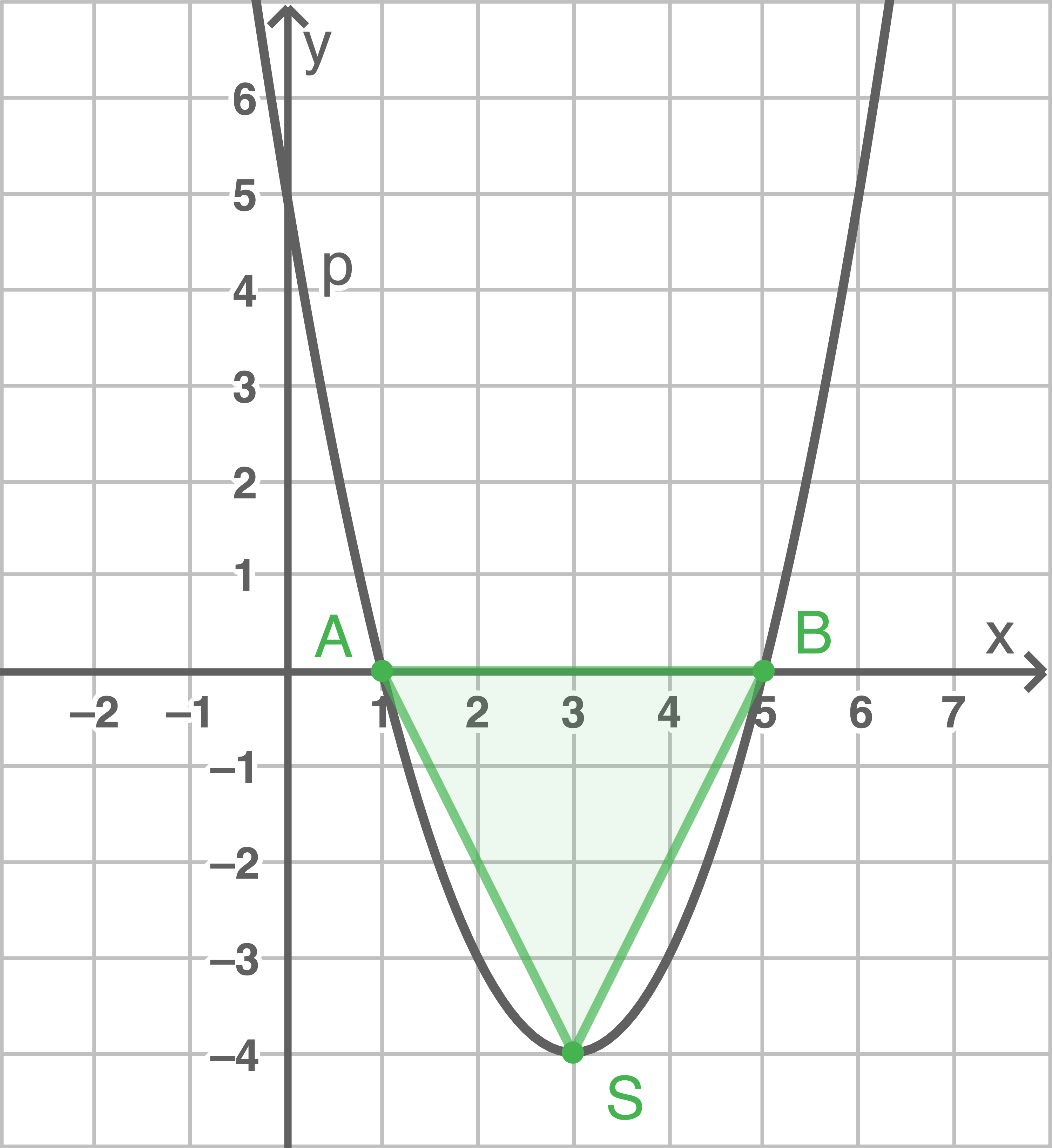
Bestimme den Scheitelpunkt und zeichne die Parabel in ein Koordinatensystem.
Die beiden Schnittpunkte der Parabel mit der
gegeben.
Bestimme den Scheitelpunkt und zeichne die Parabel in ein Koordinatensystem.
Die beiden Schnittpunkte der Parabel mit der  -Achse und der Scheitelpunkt bilden ein Dreieck.
Berechne den Umfang des Dreiecks.
-Achse und der Scheitelpunkt bilden ein Dreieck.
Berechne den Umfang des Dreiecks.
Musterprüfung 1
(3 P)
Aufgabe 9
Eine nach oben geöffnete Normalparabel  hat die Funktionsgleichung
hat die Funktionsgleichung  mit dem Scheitelpunkt
mit dem Scheitelpunkt  Der Punkt
Der Punkt  liegt auf der Parabel
liegt auf der Parabel  Berechne die Länge der Strecke
Berechne die Länge der Strecke 
Musterprüfung 2
(3 P)
Aufgabe 10
Löse die Gleichung:


Abschlussprüfung 2020
(3,5 P)
Aufgabe 11
Gegeben sind fünf Funktionsgleichungen und drei Graphen.
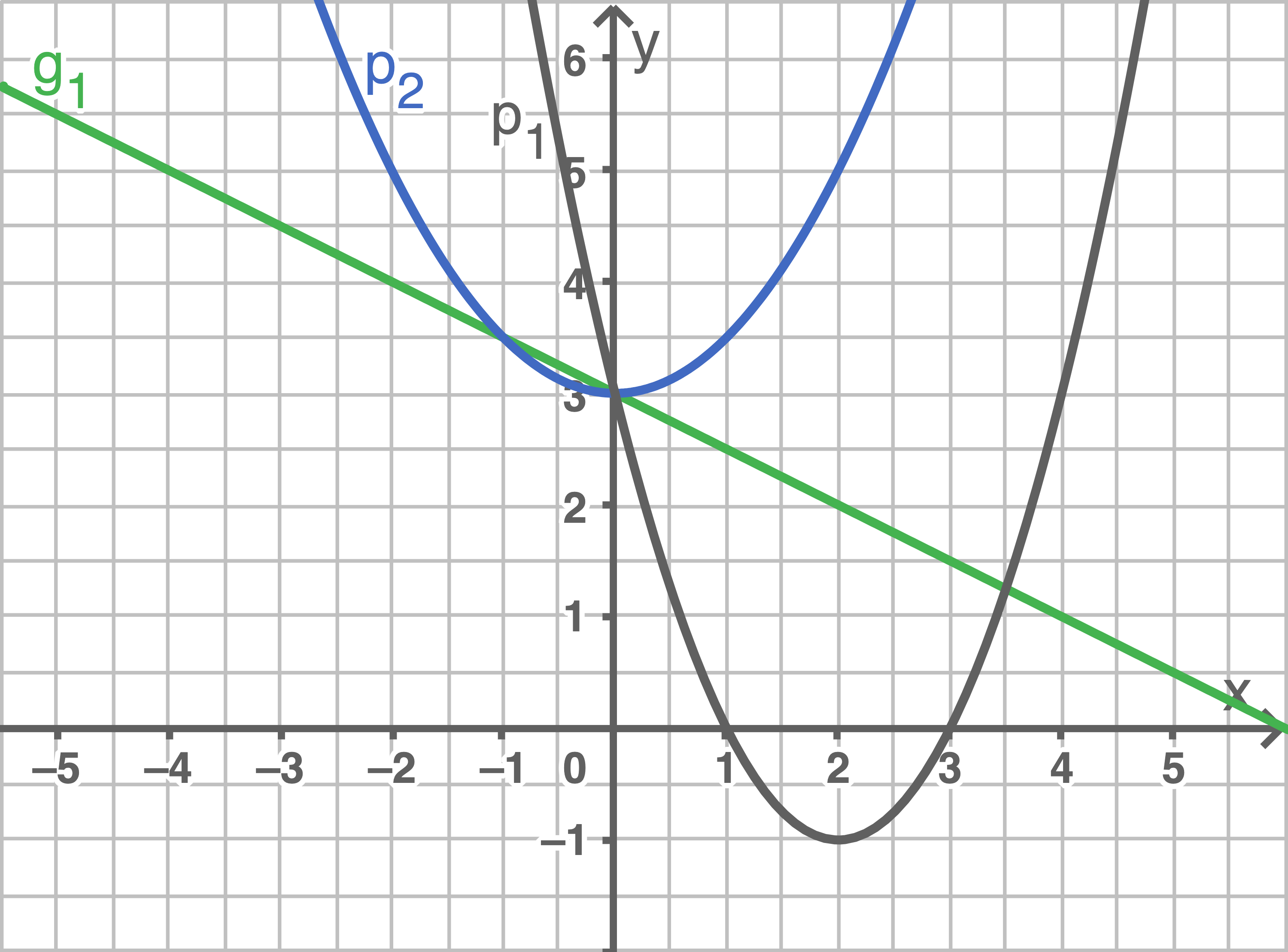 Ordne jedem Graphen die zugehörige Funktionsgleichung zu.
Ordne jedem Graphen die zugehörige Funktionsgleichung zu.
Begründe deine Entscheidung. Zeichne die beiden fehlenden Graphen in das Koordinatensystem ein.
Abschlussprüfung 2020
(1)  (2)
(2)  (3)
(3)  (4)
(4)  (5)
(5) 

Begründe deine Entscheidung. Zeichne die beiden fehlenden Graphen in das Koordinatensystem ein.
(4 P)
Aufgabe 12
Löse das Gleichungssystem:

Abschlussprüfung 2019
(3,5 P)
Aufgabe 13
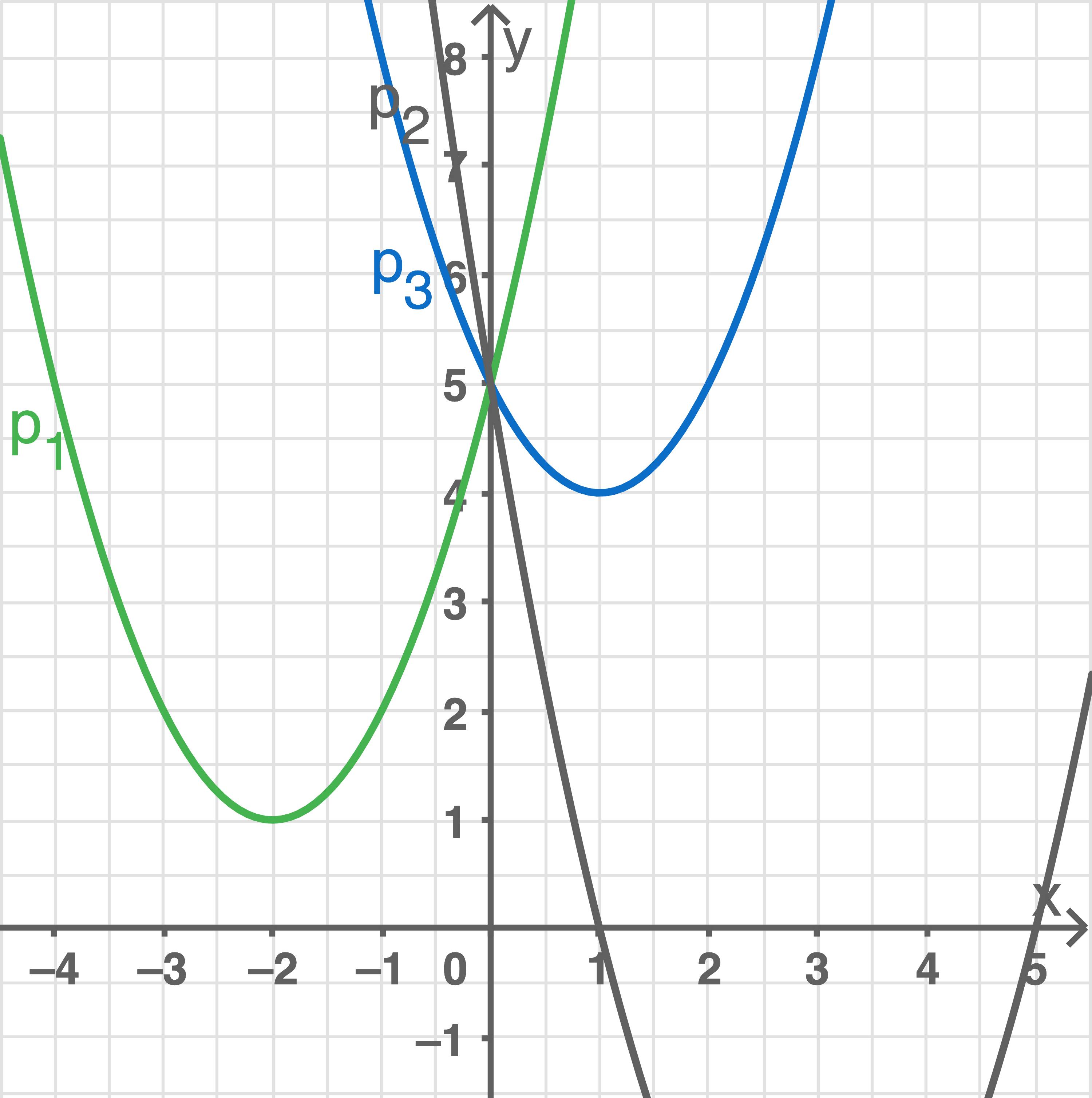
Gegeben sind eine Wertetabelle, die Graphen von zwei verschobenen Normalparabeln und drei Funktionsgleichungen.

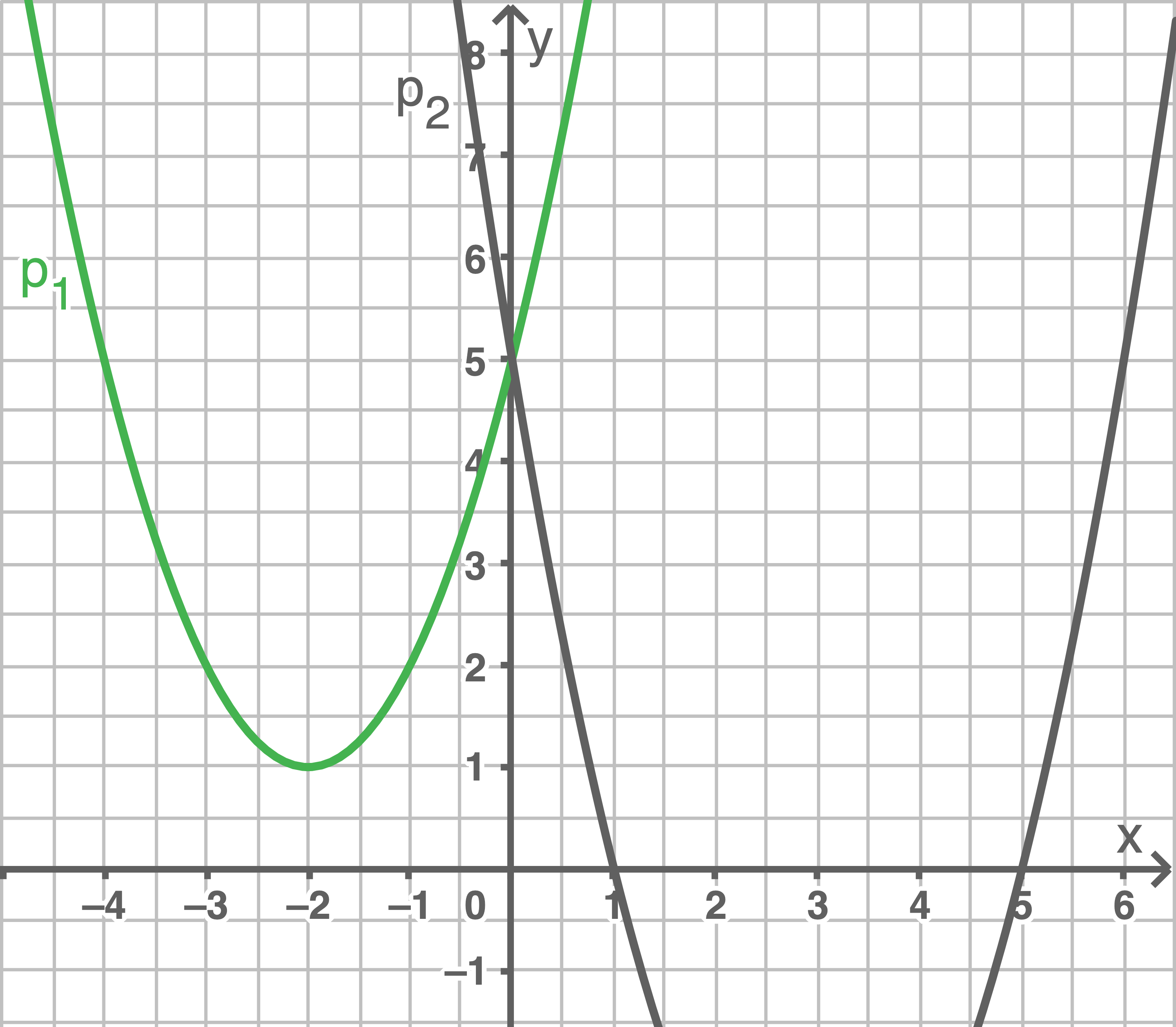 Zur Wertetabelle gehören einer der beiden Graphen sowie eine der drei Funktionsgleichungen.
Ordne der Wertetabelle ihren Graphen und ihre Funktionsgleichung zu. Begünde deine Entscheidung.
Im Schaubild fehlt der Graph
Zur Wertetabelle gehören einer der beiden Graphen sowie eine der drei Funktionsgleichungen.
Ordne der Wertetabelle ihren Graphen und ihre Funktionsgleichung zu. Begünde deine Entscheidung.
Im Schaubild fehlt der Graph  der dritten Parabel. Zeichne den fehlenden Graphen
der dritten Parabel. Zeichne den fehlenden Graphen  in das Koordinatensystem ein.
in das Koordinatensystem ein.

(4 P)
Aufgabe 14
Gib die Definitions- und Lösungsmenge der Gleichung an:

Abschlussprüfung 2018
(3,5 P)
Aufgabe 15
Zu einer verschobenen, nach oben geöffneten Normalparabel  gehört die teilweise ausgefüllte Wertetabelle.
gehört die teilweise ausgefüllte Wertetabelle.
Gib die Funktionsgleichung der Parabel  an.
an.
Ergänze die fehlenden Werte in der Tabelle.
Durch den Schnittpunkt der Parabel
der Parabel  mit der
mit der  -Achse und den Scheitelpunkt
-Achse und den Scheitelpunkt  verläuft die Gerade
verläuft die Gerade 
Berechne die Steigung der Geraden
der Geraden 
Abschlussprüfung 2018
Ergänze die fehlenden Werte in der Tabelle.
Durch den Schnittpunkt
Berechne die Steigung
(4 P)
Aufgabe 16
Das Schaubild zeigt den Ausschnitt einer verschobenen Normalparapel  .
.
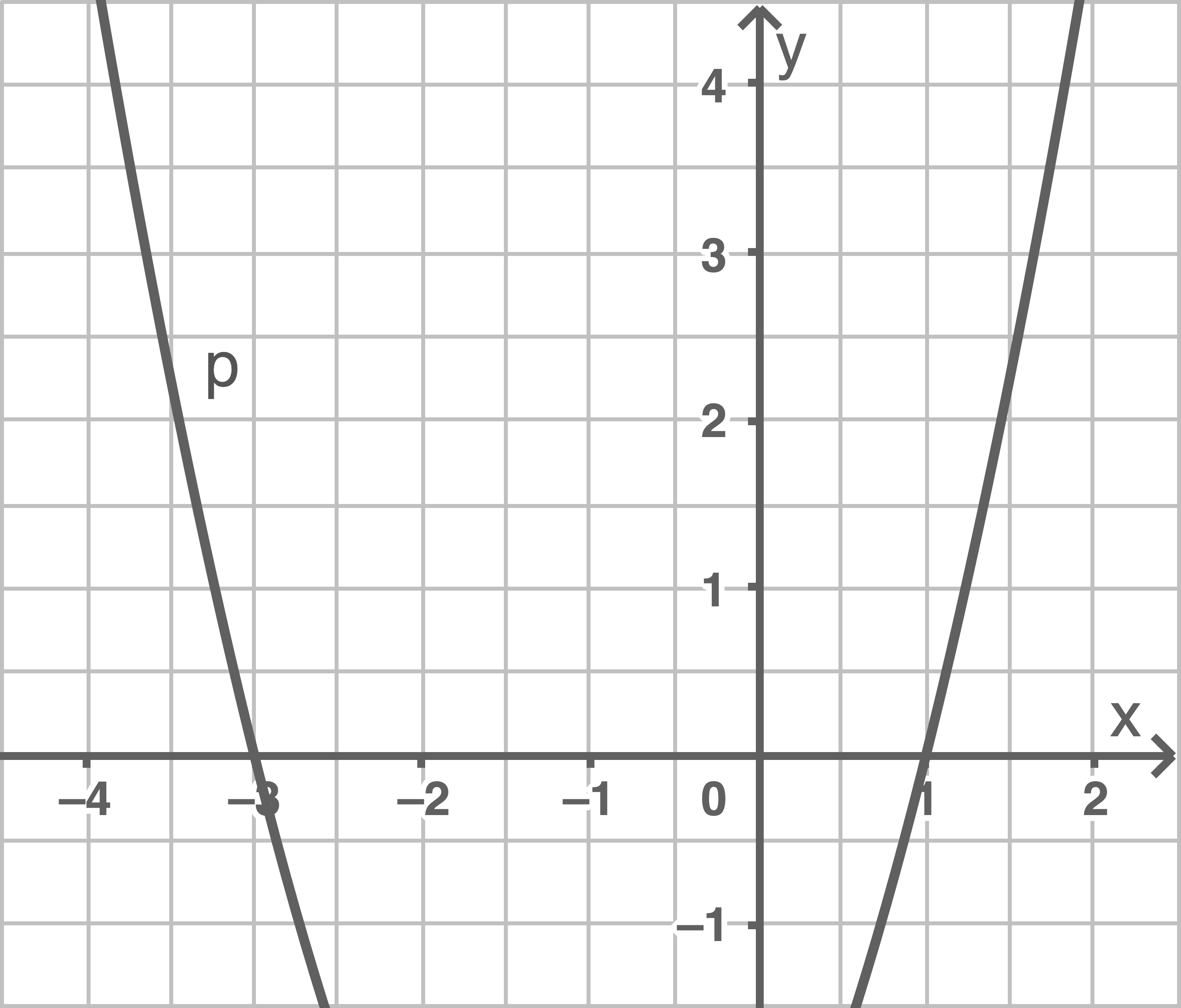 Die Gerade
Die Gerade  mit der Gleichung
mit der Gleichung  geht durch den Scheitelpunkt
geht durch den Scheitelpunkt  der Parabel
der Parabel  .
Berechne die Koordinaten des zweiten Schnittpunktes
.
Berechne die Koordinaten des zweiten Schnittpunktes  von
von  und
und  .
.

(3,5 P)
Aufgabe 17
Löse die Gleichung:

Abschlussprüfung 2017
(3,5 P)
Aufgabe 18
Gib die Definitionsmenge und die Lösungsmenge der Gleichung an:


Abschlussprüfung 2016
(3,5 P)
Aufgabe 19
Die Parabel  hat die Gleichung
hat die Gleichung 
Eine Gerade mit der Steigung
mit der Steigung  geht durch den Scheitelpunkt der Parabel
geht durch den Scheitelpunkt der Parabel  .
Berechne die Koordianten des zweiten Schnittpunkts
.
Berechne die Koordianten des zweiten Schnittpunkts  der Parabel
der Parabel  und der Geraden
und der Geraden  .
.
Abschlussprüfung 2016
Eine Gerade
(3,5 P)
Aufgabe 20
Das Schaubild zeigt die Ausschnitte von vier Parabeln.
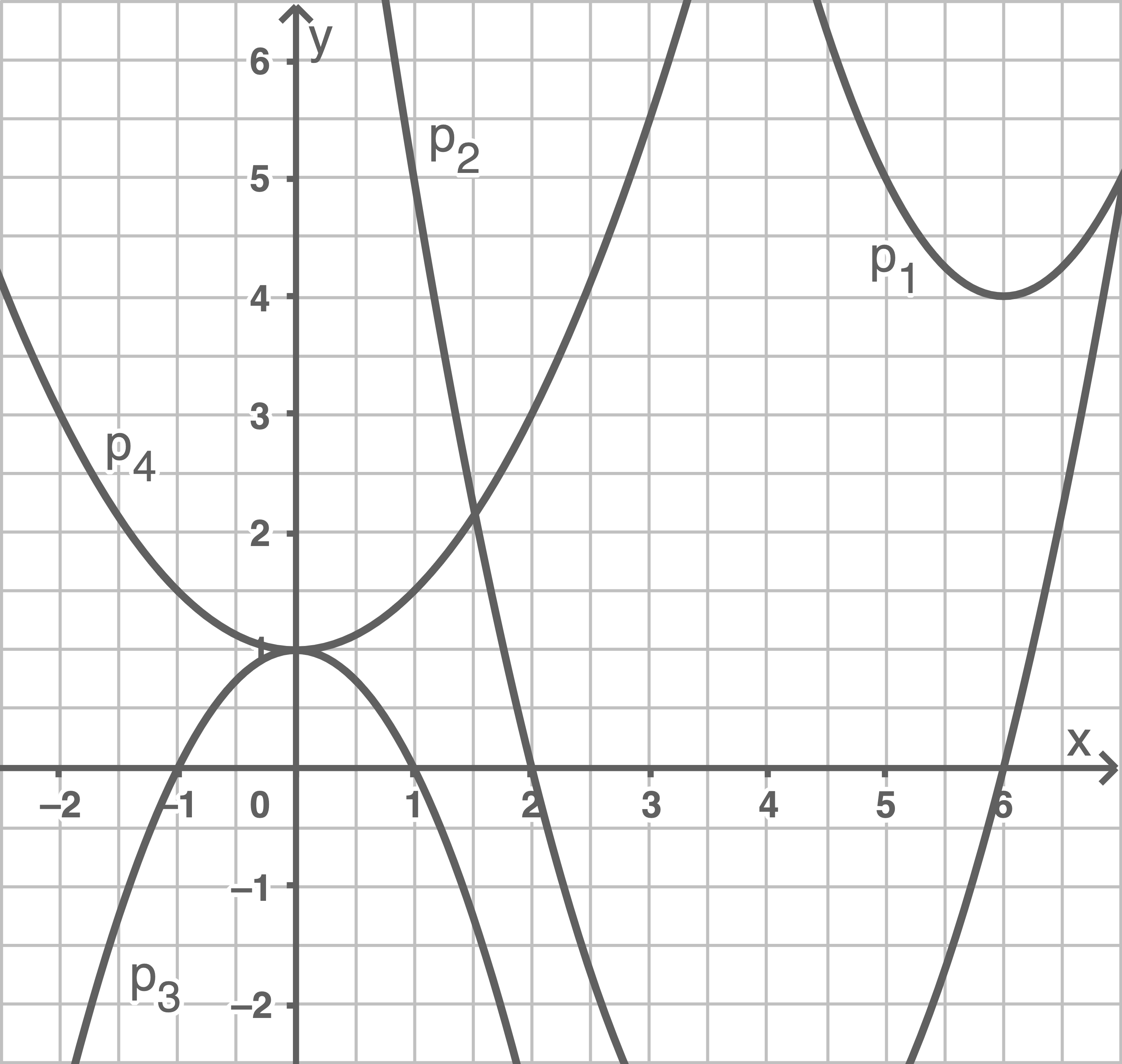
Welcher Graph gehört zur angegebenen Wertetabelle?
Begründe deine Entscheidung.
Berechne die Koordinaten des Schnittpunktes der beiden verschobenen Normalparabeln
der beiden verschobenen Normalparabeln  und
und  .
Wie heißt die Gleichung der Parabel
.
Wie heißt die Gleichung der Parabel  ?
?
Entnimm dazu erforderliche Werte dem Schaubild.

| 0 | 1 | 2 | 3 | |
| 1 | 0 | -3 | -8 |
Begründe deine Entscheidung.
Berechne die Koordinaten des Schnittpunktes
Entnimm dazu erforderliche Werte dem Schaubild.
(4 P)
Aufgabe 21
Löse das Gleichungssystem:
Abschlussprüfung 2015
| (1) | |
| (2) |
(3 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
Graphen zu Funktionsgleichungen zuordnenDer Graph der Funktion ist nach unten geöffnet.
Der Graph der Funktion ist um drei Einheiten nach rechts und um vier nach unten verschoben. Für
Lösung 2
Mit der pq-Formel folgt:Lösung 3
Einsetzungsverfahren
 Einsetzen von (2'') in (1):
Einsetzen von (2'') in (1):
![\(\begin{array}[t]{rll}
3\cdot (6y+5-y)&=&y+8 \\[5pt]
15y+15&=&y+8 &\quad \scriptsize \mid\;-y-15\\[5pt]
14y&=&-7&\quad \scriptsize \mid\;:14\\[5pt]
y&=&\underline{\underline{-\dfrac{1}{2}}}
\end{array}\)](https://mathjax.schullv.de/63bd1f433db93fb3be2b8d0bdc9f439947079dbd013bff61ee7a3a096a242060?color=5a5a5a) Einsetzen von \(y=-\dfrac{1}{2}\) in (2''):
Einsetzen von \(y=-\dfrac{1}{2}\) in (2''):


Abschlussprüfung 2023
Lösung 4
Funktionsgleichung bestimmen
Aus der Zeichnung lassen sich die Schnittpunkte von  mit der
mit der  -Achse ablesen:
-Achse ablesen: 
 Daraus folgt für den Scheitelpunkt:
Die
Daraus folgt für den Scheitelpunkt:
Die  -Koordinate des Scheitelpunkts liegt bei
-Koordinate des Scheitelpunkts liegt bei  Die
Die  -Koordinate des Scheitelpunkts liegt bei
-Koordinate des Scheitelpunkts liegt bei 
 Koordinaten berechnen
Geradengleichung aufstellen:
Koordinaten berechnen
Geradengleichung aufstellen:

 in
in 
 also
also 
 Gleichsetzen:
Gleichsetzen:
![\(\begin{array}[t]{rll}
(x-4)^2-9&=&-2x+2\\[5pt]
x^2-8x+16-9&=&-2x+2 \quad \scriptsize \mid\;+2x-2 \\[5pt]
x^2-6x+5&=&0\\[5pt]
\end{array}\)](https://mathjax.schullv.de/3e6e5c7bbeecd8a7ddbde062c078a24579ff25035b6314f26c549208ae8d58d7?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-6}{2} \pm \sqrt{\left(\dfrac{-6}{2}\right)^2-5} \\[5pt]
x_{1,2}&=& 3 \pm 2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/196ad652988732b1a22ce2a36c4ce810a030bf8731a35b1c323c7e322becbc08?color=5a5a5a)


 in
in 

 in
in 



Abschlussprüfung 2023
Lösung 5
Abschlussprüfung 2022Lösung 6
Funktionsgleichung von  bestimmen
Graphische Lösung mit der Symmetrieachse
bestimmen
Graphische Lösung mit der Symmetrieachse
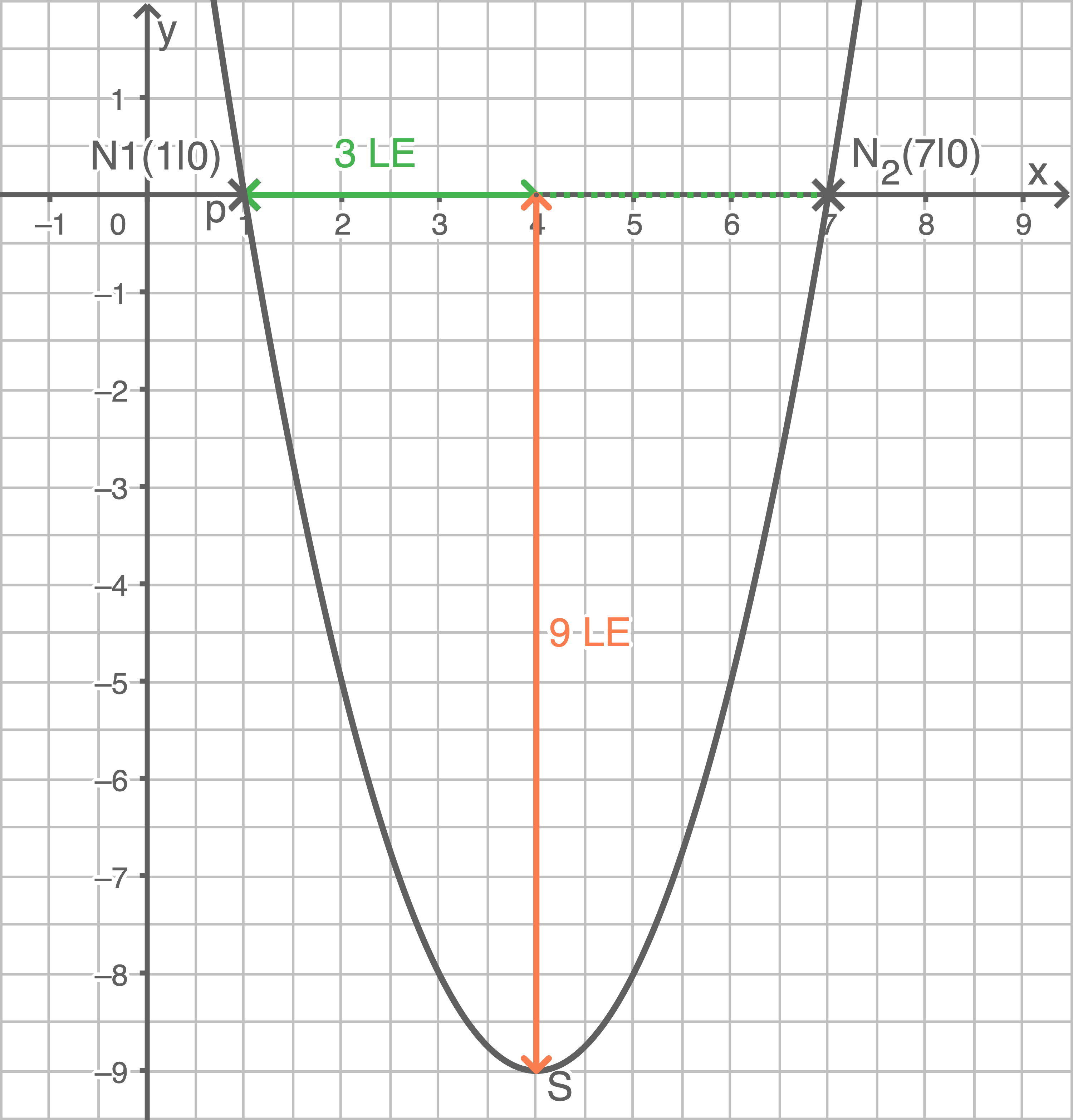
 Daraus folgt:
Daraus folgt:  in Scheitelpunktform
Rechnerische Lösung mit einem LGS
1. Schritt: Funktionsgleichung der Parabel aufstellen
Allgemeine Funktionsgleichung der Normalparabel:
in Scheitelpunktform
Rechnerische Lösung mit einem LGS
1. Schritt: Funktionsgleichung der Parabel aufstellen
Allgemeine Funktionsgleichung der Normalparabel:  2. Schritt: LGS mit
2. Schritt: LGS mit  und
und  aufstellen
aufstellen
 3. Schritt:
3. Schritt:  in (1) einsetzen
in (1) einsetzen
![\(\begin{array}[t]{rll}
0&=& 1+(-8)\cdot 1+c \\[5pt]
0&=&-7+c&\quad \mid\;+7 \\[5pt]
c&=&7 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/676cb1b576ded9c14c73d86c518a6faa94ad99a65dbf3cacfd657176bf6cae6d?color=5a5a5a) Daraus folgt:
Daraus folgt:  in Normalform
Fehlende
in Normalform
Fehlende  -Werte in der Wertetabelle ergänzen
1. Rechnung:
-Werte in der Wertetabelle ergänzen
1. Rechnung:  in
in  einsetzen
einsetzen
 2. Rechnung:
2. Rechnung:  in
in  einsetzen
einsetzen
 3. Rechnung:
3. Rechnung:  in
in  einsetzen
einsetzen
 4. Rechnung:
4. Rechnung:  in
in  einsetzen
einsetzen

Koordinaten der Schnittpunkte berechnen
1. Schritt:  -Koordinaten berechnen
-Koordinaten berechnen
![\(\begin{array}[t]{rll}
(x-4)^2-9&=&-2x+2 \\[5pt]
x^2-8x+16-9&=&-2x+2 \\[5pt]
x^2-6x+5&=&0&
\end{array}\)](https://mathjax.schullv.de/1d7df51777adf65dbb3b9f1407c9166924c058236b4fe8d61a346c62a2f1d101?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=&-\dfrac{-6}{2}\pm\sqrt{\left(\dfrac{-6}{2}\right)^2-5}& \\[5pt]
x_{1,2}&=&3\pm\sqrt{4}& \\[5pt]
x_1&=&3+2=5& \\[5pt]
x_2&=&3-2=1& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/58298bbfab75bd6f0db3dc64f177d794c2da852387b2d101c30fe02a2d81fb66?color=5a5a5a) 2. Schritt:
2. Schritt:  -Koordinaten berechnen
-Koordinaten berechnen
![\(\begin{array}[t]{rll}
y_1&=&-2\cdot 5+2 \\[5pt]
y_1&=&-8
\end{array}\)](https://mathjax.schullv.de/4414be929b2c637db70874efa818600211ca92e77e005bd49487f295228536c3?color=5a5a5a)

![\(\begin{array}[t]{rll}
y_2&=&-2\cdot 1+2 \\[5pt]
y_2&=&0
\end{array}\)](https://mathjax.schullv.de/0a714d76f41c6c8c187349a68004cd95e07c1928725e0f485bc74c953462e487?color=5a5a5a)

Abschlussprüfung 2022

- Durch Abzählen ergeben sich
bis zur Symmetrieachse
- Somit gilt:
bis zum Scheitelpunkt
| -3 | -2 | -1 | 0 | |
| 40 | 27 | 16 | 7 |
Lösung 7
Koordinaten des zweiten Schnittpunkts  der Parabel
der Parabel  mit der Geraden
mit der Geraden  berechnen.
1. Schritt: Scheitelpunkt mit der quadratischen Ergänzung bestimmen
berechnen.
1. Schritt: Scheitelpunkt mit der quadratischen Ergänzung bestimmen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10 \\[5pt]
&=& x^2-2\cdot 3x+10 \\[5pt]
&=& x^2-2\cdot 3x+3^2-3^2+10 \\[5pt]
&=& (x-3)^2-9+10\\[5pt]
&=& (x-3)^2+1
\end{array}\)](https://mathjax.schullv.de/66a34788f5fbce840aa499bb5b8d7e8fb4d3a0a01e76e0c660a89b05a2b1312c?color=5a5a5a) Der Scheitelpunkt lässt sich ablesen mit
Der Scheitelpunkt lässt sich ablesen mit  2. Schritt: Geradengleichung von
2. Schritt: Geradengleichung von  aufstellen
aufstellen

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
1&=& -2\cdot 3+c &\quad \scriptsize \\[5pt]
1&=& -6+c \quad \scriptsize \mid\; +6\\[5pt]
7&=& c \\
c&=& 7
\end{array}\)](https://mathjax.schullv.de/f6bb6f7ad5b2d6d1b1c3862eae817a19d2d6f1a9bf09fea558a271181a521634?color=5a5a5a) Daraus folgt:
Daraus folgt:  3. Schritt: Schnittpunkte berechnen
3. Schritt: Schnittpunkte berechnen
![\(\begin{array}[t]{rll}
-2x+7&=&x^2-6x+10 \quad \scriptsize \mid\;+2x-7 \\[5pt]
0&=&x^2-4x+3 \\[5pt]
x_{1/2}&=&-\dfrac{(-4)}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-3} \\[5pt]
x_{1/2}&=& 2 \pm \sqrt{(-2)^2-3} \\[5pt]
x_{1/2}&=& 2 \pm \sqrt{4-3} \\[5pt]
x_{1/2}&=& 2\pm 1 \\[5pt]
x_1&=& 2+1=3 \\[5pt]
x_2&=& 2-1=1
\end{array}\)](https://mathjax.schullv.de/b306d1fd4580da01c0f03737e96a8cd3fae4d725dbc2ac9cbffb28ee0c16ff0e?color=5a5a5a)
 in
in  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
y&=& -2\cdot 1+7 &\quad \scriptsize \\[5pt]
&=& 5
\end{array}\)](https://mathjax.schullv.de/cd232977fc08917a9115e470576da34b7461e02e37e628e4a06b6c67d9bfea3b?color=5a5a5a) Somit folgt für den zweiten Schnittpunkt:
Somit folgt für den zweiten Schnittpunkt:  Funktionsgleichung der Geraden
Funktionsgleichung der Geraden  berechnen
1. Schritt: Steigung
berechnen
1. Schritt: Steigung  der Geraden
der Geraden  bestimmen
bestimmen
 2. Schritt: Geradengleichung aufstellen
2. Schritt: Geradengleichung aufstellen

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
5&=& \dfrac{1}{2}\cdot 1+c \quad \scriptsize \\[5pt]
5&=& 0,5+c \quad \scriptsize \mid\; -0,5\\[5pt]
4,5&=& c\\
c&=& 4,5
\end{array}\)](https://mathjax.schullv.de/7602598800ef2488599aa7cf96f1ee2eb6c63259eb2a8ed14851056e5c65ec5c?color=5a5a5a) Somit lautet die Funktionsgleichung
Somit lautet die Funktionsgleichung 
Abschlussprüfung 2021
Lösung 8
Scheitelpunkt mit der quadratischen Ergänzung bestimmen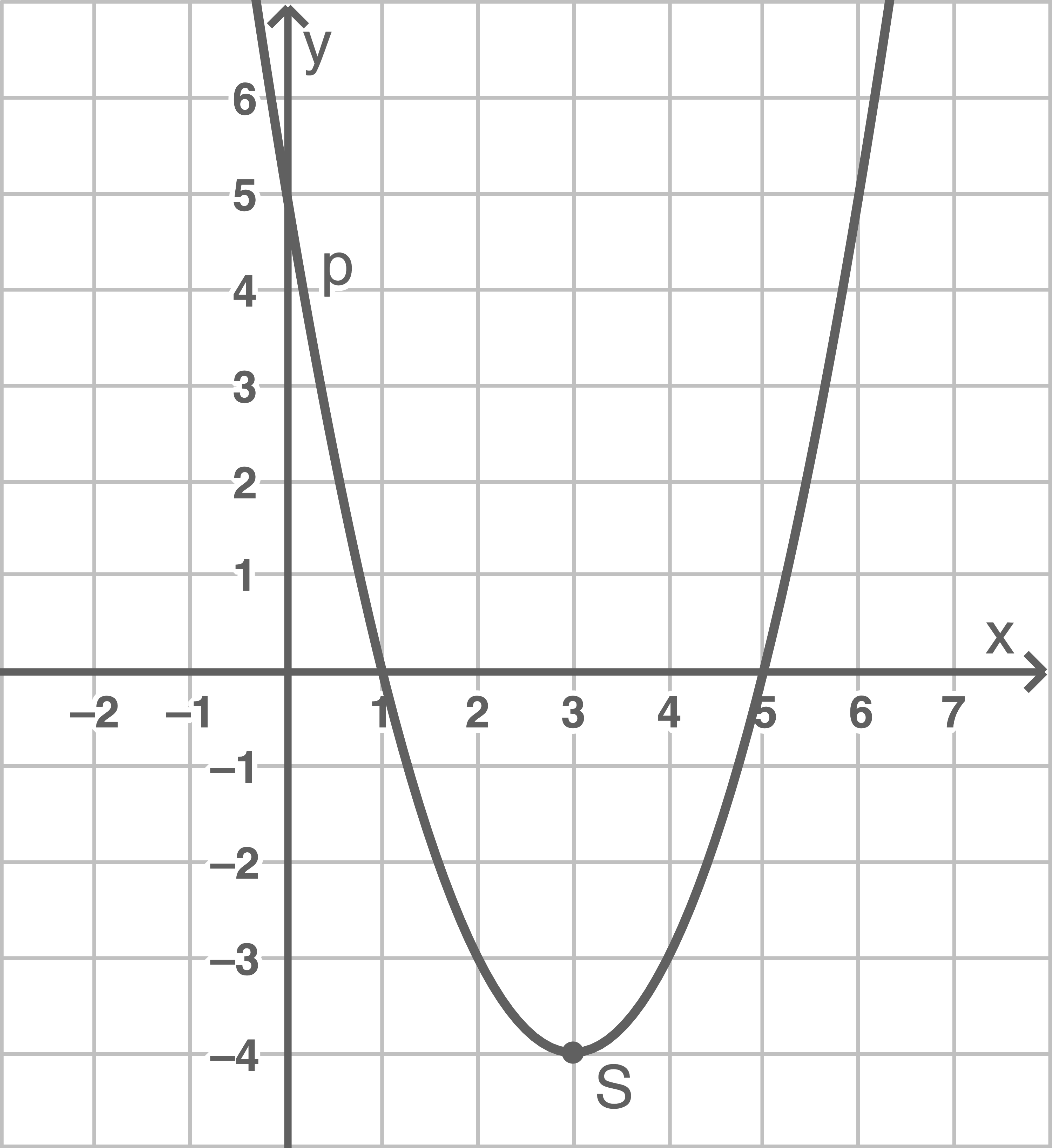
Lösung 9
1. Schritt: Scheitelpunkt über die Scheitelpunktform ermitteln
![\(\begin{array}[t]{rll}
y&=&x^2-8x+4& \\[5pt]
y&=&x^2-8\cdot x+4\quad \scriptsize \mid\ \,\text{quadr. Ergänzung} \\[5pt]
y&=&x^2-8\cdot x+16-16+4 \\[5pt]
y&=&(x-4)^2-16+4 \\[5pt]
y&=&(x-4)^2-12 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c2e03eeef03db76b9b11b23fa80f47d699674c2e3de50c2f4016d021b76d1277?color=5a5a5a)

2. Schritt: Fehlende -Koordinate von Punkt
-Koordinate von Punkt  berechnen
berechnen
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&2^2-8\cdot 2+4 \\[5pt]
y&=&4-16+4 \\[5pt]
y&=&-8 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7aaa085d0d7d7e09093ce2334272daa1729dddb0748394a517fbb1cd9bee905d?color=5a5a5a)

3. Schritt: Länge der Strecke berechnen
berechnen
 und
und 
![\(\begin{array}[t]{rll}
{\overline{AS}}&=&\sqrt{(x-x_p)^2+(y-y_p)^2} & \\[5pt]
&=&\sqrt{(4-2)^2+(-12-(-8))^2} \\[5pt]
&=&\sqrt{2^2+(-4)^2} \\[5pt]
&=&\sqrt{4+16} \\[5pt]
&=&\sqrt{20} \\[5pt]
{\overline{AS}}&=&\underline{\underline{ 4,5}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1300e365929df1c9f460284e4efc38349e2badb0c6789605561db39f8d2530bb?color=5a5a5a) Der Abstand beträgt
Der Abstand beträgt 
Musterprüfung 2
2. Schritt: Fehlende
3. Schritt: Länge der Strecke
Lösung 10
Abschlussprüfung 2020Lösung 11
Graphen zuordnen

 kein passender Graph
Die Funktionsgleichung beschreibt eine Gerade mit positiver Steigung
kein passender Graph
Die Funktionsgleichung beschreibt eine Gerade mit positiver Steigung  und dem
und dem  -Achsenabschnitt
-Achsenabschnitt  Da es keine steigende Gerade gibt, kann die Funktionsgleichung keinem Graphen zugeordnet werden. Der Graph muss neu eingezeichnet werden.
Da es keine steigende Gerade gibt, kann die Funktionsgleichung keinem Graphen zugeordnet werden. Der Graph muss neu eingezeichnet werden.

 kein passender Graph
Umformung mit quadratischer Ergänzung:
kein passender Graph
Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2+4x+3 \\[5pt]
y&=&x^2+2\cdot 2x+3 \\[5pt]
y &=&x^2+2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x+2)^2-1
\end{array}\)](https://mathjax.schullv.de/cd7edf9aaee45253702a437acf573f94ba901d2a698e64beff792f1fe0b4ed44?color=5a5a5a) Der zugehörige Graph besitzt den Scheitelpunkt
Der zugehörige Graph besitzt den Scheitelpunkt  Da es keinen Graphen mit diesem Scheitelpunkt gibt, muss der Graph dieser Funktion neu eingezeichnet werden.
Da es keinen Graphen mit diesem Scheitelpunkt gibt, muss der Graph dieser Funktion neu eingezeichnet werden.


 Die Funktionsgleichung beschreibt eine Parabel, die durch ihren
Die Funktionsgleichung beschreibt eine Parabel, die durch ihren  -Achsenabschnitt um
-Achsenabschnitt um  Einheiten nach oben verschoben ist, mit dem Faktor
Einheiten nach oben verschoben ist, mit dem Faktor  gestaucht wurde und den Scheitelpunkt
gestaucht wurde und den Scheitelpunkt  besitzt.
Diese Eigenschaften treffen auf den Graphen
besitzt.
Diese Eigenschaften treffen auf den Graphen  zu.
zu.


 Umformung mit quadratischer Ergänzung:
Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2-4x+3 \\[5pt]
y &=&x^2-2\cdot 2x+3 \\[5pt]
y &=&x^2-2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x-2)^2-1
\end{array}\)](https://mathjax.schullv.de/7c8c733974479bbec3284f43dcd2fcca8e11ea714bd696f72d4ed55254f31312?color=5a5a5a) Der Graph besitzt den Scheitelpunkt
Der Graph besitzt den Scheitelpunkt  .
Deshalb kann die Funktionsgleichung dem Graphen
.
Deshalb kann die Funktionsgleichung dem Graphen  zugeordnet werden.
zugeordnet werden.


 Die Funktionsgleichung beschreibt eine Gerade mit negativer Steigung
Die Funktionsgleichung beschreibt eine Gerade mit negativer Steigung  und mit dem
und mit dem  -Achsenabschnitt
-Achsenabschnitt  .
Dies trifft auf den Graphen
.
Dies trifft auf den Graphen  zu.
Fehlende Graphen einzeichnen
zu.
Fehlende Graphen einzeichnen
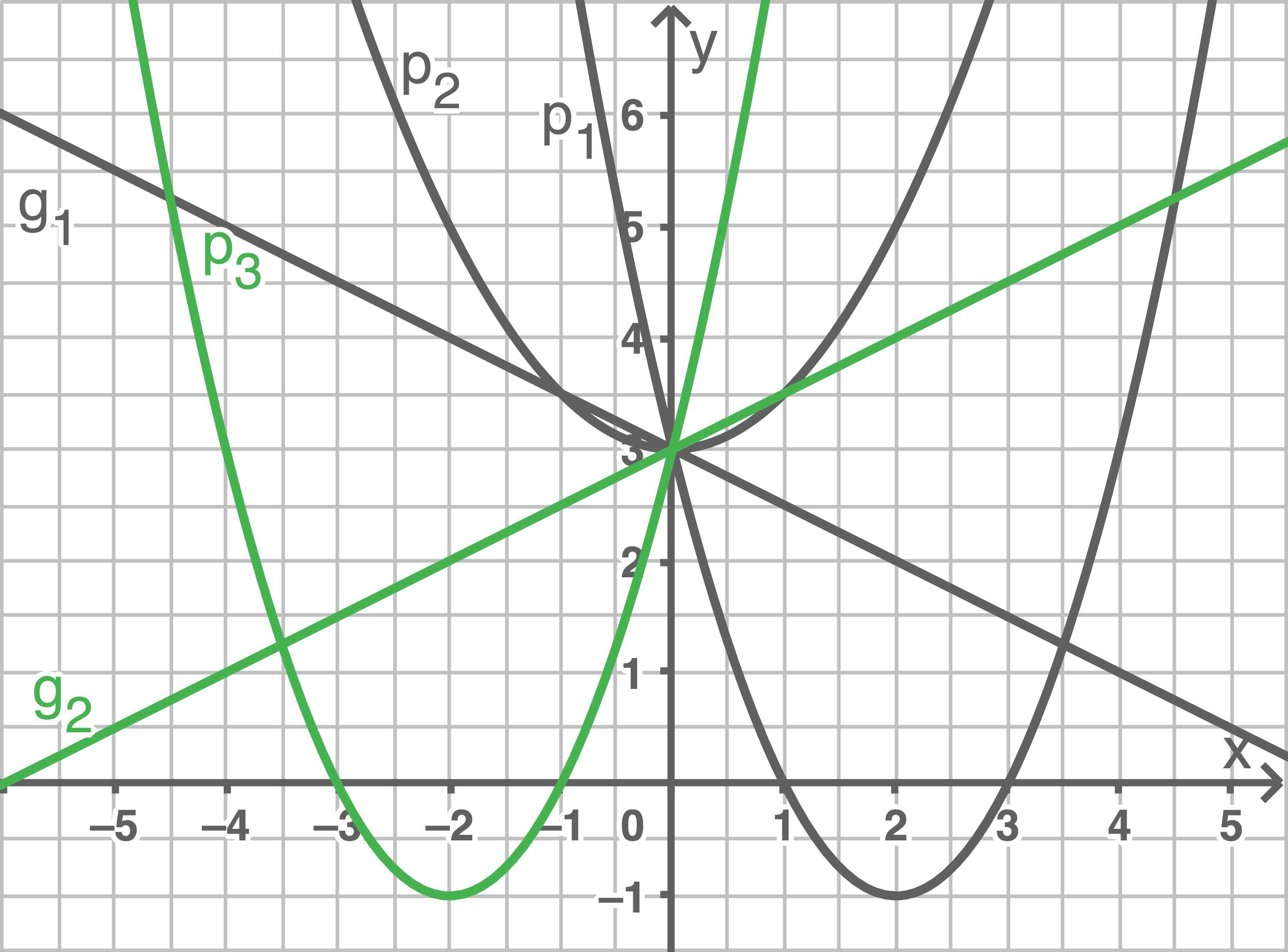
Abschlussprüfung 2020
(1)
(2)
(3)
(4)
(5)

Lösung 12
1. Schritt:Lösung 13
Wertetabelle, Graph und Funktionsgleichung zuordnen In der Wertetabelle ist das WertepaarDie Funktionsgleichung
- Verschobene Normalparabel
- Nach oben geöffnet
- Scheitelpunkt
Lösung 14
Definitionsmenge bestimmen Einschränkung: Der Nenner eines Bruchs darf nicht Null sein.- Der erste Nenner
ist für
gleich Null
- Der zweite Nenner
ist für
gleich Null
- Für den dritten Nenner gilt:
Daraus folgt:
und
Es gilt
Lösung 15
FunktionsgleichungLösung 16
1. Schritt: Scheitelpunktform der verschobenen NormalparabelSomit ist
- Scheitelpunktform:
- Koordinaten des Scheitelpunkts:
2. Schritt: Geradengleichung  aufstellen
Scheitelpunkt in die Geradengleichung
aufstellen
Scheitelpunkt in die Geradengleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-4&=& 3\cdot (-1)+b \\[5pt]
-4&=& -3+b &\quad \scriptsize \mid\; +3 \\[5pt]
b&=&-1
\end{array}\)](https://mathjax.schullv.de/c7b4d4c485211969761d96866459fdc1d53ed5a31fe705e6afc006a5792a8fa0?color=5a5a5a)

![[ALT-TAG]](https://www.schullv.de/resources/images/mathe/desktop/bw_rs2017_p5_lsg.png)
Lösung 17
Lösung 18
1. Hauptnenner bestimmen
 2. Schritt: Definitionsmenge angeben
2. Schritt: Definitionsmenge angeben

 3. Schritt: Lösungsmenge angeben
Weiter mit der
3. Schritt: Lösungsmenge angeben
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\left(\dfrac{3}{2}\right)^2-(-18)} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{9}{4}+18} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{81}{4}} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm \dfrac{9}{2} \\[5pt]
x_1&=&-\dfrac{3}{2}+ \dfrac{9}{2}= \dfrac{6}{2}=3\\[5pt]
x_2&=&-\dfrac{3}{2}- \dfrac{9}{2}= -\dfrac{12}{2}=-6 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9310cedb7065897ccd9fbc9df86b1c85961787ca077f2feb543c0a8572894c39?color=5a5a5a)

 zählt nicht in die Lösungsmenge, da dies in der Definitionsmenge ausgeschlossen wurde.
zählt nicht in die Lösungsmenge, da dies in der Definitionsmenge ausgeschlossen wurde.
Abschlussprüfung 2016
Lösung 19
1. Schritt: Koordinaten des Scheitelpunkts der Parabel  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10,5 \\[5pt]
y&=& x^2-2\cdot 3x+10,5 &\quad \scriptsize \\[5pt]
y&=& x^2-2\cdot 3x+3^2-3^2+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2-9+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2+1,5
\end{array}\)](https://mathjax.schullv.de/2e783a0b5e7a3ca8b32b9afb2fa58884235fe2c199eb4ba81c4d21a36b90a24f?color=5a5a5a) Daraus folgt:
Daraus folgt:  2. Schritt: Geradengleichung von
2. Schritt: Geradengleichung von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
y&=&mx+c \quad \scriptsize \mid\;-mx \\[5pt]
c&=& y-mx \quad \scriptsize \mid\;S(3\mid 1,5), m=2 \\[5pt]
c&=&1,5-2\cdot 3& \\[5pt]
c&=&-4,5
\end{array}\)](https://mathjax.schullv.de/2842eb35d776606606329e8af2fca32eb5e85a205f73723442c49216d58cfc3c?color=5a5a5a) Es gilt also
Es gilt also  3. Schritt: Koordinaten des Schnittpunkts
3. Schritt: Koordinaten des Schnittpunkts  berechnen
berechnen
![\(\begin{array}[t]{rll}
p&=&g \\[5pt]
x^2-6x+10,5&=& 2x-4,5 \quad \scriptsize \mid\;-\, 2x\, +4,5 \\[5pt]
x^2-8x+15&=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/03bb6b582551cdf3f1ad7a97bc8c3a721b87d6df1f8d5f69f0ce0594cac4c252?color=5a5a5a) Weiter mit der
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{(-8)}{2}\pm \sqrt{\left(\dfrac{-8}{2}\right)^2-15} \\[5pt]
x_{1/2} &=&4\pm \sqrt{16-15} \\[5pt]
x_{1/2} &=&4\pm 1 \\[5pt]
x_1&=&5 \\[5pt]
x_2&=&3
\end{array}\)](https://mathjax.schullv.de/b33372fad3e8bcb2590d694a2c8741ff3919b0cca098f5f2b5130cdad820ede5?color=5a5a5a)
 ist die
ist die  -Koordinate des bekannten Schnittpunkts
-Koordinate des bekannten Schnittpunkts  Deswegen wird
Deswegen wird  in
in  eingesetzt:
eingesetzt:
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& 2\cdot 5 - 4,5 \\[5pt]
y&=& 10-4,5 \\[5pt]
y&=& 5,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2a80286a5ee0281db1e9554124fd82cf44efaa9dfea08550311f1f6d1434a2e3?color=5a5a5a) Somit gilt:
Somit gilt: 
Abschlussprüfung 2016
Lösung 20
Welcher Graph gehört zur angegebenen Wertetabelle? Durch die Punktprobe können die verschiedenen Werte geprüft werden:- Punkt
: Da nur die Parabeln
und
durch diesen Punkt verlaufen, können die anderen beiden Parabeln ausgeschlossen werden.
- Punkt
: Nur Parabel
verläuft durch diesen Punkt. Die gegebene Wertetabelle gehört also zur Parabel
.
Es gilt also: