Geometrie im Raum
Aufgabe 1
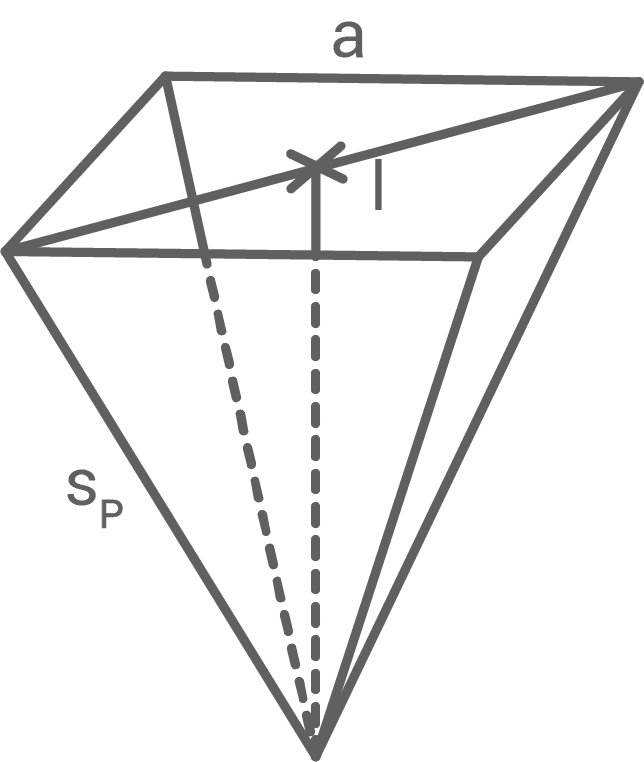
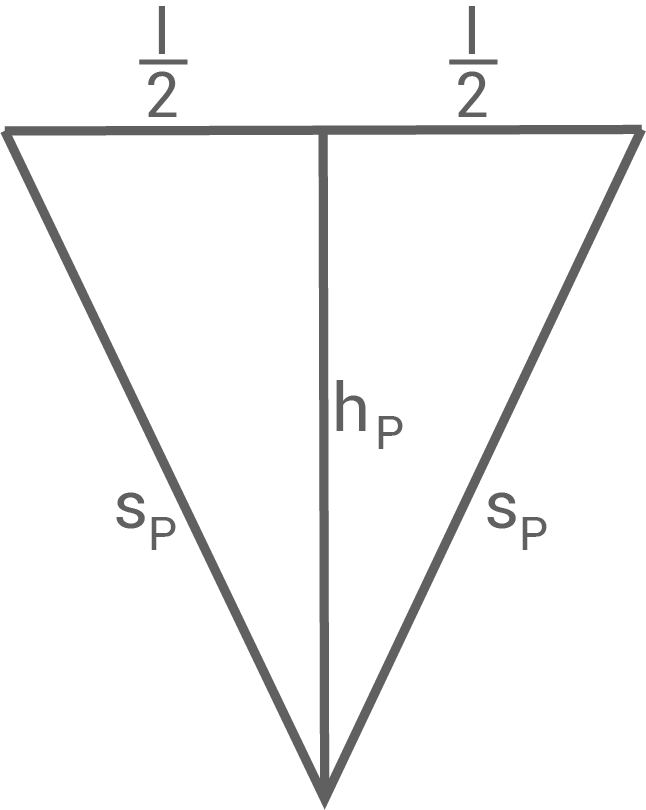
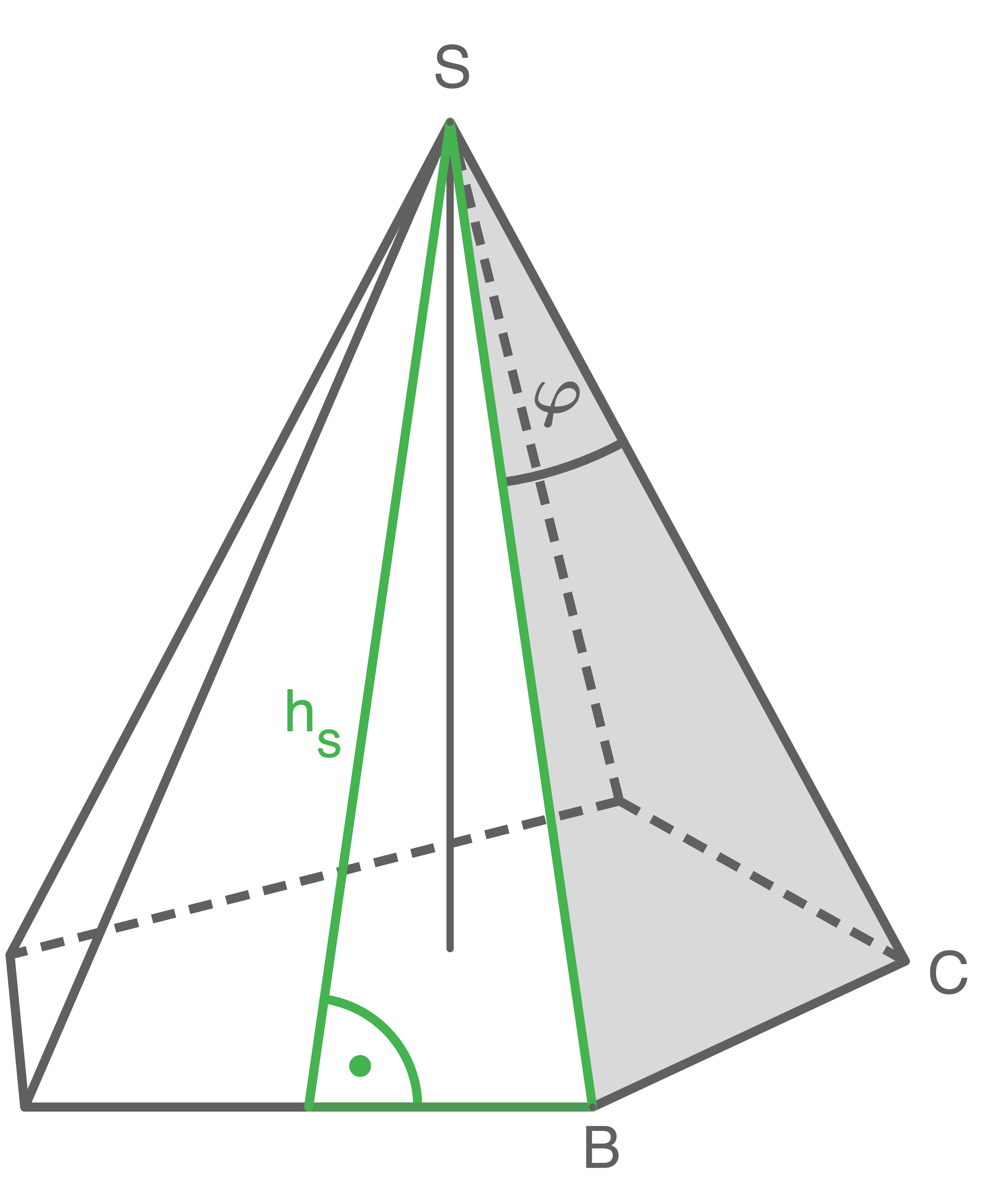
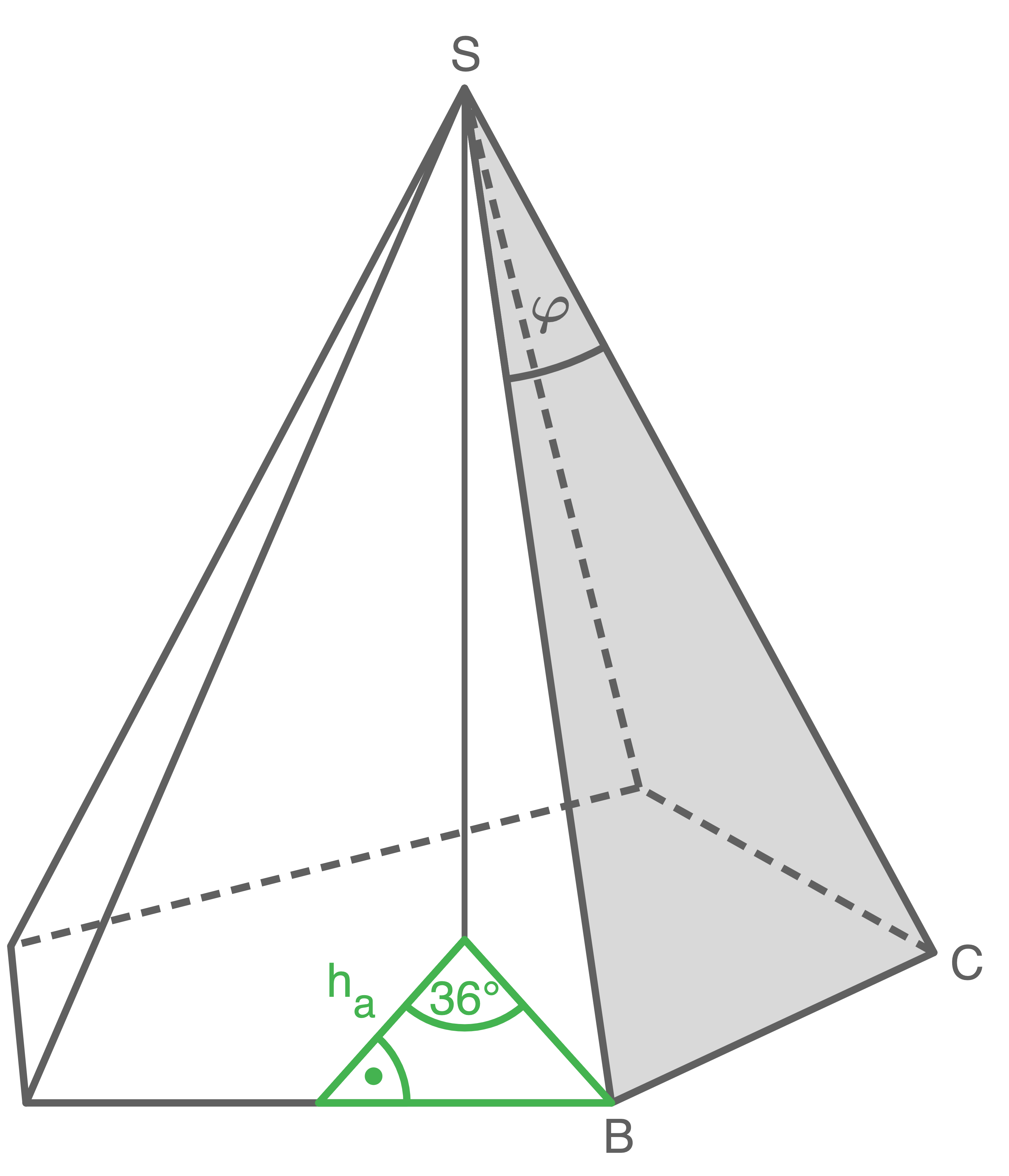
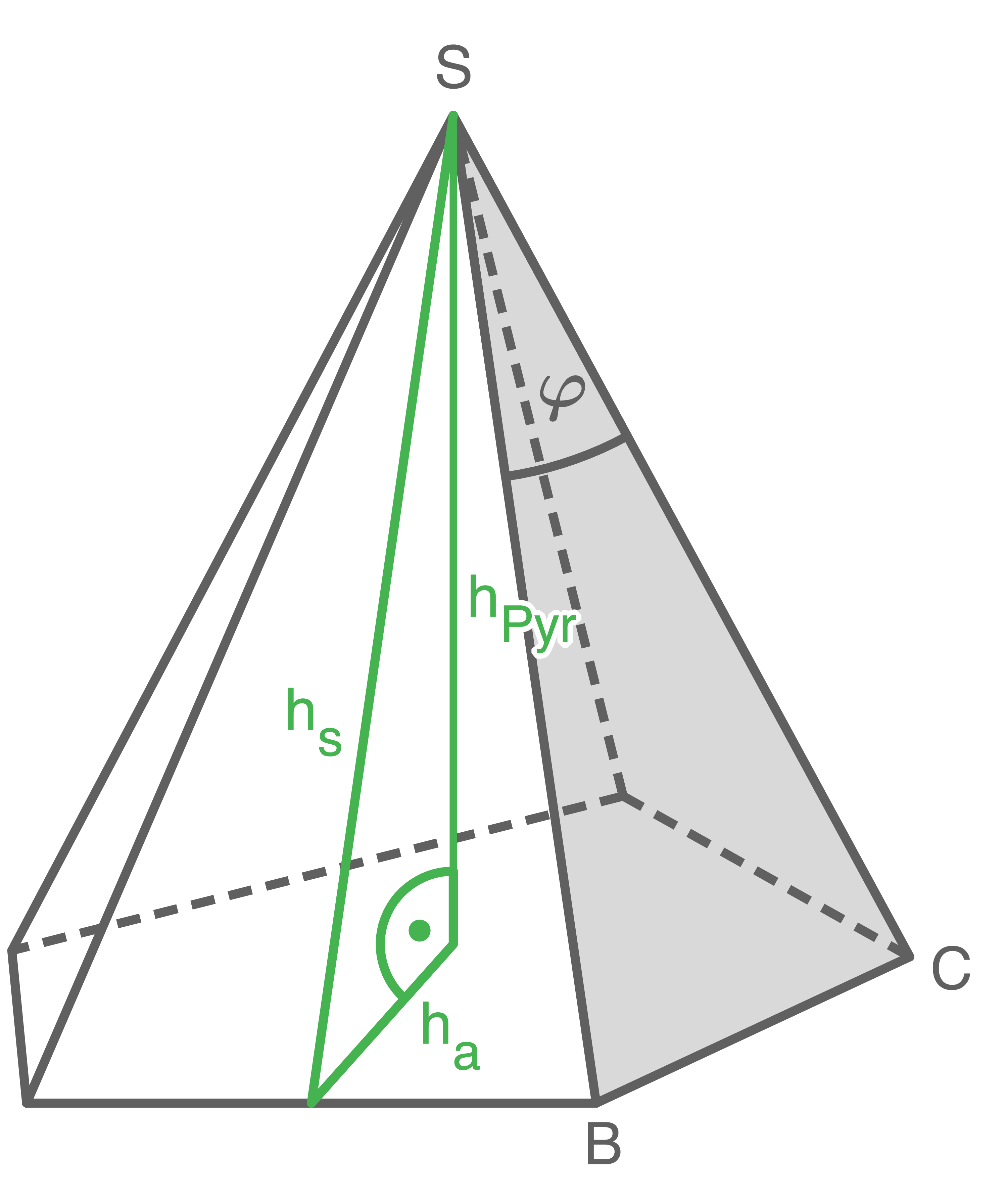
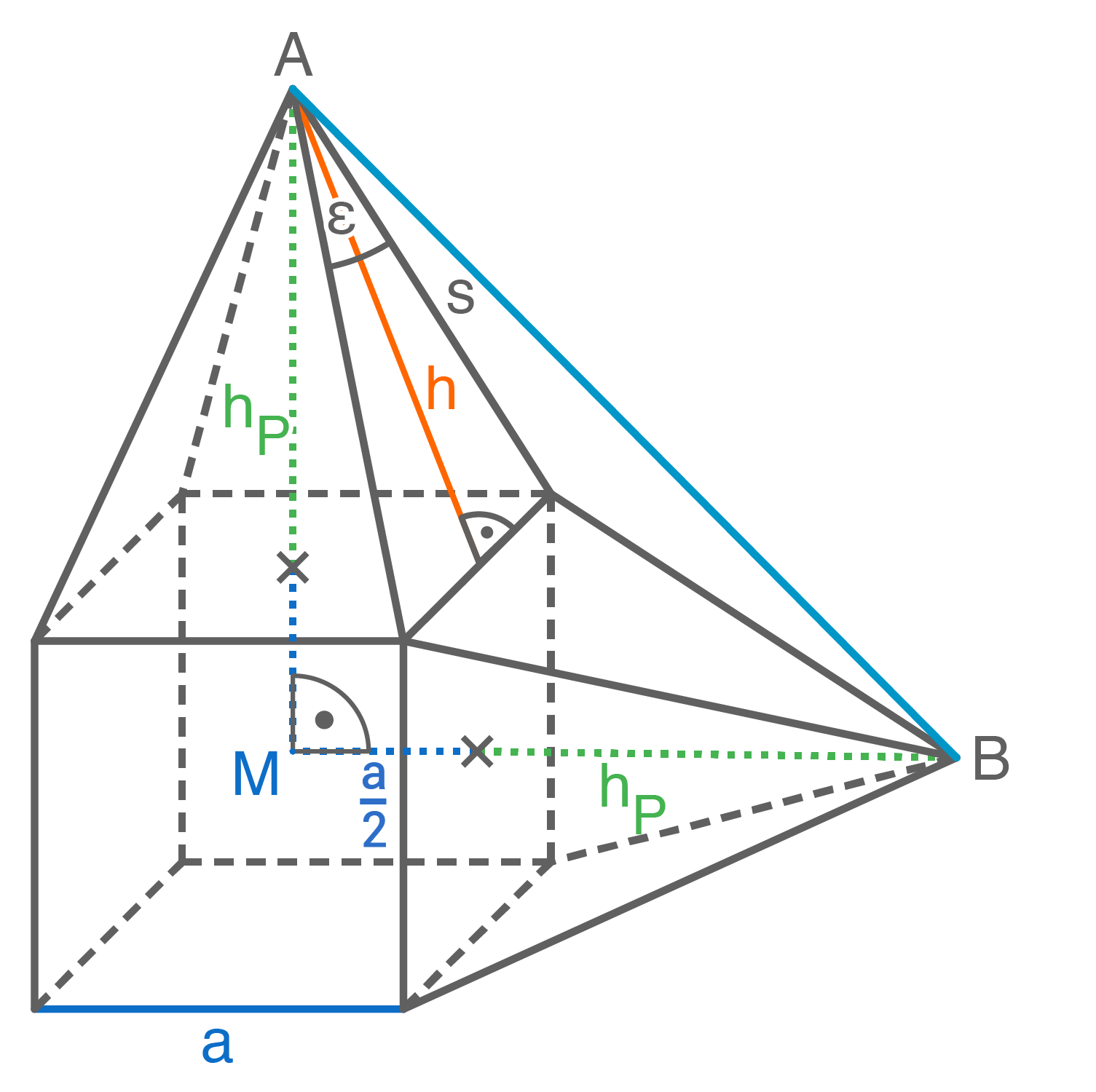
Eines der Manteldreiecke der regelmäßigen fünfseitigen Pyramide ist grau gefärbt.
Es gilt:
![\(\begin{array}[t]{rll}
\overline{B S} &=& 12,0\,\text{cm} \\
\varphi &=& 40,0^{\circ}
\end{array}\)](https://mathjax.schullv.de/ce49dafc5f827f92aa4519b7a7c6bd73535bcf9b7f925384da540e661bba9d5c?color=5a5a5a) Berechne das Volumen der Pyramide.
Berechne das Volumen der Pyramide.
(3,5 P)
Abschlussprüfung 2024
Aufgabe 2
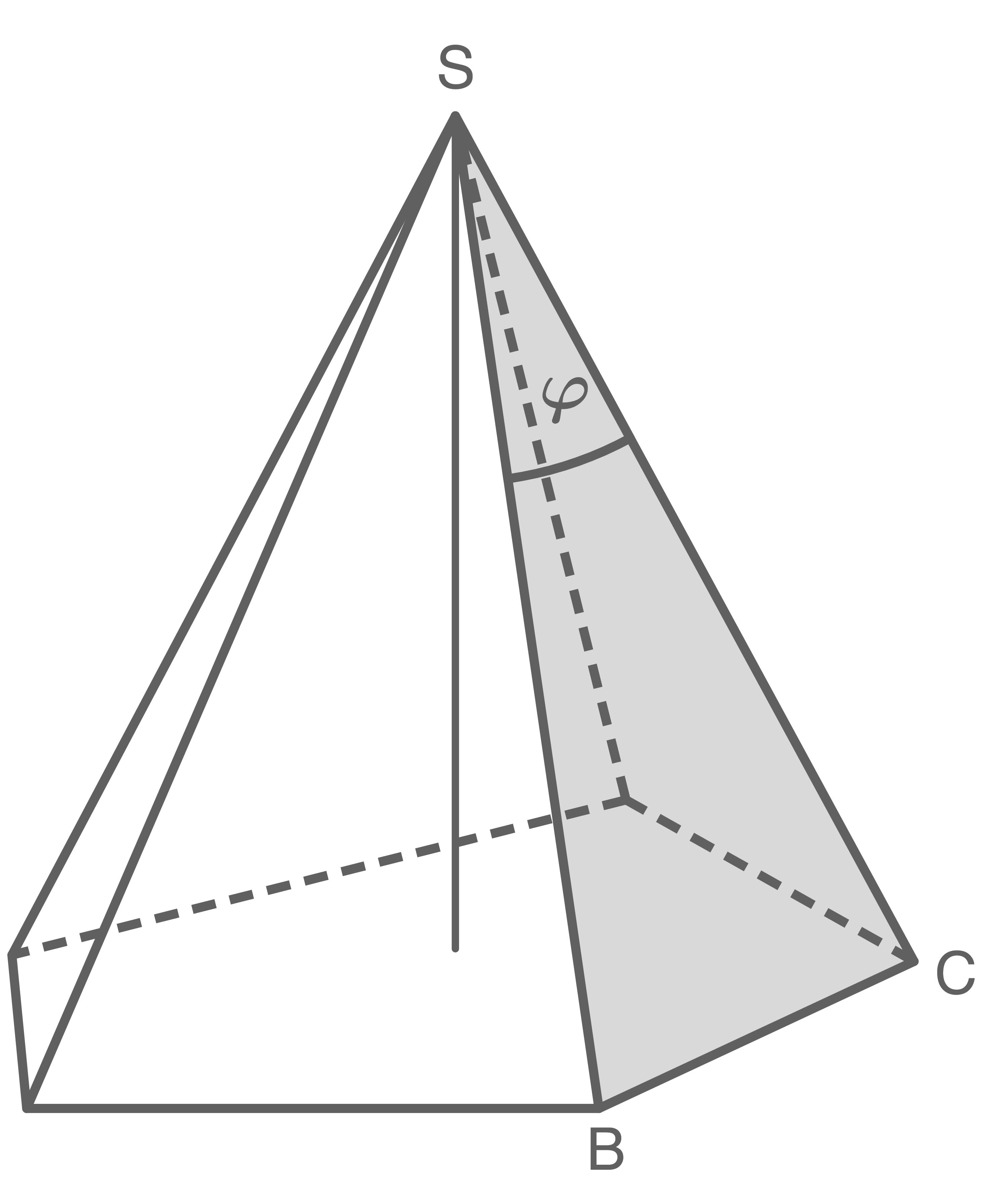
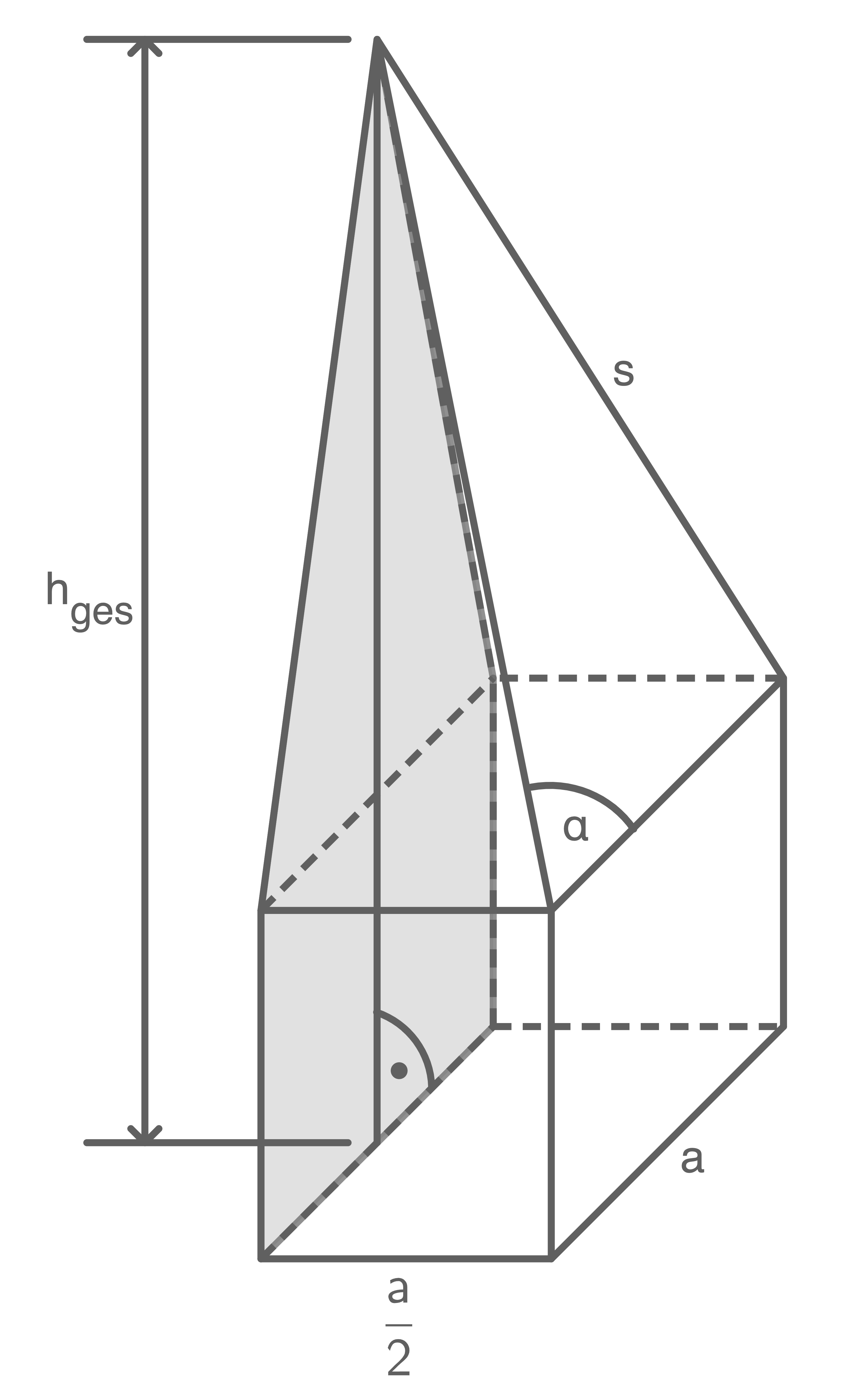
Ein zusammengesetzter Körper besteht aus einem quadratischen Prisma mit aufgesetzter quadratischer Pyramide. Dieser zusammengesetzte Körper wurde durch einen Parallelschnitt halbiert.
Die Schnittfäche ist grau eingefärbt.
Es gilt:
ist grau eingefärbt.
Es gilt:
![\(\begin{array}[t]{rll}
s&=&16,3\,\text{cm}\\
\alpha&=&68,9^\circ\\
h_{\text {ges}}&=&20,6\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/7d1814f05451741d6d7996295d7fca02941bb001cdbfdb3e02079a868bc23de9?color=5a5a5a) Berecḥne den Flächeninhalt der Schnittfläche
Berecḥne den Flächeninhalt der Schnittfläche 
Die Schnittfäche
(4 P)
Aufgabe 3
1000 Wachskugeln werden eingeschmolzen. Sie haben jeweils einen Radius von 1,5 cm. Mit diesem eingeschmolzenen Wachs werden quadratische Pyramiden gegossen. Dazu wird die abgebildete Gussform verwendet. Diese wird vollständig mit Wachs gefüllt.
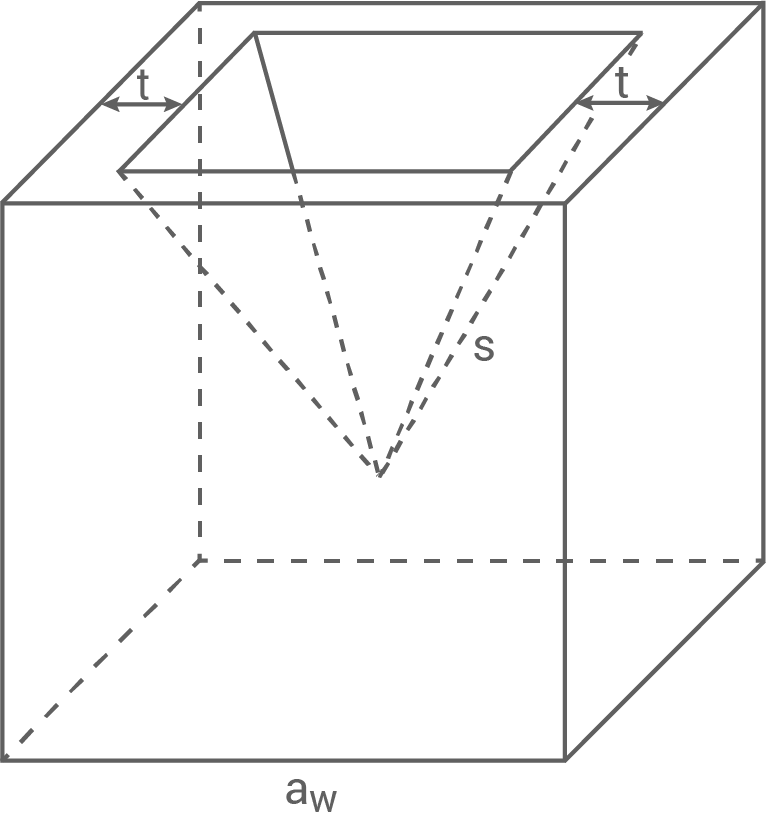 Es gilt:
Es gilt:
 Wie viele solcher Pyramiden können mit dem eingeschmolzenen Wachs gegossen werden?
Wie viele solcher Pyramiden können mit dem eingeschmolzenen Wachs gegossen werden?

(3,5 P)
Aufgabe 4
Ein Kunstwerk setzt sich aus einer Halbkugel und einem Kegel zusammen.
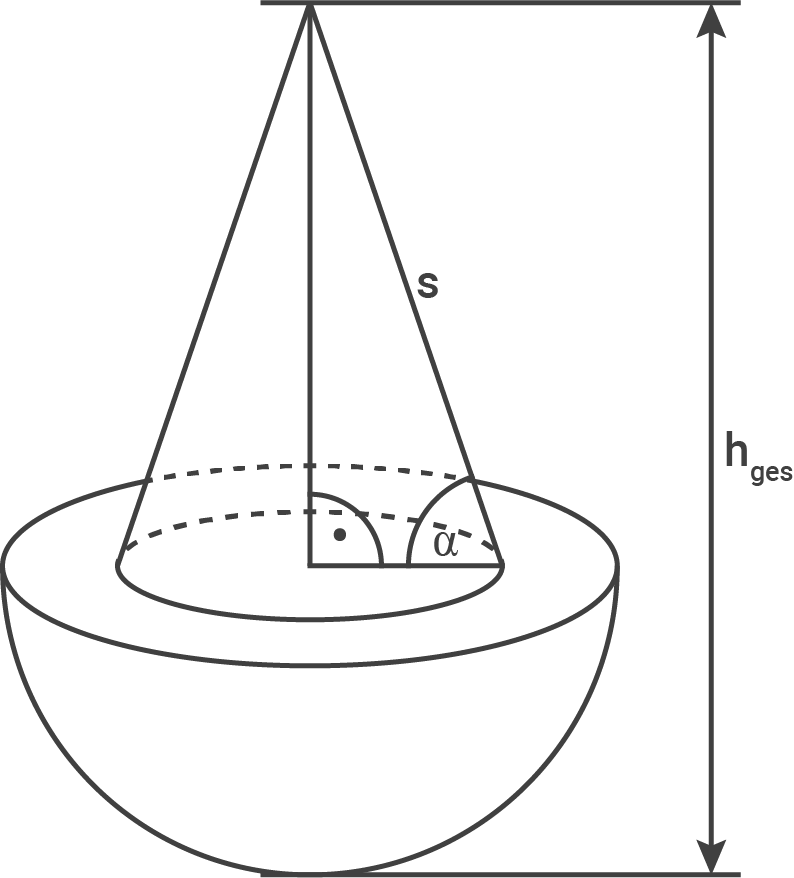 Es gilt:
Es gilt:



Eine 1-Liter-Farbdose reicht für

- Berechne den Oberflächeninhalt des zusammengesetzten Körpers.
Eine 1-Liter-Farbdose reicht für
- Wie viele Dosen müssen gekauft werden?
(3,5 P)
Aufgabe 5
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel.
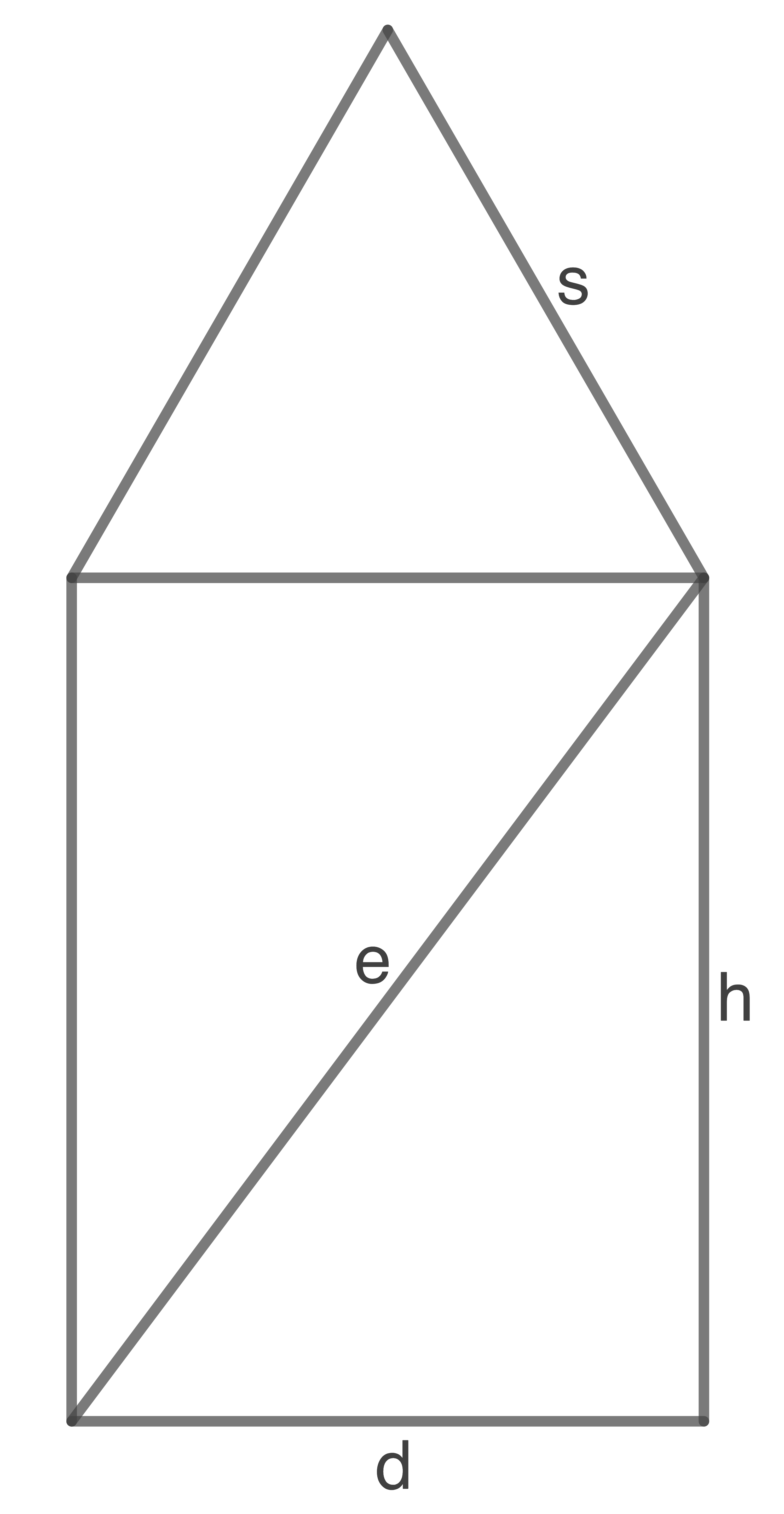 (Querschnitt des Körpers, Skizze nicht maßstäblich)
Es gilt:
(Querschnitt des Körpers, Skizze nicht maßstäblich)
Es gilt:
 (Grundfläche des Kegels)
(Grundfläche des Kegels)
 Der Durchmesser
Der Durchmesser  entspricht der Seitenkante
entspricht der Seitenkante  des Kegels.
Berechne die Oberfläche des zusammengesetzten Körpers
des Kegels.
Berechne die Oberfläche des zusammengesetzten Körpers
 (Querschnitt des Körpers, Skizze nicht maßstäblich)
(Querschnitt des Körpers, Skizze nicht maßstäblich)
(4 P)
Aufgabe 6
Gegeben ist eine quadratische Pyramide.
Es gilt:
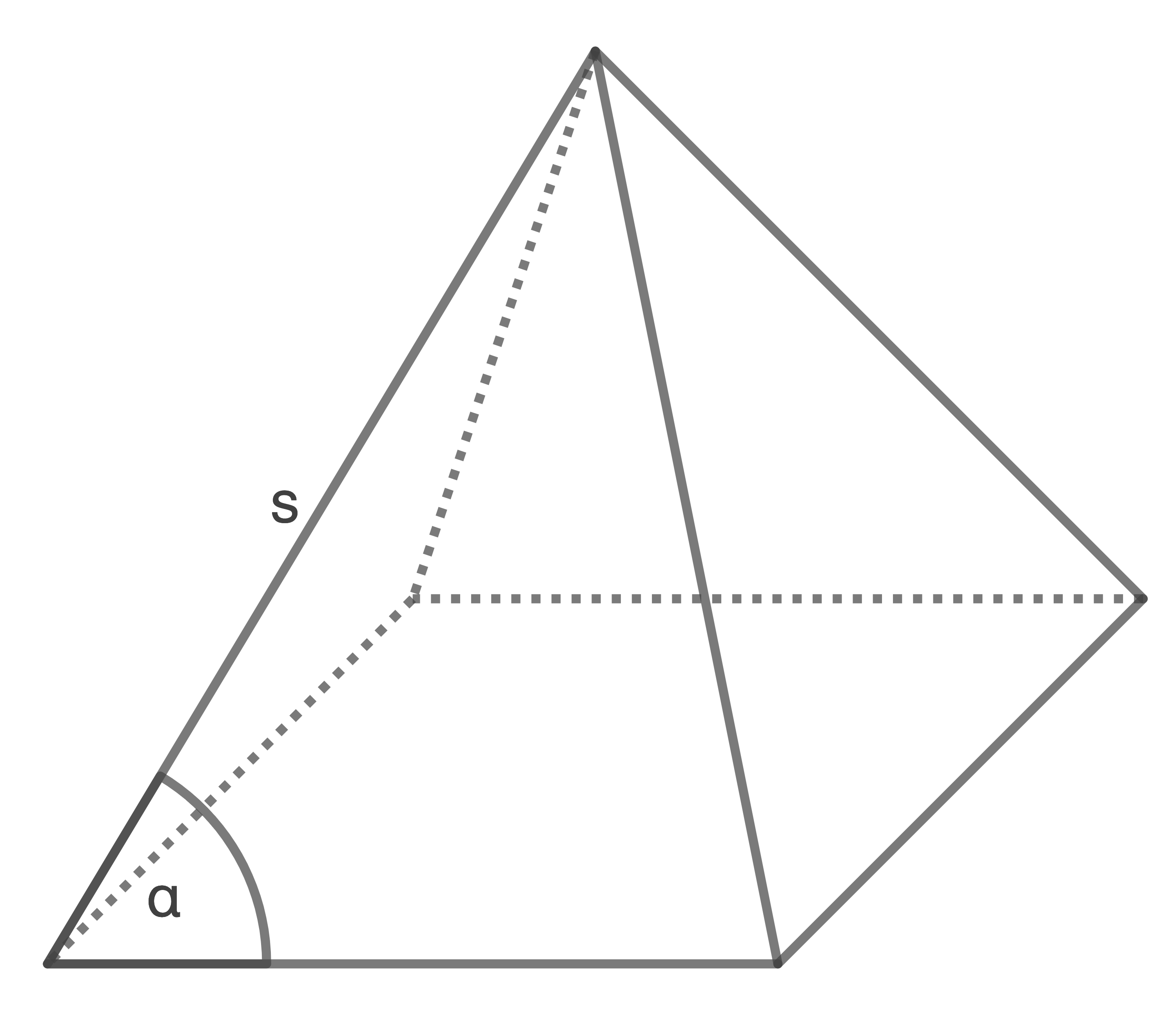
(Skizze nicht maßstäblich)
(3 P)
Aufgabe 7
Ein Werkstück besteht aus einem Kegel und einem halben Zylinder.
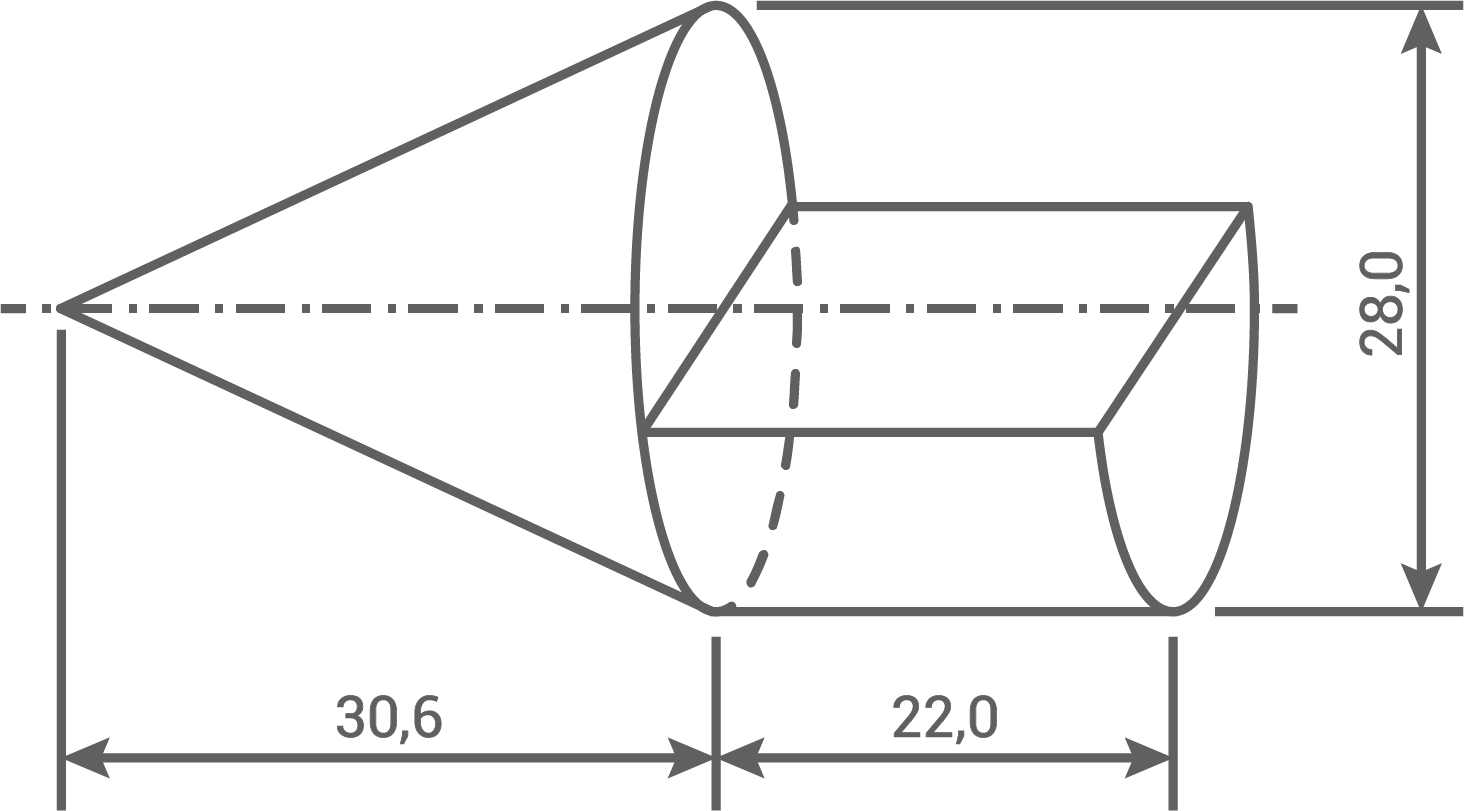 Berechne den Oberflächeninhalt des Werkstücks.
Berechne den Oberflächeninhalt des Werkstücks.

(Maße in cm)
(3,5 P)
Aufgabe 8
Ein zusammengesetzter Körper besteht aus einem Würfel und zwei quadratischen Pyramiden.
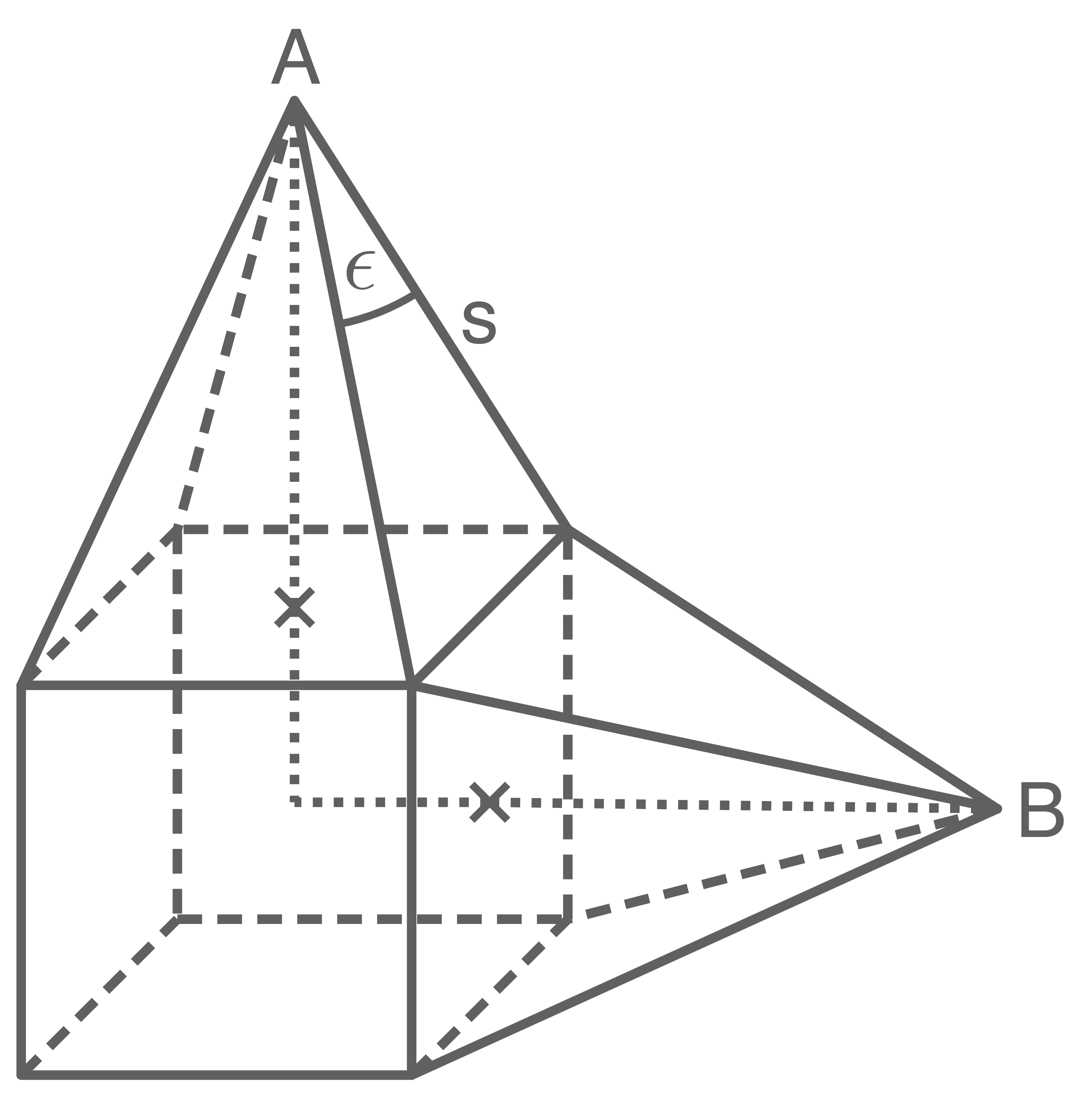 Die Pyramiden haben die gleiche Höhe.
Die Pyramiden haben die gleiche Höhe.
Es gilt: und
und  voneinander entfernt?
voneinander entfernt?

Es gilt:
(4 P)
Aufgabe 9
Die Abbildung zeigt ein quadratisches Prisma und einen zusammengesetzten Körper.
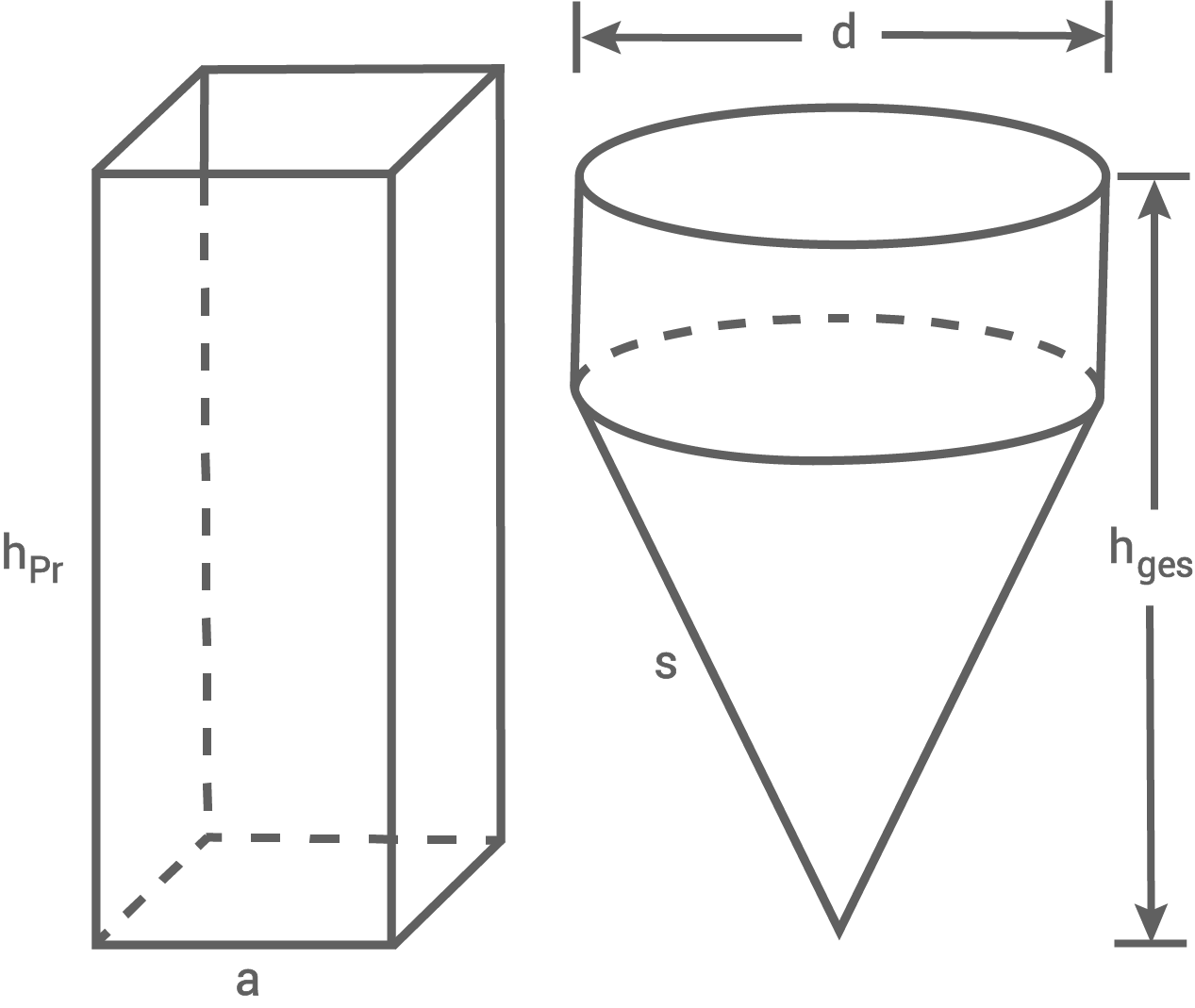 Der zusammengesetzte Körper besteht aus einem Kegel mit aufgesetztem Zylinder.
Das quadratische Prisma ist vollständig mit Wasser gefüllt. Dieses Wasser wird in den zusammengesetzten Körper umgefüllt.
Der zusammengesetzte Körper besteht aus einem Kegel mit aufgesetztem Zylinder.
Das quadratische Prisma ist vollständig mit Wasser gefüllt. Dieses Wasser wird in den zusammengesetzten Körper umgefüllt.
Es gilt:

Es gilt:
(4 P)
Aufgabe 10
Ein Körper setzt sich aus einem halben Zylinder und einer quadratischen Pyramide zusammen.
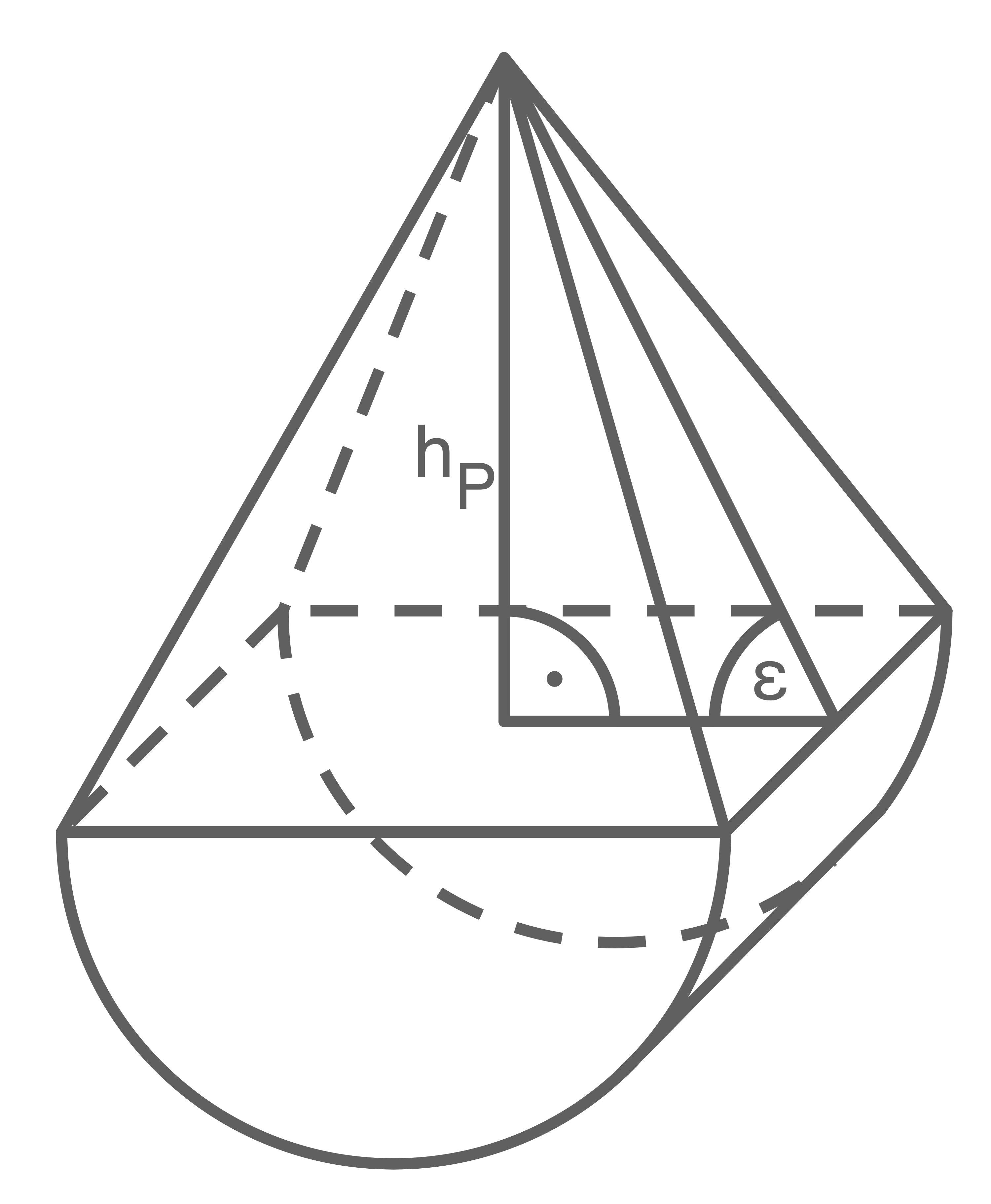 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
h_P&=&16,0 \text{ cm} \\[5pt]
\epsilon&=&58,0 ^{\circ}
\end{array}\)](https://mathjax.schullv.de/c5139acfebaf7f889cb8f753abf7409b75d6cbff8cd8a8d6fc16856a7dda67d4?color=5a5a5a) Berechne die Oberfläche des zusammengesetzten Körpers.
Berechne die Oberfläche des zusammengesetzten Körpers.

(4,5 P)
Aufgabe 11
Ein Zylinder und ein Kegel haben gleich große Mantelflächen. Die Durchmesser der beiden Grundflächen sind ebenfalls gleich.
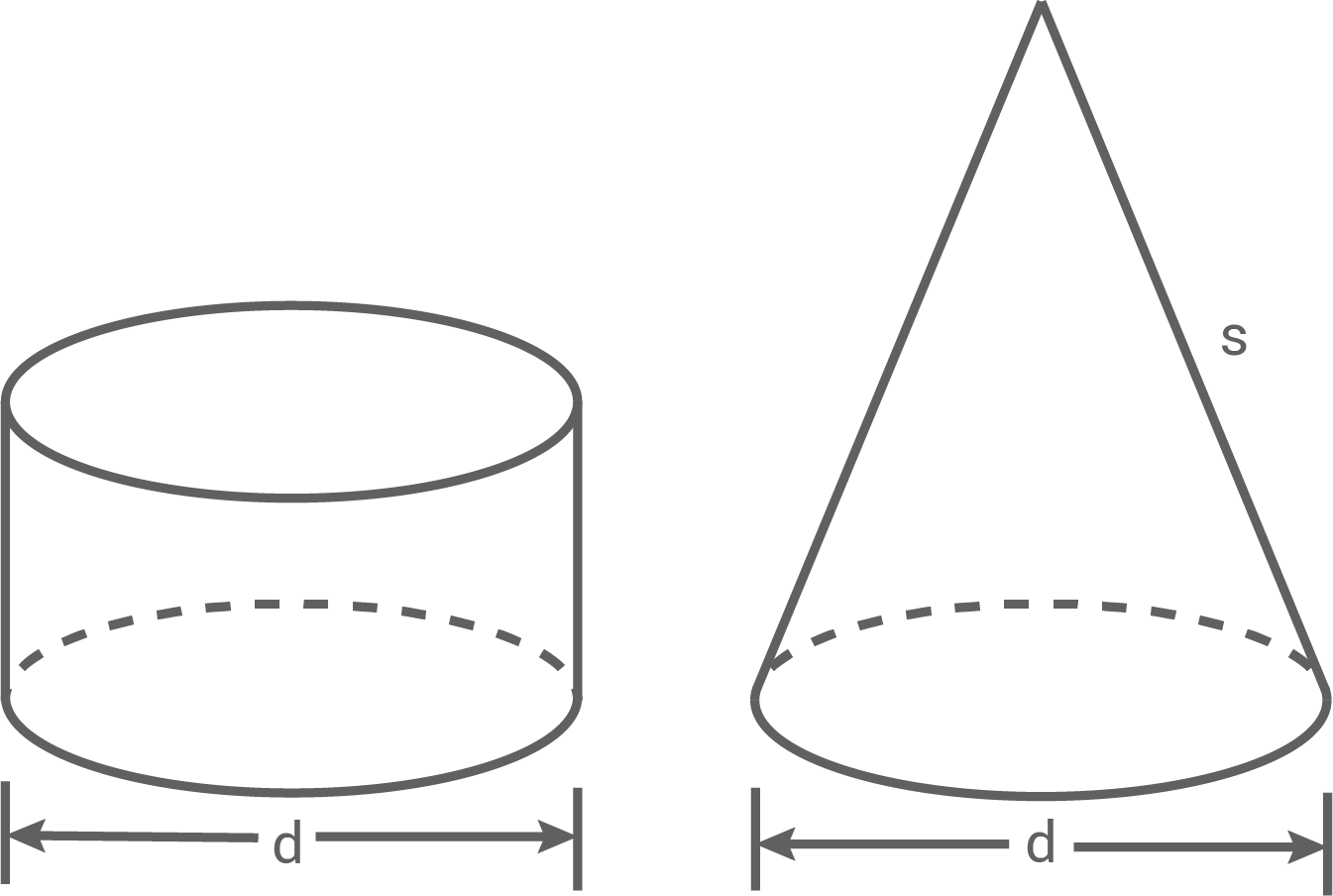 Es gilt:
Es gilt:
Abschlussprüfung 2016

(4 P)
Aufgabe 12
Ein Kegel ist teilweise mit Wasser gefüllt. Dabei nimmt das Wasser die Hälfte des Kegelvolumens ein.
Dieses Wasser soll vollständig in eine quadratische Pyramide umgefüllt werden.
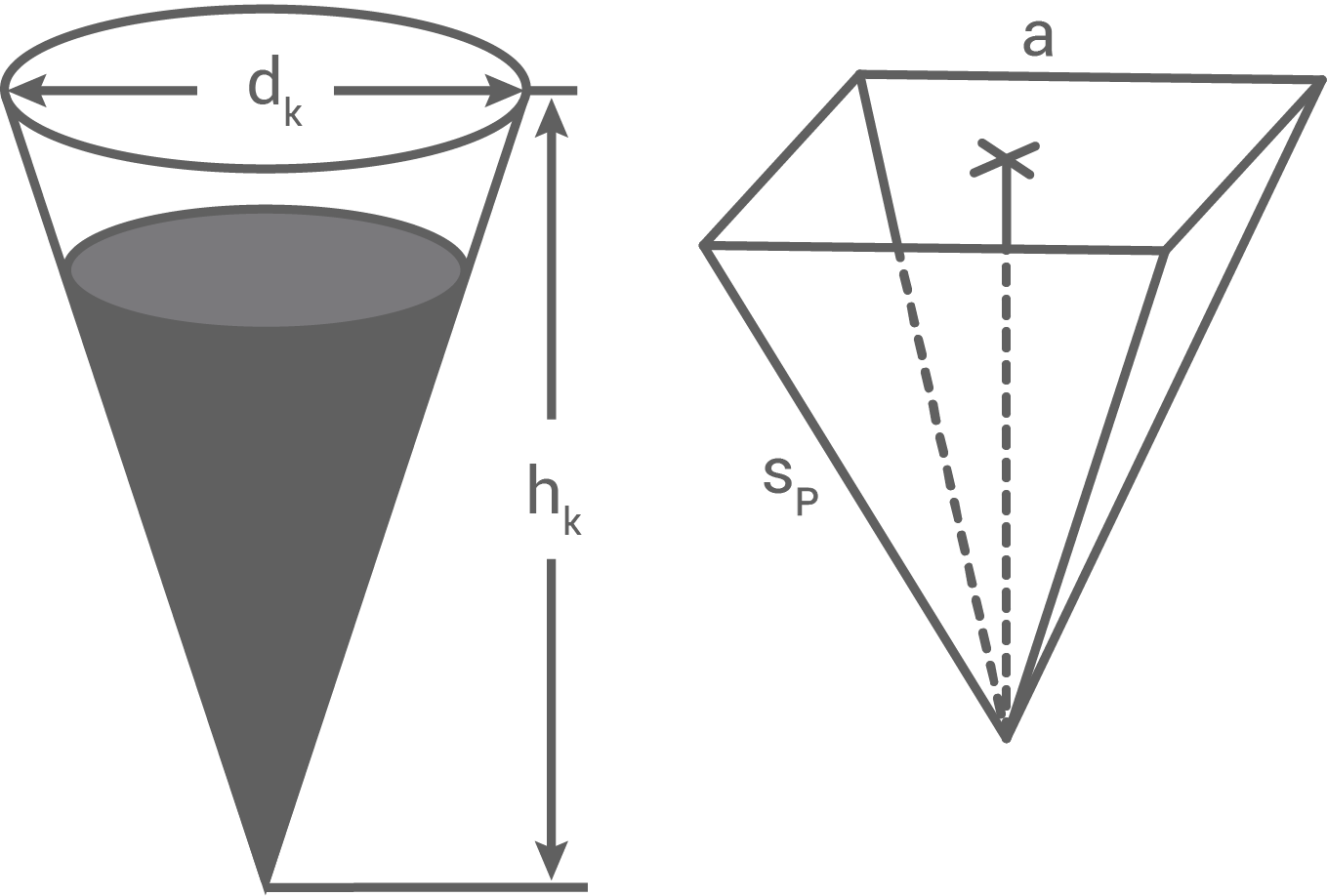 Es gilt:
Es gilt:




Läuft das Wasser über?
Überprüfe durch Rechnung.
Dieses Wasser soll vollständig in eine quadratische Pyramide umgefüllt werden.

Läuft das Wasser über?
Überprüfe durch Rechnung.
(3,5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
1. Schritt:
2. Schritt: Höhe  einer Seitenfläche berechnen
einer Seitenfläche berechnen
4. Schritt:  berechnen
berechnen
Lösung 2
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos\alpha&=&\dfrac{\frac{a}{2}}{s} \quad \scriptsize \mid\;\cdot s \\[5pt]
\cos\alpha\cdot s&=&\dfrac{a}{2}\quad \scriptsize \mid\;\cdot 2 \\[5pt]
2\cos\alpha\cdot s&=&a\\[5pt]
a&=&2\cos\alpha\cdot s\\[5pt]
&=&2\cos 68,9^\circ\cdot 16,3\,\text{cm}\\[5pt]
a&=&\underline{11,74\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/b9c78ba7ce828b7dfb3a879a1b80fe706fa061a35ec6b1334125fa0a4d679820?color=5a5a5a) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\alpha&=&\dfrac{h_s}{s}\quad \scriptsize \mid\;\cdot s \\[5pt]
\sin\alpha\cdot s&=& h_s\\[5pt]
h_s&=&\sin 68,9^\circ\cdot 16,3\,\text{cm}\\[5pt]
h_s&=&\underline{15,21\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/3fdfffcda482b0b502bbd6b7b001032803eaa5f51851d8329926e0a6c2cc212d?color=5a5a5a) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_\text{Pyramide}^2&=&h_s^2-\left(\frac{a}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
h_\text{Pyramide}&=&\sqrt{h_s^2-\left(\frac{a}{2}\right)^2}\\[5pt]
&=&\sqrt{(15,21\,\text{cm})^2-\left(\frac{11,74\,\text{cm}}{2}\right)^2}\\[5pt]
h_\text{Pyramide}&=&\underline{14,03\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/058eee2f599cfb2ba65822e55a16f66776f9bd2ee6a36bbaf74e41d49c7acd59?color=5a5a5a) 3. Schritt: Länge von
3. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_\text{Prisma}&=&h_\text{ges}-h_\text{Pyramide} \\[5pt]
&=&20,6\,\text{cm}-14,03\,\text{cm} \\[5pt]
h_\text{Prisma}&=&\underline{6,57\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/5e65e9c35d125047b72410d9697ec6d0c4f5c21436db63cabd2889641cfb7b59?color=5a5a5a) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_S&=&h_\text{Prisma}\cdot a+\dfrac{1}{2}h_\text{Pyramide}\cdot a \\[5pt]
&=&6,57\,\text{cm}\cdot 11,74\,\text{cm}+\dfrac{1}{2}\cdot 14,03\,\text{cm}\cdot 11,74\,\text{cm}\\[5pt]
A_S&=&\underline{\underline{159,5\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/1058e7bdbf19cf14761a4d35d25b79b8727660bc5f10a26212adb083f433c0ae?color=5a5a5a)
Abschlussprüfung 2023
Lösung 3
1. Schritt: Volumen der Schmelze berechnen
![\(\begin{array}[t]{rll}
V_{\,\text{Schmelze}}&=&\dfrac{4}{3}\cdot \pi\cdot r^3\cdot 1000 \\[5pt]
&=&\dfrac{4}{3}\cdot \pi\cdot (1,5\,\text{cm})^3\cdot 1000 \\[5pt]
V_{\,\text{Schmelze}}&=& \underline{ 14137\,\text{cm}^3}
\end{array}\)](https://mathjax.schullv.de/a62f17fc588efae9723f89592eeccdb60177b7bf8c248264a9a9f68f37e737ab?color=5a5a5a) 2. Schritt: Länge der Seite
2. Schritt: Länge der Seite  berechnen
berechnen
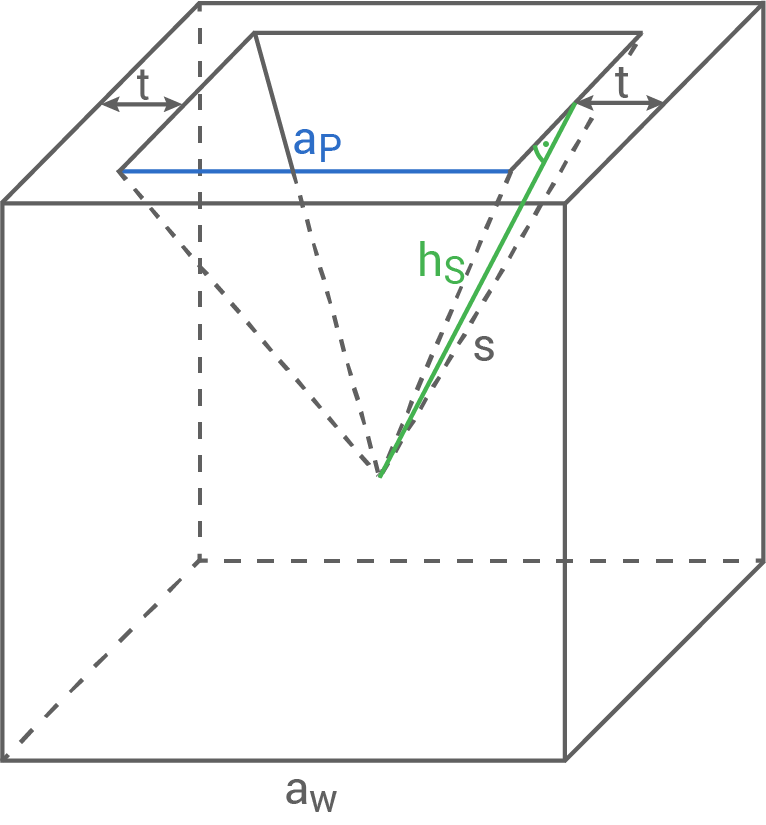
![\(\begin{array}[t]{rll}
a_P&=&a_w-2\cdot t \\[5pt]
&=& 10,0 \,\text{cm} -2\cdot 1,0\,\text{cm} \\[5pt]
&=& \underline{ 8,0\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/b16eabd4f0d1a1aa9780c687ac78d9c2bf27ce2fcc11a4faeab418ebe2d04cbf?color=5a5a5a) 3. Schritt: Länge der Seite
3. Schritt: Länge der Seite  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_S^2+\left(\dfrac{a_P}{2}\right)^2&=& s^2 \qquad \scriptsize \mid\;-\left(\dfrac{a_P}{2}\right)^2 \\[5pt]
h_S^2&=& s^2 -\left(\dfrac{a_P}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,\,} \\[5pt]
&=& \sqrt{s^2 -\left(\dfrac{a_P}{2}\right)^2} \\[5pt]
&=& \sqrt{(9\,\text{cm})^2 -(4\,\text{cm})^2} \\[5pt]
h_S&=& \underline{ 8,06\,\text{cm} } \\[5pt]
\end{array}\)](https://mathjax.schullv.de/227b66ac0c53c7990199bac345826c73f83c3779d3a24dcaeb6ba685d5a33789?color=5a5a5a) 4. Schritt: Länge der Höhe
4. Schritt: Länge der Höhe  berechnen
berechnen
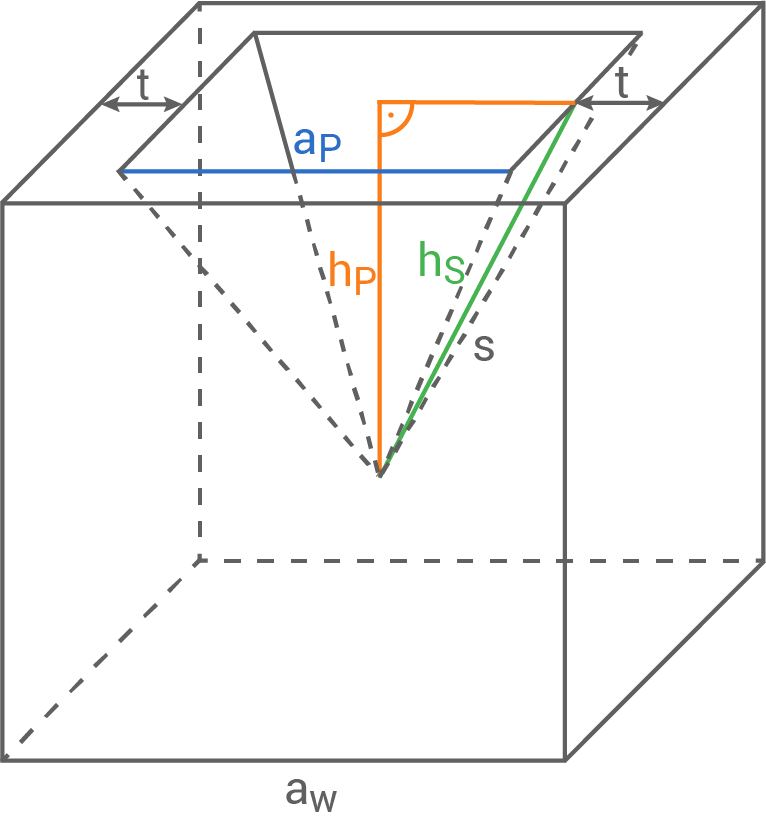
![\(\begin{array}[t]{rll}
h_P^2+\left(\dfrac{a_P}{2}\right)^2&=& h_S^2 \qquad \scriptsize \mid\;-\left(\dfrac{a_P}{2}\right)^2
\end{array}\)](https://mathjax.schullv.de/d5b0401daa25c5da9a9a2fbcc570d1f62a8eacdc5e810d5d1c2bf84b60c7c700?color=5a5a5a)
![\(\begin{array}[t]{rll}
h_P^2&=& h_S^2 -\left(\dfrac{a_P}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,\,} \\[5pt]
h_P&=& \sqrt{h_S^2 -\left(\dfrac{a_P}{2}\right)^2} \\[5pt]
&=& \sqrt{(8,06\,\text{cm})^2 -(4\,\text{cm})^2} \\[5pt]
h_P&=& \underline{ 7,0\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6bdcf29b3d9dcb8cdb4ba9361c52bb6e59db4598dcc2b37087f916c221892650?color=5a5a5a) 5. Schritt: Volumen der Pyramide berechnen
5. Schritt: Volumen der Pyramide berechnen
![\(\begin{array}[t]{rll}
V_P&=& \dfrac{1}{3}\cdot a_P^2\cdot h_P \\[5pt]
&=& \dfrac{1}{3}\cdot (8\,\text{cm})^2\cdot 7,0\,\text{cm} \\[5pt]
V_P&=& \underline{ 149 \,\text{cm}^3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/798c7e4afea37aa243e586fd32ddfa79f536bc7802e8edf017f59329a41957bb?color=5a5a5a) 6. Schritt: Anzahl der Pyramiden berechnen
6. Schritt: Anzahl der Pyramiden berechnen

 Es können
Es können  aus dem Wachs gegossen werden.
aus dem Wachs gegossen werden.
Abschlussprüfung 2022


Lösung 4
Oberflächeninhalt des zusammengesetzten Körpers berechnen
A) Mantelflächeninhalt des Kegels
1. Schritt: Radius  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{r_{\text{Kegel}}}{s} \quad \scriptsize \mid\; \cdot s\\[5pt]
\cos(\alpha)\cdot s&=& r_{\text{Kegel}} \\[5pt]
\cos(72^{\circ})\cdot 3,7\,\text{m} &=& r_{\text{Kegel}} \\[5pt]
1,14\,\text{m}&=& r_{\text{Kegel}} \\[5pt]
r_{\text{Kegel}}&=& \underline{ 1,14\,\text{m}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1daf5df26efd0f2f44413810a13738461541f1b79cf1dd19dc3ef6ae46cfa00e?color=5a5a5a) 2. Schritt: Mantelfächeninhalt des Kegels berechnen
2. Schritt: Mantelfächeninhalt des Kegels berechnen
![\(\begin{array}[t]{rll}
M_{\,\text{Kegel}}&=& \pi \cdot r_{\,\text{Kegel}} \cdot s \\[5pt]
&=& \pi\cdot 1,14\,\text{m}\cdot 3,7\,\text{m} \\[5pt]
&=& \underline{ 13,25\,\text{m}^2}
\end{array}\)](https://mathjax.schullv.de/22a85f69f9a36faf4ded267ba8edb3a01b990241b024fb08ad06d406c1cfe9c2?color=5a5a5a) B) Oberflächeninhalt der Halbkugel
1. Schritt: Höhe
B) Oberflächeninhalt der Halbkugel
1. Schritt: Höhe  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{h_\text{Kegel}}{s} \quad \scriptsize \mid\;\cdot s \\[5pt]
\sin(\alpha)\cdot s &=& h_\text{Kegel} \\[5pt]
\sin(72^{\circ})\cdot 3,7\,\text{m} &=& h_\text{Kegel} \\[5pt]
3,52\,\text{m}&=& h_\text{Kegel} \\[5pt]
h_\text{Kegel}&=& \underline{ 3,52\,\text{m}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3ec8dea06170dc70f785bd26c732d75ec723535ad4f2fdbd67670c9253b32a58?color=5a5a5a) 2. Schritt: Radius
2. Schritt: Radius  berechnen
berechnen
![\(\begin{array}[t]{rll}
r_\text{Halbkugel}&=& h_{ges} - h_\text{Kegel} \\[5pt]
&=& 5,1\,\text{m}-3,52\,\text{m} \\[5pt]
&=& \underline{ 1,58\,\text{m}}
\end{array}\)](https://mathjax.schullv.de/c178aa8856c9395b55638ffe159c56f0522bfca35f16c2e36102477af26c25c4?color=5a5a5a) 3. Schritt: Oberflächeninhalt der Halbkugel berechnen
C) Grundfläche des Kegels berechnen
3. Schritt: Oberflächeninhalt der Halbkugel berechnen
C) Grundfläche des Kegels berechnen
![\(\begin{array}[t]{rll}
A&=& \pi \cdot r_{\text{Kegel}}^2 \\[5pt]
&=& \pi \cdot (1,14\,\text{m})^2 \\[5pt]
&=& \underline{ 4,08\,\text{m}^2}
\end{array}\)](https://mathjax.schullv.de/7921a624d968d66a59bfe5b7953019504b31c75523b46a2d5b12c4f6091519c6?color=5a5a5a) D) Oberflächeninhalt des Kunstwerks berechnen
D) Oberflächeninhalt des Kunstwerks berechnen
![\(\begin{array}[t]{rll}
O&=& M_\text{Kegel}+O_\text{Halbkugel}-A \\[5pt]
&=& 13,25\,\text{m}^2+23,53\,\text{m}^2-4,08\,\text{m}^2 \\[5pt]
&=& \underline{\underline{ 32,7\,\text{m}^2}}
\end{array}\)](https://mathjax.schullv.de/71c3231cb21470aa7cff883aca06429645a2d0137573f3676f0c22053486e0f2?color=5a5a5a) Wie viele Dosen müssen gekauft werden?
Wie viele Dosen müssen gekauft werden?
 Es werden also
Es werden also  benötigt.
benötigt.
Abschlussprüfung 2021
Lösung 5
1. Schritt: Mantelflächeninhalt des Kegels berechnen RadiusLösung 6
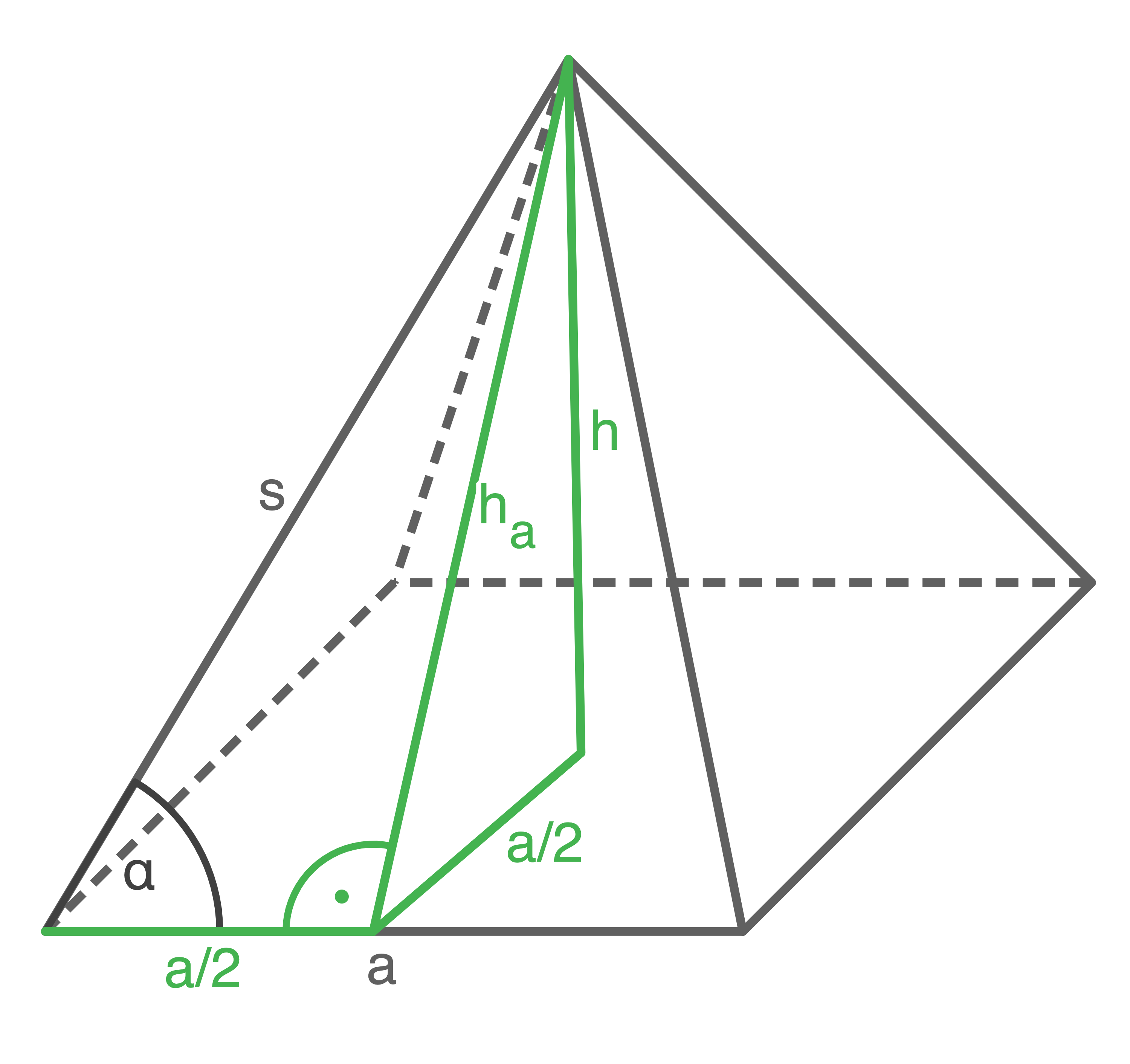
2. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke
4. Schritt: Volumen der Pyramide berechnen
Lösung 7
Radius des Kegels berechnen
 Kantenlänge des Kegelmantels berechnen
Kantenlänge des Kegelmantels berechnen
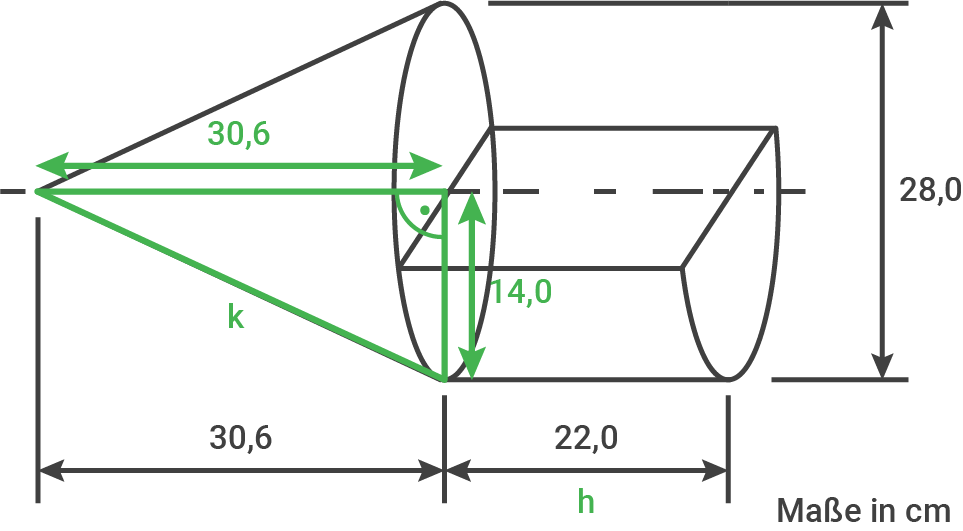
![\(\begin{array}[t]{rll}
k^2&=&(30,6\,\text{cm})^2+(14,0\,\text{cm})^2\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
k&=&\sqrt{(30,6\,\text{cm})^2+(14,0\,\text{cm})^2} \\[5pt]
k&=&\underline{ 33,65\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/1ba9ae324cd392080a11c8123282e8172c4837d41468890db04e879ff168a25f?color=5a5a5a) Oberflächeninhalt berechnen
Oberflächeninhalt berechnen
Abschlussprüfung 2020

Lösung 8
Berechnung des Oberflächeninhalts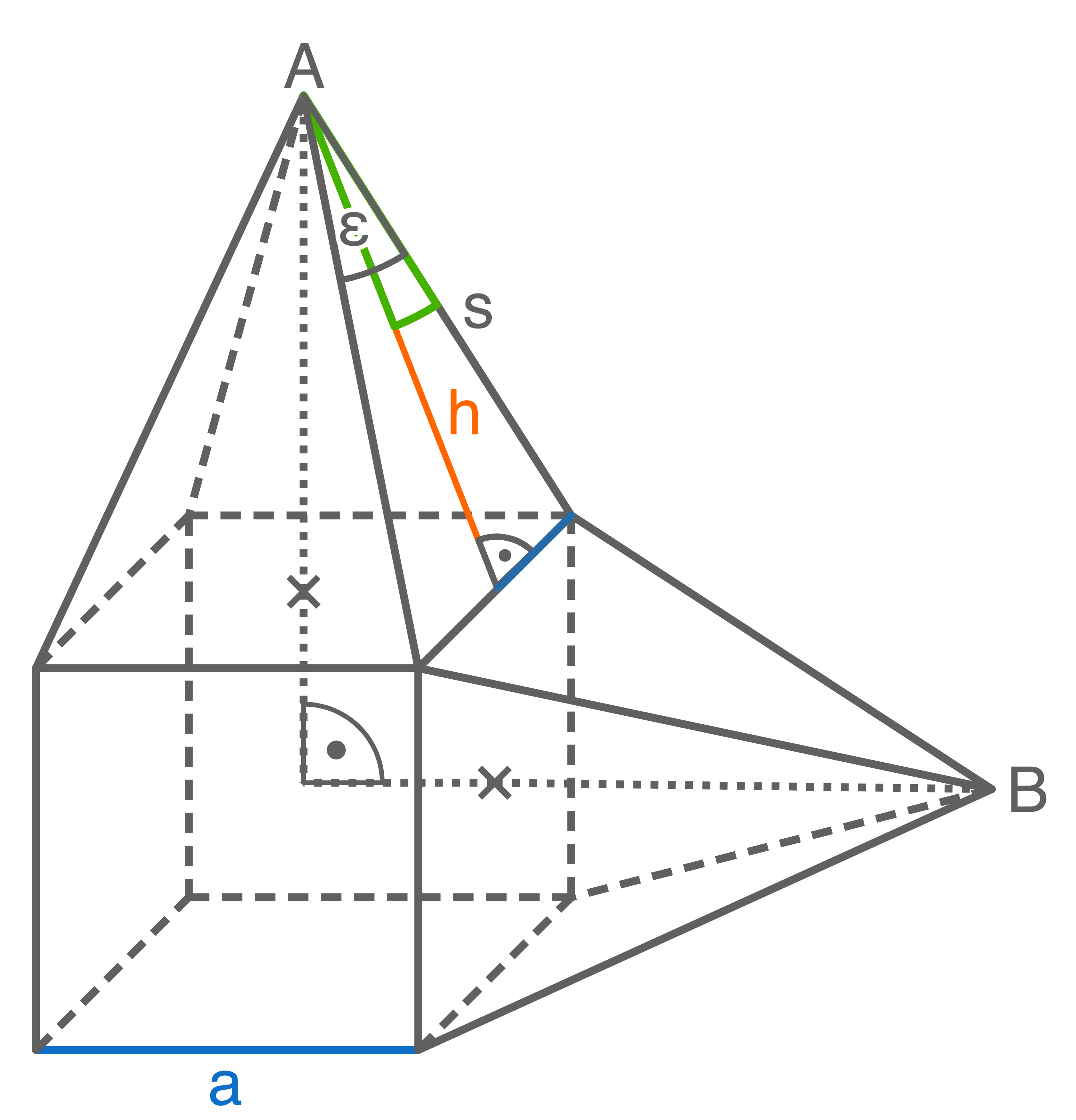
Lösung 9
1. Schritt: Volumen des Wassers berechnen Volumen des Prismas = Volumen des Wassers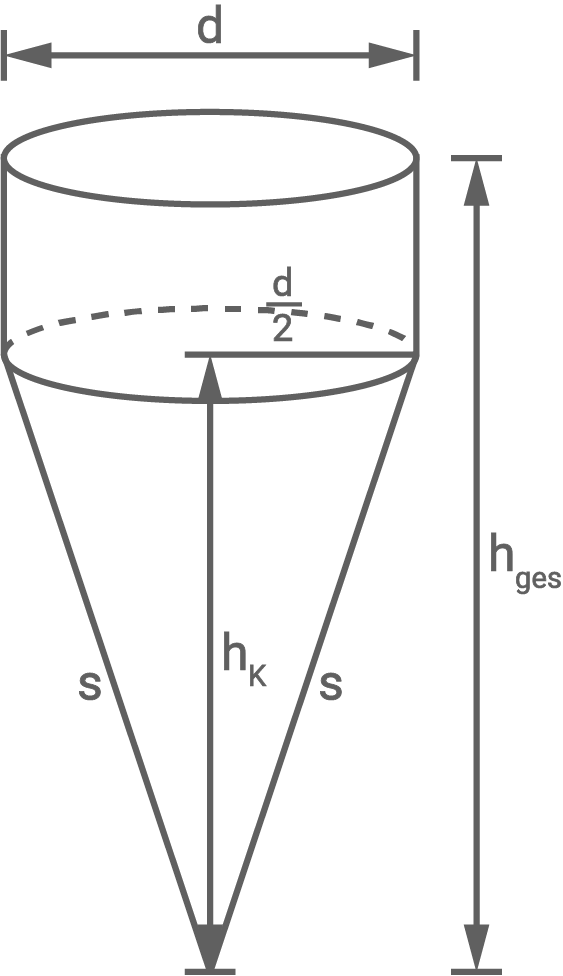
Lösung 10
1. Schritt: Mantelfläche der Pyramide berechnen
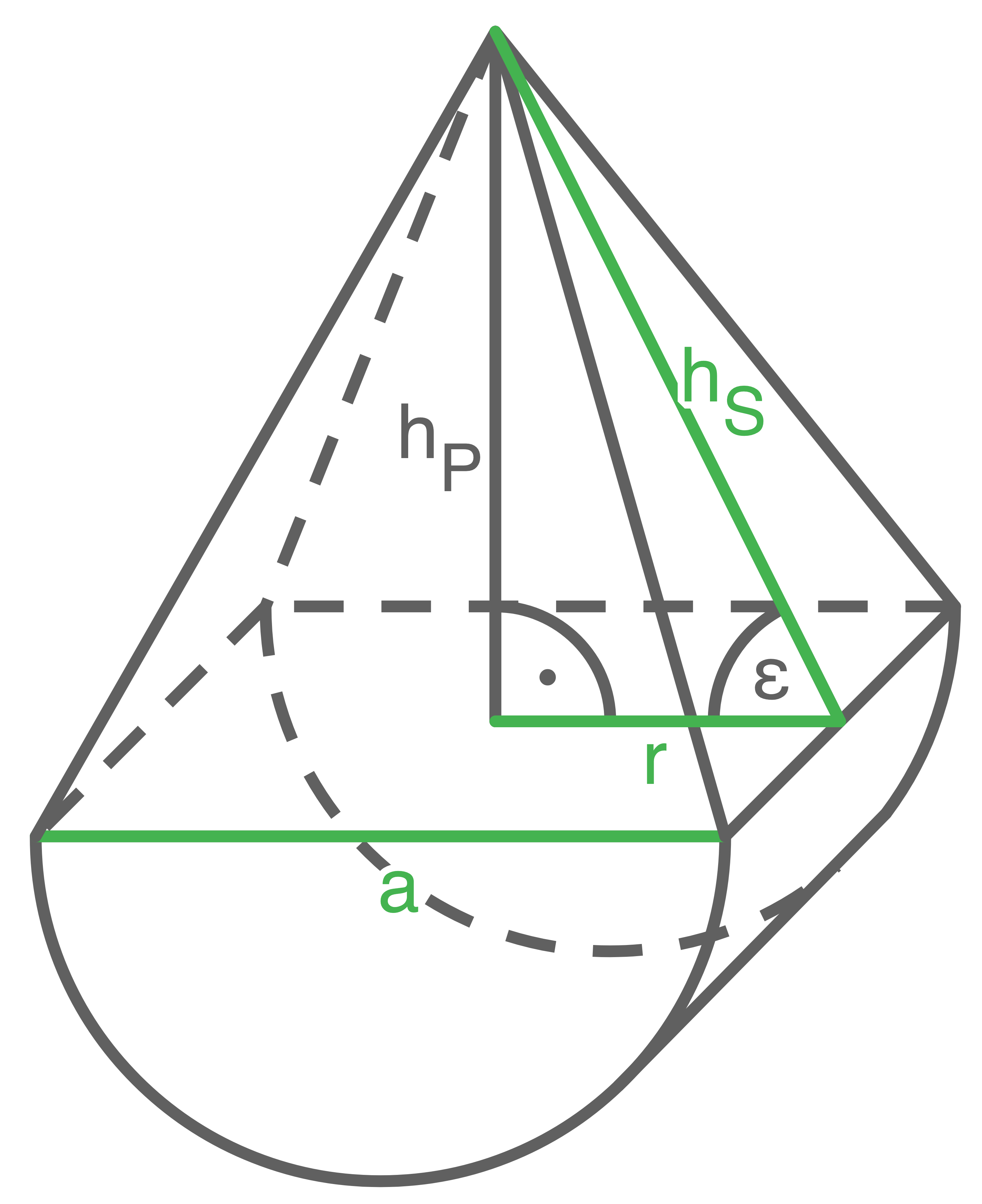 Länge der Strecken
Länge der Strecken  und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
h_S^2&=& r^2 + h_P^2 \\[5pt]
(18,87\,\text{cm})^2-(16\,\text{cm})^2 &=& r^2 \quad \scriptsize \mid\; \sqrt{\,\,} \\[5pt]
r&=& \underline{10 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/dad1f4d5f0282b96f4aaa3fabe879696c77db9fe123e58c524a64b62982b610b?color=5a5a5a) Damit ergibt sich
Damit ergibt sich  Inhalt der Mantelfläche der Pyramide berechnen
Inhalt der Mantelfläche der Pyramide berechnen
![\(\begin{array}[t]{rll}
M_{\,\text{P}}&=& 2 \cdot a \cdot h_S \\[5pt]
&=& 2 \cdot 20 \,\text{cm} \cdot 18,87 \,\text{cm} \\[5pt]
&=& \underline{754,80 \,\text{cm}^2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/bed0a09ca91c71f3f7821bb67336f5604ee3e3280d35298bacf17136792d86da?color=5a5a5a) 2. Schritt: Inhalt der Mantelfläche des Zylinders berechnen
2. Schritt: Inhalt der Mantelfläche des Zylinders berechnen
![\(\begin{array}[t]{rll}
O_Z&=& \dfrac{1}{2} (2 \pi r\cdot (r+a)) \\[5pt]
&=& \frac{1}{2} (2 \pi \cdot 10\,\text{cm}\cdot (10\,\text{cm}+20\,\text{cm} )) \\[5pt]
&=& \underline{942,48 \,\text{cm}^2 }
\end{array}\)](https://mathjax.schullv.de/889808f555547ad0eb5da5465911b9b13365453fa3c0dbd25c396e507a469f71?color=5a5a5a) 3. Schritt: Oberflächeninhalt des zusammengesetzten Körpers berechnen
3. Schritt: Oberflächeninhalt des zusammengesetzten Körpers berechnen
![\(\begin{array}[t]{rll}
O_{\text{gesamt}}&=& M_{\,\text{P}} + O_{\text{Z}} \\[5pt]
&=& 754,80 \,\text{cm}^2 + 942,48 \,\text{cm}^2 \\[5pt]
&=& 1697,28 \,\text{cm}^2\\[5pt]
O_{\text{gesamt}}&=& \underline{\underline{1697,3 \,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/7a334045d3a9f34514e18dfb122ff8edd88a4e885c78d86aaa6ea2bb7240667f?color=5a5a5a)
Abschlussprüfung 2017
Höhe  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\sin(\varepsilon)&=& \dfrac{h_P}{h_S} \quad \scriptsize \mid\; \cdot h_S \,\, \mid\; :\sin(\varepsilon)\\[5pt]
h_S&=& \dfrac{h_P}{\sin(\varepsilon)} \\[5pt]
&=& \dfrac{16 \,\text{cm}}{\sin(58^{\circ})} \\[5pt]
h_S&=& \underline{18,87\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/1eaeddeaca0135f74b8e1d25fa60fb35ce3c546aa43f6ae4b5483640f7271d69?color=5a5a5a)

Lösung 11
LS_1.png)
Lösung 12
Volumen der Pyramide berechnen 1. Schritt: Länge der Diagonale