Anwendungsaufgaben
Aufgabe 1
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Die Vorderseite einer Tennishalle hat annähernd die Form einer Parabel.
Sie lässt sich mit der Funktionsgleichung
beschreiben.
Die maximale Höhe der Halle beträgt 
Die Halle hat am Boden eine Breite von 
Die Fensterfläche soll eine Höhe von
haben.
Die beiden oberen Eckpunkte berühren den Parabelbogen (siehe Abbildung).
Die Fensterfläche soll eine Breite von
haben.
Abschlussprüfung 2024
Sie lässt sich mit der Funktionsgleichung
- Gib eine mögliche Funktionsgleichung an.
Die Fensterfläche soll eine Höhe von
Die beiden oberen Eckpunkte berühren den Parabelbogen (siehe Abbildung).
- Berechne den Flächeninhalt dieser Fensterfläche.
Die Fensterfläche soll eine Breite von
- Berechne die größtmögliche Höhe dieser Fensterfläche.
- Welche der beiden Fensterflächen ist größer? Berechne.
(5 P)
Aufgabe 2
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Die Abbildung zeigt den Sprung eines Frosches, der annähernd die Form einer Parabel mit der Gleichung 
hat.
Die maximale Höhe des Sprungs ist
. Die Sprungweite beträgt 
.
nach dem Absprung befindet sich ein Schilfrohr, das 
aus dem Wasser ragt.
dargestellt werden.
Die maximale Höhe des Sprungs ist
- Gib eine mögliche Gleichung der zugehörigen Parabel an.
- In welchem Abstand springt der Frosch darüber?
- Welcher der beiden Frösche springt weiter?
Berechne die Differenz der Sprungweiten.
(5 P)
Aufgabe 3
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Das Foto zeigt ein „Tiny House“.
Die Vorderseite des Hauses ist annähernd parabelförmig.
Die maximale Höhe des Hauses beträgt 3,00 m.
Am Boden ist es 2,70 m breit.
Quelle: https://tiny-house-de
Die maximale Höhe des Hauses beträgt 3,00 m.
Am Boden ist es 2,70 m breit.
- Berechne eine mögliche Funktionsgleichung für die parabelförmige Außenkante des Hauses.
- Berechne die Länge dieses Vordachs.
- Berechne den Flächeninhalt der Tür.
(5 P)
Aufgabe 4
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
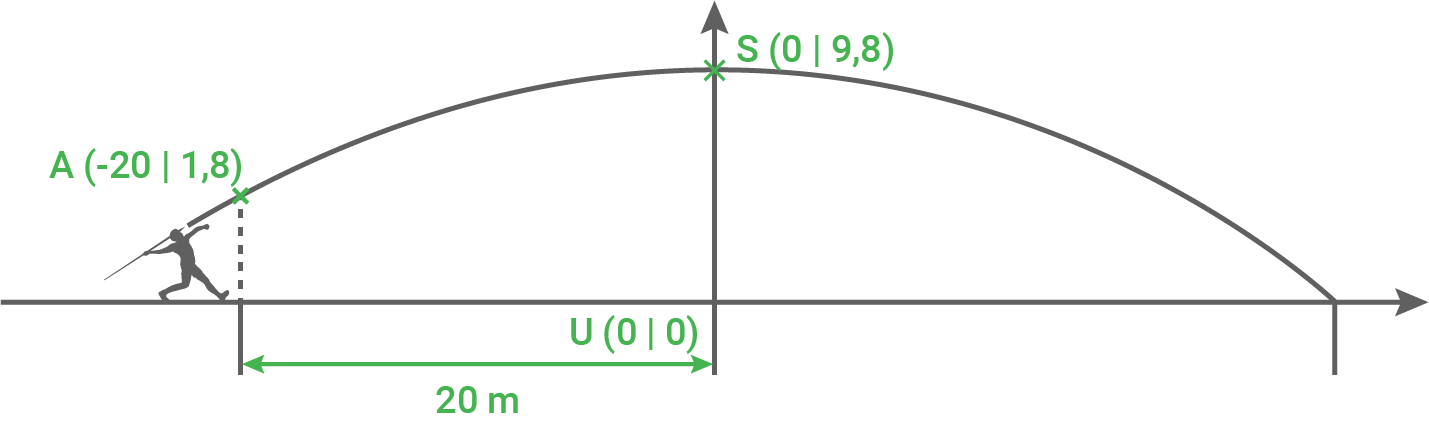
Die Flugbahn eines Speers ist nahezu parabelförmig.
(Skizze nicht maßstabsgetreu)
Der Abwurfpunkt A liegt 1,80 m über der Abwurflinie.
Der Speer erreicht nach 20 m, in horizontaler Richtung von der Abwurflinie gemessen, seine maximale Höhe von 9,80 m.
beschrieben werden. Die Wurfweite beträgt 38,15 m.
(Skizze nicht maßstabsgetreu)
Der Speer erreicht nach 20 m, in horizontaler Richtung von der Abwurflinie gemessen, seine maximale Höhe von 9,80 m.
- Berechne eine mögliche Funktionsgleichung der Flugkurve des Speers.
- Wie weit fliegt der Speer?
- Gib die Höhe dieses Abwurfpunktes an.
(5 P)
Abschlussprüfung 2021
Aufgabe 5
a)
Die Teilaufgabe a) wurde in das Thema "Geometrie in der Ebene" eingeordnet.
b)
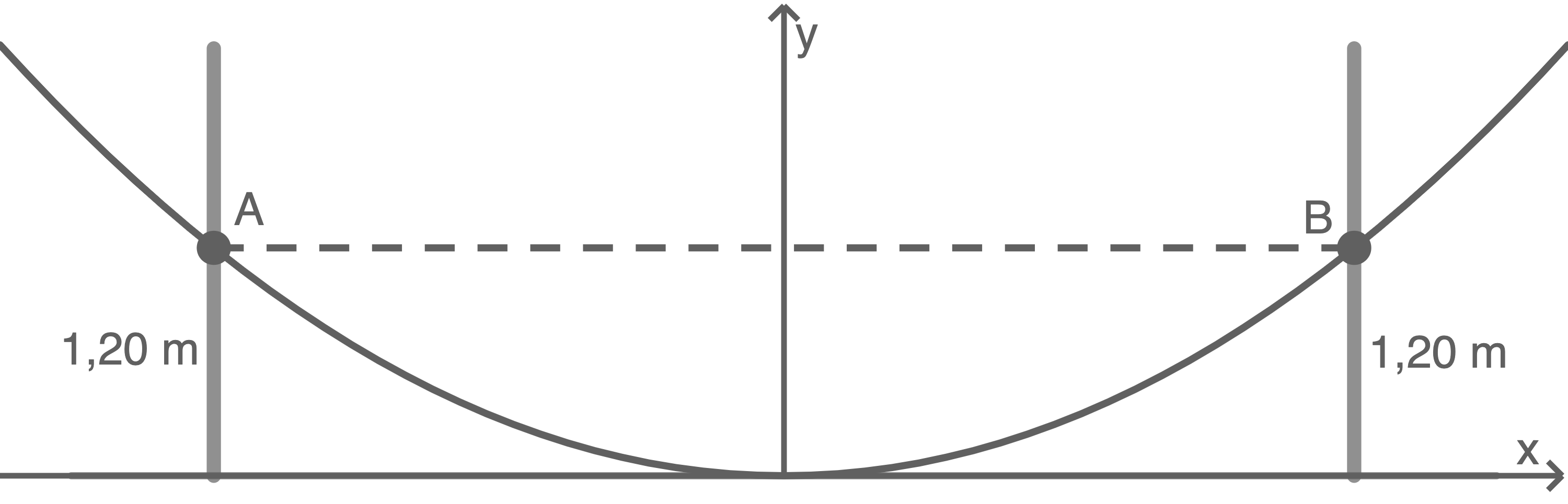
Die Abbildung zeigt eine vereinfachte Darstellung einer Hängematte, die zwischen zwei Bäumen befestigt ist. Der Abstand der beiden Bäume beträgt 8 m.
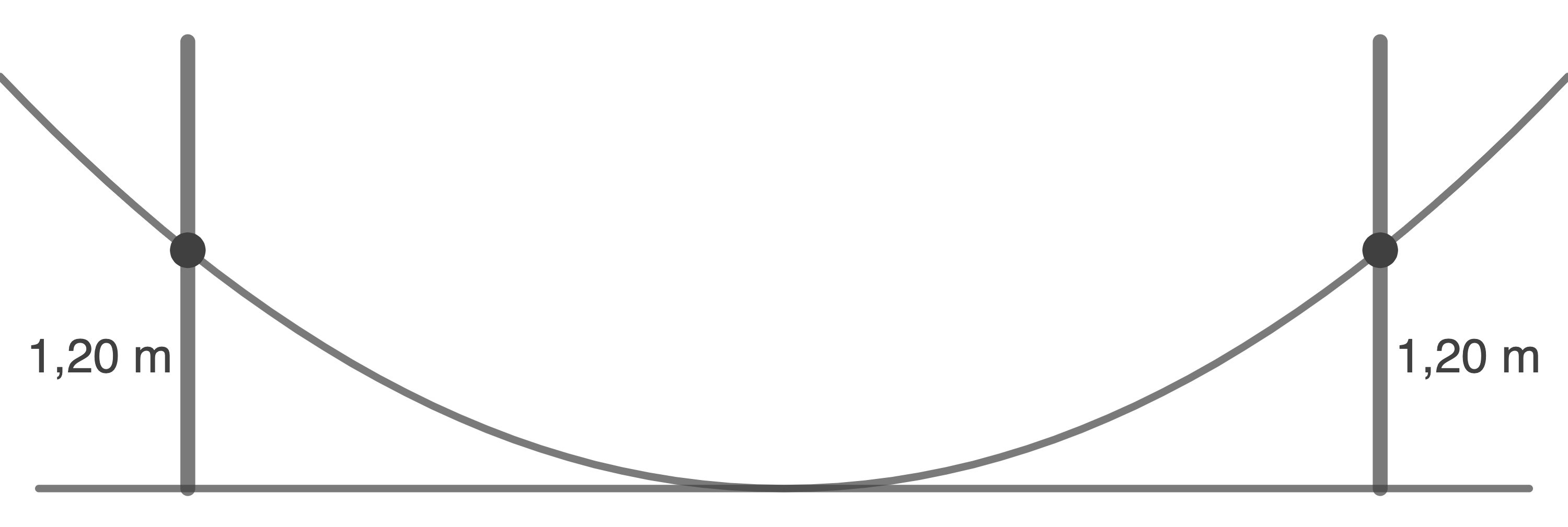
- Die Hängematte hat die Form einer Parabel. Bestimme die Funktionsgleichung dieser Parabel.
- Wenn die Parabel mit der Gleichung
beschrieben werden soll und die Hängematte in der gleichen Höhe an den Bäumen befestigt werden soll, wie weit müssten dann die Bäume auseinander stehen?
(5 P)
Aufgabe 6
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Thea trainiert Aufschläge beim Volleyball (siehe Skizze).
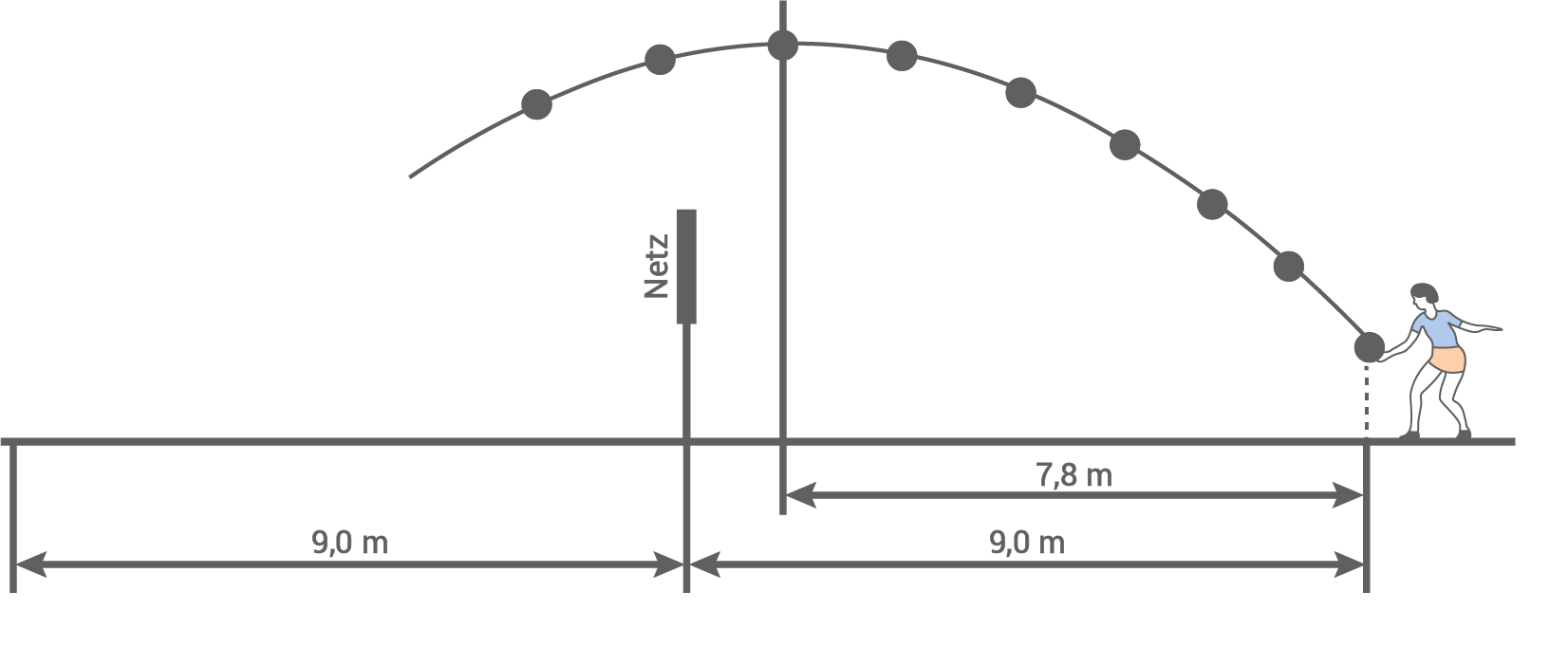Die Flugkurve des Balles lässt sich mit einer Funktionsgleichung der Form 
annähernd beschreiben. Der Ball verlässt beim Aufschlag von unten die Hand in einer Höhe von 
über der Grundlinie.
Nach
(horizontal gemessen) erreicht die Flugkurve des Balles ihre maximale Höhe von 
Gib eine mögliche Funktionsgleichung der zugehörigen Parabel
an.
ln welchem Abstand überquert der Ball das 
hohe Netz?
Die Grundlinien des Volleyballspielfeldes sind jeweils 
vom Netz entfernt (siehe Skizze).
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
Nach
Gib eine mögliche Funktionsgleichung der zugehörigen Parabel
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
(4,5 P)
Aufgabe 7
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
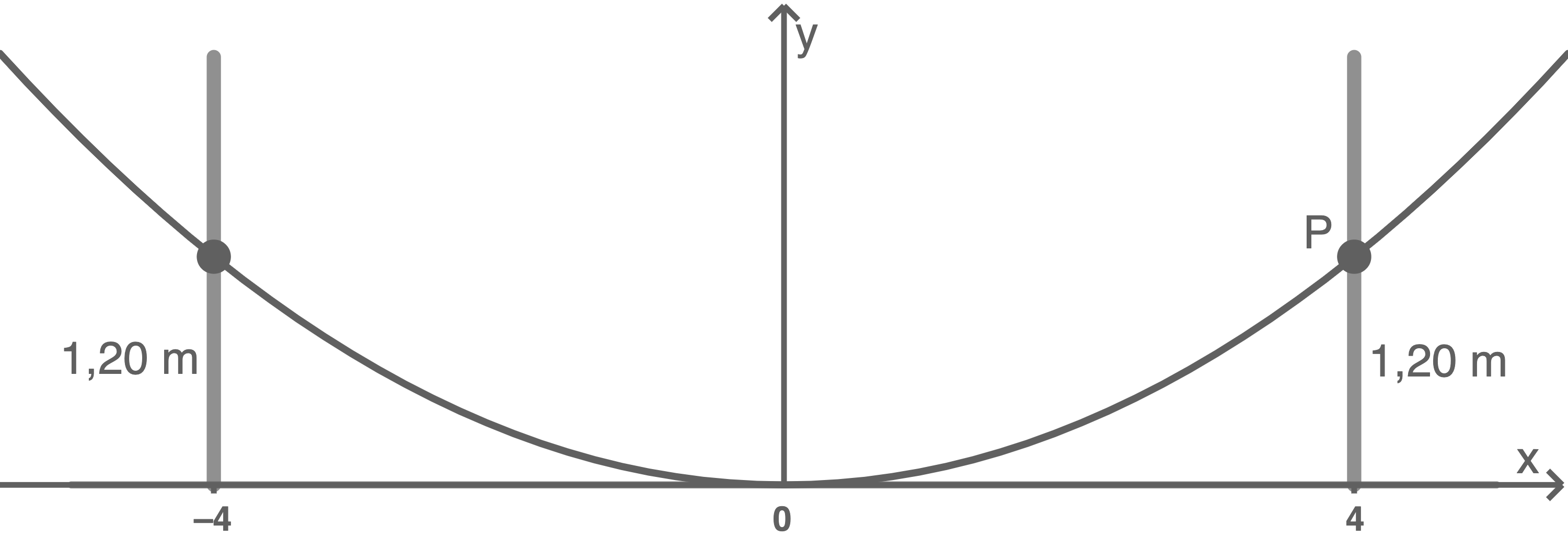
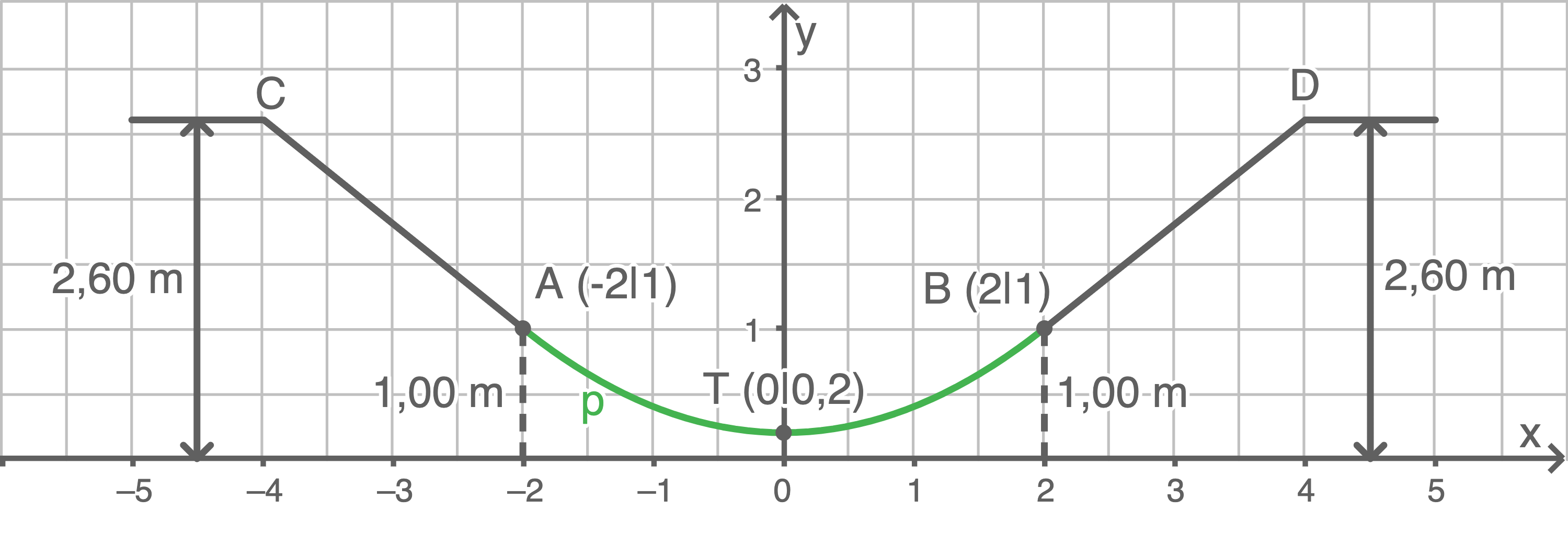
Im Querschnitt einer Skater-Rampe sieht man die beiden geraden Teilstücke 
und 
sowie das parabelförmige Teilstück 
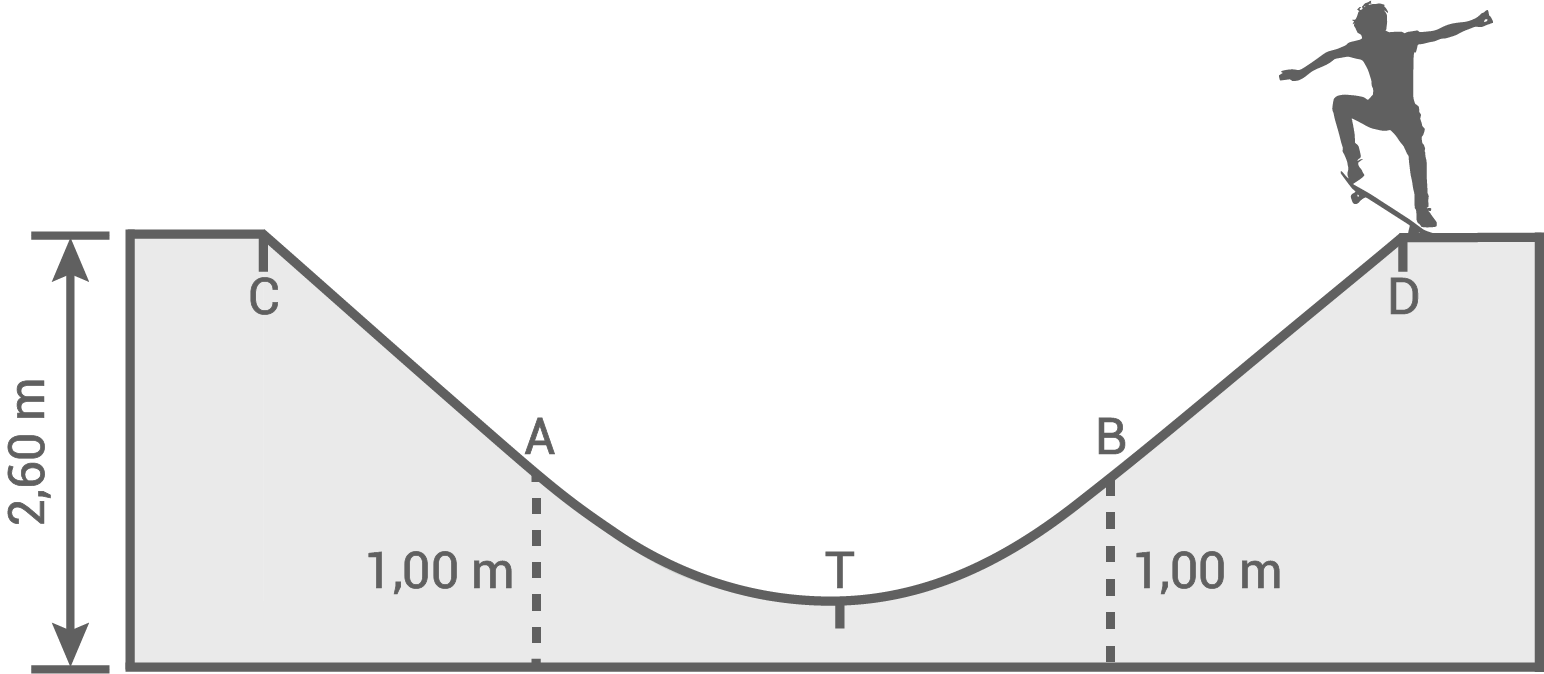Die beiden Punkte 
und 
liegen auf gleicher Höhe und sind 
voneinander entfernt.
Der tiefste Punkt
der Skater-Rampe liegt 
über dem Boden.
Bestimme eine mögliche Funktionsgleichung für das parabelförmige Teilstück
Die beiden Punkte 
und 
liegen ebenfalls auf gleicher Höhe und sind 
voneinander entfernt.
Bestimme eine mögliche Funktionsgleichung für die Gerade, auf der das gerade Teilstück liegt.
(Skizze nicht maßstabsgetreu)
Der tiefste Punkt
(4 P)
Aufgabe 8
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Ein Golfspieler schlägt seinen Golfball ab. Die Flugbahn des Golfballes ist annähernd parabelförmig.
In einer horizontalen Entfernung von 95 m zum Abschlag erreicht der Ball seine maximale Flughöhe von 25 m über dem Boden.
Gib eine Gleichung der zugehörigen Parabel an.
Ein 15 m hoher Baum steht in 45 m Entfernung vom Abschlag. In welchem Abstand überfliegt der Ball die Baumspitze?
Das Loch befindet sich auf einer 2 m höher gelegenen Ebene in 180 m horizontaler Entfernung vom Abschlag.
In welcher Entfernung vom Loch trifft der Ball auf der höher gelegenen Ebene auf?
(Skizze nicht maßstäblich)
(4,5 P)
Aufgabe 9
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
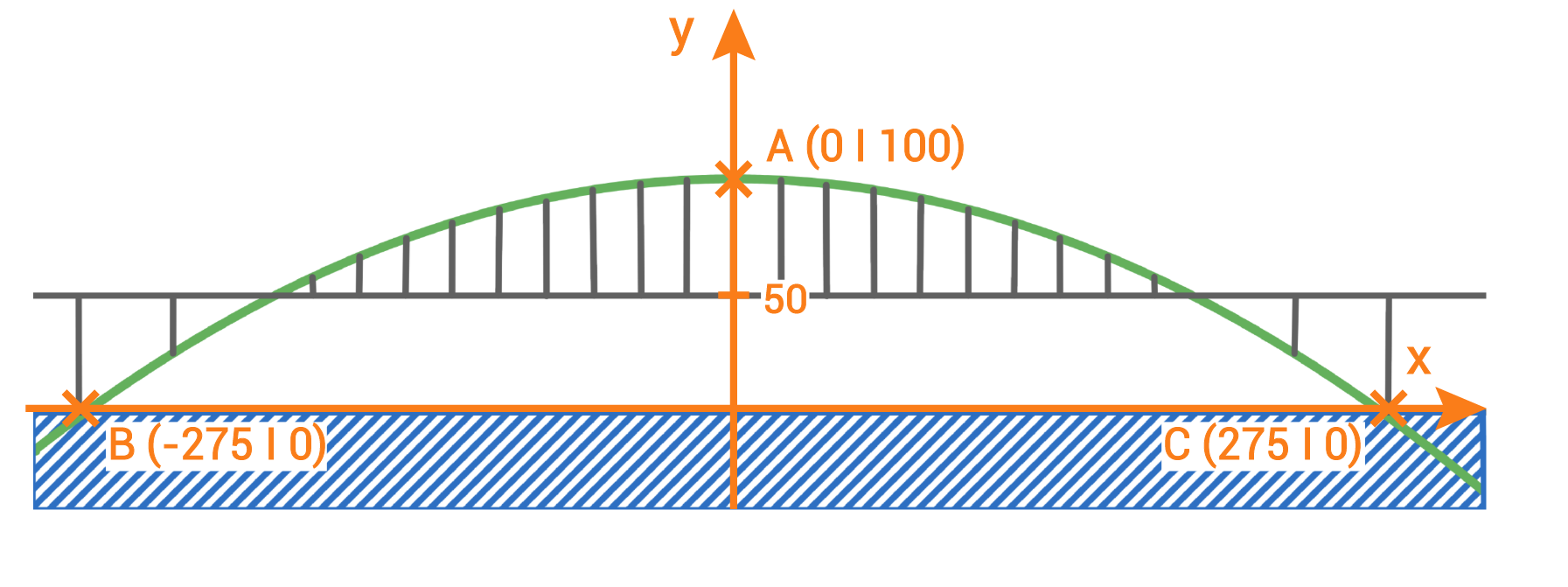
Die Lupu-Brücke überspannt den Fluss Huangpu in Shanghai.
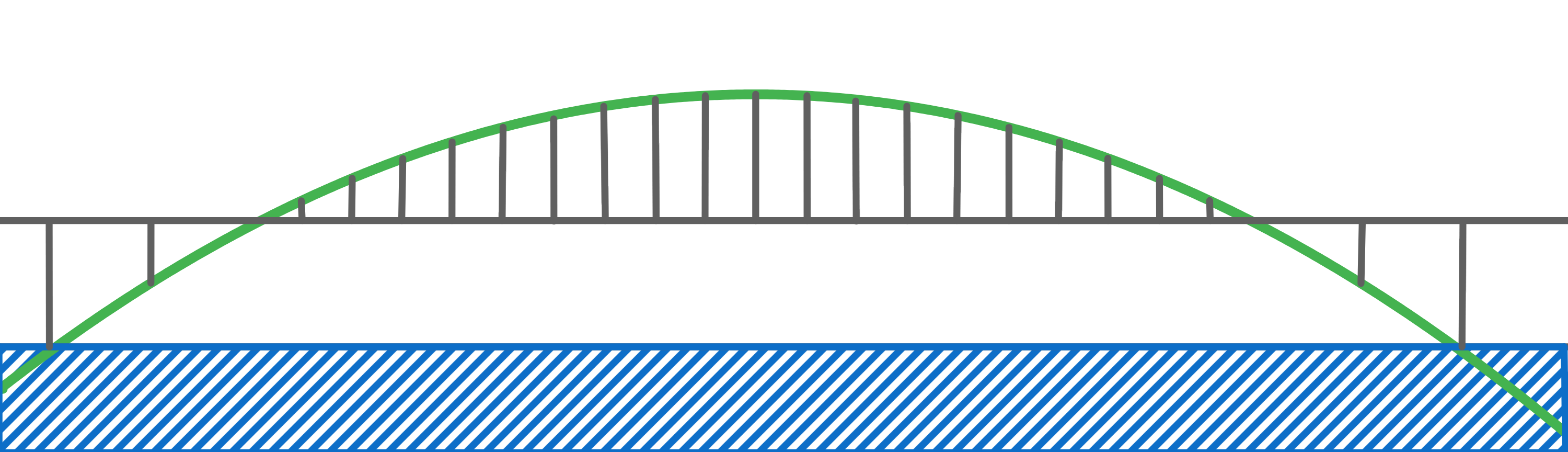Sie ist die zweitlängste Bogenbrücke der Welt und hat annähernd die Form einer Parabel.
Sie kann mit der Funktionsgleichung beschrieben werden.
Die Bogenbrücke hat auf Höhe der Wasseroberfläche eine Weite von 550 m.
Die Fahrbahn befindet sich 50 m über der Wasseroberfläche.
Das ist die Hälfte der maximalen Höhe der Brücke. Bestimme eine mögliche Funktionsgleichung für den Brückenbogen. Berechne die Länge der Fahrbahn innerhalb des Brückenbogens.
Sie kann mit der Funktionsgleichung
Die Fahrbahn befindet sich 50 m über der Wasseroberfläche.
Das ist die Hälfte der maximalen Höhe der Brücke. Bestimme eine mögliche Funktionsgleichung für den Brückenbogen. Berechne die Länge der Fahrbahn innerhalb des Brückenbogens.
(4,5 P)
Aufgabe 10
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Theo wirft im Basketballtraining auf den Korb (siehe Skizze).
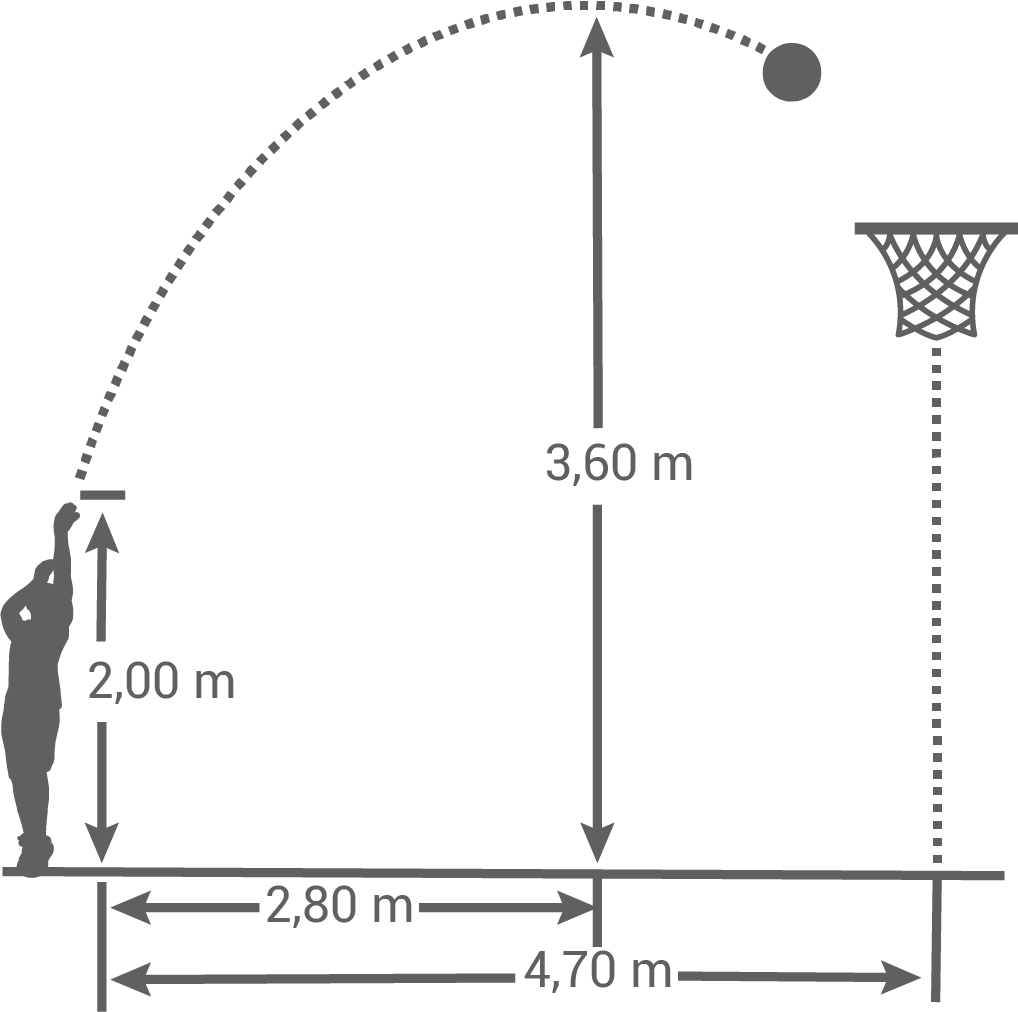Die annähernd parabelförmige Flugkurve des Balles lässt sich mit der Gleichung beschreiben.
Gib eine mögliche Gleichung der zugehörigen Parabel
an.
Trifft Theo bei diesem Wurf direkt in den Korb, der in einer Höhe von 
hängt?
Begründe durch Rechnung. Vor Theo steht der Abwehrspieler Dennis im Abstand von
Mit nach oben gestreckten Armen erreicht Dennis eine Höhe von 
Berührt er den Ball, ohne hochzuspringen?
Begründe durch Rechnung.
Gib eine mögliche Gleichung der zugehörigen Parabel
Begründe durch Rechnung. Vor Theo steht der Abwehrspieler Dennis im Abstand von
Berührt er den Ball, ohne hochzuspringen?
Begründe durch Rechnung.
(4,5 P)
Aufgabe 11
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
David und Tim messen sich im Kugelstoßen. Beim Stoß von David verlässt die Kugel seine Hand in einer Höhe von 
(siehe Skizze).
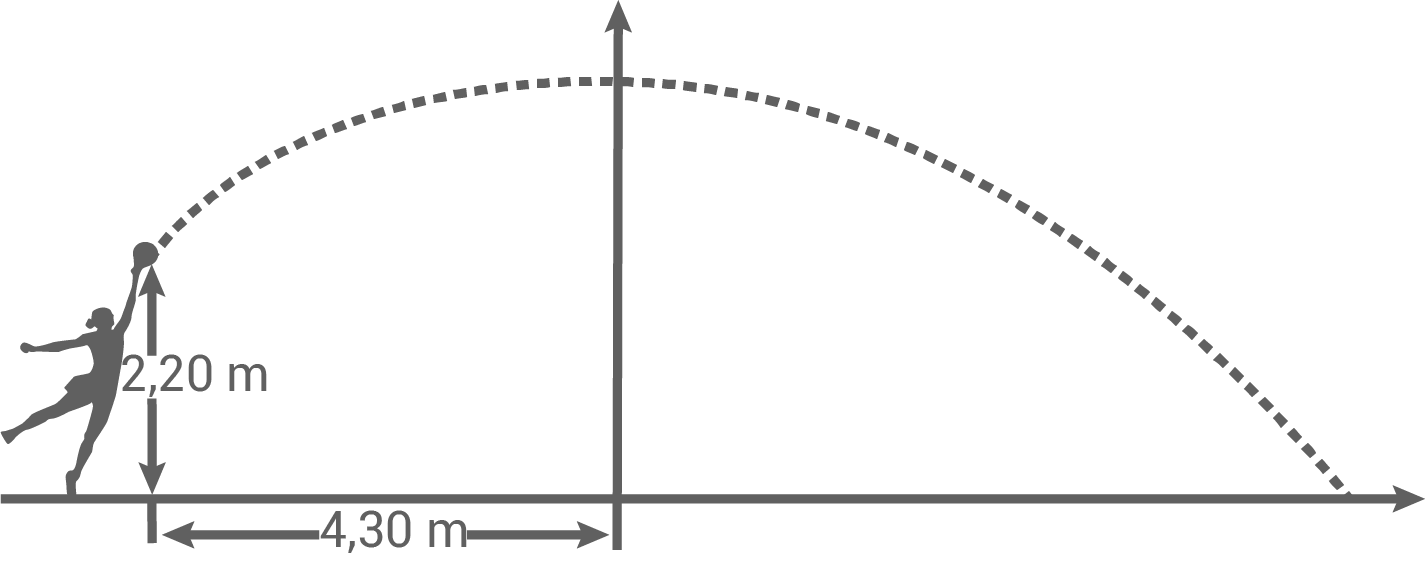Nach einer horizontalen Entfernung von 
hat die Kugel ihre maximale Höhe von 
erreicht.
Die Flugbahn der Kugel lässt sich annähernd durch eine Parabel mit der Funktionsgleichung beschreiben.
Welche Weite hat David erzielt?
Tim stößt die Kugel ebenfalls aus dem Stoßkreis. Die Kugel verlässt seine Hand in einer Höhe von 
.
Die Parabelgleichung für diesen Stoß lautet:
.
Vergleiche die beiden Kugelstoßweiten.
Die Flugbahn der Kugel lässt sich annähernd durch eine Parabel mit der Funktionsgleichung
Die Parabelgleichung für diesen Stoß lautet:
Vergleiche die beiden Kugelstoßweiten.
(4,5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Funktionsgleichung angeben
Die Parabel hat den Scheitelpunkt 
Einsetzen der Koordinaten des Punktes in die allgemeine Funktionsgleichung liefert:
![\(\begin{array}[t]{rll}
12&=& a\cdot 0^2+c \\[5pt]
12&=& c
\end{array}\)](https://mathjax.schullv.de/98e62bf120309a92b767cf6e9e2b2520415e1c638ceeb3a0cb23e1274ffb7a74?color=5a5a5a)
Außerdem kommt die Halle im Punkt 
auf dem Boden auf. Einsetzen der Koordinaten liefert weiter:
![\(\begin{array}[t]{rll}
0&=& a\cdot 20^2+12 &\quad \scriptsize \mid\; -12 \\[5pt]
-12&=& a\cdot 400 &\quad \scriptsize \mid\; :400 \\[5pt]
-0,03&=& a
\end{array}\)](https://mathjax.schullv.de/09e140d1c7d1edf06c20fca568ff32a2a8269c59ea8ca3d76caf56f3e9743367?color=5a5a5a)
Eine mögliche Funktionsgleichung lautet:
Flächeninhalt der Fensterfläche berechnen
Eckpunkte auf dem Parabelbogen berechnen:
![\(\begin{array}[t]{rll}
-0,03x^2+12&=& 10 \quad \scriptsize \mid\;-12 \\[5pt]
-0,03x^2&=& -2 \quad \scriptsize \mid\;:(-0,03) \\[5pt]
x^2&=& 66,67 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x&=& \pm 8,17
\end{array}\)](https://mathjax.schullv.de/5013a4541abd3cd0537fdb7a74abedc78940204e3aa843c9917ab5ec59c4a497?color=5a5a5a)
Die Fensterfläche hat also eine Höhe von und eine Breite von 
Für den Flächeninhalt ergibt sich:
Größtmögliche Höhe berechnen
Da das Fenster symmetrisch zur 
-Achse gebaut wird, muss der Funktionswert an der Stelle 
berechnet werden.
Die Fensterfläche könnte höchstens 
hoch sein.
Fensterflächen vergleichen
Fensterfläche bei Vorschlag 2:
Die Fensterfläche von Vorschlag 1 ist größer.
Abschlussprüfung 2024
Lösung 2
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Gleichung der zugehörigen Parabel angeben
da der Scheitelpunkt bei 
die -Koordinate 
hat.
, denn von Absprung bis Landung sind es 
in 
![\(\begin{array}[t]{rll}
0&=&a\cdot 110^2+139 &\quad \scriptsize \mid\;-139 \\[5pt]
-139&=&12100a&\quad \scriptsize \mid\;:12100 \\[5pt]
-0,011&=&a\\[5pt]
a&=&-0,011
\end{array}\)](https://mathjax.schullv.de/e9fe73f154dfcf69719aba7dd4baac31ade2f3dcef1d3a18f756e8acbf21fc6e?color=5a5a5a)
Abstand berechnen
Die Parabel hat an der Stelle 
den -Wert 
Beurteilen, welcher Frosch weiter springt und Differenz berechnen
![\(\begin{array}[t]{rll}
-\dfrac{3}{200}x^2+165&=&0 \quad \scriptsize \mid\;-165 \\[5pt]
-\dfrac{3}{200}x^2&=&-165 \quad \scriptsize \mid\;:(-\dfrac{3}{200})\\[5pt]
x^2&=& 165\cdot \dfrac{200}{3}\\[5pt]
x_1&=& 104,9\\[5pt]
x_2&=& -104,9
\end{array}\)](https://mathjax.schullv.de/b3441cda9829135a8cdfc106e7ff3b773f4af34b59deca78442526f4cbf612d5?color=5a5a5a)
Frosch 2 springt also ![\(104,9\cdot 2=209,8\,\left[\text{cm}\right]\)](https://mathjax.schullv.de/96a1239f36b2ed7607f63baf2c2d738c9d12fc6e061e5bdff9241a5d1cced5d6?color=5a5a5a)
weit.
Frosch 1 springt demnach ca. 
weiter.
Lösung 3
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Mögliche Funktionsgleichung berechnen
da der Scheitelpunkt die Koordinaten 
hat.
Der Punkt 
liegt auf der Parabel. Eingesetzt in ergibt:
Länge des Vordachs berechnen
![\(\begin{array}[t]{rll}
2+1,65x^2&=&3,00 \quad \scriptsize \mid\;-2 \\[5pt]
1,65x^2&=&1\quad \scriptsize \mid\;:1,65\\[5pt]
x^2&=&\dfrac{1}{1,65}\quad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
x&=&0,78
\end{array}\)](https://mathjax.schullv.de/c6e3079dbe393e02bbfcddbee3dfc844f3b93fc2c72c916bf55f1b0a79d4ef16?color=5a5a5a)
Länge des Vordachs: 
Flächeninhalt der Tür berechnen
![\(\begin{array}[t]{rll}
1+1,65x^2&=&3,00 \quad \scriptsize \mid\;-1 \\[5pt]
1,65x^2&=&2\quad \scriptsize \mid\;:1,65\\[5pt]
x^2&=&\dfrac{2}{1,65}\quad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
x&=&1,1
\end{array}\)](https://mathjax.schullv.de/0a3757ebded32d488f6f14a30d4581f095ef46b798b06c3fdef202b70ed32217?color=5a5a5a)
Abschlussprüfung 2022
Lösung 4
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Funktionsgleichung berechnen
Parabelform:
daher gilt: 
Punkt 
einsetzen:
![\(\begin{array}[t]{rll}
1,8&=& a \cdot (-20)^2+9,8 \quad \scriptsize \mid\; -9,8\\[5pt]
-8&=& a \cdot 400 \quad \scriptsize \mid\; :400\\[5pt]
-0,02&=& a\\
a&=& -0,02
\end{array}\)](https://mathjax.schullv.de/1ce6a7e369415d231547867770a5561de2f6e07b2dfd662de4bcb04f69830958?color=5a5a5a)
Eine mögliche Funktionsgleichung lautet also: 
Wie weit fliegt der Speer?
Nullstellen der Parabel berechnen:
![\(\begin{array}[t]{rll}
-0,02x^2+9,8&=& 0 \quad \scriptsize \mid\; -9,8 \\[5pt]
-0,02x^2&=& -9,8 \quad \scriptsize \mid\; :(-0,02)\\[5pt]
x^2&=& 490 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&=& -22,14 \\[5pt]
x_2&=& +22,14
\end{array}\)](https://mathjax.schullv.de/dabf98f1e1d50182303e60bc6181549b8495c52d3a618ba591af6766e5c0311d?color=5a5a5a)
Der Speer stößt also am Punkt 
auf dem Boden auf.
Wurfweite 
berechnen:
![\(\begin{array}[t]{rll}
w&=& x_N -x_A &\quad \scriptsize \\[5pt]
&=& 22,14 - (-20) &\quad \scriptsize \\[5pt]
&=& 42,14\\[5pt]
w&=& \underline{\underline{ 42,1}}
\end{array}\)](https://mathjax.schullv.de/cb1f93cf491c002303bd53544e72b79e93e88e021a8d28facad3efe6311945d6?color=5a5a5a)
Der Speer fliegt also 
weit.
Höhe des Abwurfpunktes angeben
Nullstellen der Parabel berechnen:
![\(\begin{array}[t]{rll}
-\dfrac{1}{30}\cdot x^2+13&=&0 \quad \scriptsize \mid\; -13 \\[5pt]
-\dfrac{1}{30}\cdot x^2&=&-13 \quad \scriptsize \mid\; :\left(-\dfrac{1}{30}\right)\\[5pt]
x^2&=& 390\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&=& -19,75\\[5pt]
x_2&=& +19,75
\end{array}\)](https://mathjax.schullv.de/bb0d9cf718e5b85da77f32b1f42c944298c5bfe91857524d533a6ceebcd99534?color=5a5a5a)
-Koordinate des Abwurfspunkts berechnen:
![\(\begin{array}[t]{rll}
x_{A2}&=& x_2- \,\text{Wurfweite} &\quad \scriptsize \\[5pt]
&=& 19,75- 38,15 &\quad \scriptsize \\[5pt]
&=& -18,4
\end{array}\)](https://mathjax.schullv.de/1c902a7dcaa57466628967dfa5f8cad11b3b86c36a284b5be66e6588e3716f81?color=5a5a5a)
-Koordinate des Abwurfspunkts berechnen:
![\(\begin{array}[t]{rll}
y&=&-\dfrac{1}{30}x^2+13 \quad \scriptsize \mid\; x_{A2}=-18,4\\[5pt]
y&=&-\dfrac{1}{30}\cdot (-18,4)^2+13 &\quad \scriptsize \\[5pt]
&=& 1,71
\\[5pt]
y&=& \underline{\underline{ 1,7}}
\end{array}\)](https://mathjax.schullv.de/8b66a255e77e81cfb31065138b46d687715512badeb6559f8fb208d2d269a27a?color=5a5a5a)
Der Abwurfpunkt befindet sich auf einer Höhe von ungefähr 
Lösung 5
a)
Die Teilaufgabe a) wurde in das Thema "Geometrie in der Ebene" eingeordnet.
b)
Funktionsgleichung der Parabel berechnen
Punkt 
in die allgemeine Parabelgleichung einsetzen:
![\(\begin{array}[t]{rll}
p:y&=& a\cdot x^2 \\[5pt]
1,2 &=& a\cdot 4^2 &\quad \scriptsize \mid\; :4^2 \\[5pt]
a &=& \dfrac{1,2}{4^2} = 0,075
\end{array}\)](https://mathjax.schullv.de/9aa3844d6336920ce00f852c343ed6be3724cf3ae2058f61632f436e1b5a0753?color=5a5a5a)
Wie weit müssten die Bäume dann auseinander stehen?
![\(\begin{array}[t]{rll}
y&=&0,15x^2 \quad \scriptsize \mid\; y=1,2 \\[5pt]
1,2&=&0,15x^2 \quad \scriptsize \mid\; :0,15 \\[5pt]
8&=& x^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
x_1&=&2,83 \\[5pt]
x_2&=& -2,83
\end{array}\)](https://mathjax.schullv.de/1a59f4cfce89e42fe58eb10ce03aadfcc64819bd25d48cb589c7a71641950460?color=5a5a5a)
Der Abstand zwischen den beiden Bäumen beträgt 
Lösung 6
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Mögliche Funktionsgleichung berechnen
Der höchste Punkt der Flugbahn entspricht dem Scheitelpunkt der Parabel:
Scheitelpunkt: 
Da dieser auf der -Achse liegt, gilt 
Aufschlagspunkt: 
![\(\begin{array}[t]{rll}
p \; y&=& ax^2+c &\quad \scriptsize \mid\;c=4 \\[5pt]
y&=& ax^2+4 &\quad \scriptsize \mid\;P(7,8\mid0,9) \\[5pt]
0,9&=& a \cdot 7,8^2 +4&\quad \scriptsize \mid\;-4 \\[5pt]
-3,1&=& a \cdot 7,8^2 &\quad \scriptsize \mid\;:7,8^2 \\[5pt]
-\dfrac{3,1}{7,8^2}&=& a \\[5pt]
a &=& -\dfrac{3,1}{7,8^2} \\[5pt]
a &=& -\dfrac{155}{3042}
\end{array}\)](https://mathjax.schullv.de/100233be7a22fb675784e35ef4aade5ff3cda7e87f8e9020c2526d6c2dee8b92?color=5a5a5a)
Eine mögliche Funktionsgleichung der Parabel lautet also:
ln welchem Abstand überquert der Ball das Netz?
Berechnung der -Koordinate des Überflugpunkts:
in einsetzen:
![\(\begin{array}[t]{rll}
y&=& -\dfrac{155}{3042}\cdot (-1,2)^2+4 \\[5pt]
y&= & 3,93
\end{array}\)](https://mathjax.schullv.de/0b19b557ed06862aa15015fbc9c2039df4d3693a2a2046ecea6edc3a9fcb7aa4?color=5a5a5a)
Abstand 
zum Netz berechnen:
![\(\begin{array}[t]{rll}
d &=& 3,93\,\text{m}- 2,24\,\text{m} \\[5pt]
&=& 1,69\,\text{m}
\\[5pt]
d&=& \underline{\underline{ 1,7\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/7f2326fd72e27a9cf0716f22d5d45797f5826b9cfe2e2c4cb0d92142e5a69c9e?color=5a5a5a)
Der Ball überquert das Netz mit einem Abstand von 
ln welcher Entfernung zur Grundlinie trifft der Ball auf dem Boden auf?
Der Boden wird durch die -Achse dargestellt.
![\(\begin{array}[t]{rll}
-\dfrac{155}{3042}x^2+4 &=& 0 &\quad \scriptsize \mid\;-4 \\[5pt]
-\dfrac{155}{3042}x^2&=& -4 &\quad \scriptsize \mid\;\cdot \left(-\dfrac{3042}{155}\right)\\[5pt]
x^2&=& \dfrac{12168}{155} &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
x_1&=& 8,86 \\[5pt]
x_2&=& -8,86
\end{array}\)](https://mathjax.schullv.de/2e69966e5681d55cd0e75f55eeb102a77c7efbff6efba69aefe332529119fbb9?color=5a5a5a)
Abstand der Grundlinie zum Netz 
berechnen:
![\(\begin{array}[t]{rll}
n&=& 9\,\text{m}+1,2\,\text{m} \\[5pt]
&=& 10,2\,\text{m}
\end{array}\)](https://mathjax.schullv.de/7b0f1cecdfe794ba8720cc8f91f69ebc498a940c875dad310e6f6758ad71998b?color=5a5a5a)
Die Grundlinie des Gegners ist 
vom Nullpunkt entfernt.
Abstand der gegenerischen Grundlinie und des Aufprallpunkts 
berechnen:
![\(\begin{array}[t]{rll}
g&=& 10,2\,\text{m}-8,86\,\text{m} \\[5pt]
&=& 1,34\,\text{m}
\end{array}\)](https://mathjax.schullv.de/457f342e00d44a1a34ec19816e9855e8fb14c1661c04aa69b43f052558915fb5?color=5a5a5a)
ln einer Entfernung von 
zur gegnerischen Grundlinie trifft der Ball auf dem Boden auf.
Abstand der eigenen Grundlinie und des Aufprallpunkts 
berechnen:
![\(\begin{array}[t]{rll}
e&=& 7,8\,\text{m} + 8,86\,\text{m} \\[5pt]
&=& 16,66\,\text{m}
\\[5pt]
&=& \underline{\underline{ 16,7\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/05be47dad39a20a4ca54d28a2f526d83c77c61fda2f993e1e3c6dda37c1bc5c9?color=5a5a5a)
ln einer Entfernung von 
zur eigenen Grundlinie trifft der Ball auf dem Boden auf.
Abschlussprüfung 2020
Lösung 7
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Eine mögliche Funktionsgleichung für das parabelförmige Teilstück bestimmen
Es gilt:
Somit gilt für den Vorfaktor 
![\(\begin{array}[t]{rll}
y&=&ax^2+c &\quad \scriptsize \mid\;-\,c \\[5pt]
ax^2&=&y-c &\quad \scriptsize \mid\;:x^2 \\[5pt]
a&=&\dfrac{y-c}{x^2} &\quad \scriptsize \mid\; c=0,2, \, B(2|1)\\[5pt]
a&=&\dfrac{1-0,2}{2^2} \\[5pt]
a&=&\dfrac{0,8}{4} \\[5pt]
a&=&0,2 \\[10pt]
\end{array}\)](https://mathjax.schullv.de/bc4938917352a4eaa4ae014817ca19c270bf485e46d819473cc3cd3702691c3f?color=5a5a5a)
Damit folgt 
Eine mögliche Funktionsgleichung für die Gerade bestimmen
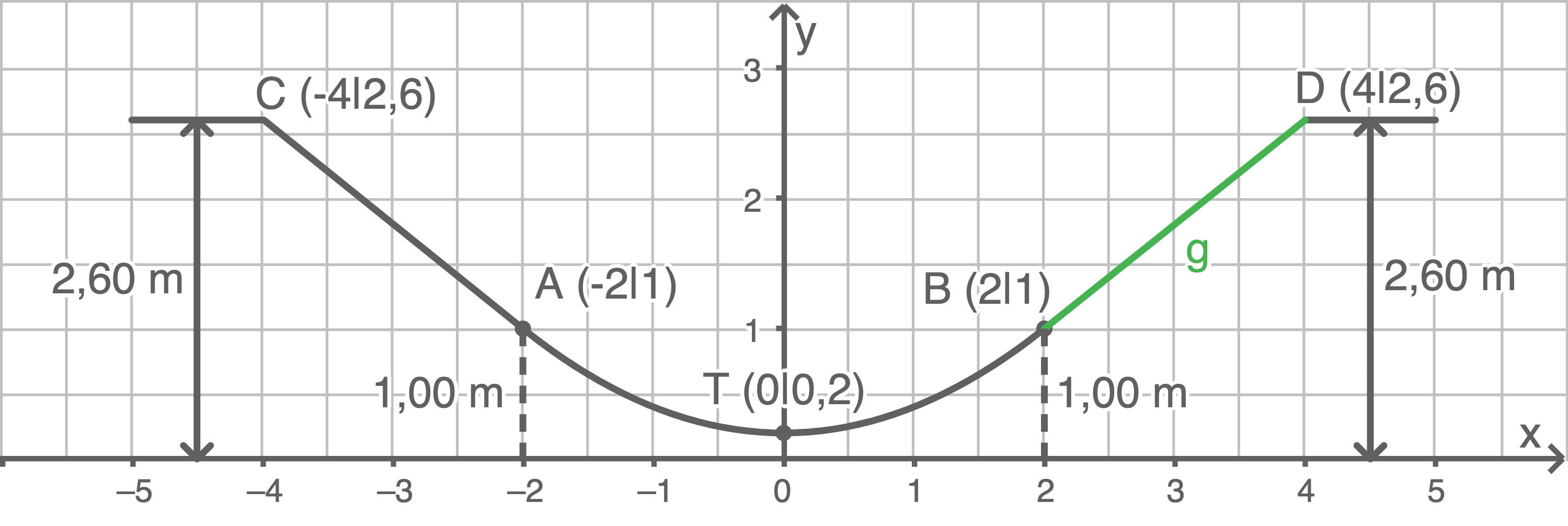
Abschlussprüfung 2019
- Allgemeine Funktionsgleichung:
- Scheitelpunkt
- Allgemeine Funktionsgleichung:
- Für den Steigungsfaktor
gilt:
- Also gilt für
Lösung 8
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Gleichung der zugehörigen Parabel angeben
Da die Koordinaten 
die höchste Flughöhe des Balls beschreiben, bilden sie den Scheitelpunkt.
Mithilfe der Scheitelpunktform hat die Parabel dann folgende vorläufige Gleichung:
Der Parameter 
kann nun mit Hilfe einer Punktprobe so bestimmmt werden, dass der Abschlagspunkt, also der Koordinatenursprung 
auf der Parabel liegt.
![\(\begin{array}[t]{rll}
p:y &=& a\cdot (x-95)^2 +25 \quad \scriptsize \mid\; (0\mid 0) \\[5pt]
0&=& a\cdot (0-95)^2 +25 \\[5pt]
0&=& a\cdot 9025 +25 \quad \scriptsize \mid\;-25 \\[5pt]
-25 &=& a\cdot 9025 \quad \scriptsize \mid\;:9025 \\[5pt]
-\dfrac{1}{361}&=& a
\end{array}\)](https://mathjax.schullv.de/cb6568127cf2c437c8c5c0f26f21231ae169e4c9be1994a76af02534ae65ad90?color=5a5a5a)
Eine Gleichung der zugehörigen Parabel lautet also 
In welchem Abstand überfliegt der Ball die Baumspitze?
Die Flughöhe des Balles an der Stelle des Baumes wird durch an der Stelle 45 beschrieben:
![\(\begin{array}[t]{rll}
y&=& -\dfrac{1}{361} \cdot (45-95)^2 +25 \\[5pt]
&=& 18,07 \\[5pt]
y&=& 18,1
\end{array}\)](https://mathjax.schullv.de/a84825f091f0b841dcb392033fd94ad20622c8d28e17e02b0172b211feda9996?color=5a5a5a)
Über dem Baum befindet sich der Ball also in einer Höhe von 
über dem Erdboden. Da der Baum 
hoch ist, überfliegt er die Baumspitze mit einem Abstand von ca. 
In welcher Entfernung vom Loch trifft der Ball auf der höher gelegenen Ebene auf?
Für die beiden Stellen ergibt sich also:
![\(\begin{array}[t]{rll}
x_1&=& 95-\sqrt{8303} \\[5pt]
&=& 3,88 \\[5pt]
x1&=& 3,9 \\[10pt]
x_2&=& 95+\sqrt{8303} \\[5pt]
&=& 186,12 \\[5pt]
x_2&=& 186,1
\end{array}\)](https://mathjax.schullv.de/53091b40fd4f93566c3716a5090674e61de8b9ff2c13937783edd2644ab3e9e6?color=5a5a5a)
beschreibt den ersten Punkt nach dem Abschlag, an dem der Ball eine Höhe von 2 m erreicht hat.
ist für diese Aufgabe relevant und gibt den gesuchten Auftreffpunkt an.
Das Loch befindet sich an der Stelle
180. Der Ball trifft also in einer Entfernung von ca. 
zum Loch auf der höher gelegenen Ebene auf.
Abschlussprüfung 2018
Mithilfe der Scheitelpunktform hat die Parabel
Das Loch befindet sich an der Stelle
Lösung 9
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Eine mögliche Funktionsgleichung für den Brückenbogen bestimmen
1. Schritt: Gegebene Punkte einzeichnen
2. Schritt: Funktionsgleichung bestimmen
Wegen 
gilt 
und 
einsetzen in 
![\(\begin{array}[t]{rll}
y &=& ax^2 + c \\[5pt]
0&=& a\cdot 275^2+100 \quad \scriptsize \mid\; -a\cdot 275^2 \\[5pt]
-275^2\cdot a &=& 100 \quad \scriptsize \mid\; : (-275^2) \\[5pt]
a&=& \underline{ -\dfrac{4}{3025}}
\end{array}\)](https://mathjax.schullv.de/8ba7040cb95b48604c257b7ee7f1e1a7e358221c44ddcaf4690d667ca257f70f?color=5a5a5a)
Eine mögliche Funktionsgleichung für den Brückenbogen lautet also:
Länge der Fahrbahn innerhalb des Brückenbogens berechnen
Der Verlauf der Fahrbahn kann durch die Gerade mit der Gleichung 
beschrieben werden.
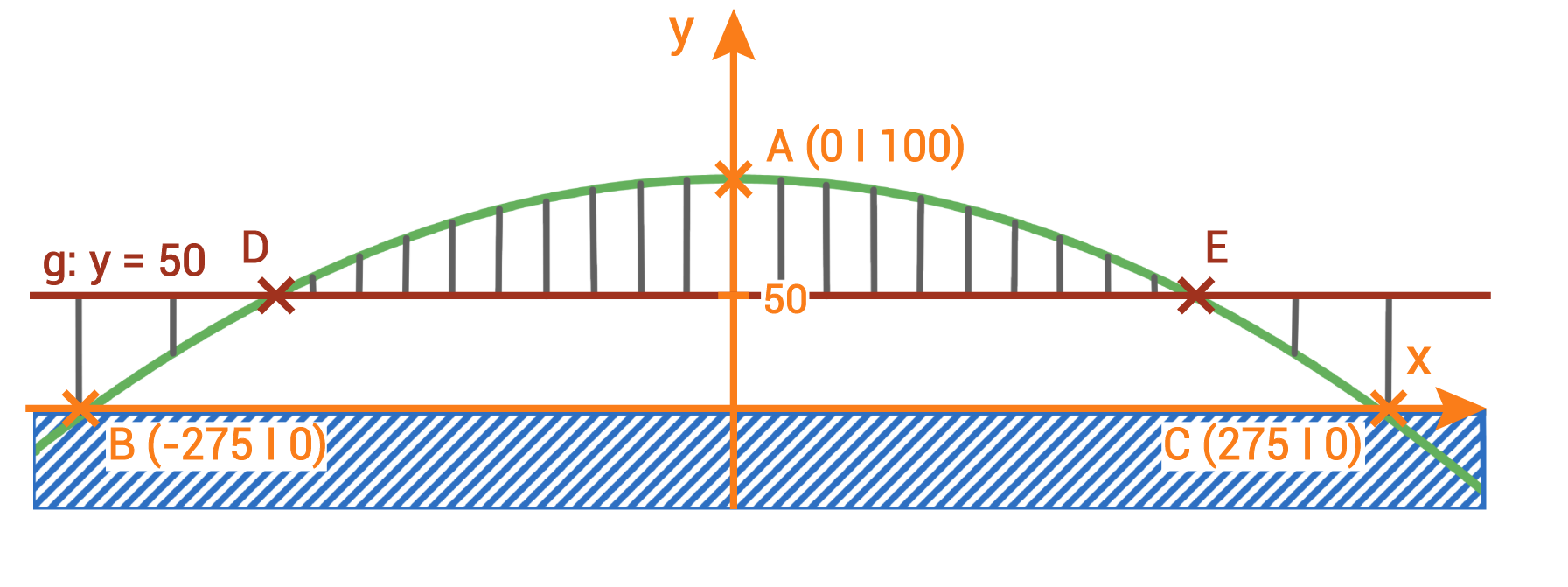
![\(\begin{array}[t]{rll}
50&=&-\frac{4}{3025}x^2+100 &\quad \scriptsize \mid\; +\frac{4}{3025}x^2 ;-50 \\[5pt]
\frac{4}{3025}x^2&=& 50 &\quad \scriptsize \mid\; \cdot \frac{3025}{4} \\[5pt]
x^2&=& \frac{75625}{2} &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
x_{1/2}&=& \underline{ \pm 194,45}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/3f588d45b0ec284f4255e9fb0247dbe326e2d0ee1f04c8d626baa3b8a26f6431?color=5a5a5a)
Damit gilt für die Länger der Fahrbahn 
:
![\(\begin{array}[t]{rll}
l&=& |x_1|+|x_2| \\[5pt]
&=& |194,45|+|-194,45| \\[5pt]
&=& \underline{\underline{ 388,9\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/b3b80f98daf2093dd17b195e523080f77fa5724cc866132490f6981dbeab5676?color=5a5a5a)
Somit beträgt die Länge der Fahrbahn 
Abschlussprüfung 2017
- Die
- Die
- Der höchste Punkt der Brücke liegt
über der Wasseroberfläche. Er kann mit
- Die Brücke ist
lang. Die beiden Schnittpunkte der Parabel mit der
Lösung 10
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Eine mögliche Gleichung der Parabel angeben
Es gilt:
Somit gilt für den Vorfaktor
![\(\begin{array}[t]{rll}
y&=&ax^2+c &\quad \scriptsize \mid\;-\,c \\[5pt]
ax^2&=&y-c &\quad \scriptsize \mid\;:x^2 \\[5pt]
a&=&\dfrac{y-c}{x^2} &\quad \scriptsize \mid\; c=3,6, \, D(-2,8|2)\\[5pt]
a&=&\dfrac{2-3,6}{(-2,8)^2} \\[5pt]
a&=& \underline{ -0,20}
\end{array}\)](https://mathjax.schullv.de/37e3af4b2974c31b68910e5d7d3afe93e5240317a140d14f3af3b31e84d04adb?color=5a5a5a)
Eine mögliche Parabel lautet also 
Trifft Theo bei diesem Wurf direkt in den Korb?
1. Schritt: Koordinaten des Korbringmittelpunkts ermitteln
2. Schritt: Punktprobe durchführen
![\(\begin{array}[t]{rll}
y &=& -0,2x^2+3,6\quad \scriptsize \mid\; K(1,9|3,5)\text{ einsetzen}\\[5pt]
3,05 &=& -0,2 \cdot (1,9)^2+3,6 \\[5pt]
3,05 &\neq& 2,878\\[5pt]
\end{array}\)](https://mathjax.schullv.de/4c313d91118d6caeca14037026e4cbb0f52786953be49573fa98ead66279a0c9?color=5a5a5a)
Der Punkt liegt nicht auf der Parabel. Theo trifft bei diesem Wurf also nicht in den Korb.
Berührt Dennis den Ball, ohne hochzuspringen?
1. Schritt: Koordinaten des Punktes ermitteln, den Dennis mit ausgestreckten Händen und ohne hochzuspringen, erreicht
2. Schritt: Flughöhe des Balls bei 
berechnen
![\(\begin{array}[t]{rll}
y &=& -0,2x^2+3,6\quad \scriptsize \mid\; x_\text{D}=-2,2\\[5pt]
y &=& -0,2 \cdot (-2,2)^2+3,6 \\[5pt]
y&=& \underline{ 2,63}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/67b9c3be27a47362da53de62ab9db9afe20ddec114303c9a4605a39ec08a7912?color=5a5a5a)
Dennis kann den Ball mit ausgestreckten Händen nicht berühren, da der Ball 
höher fliegt.
Abschlussprüfung 2016
- Der höchste Punkt (= Scheitelpunkt) liegt bei
- Der Abwurfpunkt liegt bei
links vom Ursprung
Lösung 11
a)
Die Teilaufgabe a) wurde in das Thema "Wahrscheinlichkeiten" eingeordnet.
b)
Davids Stoßweite berechnen
1. Schritt: Parabelgleichung aufstellen
Die Parabelgleichung von Davids Kugelstoß lautet also 
2. Schritt: Nullstellen berechnen
![\(\begin{array}[t]{rll}
0&=& -0,09\cdot x^2+3,9 \quad \scriptsize \mid\; -3,9\\[5pt]
-3,9&=&-0,09\cdot x^2 \quad \scriptsize \mid\; :(-0,09) \\[5pt]
\dfrac{3,9}{0,09}&=& x^2\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x&=& \underline{ \pm 6,58}
\end{array}\)](https://mathjax.schullv.de/4d660a5f21cd32ca0847253b3107422d77108db4e0a299293c23dd31e2b5b76c?color=5a5a5a)
3. Schritt: Davids Stoßweite 
berechnen
![\(\begin{array}[t]{rll}
W_D&=& 6,58\,\text{m}- (-4,30\,\text{m}) &\quad \scriptsize \\[5pt]
&=& \underline{ \underline{ 10,9\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/02ce29a8a918bd88d3a9ffd0df9d1267fe3aff1b6ff505b0037536eb9023ba1c?color=5a5a5a)
Tims Stoßweite berechnen
1. Schritt: Koordinaten des Abstoßpunkts berechnen
![\(\begin{array}[t]{rll}
y&=& -\dfrac{1}{10}\cdot x^2+3,5 \quad \scriptsize \mid\; (x\mid 1,90)\\[5pt]
1,90&=& -\dfrac{1}{10}\cdot x^2+3,5\quad \scriptsize \mid\; -3,5\\[5pt]
-1,60&=& -\dfrac{1}{10}\cdot x^2\quad \scriptsize \mid\; :(-\dfrac{1}{10}) \\[5pt]
16&=& x^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
x&=& \pm 4
\end{array}\)](https://mathjax.schullv.de/2d40541ebd7ec478c08fd8ffbf93c4c20b52daa1ada869a8b1fb1a3e75334494?color=5a5a5a)
Da der Abstoß links neben der -Achse erfolgt ist, sind die Koordinaten 
2. Schritt: Nullstellen berechnen
![\(\begin{array}[t]{rll}
0&=& -\dfrac{1}{10}\cdot x^2+3,5 \quad \scriptsize \mid\;-3,5 \\[5pt]
-3,5&=& -\dfrac{1}{10}\cdot x^2 \quad \scriptsize \mid\; :(-\dfrac{1}{10})\\[5pt]
35&=& x^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x&=& \underline{ \pm 5,92}
\end{array}\)](https://mathjax.schullv.de/546bec62038c8f1c977313382b75188ddf385e4bea64122cb1a561e5dd526c28?color=5a5a5a)
3. Schritt: Tims Stoßweite 
berechnen
![\(\begin{array}[t]{rll}
W_T&=& 5,92\,\text{m} - (-4\,\text{m}) &\quad \scriptsize \\[5pt]
&=& \underline{\underline{ 9,9\,\text{m}}}
\end{array}\)](https://mathjax.schullv.de/7e2d33263b4fff1830fd28883f3f763ad8f6f48b63cc00ba1079ffc79ba589e9?color=5a5a5a)
Stoßweiten vergleichen
![\(\begin{array}[t]{rll}
W&=& 10,9\,\text{m} -9,9\,\text{m} &\quad \scriptsize \\[5pt]
&=& \underline{ 1\,\text{m}}
\end{array}\)](https://mathjax.schullv.de/835408a7a4cd4f1c2a87c76065351811e0ed3fdc4e720b3afa7518dce9b8562d?color=5a5a5a)
David hat seine Kugel also 
weiter als Tim gestoßen.
Abschlussprüfung 2015