Geometrie im Raum
Aufgabe 1
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
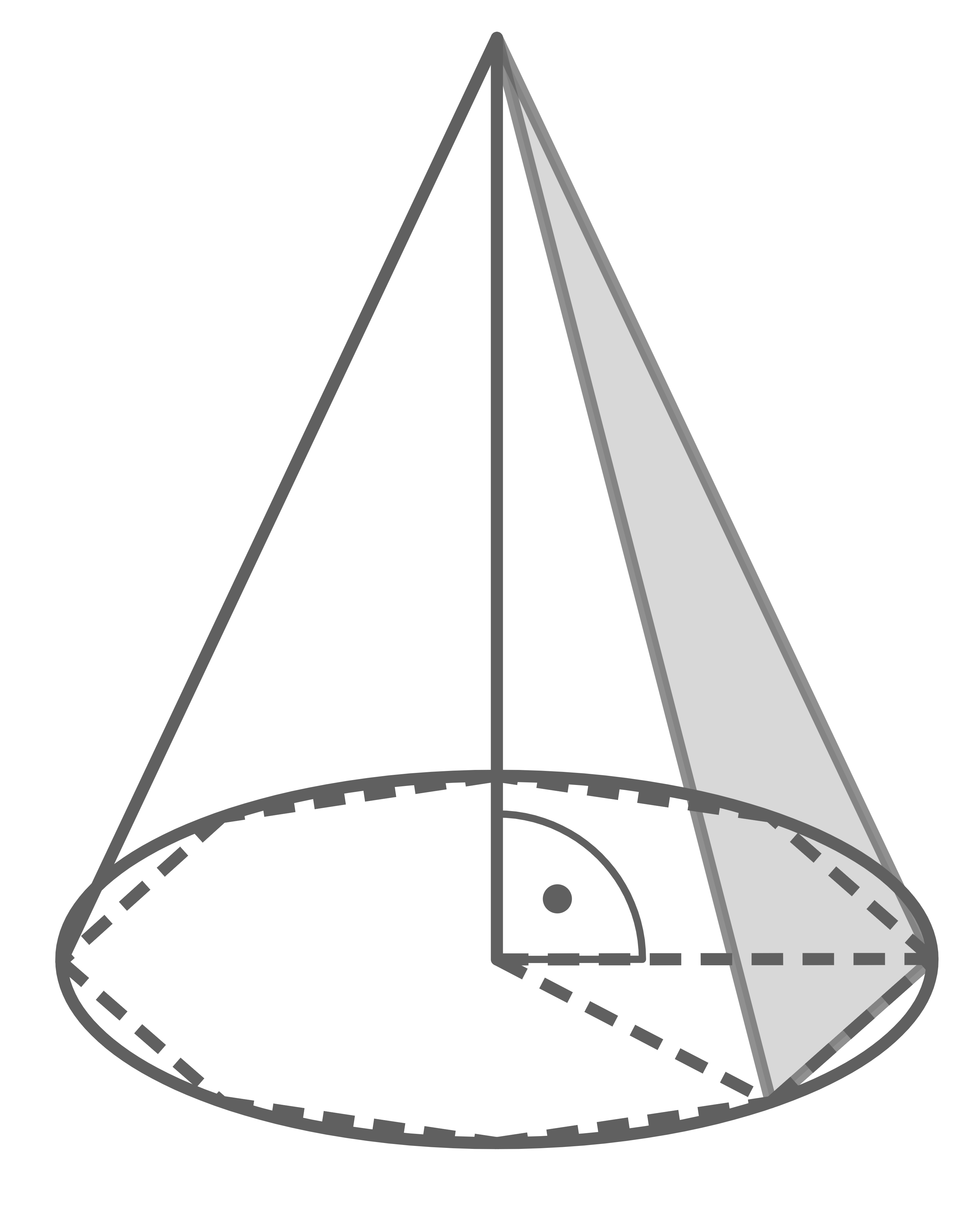
Die Abbildung zeigt den Achsenschnitt eines zusammengesetzten Körpers und den Parallelschnitt einer quadratischen Pyramide.
Der zusammengesetzte Körper besteht aus einer Halbkugel und einem Kegel. Es gilt:![\(\begin{array}[t]{rll}
s & =& 14,4 \mathrm{~cm} \\
\delta & =& 42,0^{\circ} \\
h_{\text {ges }} & =& h_{\text {Pyr }}
\end{array}\)](https://mathjax.schullv.de/cce294c1fecb55312e9c1199aa5392433c17466f98bfc99b7b425376404e0b1f?color=5a5a5a)
Der zusammengesetzte Körper besteht aus einer Halbkugel und einem Kegel. Es gilt:
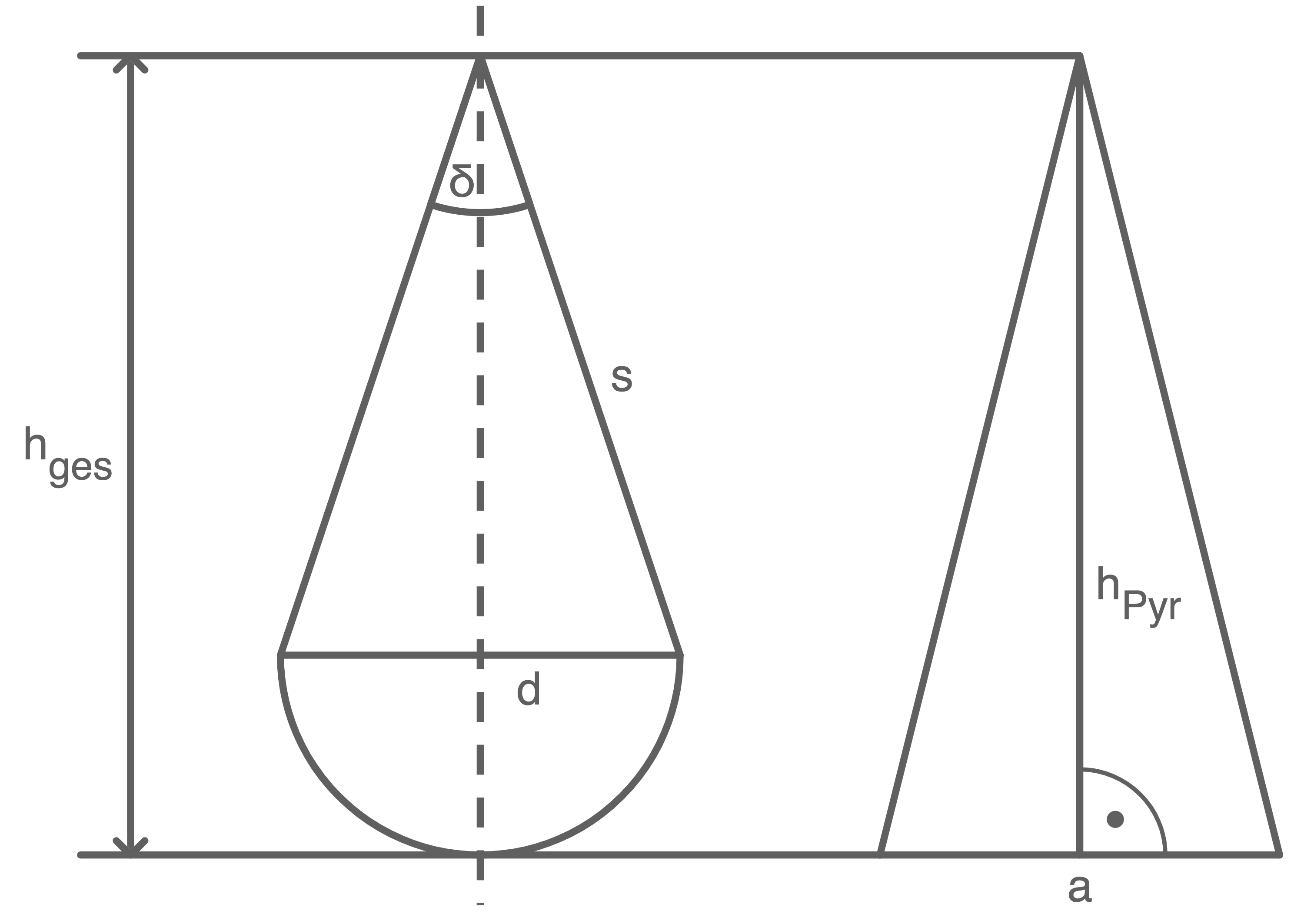
- Berechne die Differenz der Oberflächeninhalte der beiden Körper.
(5 P)
Aufgabe 2
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
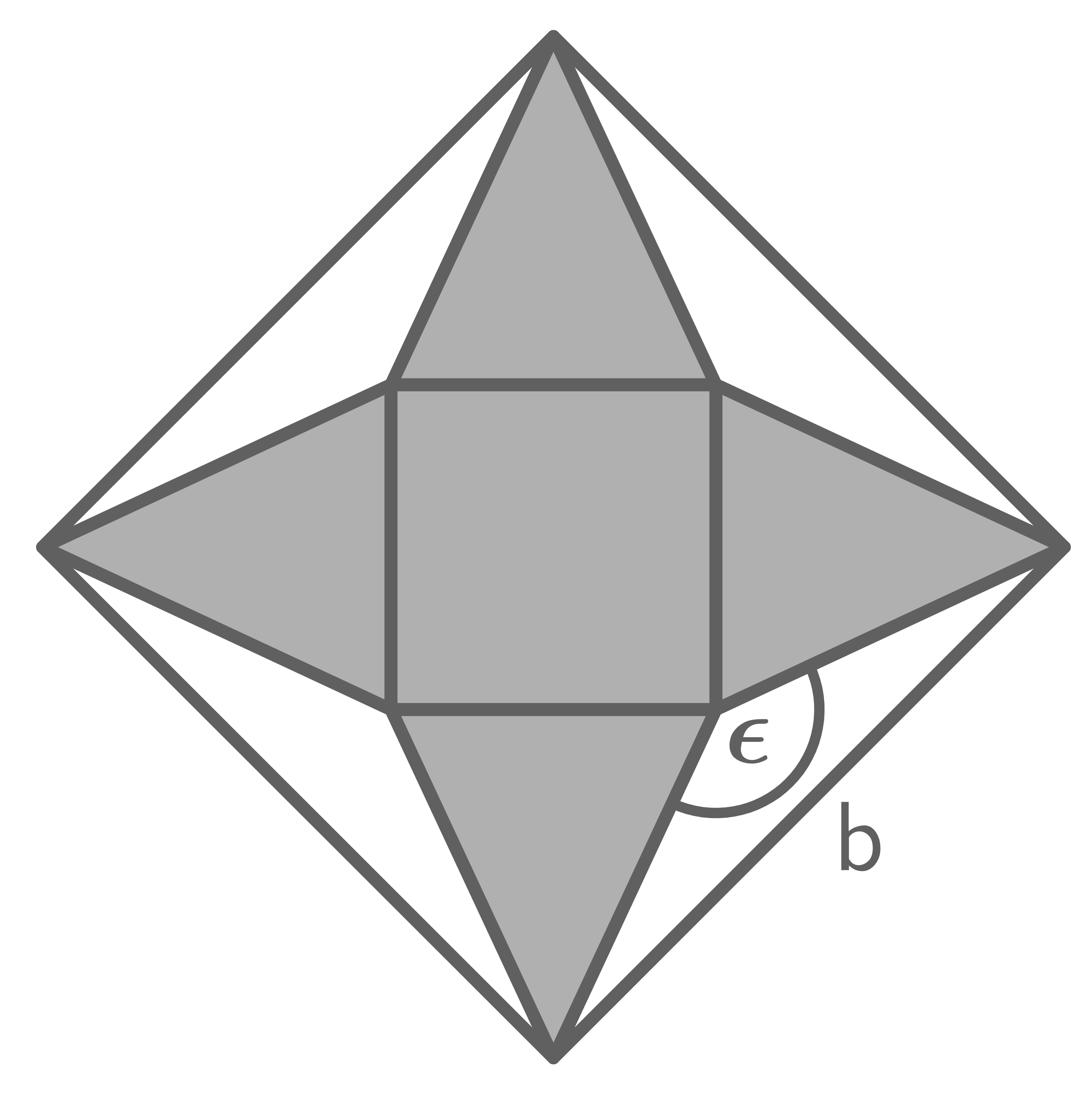
Aus einem Kegel wird eine regelmäßige fünfseitige Pyramide herausgearbeitet (siehe Abbildung).
Die Eckpunkte der Grundfläche der fünfseitigen Pyramide liegen auf der Kreislinie der Grundfläche des Kegels.
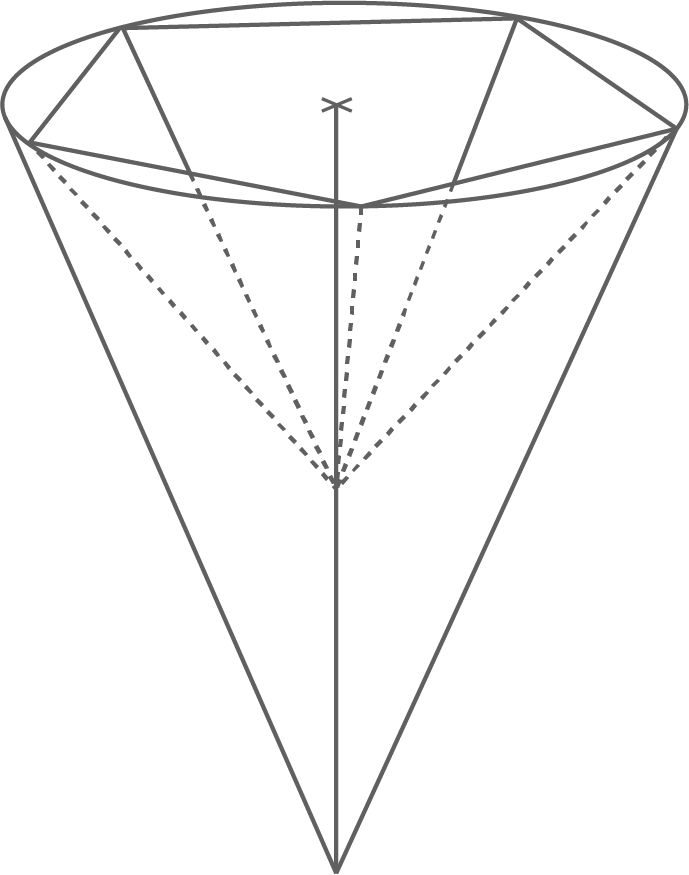Es gilt:
(Grundkante der Pyramide)
(Körperhöhe des Kegels)
(Körperhöhe der Pyramide)
Um wie viele
unterscheiden sich die Inhalte der Mantelflächen des Kegels und der Pyramide?
Die Eckpunkte der Grundfläche der fünfseitigen Pyramide liegen auf der Kreislinie der Grundfläche des Kegels.
Um wie viele
(5 P)
Aufgabe 3
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
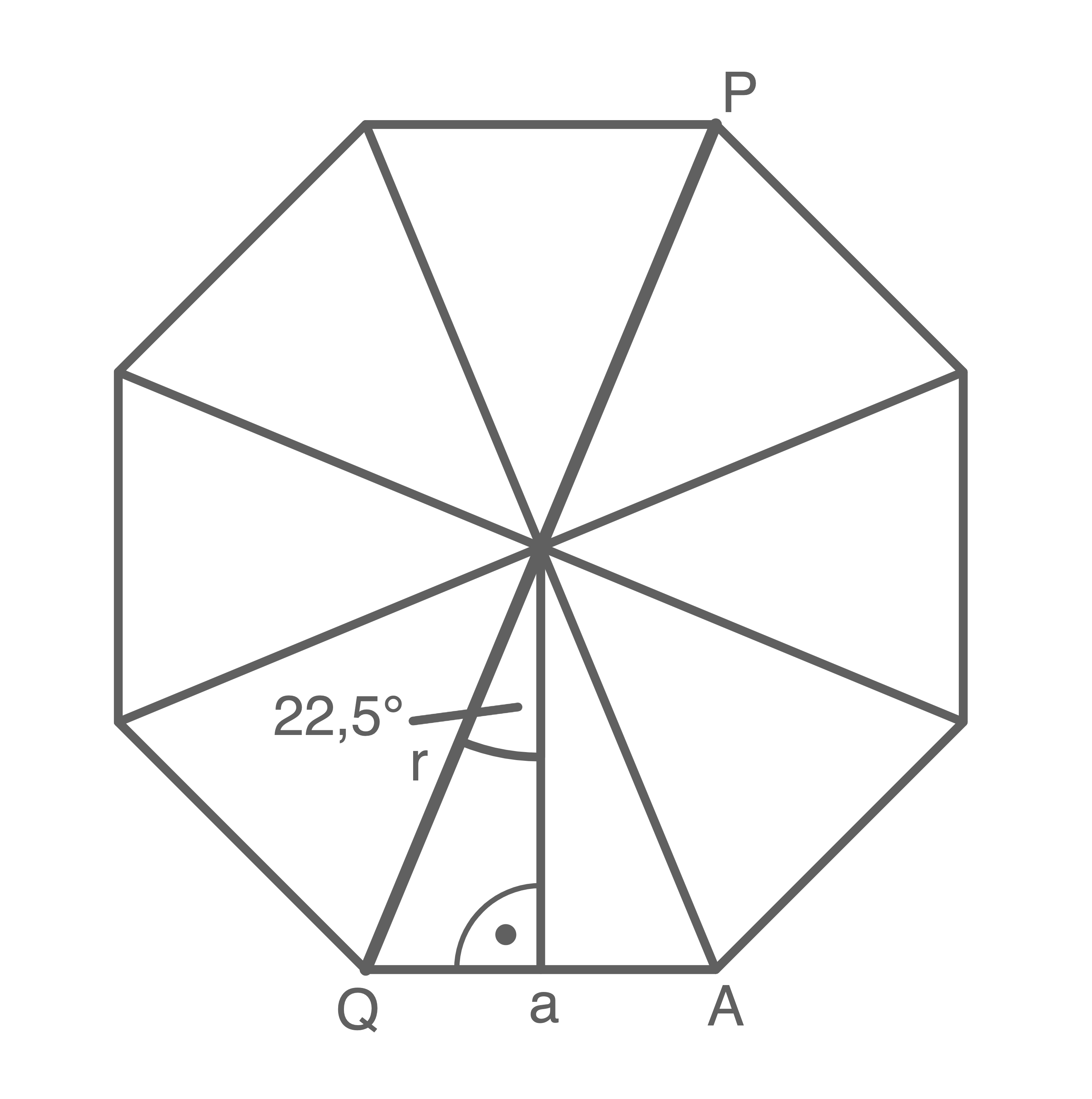
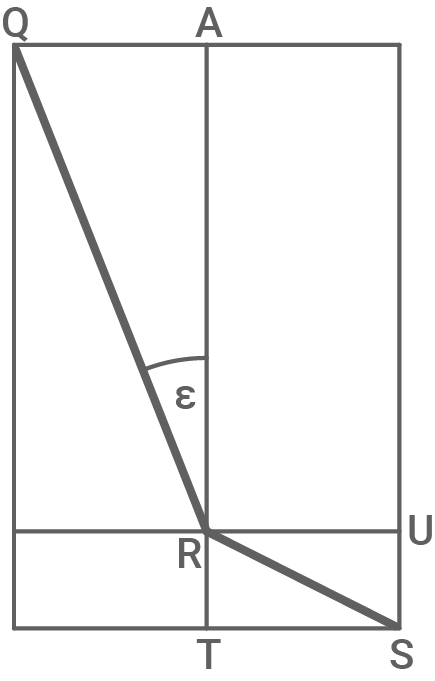
Auf einem regelmäßigen achtseitigen Prisma liegt der Streckenzug 
mit der Länge 
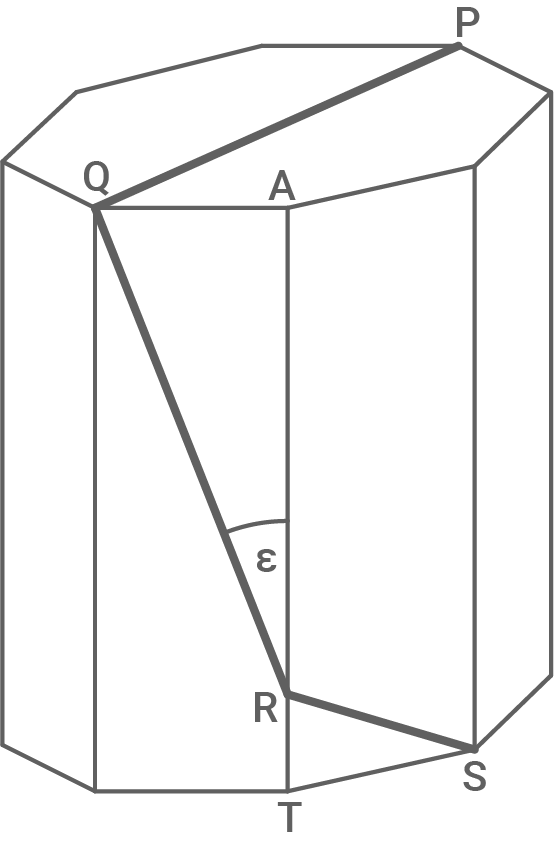Es gilt:
![\(\begin{array}[t]{rll}
\overline{AR}&=&14,2\,\text{cm}\\
\varepsilon&=&23,0^\circ
\end{array}\)](https://mathjax.schullv.de/86bace01aeef13653cea60bb3f7cc0d884d7030b051c516697fe275db44c6592?color=5a5a5a)
Berechne die Höhe des achtseitigen Prismas.
(5 P)
Aufgabe 4
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Ein zusammengesetzter Körper besteht aus einem regelmäßigen Fünfecksprisma mit aufgesetzter regelmäßiger fünfseitiger Pyramide.
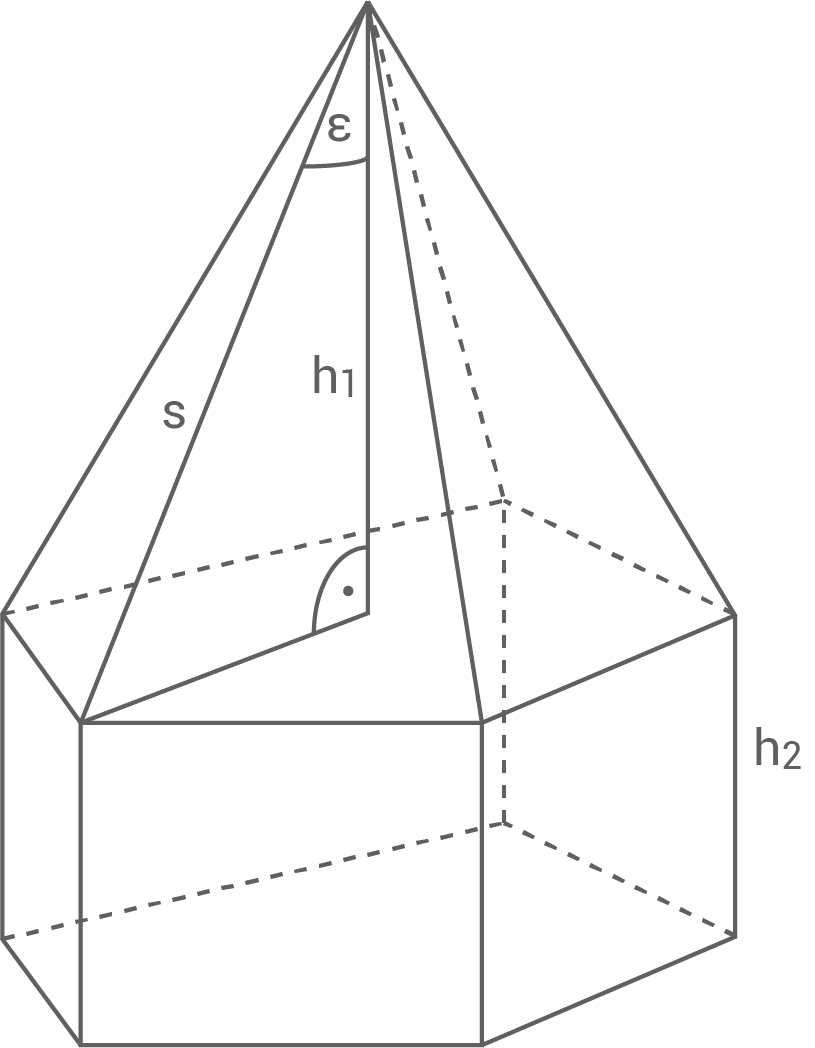Es gilt:
Berechne den Oberflächeninhalt des zusammengesetzten Körpers.
(5 P)
Aufgabe 5
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
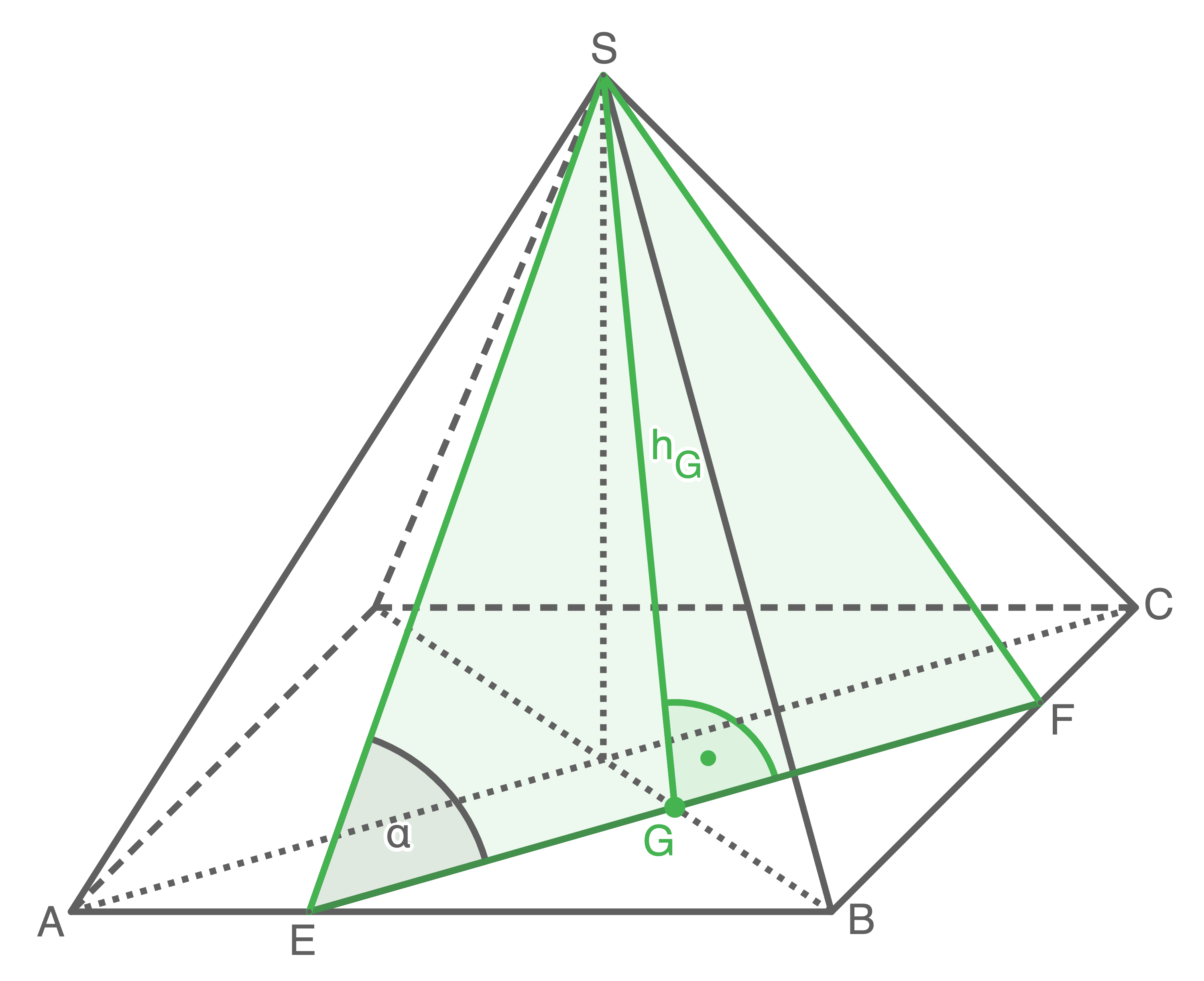
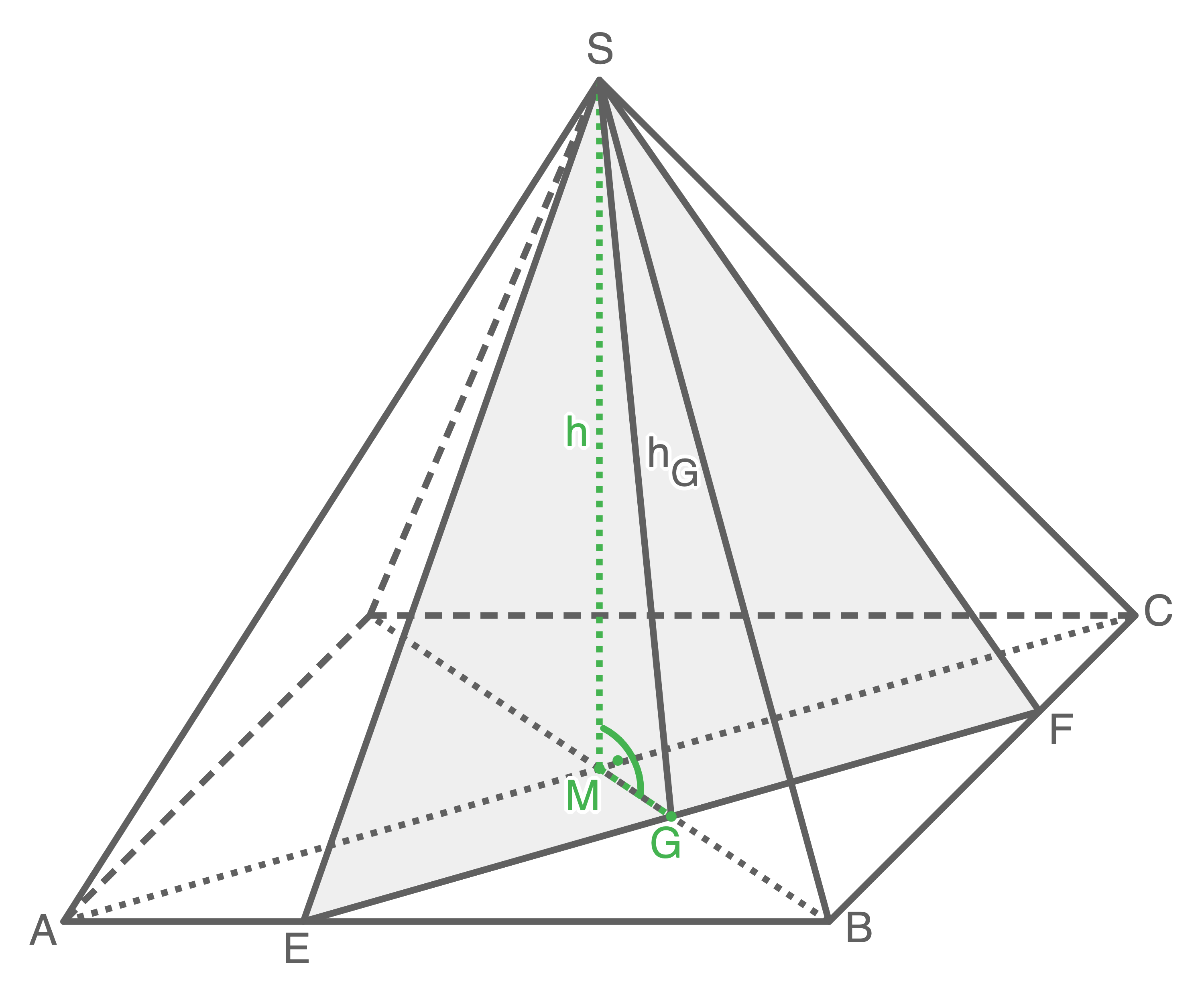
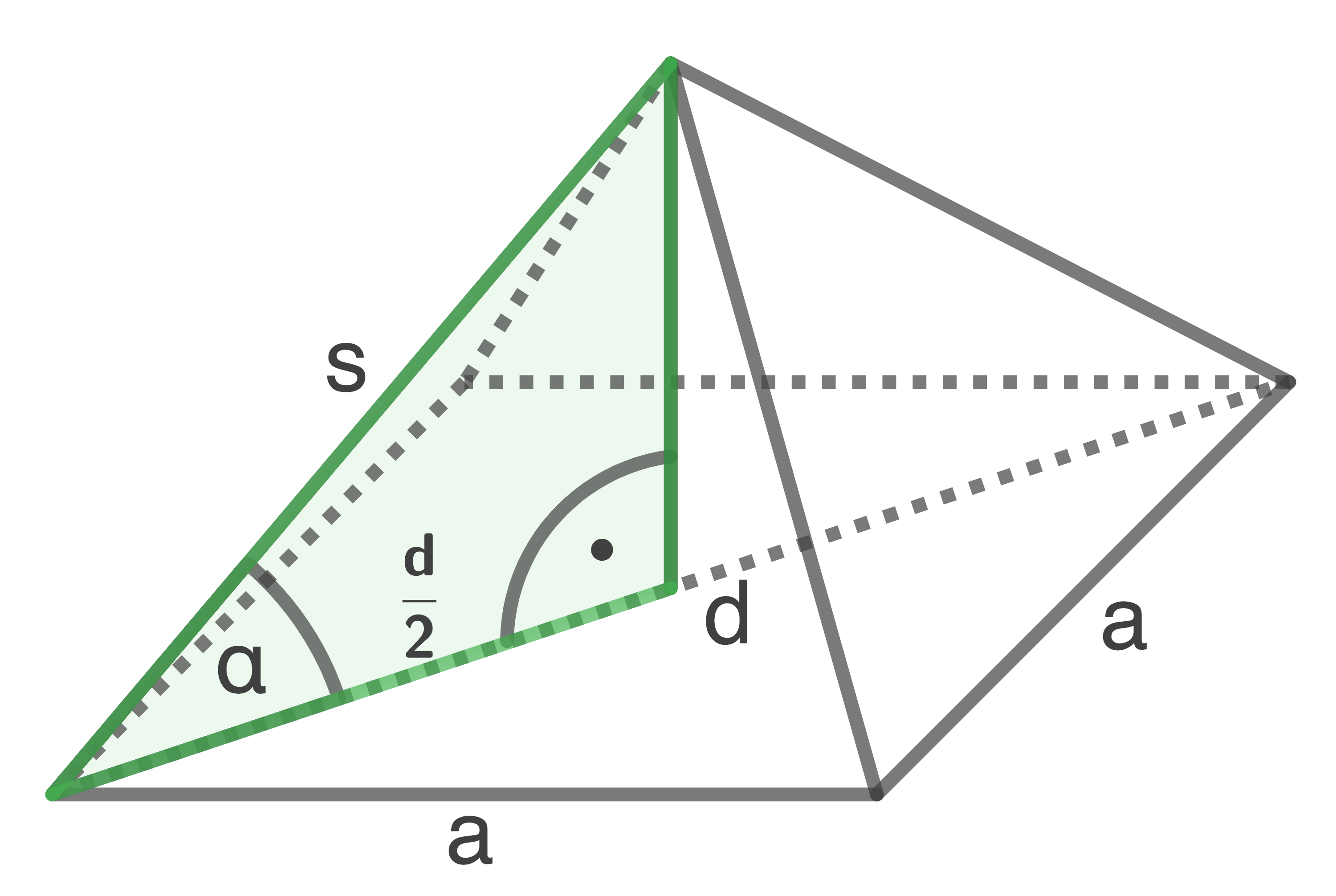
In einer quadratischen Pyramide liegt das gleichschenklige Dreieck 
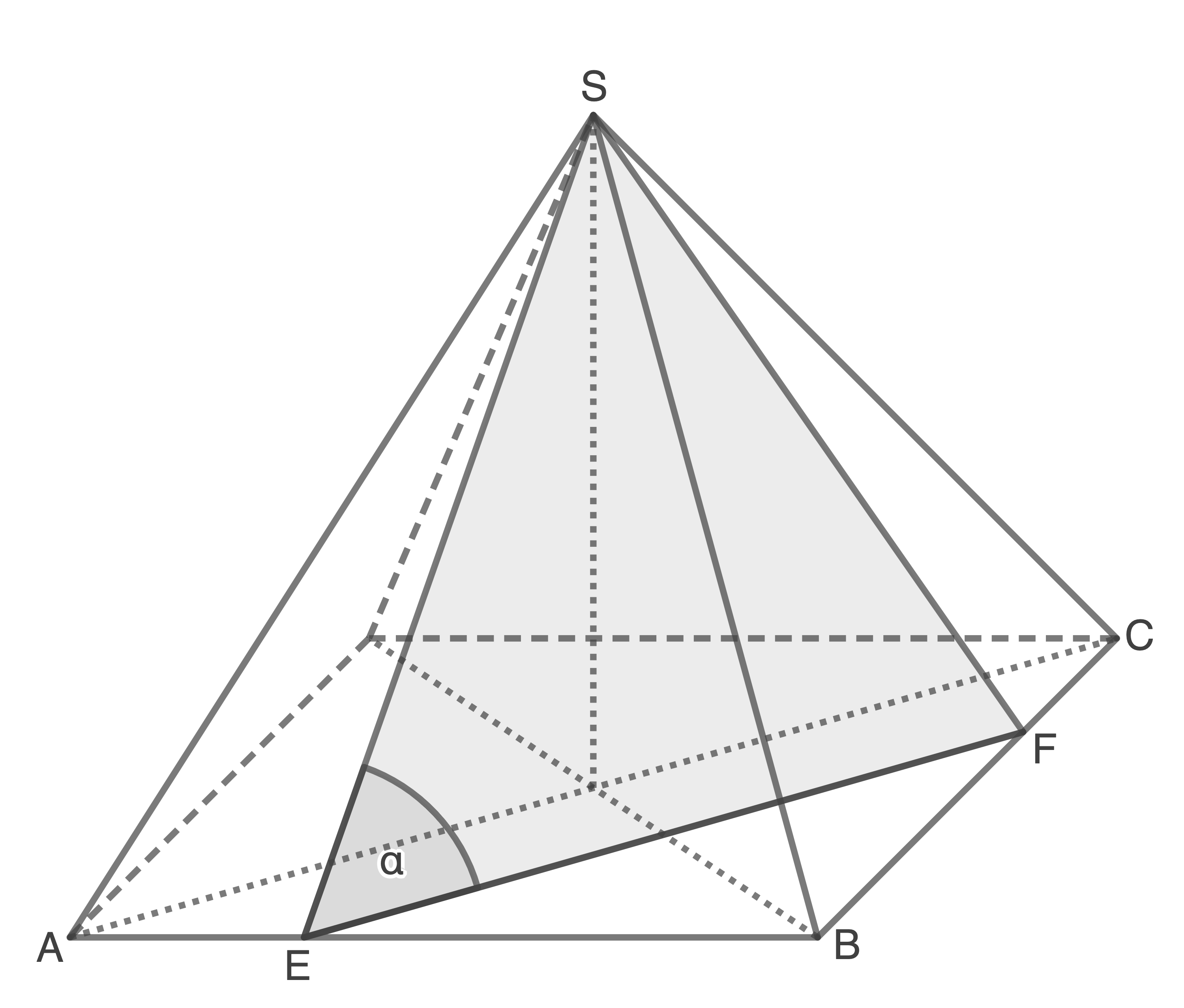Es gilt:
- Berechne den Flächeninhalt des Dreiecks
- Berechne das Volumen der quadratischen Pyramide.
Aufgabe 6
a)
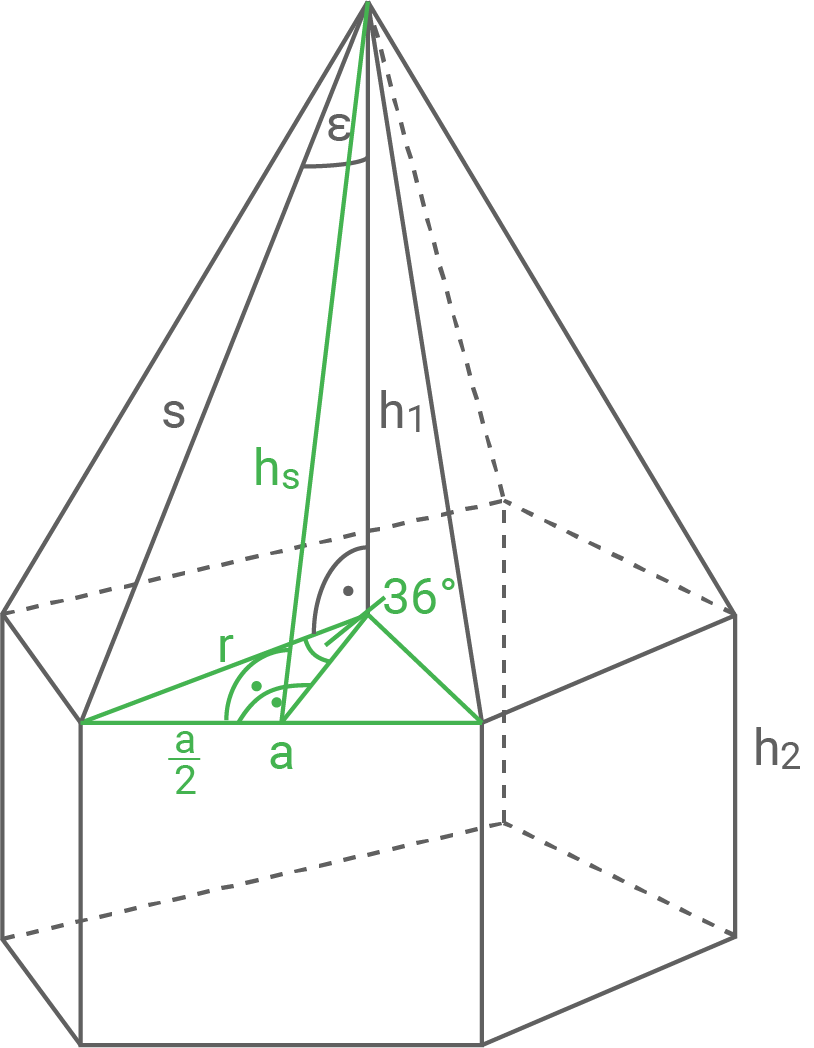
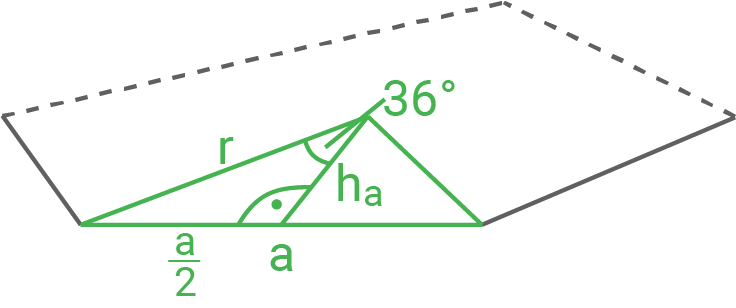
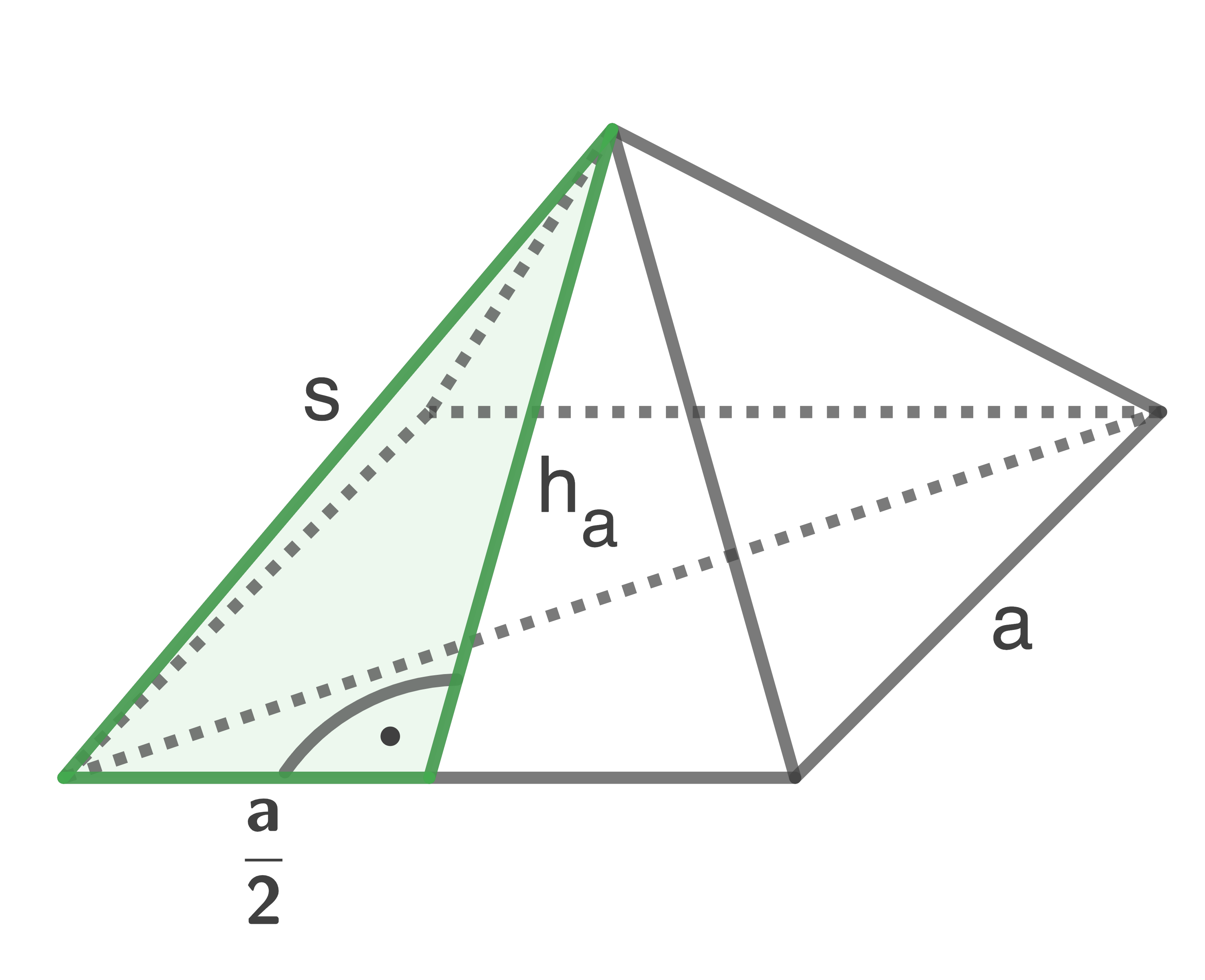
Die Abbildung zeigt einen zusammengesetzten Körper, der aus einem Quader mit aufgesetzter Pyramide besteht.
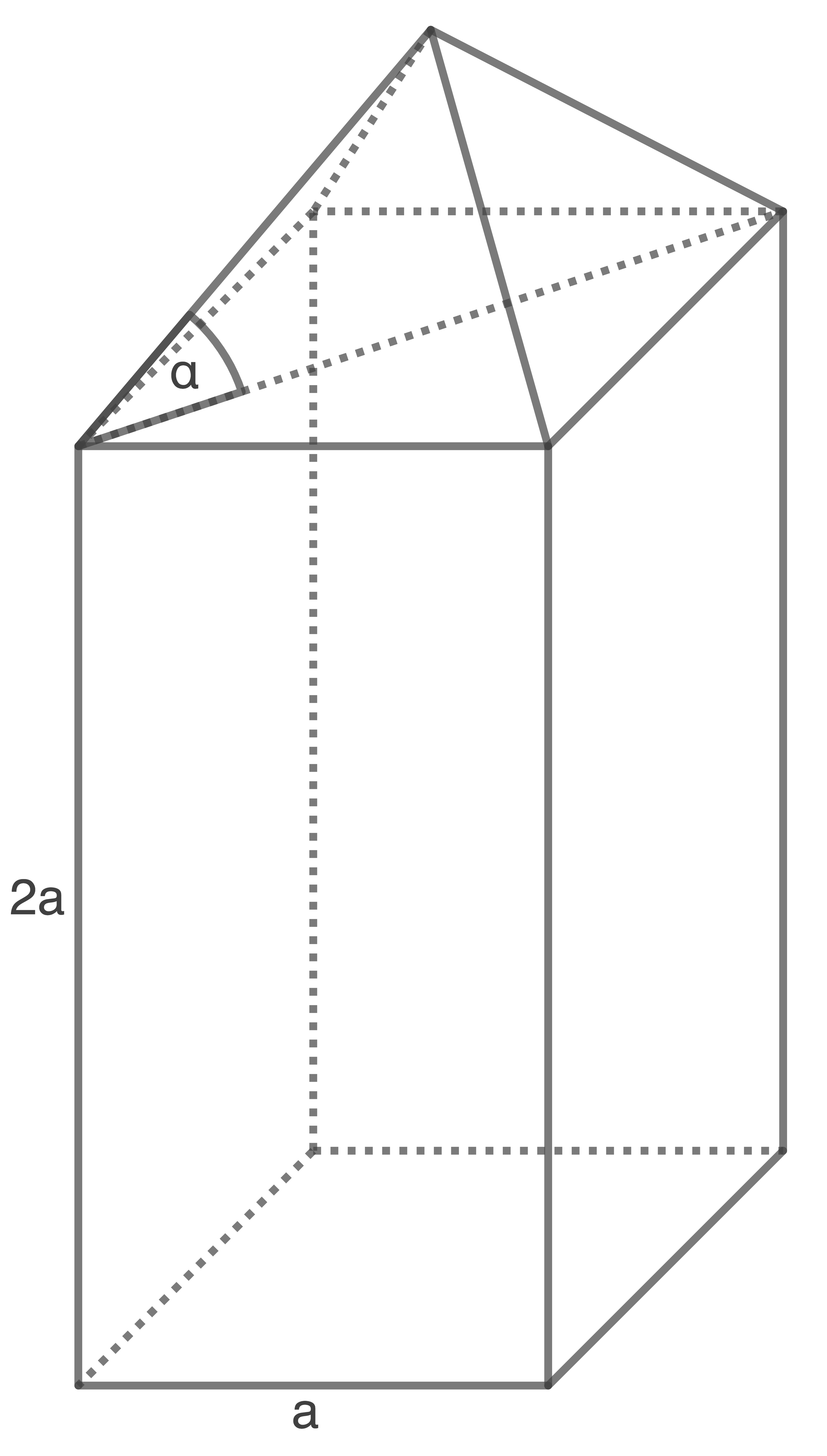Es gilt:
(Skizze nicht maßstäblich)
(5,5 P)
b)
Die Teilaufgabe b) wurde in kein Thema eingeordnet.
Aufgabe 7
a)
Aus einem großen Zylinder ist ein weiterer schmalerer Zylinder herausgefräst worden.
Es gilt:
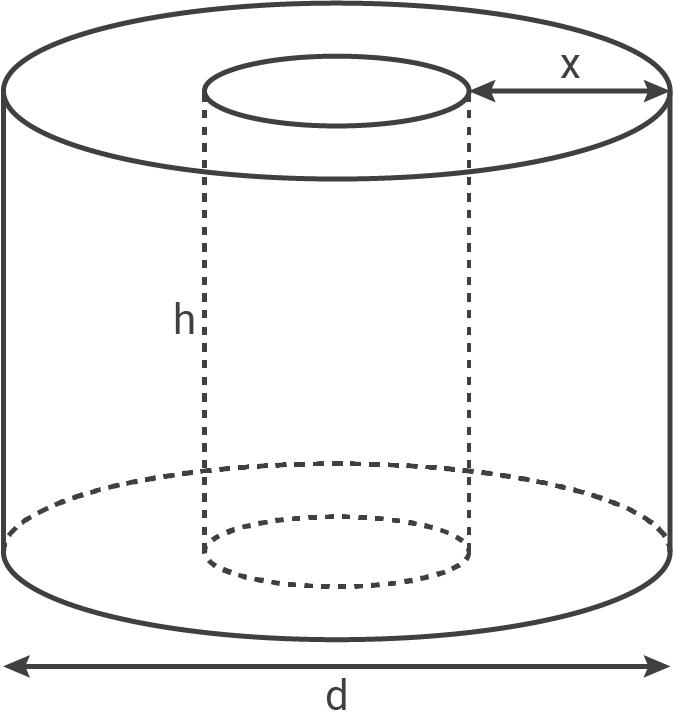
(5 P)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Aufgabe 8
a)
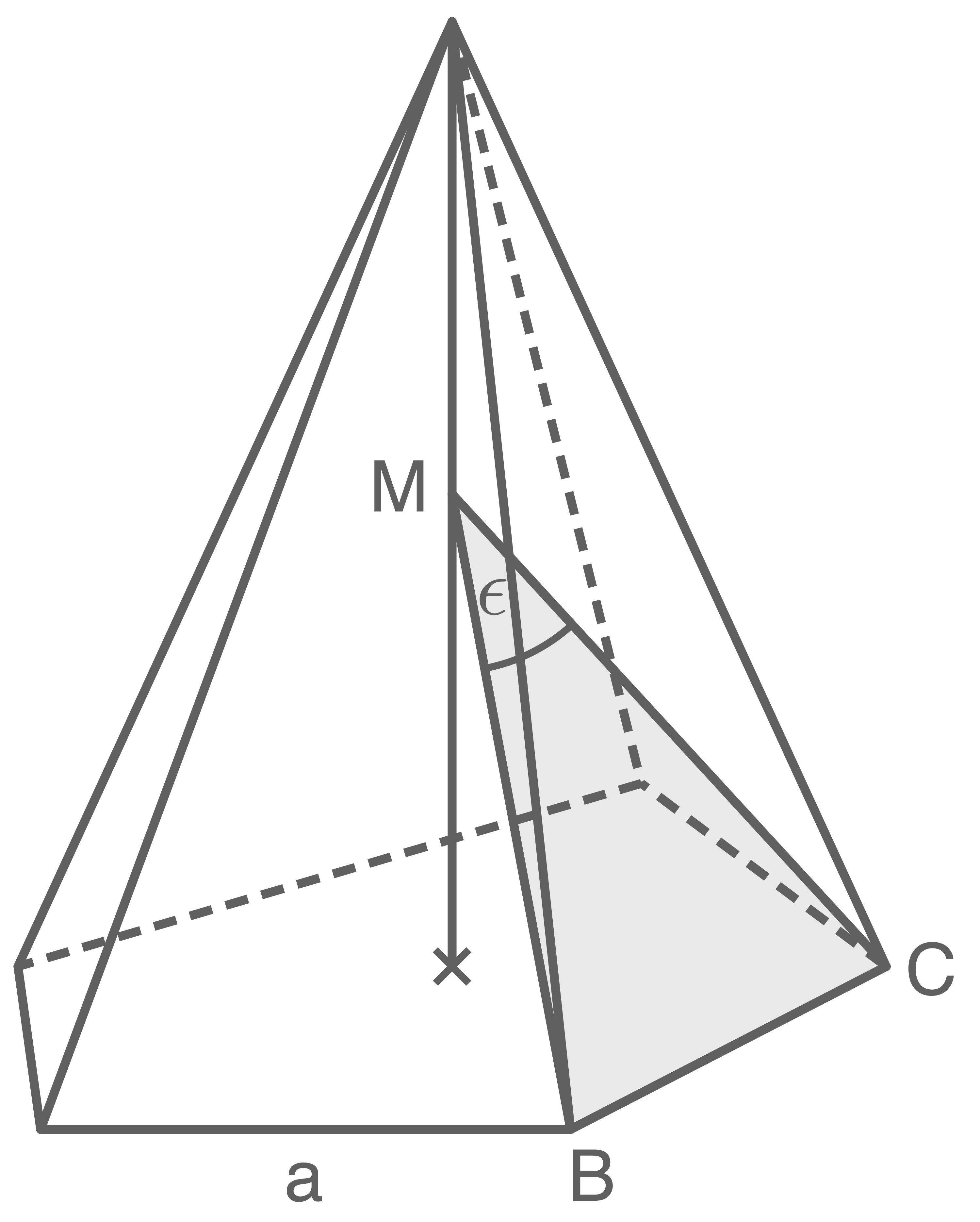
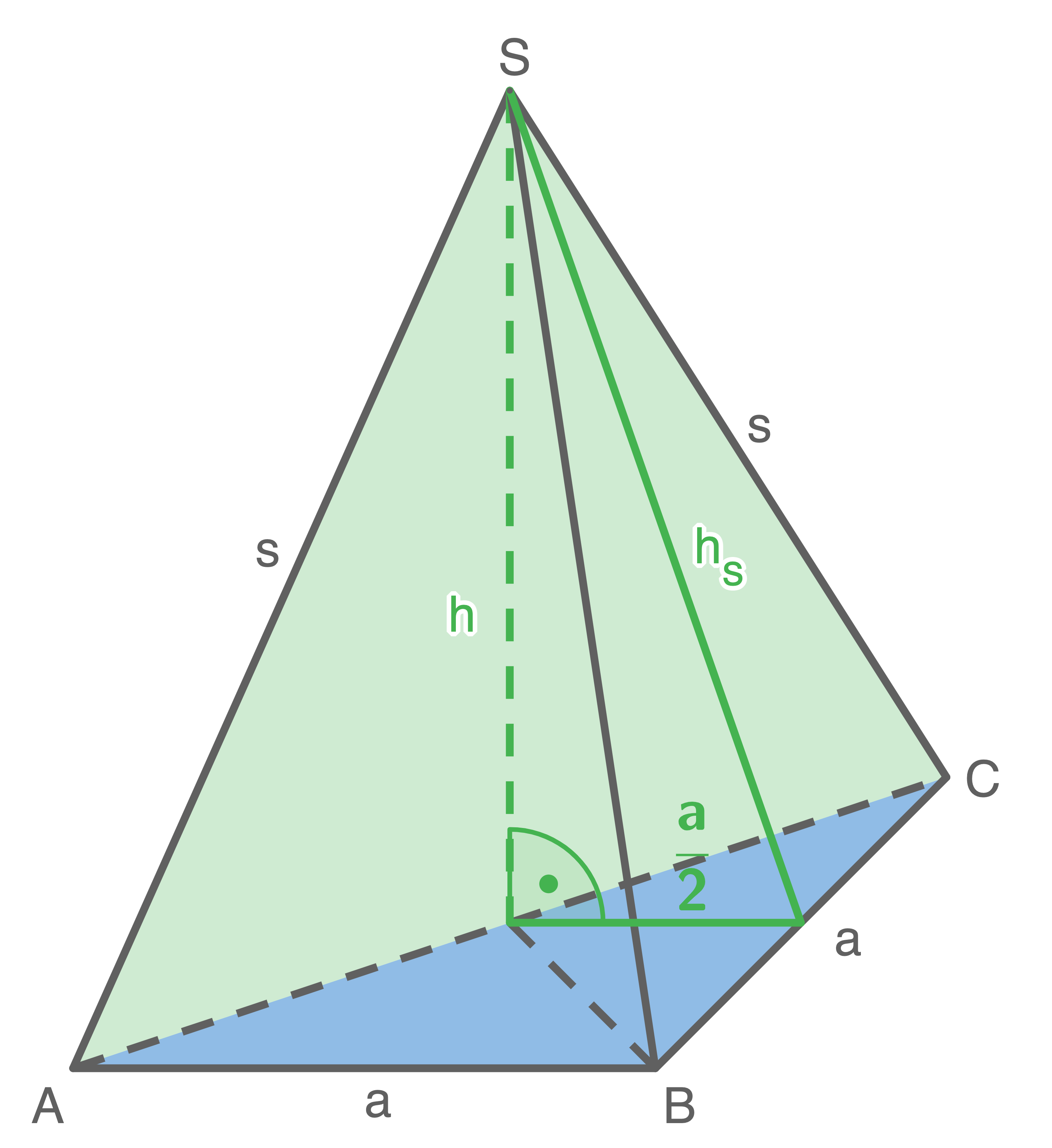
Von einer regelmäßigen achtseitigen Pyramide sind bekannt:
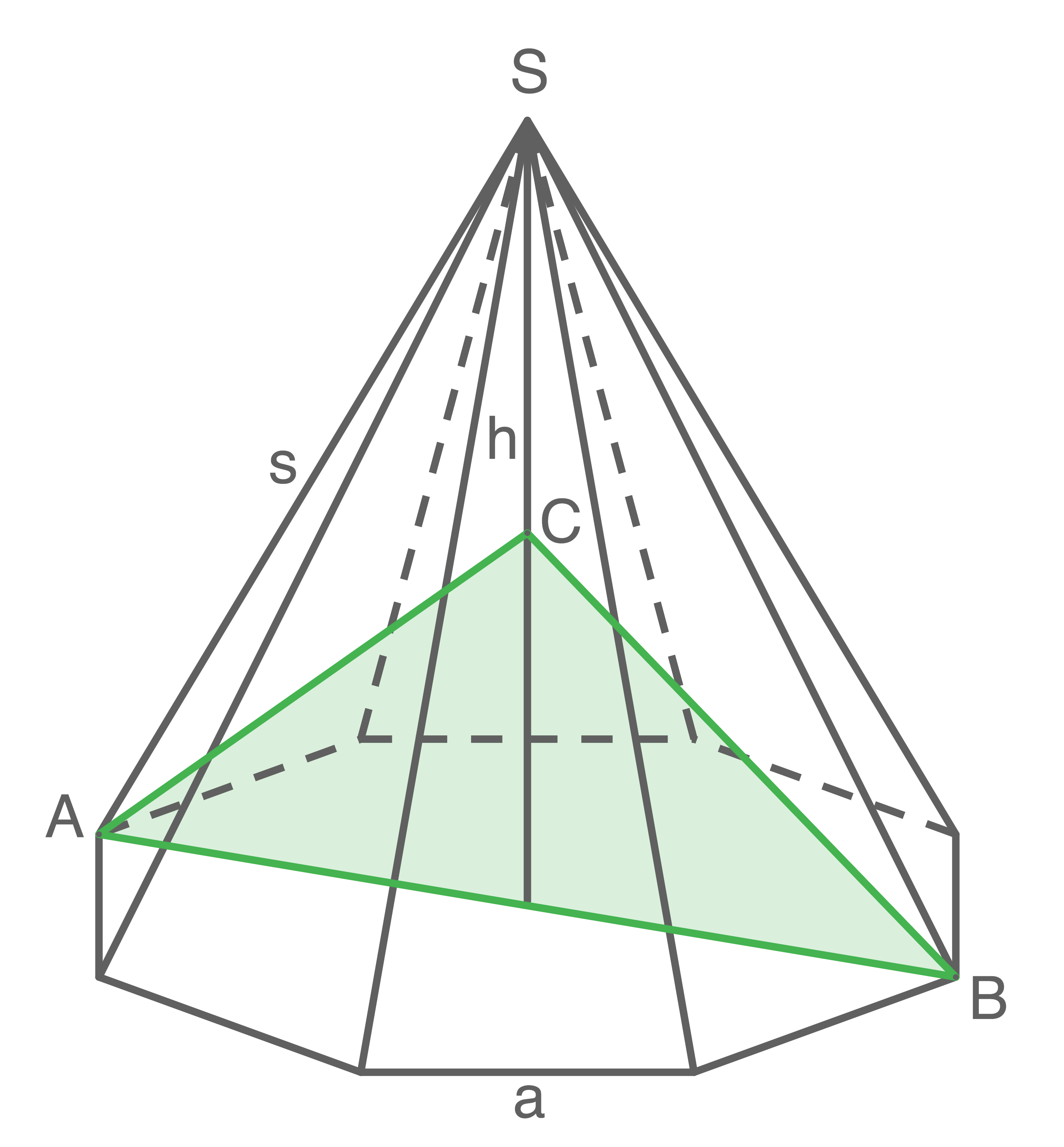Der Punkt 
liegt auf der Höhe 
der Pyramide. Das Dreieck 
soll den gleichen Flächeninhalt haben wie eines der Manteldreiecke.
Berechne die Länge von 
(5,5 P)
b)
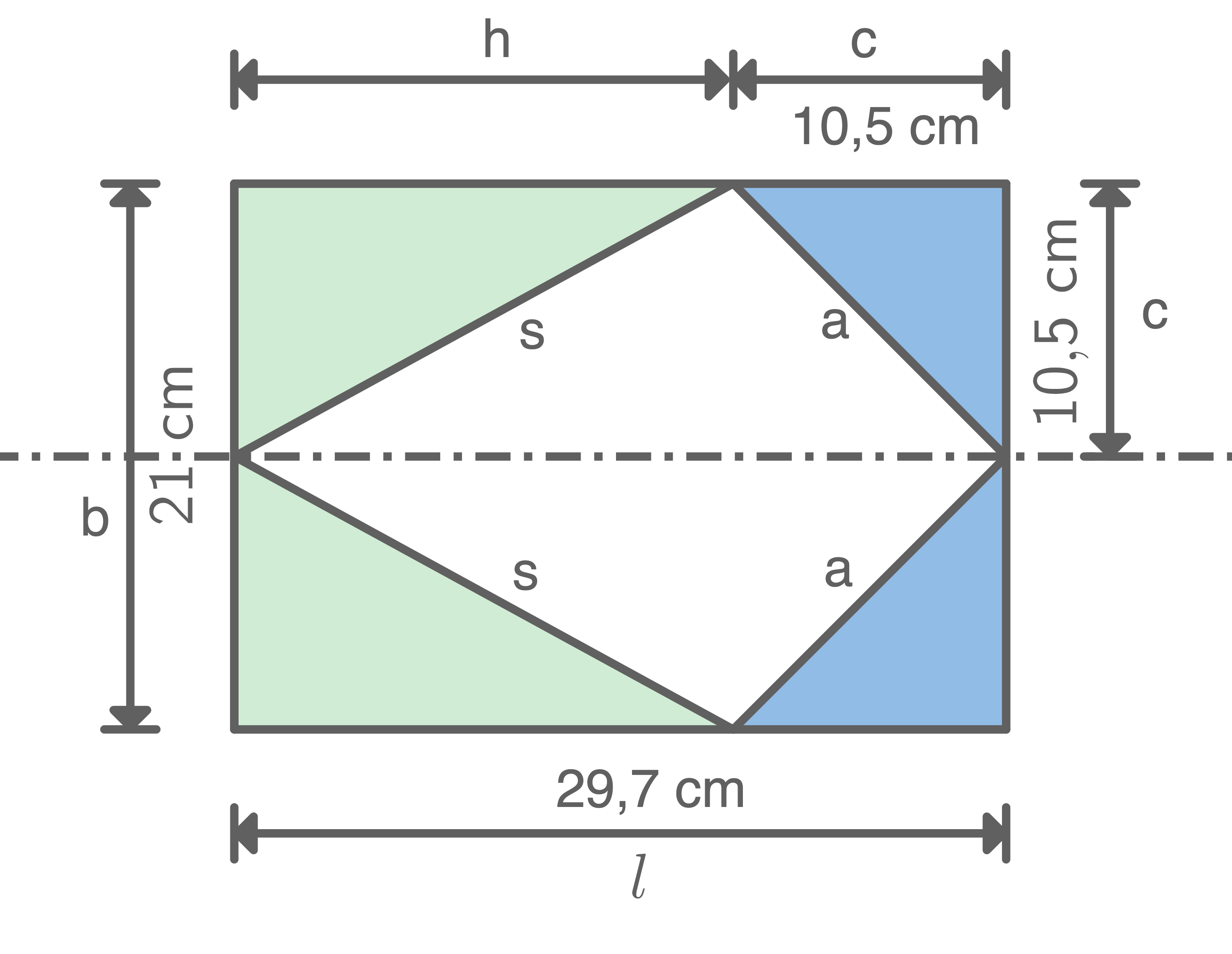
Von einem DIN-A4-Blatt 
werden die vier eingefärbten Dreiecke abgeschnitten.
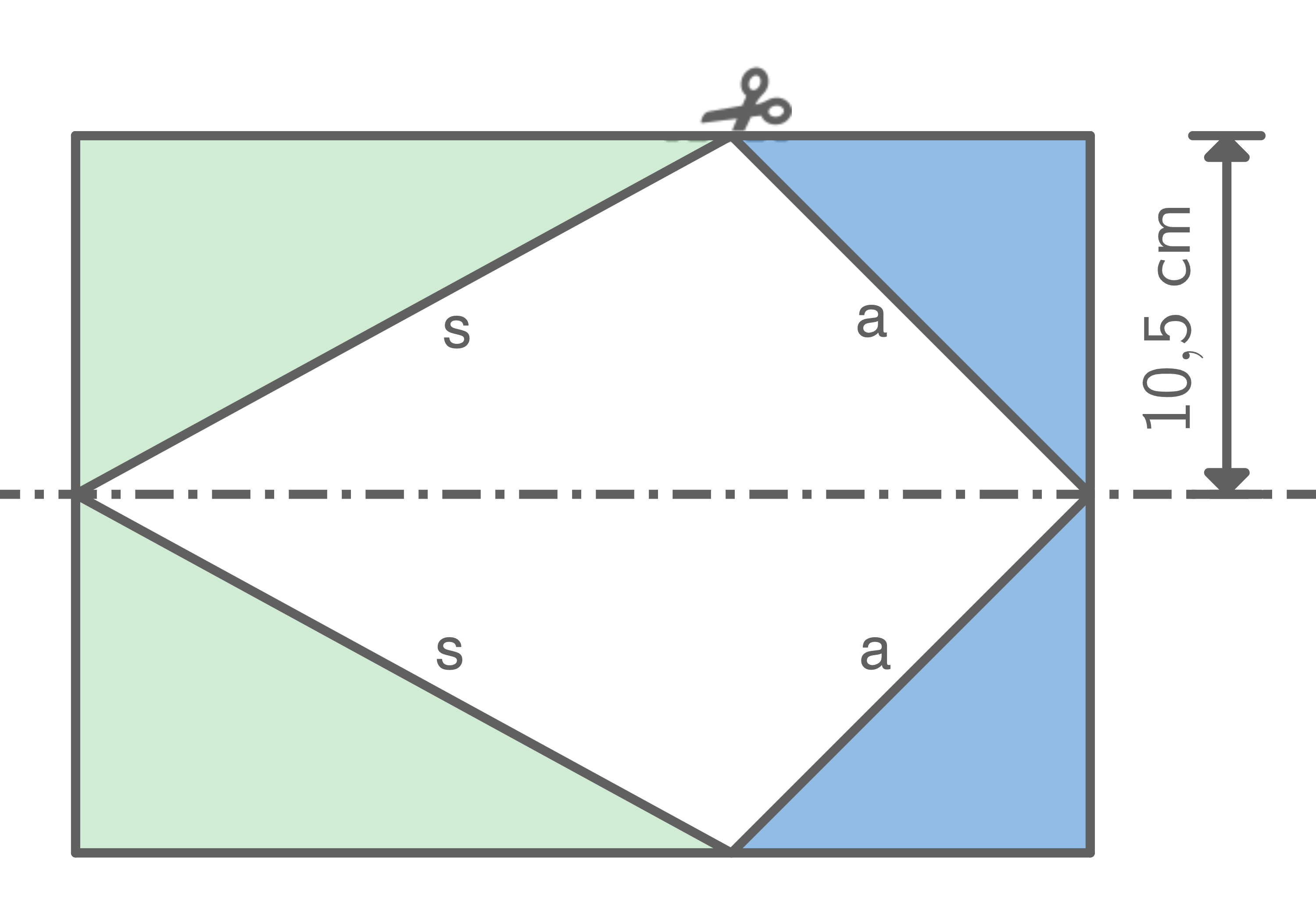
Mit diesen vier Dreiecken werden die Diagonalschnittfläche
und die Grundfläche einer halben massiven quadratischen Pyramide vollständig beklebt.
Lena behauptet: „Die beiden Manteldreiecke 
und 
haben zusammen den gleichen Flächeninhalt wie die Restfläche des DlN-A4-Blatts.“
Hat Lena Recht? Begründe durch Rechnung.
Mit diesen vier Dreiecken werden die Diagonalschnittfläche
(4,5 P)
Aufgabe 9
a)
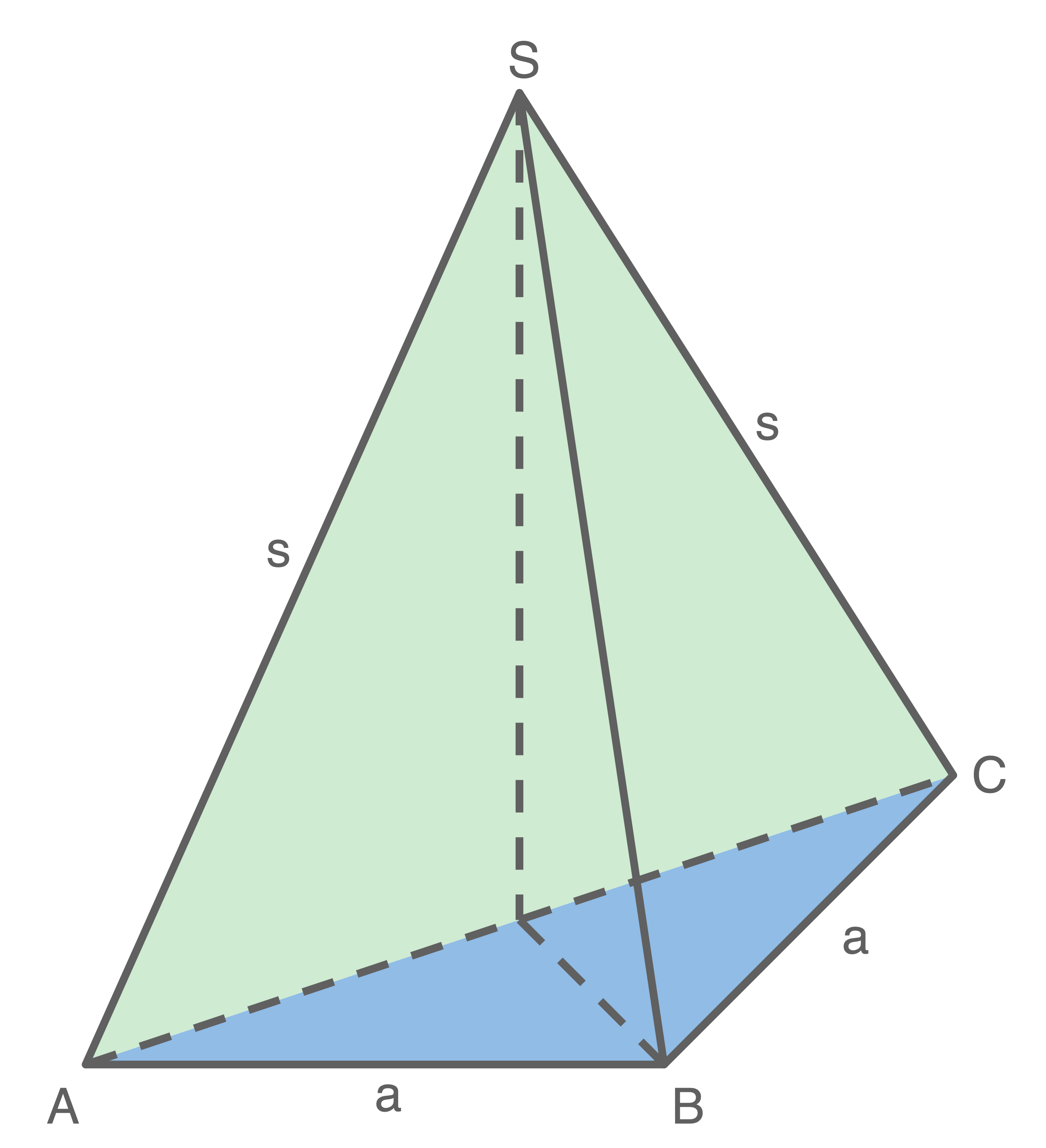
In einer regelmäßigen fünfseitigen Pyramide liegt das gleichschenklige Dreieck 
Es gilt:
Der Punkt
bewegt sich auf der Höhe der Pyramide.
Dadurch entsteht das Dreieck
Berechne den minimalen und den maximalen Flächeninhalt, den das Dreieck 
annehmen kann.
Der Punkt
Dadurch entsteht das Dreieck
(5,5 P)
b)
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel (siehe Achsenschnitt).
Zeige, dass für das Volumen des zusammengesetzten Körpers gilt:
(4,5 P)
Aufgabe 10
a)
(5 P)
b)
Aus einem quadratischen Blatt Papier wird das Netz einer quadratischen Pyramide hergestellt.
Es gilt:
(5 P)
Aufgabe 11
a)
Für einen Zylinder gilt:
![\(\begin{array}[t]{rll}
r&=&3,5 \text{ cm} \\[5pt]
h&=&12,0 \text{ cm}
\end{array}\)](https://mathjax.schullv.de/2c534d08b688773bd3b31d717264990557acd6e3a5ca8eee5aea091d8ff3540b?color=5a5a5a)
Die Mantelfläche des Zylinders wird abgerollt.
).png)
Mit den Einzelteilen dieses Rechtecks wird die Mantelfläche einer regelmäßigen fünfseitigen Pyramide vollständig beklebt.
Berechne das Volumen dieser Pyramide.
(5 P)
b)
Die Eckpunkte des gleichschenkligen Trapezes 
liegen auf den Kanten bzw. Eckpunkten einer quadratischen Pyramide.
Es gilt:
![\(\begin{array}[t]{rll}
O_{Pyr}&=&357 \text{ cm}^2 \\[5pt]
a&=&10,0 \text{ cm} \\[5pt]
\overline{AB}&=&\overline{BS}
\end{array}\)](https://mathjax.schullv.de/56d299627bc9a11e1fc26a2ec4417351d9def064c6aa852d07869165be0357c5?color=5a5a5a)
Berechne den Umfang des Trapezes 
(5 P)
Aufgabe 12
a)
Aus einer Kreisfläche wird die Mantelfläche einer regelmäßigen fünfseitigen Pyramide ausgeschnitten.
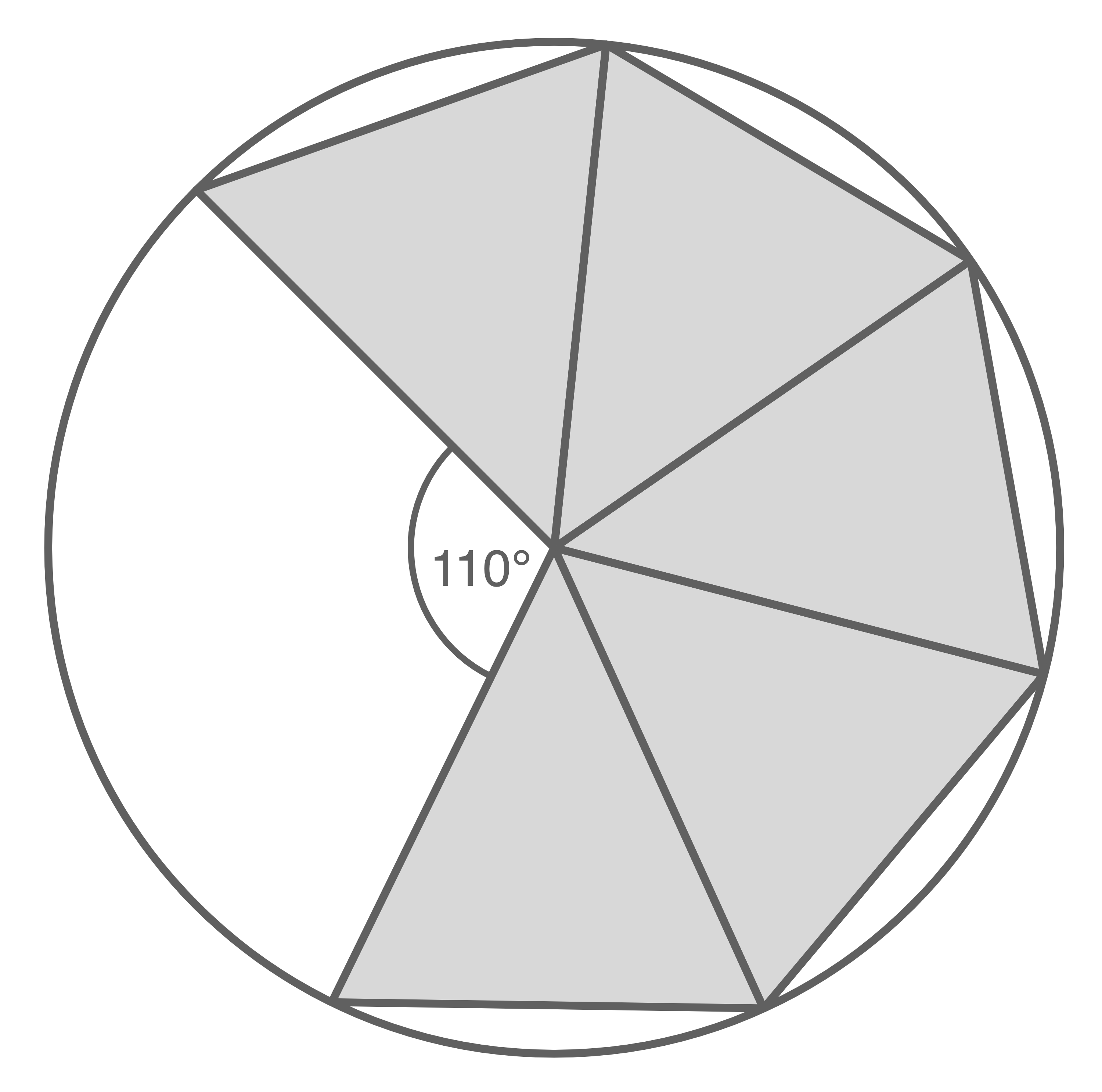Der Kreis hat einen Radius von 
.
Berechne das Volumen der Pyramide.
(5,5 P)
b)
Eine quadratische Pyramide ist zweimal abgebildet.
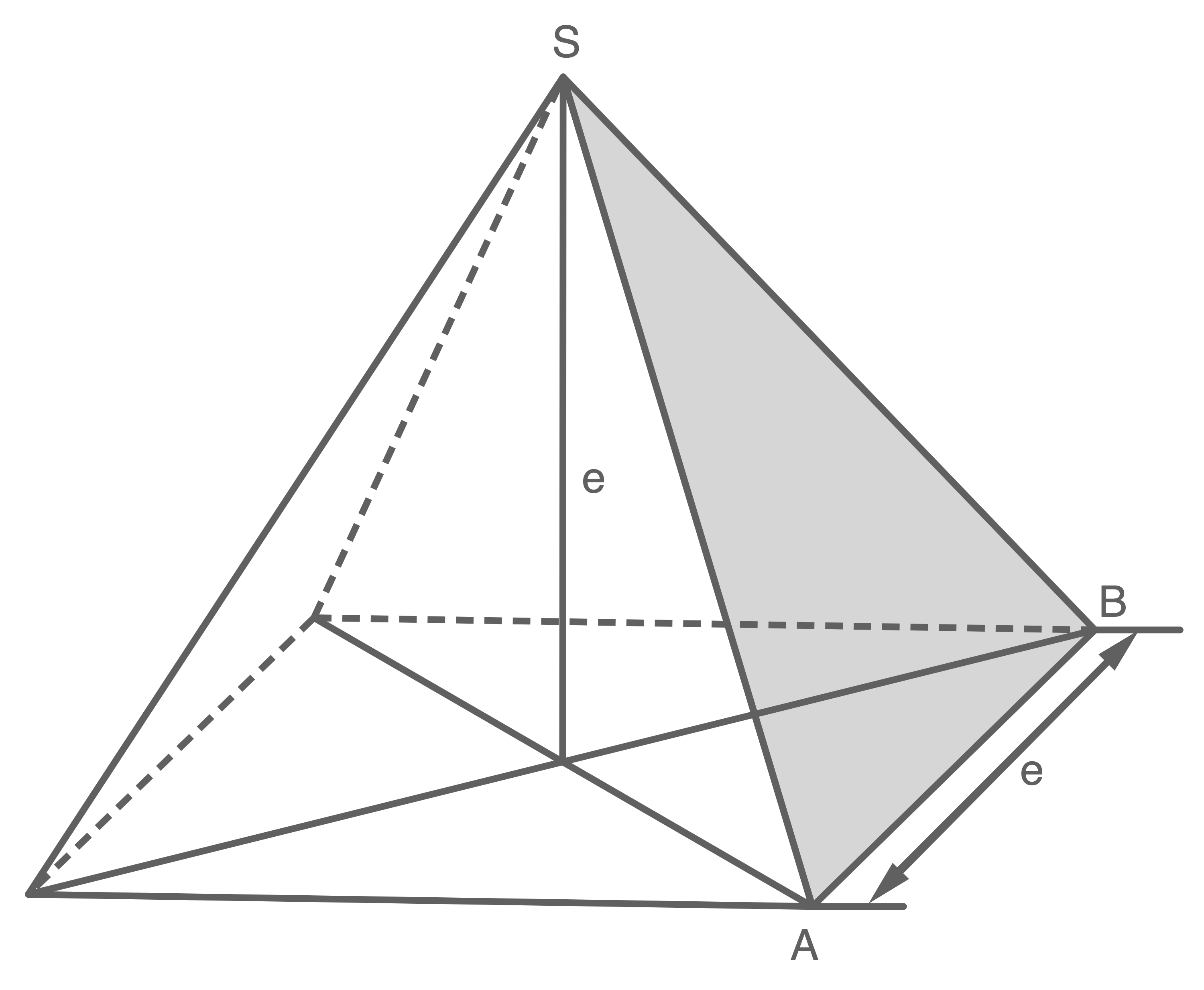
In der linken Abbildung ist das Dreieck markiert und in der rechten das Dreieck 
.
Die Punkte und 
halbieren jeweils die Grundkante.
Welche der folgenden Formeln gehört zur Dreiecksfläche und welche zur Dreiecksfläche ? Begründe deine Entscheidung ohne Verwendung gerundeter Werte.
(1) 
![\(\begin{array}[t]{rll}
A&=& \dfrac{3e^2}{8} &\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5f48ee989f04a418fe86ce37a008a17061dd5c4da246e3ebae0814e3aeb4cc4a?color=5a5a5a)
(2) ![\(\begin{array}[t]{rll}
A&=& \dfrac{e^2}{4}\sqrt{6} &\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8bd0d4ee068ccdbc0079a9468613005ce1aa52418733a59d84a74e188f55e9c2?color=5a5a5a)
(3) ![\(\begin{array}[t]{rll}
A&=& \dfrac{e^2}{4}\sqrt{5} &\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6e1df4168764250fba0b2725d9885f2358d4fa19f452befe7ad026a7f80decb0?color=5a5a5a)
Die Punkte
(4,5 P)
Aufgabe 13
a)
Gegeben sind zwei Dreiviertelkreise.
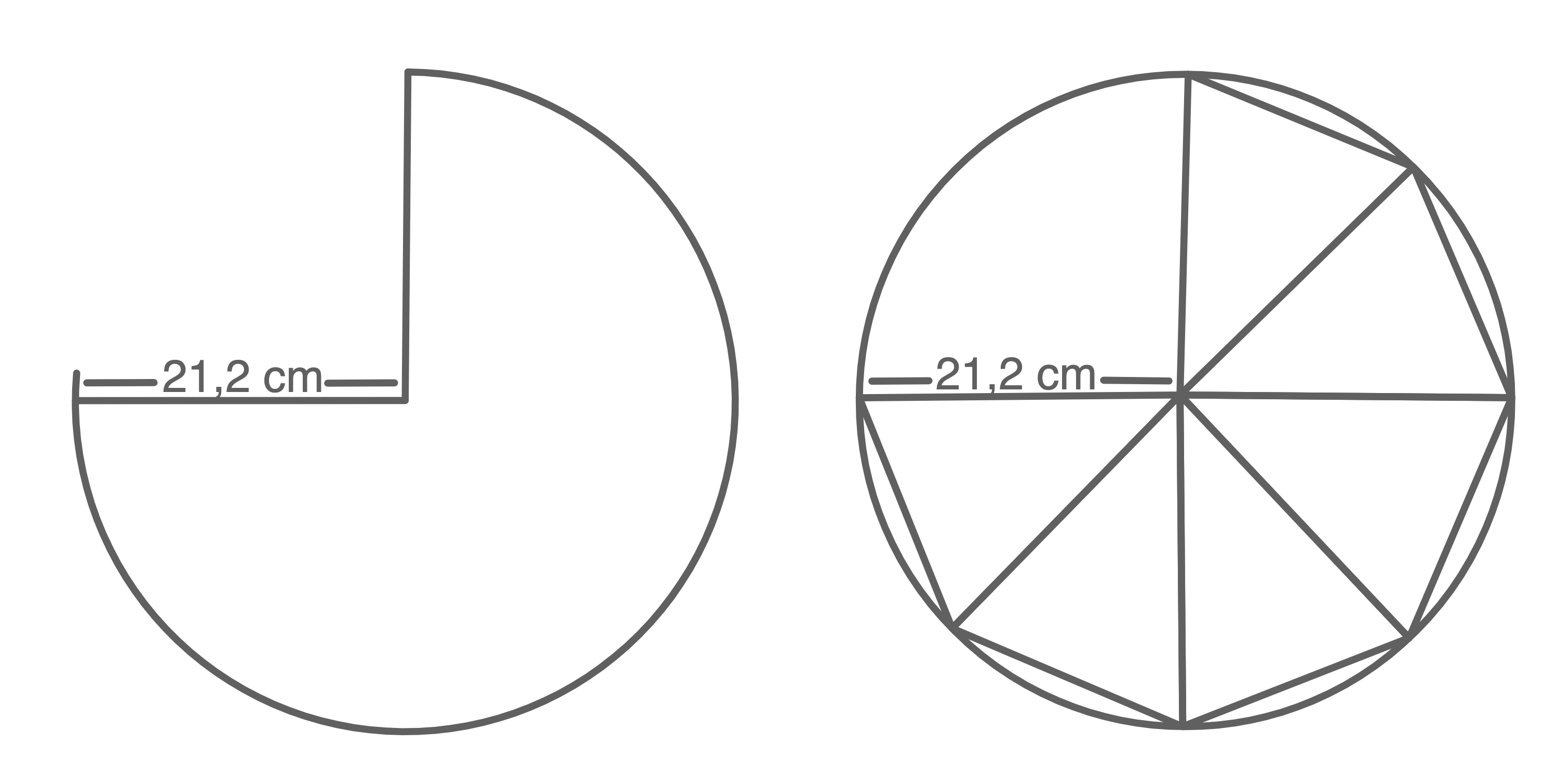Aus ihnen werden der Mantel eines Kegels und der Mantel einer regelmäßigen sechsseitigen Pyramide gefertigt.
Berechne die Differenz der beiden Körperhöhen.
Berechne die Differenz der beiden Körperhöhen.
(5,5 P)
b)
Ein zusammengesetzter Körper besteht aus einem gleichschenkligen Dreiecksprisma und einem halben Kegel (siehe Skizze).
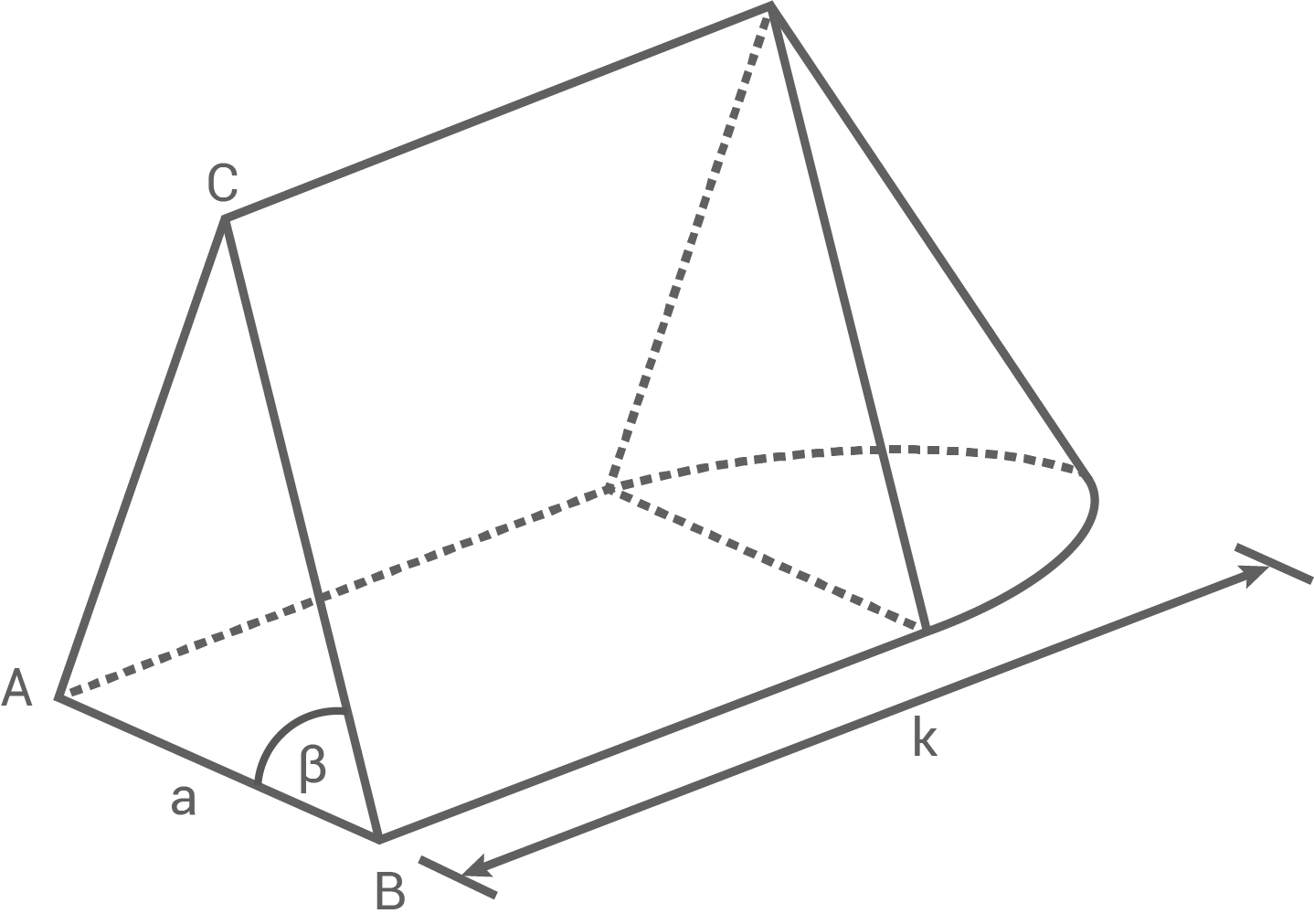Es gilt:
![\(\begin{array}[t]{rll}
\overline{AC}&=& \overline{BC}\\[5pt]
\overline{AB}&=& 11,4 \,\text{cm} \\[5pt]
\beta&=& 62,0 ^{\circ} \\[5pt]
V_{\,\text{ges}}&=& 1 \,280 \,\text{cm}^3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7a5d7545751b391cbf2ef6c0986486a5c390935cad222eb9eb5f35fa5765e4dd?color=5a5a5a)
(Volumen des zusammengesetzten Körpers)
Berechne die Gesamtlänge
des zusammengesetzten Körpers.
(Volumen des zusammengesetzten Körpers)
Berechne die Gesamtlänge
(4,5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
1. Schritt: Radius 
berechnen
2. Schritt: 
berechnen
![\(\begin{array}[t]{rll}
\tan \dfrac{\delta}{2}&=& \dfrac{r}{h_\text{Ke}} \\[5pt]
\tan 21,0°&=& \dfrac{5,16\,\text{cm}}{h_\text{Ke}} \quad \scriptsize \mid\;\cdot h_\text{Ke} \\[5pt]
\tan 21,0°\cdot h_\text{Ke}&=& 5,16\,\text{cm} \quad \scriptsize \mid\; :\tan 21,0° \\[5pt]
h_\text{Ke}&=& \dfrac{5,16\,\text{cm}}{\tan 21,0°} \\[5pt]
h_\text{Ke}&=& \underline{13,44\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/49ffe5b6098dbe1793f1dcf47dd00d3d64aee93025c45b36e88ab91a4196c8e8?color=5a5a5a)
3. Schritt: 
berechnen
![\(\begin{array}[t]{rll}
h_{\text{Pyr}}&=& h_{\text{Ke}}+r \\[5pt]
&=& 13,44\,\text{cm}+5,16\,\text{cm} \\[5pt]
&=& \underline{18,60\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/aff030f5dfbb3da272122fd884df415ce71d5c6ac5b26038629761c24d170aa0?color=5a5a5a)
4. Schritt: Höhe 
der Seitenflächen der Pyramide berechnen
![\(\begin{array}[t]{rll}
h_s^2&=& h_\text{Pyr}^2+\left(\dfrac{a}{2}\right)^2 \\[5pt]
h_s^2&=& (18,60\,\text{cm})^2+(5,16\,\text{cm})^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
h_s&=& \sqrt{(18,60\,\text{cm})^2+(5,16\,\text{cm})^2} \\[5pt]
h_s&=& \underline{19,30\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/a3cba1c02ba50ff3a468a1609ba8e3ab7b4ea8567ba628c8e8c03da91be3c368?color=5a5a5a)
5. Schritt: Differenz der Oberflächeninhalte berechnen
![\(\begin{array}[t]{rll}
O_\text{Diff}&=& 505\,\text{cm}^2-401\,\text{cm}^2 \\[5pt]
&=& \underline{\underline{104\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/a56bcae37d143b2ccc6c5469c7a313e1368c8109a21b49cec3a4bbea10f133de?color=5a5a5a)
Abschlussprüfung 2024
Lösung 2
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
1. Schritt: Radius 
des Kegels berechnen
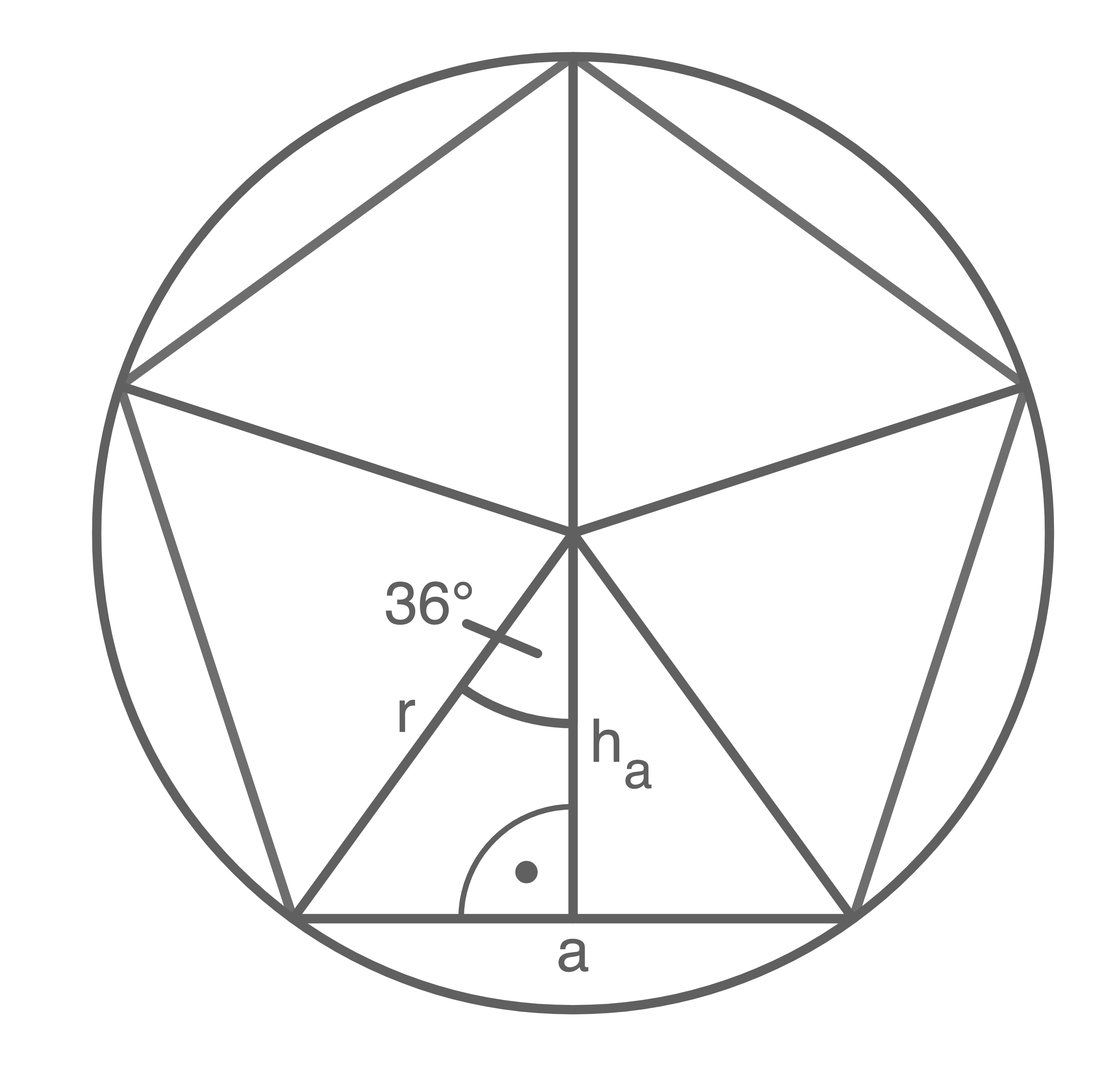
![\(\begin{array}[t]{rll}
\sin 36^\circ&=&\dfrac{\frac{a}{2}}{r} \quad \scriptsize \mid\;\cdot r \\[5pt]
\sin 36^\circ\cdot r&=&\dfrac{a}{2} \quad \scriptsize \mid\;: \sin 36^\circ \\[5pt]
r&=&\dfrac{a}{2\cdot \sin 36^\circ} \\[5pt]
&=&\dfrac{8,6\,\text{cm}}{2\cdot \sin 36^\circ} \\[5pt]
r&=&\underline{7,32\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/23c47a9369826e2f9fcc2618cf6e734a03aad40f04e2964a1c6c4a87fbb7c687?color=5a5a5a)
2. Schritt: Höhe 
berechnen
![\(\begin{array}[t]{rll}
h_a^2&=&r^2-\left(\frac{a}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
h_a&=&\sqrt{r^2-\left(\frac{a}{2}\right)^2} \\[5pt]
&=&\sqrt{(7,32\,\text{cm})^2-\left(\frac{8,6\,\text{cm}}{2}\right)^2} \\[5pt]
h_a&=&\underline{5,92\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/2f576e8b459f8f947915b4340c9d8ca30b8a28559677d8fdb32549859d171bee?color=5a5a5a)
3. Schritt: Höhe 
berechnen
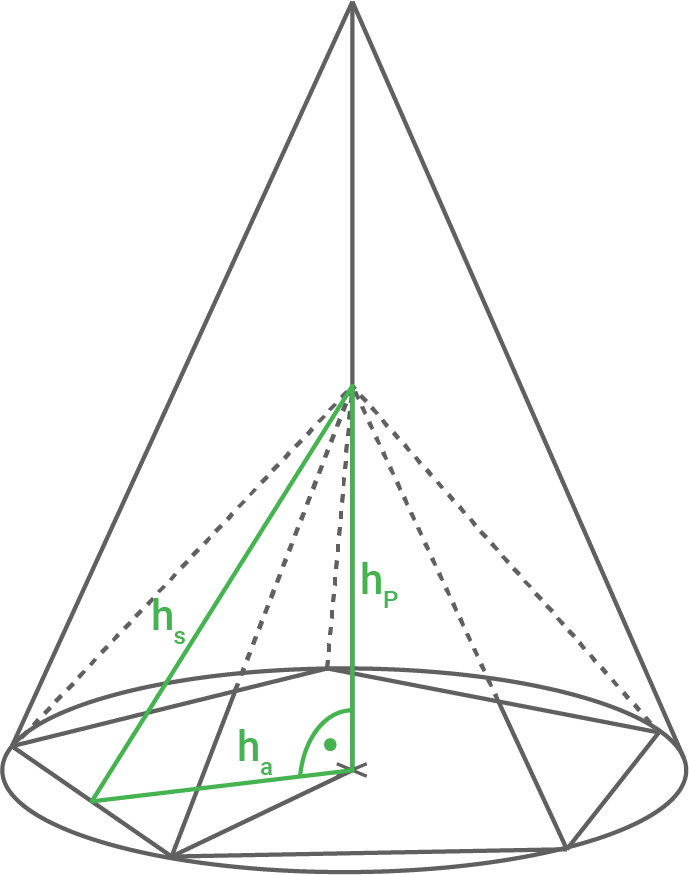
![\(\begin{array}[t]{rll}
h_s^2&=&h_P^2+h_a^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h_s&=&\sqrt{h_P^2+h_a^2}\\[5pt]
&=&\sqrt{(7,6\,\text{cm})^2+(5,92\,\text{cm})^2}\\[5pt]
h_s&=&\underline{9,63\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/6a7fefd1853a73ed49879650653ba175b5514e8a9dc1c5e935d430c532e13ed2?color=5a5a5a)
4. Schritt: Länge von 
berechnen
ist die Mantellinie des Kegels.
![\(\begin{array}[t]{rll}
s_K^2&=&r^2+h_K^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
s_K&=&\sqrt{r^2+h_K^2}\\[5pt]
&=&\sqrt{(7,32\,\text{cm})^2+(15,2\,\text{cm})^2}\\[5pt]
s_K&=&\underline{16,87\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/94e1b268642319f9b594c579920f062656ef713e1709737c7e88ed80e4dbfb43?color=5a5a5a)
5. Schritt: Mantelflächeninhalt der Pyramide berechnen
![\(\begin{array}[t]{rll}
M_P&=&5\cdot A_\text{Seitenfläche} \\[5pt]
&=&5\cdot \dfrac{a\cdot h_s}{2} \\[5pt]
&=&5\cdot \dfrac{8,6\,\text{cm}\cdot 9,63\,\text{cm}}{2}\\[5pt]
M_P&=&\underline{207,05\,\text{cm}^2}
\end{array}\)](https://mathjax.schullv.de/c0b9e2370e33b1a6c60c5fcd72cff7e17ed179fa3feaf50e56d93655d33f4c96?color=5a5a5a)
6. Schritt: Mantelflächeninhalt des Kegels berechnen
![\(\begin{array}[t]{rll}
M_K&=&\pi\cdot r\cdot s_K \\[5pt]
&=&\pi\cdot 7,32\,\text{cm}\cdot 16,87\,\text{cm}\\[5pt]
M_K&=&\underline{387,95\,\text{cm}^2}
\end{array}\)](https://mathjax.schullv.de/97e2519e62c939c79691ce72a35867e6a0ddde1e621a5dfe3fd2663a62c8fa5e?color=5a5a5a)
7. Schritt: Differenz der Mantelflächeninhalte berechnen
![\(\begin{array}[t]{rll}
M_\text{Differenz}&=&M_K-M_P\\[5pt]
&=&387,95\,\text{cm}^2-207,05\,\text{cm}^2\\[5pt]
M_\text{Differenz}&=&\underline{\underline{180,9\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/ea3ebcdbc196b4dc98123f2423e5795a1b177e93831ecb26e0cca277c69e23d9?color=5a5a5a)
Lösung 3
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Lösung 4
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Lösung 5
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
Flächeninhalt des Dreiecks 
berechnen
Formel zur Berechnung des Flächeninhalts: 
1. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{EG}&=&\dfrac{1}{2}\cdot \overline{EF}\\[5pt]
&=& \dfrac{1}{2}\cdot 12,6\,\text{cm} \\[5pt]
&=& \underline{ 6,3\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a5aff0b1a2368974bf83d0d58824de5e666d1c2920ee4e5cf1e93f3f05448bf9?color=5a5a5a)
2. Schritt: Länge der Strecke 
berechnen
3. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{EFS}&=& \dfrac{1}{2}\cdot 12,6\,\text{cm}\cdot 19,39\,\text{cm}&\quad \scriptsize \\[5pt]
& =& 122,16\,\text{cm}^2
\\[5pt]
& =& \underline{\underline{ 122,2\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/658f45eff5938b71ca33ff7bdcc542bc846cf4a25f54688116e8b03f22564462?color=5a5a5a)
Volumen der quadratischen Pyramide berechnen
Formel zur Berechnung des Volumens: 
1. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2&=& \overline{AB}^2+\overline{BC}^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\overline{AC} &=& \sqrt{\overline{AB}^2+\overline{BC}^2} \\[5pt]
\overline{AC} &=& \sqrt{(12,6\,\text{cm})^2+(12,6\,\text{cm})^2} \\[5pt]
\overline{AC}&=& \underline{ 17,82\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/0957378fa0c3a2ee81eb32f6f8b13cea0e20addb49ded35a61c8edf8bb8131f7?color=5a5a5a)
2. Schritt: Länge von 
berechnen
![\(\begin{array}[t]{rll}
\overline{MB}=\overline{AM}&=& \dfrac{1}{2}\cdot \overline{AC}&\\[5pt]
&=&\dfrac{1}{2}\cdot 17,82 \,\text{cm} \\[5pt]
&=&\underline{ 8,91 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a0c12bede9132bbf831462d78cb77732133aee2551d207d551faa1ed6557a9f0?color=5a5a5a)
3. Schritt: Länge der Strecke 
mit dem Zweiten Strahlensatz berechnen
4. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{MG}&=& \overline{MB}-\overline{GB} \\[5pt]
&=& 8,91\,\text{cm}-6,3\,\text{cm} \\[5pt]
&=& \underline{ 2,61\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/f97038fbbc195d314942b33767942561de32148db25fdac1201f82f255fcd7f8?color=5a5a5a)
5. Schritt: Länge der Strecke berechnen
6. Schritt: Volumen berechnen
![\(\begin{array}[t]{rll}
V &=& \dfrac{1}{3}\cdot \overline{AB}^2\cdot h \\[5pt]
&=& \dfrac{1}{3}\cdot (12,6\,\text{cm})^2\cdot 19,21\,\text{cm} \\[5pt]
&=& 1016,59\,\text{cm}^3
\\[5pt]
V &=& \underline{\underline{ 1016,6\,\text{cm}^3}}
\end{array}\)](https://mathjax.schullv.de/af1276eda5c255348c01df36fee826382384f4e3ce9c2317a1a17f03c9c405f4?color=5a5a5a)
Lösung 6
a)
b)
Die Teilaufgabe b) wurde in kein Thema eingeordnet.
Musterprüfung 1
Lösung 7
a)
1. Schritt: Oberfläche des großen Zylinders berechnen
![\(\begin{array}[t]{rll}
O_{\,\text{großer Zyl.}}&=& 2 \pi \cdot r_{\,\text{groß}} \cdot (r_{\,\text{groß}} + h) \\[5pt]
&=& 2 \pi \cdot \frac{16}{2} \cdot (\frac{16}{2} + 12) \\[5pt]
&= & \underline{ 1005,31\,\text{cm}^2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7652cced926147209e557b67fc47ae28beea10044acf10025b14f8b20d9a122d?color=5a5a5a)
2. Schritt: Deckfläche des kleinen Zylinders berechnen
![\(\begin{array}[t]{rll}
D_{\,\text{kleiner Zyl.}}&=& \pi \cdot r_{\,\text{klein}}^2\\[5pt]
&=& \pi \cdot 2,5^2 \\[5pt]
&= & \underline{ 19,63\,\text{cm}^2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7b2b1ac59cbe45c35b09360bfe1394cdb6d27c8767ad97dc5c724e108351ebeb?color=5a5a5a)
3. Schritt: Mantelfläche des kleinen Zylinders berechnen
![\(\begin{array}[t]{rll}
M_{\,\text{kleiner Zyl.}}&=& 2 \cdot \pi \cdot r_{\,\text{klein}} \cdot h &\quad \scriptsize \\[5pt]
&=& 2 \cdot \pi \cdot 2,5 \cdot 12 &\quad \scriptsize \\[5pt]
&= & \underline{ 188,50\,\text{cm}^2} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/807d47ced8b36c192cdd0858c967ccb6279d660791dccb610a7220072939a1f5?color=5a5a5a)
4. Schritt: Oberfläche des gesamten Körpers berechnen
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Lösung 8
a)
1. Schritt: Flächeninhalt des Manteldreiecks berechnen
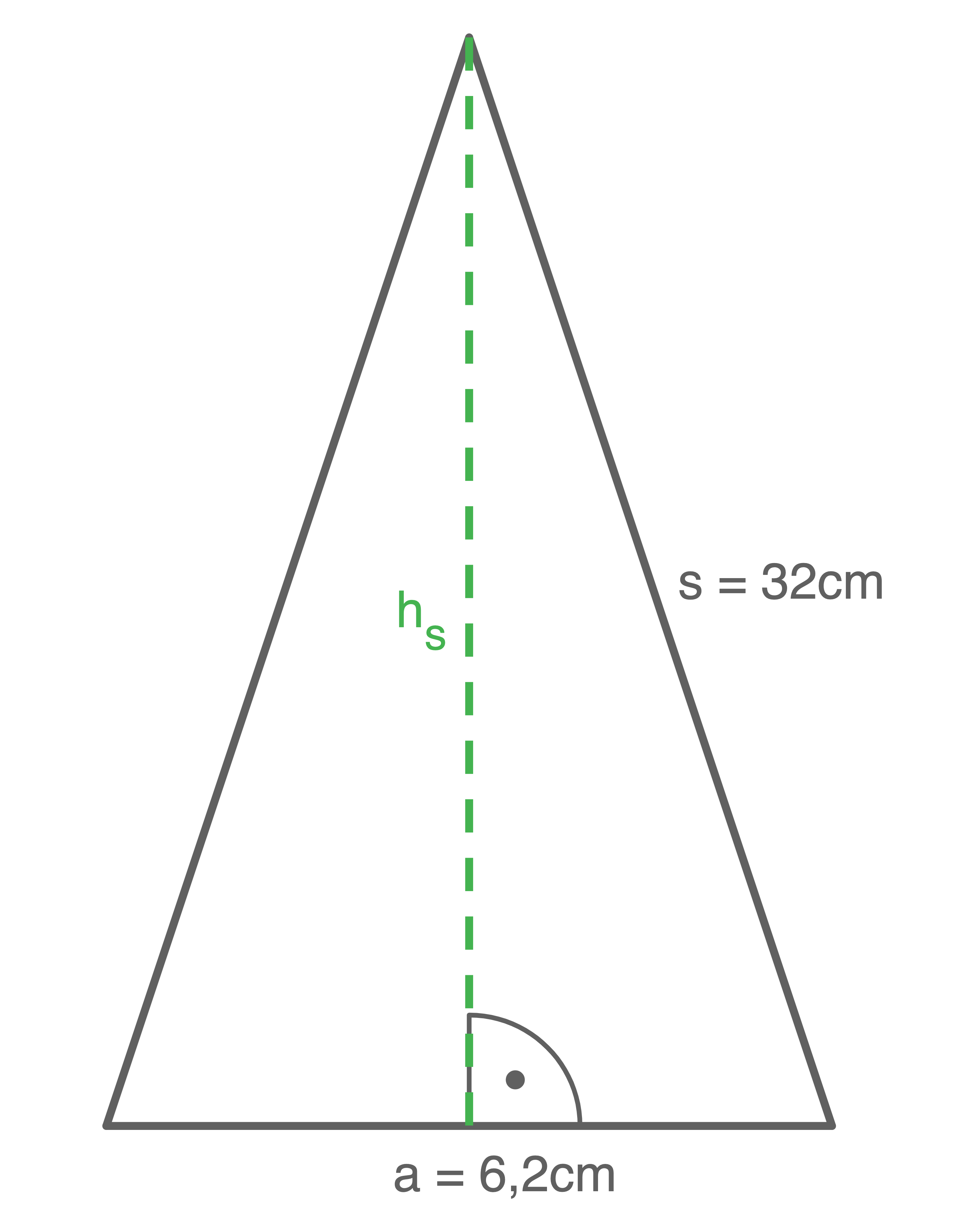Da die Pyramide regelmäßig ist, sind die Manteldreiecke gleichschenklig und es gilt:
![\(\begin{array}[t]{rll}
A_{\,\text{Manteldreieck}}&=&\dfrac{1}{2} \cdot a \cdot h_s \\[5pt]
&=&\dfrac{1}{2} \cdot 6,2\,\text{cm} \cdot 31,85\,\text{cm} \\[5pt]
&= &\underline{ 98,74\,\text{cm}^2}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8128474d47eb08f86f8e8314aa41bd71ecdaf0cbc951ccfac7a05ef4323a901c?color=5a5a5a)
2. Schritt: Länge der Strecke 
berechnen
Die Grundfläche der Pyramide lässt sich in acht gleichschenklige Dreiecke einteilen:
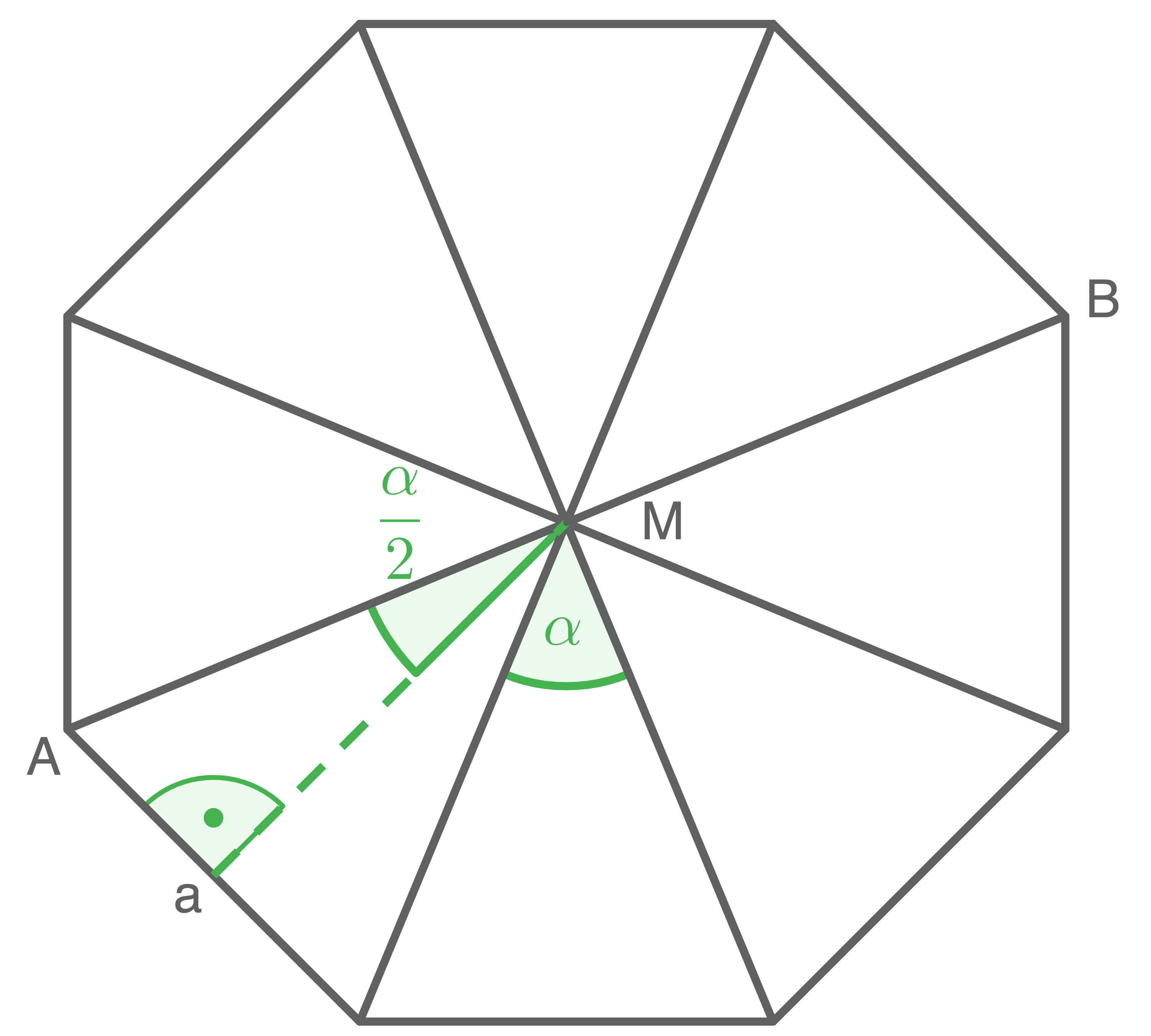
![\(\begin{array}[t]{rll}
\alpha&=& 360^{\circ}:8 \\[5pt]
&=& 45^{\circ}
\end{array}\)](https://mathjax.schullv.de/be2ddfc757b74964274e70b9de13be6519698b1301ea5459119f8dc9070011fe?color=5a5a5a)
![\(\begin{array}[t]{rll}
\sin\left(\dfrac{\alpha}{2}\right)&=&\dfrac{\dfrac{a}{2}}{\overline{AM}} \\[5pt]
\sin(22,5°)&=&\dfrac{3,1\,\text{cm}}{\overline{AM}} \quad \scriptsize \mid\; \cdot \overline{AM}\\[5pt]
\sin(22,5°)\cdot \overline{AM} &=& 3,1\,\text{cm} \quad \scriptsize \mid\; : \sin(22,5^{\circ} ) \\[5pt]
\overline{AM} &=& \dfrac{3,1\,\text{cm}}{ \sin(22,5^{\circ}) } \\[5pt]
\overline{AM} &= &8,1\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a1c210361b5570e016187e8d54c623b3b2f30e7601226ba18b080e7fca9d011a?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overline{AB}&=& \overline{AM}\cdot 2 \\[5pt]
&=& 8,1\,\text{cm} \cdot 2 \\[5pt]
&=& \underline{ 16,2\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/be84e74c04eb056dcc3c7cb17a35099b6f1c336f3f9d66aadf1f0c933860e0ec?color=5a5a5a)
3. Schritt: Höhe des Dreiecks 
berechnen
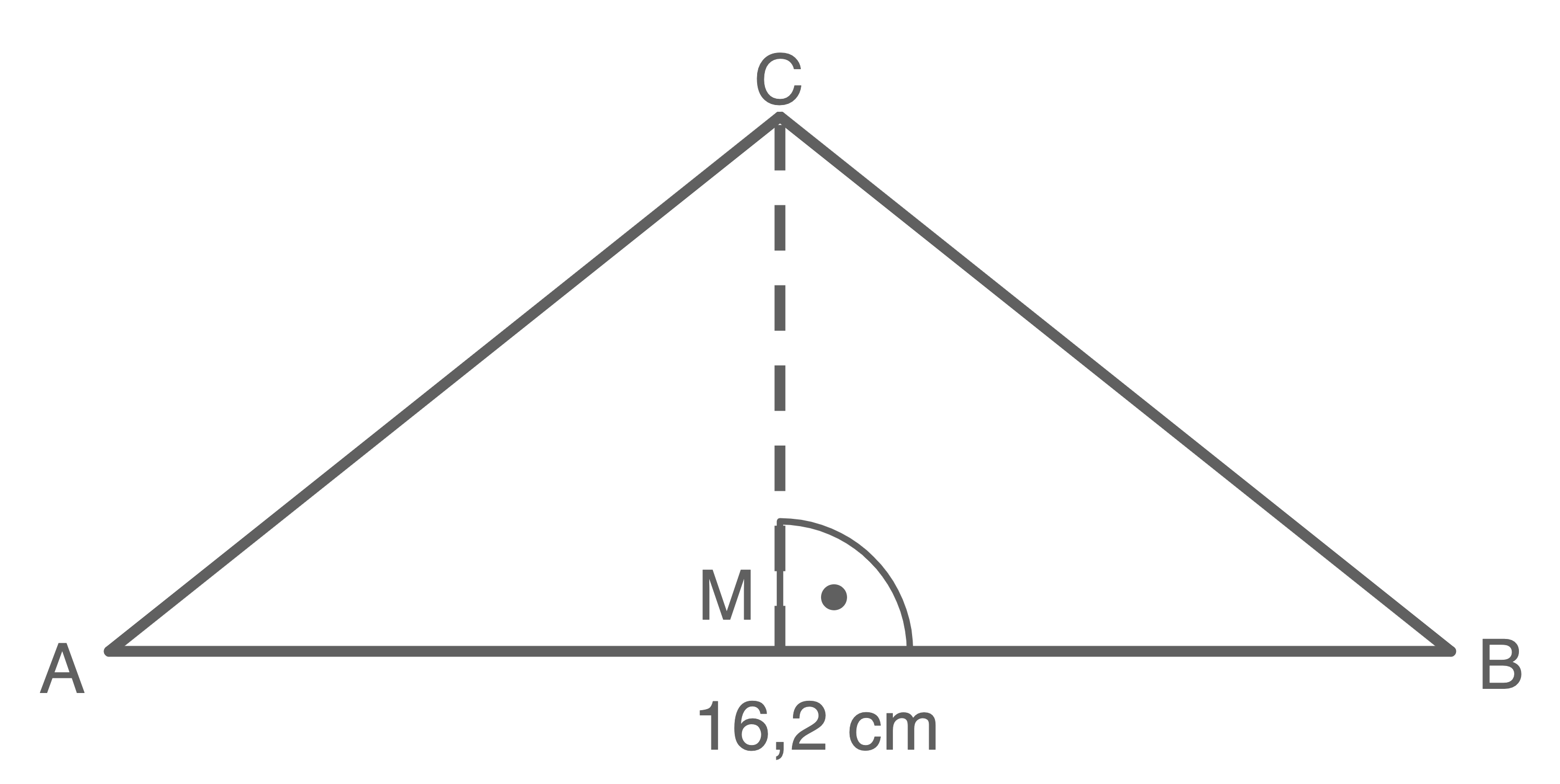
![\(\begin{array}[t]{rll}
A_{ABC}&=&\dfrac{1}{2} \cdot \overline{AB} \cdot \overline{MC} \\[5pt]
98,74\,\text{cm}^2&=&\dfrac{1}{2} \cdot 16,2\,\text{cm} \cdot \overline{MC} \\[5pt]
98,74\,\text{cm}^2&=& 8,1\,\text{cm} \cdot \overline{MC} \quad \scriptsize \mid\; :8,1 \,\text{cm} \\[5pt]
\dfrac{ 98,74\,\text{cm}^2}{ 8,1\,\text{cm}} &=& \overline{MC} \\[5pt]
\overline{MC} &=& \dfrac{ 98,74\,\text{cm}^2}{ 8,1\,\text{cm}}\\[5pt]
\overline{MC} &=& \underline{ 12,19\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/eda3ce87d60a1d42169806145e6e82cda5b03b1be0284f351d90b2331bed99e8?color=5a5a5a)
4. Schritt: Höhe der Pyramide berechnen
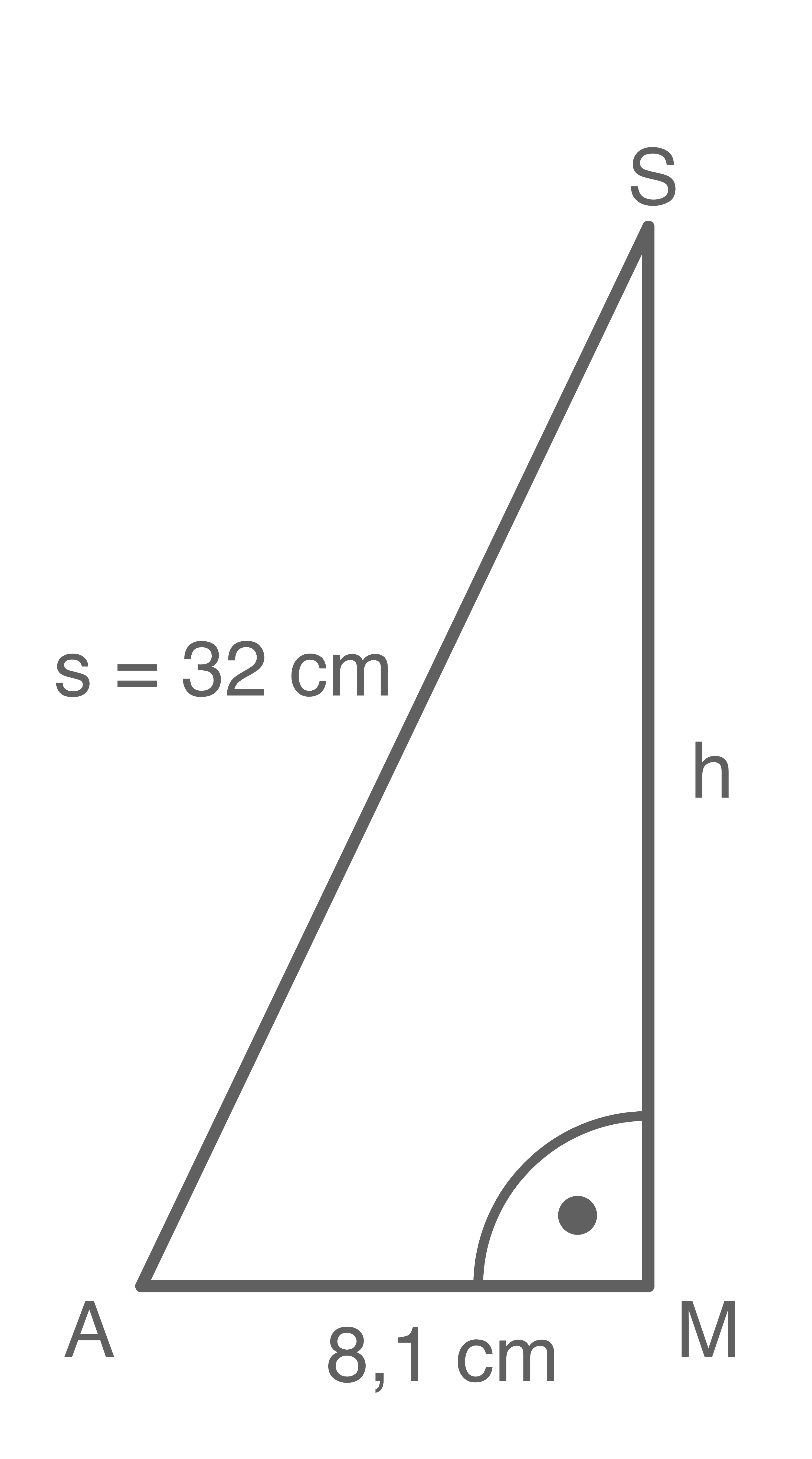5. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{SC}&=& h-\overline{MC} \\[5pt]
&=& 30,96\,\text{cm}-12,19\,\text{cm} \\[5pt]
&=&18,77\,\text{cm}\\[5pt]
\overline{SC}&=& \underline{\underline{ 18,8\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/a15342055a4c8ecdebd9068d0732f689e3f741a51d9fefb083ffa1524a7a99f9?color=5a5a5a)
b)
Lösung 9
a)
Berechnung der Höhe der Pyramide
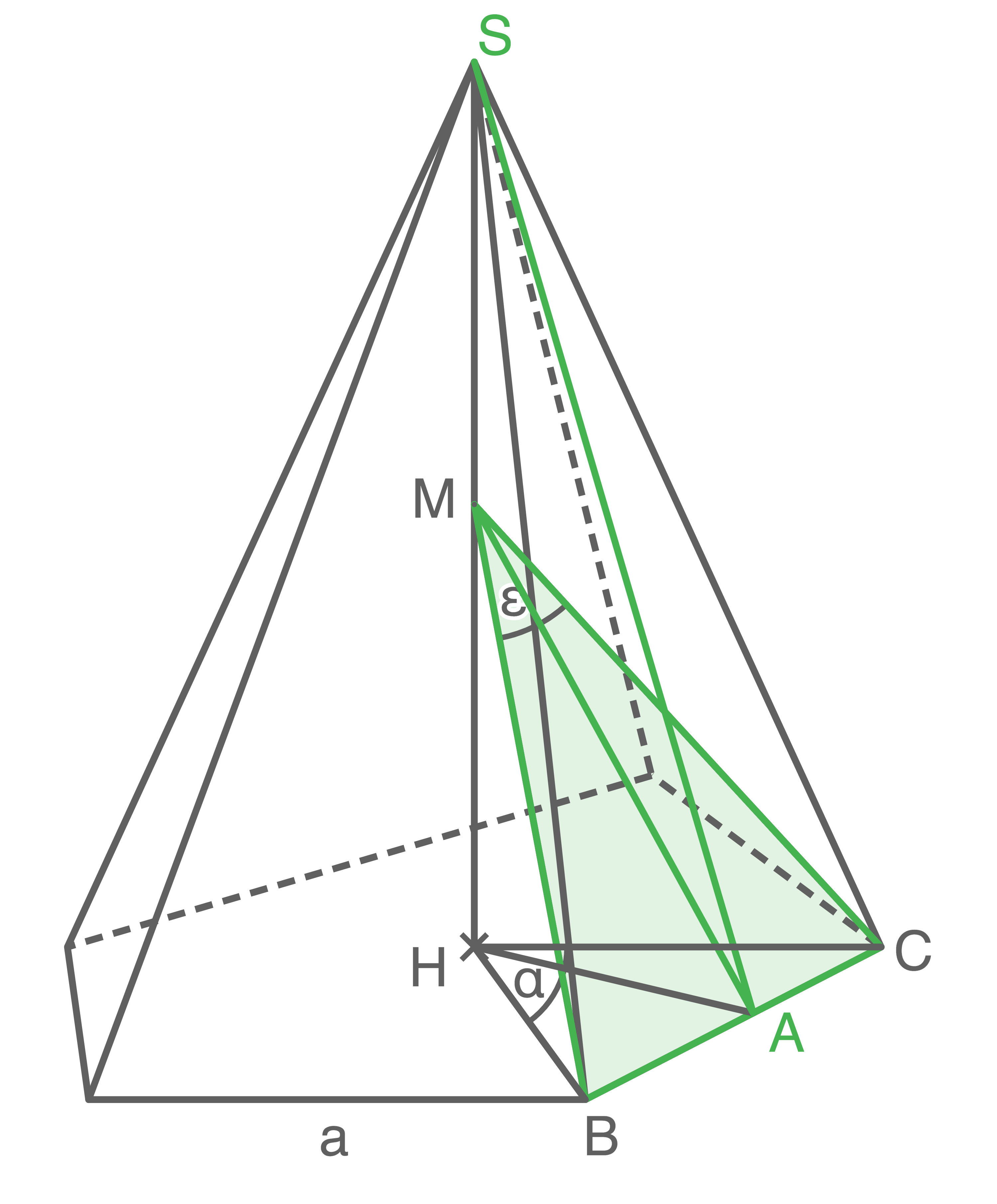1. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\epsilon}{2}\right)&=&\dfrac{\overline{AM}}{\overline{BM}} &\quad \scriptsize \mid\;\cdot\overline{BM} \\[5pt]
\overline{AM}&=&\overline{BM}\cdot \cos\left(\dfrac{\epsilon}{2}\right) \\[5pt]
\overline{AM}&=&8,0 \,\text{cm}\cdot \cos\left(\dfrac{48^{\circ}}{2}\right)\\[5pt]
\overline{AM}&=&\underline{ 7,31 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/73e7149ff137337f0d06da8c2ab99bcce885803227c96921f0a7efd8bfdae7ca?color=5a5a5a)
2. Schritt: Länge der Strecke berechnen
![\(\begin{array}[t]{rll}
\sin\left(\dfrac{\epsilon}{2}\right)&=&\dfrac{\overline{AB}}{BM} &\quad \scriptsize \mid\;\cdot\overline{BM} \\[5pt]
\overline{AB}&=&\overline{BM}\cdot \sin\left(\dfrac{\epsilon}{2}\right) \\[5pt]
\overline{AB}&=&8,0 \,\text{cm} \cdot \sin\left(\dfrac{48^{\circ}}{2}\right) \\[5pt]
\overline{AB}&=&\underline{ 3,25 \,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ba83353a7feaa02979f5269c5a94ff60eca9318ee9309fe3275dd9715c732964?color=5a5a5a)
3. Schritt: Größe des Mittelpunktswinkels 
berechnen
4. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\alpha}{2}\right)&=&\dfrac{\overline{AB}}{AH} &\quad \scriptsize \mid\;\cdot\overline{AH} \\[5pt]
\overline{AH}\cdot \tan\left(\dfrac{\alpha}{2}\right) &=&\overline{AB}&\quad \scriptsize \mid\;: \tan\left(\dfrac{\alpha}{2}\right) \\[5pt]
\overline{AH}&=&\dfrac{\overline{AB}}{\tan\left(\dfrac{\alpha}{2}\right)} \\[5pt]
\overline{AH}&=&\dfrac{3,25 \,\text{cm}}{\tan\left(\dfrac{72^{\circ}}{2}\right)} \\[5pt]
\overline{AH}&=&\underline{ 4,47 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/af8950ee06be72f9509a085cd1b4009fe31023e045d4370c222989566acff181?color=5a5a5a)
5. Schritt: Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{AM}^2&=&\overline{MH}^2+\overline{AH}^2 \quad \scriptsize \mid\;-\overline{AH}^2 \\[5pt]
\overline{MH}^2&=&\overline{AM}^2-\overline{AH}^2 \quad \scriptsize \mid\;\sqrt{\,\,\,}\\[5pt]
\overline{MH}&=& \sqrt{(7,31\,\text{cm})^2-(4,47\,\text{cm})^2}\\[5pt]
\overline{MH}&=&\underline{ 5,78\,\text{cm} }\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bfbb05a78313b169b45670906db180100ef7fe838a150c51e17c3e3331b30de1?color=5a5a5a)
6. Schritt: Höhe der Pyramide berechnen
![\(\begin{array}[t]{rll}
\overline{SH}&=&2\cdot \overline{MH} & \\[5pt]
&=& 2\cdot 5,78\,\text{cm} \\[5pt]
&=& 11,56\,\text{cm} \\[5pt]
\overline{SH}&=&\underline{\underline{ 11,6\,\text{cm}}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cca1fc4ce816f4b32039e484c723941288444e5a25624f9c2b782dc2db17bae4?color=5a5a5a)
Berechnung des minimalen Flächeninhalts
![\(\begin{array}[t]{rll}
A_{\,\text{min}}&=&\dfrac{1}{2}\cdot \overline{BC}\cdot \overline{AM](https://mathjax.schullv.de/19ee3d26fca41873b30e02adf2d6bfff2d20e9ba9e8671ca12e7af4b8c56ba3e?color=5a5a5a)
Berechnung des maximalen Flächeninhalts
Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{AS}^2&=&\overline{SH}^2+\overline{AH}^2 & \\[5pt]
\overline{AS}^2&=&(11,6\,\text{cm})^2+(4,47\,\text{cm})^2 &\quad \scriptsize \mid\;\sqrt{\quad} \\[5pt]
\overline{AS}&=& \sqrt{(11,6\,\text{cm})^2+(4,47\,\text{cm})^2} \\[5pt]
\overline{AS}&=&\underline{ 12,43\,\text{cm}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2cc28c461894bb663f645fac185a98ee21ba7b18a752d2c8791dde2dc37a8db2?color=5a5a5a)
Somit gilt:
![\(\begin{array}[t]{rll}
A_{\,\text{max}}&=&\dfrac{1}{2}\cdot \overline{BC}\cdot \overline{AS} & \\[5pt]
&=&\dfrac{1}{2}\cdot (2\cdot \overline{AB})\cdot \overline{AS} & \\[5pt]
&=&\dfrac{1}{2}\cdot (2\cdot 3,25\,\text{cm}) \cdot 12,43\,\text{cm} \\[5pt]
A_{\,\text{max}}&=&\underline{\underline{ 40,4\,\text{cm}^2}}
\end{array}\)](https://mathjax.schullv.de/1a92cf3991e21c6614f446a85deaa28ea9fe94cfe87b4dac18d24bf8e96feb2c?color=5a5a5a)
b)
.png)
Lösung 10
a)
Um das Volumen berechnen zu können, werden folgende Größen benötigt:
- Flächeninhalt der Pyramidengrundfläche, also des regelmäßigen Achtecks.
- Die Höhe der Pyramide.
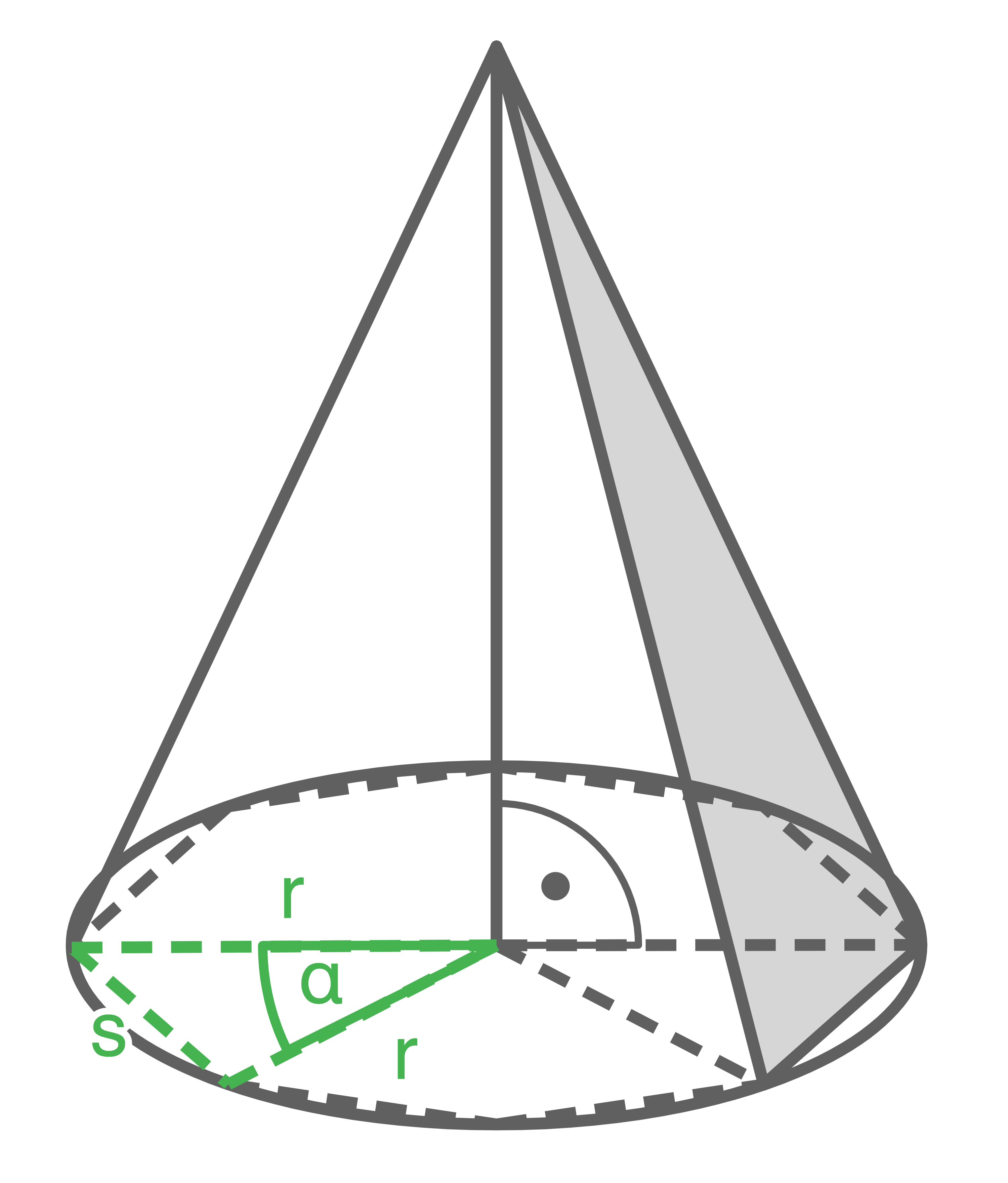
b)
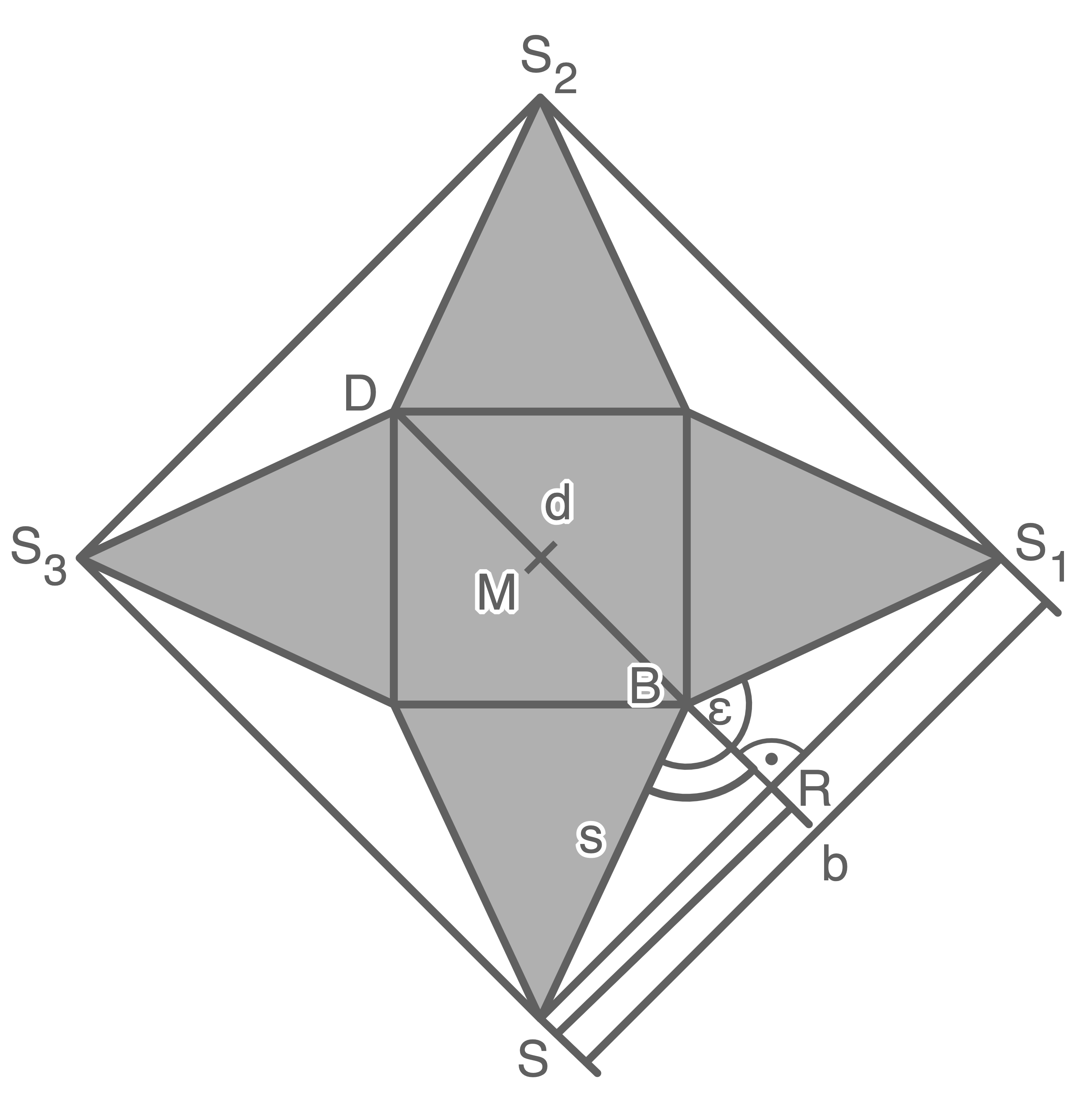
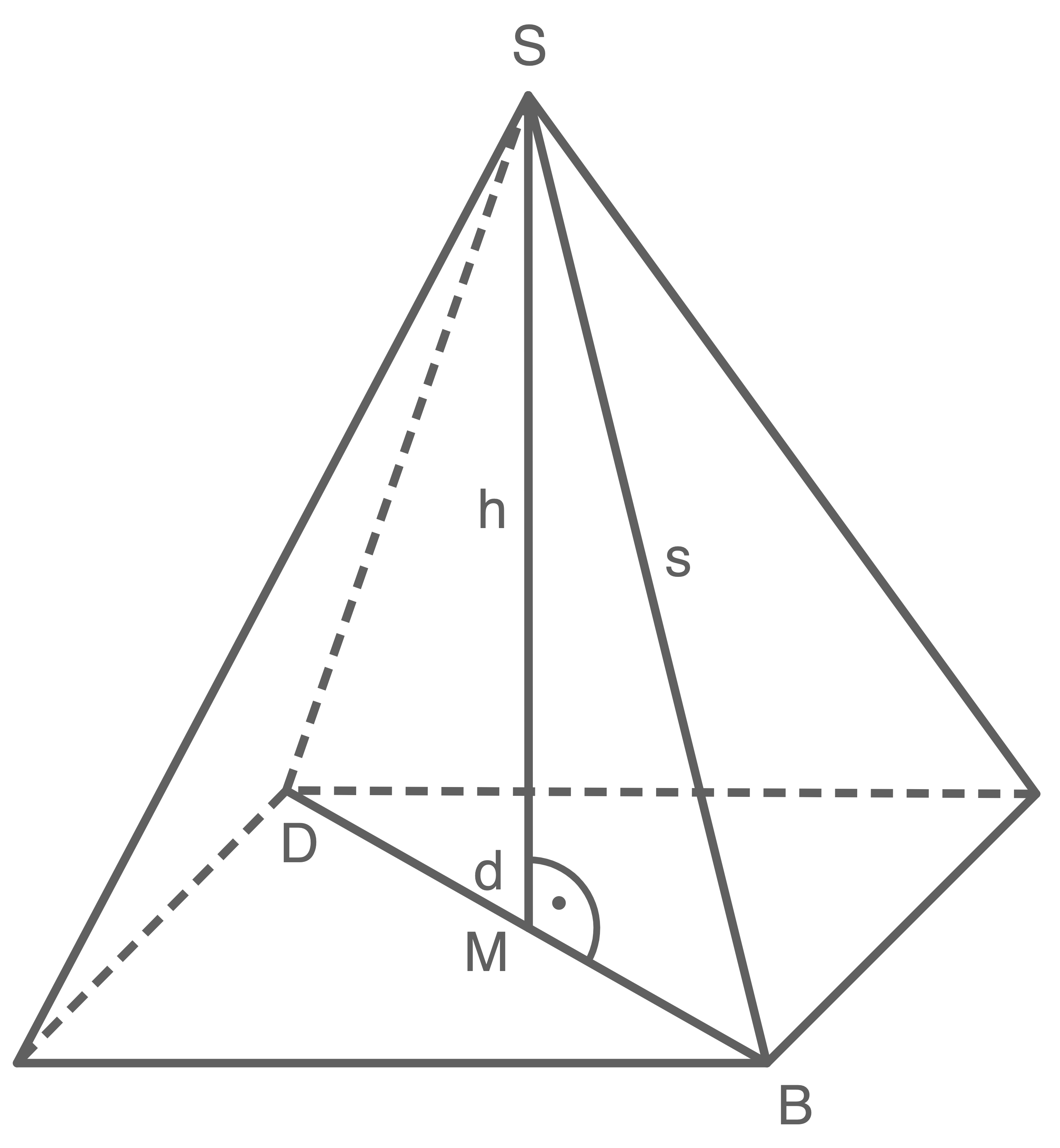
Lösung 11
a)
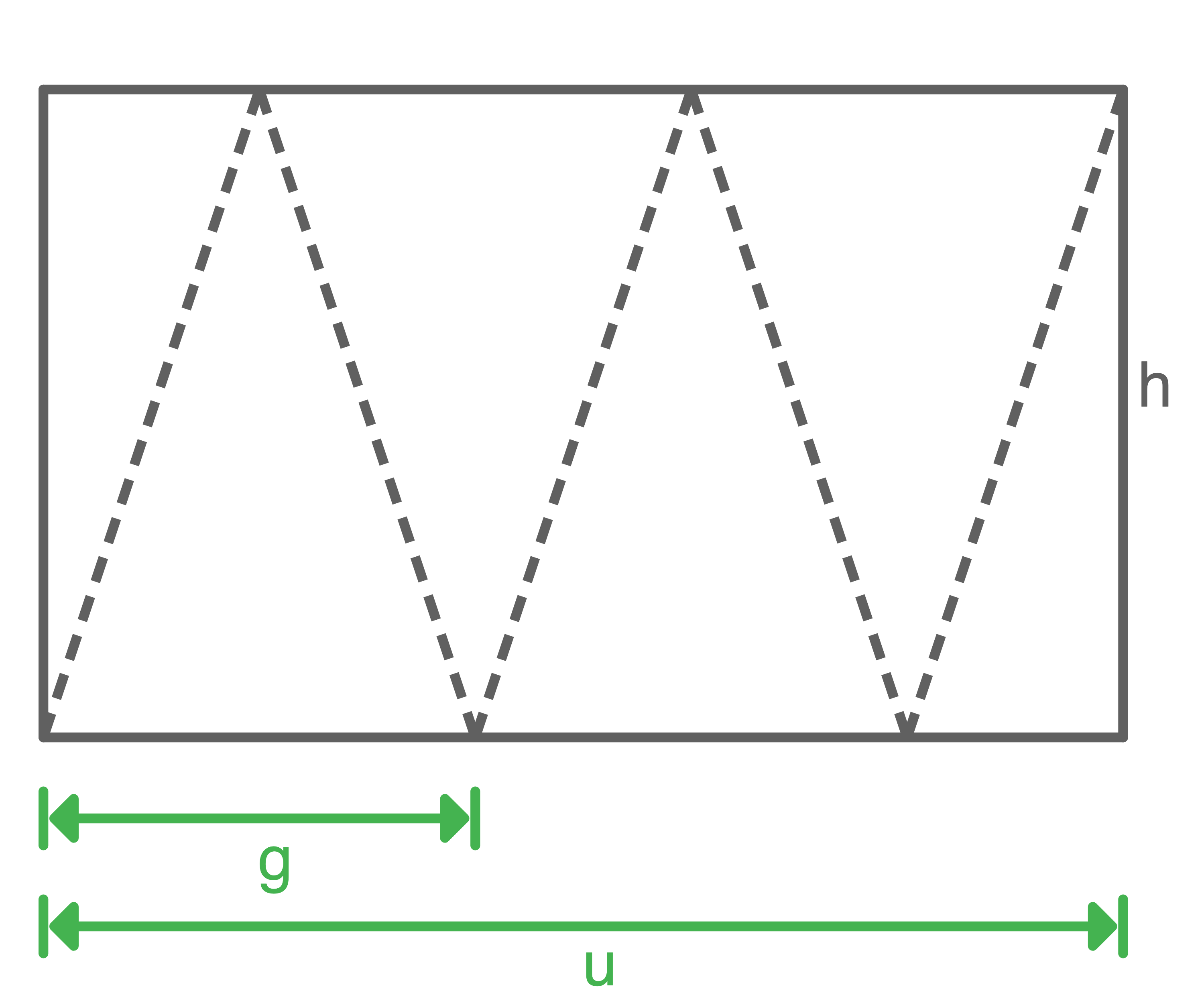
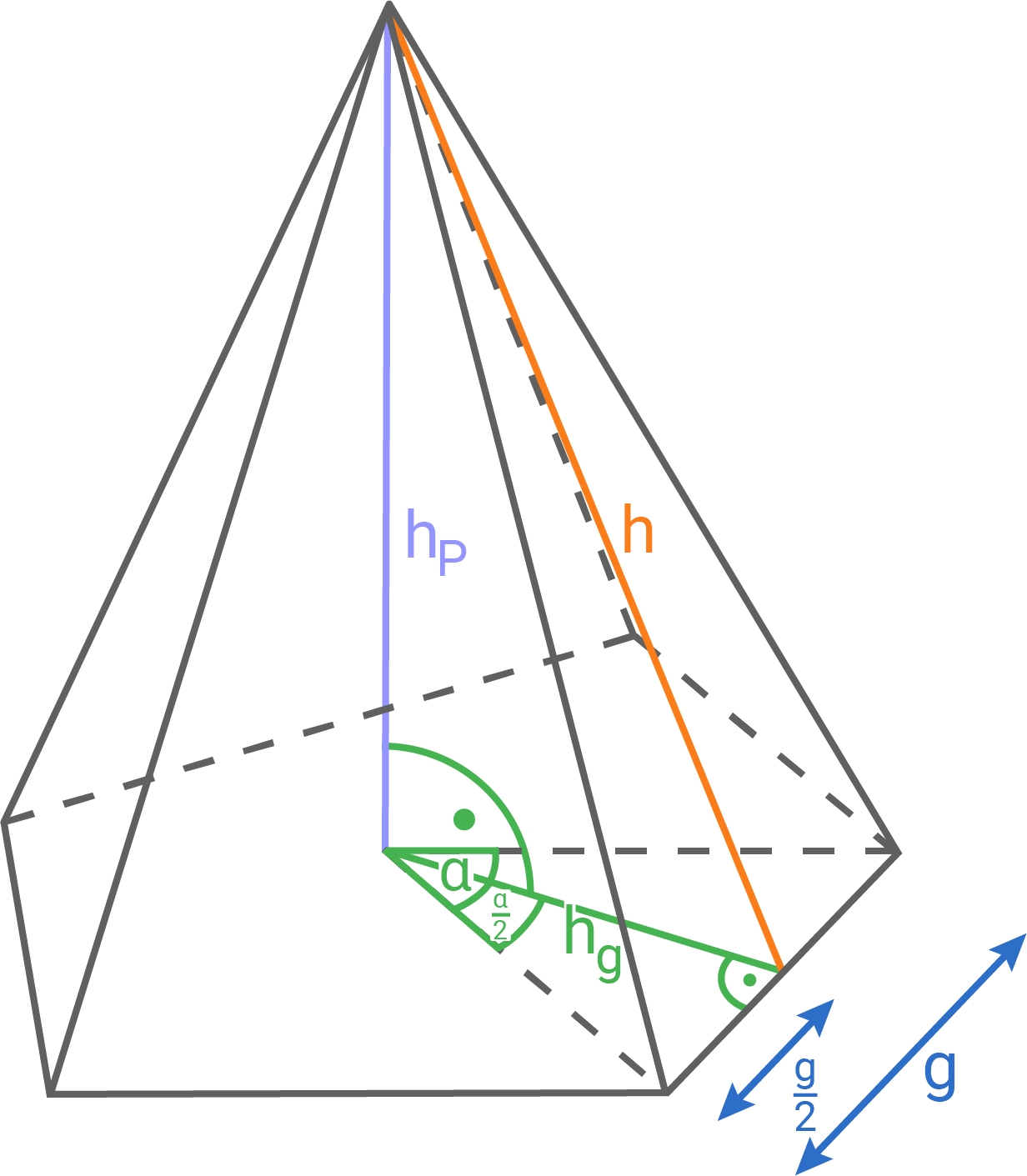
b)
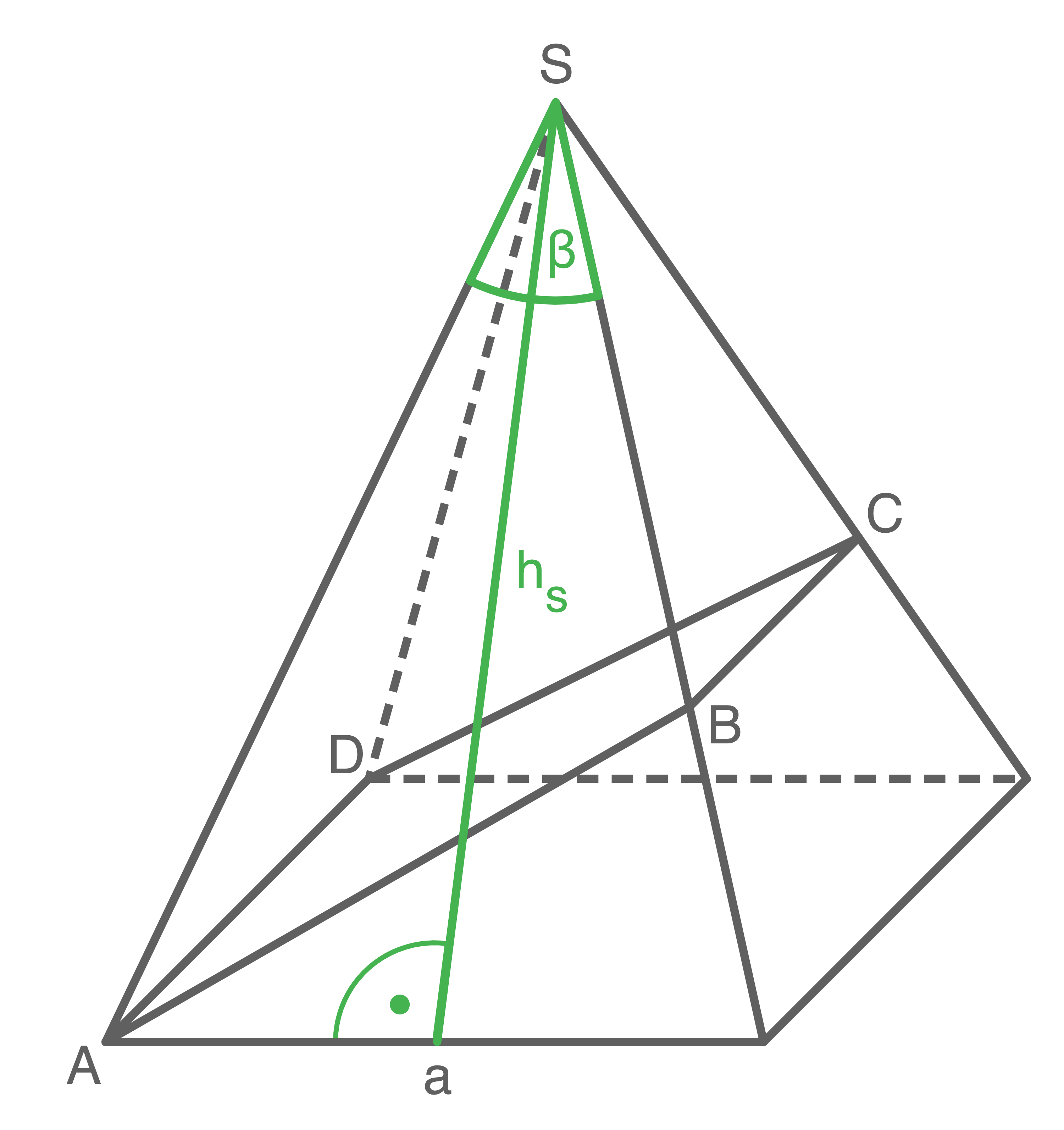
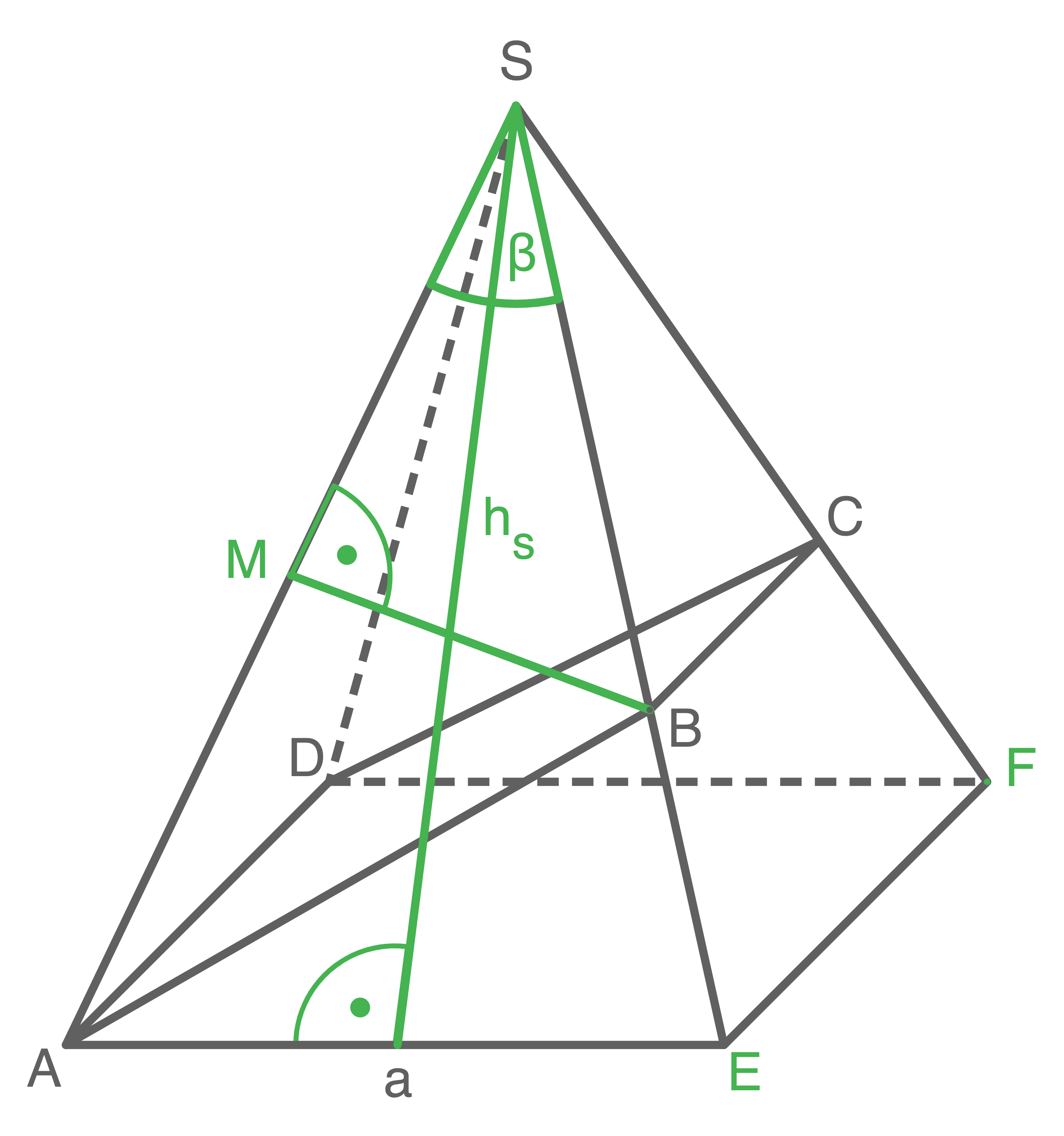
Lösung 12
a)
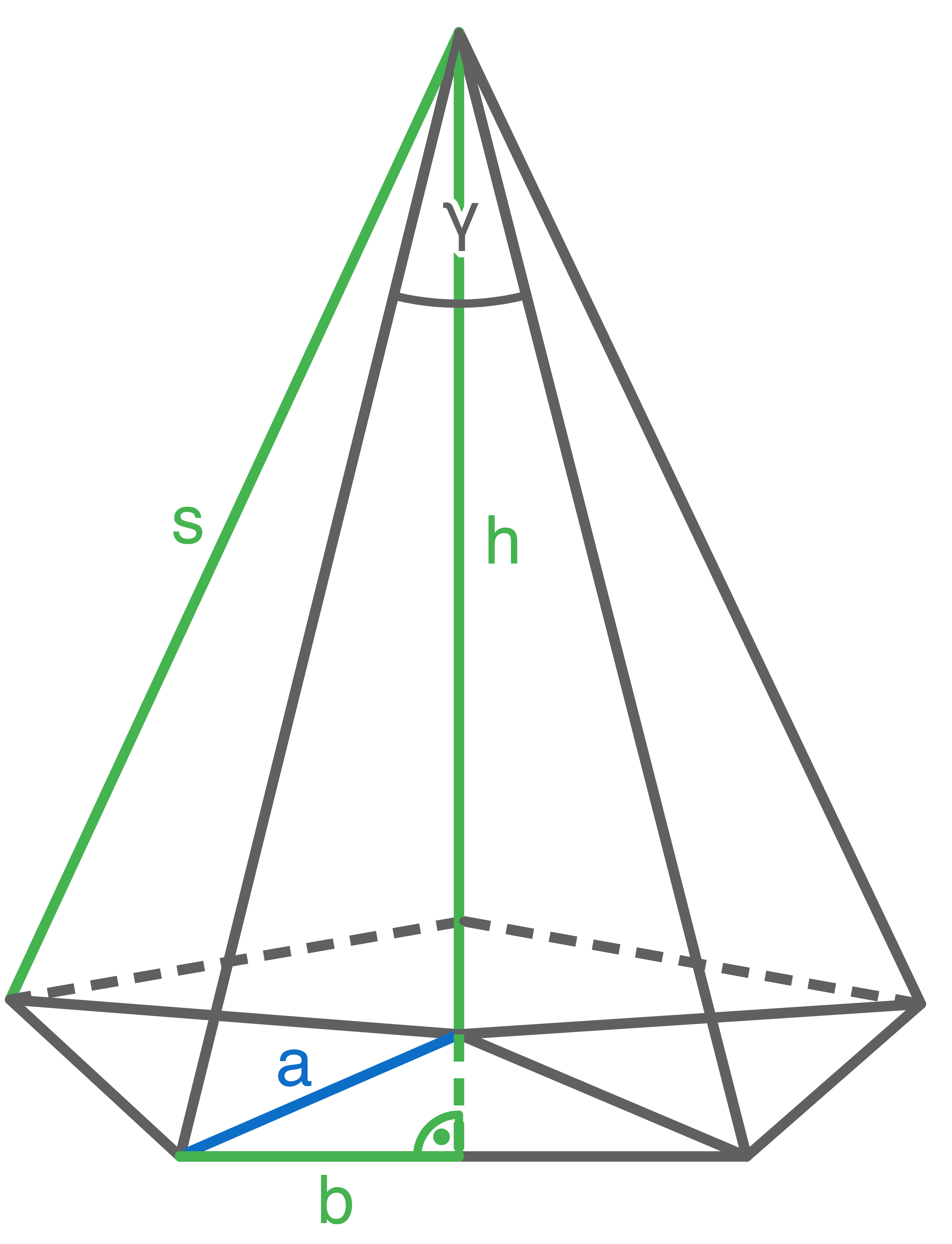
Skizze der Pyramide
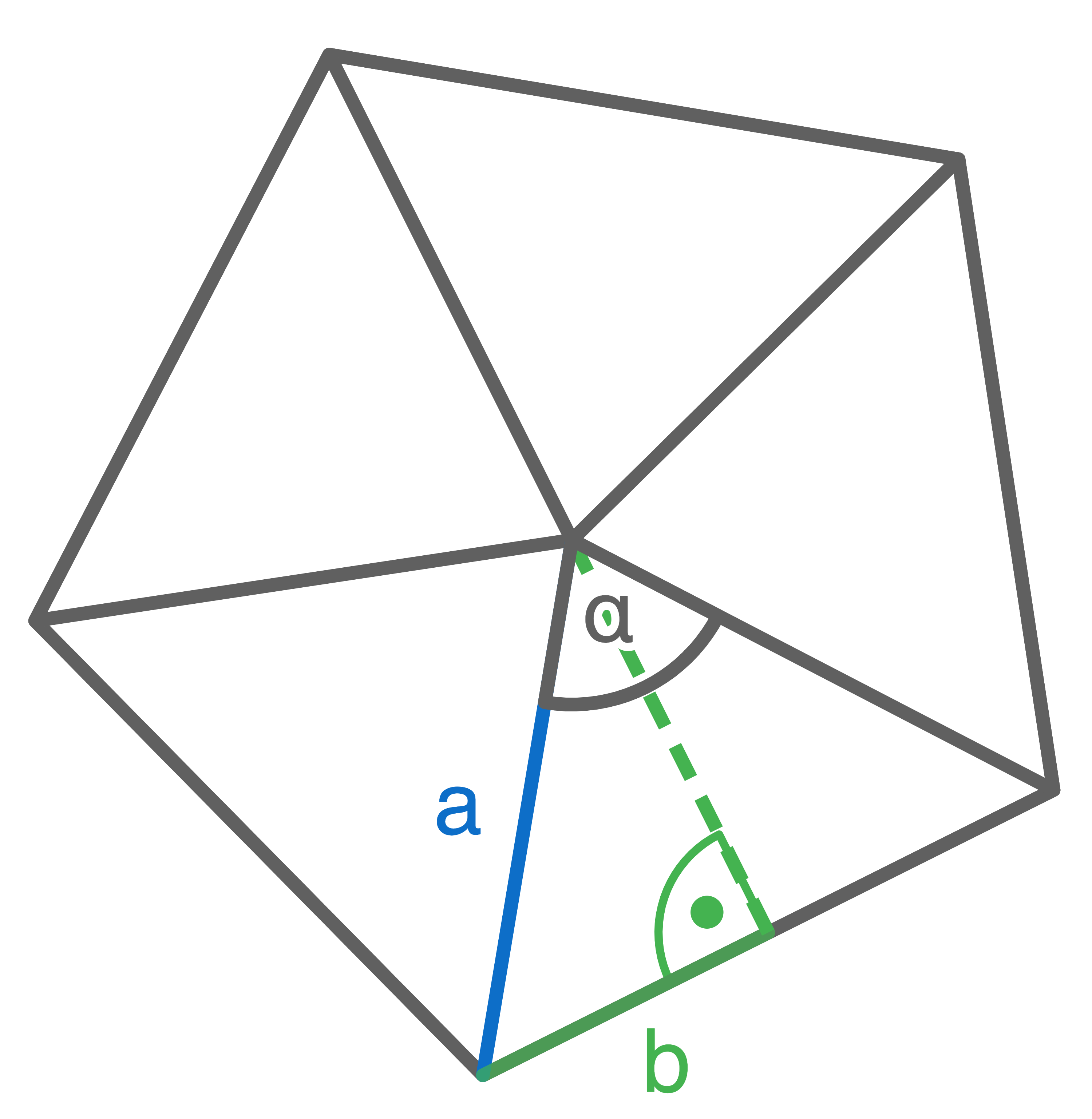
Skizze der Grundfläche
b)
Flächeninhalt des Dreiecks 
berechnen
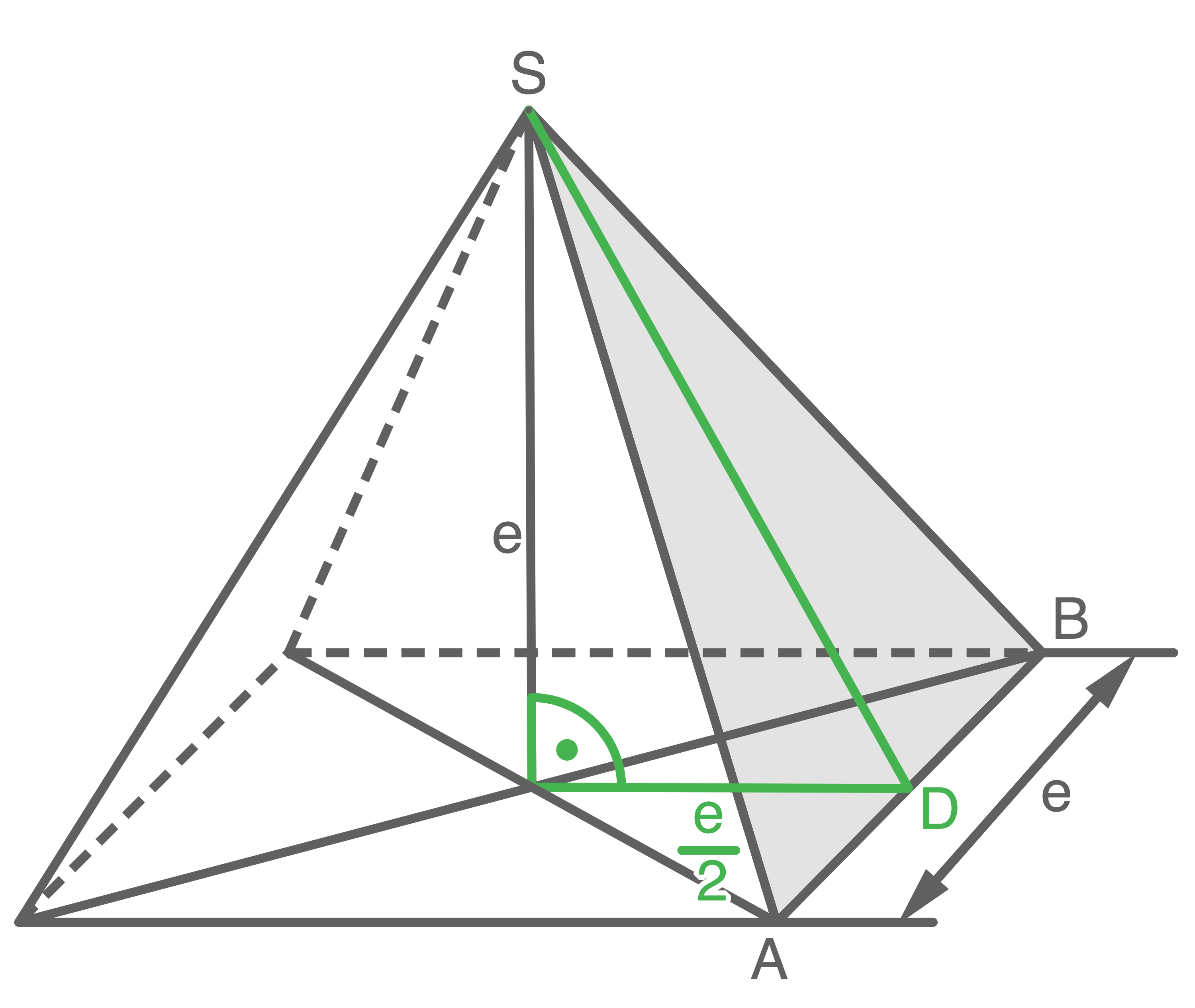Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{SD}^2 &=& e^2+\left(\dfrac{e}{2}\right)^2\quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
\overline{SD} &=&\sqrt{e^2+\left(\dfrac{e}{2}\right)^2} \\[5pt]
\overline{SD} &=&\sqrt{e^2+\dfrac{e^2}{4}} \\[5pt]
\overline{SD} &=&\sqrt{\dfrac{5}{4}e^2} \\[5pt]
\overline{SD} &=&\underline{ \dfrac{e}{2}\sqrt{5}}
\end{array}\)](https://mathjax.schullv.de/12a394a7d6f087a119a3dd1f4e271076ec388557c32b6dcf4435d5debad8d277?color=5a5a5a)
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{ABS}&=& \dfrac{1}{2}\cdot\text{e}\cdot \overline{SD}\\[5pt]
A_{ABS}&=&\dfrac{1}{2}\cdot e \cdot \dfrac{e}{2}\sqrt{5}\\[5pt]
A_{ABS}&=&\underline{ \dfrac{e^2}{4}\cdot\sqrt{5}}
\end{array}\)](https://mathjax.schullv.de/aa8b80280642055ac5a4223d1b86e63b7609df9a4f51f8c5fd5368d3c0d7dde5?color=5a5a5a)
Somit gehört Formel (3) zur Dreiecksfläche 
Flächeninhalt des Dreiecks 
berechnen
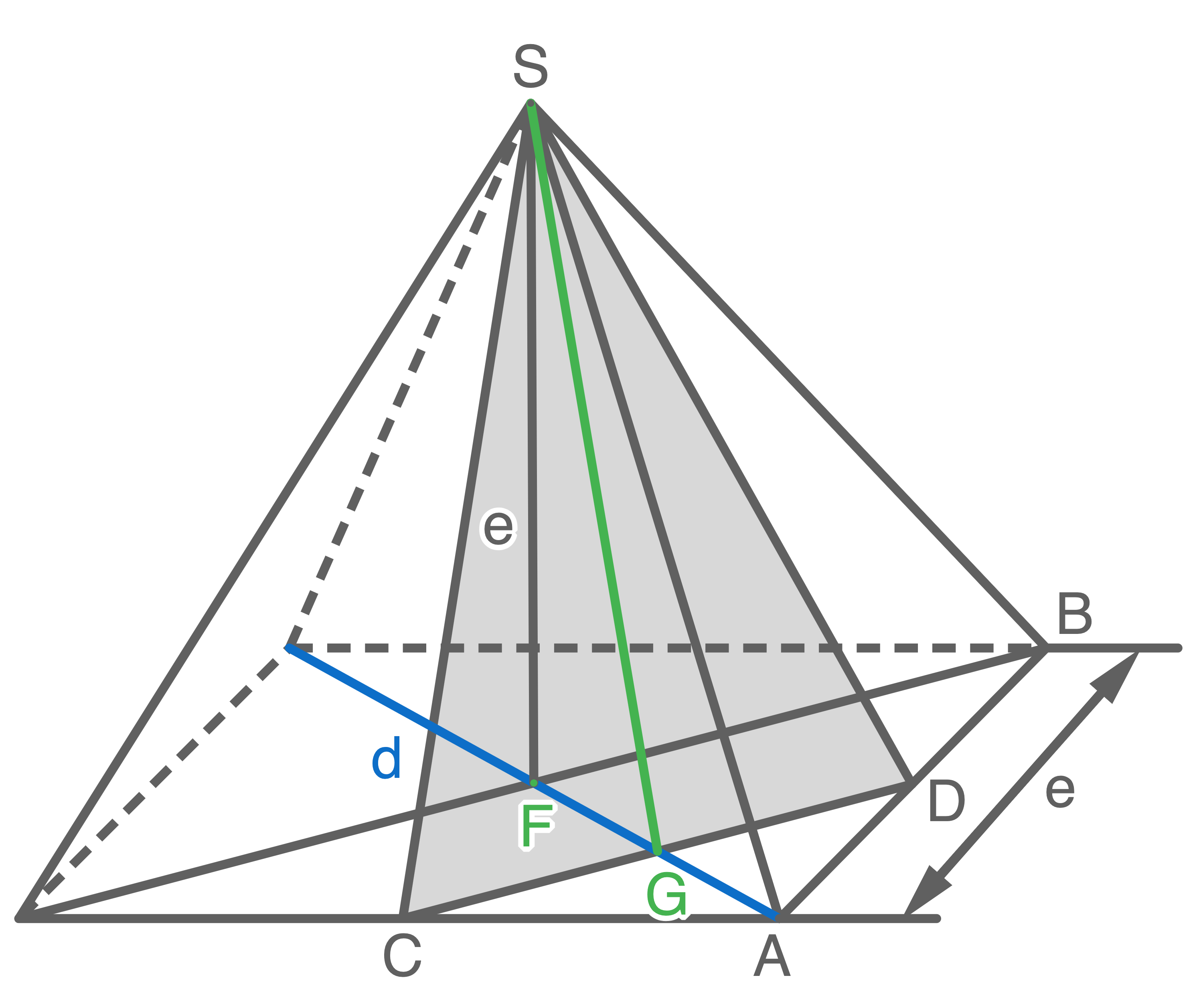Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}^2&=& \overline{CA}^2+\overline{AD}^2 \quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
\overline{CD}&=& \sqrt{\overline{CA}^2+\overline{AD}^2} &\\[5pt]
\overline{CD}&=& \sqrt{\left(\dfrac{e}{2}\right)^2+\left(\dfrac{e}{2}\right)^2}\\[5pt]
\overline{CD}&=& \sqrt{\dfrac{e^2}{4}+\dfrac{e^2}{4}}\\[5pt]
\overline{CD}&=&\sqrt{\dfrac{2e^2}{4}}\\[5pt]
\overline{CD}&=&\underline{ \dfrac{1}{2}e\sqrt{2}}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/4318de65099b154129b758720f10cd0a291acfdd2e5ebba6cd416001399c88c9?color=5a5a5a)
Länge der Strecke 
mit der Diagonale 
berechnen
![\(\begin{array}[t]{rll}
d^2&=&e^2+e^2 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
d&=& \sqrt{e^2+e^2} & \\[5pt]
d&=& \sqrt{2e^2} & \\[5pt]
d&=& e\sqrt{2} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0818433e5032bab639cf86d5c9245af2ef430586df0431a4f9f067507673dc68?color=5a5a5a)
Daraus folgt: 
Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\dfrac{\overline{FG}}{\overline{FA}}&=&\dfrac{\overline{DB}}{\overline{AB}} &\quad \scriptsize \mid\;\cdot \overline{FA} \\[5pt]
\overline{FG}&=&\dfrac{\overline{DB}}{\overline{AB}}\cdot \overline{FA} & \\[5pt]
\overline{FG}&=&\dfrac{\dfrac{e}{2}}{e} \cdot \dfrac{1}{2}e\sqrt{2}& \\[5pt]
\overline{FG}&=&\dfrac{1}{2}\cdot \dfrac{1}{2}e\sqrt{2} &\quad \scriptsize \\[5pt]
\overline{FG}&=&\underline{ \dfrac{1}{4}e\sqrt{2}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/48d8ec9d1e4032e7b760731c8b21b031aaaf0dd06ddfd54a6e46b9811ddd4dc9?color=5a5a5a)
Länge der Strecke 
berechnen
![\(\begin{array}[t]{rll}
\overline{SG}^2&=&\overline{SF}^2+\overline{FG}^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\overline{SG}&=&\sqrt{\overline{SF}^2+\overline{FG}^2 }& \\[5pt]
\overline{SG}&=&\sqrt{e^2+\left(\dfrac{1}{4}e\sqrt{2}\right)^2 }& \\[5pt]
\overline{SG}&=&\sqrt{e^2+\dfrac{1}{16}e^2\cdot 2 }& \\[5pt]
\overline{SG}&=&\sqrt{\dfrac{9}{8}e^2}& \\[5pt]
\overline{SG}&=&\dfrac{3}{2\sqrt{2}}e \quad \scriptsize \mid\; \text{Nenner rational machen} \\[5pt]
\overline{SG}&=&\dfrac{3\sqrt{2}}{2\sqrt{2}\sqrt{2}}e&\\[5pt]
\overline{SG}&=&\dfrac{3\sqrt{2}}{2\cdot 2}e&\\[5pt]
\overline{SG}&=&\underline{ \dfrac{3\sqrt{2}}{4}e}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/19d56784f8c76b37751c80c16b27173d5d16cadf2a6f8bac09ae5d518335d3f4?color=5a5a5a)
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{CDS}&=& \dfrac{1}{2}\cdot\overline{CD}\cdot \overline{SG}\\[5pt]
&=& \dfrac{1}{2}\cdot \dfrac{1}{2}e\sqrt{2}\cdot \dfrac{3\sqrt{2}}{4}e\\[5pt]
&=& \dfrac{1}{4}e^2\cdot \dfrac{3\cdot 2}{4}\\[5pt]
A_{CDS}&=& \underline{ \dfrac{3}{8}e^2}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ee02a7cd20900ea5cb8206457762ffe8b40202847da148a022cb0bef7f92bb37?color=5a5a5a)
Somit gehört Formel (1) zur Dreiecksfläche
Abschlussprüfung 2016
Lösung 13
a)
Höhe des Kegels berechnen
1. Schritt: Radius der Grundfläche berechnen
Umfang Dreiviertelkreis:
![\(\begin{array}[t]{rll}
U_{\,\text{Dr}}&=& \dfrac{3}{4}\cdot 2\cdot \pi \cdot r_K &\quad \scriptsize \\[5pt]
&=& \dfrac{3}{4}\cdot 2\cdot \pi \cdot 21,2\,\text{cm} &\quad \scriptsize \\[5pt]
U_{\,\text{Dr}}&=& \dfrac{159}{5}\cdot \pi \,\text{cm}
\end{array}\)](https://mathjax.schullv.de/943b8b82a51c1b528ef36d2a1baff47274e639d09b96811d6b1c11dd3b888eee?color=5a5a5a)
Umfang Dreiviertelkreis = Umfang Grundfläche
Umfang Grundfläche
![\(\begin{array}[t]{rll}
U_G&=&2\cdot \pi \cdot r_K \quad \scriptsize \mid\; : 2\pi \\[5pt]
r_K&=&\dfrac{U_G}{2\pi} \quad \scriptsize \mid\; U_G=\dfrac{159}{5}\cdot \pi \,\text{cm} \\[5pt]
r_K&=& \dfrac{\dfrac{159}{5}\cdot \pi \,\text{cm} }{2\pi} &\quad \scriptsize \\[5pt]
r_K&=& \underline{ 15,9\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/0b1550592883ba5c42d468ef988bbdec8a980b4ba125765f2610fa7923027fa7?color=5a5a5a)
2. Schritt: Höhe des Kegels berechnen
Höhe der Pyramide berechnen
1. Schritt: Seitenlänge der Grundfläche berechnen
Größe des Winkels 
berechnen
Die Winkelsumme eines Dreiviertelkreis wird in sechs regelmäßige Dreiecke aufgeteilt. Für 
gilt also:
![\(\begin{array}[t]{rll}
\gamma&=&\dfrac{360^{\circ} \cdot \dfrac{3}{4}}{6} &\quad \scriptsize \\[5pt]
\gamma&=&\dfrac{270^{\circ}}{6} \\[5pt]
\gamma&=& 45^{\circ}
\end{array}\)](https://mathjax.schullv.de/e72daab514181f9a751c9a97cceabc49de11fac9cc3bf7eb4ea13d71dcbcc660?color=5a5a5a)
Länge von 
berechnen
![\(\begin{array}[t]{rll}
\sin\left(\dfrac{\gamma}{2}\right)&=& \dfrac{\dfrac{a}{2}}{s_P}\quad \scriptsize \mid\;\cdot s_P \\[5pt]
\dfrac{a}{2}&=&\sin\left(\dfrac{\gamma}{2}\right) \cdot s_P &\quad \scriptsize \\[5pt]
\dfrac{a}{2}&=&\sin(22,5^{\circ})\cdot 21,2\,\text{cm} \quad \scriptsize \mid\; \cdot 2\\[5pt]
a&=& \underline{ 16,2\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/1aeada8828554af5e4b5bcd4ed4eb6f4cef4ad7a5fe0bdda3f84a78b3b5f5eae?color=5a5a5a)
2. Schritt: Höhe der Pyramide berechnen
![\(\begin{array}[t]{rll}
d&=& h_K-h_P &\quad \scriptsize \\[5pt]
&=& 14\,\text{cm}-13,7\,\text{cm} &\quad \scriptsize \\[5pt]
d&=& \underline{\underline{ 0,3\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/4862d61f2381f1fc01e53051bdc144ad983955f053e740d67d100e2c854c48ca?color=5a5a5a)
Vogelsicht der Pyramide:
Querschnitt der Pyramide:
Differenz D der Körperhöhen berechnen
b)
Kegelvolumen berechnen
Volumenformel für einen halben Kegel: 
2. Schritt: Kegelhöhe berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{h}{\overline{BM}} \quad \scriptsize \mid\; \cdot \overline{BM} \\[5pt]
h&=&\tan(\beta)\cdot \overline{BM} &\quad \scriptsize \\[5pt]
h&=&\tan(62^{\circ})\cdot 5,7\,\text{cm} &\quad \scriptsize \\[5pt]
h &= & \underline{ 10,72 \,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/77ea737a2f43b0729f4636b44c198b7654da43ecc18be7de3ec5dcc5557a1bb7?color=5a5a5a)
3. Schritt: Volumen des halben Kegels berechnen
![\(\begin{array}[t]{rll}
V_K&=&\dfrac{\dfrac{1}{3}\cdot \pi \cdot r^2\cdot h}{2} &\quad \scriptsize \\[5pt]
&=& \dfrac{\dfrac{1}{3}\cdot \pi \cdot (5,7\,\text{cm})^2\cdot 10,72\,\text{cm} }{2} &\quad \scriptsize \\[5pt]
V_K&=&\underline{ 182,37 \,\text{cm}^3}
\end{array}\)](https://mathjax.schullv.de/6cc43836b23448304d6799e3986973bbf8169ac0fa56e63001e581c3084bcd3c?color=5a5a5a)
Differenz der bekannten Volumina berechnen
![\(\begin{array}[t]{rll}
V_P&=&V_{\,\text{Ges}}-V_K &\quad \scriptsize \\[5pt]
&=& 1280\,\text{cm}^3-182,37\,\text{cm}^3&\quad \scriptsize \\[5pt]
V_P&=& \underline{ 1\,097,63 \,\text{cm}^3}
\end{array}\)](https://mathjax.schullv.de/c56071cced2b0048a293f4ab965f8e9a5a733d39272588e937b2439029b0d2d1?color=5a5a5a)
Volumen des Dreiecksprismas berechnen
1. Schritt: Grundfläche 
berechnen
![\(\begin{array}[t]{rll}
G&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot \overline{AB}\cdot h &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 11,4\,\text{cm}\cdot 10,72\,\text{cm} &\quad \scriptsize \\[5pt]
G&=&\underline{ 61,10\,\text{cm}^3}
\end{array}\)](https://mathjax.schullv.de/3b9c4e14b1e233ae358b4daea36de11855122f289882346bba2feb24b80dc8e3?color=5a5a5a)
2. Schritt: Länge des Dreiecksprismas berechnen
![\(\begin{array}[t]{rll}
V_P&=&G\cdot l_P \quad \scriptsize \mid\; :G \\[5pt]
l_P&=&\dfrac{V_P}{G} &\quad \scriptsize \\[5pt]
l_P&=& \dfrac{1097,63\,\text{cm}^3}{61,1\,\text{cm}^2}&\quad \scriptsize \\[5pt]
l_P&= & \underline{ 17,96\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/7f369fd07a0dc50a8959dd7d6580c3a4c5cd42eb8ba43ef16703041354f14ba8?color=5a5a5a)
Gesamtlänge des Körpers berechnen
![\(\begin{array}[t]{rll}
l_{\,\text{Ges}}&=& l_K+l_P&\quad \scriptsize \\[5pt]
&=& r_K+l_P&\quad \scriptsize \\[5pt]
&=& 5,7\,\text{cm}+17,96\,\text{cm}&\quad \scriptsize \\[5pt]
l_{\,\text{Ges}}&=& \underline{\underline{ 23,7\,\text{cm}}}
\end{array}\)](https://mathjax.schullv.de/0dd45ff6c7bef5f62844be08f2ab6f9b84de32481037fbfc7495fdd4d6e53cea?color=5a5a5a)
Abschlussprüfung 2015
1. Schritt: Kegelradius berechnen
![\(\begin{array}[t]{rll}
\overline{BM}&=&\dfrac{\overline{AB}}{2} &\quad \scriptsize \\[5pt]
\overline{BM}&=& \dfrac{11,4\,\text{cm}}{2}&\quad \scriptsize \\[5pt]
\overline{BM} &=& \underline{ 5,70\,\text{cm}} = r
\end{array}\)](https://mathjax.schullv.de/43db8d8bf51b98841e182e3f8b1d893d11d78d243ceccb750d5c6e58558f4674?color=5a5a5a)