Wahlaufgaben
8.
Funktionen
8.1
Gegeben ist eine lineare Zuordnung 
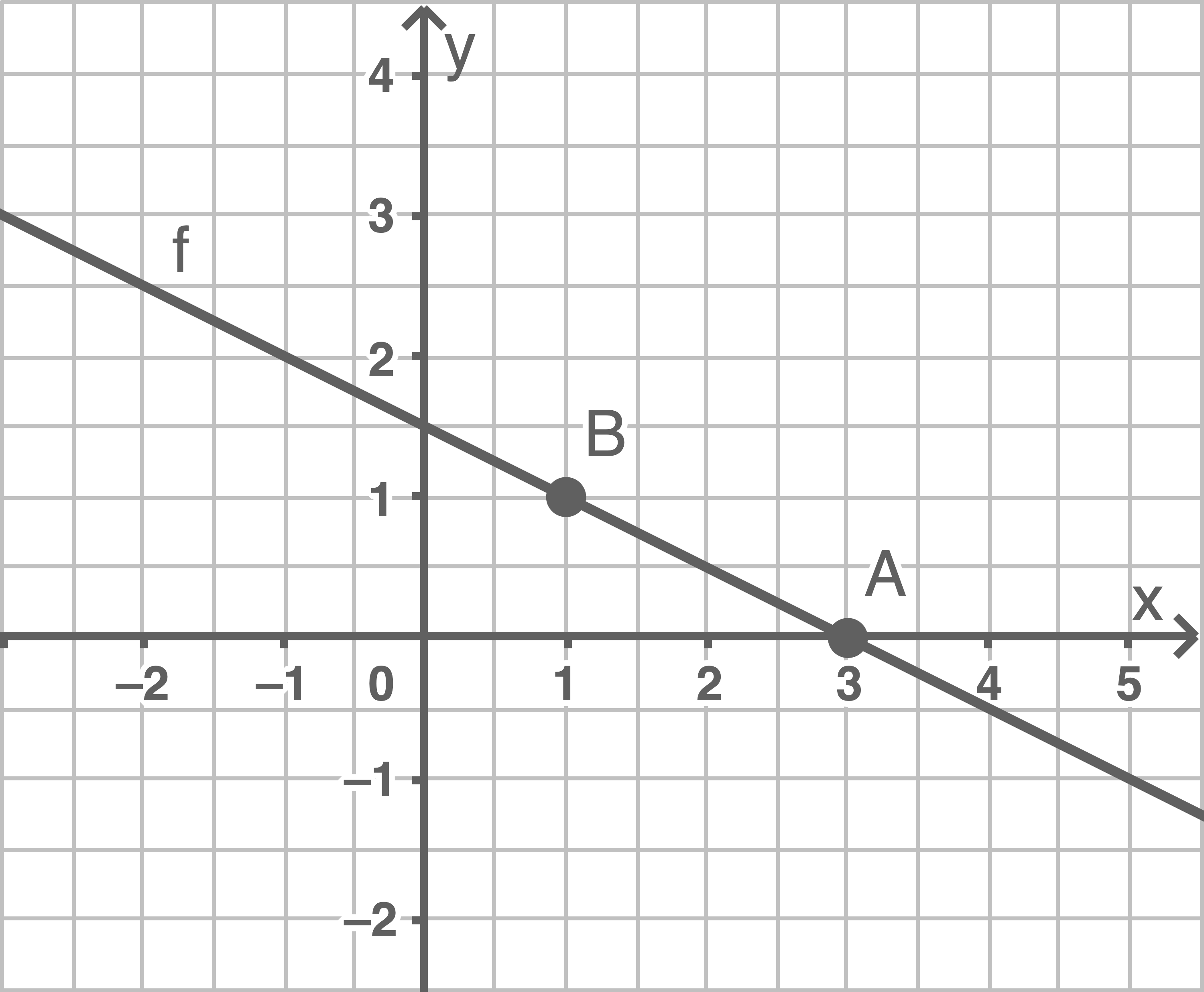
Der Graph von verläuft durch die Punkte
verläuft durch die Punkte  und
und  .
.
 durch
durch  Die Graphen von
Die Graphen von  und
und  schneiden sich im Punkt
schneiden sich im Punkt 
 mit der
mit der  -Achse ist der Punkt
-Achse ist der Punkt 
Der Graph von
a)
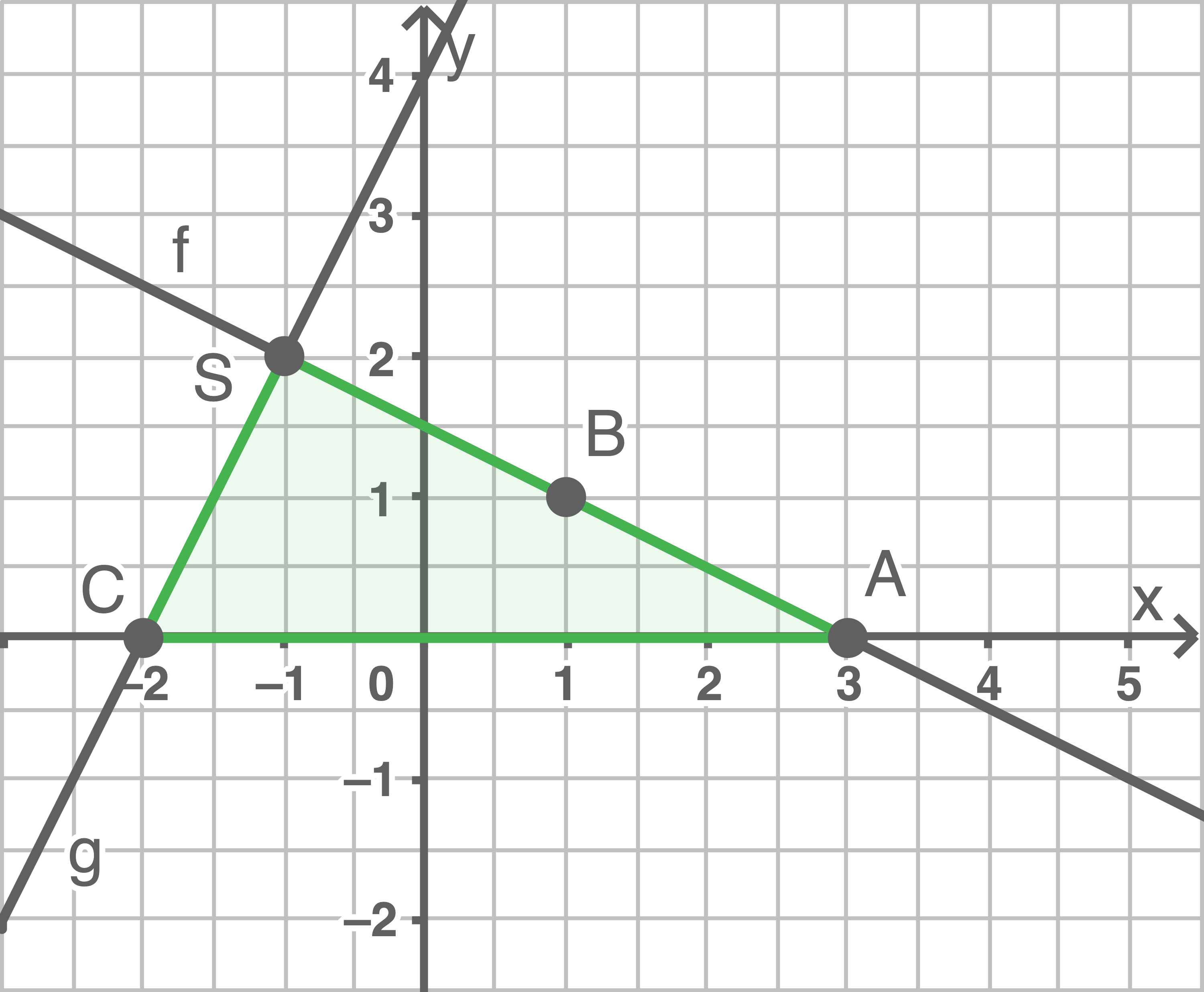
Stelle den Graph der Zuordnung  in einem Koordinatensystem dar.
in einem Koordinatensystem dar.
(Eine Längeneinheit entspricht )
)
Gegeben ist eine weitere lineare Zuordnung (Eine Längeneinheit entspricht
(3 BE)
b)
Ermittle die Koordinaten von 
Der Schnittpunkt des Graphen von
(2 BE)
c)
Berechne den Flächeninhalt des Dreiecks 
(3 BE)
8.2
Für 50 Personen der 9. Klassen wird zum Wandertag ein Bus gebucht.
Jede Person muss dafür bezahlen.
bezahlen.
Zwei Personen können nicht am Wandertag teilnehmen. Berechne den neuen Preis pro Person in Euro.
Jede Person muss dafür
Zwei Personen können nicht am Wandertag teilnehmen. Berechne den neuen Preis pro Person in Euro.
(2 BE)
9.
Geometrie
9.1
Ein Würfel hat eine Kantenlänge von 
a)
Zeichne das Schrägbild dieses Würfels auf unliniertem Papier.
(2 BE)
b)
Berechne das Volumen dieses Würfels.
(2 BE)
Das dargestellte Würfelnetz soll auf ein A4-Blatt ( breit,
breit,  lang) gezeichnet werden. Der entstehende Würfel soll möglichst groß sein.
lang) gezeichnet werden. Der entstehende Würfel soll möglichst groß sein.
(Klebeflächen werden nicht berücksichtigt.)
(Klebeflächen werden nicht berücksichtigt.)

c)
Ermittle den Oberflächeninhalt des Würfels.
(3 BE)
9.2
Ein Modell der Erde auf einem Brunnen hat einen Durchmesser von 
Der Durchmesser der Erde beträgt etwa Drei Schüler haben den verwendeten Maßstab bestimmt:
Drei Schüler haben den verwendeten Maßstab bestimmt:
![\(\begin{array}[t]{ll}
\text{Anton}& 1:8\,500\,000\\[5pt]
\text{Ben}& 1:850\,000\\[5pt]
\text{Max}& 1:85\,000
\end{array}\)](https://mathjax.schullv.de/cc43bc1f51e480b80a43cf49d0ddce1ca3ba08f61c2708d2e6794e77442ce512?color=5a5a5a) Begründe, wer Recht hat.
Begründe, wer Recht hat.
Der Durchmesser der Erde beträgt etwa

(3 BE)
10.
Arithmetik/Algebra
10.1
Jonas und Alina unternehmen eine Wanderung.
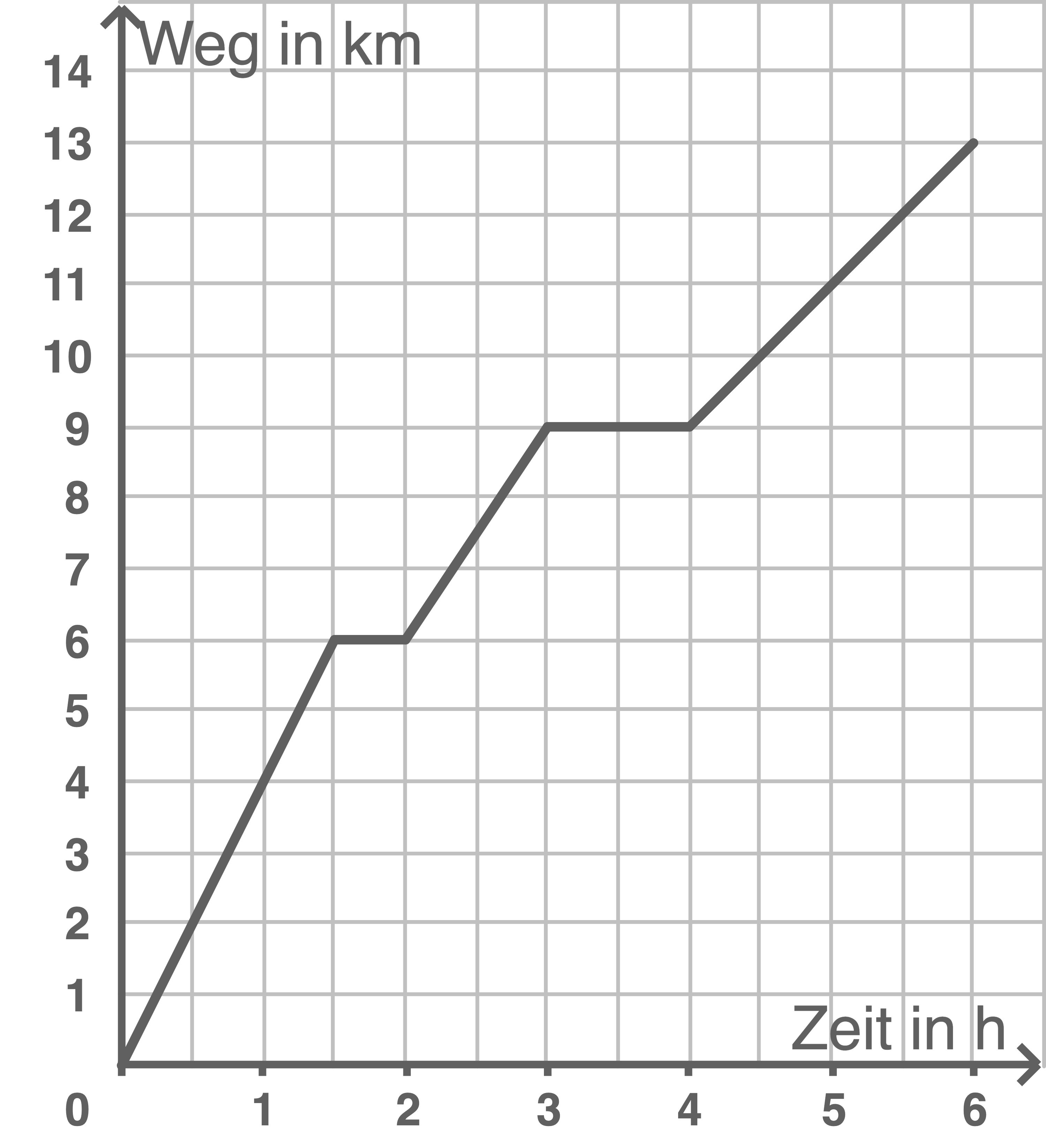
Alina stellt den zurückgelegten Weg in Abhängigkeit von der Zeit im Diagramm dar.
Alina stellt den zurückgelegten Weg in Abhängigkeit von der Zeit im Diagramm dar.
a)
Gib die Länge des gesamten Weges für diese Wanderung an.
(1 BE)
b)
Berechne den prozentualen Anteil der Pausenzeiten an der Gesamtzeit dieser Wanderung.
Jonas und Alina starten um 09:00 Uhr.
(3 BE)
c)
Gib die Ankunftszeit an.
(1 BE)
10.2
Schülerinnen und Schüler kochen in der Projektwoche „Gesunde Ernährung“ Rote-Bete-Suppe nach dem abgedruckten Rezept.
Ein Kilogramm Rote Bete kostet 3,99 €.
für vier Portionen:
450 g Rote Bete
150 g Kartoffeln
850 ml Gemüsebrühe
...
150 g Kartoffeln
850 ml Gemüsebrühe
...
a)
Ermittle den Preis der benötigten Rote Bete für 17 Portionen.
Die Suppe wird nach diesem Rezept mit
(3 BE)
b)
Berechne die Anzahl der Portionen.
(2 BE)
11.
Stochastik
In einer Regelschule wurde ein Getränkeautomat aufgestellt.
Am ersten Tag wurden folgende Getränke nacheinander verkauft:
Am ersten Tag wurden folgende Getränke nacheinander verkauft:
| C |
| C |
| W |
| A |
| W |
| A |
| S |
| S |
| A |
| W |
| C |
| C |
| W |
| W |
| A |
| S |
| S |
| A |
| W |
| C |
| A |
| W |
| A – Apfelschorle |
| C – Cola |
| S – Saft |
| W – Wasser |
a)
Erstelle eine Häufigkeitstabelle für diese verkauften Getränke.
(2 BE)
b)
Stelle die Anzahl der verkauften Getränke in einem geeigneten Diagramm dar.
(3 BE)
c)
Berechne den prozentualen Anteil des Getränkes, das an diesem Tag am häufigsten verkauft wurde.
Die Getränke kosten jeweils
(3 BE)
d)
Berechne die Einnahmen innerhalb einer fünftägigen Schulwoche.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
8.1
a)
b)
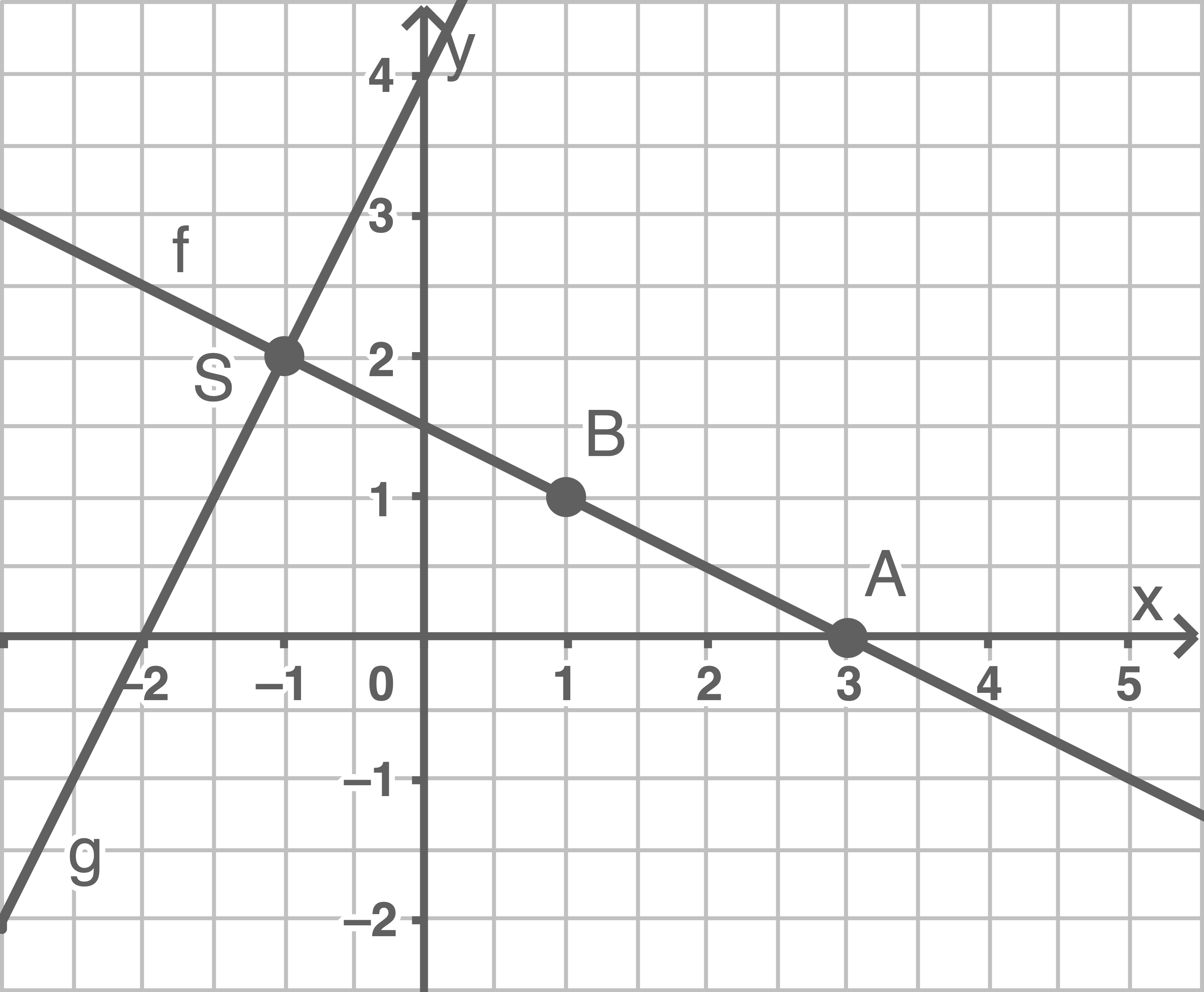
c)
8.2
Preis für den Bus:
 Neuer Preis pro Person:
Neuer Preis pro Person:

9.1
a)
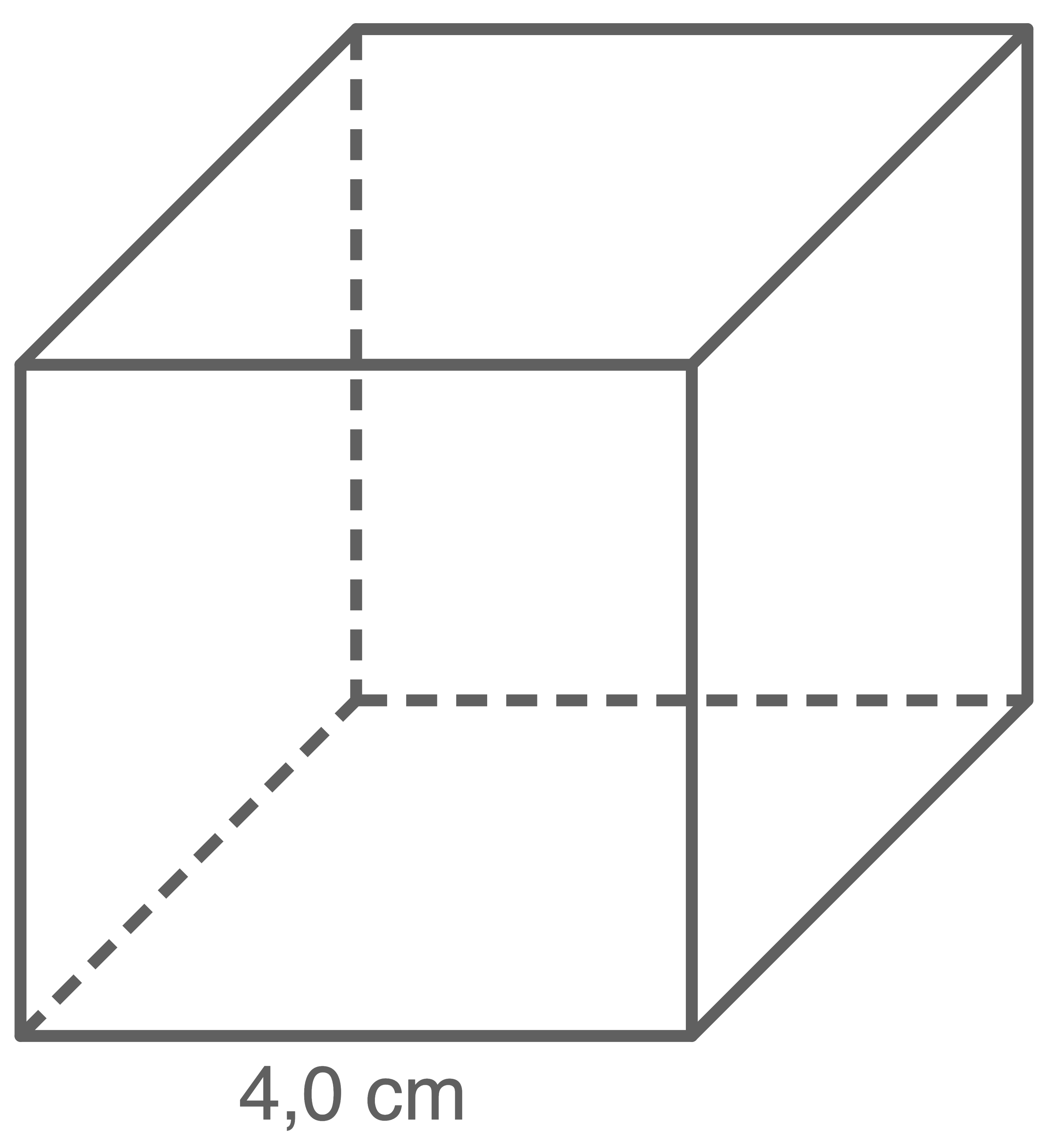
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
b)
c)
Kantenlänge des Würfels berechnen:
 Damit lässt sich der Oberflächeninhalt des Würfels berechnen:
Damit lässt sich der Oberflächeninhalt des Würfels berechnen:

9.2
10.1
a)
Der gesamte Weg ist  lang.
lang.
b)
Pausenzeiten:  Gesamtzeit:
Gesamtzeit: 
![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{90\,\text{min}}{360\,\text{min}}\cdot 100\,\% \\[5pt]
&=& 25\,\%
\end{array}\)](https://mathjax.schullv.de/992303e7a4c769ca731afc33a1ad5b857cca6a6a47a7fbc393d1ecc95457117b?color=5a5a5a) Der prozentuale Anteil beträgt
Der prozentuale Anteil beträgt 
c)
Jonas und Alina starten um 9:00 Uhr und sind 6 Stunden unterwegs.
Die Ankuftszeit ist um 15:00 Uhr.
10.2
a)
Benötigte Rote Bete mit dem Dreisatz berechnen:




![\(\begin{array}{rcl}
4 & \mathrel{\widehat{=}}& 450\,\text{g}\\[5pt]
1 & \mathrel{\widehat{=}}& 112,5\,\text{g}\\[5pt]
17 & \mathrel{\widehat{=}}& 1\,912,5\,\text{g}
\end{array}\)](https://mathjax.schullv.de/c2fa1001b7bf7bb88da20de2ae6f269871c2db18ae8d031cbde44971ac77e771?color=5a5a5a)




 Preis berechnen:
Preis berechnen:

b)
11.
a)
| A | C | S | W |
| 6 | 5 | 4 | 7 |
b)
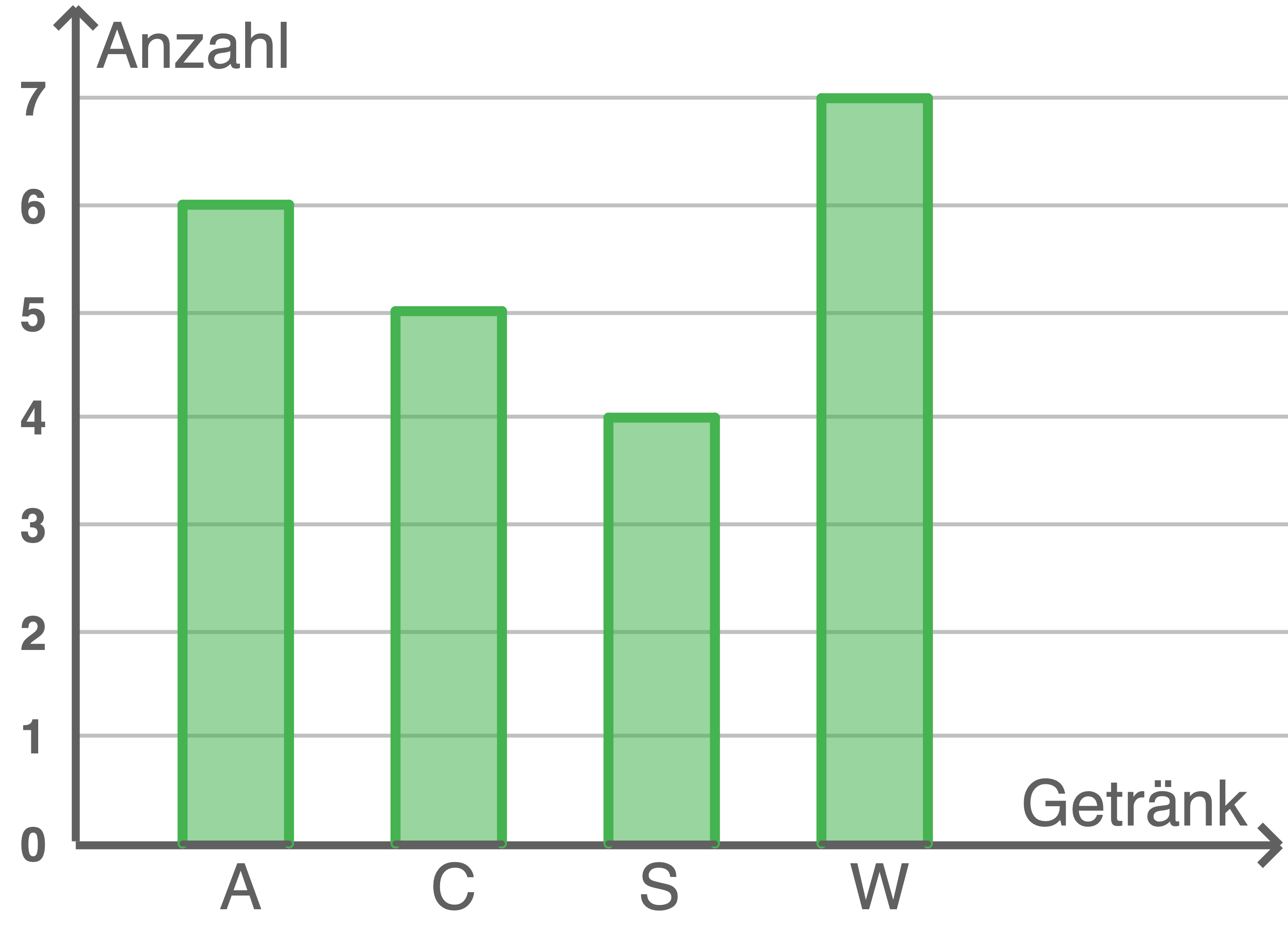
c)
Insgesamt wurden 22 Getränke verkauft. Am häufigsten wurde an diesem Tag Wasser verkauft.

d)