Wahlaufgaben

Arithmetik/Algebra

8.1

Für eine $75\,\text{m}^2$ große Wohnung sollen monatlich $637,50\,€$ Miete gezahlt werden.

Berechne die Miete für einen Quadratmeter.

(2 BE)

Für eine andere, gleichgroße Wohnung, beträgt die Miete monatlich $7,10\,€$ pro Quadratmeter.

Berechne die jährliche Ersparnis für die günstigere Wohnung.

(4 BE)

8.2

Das Doppelte einer Zahl vermehrt um sechs ist gleich dem Dreifachen dieser Zahl vermindert um $1.$
Ermittle diese Zahl.

(2 BE)

8.3

Im Schülercafé "Kubus" werden Waffeln gebacken. Das nebenstehende Rezept reicht für zehn Waffeln aus.

Die Schüler haben $875\,\text{g}$ Haferflocken zur Verfügung. Die anderen Zutaten sind ausreichend vorhanden.

Ermittle die Anzahl der Waffeln, die nach diesem Rezept maximal gebacken werden können.

Rezept

$125\,\text{g}$ Haferflocken
$\frac{1}{4}$ Liter Milch
$3$ Esslöfel Zucker
$\frac{1}{2}$ Teelöffel Zimt
$2$ Esslöffel Butter
$2$ Eier

(2 BE)

Stochastik

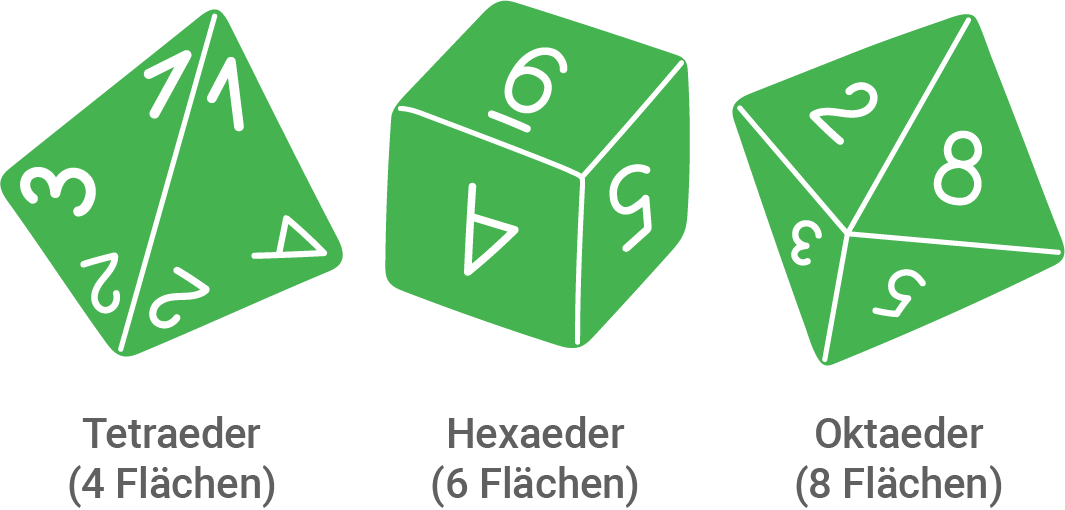
Die abgebildeten Körper können als Spielwürfel genutzt werden. Die Seitenflächen sind mit den Zahlen $1,2,3,...$ nummeriert.
Beim Tetraeder wird die geworfene Augenzahl an der Spitze abgelesen.

Spielwürfel - Thüringen Hauptschulabschluss

Ein Spielwürfel wurde $20$ -mal geworfen.

mögliche Ergebnisse	Anzahl
$1$
$2$
$3$
$4$

Entscheide, welcher Spielwürfel genutzt wurde.
Gib die relative Häufigkeit für die Augenzahl " $1$ " an.

(2 BE)

Bei einem Spiel gewinnt man, wenn die Augenzahl durch drei teilbar ist.

Wähle einen Spielwürfel so, dass du gute Gewinnchancen hast. Begründe deine Wahl.

(3 BE)

Das Hexaeder wird $300$ -mal geworfen.

Gib die Anzahl der Augenzahl "6" an, die du erwarten würdest.

(1 BE)

Die Flächen des Hexaeders wurden rot und blau gefärbt. Beim einmaligen Werfen wird mit einer Wahrscheinlichkeit von $\dfrac{1}{3}$ eine blaue Fläche geworfen.

Skizziere ein Netz dieses Hexaeders.

(2 BE)

Das Oktaeder wird einmal geworfen.

Ermittle die Wahrscheinlichkeit dafür, dass eine Primzahl geworfen wird.

(2 BE)

10.

Funktionen

Gera	Tagestarif	Nachttarif
Grundgebühr einschließlich erster Kilometer	$7,00\,€$	$7,00\,€$
jeder weitere angefangene Kilometer	$2,20\,€$	$2,30\,€$

Frau Müller fährt in Gera am Tag eine $12\,\text{km}$ lange Strecke mit dem Taxi.

Berechne den Preis für die Taxifahrt.

(2 BE)

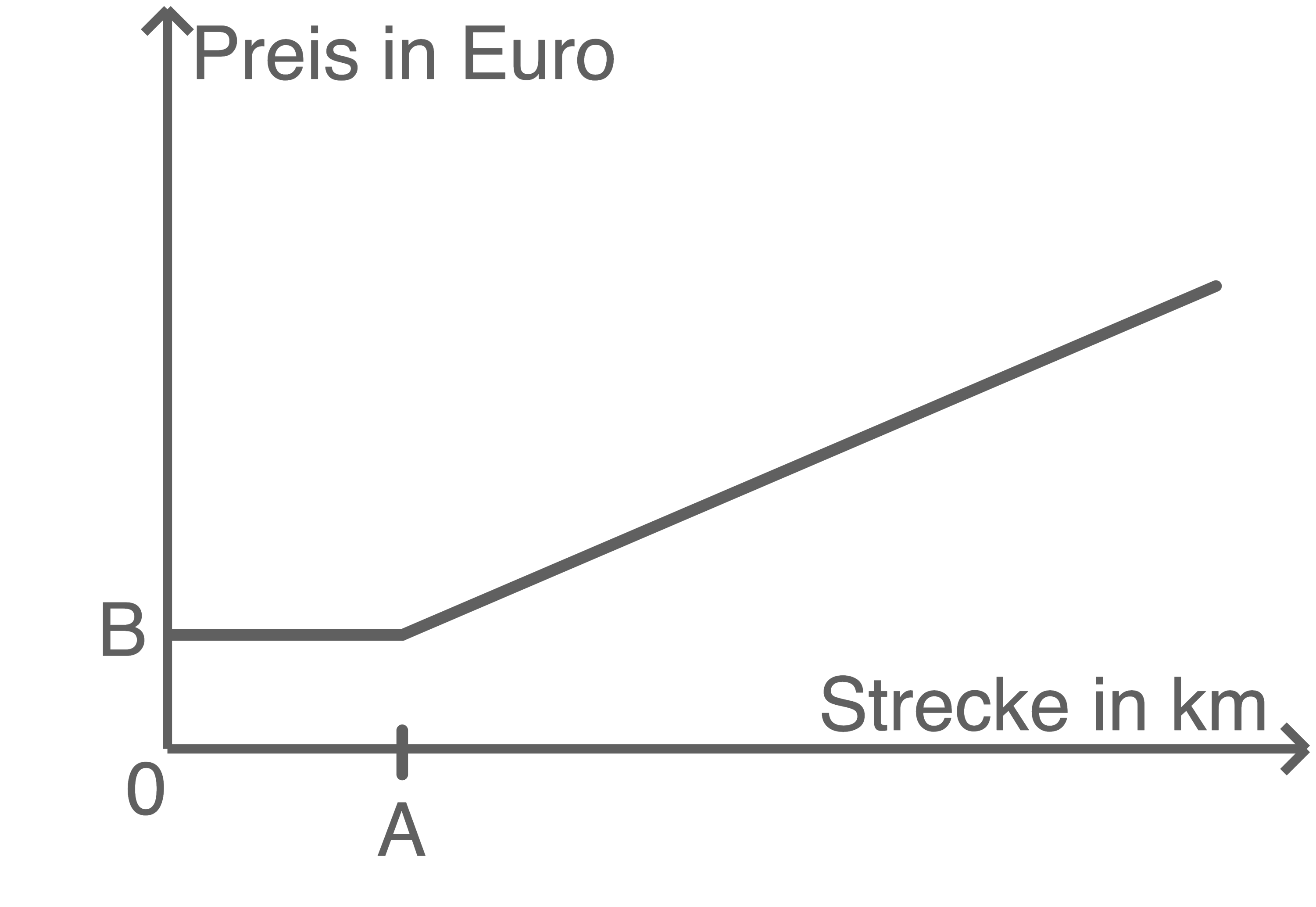
Die Darstellung passt zum Tarif in Gera.

Gib die Werte von $A$ und $B$ an.

(2 BE)

Erfurt	Tagestarif	Nachttarif
Grundgebühr	$4,70\,€$	$4,90\,€$
$1.$ bis $4.$ Kilometer, je $\text{km}$	$3,00\,€$	$3,20\,€$
jeder weitere angefangene Kilometer	$2,10\,€$	$2,30\,€$

Herr Fuchs hat noch $40,00\,€$ und möchte in Erfurt um Mitternacht mit dem Taxi fahren.

Bestimme die maximale Fahrstrecke, die er fahren kann.

(4 BE)

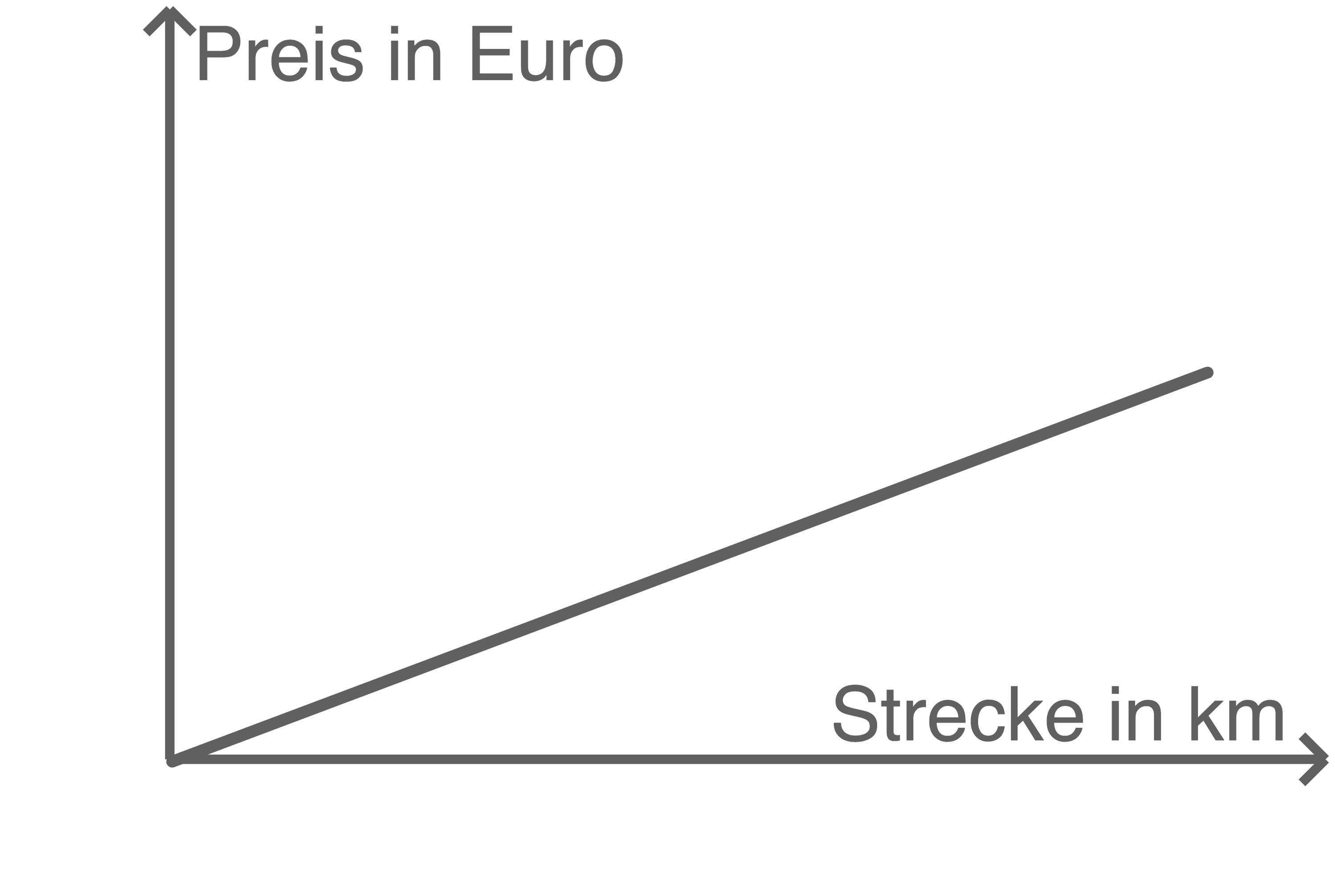
Eine andere Stadt veröffentlicht die Taxitarife in einem Diagramm.

Beschreibe einen zu diesem Diagramm passenden Sachverhalt.

(2 BE)

11.

Geometrie

In Gullivers Welt in Pudagla auf der Insel Usedom gibt es neben der riesigen Gulliver-Figur auch ein Modell seines Tellers.

Ein normaler Teller hat einen Durchmesser von $18,4\,\text{cm}.$ Das Modell ist eine $20$ -fache Vergrößerung.

Berechne den Flächeninhalt des riesigen Tellers.

(3 BE)

Kinder haben die Idee, diesen Riesenteller als Tisch zu verwenden.
Für jedes Kind planen sie $60\,\text{cm}$ Platz ein.

Ermittle die Anzahl der Kinder, die an diesem Riesentisch Platz haben.

(3 BE)

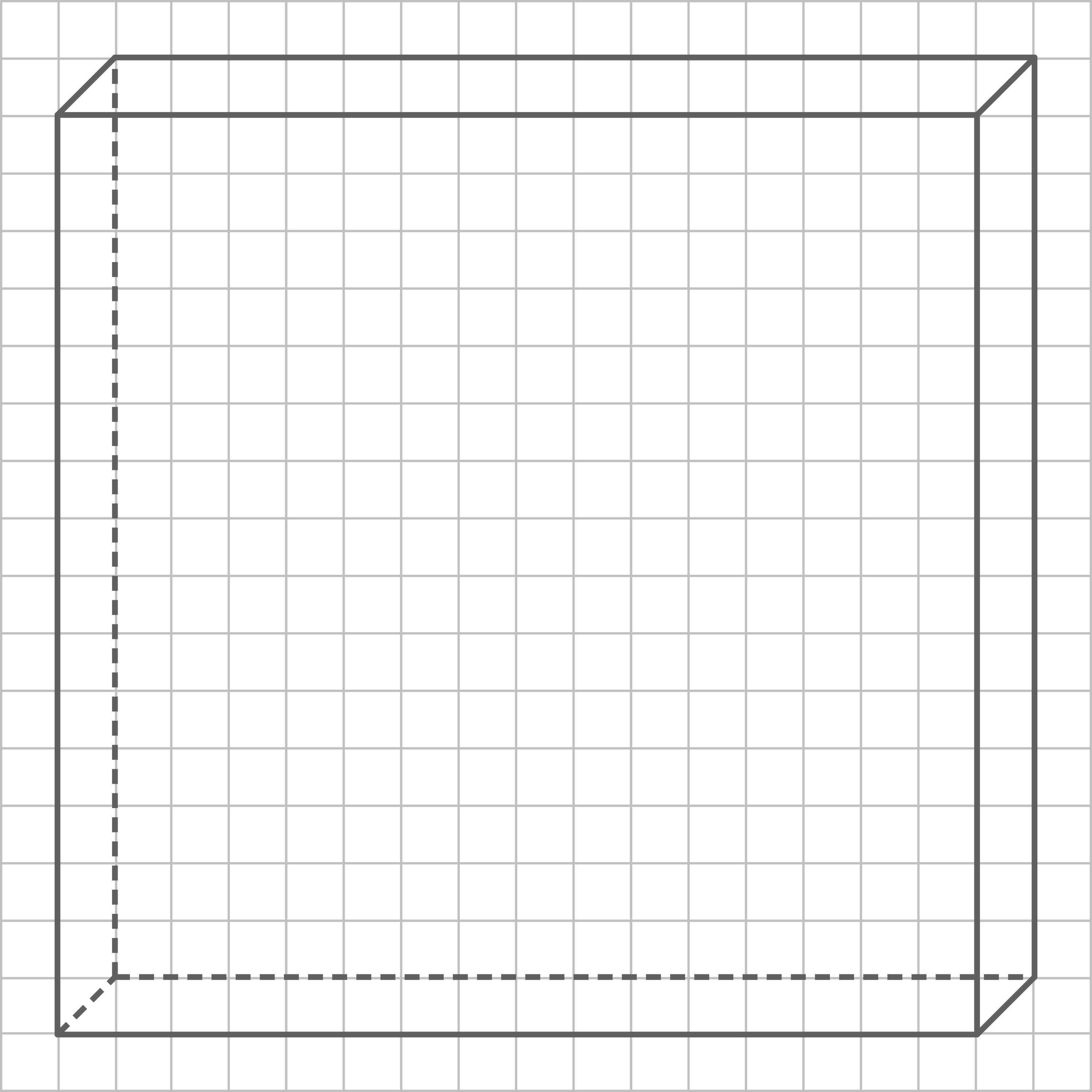
Der Riesenteller wurde zum Transport in eine quaderförmige Kiste verpackt.
Maße der Kiste:

Länge: $4\,\text{m}$
Breite: $4\,\text{m}$
Höhe: $50\,\text{cm}$

Stelle diese Kiste in einem geeigneten Maßstab auf unliniertem Papier da.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

8.1

$637,50\,€:75=\underline{\underline{8,50\,€}}$

Die Miete für einen Quadratmeter liegt also bei $8,50\,€.$

Miete für die andere Wohnung: $7,10\,€\cdot 75=532,50\,€$

Ersparnis pro Monat: $637,50\,€-532,50\,€=105\,€$

Damit beträgt die jährliche Ersparnis $105\,€\cdot 12=\underline{\underline{1260\,€}}.$

8.2

$2\cdot x+6=3\cdot x-1$

$\begin{array}[t]{rll} 2x+6&=&3x-1 &\quad \scriptsize \mid\;-2x \\[5pt] 6&=&x-1 &\quad \scriptsize \mid\;+1 \\[5pt] 7&=&x \\[5pt] x&=&\underline{\underline{7}} \end{array}$

Die Zahl, die gesucht wird, heißt $7.$

8.3

$875\,\text{g}:125\,\text{g}=7$

Da das Rezept für zehn Waffeln ausreicht, können also $7\cdot 10=\underline{\underline{70}}$ Waffeln gebacken werden.

Da als mögliche Ergebnisse nur vier Zahlen in Frage kommen, wurde der Tetraeder als Spielwürfel genutzt.

Die relative Häufigkeit für die Augenzahl "1" beträgt $\dfrac{8}{20}=0,4=\underline{\underline{40\,\%}}.$ Hierbei wird die Anzahl der Ergebnisse mit "1" durch die Gesamtanzahl der Würfe geteilt.

Es wird die Wahrscheinlichkeit bei jedem Würfel berechnet.

Tetraeder: $\dfrac{\small\text{Anzahl durch 3 teilbarer Zahlen}}{\small\text{Anzahl aller Zahlen}}=\dfrac{1}{4}$ $=0,25=25\,\%$

Hexaeder: $\dfrac{\small\text{Anzahl durch 3 teilbarer Zahlen}}{\small\text{Anzahl aller Zahlen}}=\dfrac{2}{6}$ $\approx 0,33\approx 33\,\%$

Oktaeder: $\dfrac{\small\text{Anzahl durch 3 teilbarer Zahlen}}{\small\text{Anzahl aller Zahlen}}=\dfrac{2}{8}$ $=0,25=25\,\%$

Beim Hexaeder ist die Gewinnchance also am höchsten.

$\dfrac{1}{6}\cdot 300=\underline{\underline{50}}$

Beim Hexaeder kann bei $300$ Würfen $50$ -mal mit einer "6" gerechnet werden.

Damit eine blaue Fläche mit einer Wahrscheinlichkeit von $\frac{1}{3}$ geworfen wird, müssen $2$ der $6$ Flächen gefärbt werden. Begründung: $\frac{1}{3}=\frac{2}{6}$

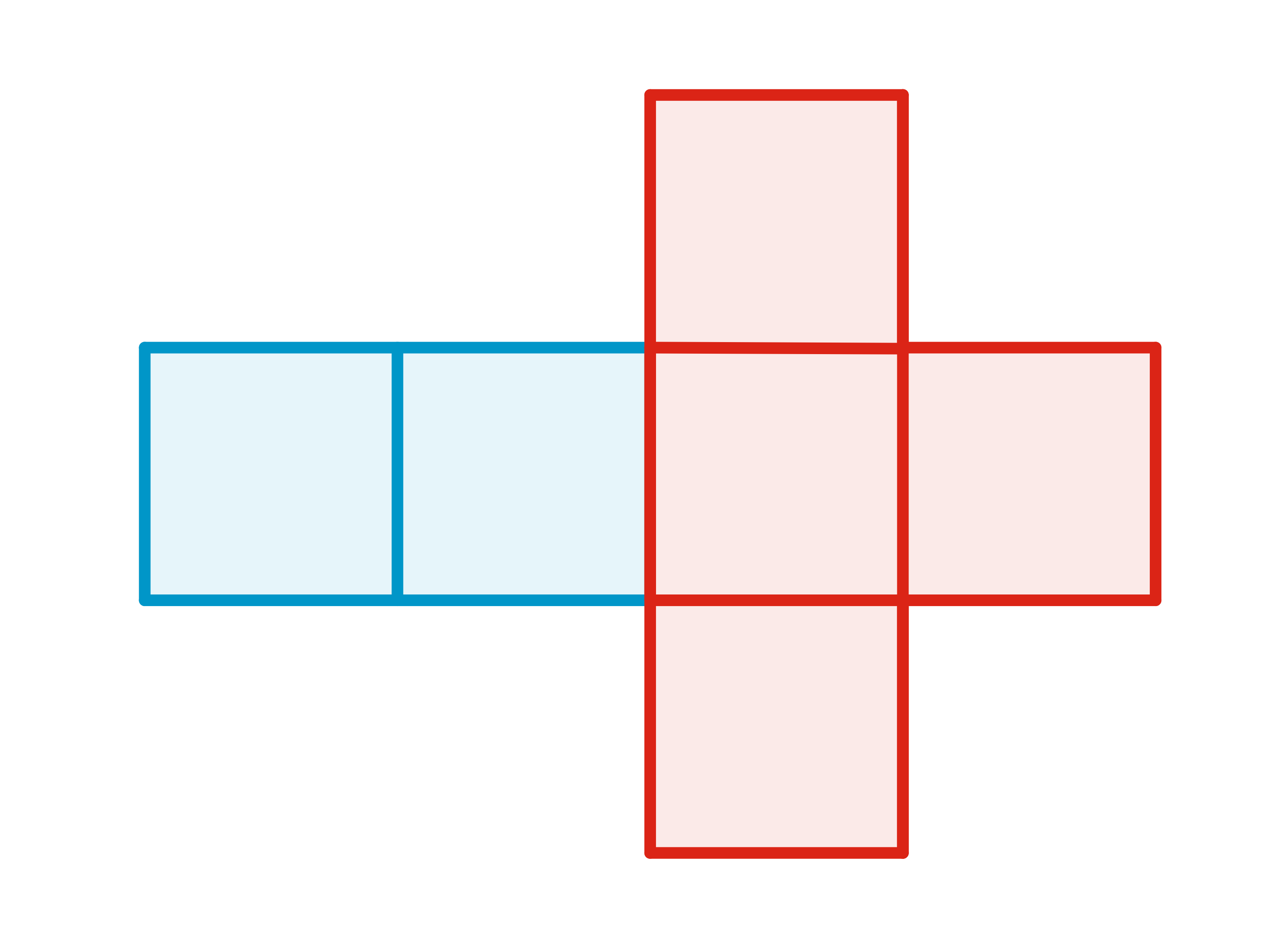
Würfelnetz - Thüringen Hauptschulabschluss

Ein Oktaeder hat folgende Primzahlen: $2,3,5$ und $7,$ also vier Primzahlen.

$P=\dfrac{4}{8}=\dfrac{1}{2}=0,5=\underline{\underline{50\,\%}}$

Mit einer Wahrscheinlichkeit von $50\,\%$ wird also eine Primzahl geworfen.

10.

$11\cdot 2,20\,€+7,00\,€=\underline{\underline{31,20\,€}}$

Für die Taxifahrt bezahlt Frau Müller also $31,20\,€.$

Zwischen $0$ und $A$ ist der Preis gleichbleibend, also konstant. Hier handelt es sich also um die Grundgebühr. Es gilt also $\underline{\underline{A=1\,\text{km}}}.$

Die Grundgebühr einschließlich dem ersten Kilometer beträgt $7,00\,€.$ Daher gilt $\underline{\underline{B=7\,€}}.$

Es gilt der Nachttarif.

Dazu kann eine Gleichung aufgestellt werden:

$\begin{array}[t]{rll} 2,30x+4\cdot 3,20+4,90&=&40\\[5pt] 2,30x+17,70&=&40 &\quad \scriptsize \mid\;-17,70 \\[5pt] 2,30x&=&22,30 &\quad \scriptsize \mid\;:2,30 \\[5pt] x&\approx&9,70 \end{array}$

Die Zahlung erfolgt pro angefangenem Kilometer, also müssen die $9,70\,\text{km}$ abgerundet werden auf $9\,\text{km}.$ Dazu kommen die ersten vier Kilometer, also beträgt die Gesamtstrecke:

$9\,\text{km}+4\,\text{km}=\underline{\underline{13\,\text{km}}}$

Herr Fuchs kann also maximal eine Strecke von $13$ Kilometern fahren.

Es gibt in dieser Stadt keine Grundgebühr. Pro Kilometeter zahlt man gleich viel.

11.

Da der Teller kreisförmig ist, gilt: $A=\pi\cdot r^2.$

Für den Radius gilt: $r=\dfrac{d}{2}=\dfrac{18,4\,\text{cm}}{2}=9,2\,\text{cm}$

Die Vergrößerung beträgt das $20$ -fache: $r_{\text{Teller}}=9,2\,\text{cm}\cdot 20=184\,\text{cm}$

$A_{\text{Teller}}=\pi\cdot (184\,\text{cm})^2$

$A_{\text{Teller}}=106361,76\,\text{cm}^2$ $\approx \underline{\underline{106362\,\text{cm}^2}}$

Der riesige Teller hat also einen Flächeninhalt von ca. $106362\,\text{cm}^2.$

Hier muss der Umfang berechnet werden:

$u=2\cdot \pi\cdot r$

$u=2\cdot \pi\cdot 184\,\text{cm}\approx1156\,\text{cm}$

$1156\,\text{cm}:60\,\text{cm}\approx 19,27\approx \underline{\underline{19}}$

Am Tisch finden also $19$ Kinder Platz.

Darstellung als Schrägbild:

Zunächst wird ein Maßstab bestimmt. Hier können z.B. die $4\,\text{m}$ als $8\,\text{cm}$ dargestellt werden: $\dfrac{8\,\text{cm}}{400\,\text{cm}}=\dfrac{1}{50},$ der Maßstab beträgt $1:50$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?