Aufgabe 3: Dreieck
Abbildung 1 zeigt das Dreieck 
mit vorgegebenen Maßangaben.
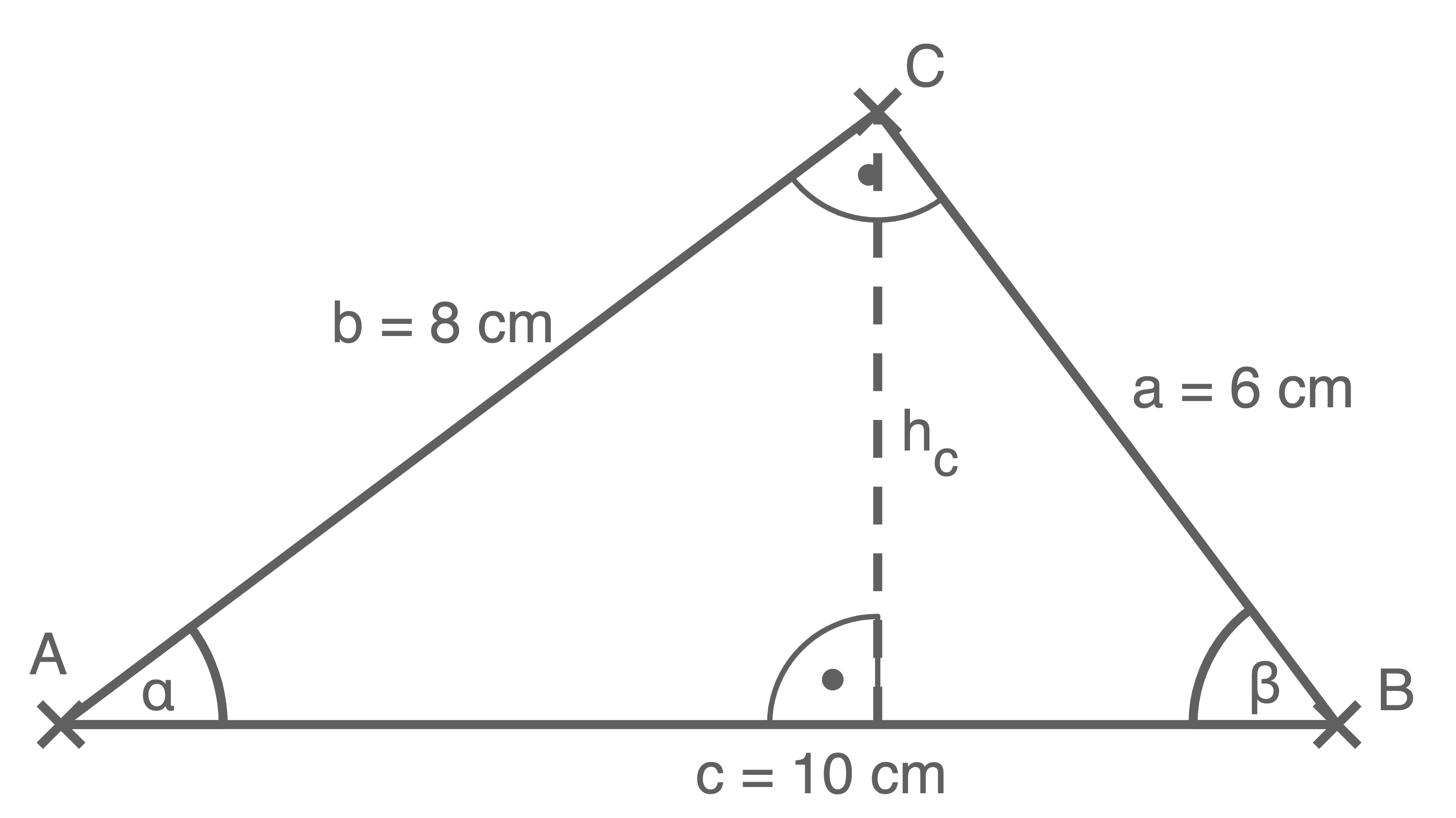
Abbildung 1: Dreieck mit Maßangaben
a)
Zeige rechnerisch, dass der Flächeninhalt dieses Dreiecks 
groß ist.
b)
Begründe, dass die folgende Gleichung gilt:
c)
Bestimme rechnerisch die Länge der Strecke 
.
d)
Bestimme rechnerisch die Größe des Winkels 
.
e)
Gegeben ist ein gleichschenkliges rechtwinkliges Dreieck mit der Basis 
und den beiden Schenkeln 
und 
(1) Skizziere eine geeignete Planfigur.
(2) Berechne die Länge der Schenkel.
f)
Kai behauptet: „Es gibt auch ein rechtwinkliges Dreieck, bei dem alle drei Seiten gleich lang sind.“
Entscheide begründet, ob Kais Behauptung stimmt.
g)
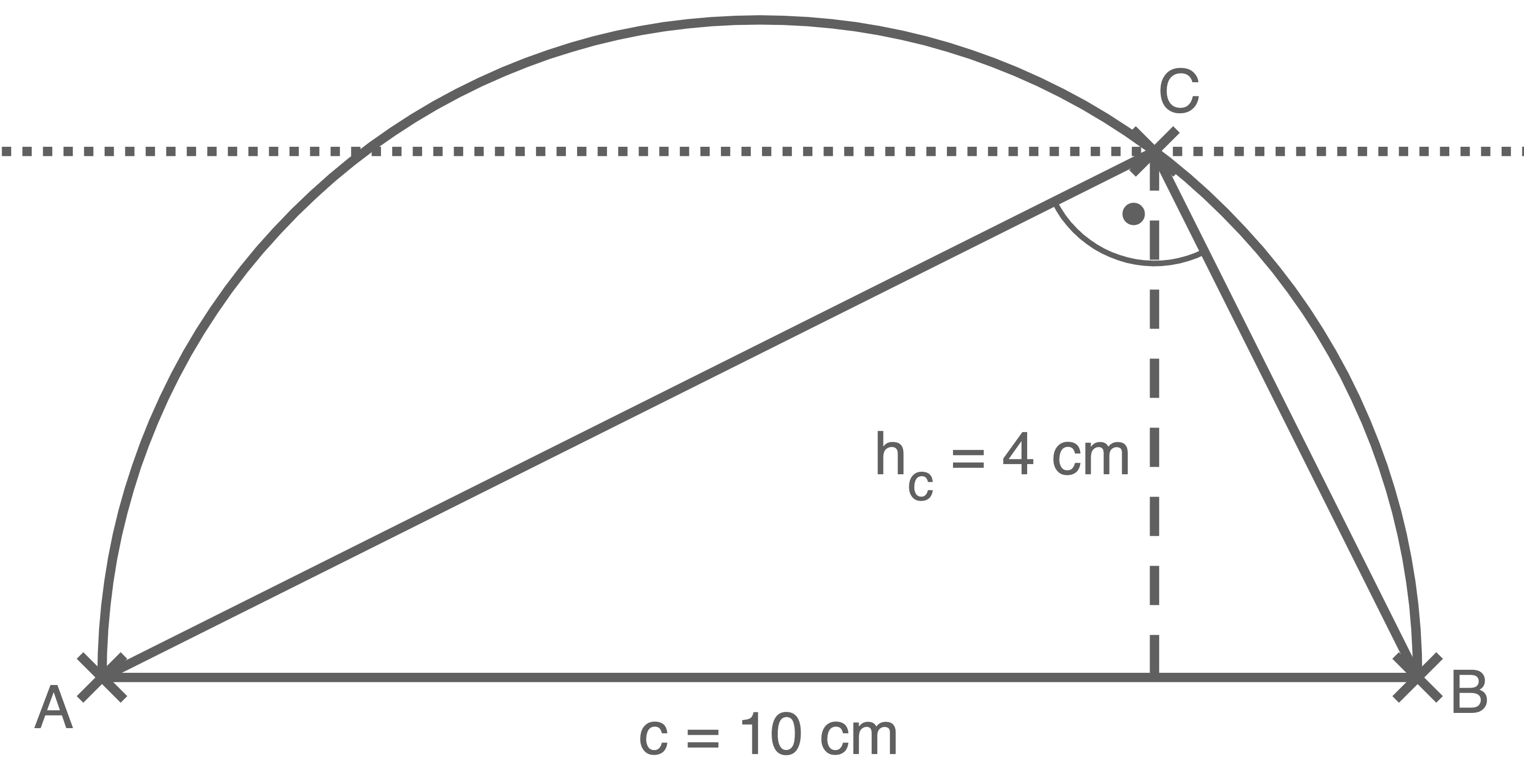
Konstruiere mithilfe des Satz des Thales ein rechtwinkliges Dreieck mit der Hypotenuse und der Höhe 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Da das Dreieck rechtwinklig ist, kann die Seite 
als Grundseite und die Seite als Höhe betrachtet werden. Mit der Formel für den Flächeninhalt eines Dreiecks folgt:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot b\cdot a \\[5pt]
&=& \dfrac{1}{2}\cdot 8\,\text{cm}\cdot 6\,\text{cm} \\[5pt]
&=& 24\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/9adbba5223eeaaf84c342943c8f7e133f48a2b5a38b76884696c9dad50c7df52?color=5a5a5a)
b)
Die Gleichung ist erfüllt, da beide Terme den Flächeninhalt des Dreiecks berechnen.
Auf der linken Seite der Gleichung wird der Flächeninhalt wie in Teilaufgabe a) mit der Grundseite und der Höhe berechnet.
Auf der rechten Seite der Gleichung wird die Seite 
als Grundseite mit der Höhe betrachtet.
c)
Der Flächeninhalt des Dreiecks beträgt 
und es gilt 
Damit folgt:
![\(\begin{array}[t]{rll}
10\,\text{cm}\cdot h_c &=& 24\,\text{cm}^2 &\quad \scriptsize \mid\; :10\,\text{cm} \\[5pt]
h_c &=& 2,4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/c48640fc391193028c33cedaa70fdc7356eee656c51e070aeee0cf269410c87a?color=5a5a5a)
d)
Im rechtwinkligen Dreieck gilt:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=& \dfrac{b}{c} \\[5pt]
\cos(\alpha)&=& \dfrac{8\,\text{cm}}{10\,\text{cm}} \quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\alpha&=& \cos^{-1}\left(\dfrac{8}{10}\right) \\[5pt]
\alpha&\approx& 36,9^\circ
\end{array}\)](https://mathjax.schullv.de/7072ac3b77a8353378c73bd270f4cb292e94cdc4e7c29dc41497546e58ead535?color=5a5a5a)
e)
(1)
Mit dem Satz des Thales folgt:
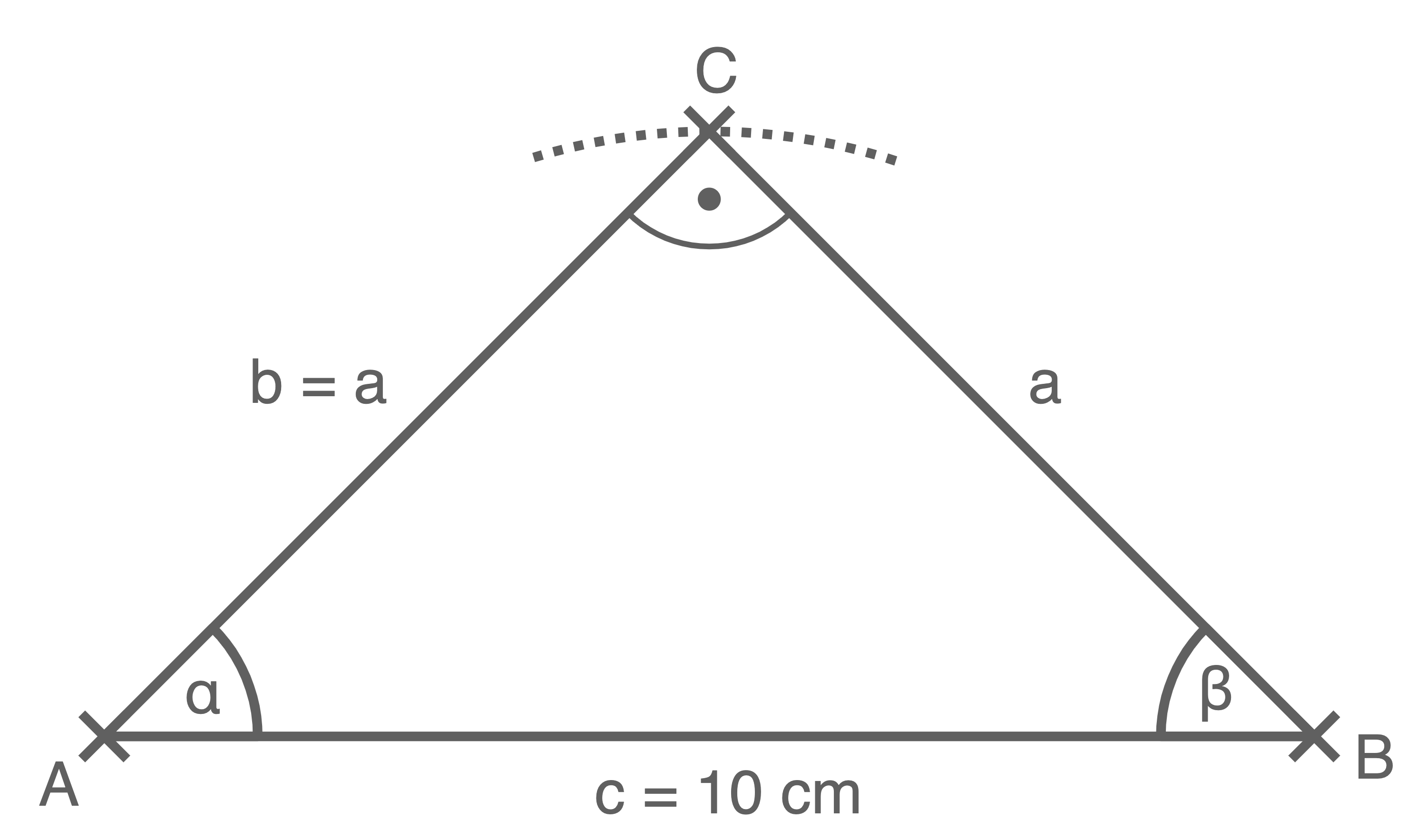Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
(2)
Da es sich um ein gleichschenkliges und rechtwinkliges Dreieck handelt, folgt mit dem Satz des Pythagoras:
![\(\begin{array}[t]{rll}
a^2+b^2&=& c^2 &\quad \scriptsize \mid\;b=a \\[5pt]
2a^2&=& c^2 \\[5pt]
2a^2&=& (10\,\text{cm})^2 \\[5pt]
2a^2&=& 100\,\text{cm}^2 &\quad \scriptsize \mid\;:2 \\[5pt]
a^2&=& 50\,\text{cm}^2 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
a&\approx& 7,07\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/19626473b1d2afc6962b302d93347dcd61f8669121181b80b9cacdfc5c6d04cb?color=5a5a5a)
Wegen 
gilt auch 
f)
Wenn in einem Dreieck alle Seiten gleich lang sind, so sind aus Symmetriegründen auch alle Winkel gleich groß, nämlich 
Das Dreieck kann dann also keinen rechten Winkel haben.
Kais Behauptung ist daher falsch.
g)
