Aufgabe 2: Varroa-Milbe

Die Varroa-Milbe ist ein Schädling, der in jedem Bienenvolk lebt. Die Schülerinnen und Schüler der Bienen-AG untersuchen die Milbe mit einem Mikroskop.

Berechne die Länge und Breite der Milbe durch Messen der Pfeillängen und Anwenden des Maßstabs (Abbildung 1).

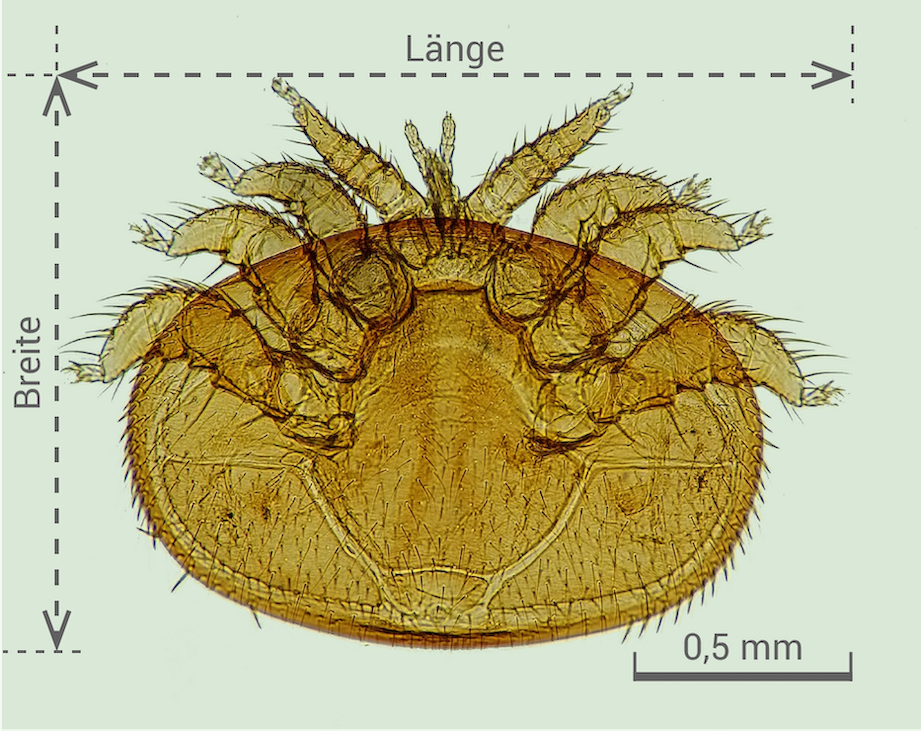
Abbildung 1: Varroma-Milbe (vergrößert)

Im Frühjahr ermitteln sie die Anzahl der Milben im Bienenvolk.

Im Internet finden sie die Faustregel, dass sich die Anzahl der Milben alle vier Wochen etwa verdoppelt. Sie kalkulieren die voraussichtliche Anzahl der Milben für die kommenden vier und acht Wochen. Die Werte halten sie in einer Tabelle fest.

	Wert 1	Wert 2	Wert 3
Zeit in Wochen	$0$	$4$	$8$
Anzahl der Milben	$308$

Ergänze die fehlenden Werte in der Tabelle.

Um die Entwicklung der Milben pro Woche vorauszusagen, beschreiben sie die Anzahl der Milben mit der folgenden Exponentialfunktion $f:$

$f(x)=308 \cdot 1,19^x \quad$ $x$ ist die Zeit in Wochen, $x=0$ ist der Beobachtungsbeginn

Gib die Bedeutung der Werte $308$ und $1,19$ im Sachzusammenhang an.

Bestätige mithilfe der Funktionsgleichung, dass nach 12 Wochen ca. 2 500 Milben vorhanden sind.

Bei einer Anzahl von ca. 10 000 Milben würde das Bienenvolk so großen Schaden nehmen, dass es nicht überleben kann.

Bestimme, nach wie vielen Wochen die Anzahl von 10 000 Milben überschritten wird.

Damit das Bienenvolk überlebt, wird nach 12 Wochen Ameisensäure eingesetzt. Dadurch wird die Anzahl von ca. 2 500 Milben einmalig um $90 \,\%$ reduziert.

Weise nach, dass durch die Behandlung mit der Ameisensäure die Anzahl von 10 000 Milben 21 Wochen nach Beobachtungsbeginn nicht überschritten wird.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Hinweis: Die Angaben können je nach Bildschirmgröße variieren.

$1,5\,\text{cm}$ entsprechen $0,5\,\text{mm}$ in der Realität.

Die Länge der Milbe beträgt ca. $5,8\,\text{cm}$ und die Breite $4,0\,\text{cm}.$ Mit dem Dreisatz folgt:

Länge:

$:1,5$

$\cdot 5,8$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 1,5\,\text{cm} & \mathrel{\widehat{=}}& 0,5\,\text{mm}\\[5pt] 1\,\text{cm} & \mathrel{\widehat{=}}& 0,33\,\text{mm}\\[5pt] 5,8\,\text{cm} & \mathrel{\widehat{\approx}}& 1,93\,\text{mm} \end{array}$

$:1,5$

$\cdot 5,8$

Breite:

$:1,5$

$\cdot 4,0$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 1,5\,\text{cm} & \mathrel{\widehat{=}}& 0,5\,\text{mm}\\[5pt] 1\,\text{cm} & \mathrel{\widehat{=}}& 0,33\,\text{mm}\\[5pt] 4\,\text{cm} & \mathrel{\widehat{\approx}}& 1,33\,\text{mm} \end{array}$

$:1,5$

$\cdot 4,0$

Die Milbe ist ca. $1,93\,\text{mm}$ lang und $1,33\,\text{mm}$ breit.

	Wert 1	Wert 2	Wert 3
Zeit in Wochen	$0$	$4$	$8$
Anzahl der Milben	$308$	$616$	$1232$

Der Wert $308$ gibt die Anzahl der Milben zum Zeitpunkt des Beobachtungsbeginns $x=0$ an.

Der Wert $1,19$ gibt den Wachstumsfaktor an, um den sich die Anzahl der Milben wöchentlich vervielfacht.

$f(12)=308\cdot 1,19^{12}\approx 2\,484$

Nach 12 Wochen sind ca. $2\,500$ Milben vorhanden.

$\begin{array}[t]{rll} 308\cdot 1,19^x &=&10\,000 &\quad \scriptsize \mid\; :308\\[5pt] 1,19^x&=& \dfrac{10\,000}{308}&\quad \scriptsize \mid\;\log \\[5pt] x &=& \log_{1,19}\dfrac{10\,000}{308} \\[5pt] x &\approx& 20 \end{array}$

Nach ungefähr 20 Wochen ist die Anzahl von $10\,000$ Milben überschritten.

Nach $12$ Wochen wird die Anzahl der Milben um $90\,\%$ reduziert:

$\begin{array}[t]{rll} p\,\%&=& \dfrac{W}{G} \\[5pt] 0,9&=& \dfrac{W}{2\,500} \quad \scriptsize \mid\; \cdot 2\,500 \\[5pt] 2\,250&=& W \end{array}$

Es sind dann also noch $2\,500-2\,250=250$ Milben im Bienenvolk.

Ab diesem Zeitpunkt haben die Milben wieder $9$ Wochen Zeit, sich zu vermehren. Die Anzahl nach den $9$ Wochen mit Startwert $250$ lässt sich wie folgt berechnen:

$250\cdot 1,19^9\approx 1\,196$

Die Anzahl von 10 000 Milben wird also nicht überschritten.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?