Aufgabe 1: Herzlich Willkommen
Eine Firma produziert herzförmige Dekoanhänger aus Metall (Abbildung 1).
Jedes Herz besteht aus einem Quadrat mit der Kantenlänge 
, an das zwei Halbkreise mit einem Radius von jeweils 
angesetzt sind (Abbildung 2).
Abbildung 1: herzförmiger Dekostecker
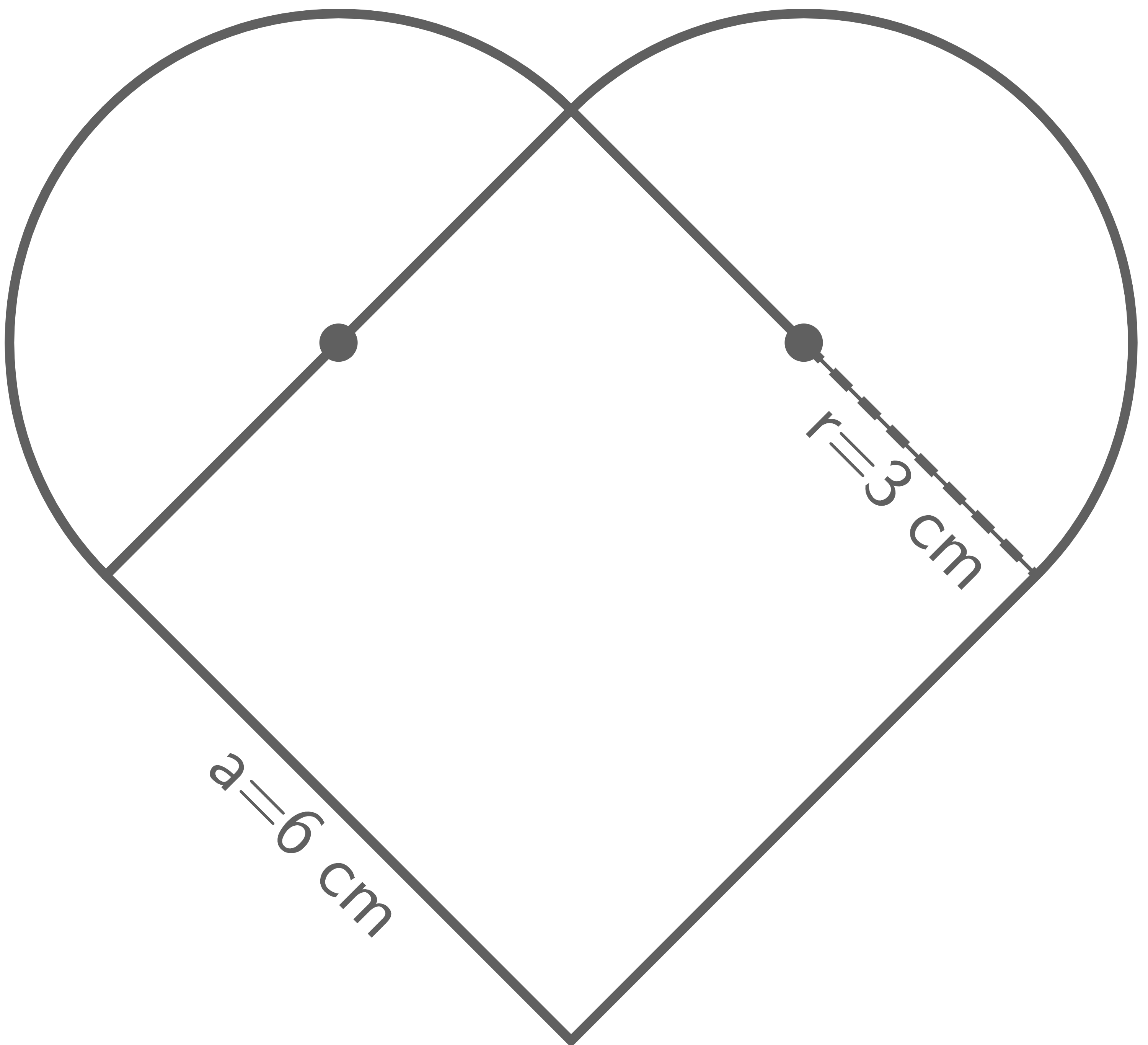
Abbildung 2: geometrische Form eines Herzens
a)
Zeichne ein Herz in Originalgröße in dein Heft.
b)
Die Herzen werden aus dünnen Metallblechen hergestellt.
des Metallblechs wiegt 
.
Berechne das Gewicht eines Herzens.
Um die Breite 
und die Höhe 
eines Herzens zu bestimmen, wird eine Skizze angefertigt (Abbildung 3). Hier gilt: Die Strecke 
entspricht der Breite 
geht durch die Mittelpunkte 
und 
der angesetzten Halbkreise.
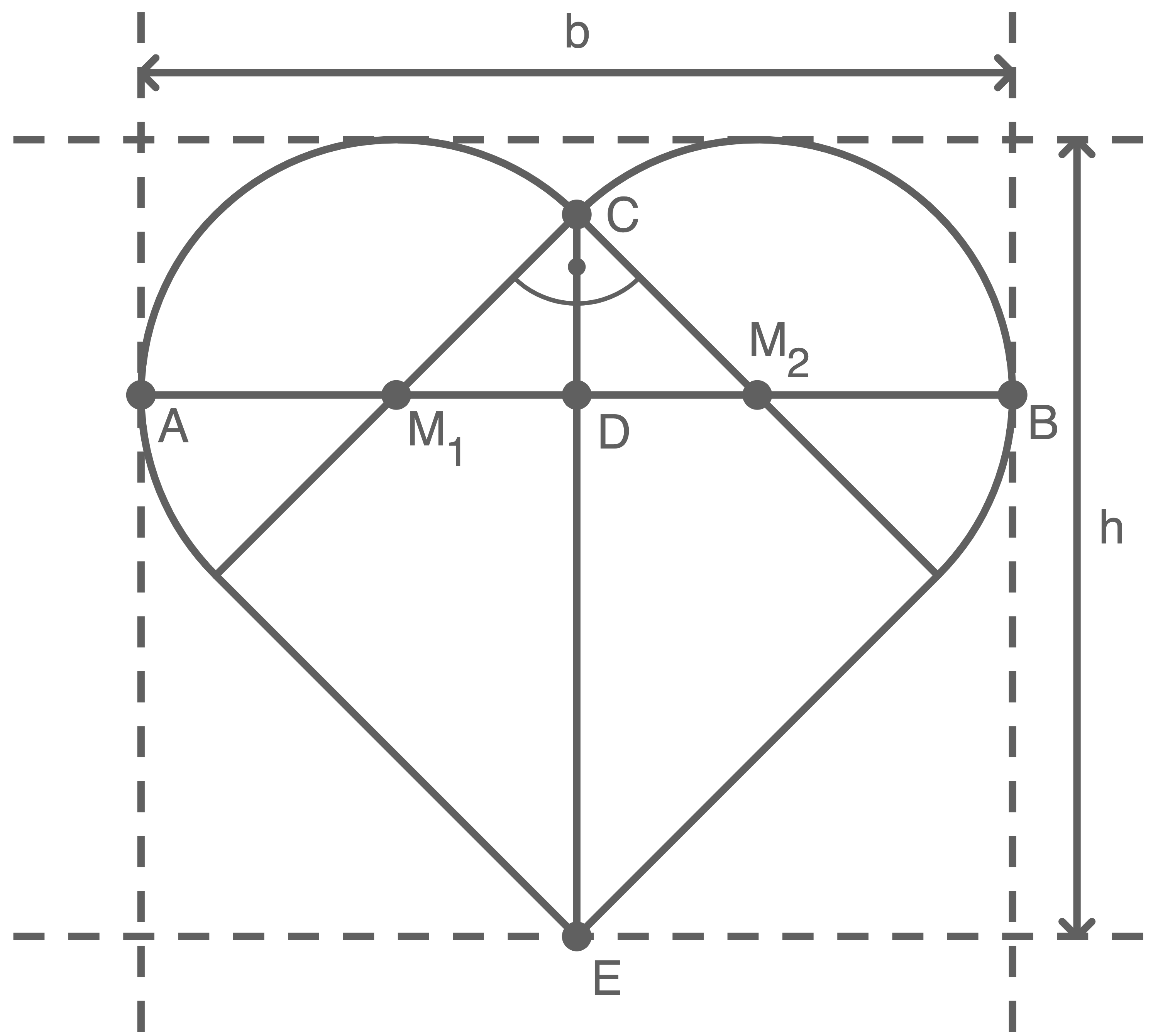
Die Herzen werden in den Farben rot und weiß produziert und farblich gemischt in Kartons verpackt. Beim Fabrikverkauf werden die Herzen angeboten. Die Kunden dürfen ohne hinzusehen nacheinander zwei Herzen aus dem Karton ziehen. Zu diesem Zufallsversuch gehört das folgende Baumdiagramm (Abbildung 4).
Abbildung 3:
Skizze zur Berechnung der Breite und der Höhe
Skizze zur Berechnung der Breite
c)
Berechne die Breite eines Herzens.
d)
Mithilfe der Abbildung 3 kann die Höhe der Herzen berechnet werden.
(1)
Berechne die Länge der Strecke 
(2)
Begründe, dass für die Höhe der Herzen gilt: 
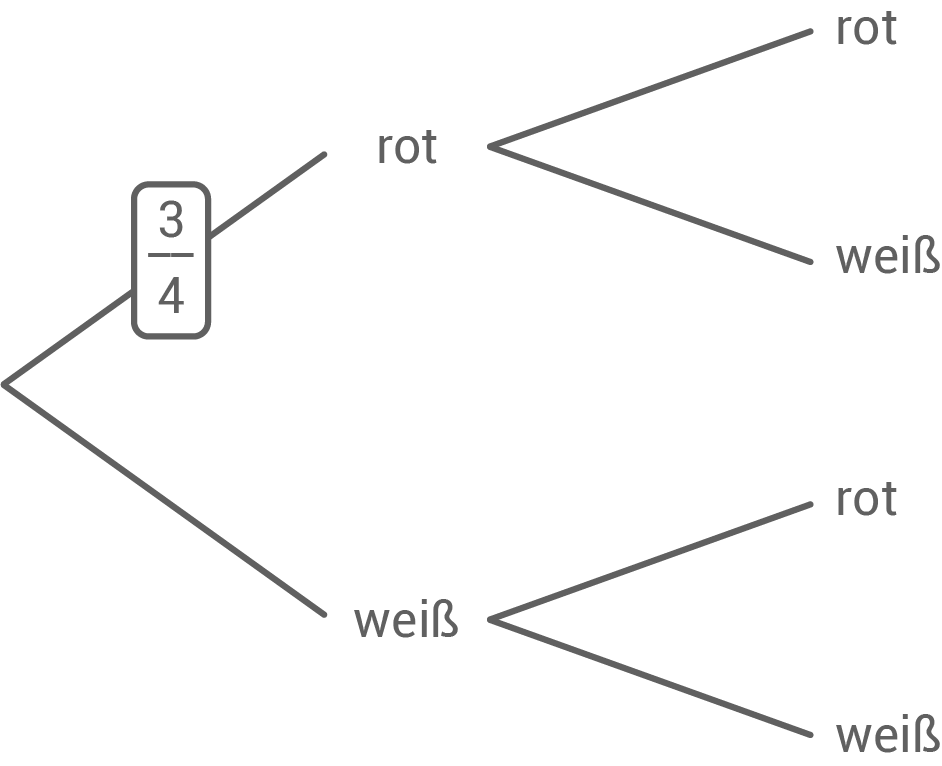
Abbildung 4: Baumdiagramm für das Ziehen von zwei Herzen ohne Zurücklegen
e)
Begründe, dass sich in dem Karton insgesamt 20 Herzen befinden.
f)
Gesucht ist die Wahrscheinlichkeit, dass zwei verschiedenfarbige Herzen gezogen werden.
(1)
Ergänze im Baumdiagramm die dafür notwendigen Wahrscheinlichkeiten.
(2)
Berechne die gesuchte Wahrscheinlichkeit.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
Zunächst muss der Flächeninhalt des Herzens berechnet werden.
Für den Flächeninhalt des Quadrats gilt:
![\(\begin{array}[t]{rll}
A_Q&=& 6\,\text{cm}\cdot 6\,\text{cm} \\[5pt]
&=& 36\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/0003d68e7e2eb05e0f1daf946c7979c91f1c937a0134efbaf0ff2b86e77ac2ac?color=5a5a5a)
Die beiden Halbkreise haben zusammen den Flächeninhalt eines Kreises mit Radius 
![\(\begin{array}[t]{rll}
A_K&=& \pi \cdot (3\,\text{cm})^2 \\[5pt]
&\approx& 28,27\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/adad6c3c58d3e1473f807496b41fb3a5384f310361596c43bbae9e618afe31d0?color=5a5a5a)
Damit folgt für den Flächeninhalt des Herzens:
![\(\begin{array}[t]{rll}
A&=& A_Q+A_K \\[5pt]
&\approx& 36\,\text{cm}^2+28,27\,\text{cm}^2 \\[5pt]
&=& 64,27\,\text{cm}^2 \\[5pt]
&=& 0,6427\,\text{dm}^2
\end{array}\)](https://mathjax.schullv.de/ba8ac9f8f555a34d0988aa2c9a911d8ae0460556ba26c680b9ffb4b825bddae0?color=5a5a5a)
Das Herz hat folglich ein Gewicht von 
c)
Da der Radius der beiden Halbkreise 
beträgt, sind die Strecken 
und 
ebenfalls lang.
Da das Dreieck 
rechtwinklig ist, lässt sich die Länge der Strecke 
mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
\overline{M_1M_2}^2&=& \overline{CM_1}^2+\overline{CM_2}^2 \\[5pt]
\overline{M_1M_2}^2&=& (3\,\text{cm})^2+(3\,\text{cm})^2 \\[5pt]
\overline{M_1M_2}^2&=& 18\,\text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{M_1M_2}&\approx& 4,24\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/4477426696d304838581de18fabdc77c7f57f88938209ec0c1e118da1aea6c67?color=5a5a5a)
Die gesamte Länge der Strecke und damit die Breite lässt sich schließlich wie folgt berechnen:
![\(\begin{array}[t]{rll}
b&=& \overline{AM_1}+\overline{M_1M_2}+\overline{BM_2} \\[5pt]
&\approx& 3\,\text{cm} + 4,24\,\text{cm} + 3\,\text{cm}\\[5pt]
&=& 10,24\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/26f5f51d159db5c9ebc9dc699be05f346ef4123c908ad46dc32a936b12e79ce5?color=5a5a5a)
d)
(1)
Die Länge der Strecke 
lässt sich mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
\overline{CE}^2&=& (6\,\text{cm})^2+(6\,\text{cm})^2 \\[5pt]
\overline{CE}^2&=& 72\,\text{cm}^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
\overline{CE}&\approx& 8,49\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/f3721a666712738b6dd9610c752a34d8de8f3f0252bab27de5c70617619d454d?color=5a5a5a)
Mit Teilaufgabe c) gilt:
Bei 
handelt es sich ebenfalls um ein rechtwinkliges Dreieck mit 
Mit dem Satz des Pythagoras folgt:
![\(\begin{array}[t]{rll}
\overline{CD}^2&=& (\overline{CM_2})^2-(\overline{DM_2})^2 \\[5pt]
\overline{CD}^2&\approx& (3\,\text{cm})^2-(2,12\,\text{cm})^2 \\[5pt]
\overline{CD}^2&\approx& 4,5056\,\text{cm}^2 \quad \scriptsize \mid\;\sqrt{\,} \\
\overline{CD} &\approx & 2,12 \,\text{cm}
\end{array}\)](https://mathjax.schullv.de/bdd98aa8c2b7585e93bb1495ada9382da383f9f96615cf4e8987aeef698880cd?color=5a5a5a)
Damit lässt sich die Länge der Strecke 
berechnen.
![\(\begin{array}[t]{rll}
\overline{DE}&\approx& 8,49\,\text{cm}-2,12\,\text{cm} \\[5pt]
&=& 6,37\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/adfb727ea78d13d0d54644fa86498db17726706d3b22483d4e17661c70bd7eb1?color=5a5a5a)
(2)
Der unterste Punkt des Herzens ist der Punkt 
die höchsten Punkte liegen auf den beiden Halbkreisen um die Punkte und 
Der Punkt
befindet sich auf Höhe der Mittelpunkte der beiden Halbkreise. Da der Radius dieser Halbkreise beträgt, gilt die angegebene Formel.
Der Punkt
e)
Aus dem Baumdiagramm lässt sich ablesen, dass 
aller Herzen rot sind. Es ist außerdem bekannt, dass 
Herzen rot sind.
![\(\begin{array}{rcl}
\dfrac{3}{4} & \mathrel{\widehat{=}}& 15\\[5pt]
1 & \mathrel{\widehat{=}}& 20\\[5pt]
\,
\end{array}\)](https://mathjax.schullv.de/ecbef00a3440215174609f43ea6725158b6ce9454fc17d16accf17356e511a4a?color=5a5a5a)
Im Karton befinden sich also insgesamt 20 Herzen.
f)
(1)
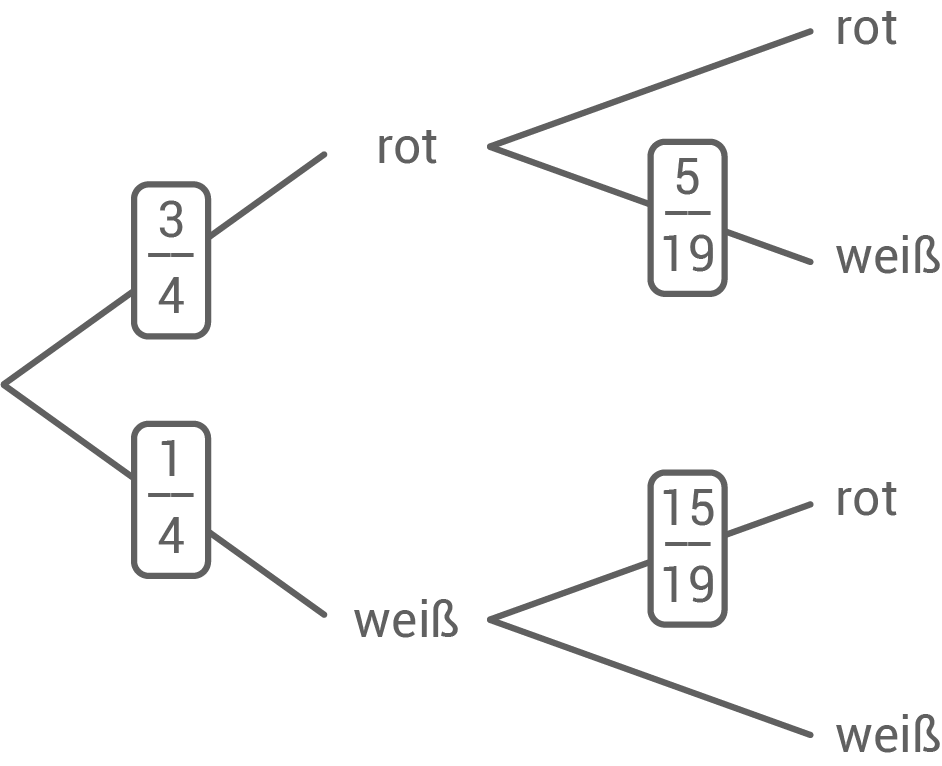
(2)
Mit den Pfadregeln folgt:
![\(\begin{array}[t]{rll}
&=& \dfrac{15}{76}+\dfrac{15}{76} \\[5pt]
&=&\dfrac{30}{76}\\[5pt]
&\approx& 0,3947\\[5pt]
&=& 39,47\,\%
\end{array}\)](https://mathjax.schullv.de/f566fda929db704ce1072fe55864ab83616b8daab2479b0797c21cc891d63c11?color=5a5a5a)
Die gesuchte Wahrscheinlichkeit beträgt ungefähr 