Prüfungsteil II (HT1/2)
Aufgabe 1: Rösti
Ein Unternehmen stellt nach eigenem Rezept aus Kartoffeln sogenannte Rösti her (Abbildung 1). Dazu wird der Teig in eine zylindrische Form gegossen (Abbildung 2) und anschließend gebacken. Für ein Rösti benötigt man 100 g Teig.

Abbildung 1: Rösti aus Kartoffeln

Abbildung 2: zylindrische Form
a)
b)
Ein Rösti soll  dick sein und ein Volumen von
dick sein und ein Volumen von  haben.
Zeige, dass die zylindrische Form einen Durchmesser von ca.
haben.
Zeige, dass die zylindrische Form einen Durchmesser von ca.  haben muss.
haben muss.
c)
Das Unternehmen möchte zusätzlich Mini-Rösti herstellen. Ein Mini-Rösti soll auch  dick sein, aber nur das halbe Volumen haben.
Ein Mitarbeiter behauptet: „Für ein Mini-Rösti brauchen wir eine Form mit halbem Durchmesser!“
Hat er recht? Begründe deine Entscheidung.
dick sein, aber nur das halbe Volumen haben.
Ein Mitarbeiter behauptet: „Für ein Mini-Rösti brauchen wir eine Form mit halbem Durchmesser!“
Hat er recht? Begründe deine Entscheidung.
Bevor die Rösti verpackt werden, wird zuerst das Gewicht und dann das Aussehen kontrolliert. Bei der Kontrolle des Gewichts erfüllen 98 % der Rösti die Vorgabe. Die anderen Rösti werden direkt aussortiert. Bei der anschließenden Kontrolle des Aussehens erfüllen 99 % die Vorgabe. Erneut werden die restlichen Rösti aussortiert.
d)
Zeichne ein Baumdiagramm, das die beschriebene Situation darstellt.
e)
Bei einer Kontrolle werden insgesamt 447 Röstis aussortiert. Entweder entsprachen das Gewicht oder das Aussehen nicht der Vorgabe.
Berechne, wie viele Röstis vermutlich kontrolliert wurden.
Aufgabe 2: Wassermelonen
Für ein Schulprojekt beschäftigt sich Sinja mit der Form und dem Wachstum von Wassermelonen.
Sinja hat eine nahezu kugelförmige Wassermelone gekauft, die einen Durchmesser von ca.  hat (Abbildung 1).
hat (Abbildung 1).

Abbildung 1: aufgeschnittene Wassermelone
a)
Zeige rechnerisch, dass diese Wassermelone ein Volumen von  hat.
hat.
b)
Die Schale der Wassermelone hat eine Dicke von  (Abbildung 1).
Berechne den prozentualen Anteil des Fruchtfleisches an der ganzen Wassermelone.
(Abbildung 1).
Berechne den prozentualen Anteil des Fruchtfleisches an der ganzen Wassermelone.
Sinja entdeckt würfelförmige Wassermelonen, die in Japan verkauft werden (Abbildung 2).
 Abbildung 2: würfelförmige Wassermelone
Abbildung 2: würfelförmige Wassermelone
 Abbildung 2: würfelförmige Wassermelone
Abbildung 2: würfelförmige Wassermelone
c)
Eine würfelförmige Wassermelone hat ebenfalls ein Volumen von  Bestätige durch eine Rechnung, dass diese Wassermelone eine Kantenlänge von ca.
Bestätige durch eine Rechnung, dass diese Wassermelone eine Kantenlänge von ca.  hat.
hat.
d)
Entscheide durch eine Rechnung, ob die kugelförmige oder die würfelförmige Wassermelone eine größere Oberfläche hat.
Wassermelonen verdoppeln ihr Gewicht pro Woche unter idealen Wachstumsbedingungen. Sinja überlegt, wie sich das Gewicht einer 400 g schweren Wassermelone unter idealen Bedingungen voraussichtlich entwickelt. Sie erstellt dazu eine Tabelle.
| Beobachtungswoche | Gewicht in g |
|---|---|
| 0 | 400 |
| 1 | 800 |
| 2 | 1600 |
| ... | ... |
e)
Berechne das Gewicht der Wassermelone nach 4 Wochen.
f)
Sinja behauptet: „Der Graph in Abbildung 3 beschreibt das Wachstum dieser Wassermelone.“
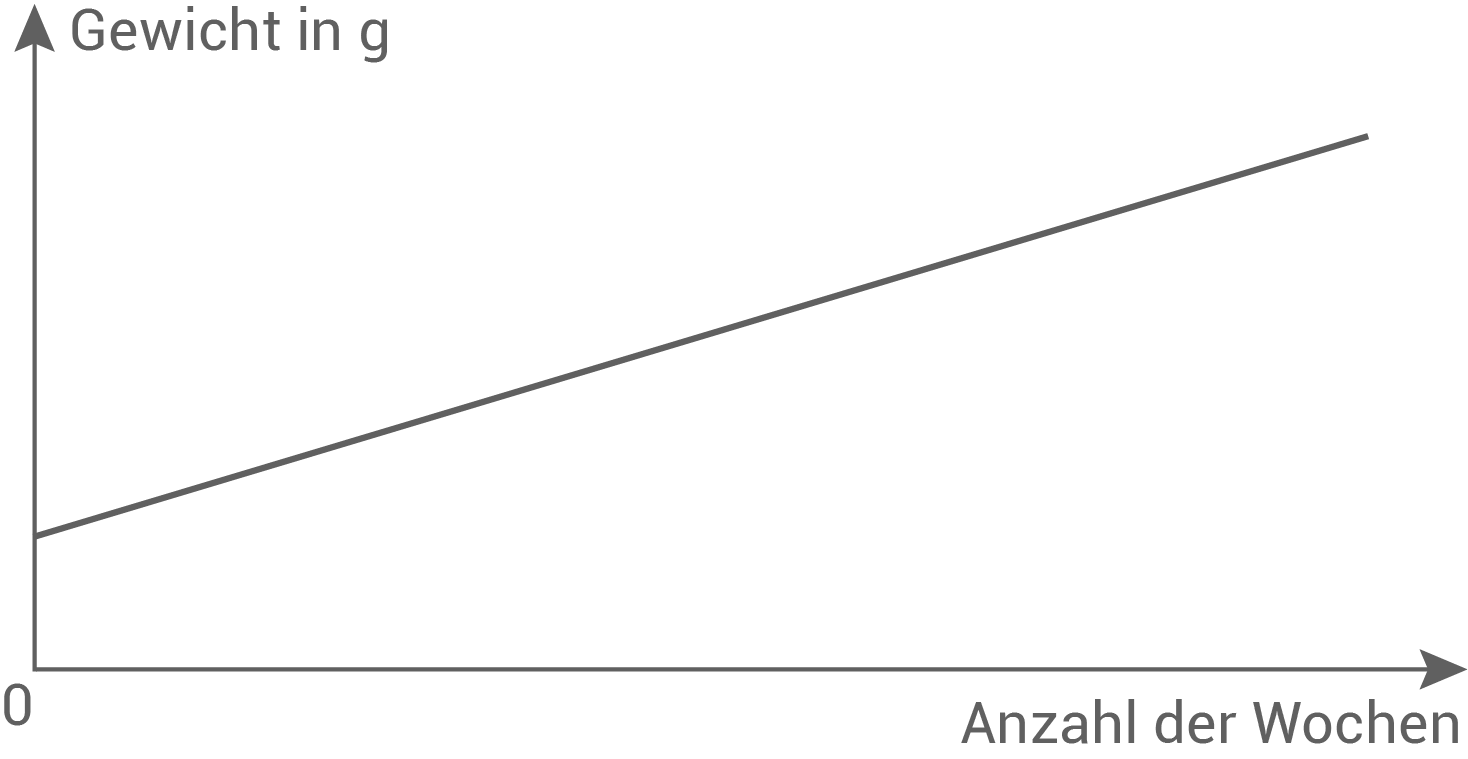 Hat Sinja recht? Begründe deine Entscheidung.
Hat Sinja recht? Begründe deine Entscheidung.

Abbildung 3: Graph zum Wachstum der Wassermelone
Aufgabe 3: Parabel und Rechteck
Julia zeichnet mithilfe einer Geometriesoftware die Parabel  mit der Funktionsgleichung
mit der Funktionsgleichung  in ein Koordinatensystem (Abbildung 1).
in ein Koordinatensystem (Abbildung 1).
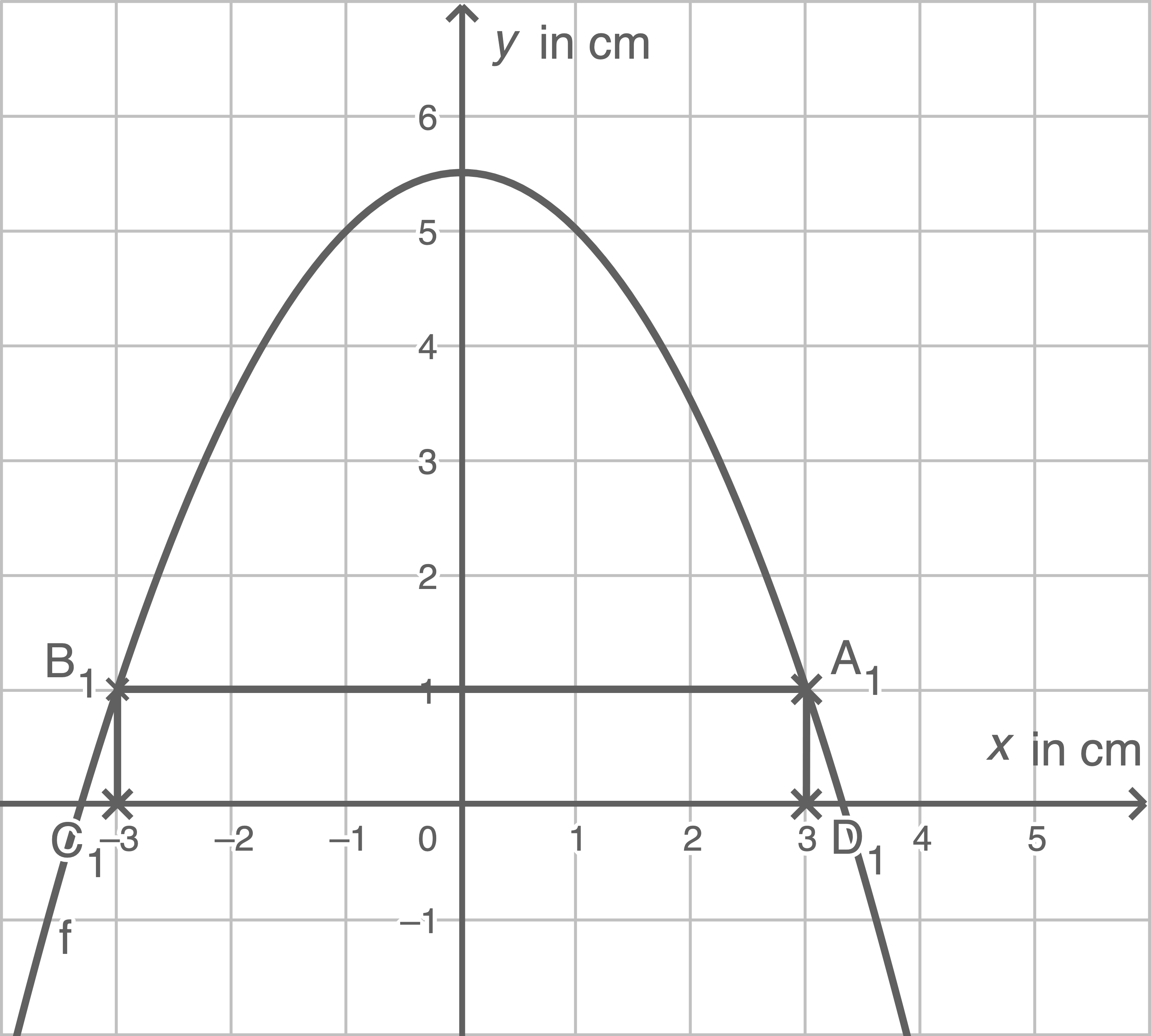

Abbildung 1: Parabel  und Rechteck
und Rechteck 
a)
Bestätige durch eine Rechnung, dass der Punkt  auf der Parabel
auf der Parabel  liegt.
liegt.
b)
Begründe mit den Eigenschaften dieser Parabel, dass der Punkt  ebenfalls auf dem Graphen von
ebenfalls auf dem Graphen von  liegt.
liegt.
c)
Die Punkte  und
und  liegen auf der
liegen auf der  -Achse und bilden mit den Punkten
-Achse und bilden mit den Punkten  und
und  das Rechteck
das Rechteck  .
Berechne den Umfang dieses Rechtecks.
.
Berechne den Umfang dieses Rechtecks.
Ausgehend von anderen Punkten auf der Parabel  kann man auf die gleiche Art weitere Rechtecke zeichnen.
kann man auf die gleiche Art weitere Rechtecke zeichnen.
d)
(1) Zeichne den Punkt  in Abbildung 1 ein.
(2) Ergänze die drei weiteren Punkte
in Abbildung 1 ein.
(2) Ergänze die drei weiteren Punkte 
 und
und  und verbinde die vier Punkte zu dem Rechteck
und verbinde die vier Punkte zu dem Rechteck 
Julia stellt den Term  auf, mit dem man den Umfang für jedes dieser Rechtecke berechnen kann.
Dazu nutzt sie die bekannte Formel zur Berechnung des Umfangs eines Rechtecks und erhält:
auf, mit dem man den Umfang für jedes dieser Rechtecke berechnen kann.
Dazu nutzt sie die bekannte Formel zur Berechnung des Umfangs eines Rechtecks und erhält:
 Dabei ist
Dabei ist  und steht für die
und steht für die  -Koordinate des zum Rechteck gehörenden Punktes
-Koordinate des zum Rechteck gehörenden Punktes  usw.
usw.
e)
Begründe, dass mit dem Term  der Umfang jedes dieser Rechtecke berechnet werden kann.
der Umfang jedes dieser Rechtecke berechnet werden kann.
Julia vereinfacht den Term  zu
zu 
Bildnachweise [nach oben]
f)
Zeige durch Termumformungen, dass die beiden Terme  und
und  gleichwertig sind.
gleichwertig sind.
g)
Julia stellt die folgende Gleichung auf:  (1) Löse die Gleichung.
(2) Erkläre das Ergebnis in Bezug auf die Rechtecke unter der Parabel
(1) Löse die Gleichung.
(2) Erkläre das Ergebnis in Bezug auf die Rechtecke unter der Parabel 
h)
Der Term  kann auch als Funktion
kann auch als Funktion  mit
mit  interpretiert werden.
(1) Bestimme den Scheitelpunkt der Funktion
interpretiert werden.
(1) Bestimme den Scheitelpunkt der Funktion  und
(2) erkläre seine Bedeutung für die Umfangsbetrachtung.
und
(2) erkläre seine Bedeutung für die Umfangsbetrachtung.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1: Rösti
a)
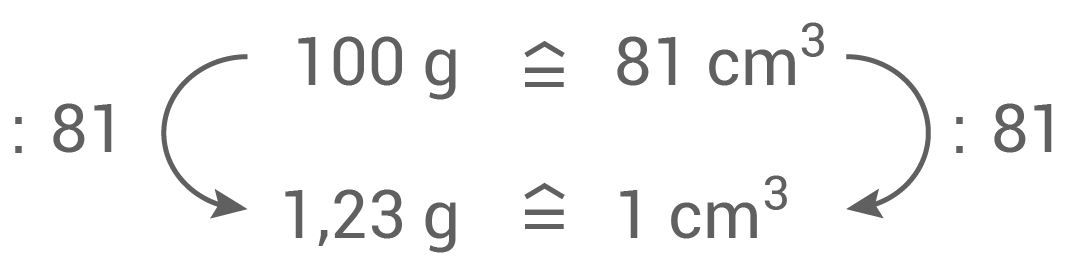 Ein Kubikzentimeter Teig wiegt also 1,23 g.
Ein Kubikzentimeter Teig wiegt also 1,23 g.
b)
Durchmesser eines Röstis berechnen:
![\(\begin{array}[t]{rll}
V_{\,\text{Rösti}}&=& \pi\cdot r^2\cdot h\qquad \scriptsize \mid\;:\pi \mid\;:h\\[5pt]
\dfrac{V_{\,\text{Rösti}}}{\pi\cdot h} &=& r^2\qquad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
\sqrt{\dfrac{V_{\,\text{Rösti}}}{\pi\cdot h}}&=& r \\[5pt]
\sqrt{\dfrac{81\,\text{cm}^3}{\pi\cdot 2\,\text{cm}}}&=& r \\[5pt]
3,6 \,\text{cm}&\approx& r \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5ce1ab340fc4818b29882a145346d90568d840081ee6c2f714cd92e4090ea9cc?color=5a5a5a) Daraus folgt
Daraus folgt  Da der Durchmesser eines Röstis bei etwa
Da der Durchmesser eines Röstis bei etwa  liegt, muss auch der Durchmesser der zylindrischen Form bei ca.
liegt, muss auch der Durchmesser der zylindrischen Form bei ca.  liegen.
liegen.
c)
Volumen eines Rösti mit halbem Durchmesser berechnen:
![\(\begin{array}[t]{rll}
V&=& \pi\cdot \left(\dfrac{r}{2}\right)^2\cdot h \\[5pt]
&=& \pi\cdot (1,8\,\text{cm})^2\cdot 2\,\text{cm} \\[5pt]
&\approx& 20,4\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/1857ebc4c563933f29f4ef545b8787b1a9b679bb0d372f8f7534c3808b1ce118?color=5a5a5a) Das Volumen eines Rösti mit halben Durchmesser wäre deutlich geringer als
Das Volumen eines Rösti mit halben Durchmesser wäre deutlich geringer als  Der Mitarbeiter hat also nicht recht.
Der Mitarbeiter hat also nicht recht.
d)
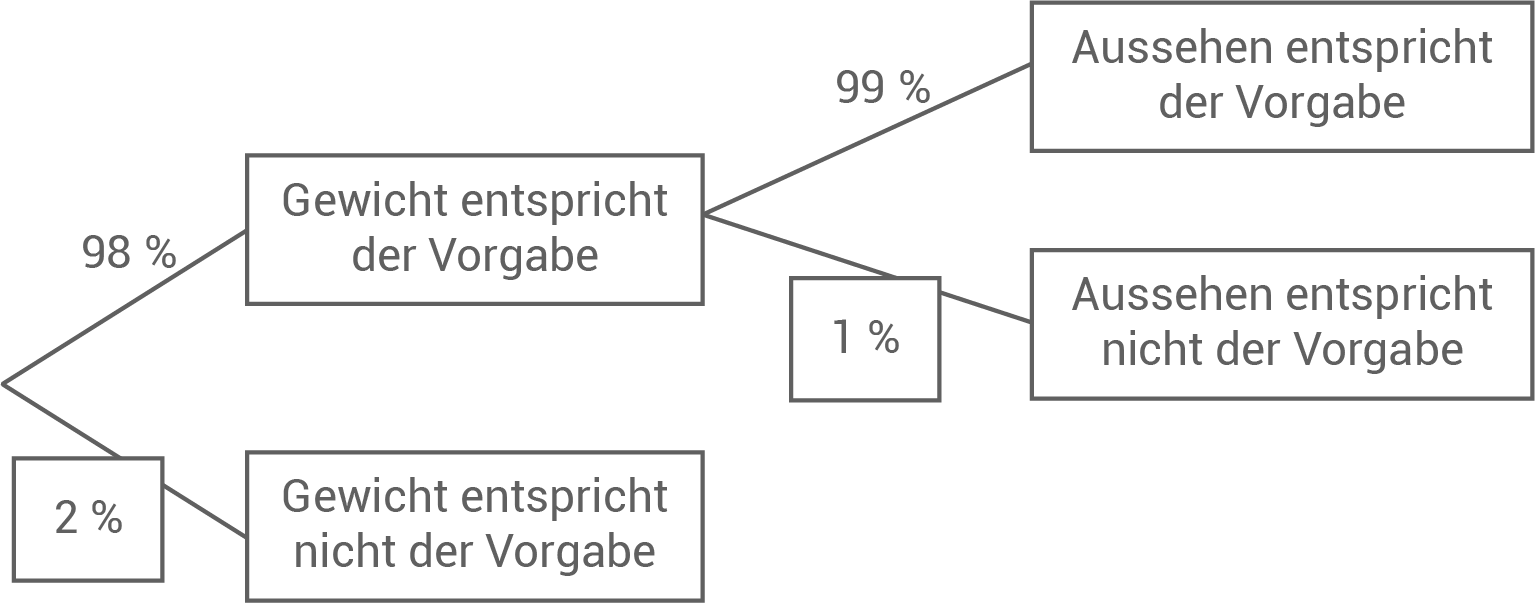
e)
Lösung 2: Wassermelonen
a)
b)
1. Schritt: Radius des Fruchtfleisches berechnen
![\(\begin{array}[t]{rll}
d_{\,\text{F}}&=& 25\,\text{cm}-1,5\,\text{cm}-1,5\,\text{cm} \\[5pt]
&=& 22\,\text{cm} \\[5pt]
r_F&=& 22\,\text{cm}:2\\[5pt]
&=& 11\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/3d6a34341d7fe385abe52ac1c0ebcef60a5b1ec6fe83abc9f32cf4070db187fb?color=5a5a5a) 2. Schritt: Volumen des Fruchtfleisches berechnen
2. Schritt: Volumen des Fruchtfleisches berechnen
![\(\begin{array}[t]{rll}
V_{\text{F}}&=& \dfrac{4}{3}\cdot \pi\cdot r_F^3 \\[5pt]
&=&\dfrac{4}{3}\cdot \pi\cdot (11\,\text{cm})^3 \\[5pt]
&\approx&5575 \,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/7e83337d6590f0673cc0a28e1b2fc717f9a50a043c36707e5a4e1341e7851f98?color=5a5a5a) 3.Schritt: Prozentualen Anteil berechnen
3.Schritt: Prozentualen Anteil berechnen


c)
d)
1. Schritt: Oberflächeninhalt der kugelförmigen Wassermelone berechnen
![\(\begin{array}[t]{rll}
O_{\text{Kugel}}&=& 4\cdot \pi\cdot r^2 \\[5pt]
&=& 4\cdot \pi\cdot (12,5\,\text{cm})^2 \\[5pt]
&\approx& 1963,50\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f461f4c2875f22afe5e5834fe828ba3527e1029144e536a3541cdddf5d5cda7e?color=5a5a5a) 2. Schritt: Oberflächeninhalt der würfelförmigen Wassermelone berechnen
2. Schritt: Oberflächeninhalt der würfelförmigen Wassermelone berechnen
![\(\begin{array}[t]{rll}
O_{\text{Würfel}}&=& 6\cdot a^2 \\[5pt]
&=& 6\cdot (20,2\,\text{cm})^2 \\[5pt]
&=& 2448,24\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fab5c14b62237e03080996e0c82fd223ad8b5bd586b0a473506f1336fa408215?color=5a5a5a) Die würfelförmige Wassermelone hat einen größeren Oberflächeninhalt.
Die würfelförmige Wassermelone hat einen größeren Oberflächeninhalt.
e)
| Beobachtungswoche | Gewicht in g |
|---|---|
| 0 | 400 |
| 1 | 800 |
| 2 | 1600 |
| 3 | 3200 |
| 4 | 6400 |
f)
Nach jedem Zeitschritt in Wochen verdoppelt sich das Gewicht. Daher handelt es sich nicht um eine lineare Zuordnung.
Sinja hat also nicht recht.
Lösung 3: Parabel und Rechteck
a)
b)
Da die Parabel symmetrisch zur  -Achse ist, unterscheiden sich gegenüberliegende Punkte immer nur im Vorzeichen ihrer
-Achse ist, unterscheiden sich gegenüberliegende Punkte immer nur im Vorzeichen ihrer  -Koordinate. Spiegelt man also den Punkt
-Koordinate. Spiegelt man also den Punkt  an der
an der  -Achse, erhält man auf der Parabel den Punkt
-Achse, erhält man auf der Parabel den Punkt 
c)
Anhand des Schaubildes können die Längen der Strecken  und
und  abgelesen werden:
abgelesen werden:
![\(\begin{array}[t]{rll}
u&=&2\cdot\overline{A_1B_1}+2\cdot \overline{B_1C_1} \\[5pt]
&=& 2\cdot 6\,\text{cm}+2\cdot 1\,\text{cm} \\[5pt]
&=& 14\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/97645df892df114ba2d1458ea32c32a3c7d65f713dd6add373a44c049d80d2e6?color=5a5a5a)
d)
(1)
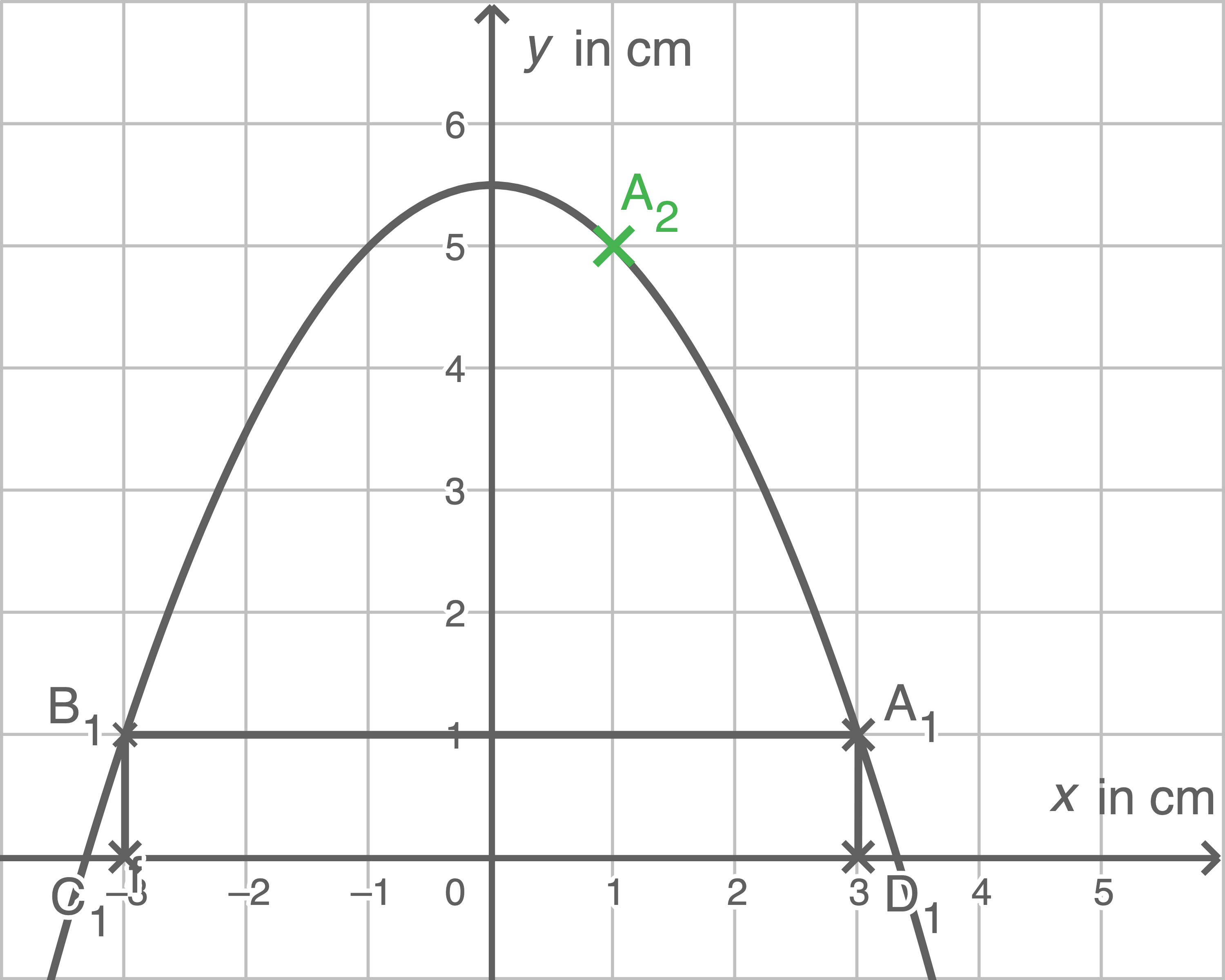 (2)
(2)
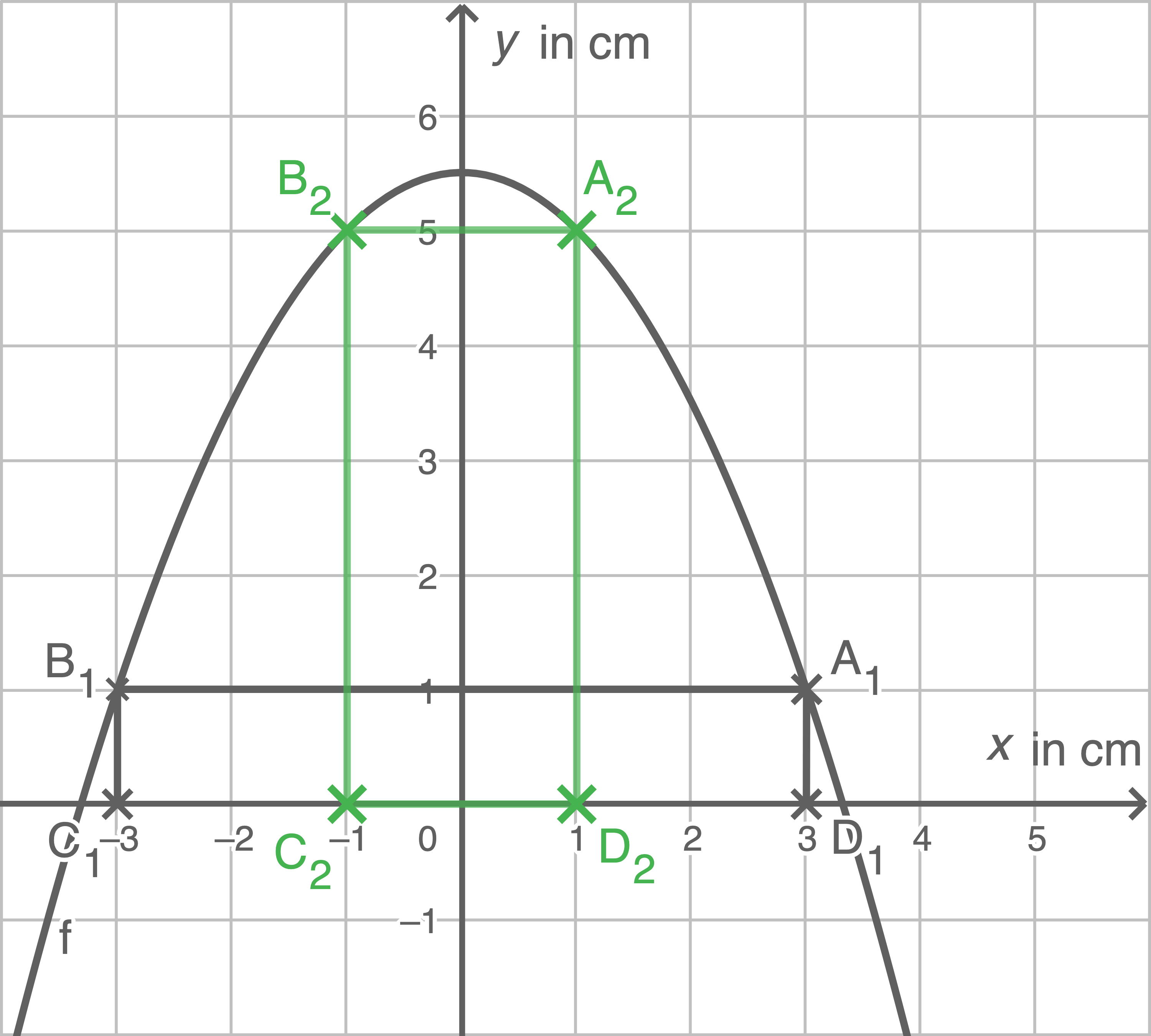


e)
Das Rechteck hat einen Umfang von  Die waagrechten Seiten des Rechtecks haben jeweils die Länge
Die waagrechten Seiten des Rechtecks haben jeweils die Länge  Die senkrechten Seiten des Rechtecks haben die Länge
Die senkrechten Seiten des Rechtecks haben die Länge  Damit hat das Rechteck einen Umfang von
Damit hat das Rechteck einen Umfang von 
f)
g)
(1) Gleichung mithilfe der  -Formel lösen:
-Formel lösen:
![\(\begin{array}[t]{rll}
-x^2+4x +11 &=& 14,75\quad \scriptsize \mid\;-14,75 \\[5pt]
-x^2+4x-3,75&=&0\quad \scriptsize \mid\;\cdot (-1) \\[5pt]
x^2-4x+3,75&=&0
\end{array}\)](https://mathjax.schullv.de/017a38e5f30d3064c11f36f86c9e2e50272c64d001845ca36792f7a5e3b36a63?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{-4}{2}\pm\sqrt{\left(\dfrac{-4}{2}\right)^2-3,75}\\[5pt]
x_{1,2}&=&2\pm\sqrt{4-3,75}\\[5pt]
x_{1,2}&=&2\pm\sqrt{0,25}\\[5pt]
x_{1}&=&2+0,5=2,5\\[5pt]
x_{2}&=&2-0,5=1,5
\end{array}\)](https://mathjax.schullv.de/e1c0a43ce5e07096b2d44be2f244ffa53d3f18fd13ce384af41e7a3c5da746d3?color=5a5a5a) (2) Unter der Parabel
(2) Unter der Parabel  gibt es zwei Rechtecke, deren Umfang bei
gibt es zwei Rechtecke, deren Umfang bei  liegt. Bei einem hat der Punkt
liegt. Bei einem hat der Punkt  die
die  -Koordiante
-Koordiante  und beim anderen
und beim anderen  Zur Veranschaulichung (ist nicht Teil der Lösung):
1. Schritt:
Zur Veranschaulichung (ist nicht Teil der Lösung):
1. Schritt:  -Koordinate des Punktes
-Koordinate des Punktes  berechnen
berechnen
 einsetzen in
einsetzen in 
![\(\begin{array}[t]{rll}
y_1&=&-0,5\cdot2,5^2+5,5 \\[5pt]
&=&2,375
\end{array}\)](https://mathjax.schullv.de/1f545a4fb62e3df470f0455dcf3d00fa3e2d68a52395381f4efefbd862018195?color=5a5a5a)
 2. Schritt:
2. Schritt:  und
und  einzeichnen
einzeichnen
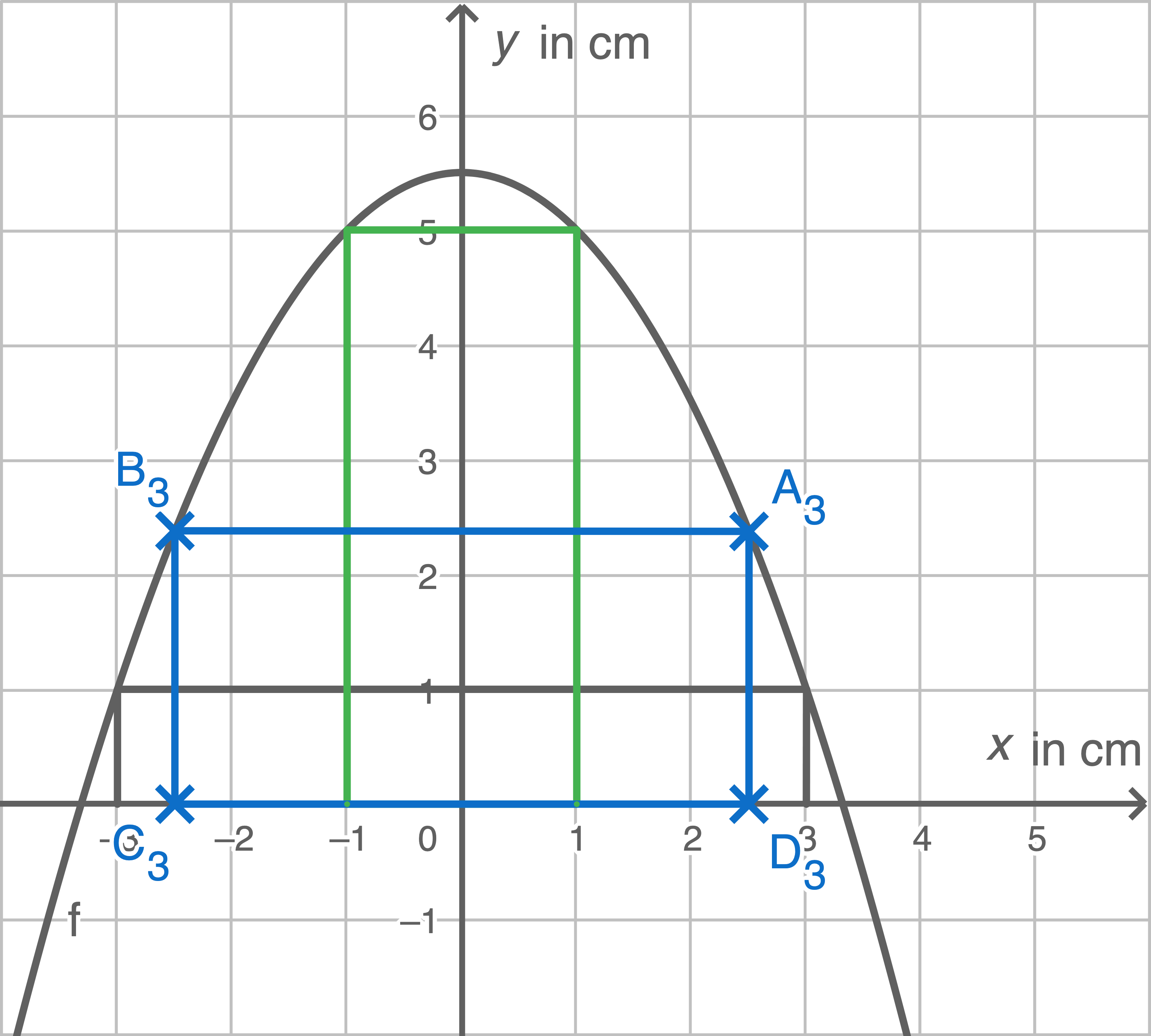 Wie man an dem Schaubild erkennt, liegt der Umfang des Rechtecks bei
Wie man an dem Schaubild erkennt, liegt der Umfang des Rechtecks bei  Gleiches gilt für
Gleiches gilt für 

h)
(1)
![\(\begin{array}[t]{rll}
u(x)&=& -x^2+4x+11 \\[5pt]
&=&-(x^2-4x-11) \\[5pt]
&=& -(x^2-4x+4-15) \\[5pt]
&=& -(x^2-4x+4)+15 \\[5pt]
&=& -(x-2)^2+15
\end{array}\)](https://mathjax.schullv.de/c730c2d4311d2ef056550a8dad344fb3b91834aaa865ee83e301e4c44870befd?color=5a5a5a)
 (2) Für
(2) Für  wird der Umfang maximal mit 15 Längeneinheiten.
wird der Umfang maximal mit 15 Längeneinheiten.