Aufgabe 1: Fruchtfliegen
Jasmin möchte für ein Biologieprojekt untersuchen, wie schnell sich Fruchtfliegen (Abbildung 1) vermehren. Sie kauft im Zoo-Center drei Zuchtboxen und bezeichnet diese mit 
und 
Abbildung 1:
Fruchtfliege (Drosophila)
Fruchtfliege (Drosophila)
Zuchtbox 
enthält anfänglich zehn Fruchtfliegen. Jasmin bewahrt die Box in ihrem warmen Zimmer auf und protokolliert in den folgenden Tagen die Anzahl der Tiere in der Box (Abbildung 2).
| Tag |
Anzahl Fruchtfliegen |
|---|---|
| 0 | 10 |
| 1 | 13 |
| 2 | 17 |
| 3 | 22 |
Abbildung 2: Tabelle
a)
Die Anzahl der Fruchtfliegen in Zuchtbox wächst täglich um ca. 
Weise dies für den Übergang von Tag 
auf Tag 
nach.
Jasmin stellt die Funktion
b)
Bestimme die voraussichtliche Anzahl an Fruchtfliegen nach 
Tagen.
c)
Bestimme, nach wie vielen Tagen die Anzahl der Fruchtfliegen erstmals größer als 
sein müsste.
Zuchtbox
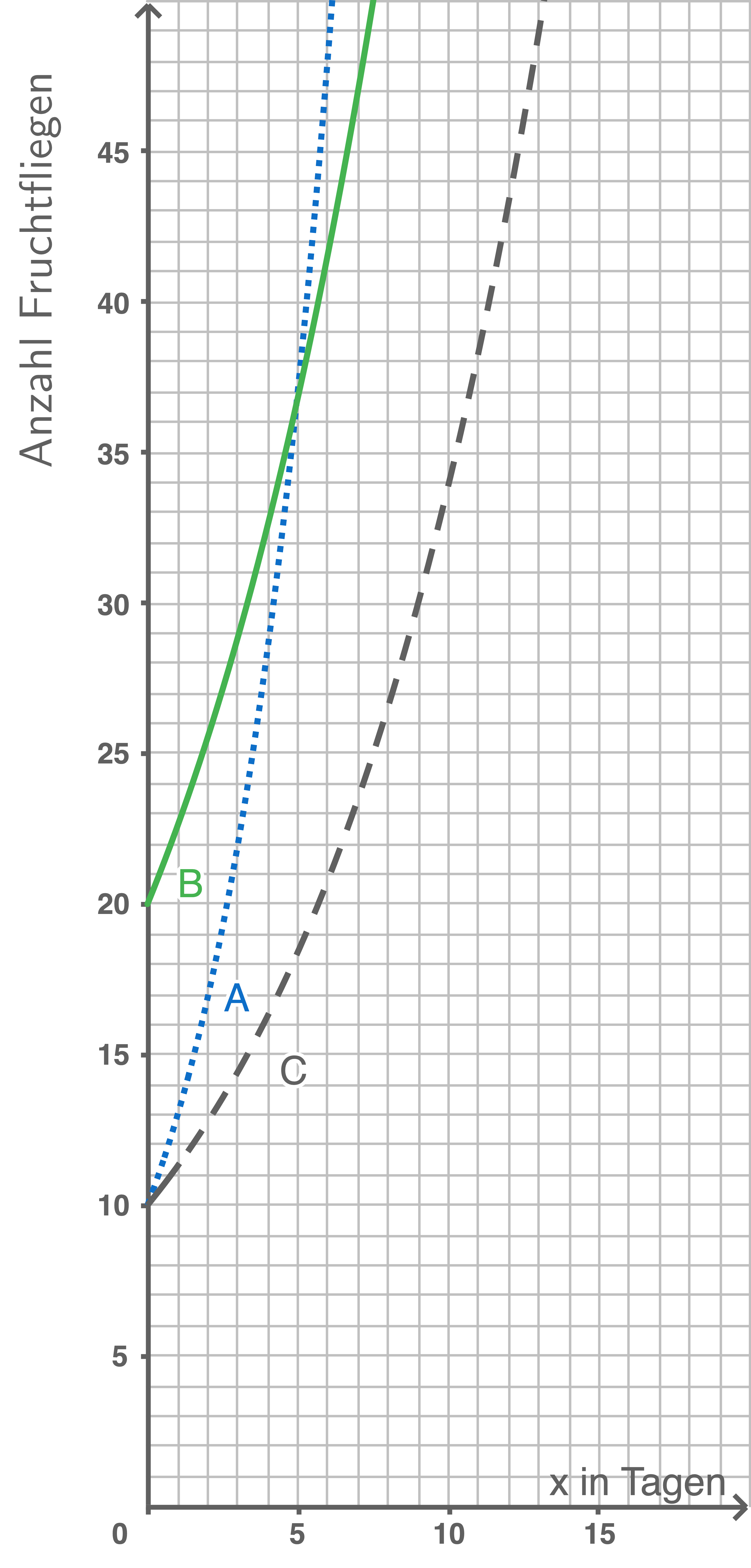
In Abbildung 3 sind die Graphen und 
dargestellt.
durch. Die Entwicklung der Anzahl an Fruchtfliegen wird mit dem Graphen beschrieben.
Abbildung 3: Graphen und
d)
Begründe, dass
(1)
die Funktion 
mit 
durch Graph dargestellt wird und
(2)
die Funktion 
mit 
durch Graph dargestellt wird.
e)
Bestimme mithilfe von Abbildung 3 den Tag, an dem die Zuchtboxen und etwa gleich viele Fruchtfliegen enthalten und gib die Anzahl an.
Jasmin führt ein drittes Experiment mit Zuchtbox
f)
Bestimme für den Graphen näherungsweise die Funktionsgleichung 
mit 
g)
Stelle eine begründete Vermutung zu den Bedingungen auf, unter denen das Experiment mit Zuchtbox durchgeführt wurde, indem du die drei abgebildeten Graphen vergleichst.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
c)
Gesucht ist die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
10\cdot 1,3^x&=& 100\,000 &\quad \scriptsize \mid\;:10 \\[5pt]
1,3^x&=& 10\,000 &\quad \scriptsize \mid\;\ln \\[5pt]
x\cdot \ln(1,3)&=& \ln(10\,000) &\quad \scriptsize \mid\;:\ln(3) \\[5pt]
x&=& \dfrac{\ln(10\,000)}{\ln(1,3)} \\[5pt]
x&\approx& 35,11
\end{array}\)](https://mathjax.schullv.de/2fd40286e6f1193ed80750c555e0add5eee960ee1d956d8a19d7cf902610162f?color=5a5a5a)
Nach 36 Tagen müsste die Anzahl der Fruchtfliegen erstmals größer als sein.
d)
(1)
Die Funktion gehört zu Zuchtbox 
Die Werte in der Tabelle in Abbildung 2 zeigen, dass der Graph von die Punkte 
und 
enthalten muss. Das ist nur für den Graph der Fall.
(2)
Es gilt 
und 
Der Graph ist der einzige, auf dem die zugehörigen Punkte liegen.
e)
Die Graphen und schneiden sich ungefähr bei 
Aus der Abbildung lässt sich 
ablesen.
Nach 5 Tagen befinden sich in den Zuchtboxen und jeweils 
Fruchtfliegen.
f)
Der Punkt liegt auf dem Graphen von Einsetzen der Koordinaten in die Funktionsgleichung von liefert:
![\(\begin{array}[t]{rll}
10&=& a\cdot q^0 \\[5pt]
10&=& a
\end{array}\)](https://mathjax.schullv.de/6e1d56ea78e65b6aff781e6da2974dc1399067a266e70ecba33a2031b1096768?color=5a5a5a)
Außerdem liegt der Punkt 
auf der Funktionsgleichung von 
Einsetzen von 
und den Koordianten dieses Punktes liefert für den Wert von 
![\(\begin{array}[t]{rll}
34&=& 10\cdot q^{10}&\quad \scriptsize \mid\;:10 \\[5pt]
3,4&=& q^{10}&\quad \scriptsize \mid\;\sqrt[10]{\,} \\[5pt]
1,13&\approx& q
\end{array}\)](https://mathjax.schullv.de/c357a22d5b130a0622b6f0d9788ca4d29dfaca7076eba1093f94b281c567635b?color=5a5a5a)
Insgesamt ergibt sich die Funktionsgleichung 
g)
Da der Graph wie der Graph an der Stelle den Wert 
annimmt, startet das Experiment mit 10 Fruchtfliegen.
Außerdem hat der Graph den gleichen Wachstumsfaktor wie der Graph von Zuchtbox B, daher wurde das Experiment vermutlich ebenfalls im Keller oder an einem anderen kühleren Ort durchgeführt.