Hauptähnlichkeitssatz Dreiecke
Stimmen zwei Dreiecke in zwei Innenwinkeln überein, so sind sie ähnlich zueinander.
(Hauptähnlichkeitssatz für Dreiecke) Das eine Dreieck kann in dem Fall z.B. dann durch das Bild einer zentrischen Streckung des anderen Dreiecks dargestellt werden.
(Hauptähnlichkeitssatz für Dreiecke) Das eine Dreieck kann in dem Fall z.B. dann durch das Bild einer zentrischen Streckung des anderen Dreiecks dargestellt werden.
1
Sind die folgenden beiden Dreiecke ähnlich?
Begründe mit dem Hauptähnlichkeitssatz für Dreiecke.
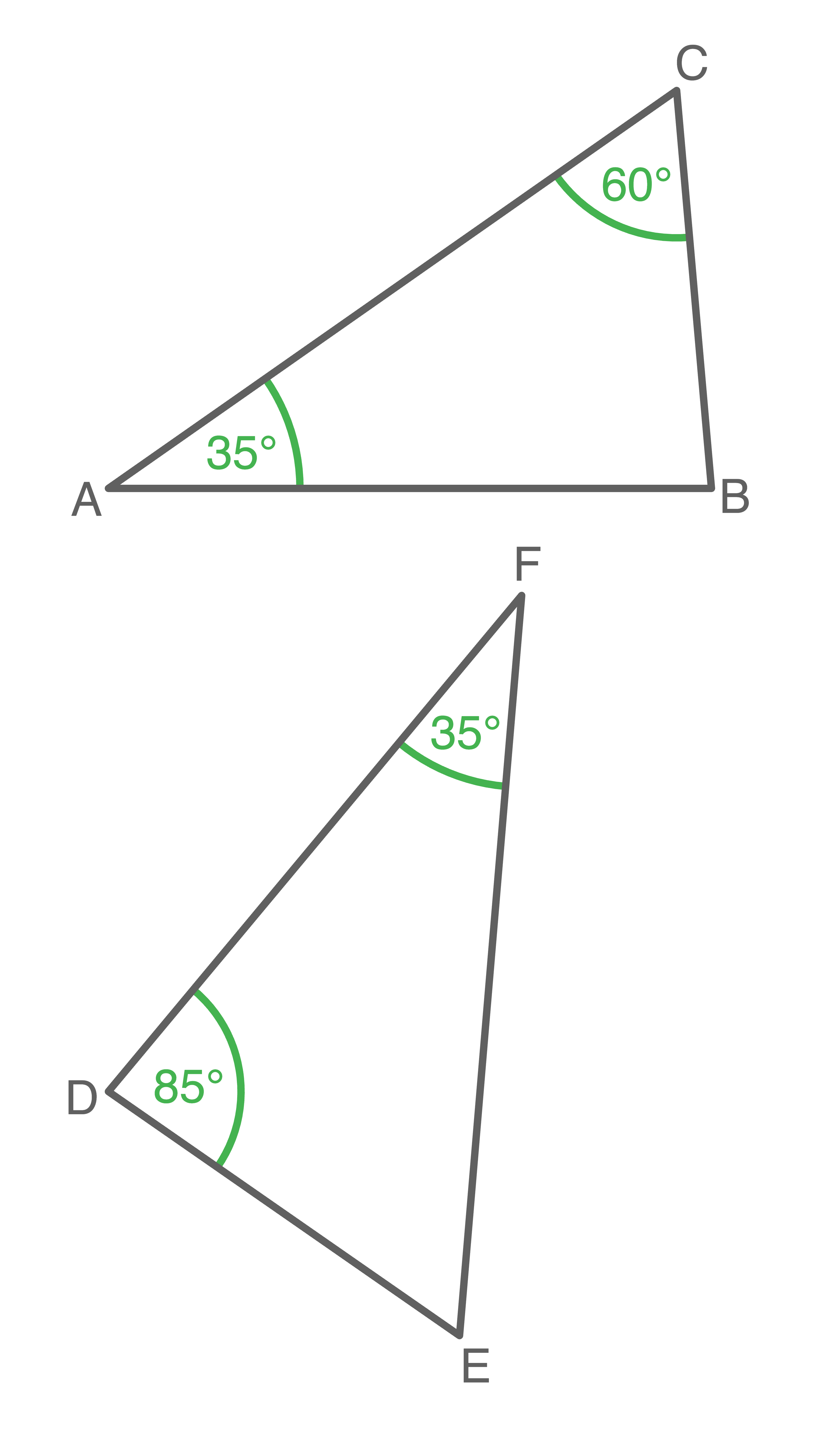
Begründe mit dem Hauptähnlichkeitssatz für Dreiecke.

2
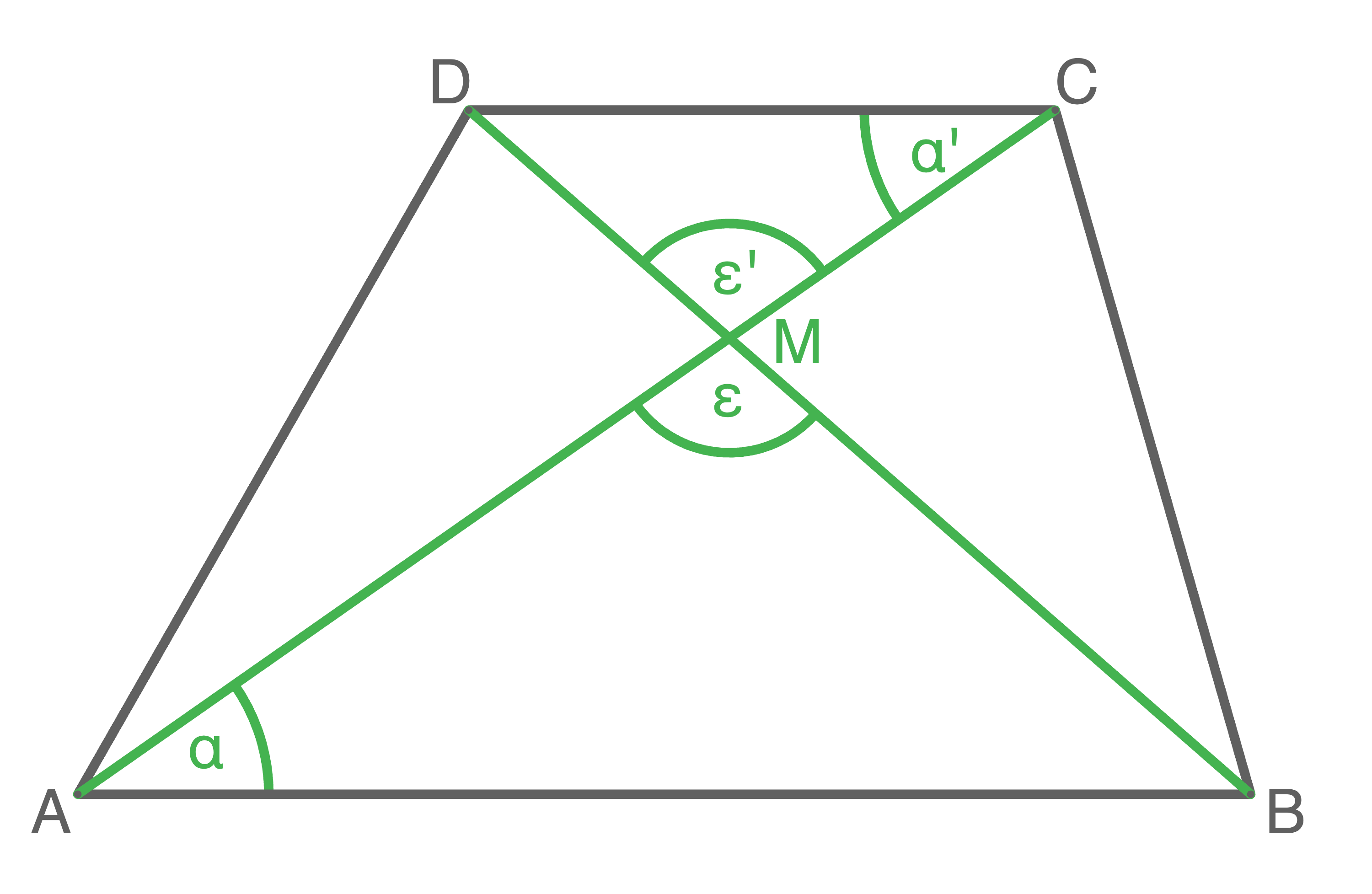
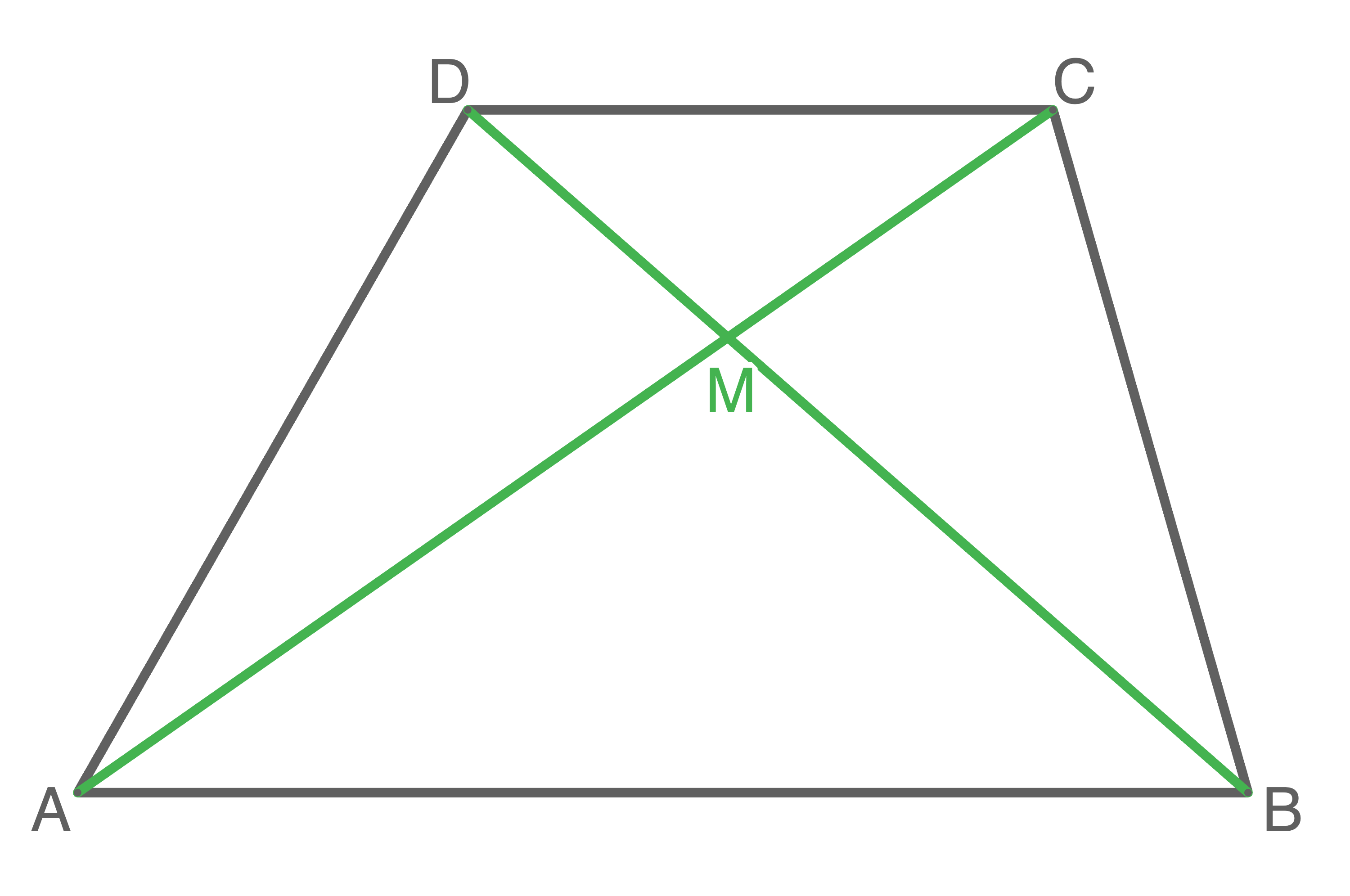
Die beiden Diagonalen  und
und  teilen das Trapez
teilen das Trapez  mit
mit  in vier Dreiecke.
Begründe mit Hilfe des Hauptähnlichkeitssatzes für Dreiecke, dass die Dreiecke
in vier Dreiecke.
Begründe mit Hilfe des Hauptähnlichkeitssatzes für Dreiecke, dass die Dreiecke  und
und  ähnlich zueinander sind.
ähnlich zueinander sind.

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Die Winkelsumme im Dreieck beträgt  Der fehlende Winkel im Dreieck
Der fehlende Winkel im Dreieck  hat die Größe
hat die Größe  Damit stimmen in beiden Dreiecken jeweils zwei Innenwinkel überein. Somit sind nach dem Hauptähnlichkeitssatz für Dreiecke die beiden Dreiecke ähnlich zueinander.
Damit stimmen in beiden Dreiecken jeweils zwei Innenwinkel überein. Somit sind nach dem Hauptähnlichkeitssatz für Dreiecke die beiden Dreiecke ähnlich zueinander.
2