Teil B – Pflichtaufgaben
Aufgabe 1
Die Münzen des Euroraumes bestehen aus verschiedenen Materialien (siehe Tabelle).


a)
Berechne, wie viel Gramm Aluminium in einer 50-Cent-Münze enthalten sind.
b)
In einer 5-Cent-Münze sind 3,70 g Eisen enthalten.
Berechne die Masse einer 5-Cent-Münze auf hundertstel Gramm genau.
Berechne die Masse einer 5-Cent-Münze auf hundertstel Gramm genau.
c)
Felix hat in seiner Sparbüchse Münzen gesammelt. Zum gesamten Inhalt der Sparbüchse hat er eine Tabelle angelegt.
Übernimm die Tabelle und ergänze die fehlenden Werte.
| Wert | Anzahl | Masse |
|---|---|---|
| 10 Cent | ||
| 20 Cent | ||
| 50 Cent | ||
| Gesamt |
Für Aufgabe 1 erreichbare BE: 6
Aufgabe 2
Gegeben sind zwei lineare Funktionen  und
und 
Die Funktion hat die Gleichung
hat die Gleichung 
Der Graph der Funktion verläuft durch die Punkte
verläuft durch die Punkte  und
und 
Die Funktion
Der Graph der Funktion
a)
Zeichne die Graphen der Funktionen  und
und  in ein rechtwinkliges Koordinatensystem mindestens im Intervall
in ein rechtwinkliges Koordinatensystem mindestens im Intervall 
b)
Gib den Anstieg  der Funktion
der Funktion  an.
an.
c)
Der Graph einer weiteren Funktion  entsteht durch Spiegelung des Graphen der Funktion
entsteht durch Spiegelung des Graphen der Funktion  an der
an der  -Achse.
-Achse.
- Zeichne den Graphen der Funktion
in dasselbe Koordinatensystem.
- Gib die Funktionsgleichung der Funktion
an.
Für Aufgabe 2 erreichbare BE: 6
Aufgabe 3
Eine Firma stellt Getriebe-Wellen her.
Bei jeder hergestellten Getriebe-Welle werden nacheinander Länge und Durchmesser kontrolliert. Jede der beiden Kontrollen wird mit „bestanden" oder „fehlerhaft" eingeschätzt.
Bei der Kontrolle der Längen sind erfahrungsgemäß 4 % der Getriebe-Wellen „fehlerhaft".
Bei der Kontrolle der Durchmesser sind erfahrungsgemäß 9 % der Getriebe-Wellen „fehlerhaft".
Das Kontrollverfahren kann als zweistufiges Zufallsexperiment betrachtet werden.
Bei der Kontrolle der Durchmesser sind erfahrungsgemäß 9 % der Getriebe-Wellen „fehlerhaft".
Das Kontrollverfahren kann als zweistufiges Zufallsexperiment betrachtet werden.
a)
Zeichne für dieses Zufallsexperiment ein Baumdiagramm.
Beschrifte alle Pfade mit den Wahrscheinlichkeiten.
Beschrifte alle Pfade mit den Wahrscheinlichkeiten.
b)
Eine Getriebe-Welle wird in beiden Kontrollen mit „bestanden" eingeschätzt.
Berechne die Wahrscheinlichkeit dafür.
Berechne die Wahrscheinlichkeit dafür.
c)
Eine Getriebe-Welle wird bei genau einer der beiden Kontrollen mit „fehlerhaft" eingeschätzt.
Berechne die Wahrscheinlichkeit dafür.
Berechne die Wahrscheinlichkeit dafür.
Für Aufgabe 3 erreichbare BE: 6
Aufgabe 4
Piloten von Segelflugzeugen müssen zum Erwerb von Leistungsabzeichen Streckenflüge zurücklegen.
Eine Karte mit dem Start und den drei Wendepunkten
und den drei Wendepunkten  ist in der Abbildung dargestellt.
ist in der Abbildung dargestellt.
Für die Berechnung werden alle Teilstrecken als geradlinig angenommen.
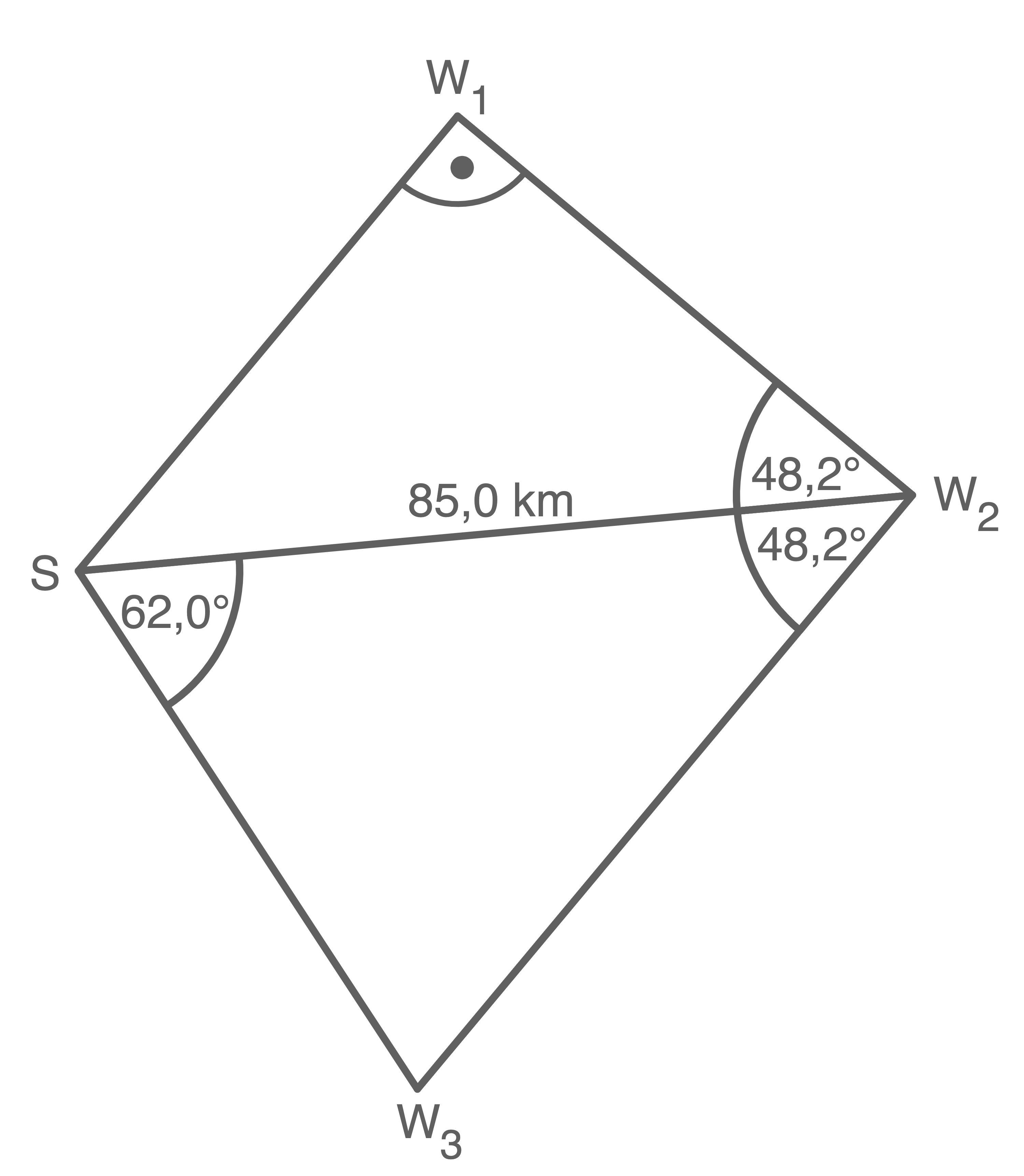
Eine Karte mit dem Start
Für die Berechnung werden alle Teilstrecken als geradlinig angenommen.

Abbildung (nicht maßstäblich)
a)
Ein Streckenflug führt vom Start  über den Wendepunkt
über den Wendepunkt  bis zum Wendepunkt
bis zum Wendepunkt  und von dort direkt zurück zum Start
und von dort direkt zurück zum Start 
- Berechne die Länge der Strecke
- Berechne die Länge dieses Streckenfluges.
b)
Andere Streckenflüge führen über den Wendepunkt  .
.
Berechne, wie weit der Wendepunkt vom Start
vom Start  entfernt ist.
entfernt ist.
Berechne, wie weit der Wendepunkt
Für Aufgabe 4 erreichbare BE: 6
Aufgabe 5
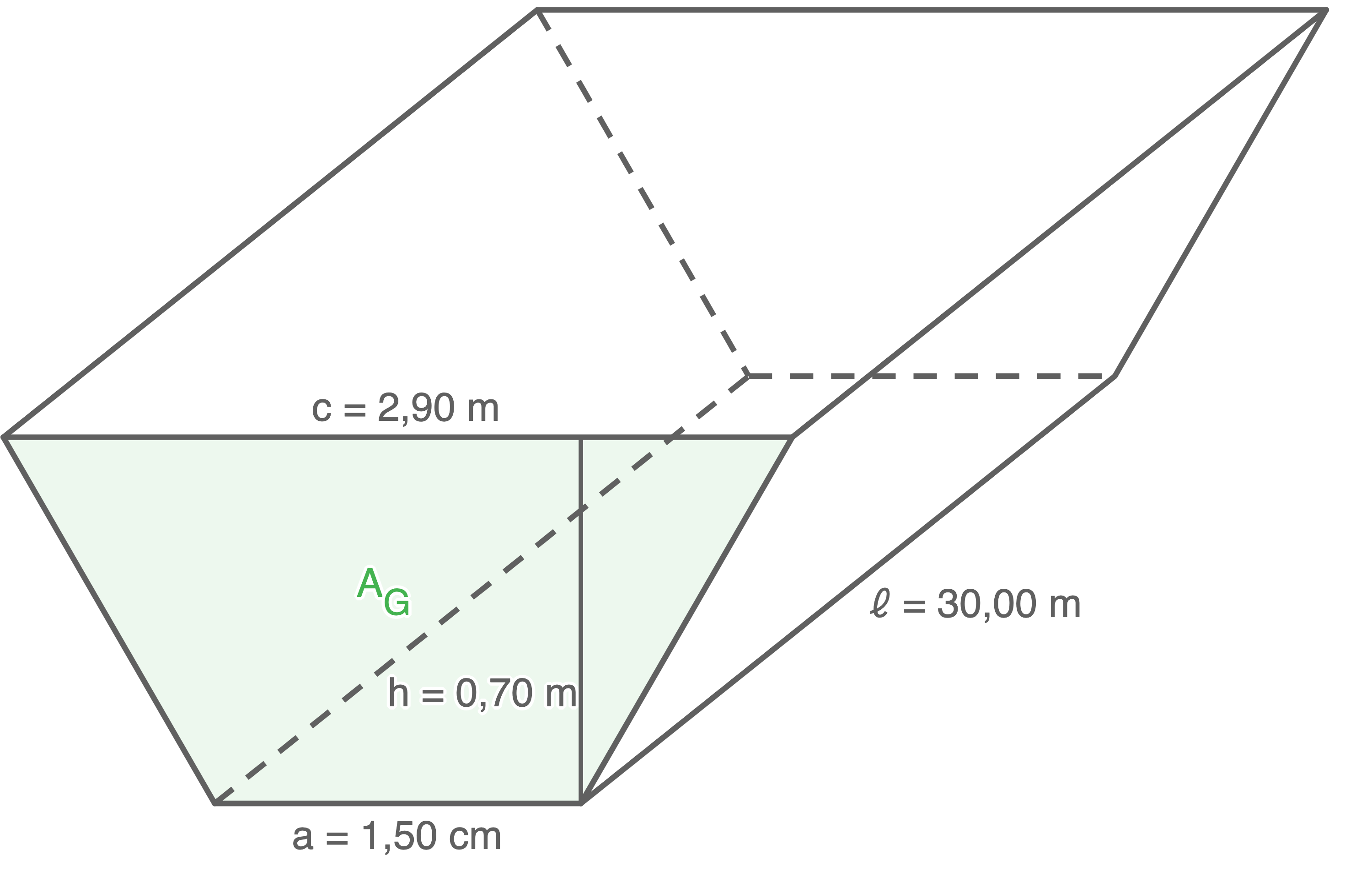
Für das Verlegen von Versorgungsleitungen müssen Gräben ausgehoben werden.
Jeder Graben hat die Form eines Prismas mit trapezförmiger Grundfläche.
Die Maße der Grundfläche sind von der Bodenbeschaffenheit abhängig.
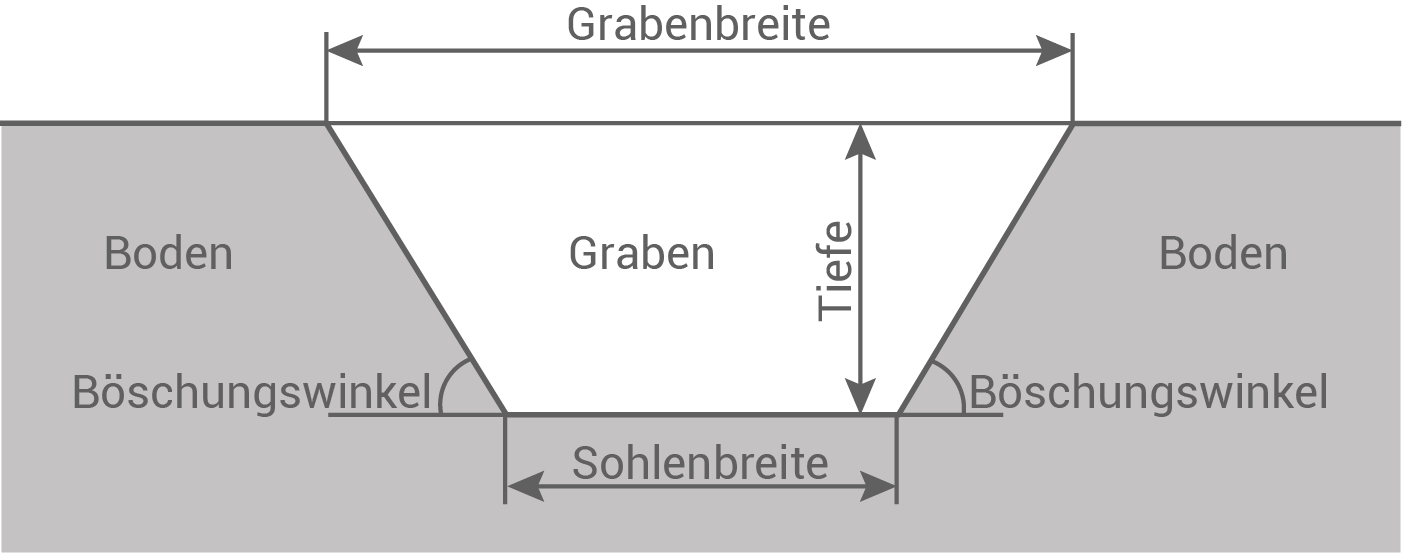
Jeder Graben hat die Form eines Prismas mit trapezförmiger Grundfläche.
Die Maße der Grundfläche sind von der Bodenbeschaffenheit abhängig.

Abbildung (nicht maßstäblich)
a)
Ein Graben im lehmhaltigen Boden hat eine Tiefe von 1,20 m.
Die Sohlenbreite beträgt ebenfalls 1,20 m.
Die beiden Böschungswinkel sind jeweils 60° groß (siehe Abbildung).
Ermittle die Grabenbreite mithilfe einer Zeichnung im Maßstab 1:20.
Die Sohlenbreite beträgt ebenfalls 1,20 m.
Die beiden Böschungswinkel sind jeweils 60° groß (siehe Abbildung).
Ermittle die Grabenbreite mithilfe einer Zeichnung im Maßstab 1:20.
b)
Ein anderer Graben im sandigen Boden hat die folgenden Maße.
Sohlenbreite .......................... 1,50 m
Grabenbreite ......................... 2,90 m
Tiefe ...................................... 0,70 m
Länge des Grabens ............ 30,00 m
Berechne das Volumen des Aushubes für diesen Graben.
Sohlenbreite .......................... 1,50 m
Grabenbreite ......................... 2,90 m
Tiefe ...................................... 0,70 m
Länge des Grabens ............ 30,00 m
Berechne das Volumen des Aushubes für diesen Graben.
Für Aufgabe 5 erreichbare BE: 6
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 7,80\,\text{g}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{7,80}{100}\,\text{g}\\[5pt]
5\,\% & \mathrel{\widehat{=}}& \dfrac{7,80}{100}\cdot 5\,\text{g}
\end{array}\)](https://www.schullv.de/resources/formulas/16dfab4f24d40216ee35141b11eee996c8f835868a87d80bea45edba95ac7609_light.svg)





Lösungsweg über die Verhältnisgleichung
![\(\begin{array}[t]{rll}
\dfrac{x}{5\,\%}&=&\dfrac{7,80\,\text{g}}{100\,\%} &\quad \scriptsize \mid\;\cdot 5 \,\%\\[5pt]
x&=&\dfrac{7,80\,\text{g}}{100\,\%}\cdot 5 \,\% \\[5pt]
x&=&\underline{\underline{ 0,39\,\text{g}}}
\end{array}\)](https://www.schullv.de/resources/formulas/1f29e1a5054f15919741c0421222887c35b69db74716191d842f14e3446742d0_light.svg)
Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
W&=&\dfrac{G\cdot p}{100} \\[5pt]
W&=&\dfrac{7,80\,\text{g}\cdot 5}{100} \\[5pt]
W&=&\underline{\underline{ 0,39\,\text{g}}}
\end{array}\)](https://www.schullv.de/resources/formulas/eeaeb4598e763bc69a6e995cf5833ef4c5b04177db7b3010fab0f2a01dd3e11e_light.svg)
Lösungsweg über den Dezimalbruch

In einer 50-Cent-Münze sind
b)
Eine 5-Cent-Münze besteht aus  aus Eisen. Um die Masse berechnen zu können, muss der Grundwert berechnet werden:
Beispielhafter Lösungsweg über die Prozentformel
aus Eisen. Um die Masse berechnen zu können, muss der Grundwert berechnet werden:
Beispielhafter Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
G&=&\dfrac{W\cdot 100}{p} \\[5pt]
G&=&\dfrac{3,70\,\text{g}\cdot 100}{94,35} \\[5pt]
G&=&\underline{\underline{ 3,92\,\text{g}}}
\end{array}\)](https://www.schullv.de/resources/formulas/8a8fd918eb58614c4cb67daf84738fd7258c0f6b1a3f1d35b89db055677b2db2_light.svg) Die Masse einer 5-Cent-Münze beträgt
Die Masse einer 5-Cent-Münze beträgt 
c)
| Wert | Anzahl | Masse |
|---|---|---|
| 10 Cent | ||
| 20 Cent | ||
| 50 Cent | ||
| Gesamt |
Lösung 2
a)
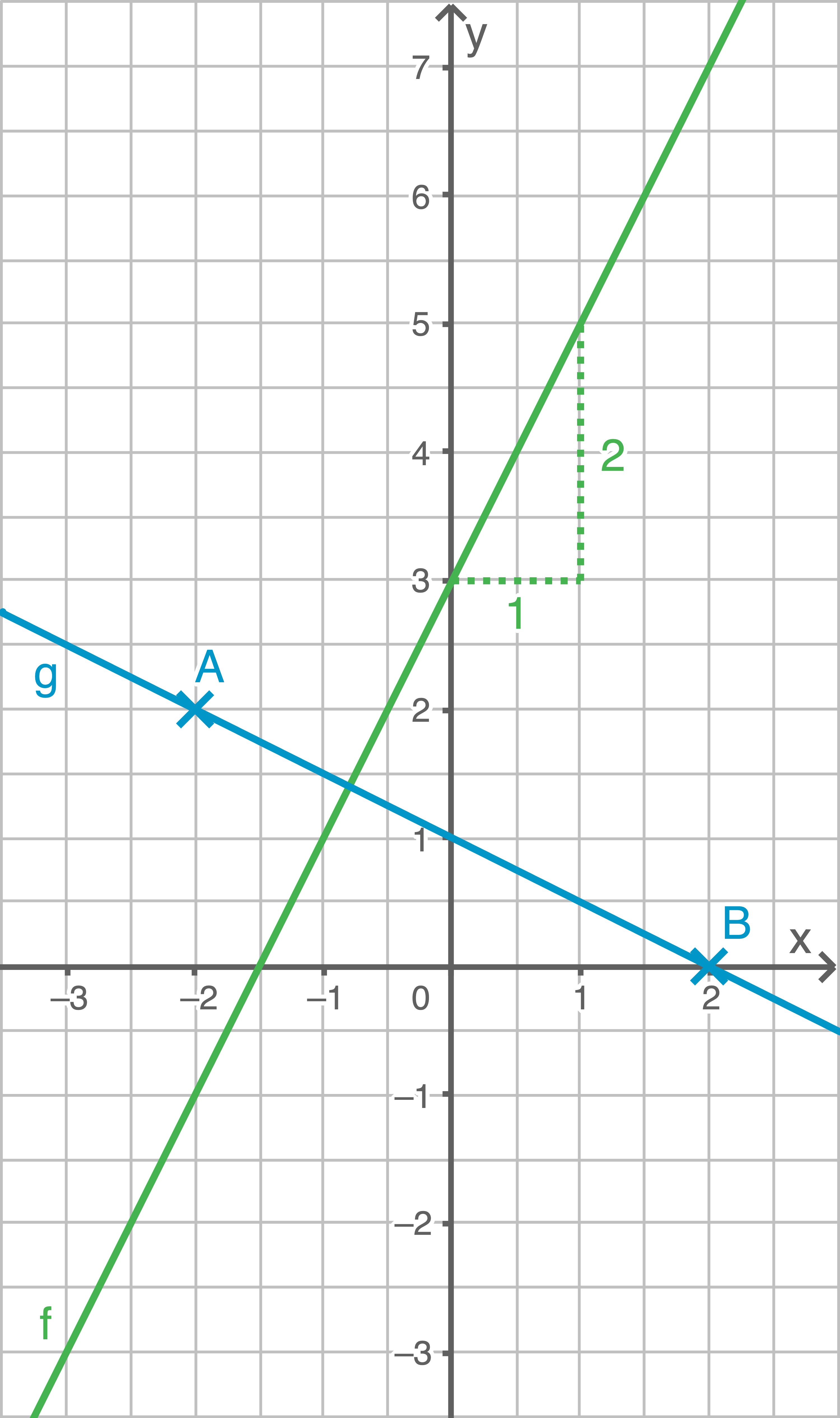
b)
Um den Anstieg  der Funktion
der Funktion  anzugeben, wird ein Steigungsdreieck eingezeichnet:
anzugeben, wird ein Steigungsdreieck eingezeichnet:
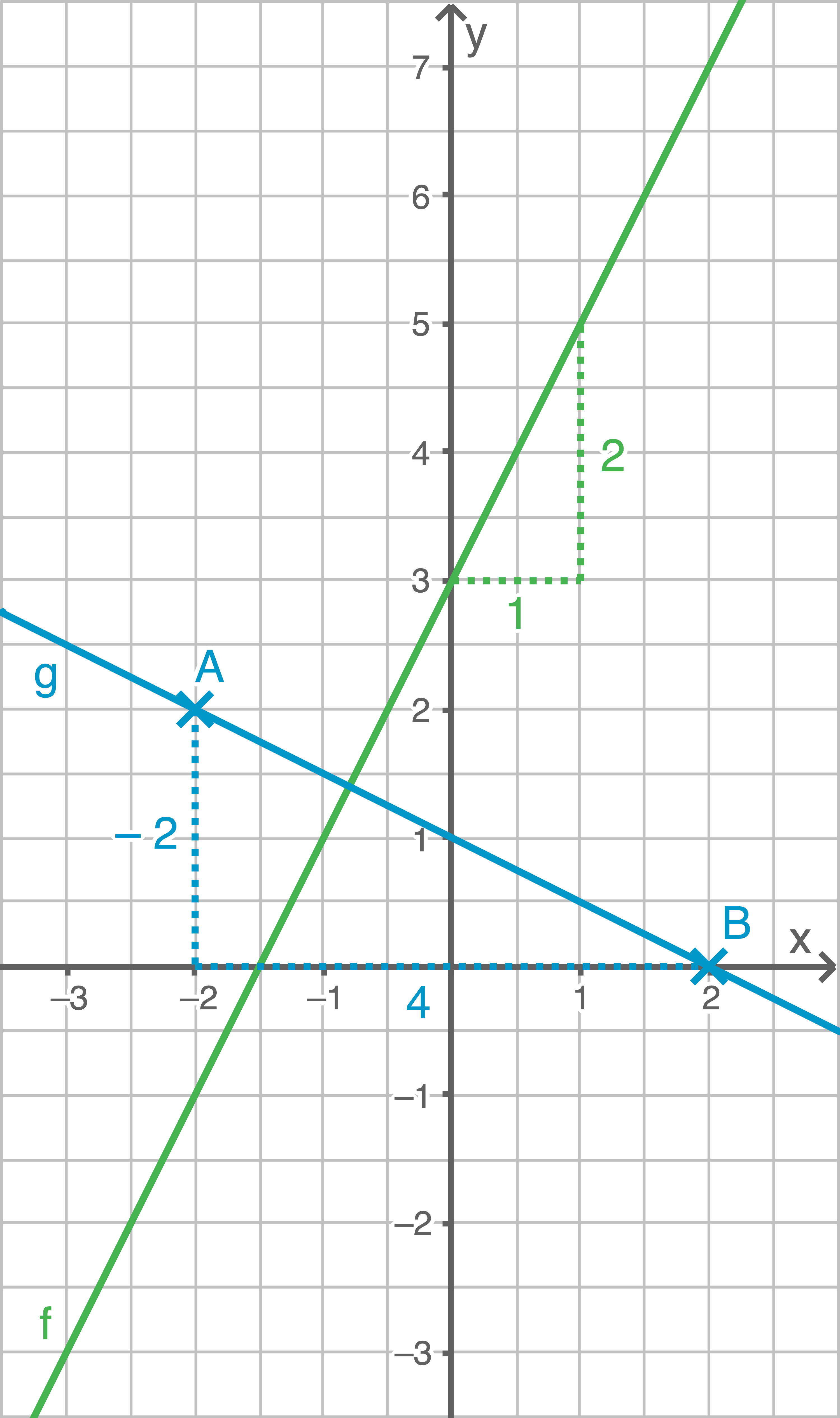 Daraus folgt für den Anstieg:
Daraus folgt für den Anstieg: 

c)
Graphen der Funktion  zeichnen
zeichnen
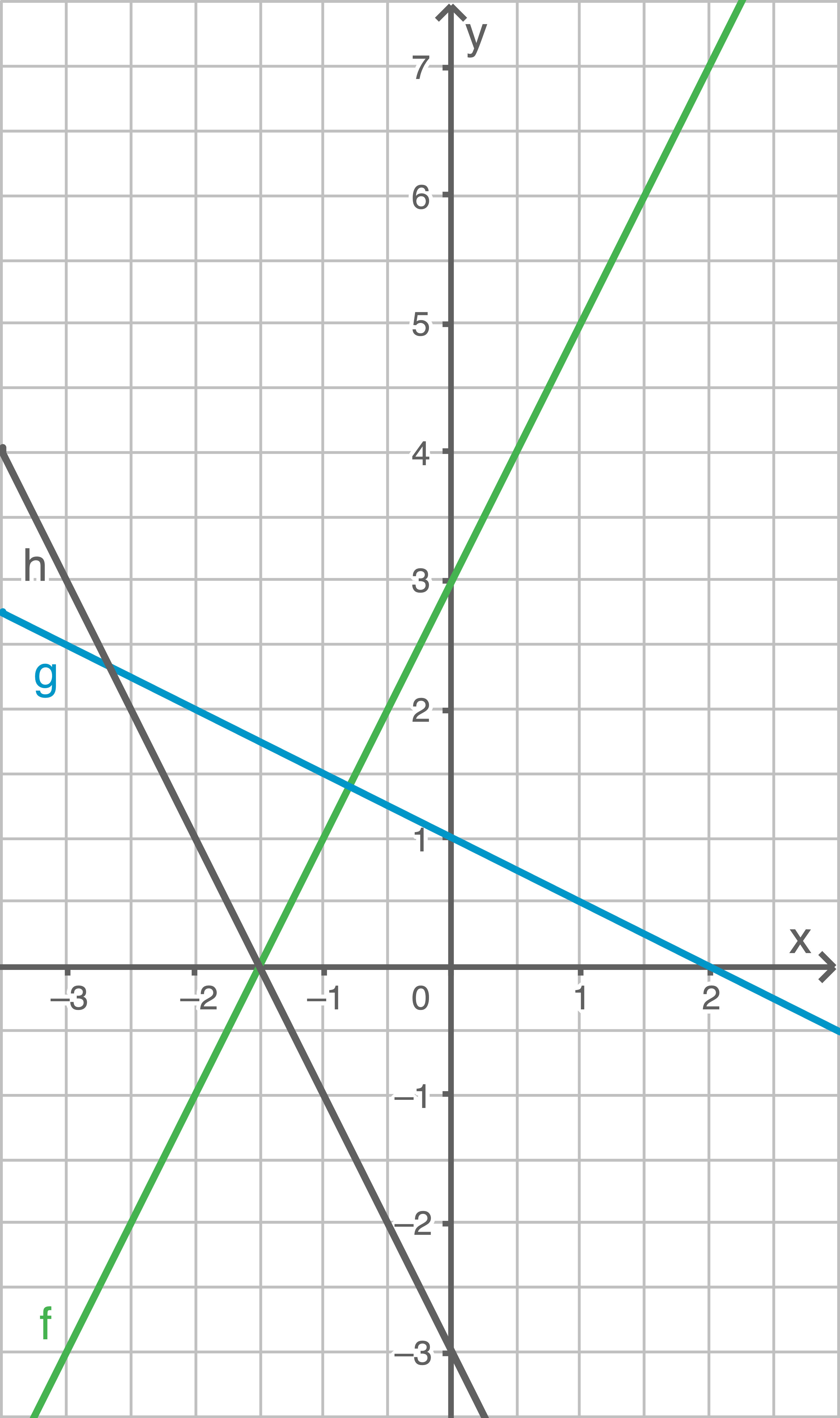 Funktionsgleichung der Funktion
Funktionsgleichung der Funktion  angeben
angeben


Lösung 3
a)

b = „bestanden“
b)
c)
Lösung 4
a)
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(48,2^{\circ})&=& \dfrac{\overline{W_1W_2}}{\overline{SW_2}} \quad \scriptsize \mid\; \cdot \overline{SW_2} \\[5pt]
\overline{W_1W_2}&=& \cos(48,2^{\circ}) \cdot \overline{SW_2} \\[5pt]
\overline{W_1W_2}&=& \cos(48,2^{\circ}) \cdot 85,0\,\text{km} \\[5pt]
\overline{W_1W_2}&\approx& \underline{\underline{ 56,66\,\text{km}}}
\end{array}\)](https://www.schullv.de/resources/formulas/6bc3c6d96fa068eca12c3220c120d3158c630b13e37c0bc96f933e51da912d37_light.svg) Die Länge der Strecke
Die Länge der Strecke  beträgt
beträgt  Länge des Streckenfluges berechnen
Satz des Pythagoras anwenden:
Länge des Streckenfluges berechnen
Satz des Pythagoras anwenden:
![\(\begin{array}[t]{rll}
\overline{SW_2}^2&=& \overline{SW_1}^2 + \overline{W_1W_2}^2 \quad \scriptsize \mid\; -\overline{W_1W_2}^2 \\[5pt]
\overline{SW_1}^2&=& \overline{SW_2}^2 - \overline{W_1W_2}^2 \quad \scriptsize \mid\; \sqrt{\,\,\,} \\[5pt]
\overline{SW_1}&=& \sqrt{\overline{SW_2}^2 - \overline{W_1W_2}^2} \\[5pt]
\overline{SW_1}&=& \sqrt{(85,0\,\text{km})^2-(56,66\,\text{km})^2} \\[5pt]
\overline{SW_1}&\approx& 63,36\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/584feb95652404a7e06562aa4425ab9803926ce19e838d3ffac51153000bd90a_light.svg) Daraus folgt für den gesamten Streckenflug:
Daraus folgt für den gesamten Streckenflug:
 Der gesamte Streckenflug hat eine Länge von
Der gesamte Streckenflug hat eine Länge von  .
.
b)
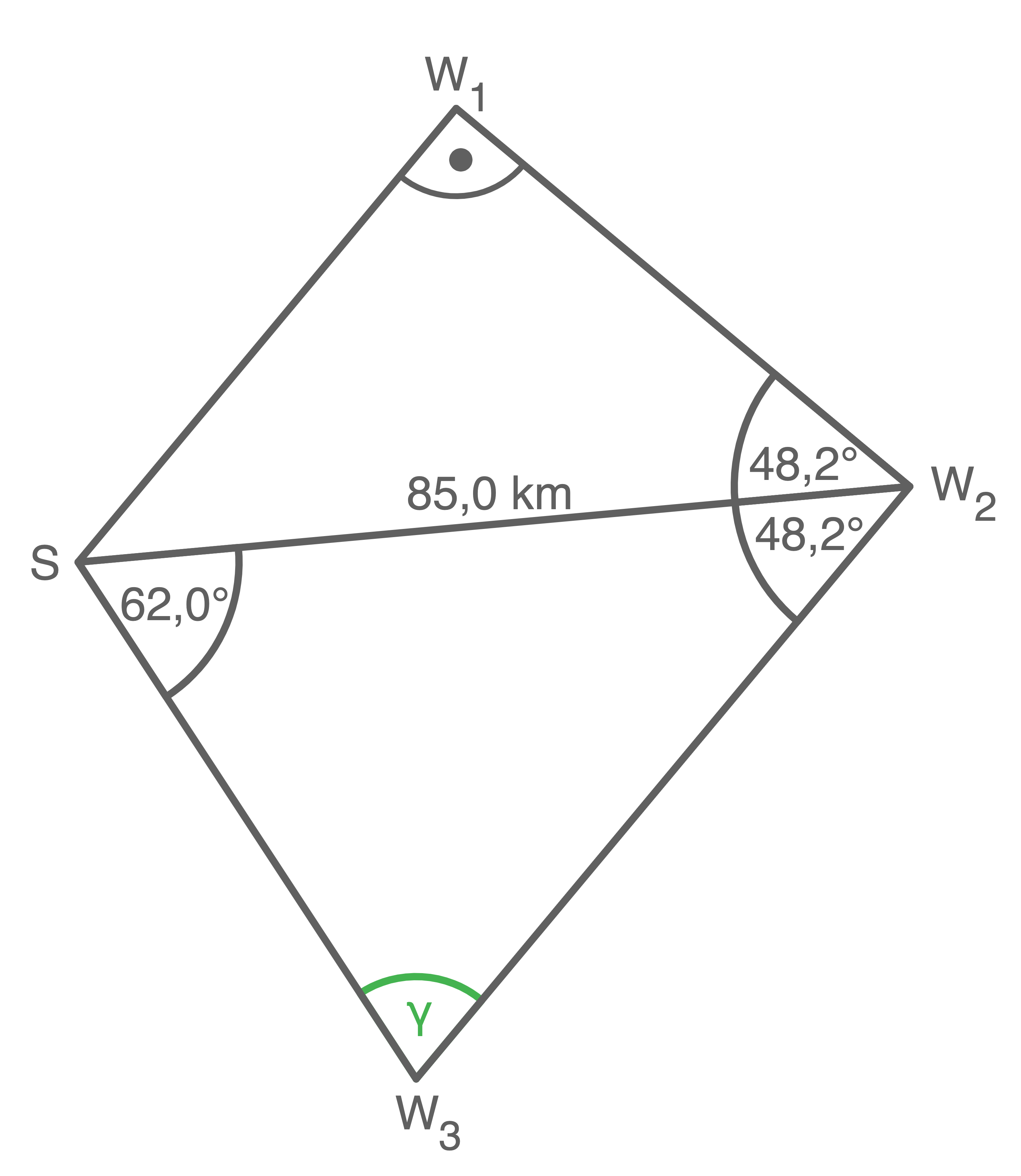
Lösung 5
a)
| Originallänge | Bildlänge im Maßstab 1:20 |
|---|---|
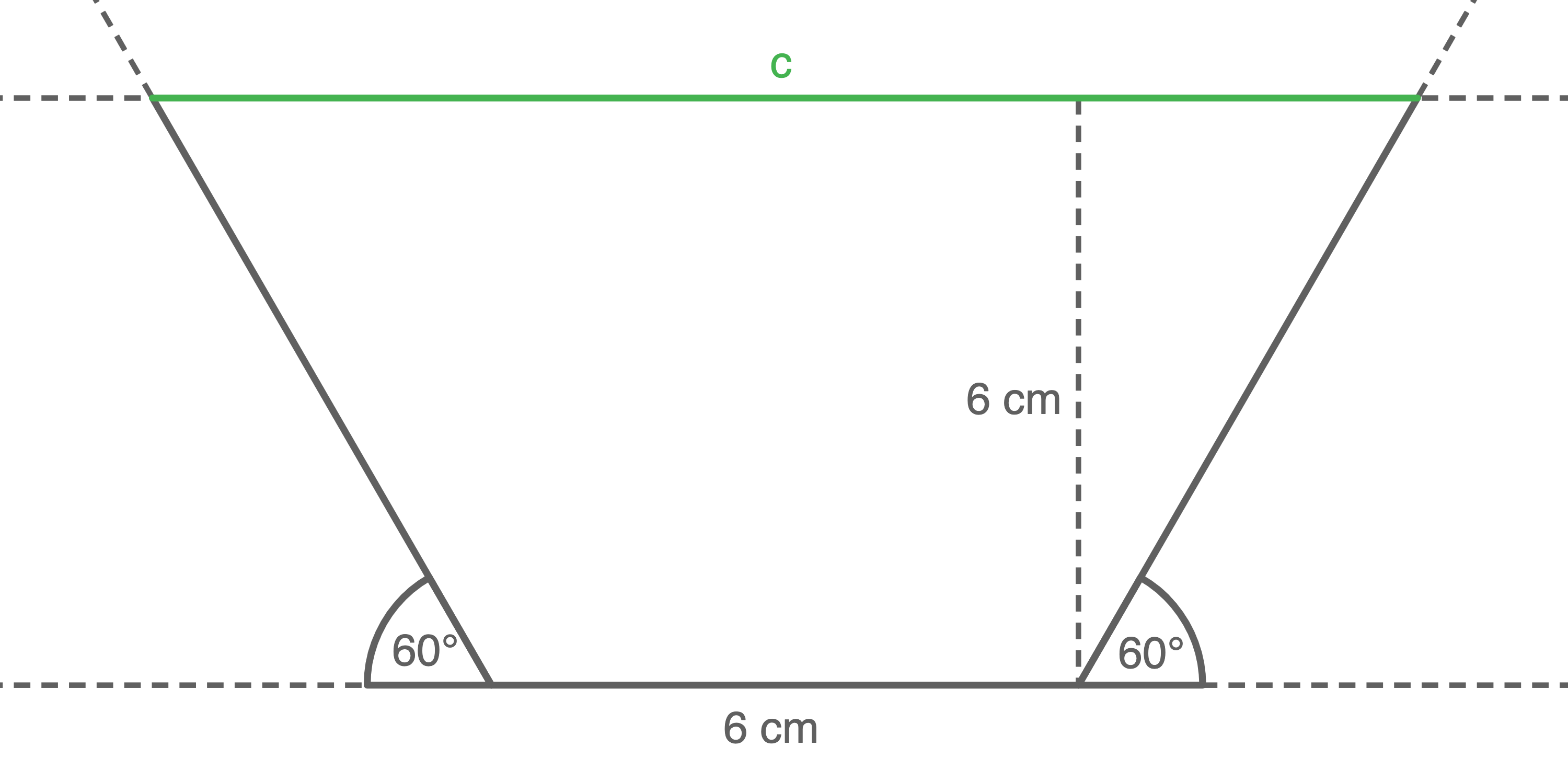
b)