Aufgabe 3: Quadratische Funktionen
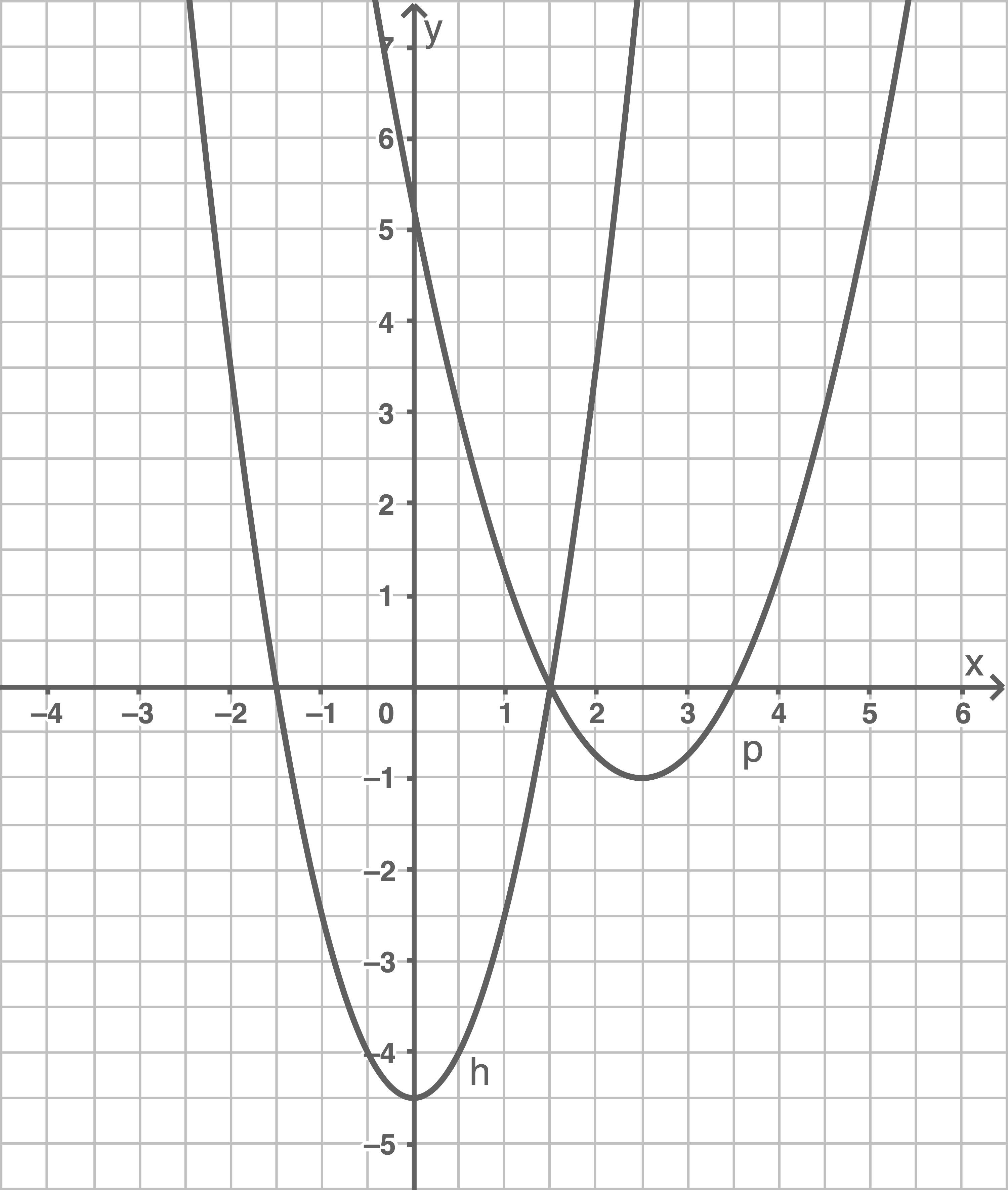
Der Graph einer quadratischen Funktion 
ist im Koordinatensystem dargestellt.
ist durch die Gleichung 
gegeben.
Der Scheitelpunkt der Parabel liegt auf der 
-Achse im Punkt 
Die Parabeln und schneiden sich im Punkt 
a)
Beschreibe, wie die Parabel aus der Normalparabel entstanden ist.
(2 P)
b)
Gib eine Gleichung der Funktion an.
Zeige, dass 
und 
die Nullstellen der Funktion sind.
Eine Parabel
(4 P)
Der Scheitelpunkt der Parabel
Die Parabeln
c)
Ermittle die Werte für die Parameter 
und 
.
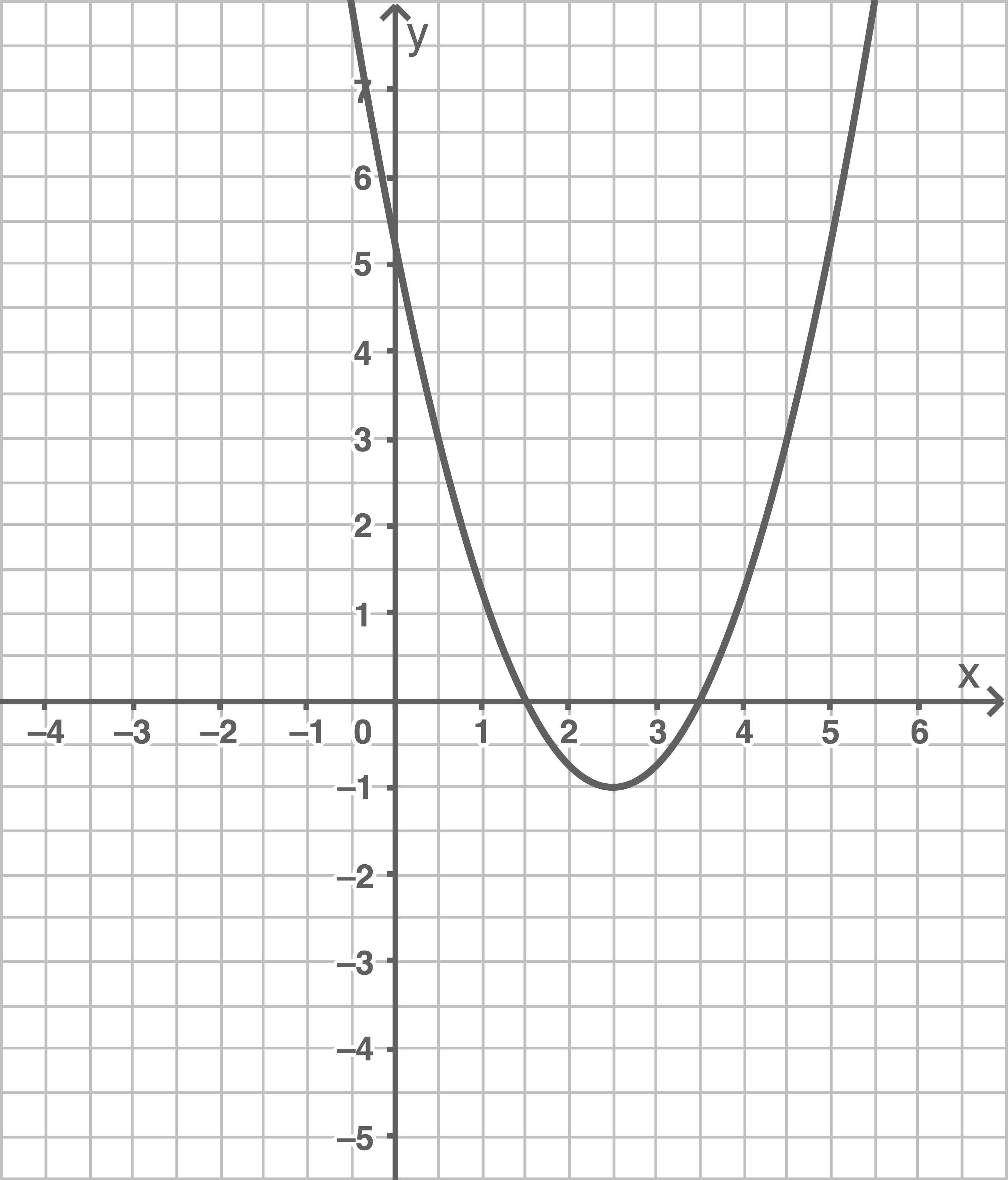
Zeichne die Parabel mindestens im Intervall 
in das vorgegebene Koordinatensystem.
(5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Verschiebung um 2,5 Einheiten in die positive 
-Richtung.
Verschiebung um eine Einheit in die negative -Richtung.
b)
Funktionsgleichung angeben
Der Scheitelpunkt 
kann aus der Abbildung abgelesen werden. Damit lässt sich die Funktionsgleichung in Scheitelpunktform angeben:
Nullstellen nachweisen
einsetzen:
![\(\begin{array}[t]{rll}
p(x_1)&=& (3,5-2,5)^2-1 &\quad \scriptsize \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/616d5e337c1416af02106bc501c976b7c523de362e4e96be6b07182f56a00241?color=5a5a5a)
einsetzen:
![\(\begin{array}[t]{rll}
p(x_2)&=&(1,5-2,5)^2-1 &\quad \scriptsize \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/4e6d845e56a914dbee0ef43a72b360ae2adbde071aaefb22f97ac9eeb87ff0d2?color=5a5a5a)
c)
Die Funktionsgleichung lautet bis dahin also
