Grundkenntnisse
1.
Ein Gewinn von  soll gleichmäßig auf
soll gleichmäßig auf  Personen aufgeteilt werden.
Personen aufgeteilt werden.
Wie viel Euro erhält jede Person?
Wie viel Euro erhält jede Person?
(1 Pkt.)
2.
Welche Zahl liegt  am nächsten? Kreuze an.
am nächsten? Kreuze an.
(1 Pkt.)
3.
Welche Figur wird durch Drehen und Verschieben spiegelsymmetrisch zur Ausgangsfigur? Kreuze an.




(1 Pkt.)
4.
Ein Kraftfuttervorrat reicht für  Kühe
Kühe  Tage lang.
Tage lang.
Wie lange würde die gleiche Menge Kraftfutter voraussichtlich für Kühe reichen?
Kühe reichen?
Wie lange würde die gleiche Menge Kraftfutter voraussichtlich für
(1 Pkt.)
5.
Wie groß ist der Umfang dieser Fläche?
Die Maße sind in angegeben.
angegeben.
Die Maße sind in

Zeichnung nicht maßstabsgetreu
(1 Pkt.)
6.
Zeichne ein rechtwinkliges Dreieck, dessen Katheten  und
und  lang sind.
lang sind.
(1 Pkt.)
7.
Der Winkel  in einem gleichschenkligen Trapez beträgt
in einem gleichschenkligen Trapez beträgt  . Gib die Größe des Winkels
. Gib die Größe des Winkels  an.
an.

Zeichnung nicht maßstabsgetreu
(1 Pkt.)
8.
Löse die Gleichung.

(1 Pkt.)
9.
Tim dreht einmal am abgebildeten Glücksrad.
 Wie groß ist die Wahrscheinlichkeit, dass der Pfeil nach dem Drehen auf ein Feld mit einer geraden Zahl zeigt?
Wie groß ist die Wahrscheinlichkeit, dass der Pfeil nach dem Drehen auf ein Feld mit einer geraden Zahl zeigt?

(1 Pkt.)
10.
Zu weIcher Geradengleichung passt der Graph? Kreuze an.


(1 Pkt.)
1.
2.
Die benachbarten Quadratzahlen zu
3.
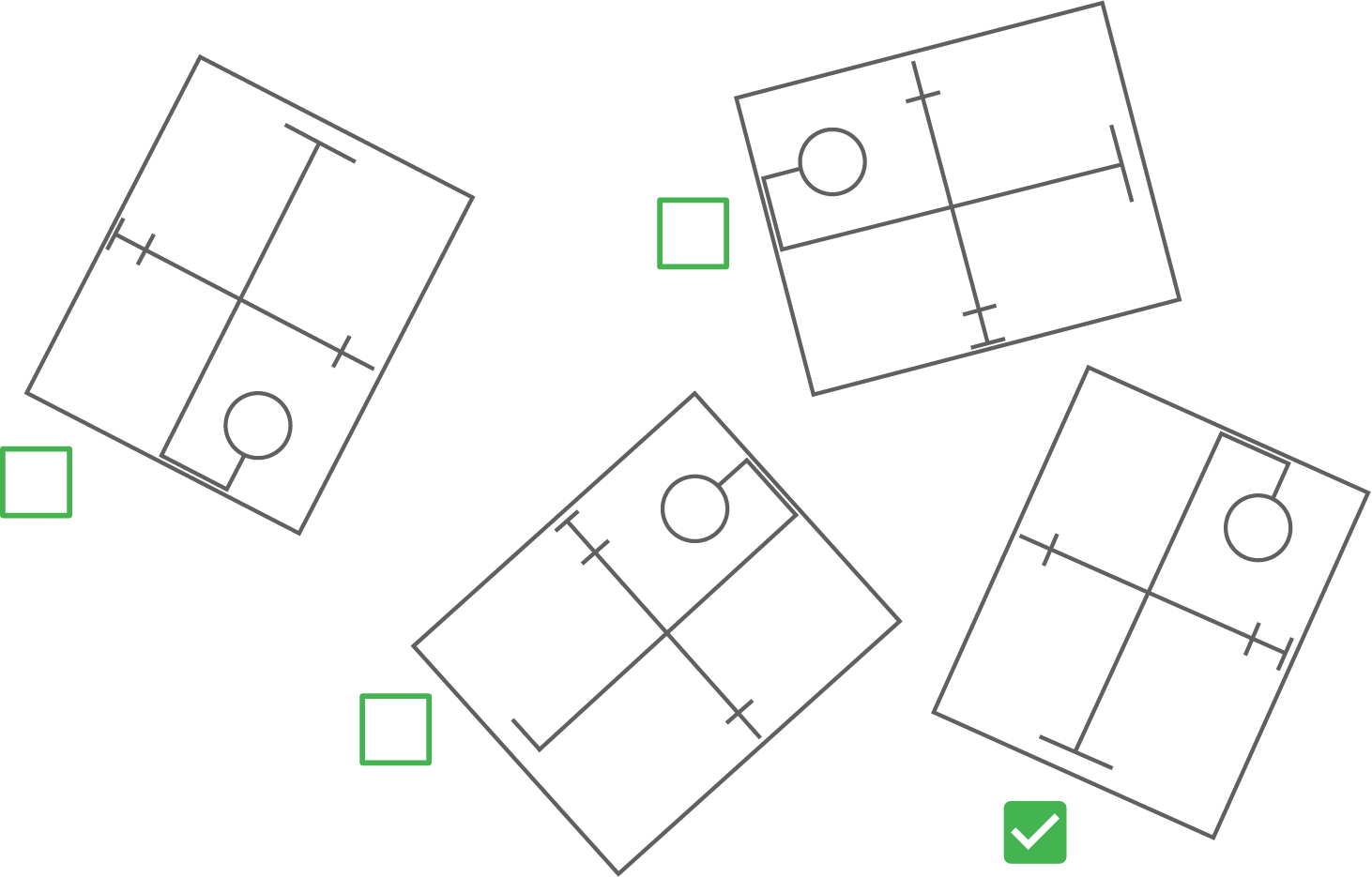
4.
Es handelt sich um eine antiproportionale Zuordnung: Je mehr Kühe, desto weniger Tage reicht das Futter.
Oder andersrum formuliert: Je weniger Kühe, desto mehr Tage reicht das Futter.




![\(\begin{array}{rcl}
10\,\text{Kühe} & \mathrel{\widehat{=}}& 30\,\text{Tage}\\[5pt]
1\,\text{Kuh} & \mathrel{\widehat{=}}& 300\,\text{Tage}\\[5pt]
15\,\text{Kühe} & \mathrel{\widehat{=}}& 20\,\text{Tage}
\end{array}\)](https://mathjax.schullv.de/6d76ce8eb286a89a56fc99aa748ca95ce0c88333e0dcfd76e14e8d0758fe21c8?color=5a5a5a)



 Die Menge Kraftfutter würde für 20 Tage reichen.
Die Menge Kraftfutter würde für 20 Tage reichen.
Oder andersrum formuliert: Je weniger Kühe, desto mehr Tage reicht das Futter.
5.
Für einen besseren Überblick werden alle Seiten mit den entsprechenden Längen versehen:
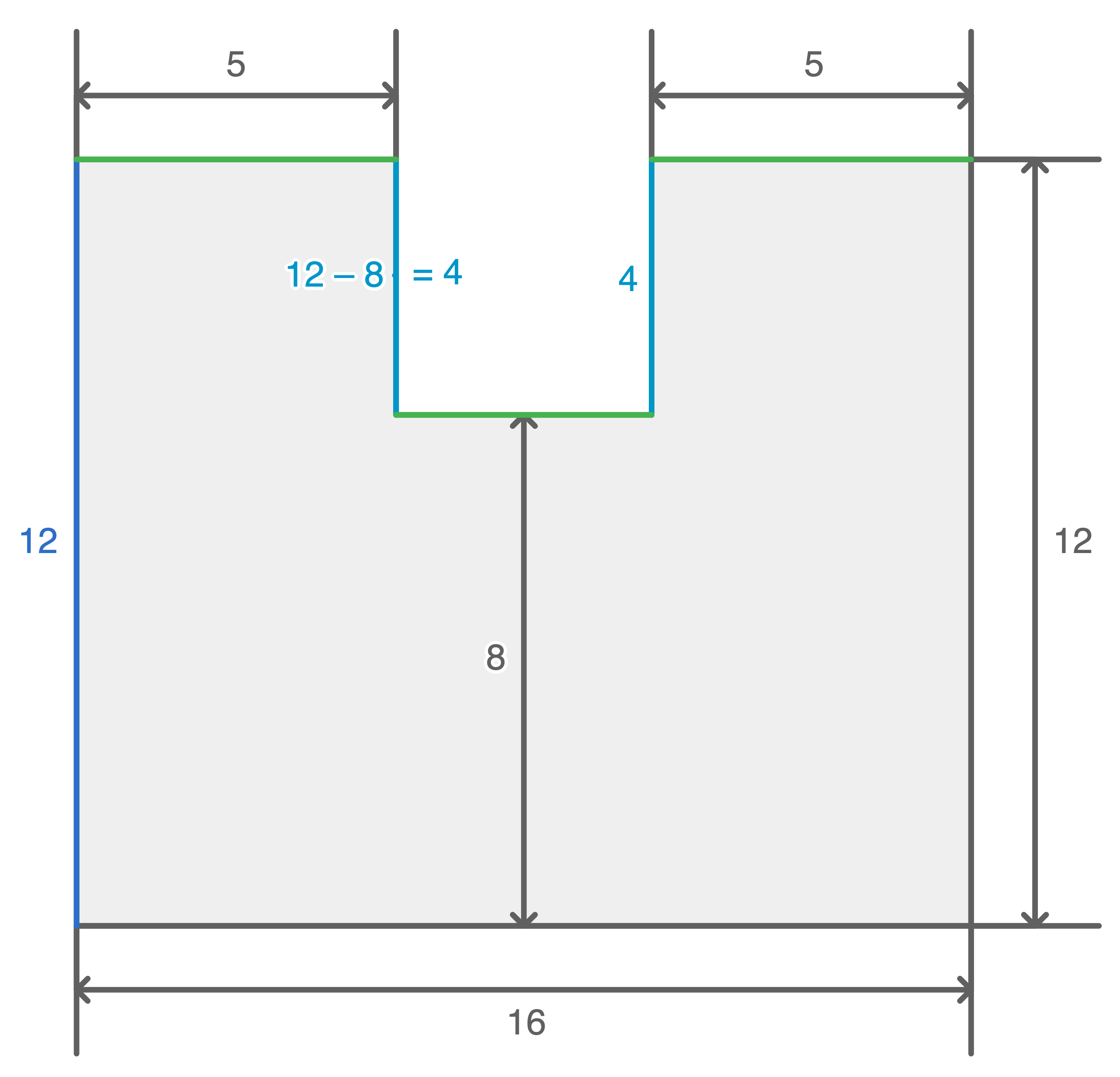 Die grünen Seiten ergeben zusammen eine Länge von
Die grünen Seiten ergeben zusammen eine Länge von  Um den Umfang zu berechnen, müssen alle Längen nur noch addiert werden:
Um den Umfang zu berechnen, müssen alle Längen nur noch addiert werden:
![\(\begin{array}[t]{rll}
u&=&2\cdot 16\,\text{cm}+2\cdot 12\,\text{cm}+2\cdot 4\,\text{cm} & \\[5pt]
u&=&32\,\text{cm}+24\,\text{cm}+8\,\text{cm} & \\[5pt]
u&=&64\,\text{cm} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/67f2b6f93f728fc29e0b04ec9c9dd680ce296eec8ed6cd852e9c6460392a82ae?color=5a5a5a)

6.
Ein mögliches Dreieck:
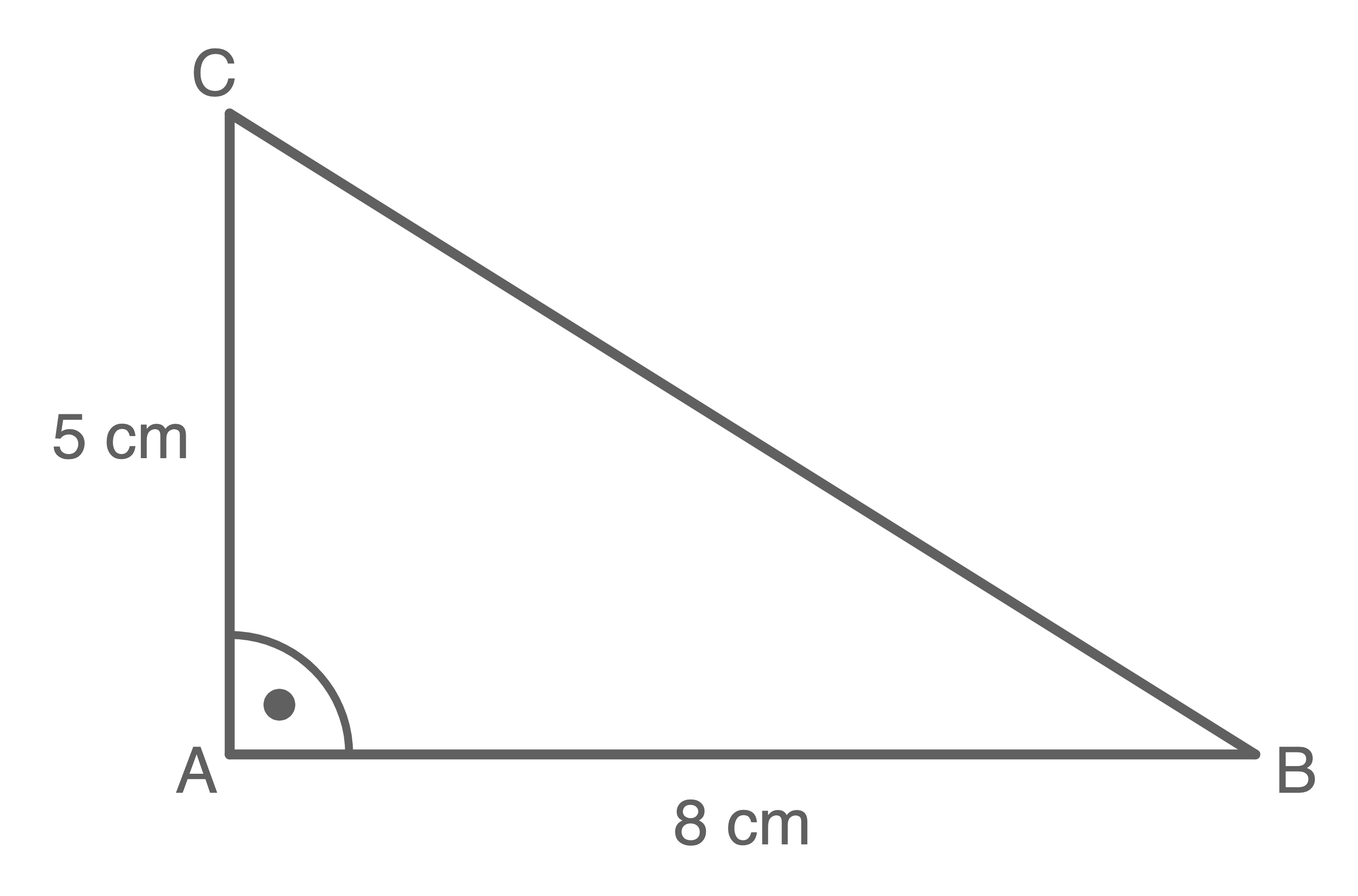

7.
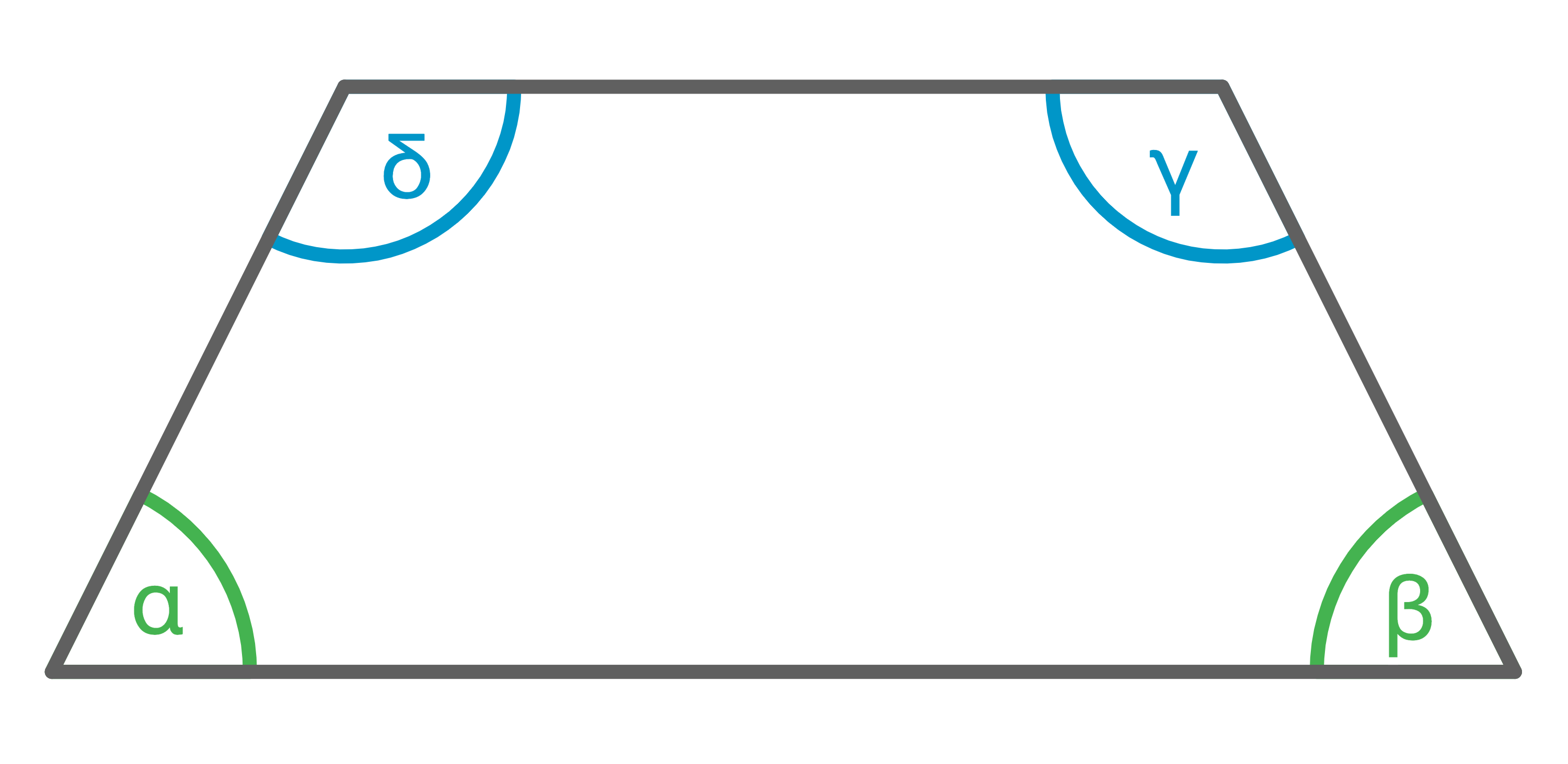
Daraus folgt:
8.
9.
Es gibt insgesamt 8 Felder. Davon sind 3 Felder mit einer geraden Zahlen beschriftet.
 Die Wahrscheinlichkeit liegt also bei
Die Wahrscheinlichkeit liegt also bei 
10.
