Wahlteil B
Aufgabe 1
a)
Im Jahr 2002 erhielt man bei einer Geldanlage noch 
Zinsen, 2022 nur noch 
Zinsen.
Frau Ziegler legte 2002 den Betrag von 
für ein Jahr an.
- Berechne den Jahreszins für 2002.
- Wie viel Geld hätte sie 2022 anlegen müssen, um den gleichen Jahreszins wie 2002 zu erhalten?
(2 Pkt.)
b)
Setze einen der beiden Lösungswege fort und berechne die Länge der Seitenkante 
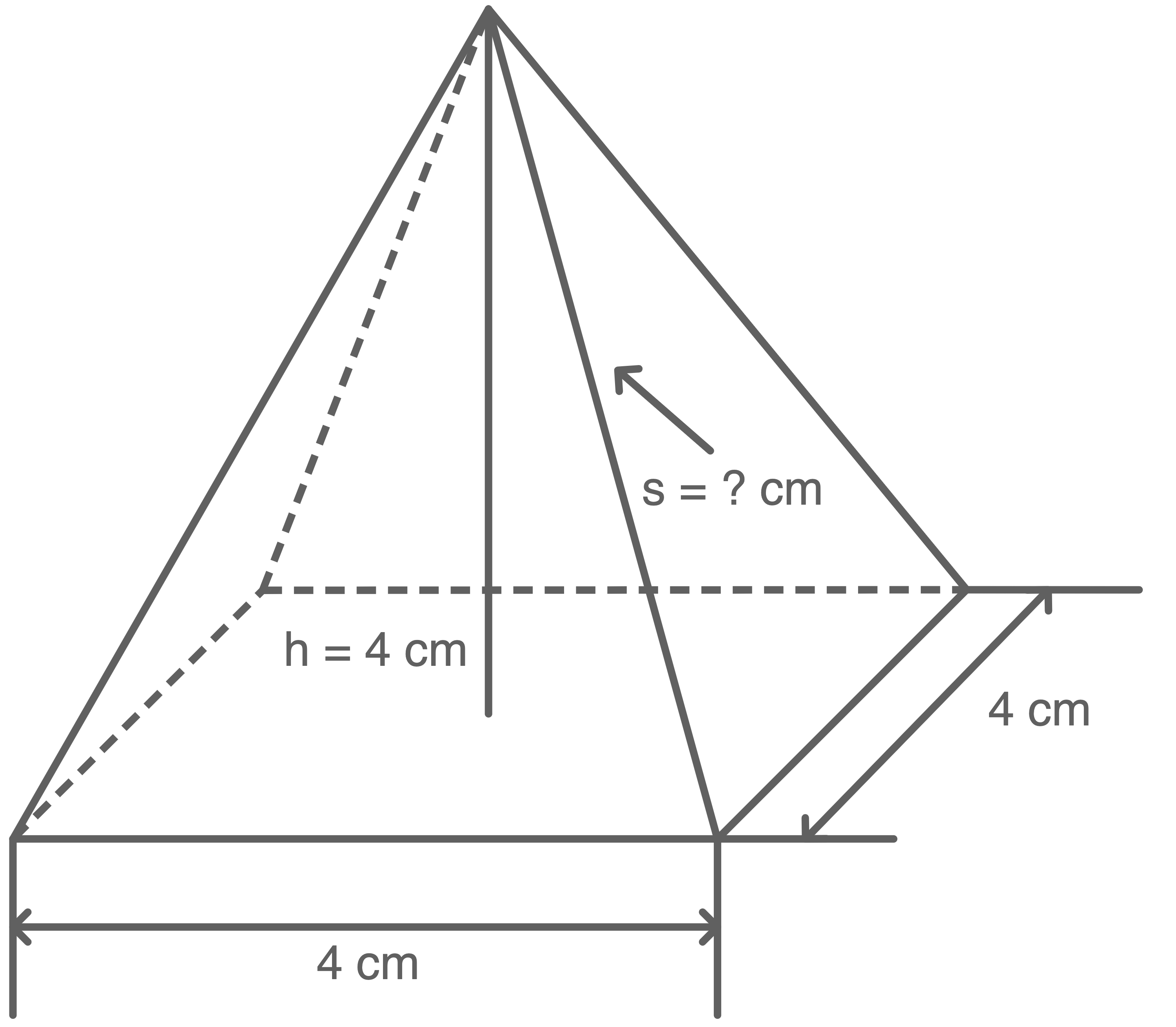
Zeichnung nicht maßstabsgetreu!
Skizze:
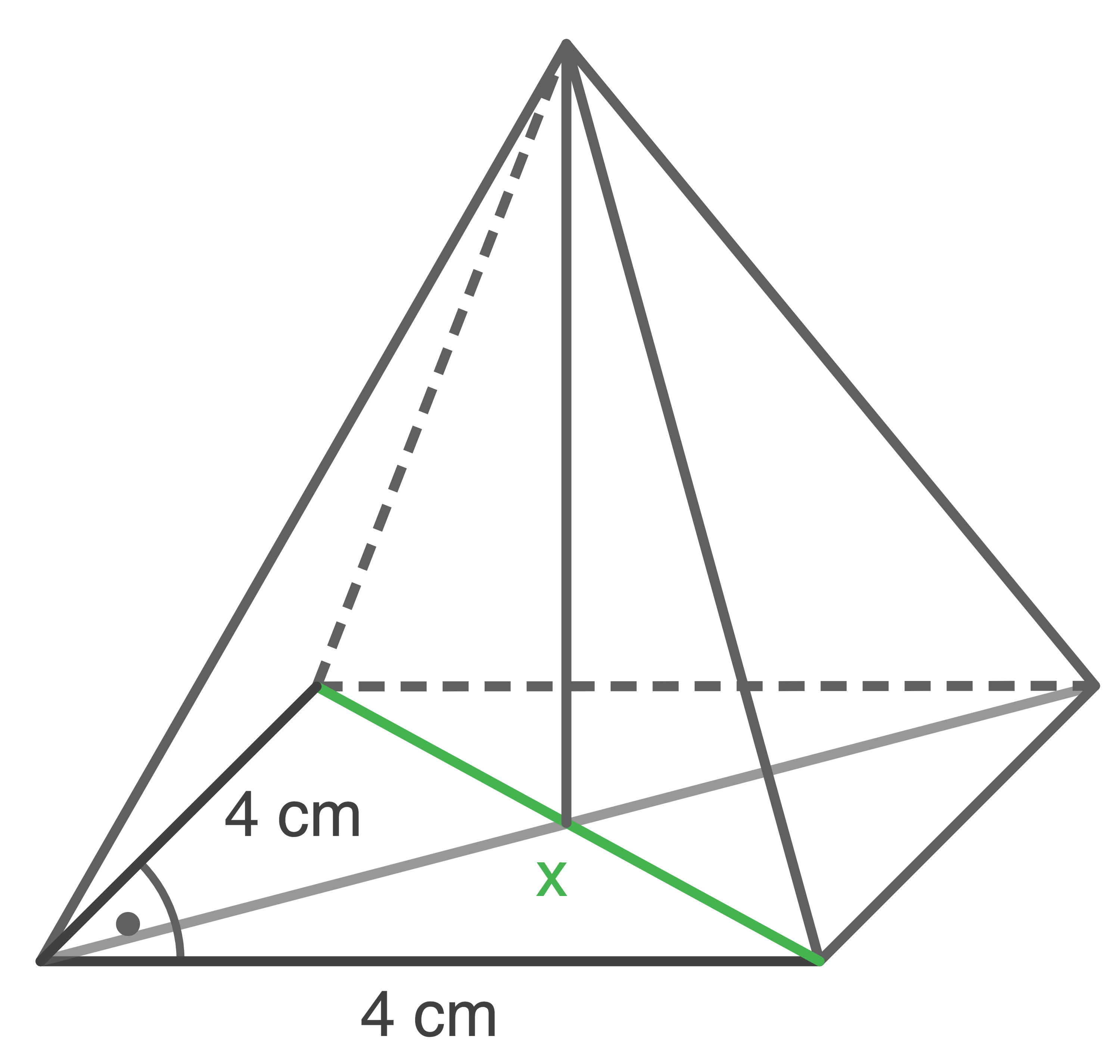
Skizze:
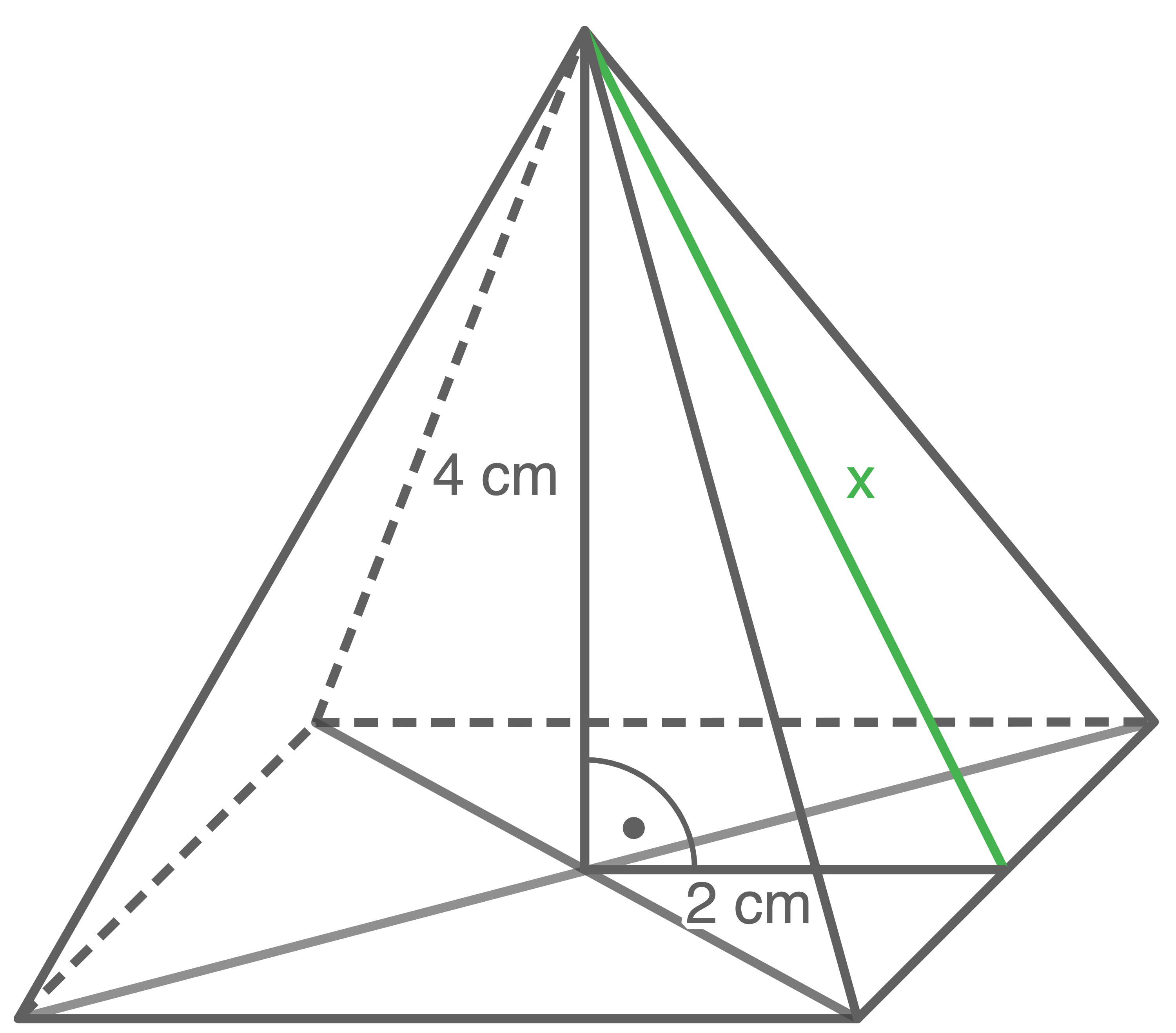
(3 Pkt.)
Aufgabe 2
a)
Claudia muss vier Ziffern eingeben, um eine Eingangstür zu öffnen.
Leider weiß sie nur noch, dass die erste Ziffer eine
ist.
Auch erinnert sie sich, dass die Ziffern
je einmal vorkommen.
Leider weiß sie nur noch, dass die erste Ziffer eine
Auch erinnert sie sich, dass die Ziffern
- Wie viele Kombinationsmöglichkeiten bleiben Claudia?
- Wie groß ist die Wahrscheinlichkeit, dass Claudia beim ersten Versuch die richtige Ziffernreihenfolge eingibt?
(2 Pkt.)
b)
Beim „Tag der offenen Tür“ führt die Klasse 9a einen Verkauf von Hotdogs durch.
Folgende Lebensmittel hat sie hierfür eingekauft.
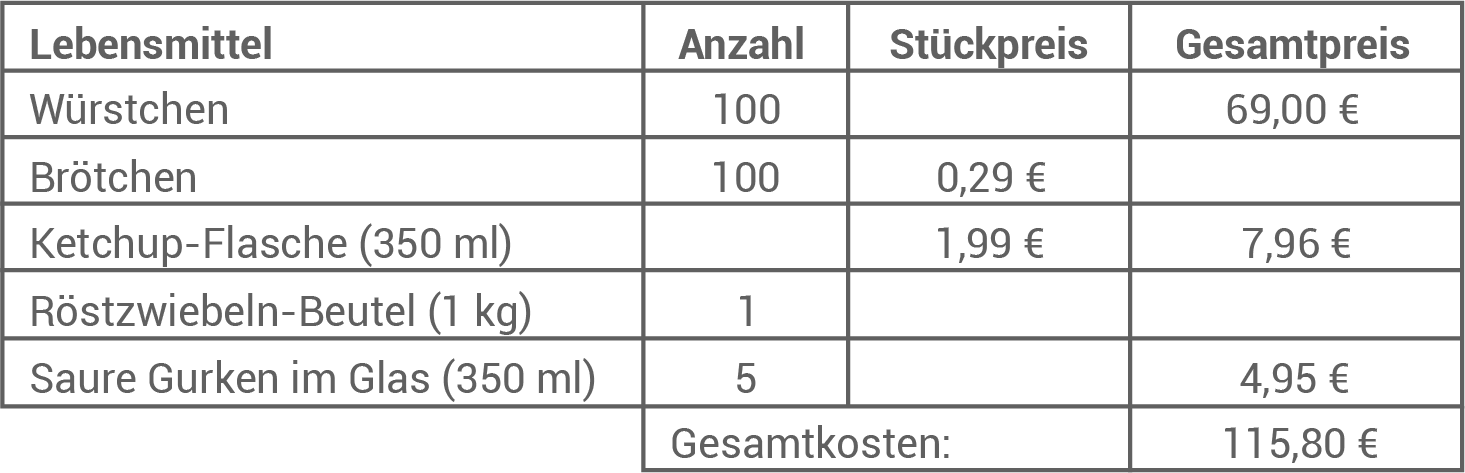
verkauft.
Die Klasse 9a möchte das Geld nach Abzug der Gesamtkosten an drei verschiedene Projekte spenden:
Schülerzeitung:
Brot für Kinder: 
Förderverein der Schule: 
Folgende Lebensmittel hat sie hierfür eingekauft.
- Ergänze die Tabelle.
Die Klasse 9a möchte das Geld nach Abzug der Gesamtkosten an drei verschiedene Projekte spenden:
Schülerzeitung:
- Berechne, wie viel
für jedes Projekt gespendet werden können.
(3 Pkt.)
Aufgabe 3
a)
Grundriss:
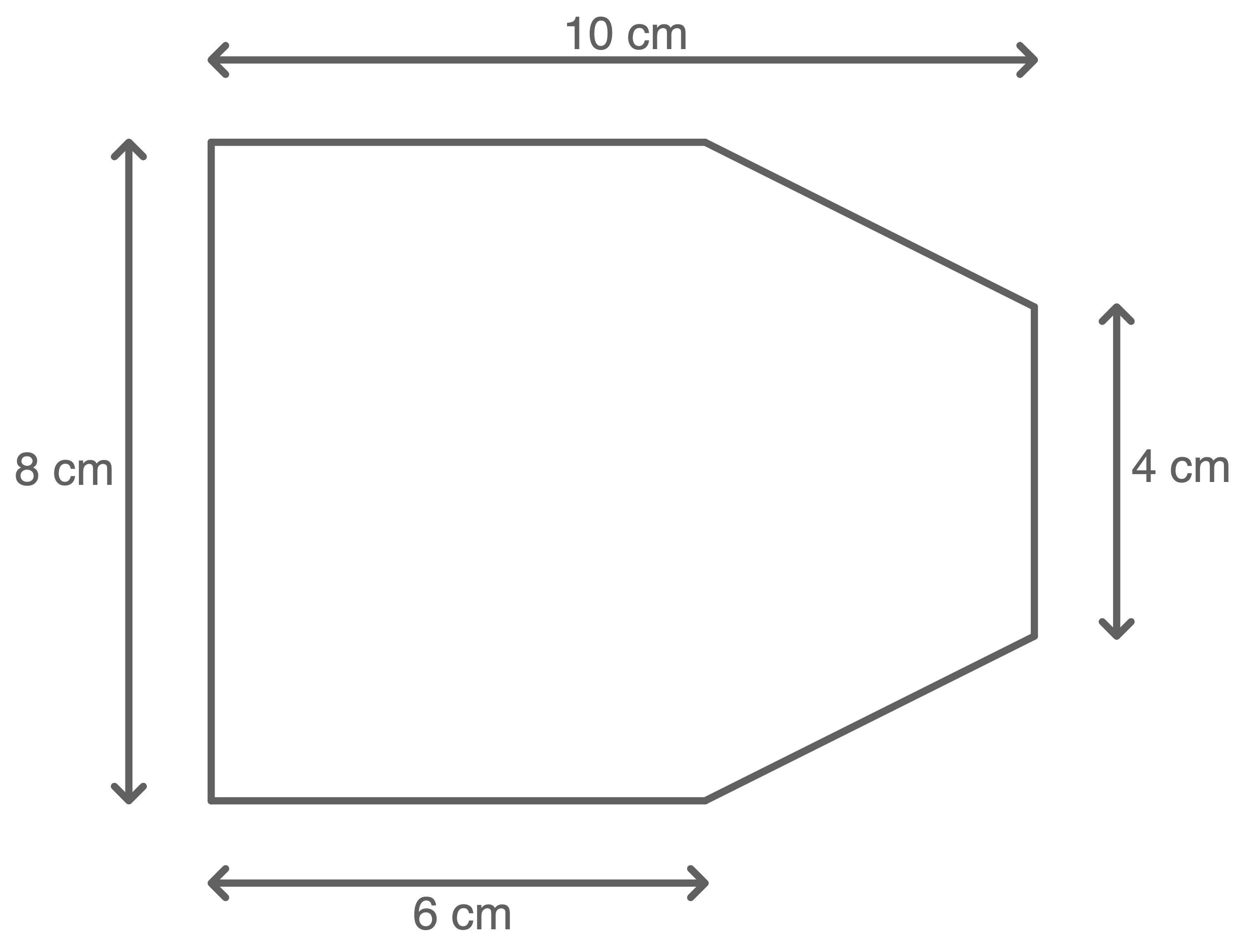
Schrägbild:
Mit welchen Formeln lässt sich das Volumen dieses Körpers bestimmen?
Zeichnung nicht maßstabsgetreu!
Kreuze für jede Formel „richtig“ oder „falsch“ an.
| Formel | richtig | falsch |
(2 Pkt.)
b)
Das Bild unten zeigt einen 
großen Mann mit einem Regenschirm.
Er steht neben einem Kunstwerk, das ebenfalls einen Regenschirm darstellt.
Stell dir vor, der Mann würde als Statue passend zum Kunstwerk gebaut werden. Wie groß müsste er sein?
Berechne. Entnimm nötige Maße der Zeichnung.
Er steht neben einem Kunstwerk, das ebenfalls einen Regenschirm darstellt.
Berechne. Entnimm nötige Maße der Zeichnung.
(3 Pkt.)
Aufgabe 4
a)
Das Schaubild zeigt den Tauchgang von Hendrik.
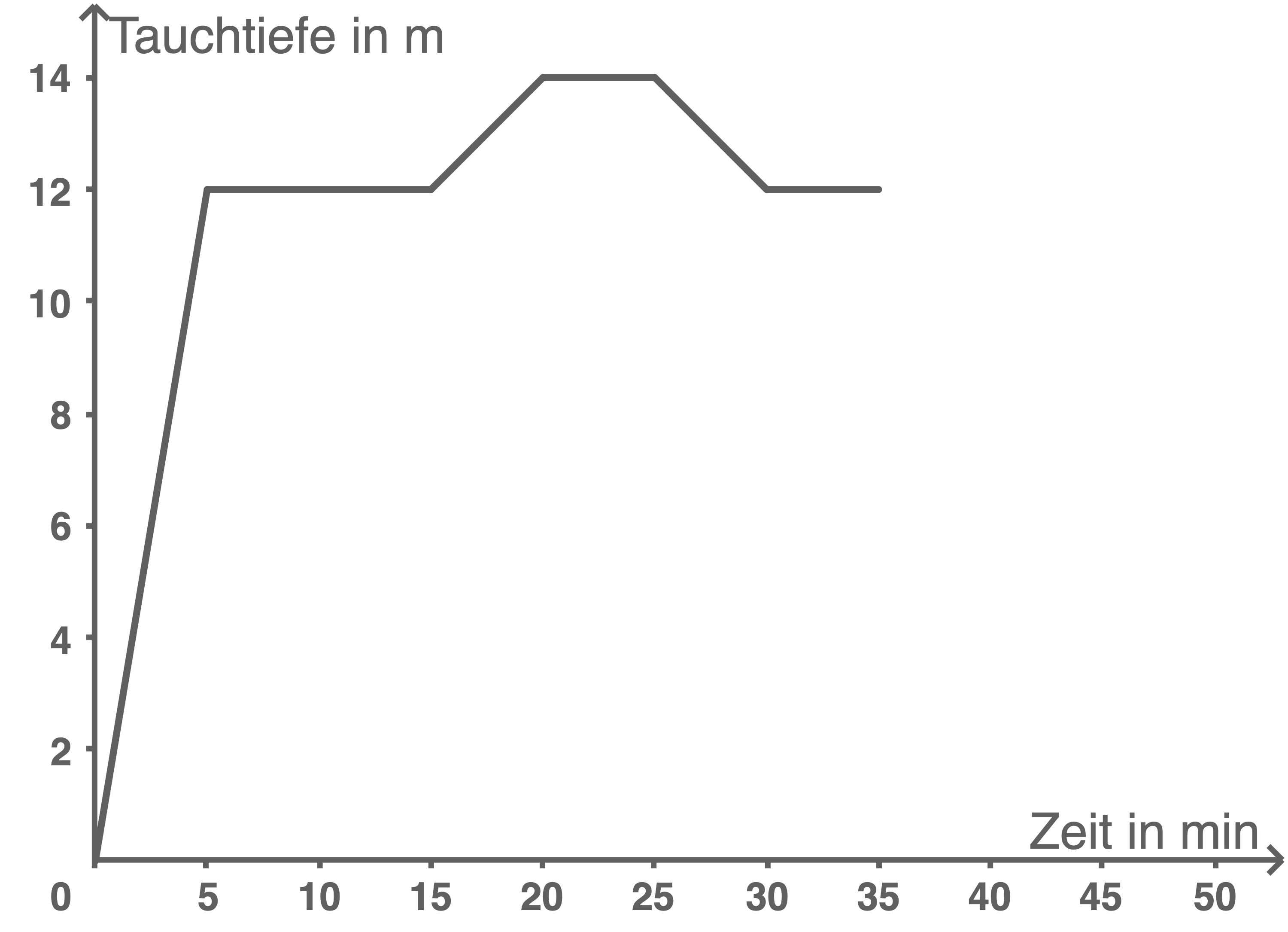
- Wie lange befindet er sich auf einer Tiefe von genau 12 Metern?
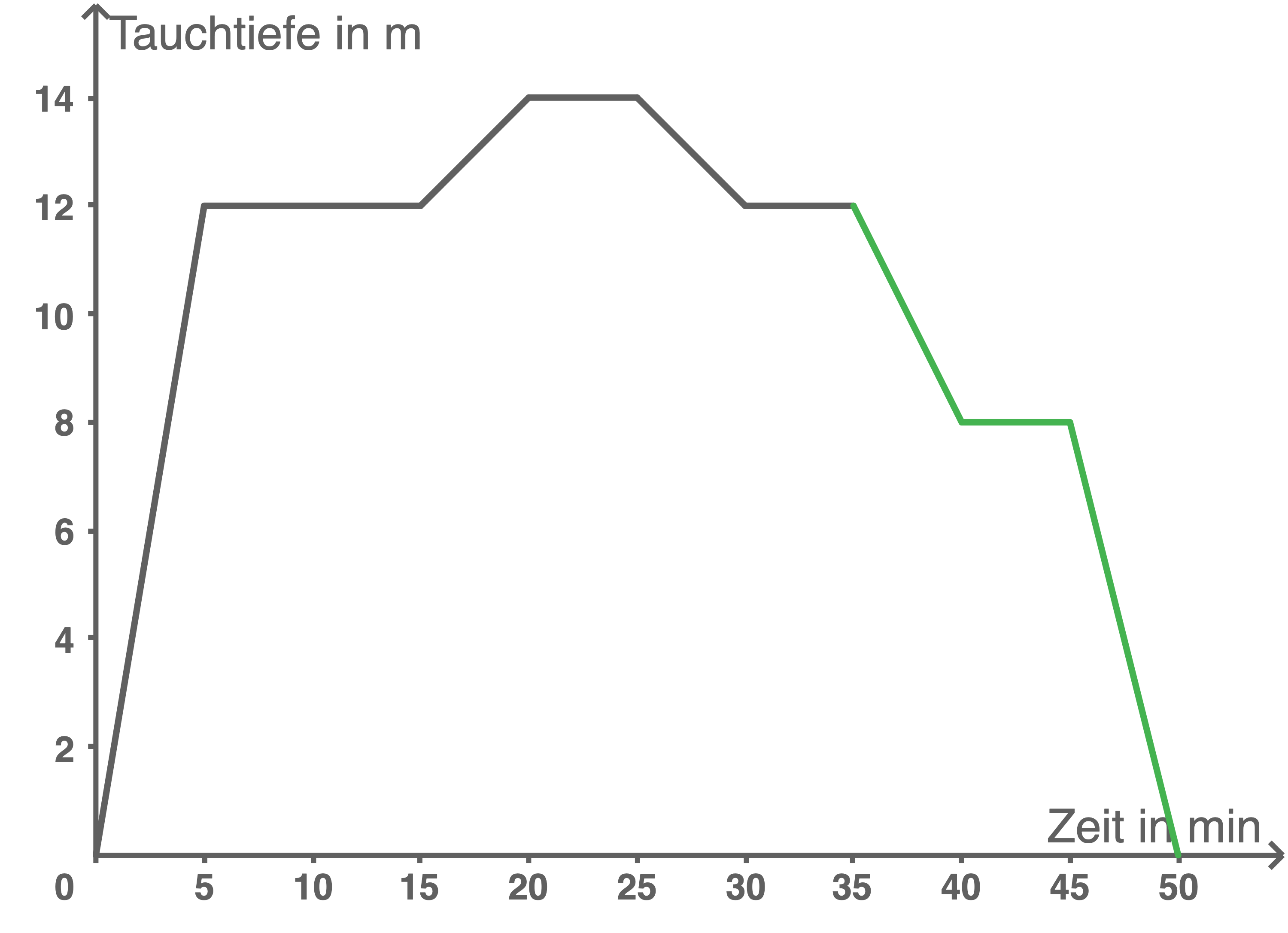
- Ergänze das Diagramm um folgende Sachverhalte:
NachMinuten steigt er gleichmäßig in
Minuten um
Meter auf.
In dieser Tiefe bleibt er
Nach weiteren
(2 Pkt.)
b)
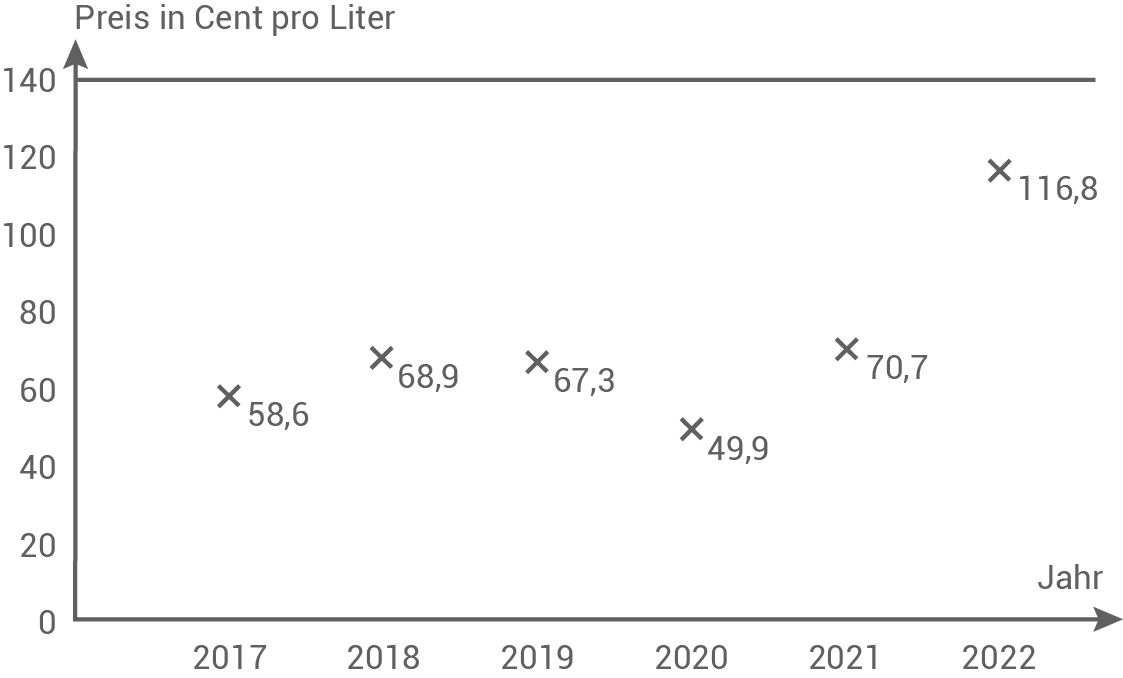
Durchschnittlicher Heizölpreis in Deutschland (in Cent pro Liter):
pro Liter.
Am Ende des Monats sinkt er wieder um.
- Berechne, um wie viel Prozent der Heizölpreis von 2020 bis 2022 angestiegen ist.
Am Ende des Monats sinkt er wieder um
- Wie ist der Heizölpreis im Vergleich zum Monatsanfang? Kreuze an und begründe deine Entscheidung.
billiger gleich teurer
(3 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Jahreszins für 2002 berechnen
Lösungsweg über den Dreisatz
![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 5\,000 \,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 50 \,€\\[5pt]
4\,\% & \mathrel{\widehat{=}}& 200 \,€
\end{array}\)](https://mathjax.schullv.de/fac3b390e00cc9aee01d3ce969ad02422b9d0cf1f83c92ac11580b699ea51b4c?color=5a5a5a)
Lösungsweg über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{5\,000 \,€\cdot 4}{100} \\[5pt]
P&=& 200 \,€
\end{array}\)](https://mathjax.schullv.de/b65fb7272f01c0a87e03fe1c0fd253b3a72d7c2177dcaa979f93110a6ea3fab3?color=5a5a5a)
Der Jahreszins beträgt 
Wie viel Geld hätte sie 2022 anlegen müssen, um den gleichen Jahreszins wie 2002 zu erhalten?
Lösungsweg über den Dreisatz
![\(\begin{array}{rcl}
0,6\,\% & \mathrel{\widehat{=}}& 200 \,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 333,33 \,€\\[5pt]
100\,\% & \mathrel{\widehat{=}}& 33\,333 \,€
\end{array}\)](https://mathjax.schullv.de/f55bf9a8fb7e1994de4f4a13fabb300c323523fbc362ba3d0755ed6e23e4a6a3?color=5a5a5a)
Lösungsweg über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100}&\quad \scriptsize \mid\;\cdot 100 \\[5pt]
P\cdot 100&=& G\cdot p&\quad \scriptsize \mid\;:p \\[5pt]
\dfrac{P\cdot 100}{p}&=& G \\[5pt]
G&=&\dfrac{P\cdot 100}{p} \\[5pt]
G&=&\dfrac{200 \,€\cdot 100}{0,6} \\[5pt]
G&\approx& 33\,333\,€
\end{array}\)](https://mathjax.schullv.de/a2a92d981bc0fb6709424ba3265d5ff917de7d746298cfb19076da30ba815631?color=5a5a5a)
Sie hätte etwa 
anlegen müssen.
b)
Lösungsweg 1 fortsetzen
Skizze:
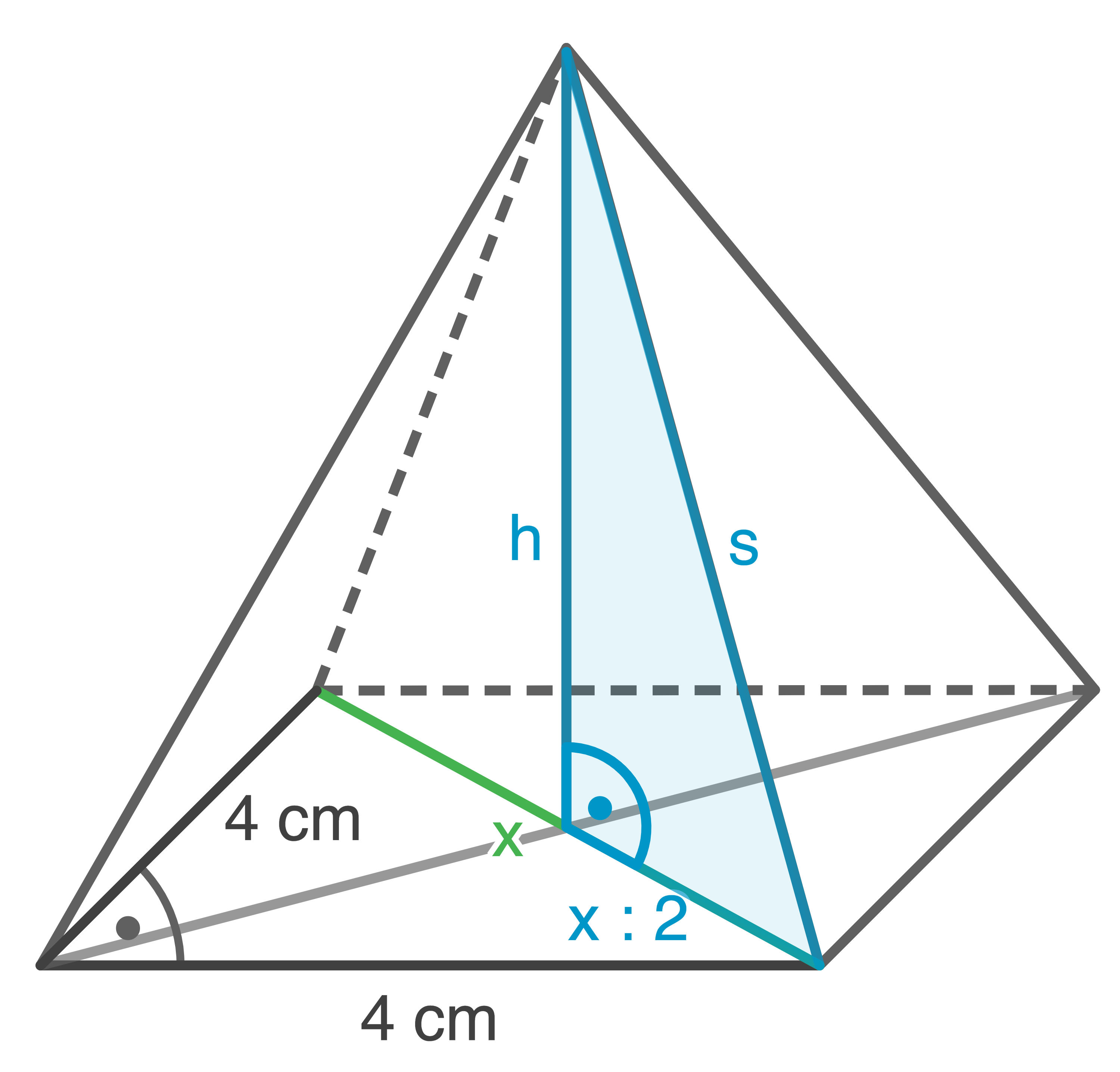
![\(\begin{array}[t]{rll}
x^2&=& (4\,\text{cm})^2 +(4\,\text{cm})^2 & \\[5pt]
x^2&=& 16\,\text{cm}^2 +16\,\text{cm}^2 \\[5pt]
x^2&=& 32\,\text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,\,\,}\\[5pt]
x&=&\underline{ 5,7\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/8c646b9bdd65ae12ed3b0ee945b6e85d178d701808dadb7147dc266724d0a808?color=5a5a5a)
Länge der Seite 
berechnen:
![\(\begin{array}[t]{rll}
s^2&=&h^2+(x:2)^2 \\[5pt]
s^2&=&(4\,\text{cm})^2+(5,7\,\text{cm}:2)^2 \\[5pt]
s^2&=&(4\,\text{cm})^2+(2,85\,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\,\,\,}\\[5pt]
s&=&\sqrt{(4\,\text{cm})^2+(2,85\,\text{cm})^2} \\[5pt]
s&=&\sqrt{24,1225\,\text{cm}^2} \\[5pt]
s&\approx&4,9\,\text{cm} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0c9f94debabdb290ffcaf9e1d2896f28730e472c20c8d16572dc626a60ce19d8?color=5a5a5a)
Lösungsweg 2 fortsetzen
Skizze:
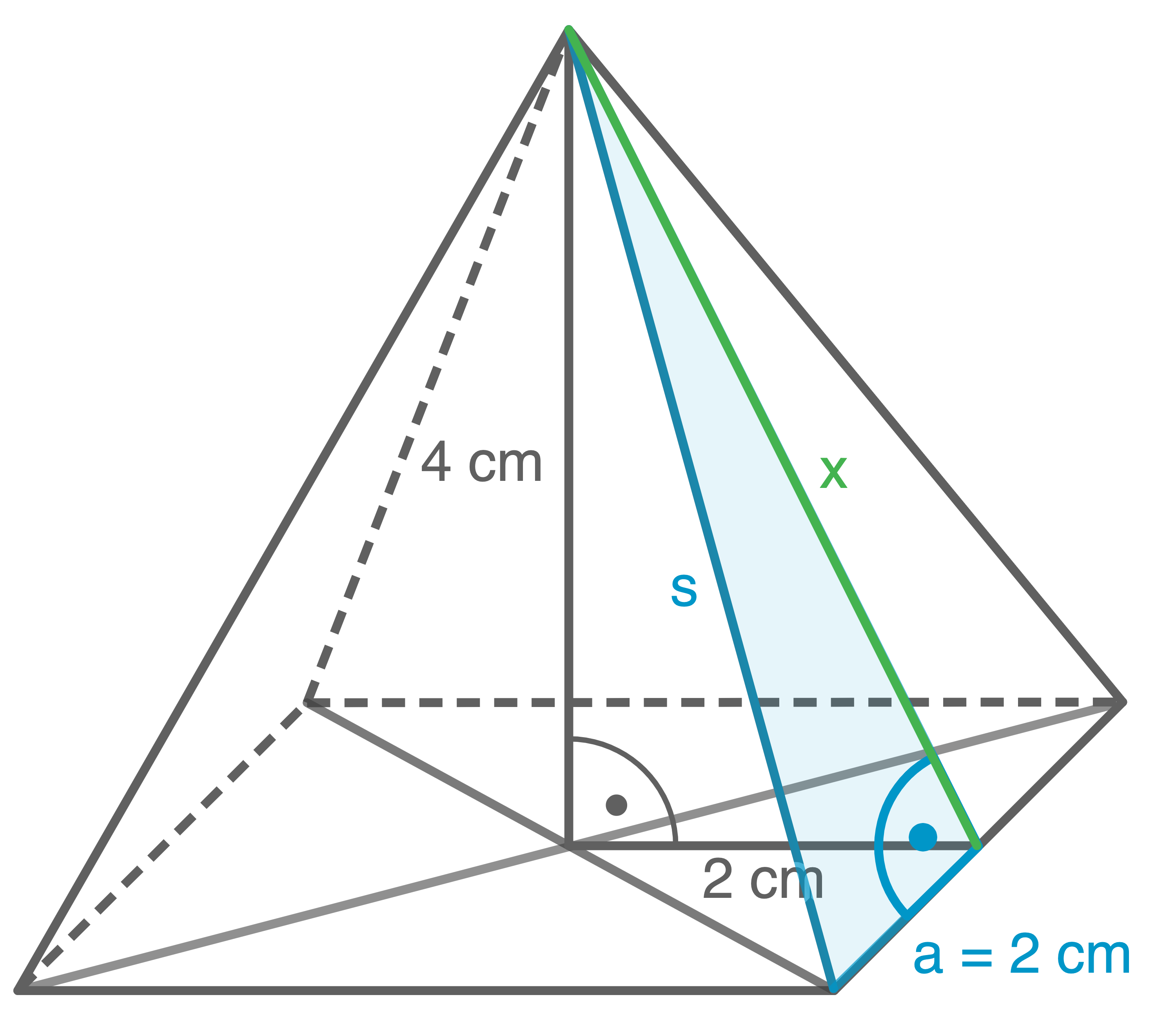
![\(\begin{array}[t]{rll}
x^2&=&(4\,\text{cm})^2 +(2\,\text{cm})^2 & \\[5pt]
x^2&=& 16\,\text{cm}^2 +4\,\text{cm}^2 \\[5pt]
x^2&=& 20 \,\text{cm}^2 \quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
x&=& \underline{ 4,5\,\text{cm} }
\end{array}\)](https://mathjax.schullv.de/801a631d5e092575c921f879431daea9805f63bf2a2f405b48da117b62f81836?color=5a5a5a)
Länge der Seite berechnen:
![\(\begin{array}[t]{rll}
s^2&=&x^2+a^2 \\[5pt]
s^2&=&(4,5\,\text{cm})^2+(2\,\text{cm})^2 &\quad \scriptsize \mid\;\sqrt{\,\,\,} \\[5pt]
s&=&\sqrt{(4,5\,\text{cm})^2+(2\,\text{cm})^2} \\[5pt]
s&=&\sqrt{24,25\,\text{cm}^2} \\[5pt]
s&\approx& 4,9\,\text{cm} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/aa86d91e7f18ab5bef8d78c5a0773d3c7e71830b0a70bda15ce8bc4a1e35acfb?color=5a5a5a)
Lösung 2
a)
Wie viele Kombinationsmöglichkeiten bleiben Claudia?
Claudia bleiben 6 Kombinationsmöglichkeiten:
bzw. 
bzw. 
- Möglichkeit:
- Möglichkeit:
- Möglichkeit:
- Möglichkeit:
- Möglichkeit:
- Möglichkeit:
b)
Tabelle ergänzen
1. Rechnung: Stückpreis der Würstchen berechnen
2. Rechnung: Gesamtpreis der Brötchen berechnen
3. Rechnung: Anzahl der Ketchup-Flaschen berechnen
4. Rechnung: Stückpreis der Gläser mit sauren Gurken berechnen
5. Rechnung: Gesamtpreis der Röstzwiebel-Beutel berechnen
6. Rechnung: Stückpreis der Röstzwiebel-Beutel berechnen
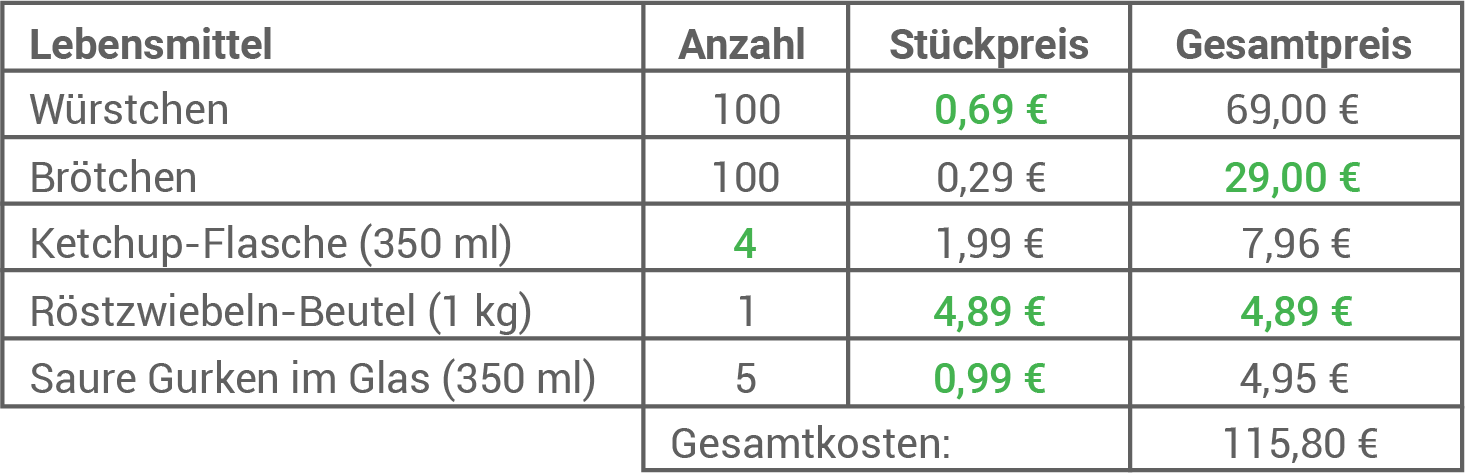Berechnen, wie viel für jedes Projekt gespendet werden können
Die Klasse hat 100 Würstchen gekauft. Somit konnte die Klasse 100 Hotdogs verkaufen.
Spende an Brot für Kinder
Spende an den Förderverein der Schule
- Einnahmen: :
- Einnahmen nach Abzug der Gesamtkosen:
Lösung 3
a)
| Formel | richtig | falsch |
b)
Der echte Regenschirm hat abgemessen eine Größe von 
Das Kunstwerk hat abgemessen eine Größe von 
Hinweis: Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch gleich.
Bei dem echten Regenschirm ist das Verhältnis zwischen Regenschirm und Mann bekannt: 
zu 
Mit diesem Verhältnis lässt sich die Größe des Mannes als Statue berechnen:
![\(\begin{array}{rcl}
2\,\text{cm} & \mathrel{\widehat{=}}& 1,80 \,\text{m}\\[5pt]
1\,\text{cm} & \mathrel{\widehat{=}}& 0,9 \,\text{m}\\[5pt]
10\,\text{cm} & \mathrel{\widehat{=}}& 9 \,\text{m}
\end{array}\)](https://mathjax.schullv.de/68182768315a93778870cd649749a1d1f138762a82e62e11b9ab34aac57abad2?color=5a5a5a)
Der Mann als Statue müsste 
groß sein.
Mit diesem Verhältnis lässt sich die Größe des Mannes als Statue berechnen:
Lösung 4
a)
Wie lange befindet er sich auf einer Tiefe von genau 12 Metern?
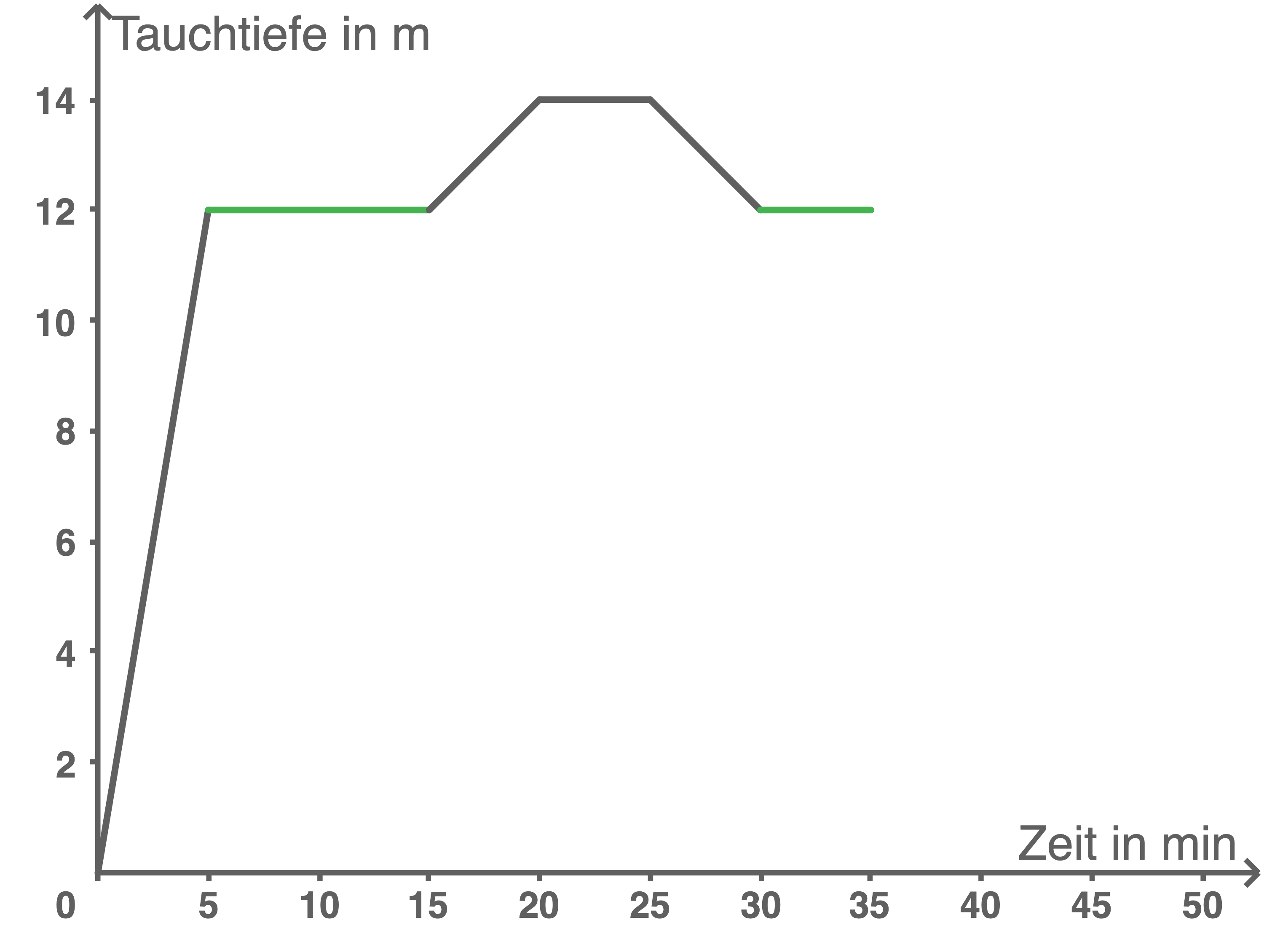Hendrik befindet sich 15 min auf einer Tiefe von genau 12 Metern.
Das Diagramm ergänzen
b)
Berechnen, um wie viel Prozent der Heizölpreis von 2020 bis 2022 angestiegen ist
Lösungsweg über den Dreisatz
![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 49,9 \,\text{ct}\\[5pt]
2\,\% & \mathrel{\widehat{=}}& 1 \,\text{ct}\\[5pt]
234\,\% & \mathrel{\widehat{=}}& 116,8 \,\text{ct}
\end{array}\)](https://mathjax.schullv.de/03477b8075605396d7a2806aba060cb9bea0d1fb4e0233d8633350d539065bf1?color=5a5a5a)
Lösungsweg über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} &\quad \scriptsize \mid\;\cdot 100 \\[5pt]
P\cdot 100&=&G\cdot p &\quad \scriptsize \mid\;:G \\[5pt]
\dfrac{P\cdot 100}{G}&=&p &\quad \scriptsize \mid\;:G \\[5pt]
p&=&\dfrac{P\cdot 100}{G} &\quad \scriptsize \mid\;:G \\[5pt]
p&=&\dfrac{116,8 \,\text{ct}\cdot 100}{49,9 \,\text{ct}} \\[5pt]
p&\approx&234
\end{array}\)](https://mathjax.schullv.de/f83a79b6220f55008ff0ad059bcaebc857649ab4c66b4ca67137343426e3ea3e?color=5a5a5a)
Von 2020 bis 2022 ist der Heizölpreis um 
gestiegen.
Wie ist der Heizölpreis im Vergleich zum Monatsanfang?
Rechnerische Begründung Angenommen der Preis liegt Anfang des Monats bei
pro Liter.
Ende des Monats abgezogen werden, höher ist. Dadurch entsprechen Ende des Monats einem höheren Wert als noch Anfang des Monats.
| billiger | |
| gleich | |
| teurer |
Rechnerische Begründung Angenommen der Preis liegt Anfang des Monats bei
- Preiserhöhung um
- Preissenkung um