Ereignisse verknüpfen

Es ist möglich Ereignisse zu verknüpfen, um neue Ereignisse zu erhalten. Dafür gibt es, bei gegebenen Ereignissen $A$ und $B,$ mehrere Möglichkeiten:

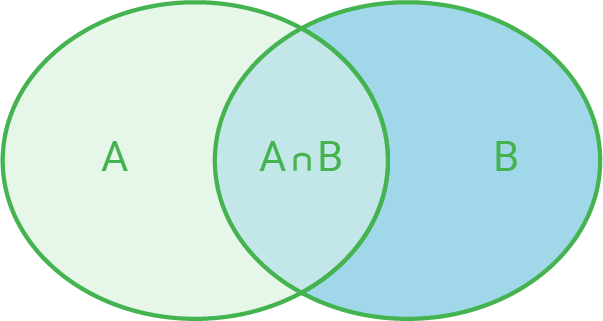
Die Vereinigungsmenge $A\cup B$ gibt das Ereignis „ $A$ oder $B$ “ an
Die Schnittmenge $A\cap B$ gibt das Ereignis „ $A$ und $B$ “ an
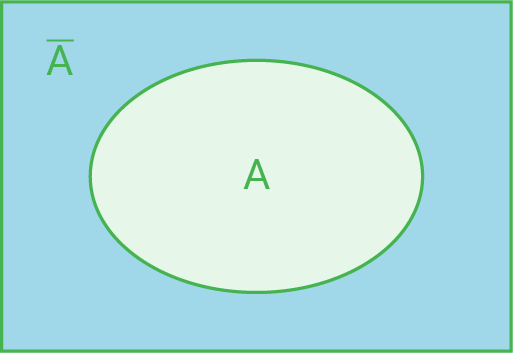
Die Komplementmenge $\overline{A}$ gibt das Gegenereignis an, also „Nicht $A$ “

Venn-Diagramm mit den Mengen A, B und der Schnittmenge AnB.

Diagramm mit einer ovalen Fläche, die das Element A darstellt, umgeben von einer blauen Fläche und einer anderen Beschriftung.

Rechenregeln

Für die Wahrscheinlichkeit des Gegenereignisses gilt $P\left(\overline{A}\right)=1-P(A).$

Der Additionssatz ist definiert durch $P(A\cup B)=P(A)+P(B)-P(A\cap B).$

Gegenereignis angeben

$\overline{A}:$

„Es werden nur gerade Zahlen gewürfelt.“

Wahrscheinlichkeit berechnen

Das viermalige Werfen eines Würfels ist ein Laplace-Experiment. Da ein Würfel sechs Seiten hat, gibt es somit insgesamt $6\cdot6\cdot6\cdot6=1296$ mögliche Ergebnisse.
Drei der Zahlen von $1$ bis $6$ sind gerade. Somit gibt es genau $3\cdot3\cdot3\cdot3=648$ Ergebnisse, die zu $\overline{A}$ gehören. Da $A$ andersherum auch das Gegenereignis von $\overline{A}$ ist, lassen sich die beiden Ausdrücke in der Formel für die Wahrscheinlichkeit des Gegenereignisses tauschen und es ergibt sich für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rlll} P(A)&=&1-P\left(\overline{A}\right) \\[5pt] &=&1-\dfrac{81}{1296} \\[5pt] &=&\dfrac{1215}{1296} \\[5pt] &=&\dfrac{15}{16} \end{array}$

Gegenereignis angeben

$\overline{B}:$

„Alle gewürfelten Zahlen sind gleich.“

Wahrscheinlichkeit berechnen

Der Würfel hat sechs verschiedene Zahlen, somit gibt es genau $6$ Möglichkeiten, dass bei vier Würfen alle gewürfelten Zahlen untereinander übereinstimmen.
Für die Wahrscheinlichkeit des Ereignisses $B$ folgt somit:

$\begin{array}[t]{rlll} P(B)&=&1-P\left(\overline{B}\right) \\[5pt] &=&1-\dfrac{6}{1296} \\[5pt] &=&\dfrac{1290}{1296} \\[5pt] &=&\dfrac{215}{216} \end{array}$

Gegenereignis angeben

$\overline{C}:$

„Die Summe der gewürfelten Zahlen betragt höchstens $6.$ “

Wahrscheinlichkeit berechnen

Um in vier Würfen eine Summe von maximal $6$ zu erzielen, existieren wenige Möglichkeiten. Ein Mal die $3$ und drei Mal die $1$ ergeben z.B. genau $6.$ Die weiteren Möglichkeiten sind zwei Mal die $2$ und zwei Mal die $1,$ ein Mal die $2$ und dreimal die $1,$ sowie ausschließlich Einser.
Da die $3$ in jedem der vier Würfe auftreten kann, gibt es für die erste Möglichkeit genau vier Ergebnisse. Mit der selben Argumentation gehören auch zu der dritten Möglichkeit $4$ Ergebnisse. Für die zweite Möglichkeiten ergeben sich die folgenden Zahlenkombinationen:

$\{(1,1,2,2);(1,2,1,2);(1,2,2,1);$ $(2,2,1,1);(2,1,2,1);(2,1,1,2)\}$

Somit ergeben sich insgesamt $4+4+6+1=15$ Ergebnisse, die zum Gegenereignis $\overline{C}$ gehören. Damit folgt:

$\begin{array}[t]{rlll} P(C)&=&1-P\left(\overline{C}\right) \\[5pt] &=&1-\dfrac{15}{1296} \\[5pt] &=&\dfrac{1281}{1296} \\[5pt] &=&\dfrac{427}{432} \end{array}$

Gegenereignis angeben

$\overline{D}:$

„Alle gewürfelten Zahlen sind unterschiedlich“

Wahrscheinlichkeit berechnen

Im ersten Wurf ist es egal welche der sechs Zahlen geworfen wird, damit am Ende alle vier Würfe unterschiedliche Zahlen zeigen. Für den zweiten Wurf kommen dann nur noch fünf der sechs Zahlen infrage. Das setzt sich weiter fort, sodass im dritten Wurf noch vier Zahlen bzw. im vierten noch drei Zahlen offen sind. Insgesamt gibt es also $6\cdot5\cdot4\cdot3=360$ verschiedene Ergebnisse für das Gegenereignis.
Die Wahrscheinlichkeit von $D$ lässt sich somit wie folgt berechnen:

$\begin{array}[t]{rlll} P(D)&=&1-P\left(\overline{D}\right) \\[5pt] &=&1-\dfrac{360}{1296} \\[5pt] &=&\dfrac{936}{1296} \\[5pt] &=&\dfrac{13}{18} \end{array}$

$A:$

„Die Person ist mit dem Auto angereist.“

$H:$

„Die Person ist Heimfan.“

Aus der Aufgabenstellung ergibt sich $P(A)=0,15$ und $P(H)=0,8.$ Von den $80\,\%$ der Fans, die die Heimmannschaft unterstützen, sind $20\,\%$ mit dem Auto gekommen. Diese Personengruppe macht somit $0,8\cdot0,2=0,16=16\,\%$ aller Fans aus, das heißt es gilt $P(A\cap H)=0,16.$ Mit dem Additionssatz folgt somit:

$\begin{array}[t]{rlll} P(A\cup H)&=&P(A)+P(H)-P(A\cap B) \\[5pt] &=&0,15+0,8-0,16 \\[5pt] &=&0,79 \\[5pt] &=&79\,\% \end{array}$

Es fallen somit insgesamt $78000\cdot0,78=60840$ Fans in diese Kategorie.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?