Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
a)
Ordne den Gleichungen die passende Lösungsmenge zu.




| Gleichung | Lösungsmenge |
|---|---|
(3 BE)
b)
Berechne.

(2 BE)
2.
a)
Gegeben sind die Funktionen  und
und  durch
durch  und
und  mit
mit 
Ermittle zeichnerisch den Schnittpunkt der Graphen von und
und  .
.
Ermittle zeichnerisch den Schnittpunkt der Graphen von

(3 BE)
b)
Gib eine Gleichung einer Sinusfunktion mit folgenden beiden Eigenschaften an:
- Die kleinste Periode ist
.
- Der Wertebereich ist
.
(2 BE)
3.
Gegeben ist ein gleichschenkliges Dreieck  Die Basis hat eine Länge von
Die Basis hat eine Länge von  und die Höhe auf der Basis hat eine Länge von
und die Höhe auf der Basis hat eine Länge von 
a)
Zeichne das Dreieck  und berechne die Länge der Schenkel dieses Dreiecks.
und berechne die Länge der Schenkel dieses Dreiecks.
(3 BE)
b)
Vervollständige die Gleichungen für dieses Dreieck 


(2 BE)
4.
a)
Ein idealer Würfel mit den Augenzahlen  wird zweimal geworfen.
Bestimme die Wahrscheinlichkeiten folgender Ereignisse.
wird zweimal geworfen.
Bestimme die Wahrscheinlichkeiten folgender Ereignisse.
 „Die Summe der Augenzahlen beträgt
„Die Summe der Augenzahlen beträgt  “
“
 „Die Summe der Augenzahlen ist größer als
„Die Summe der Augenzahlen ist größer als  “
“
(3 BE)
b)
Das Glücksrad soll so vervollständigt werden, dass die Wahrscheinlichkeit dafür, dass der Pfeil auf einen schwarzen Sektor zeigt,  beträgt.
beträgt.
Erläutere ein mögliches Vorgehen.

Erläutere ein mögliches Vorgehen.

(2 BE)
1.
a)
| Gleichung | Lösungsmenge |
|---|---|
b)
2.
a)
Die Graphen von  und
und  schneiden sich im Punkt
schneiden sich im Punkt 
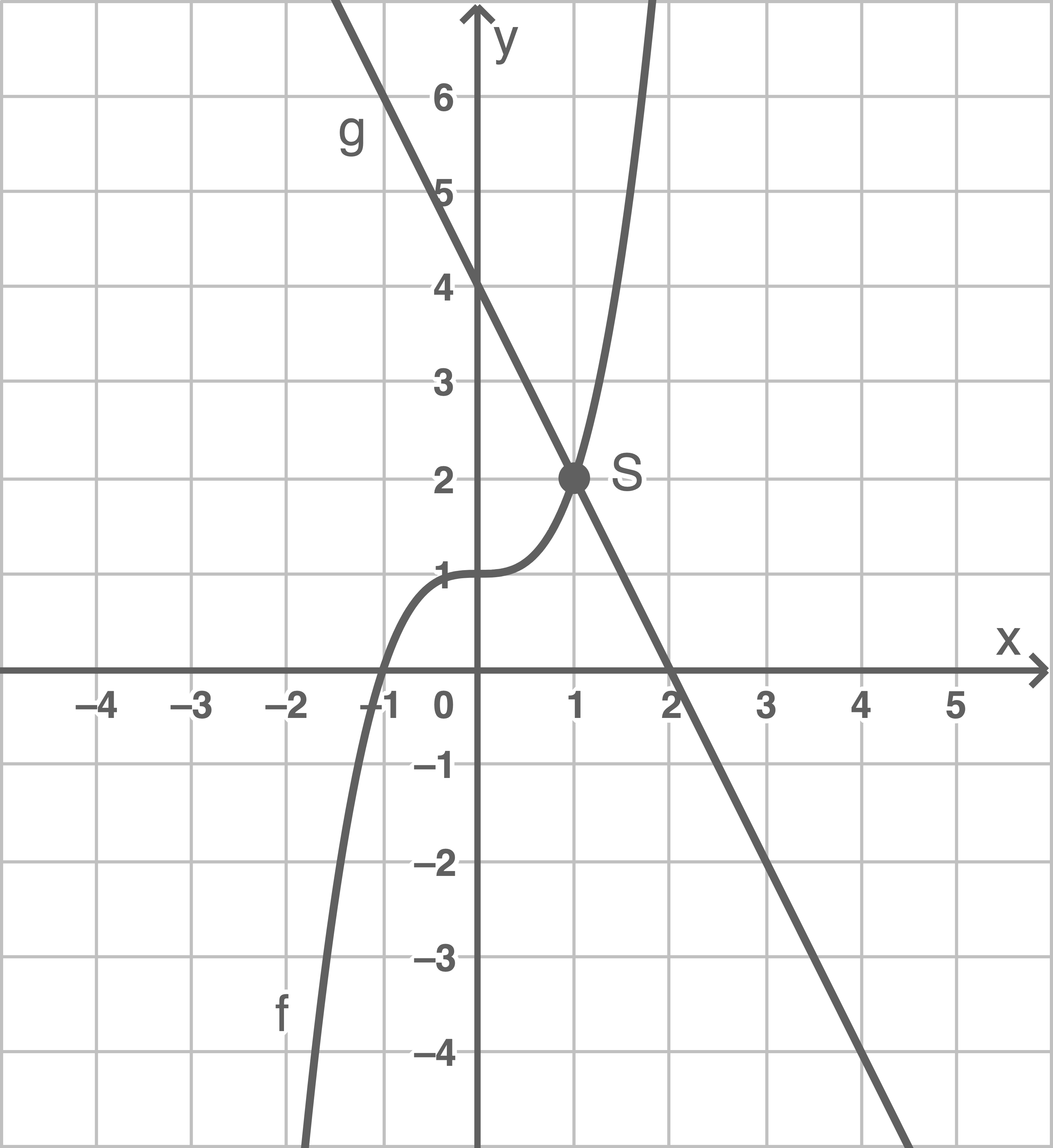

b)
Die Parameter der Funktion  sollen so gewählt werden, dass die Funktion die gegebenen Eigenschaften erfüllt.
Der Wertebereich
sollen so gewählt werden, dass die Funktion die gegebenen Eigenschaften erfüllt.
Der Wertebereich  kann durch den Faktor
kann durch den Faktor  erreicht werden.
Für die kleiste Periode soll
erreicht werden.
Für die kleiste Periode soll  gelten. Daraus folgt
gelten. Daraus folgt  Eine mögliche Funktion mit den gewünschten Eigenschaften ist also gegeben durch
Eine mögliche Funktion mit den gewünschten Eigenschaften ist also gegeben durch 
3.
a)
Dreieck zeichnen
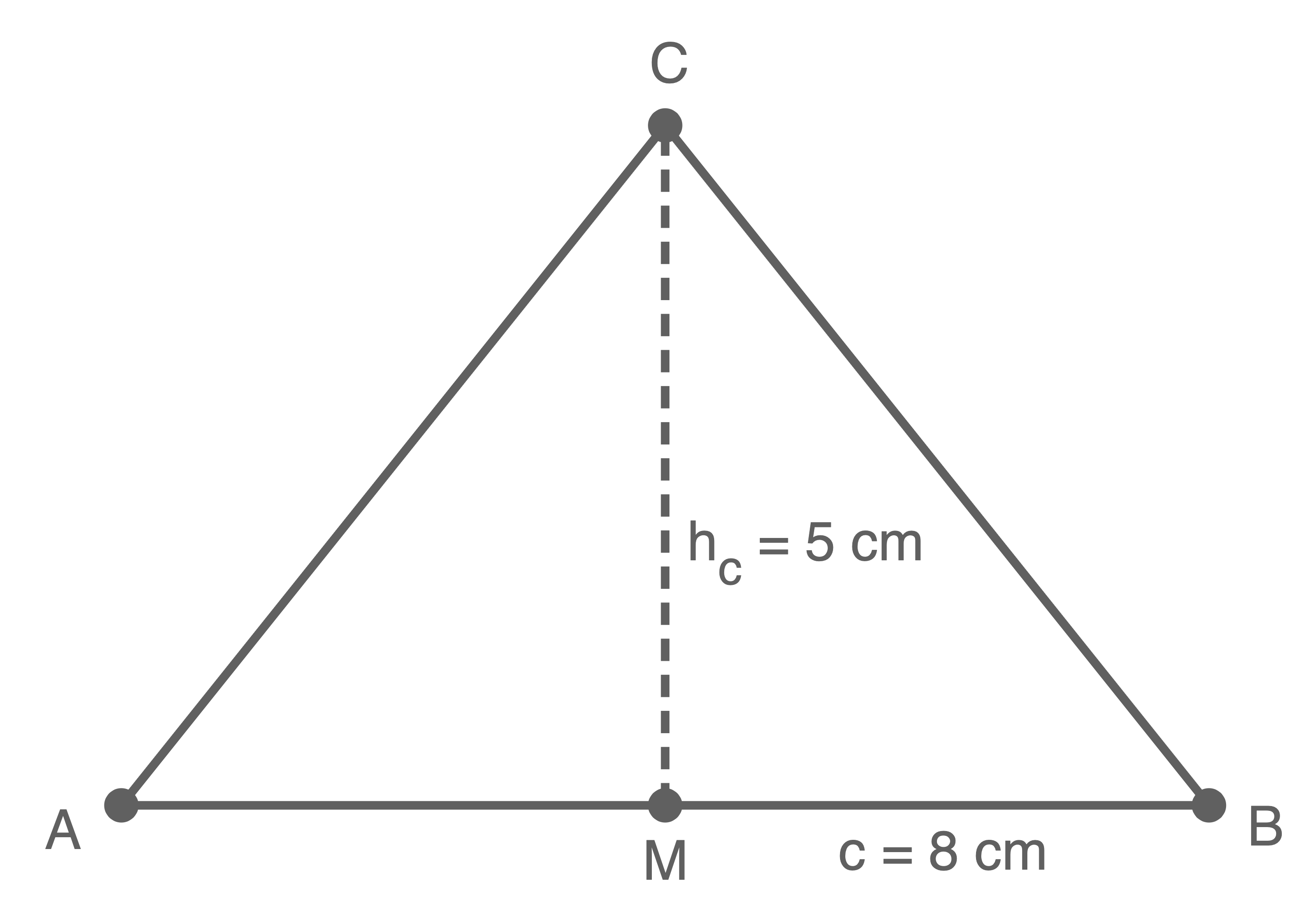 Länge der Schenkel berechnen
Die Länge der Schenkel kann mit dem Satz des Pythagoras berechnet werden:
Länge der Schenkel berechnen
Die Länge der Schenkel kann mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
s^2&=& \left(\dfrac{1}{2}c\right)^2+(h_c)^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
s &=& \sqrt{\left(\dfrac{1}{2}c\right)^2+(h_c)^2}\\[5pt]
s &=& \sqrt{\left(\dfrac{1}{2}\cdot 8\,\text{cm}\right)^2+(5\,\text{cm})^2}\\[5pt]
s &=& \sqrt{41}\,\text{cm} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2c07b92373ab0cca5799e50f606a27dba8af36b64cc17739aa44e8f66bf797da?color=5a5a5a) Die Schenkel des Dreiecks sind
Die Schenkel des Dreiecks sind  lang.
lang.

b)
4.
a)
Die höchste Summe, die erreicht werden kann, ist  Daher kann das Ereignis
Daher kann das Ereignis  nicht eintreten.
nicht eintreten.
 Eine Augensumme höher als 16 kann durch die Ereignisse
Eine Augensumme höher als 16 kann durch die Ereignisse 
 und
und  erreicht werden.
erreicht werden.

b)
Das Glücksrad könnte in 12 gleich große Sektoren eingeteilt werden, von denen 5 schwarz eingefärbt werden. Ein Sektor hätte dann einen Zentriwinkel von 