A10 – Exponentialfunktion
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
In der Abbildung ist der Graph der Funktion 
dargestellt.
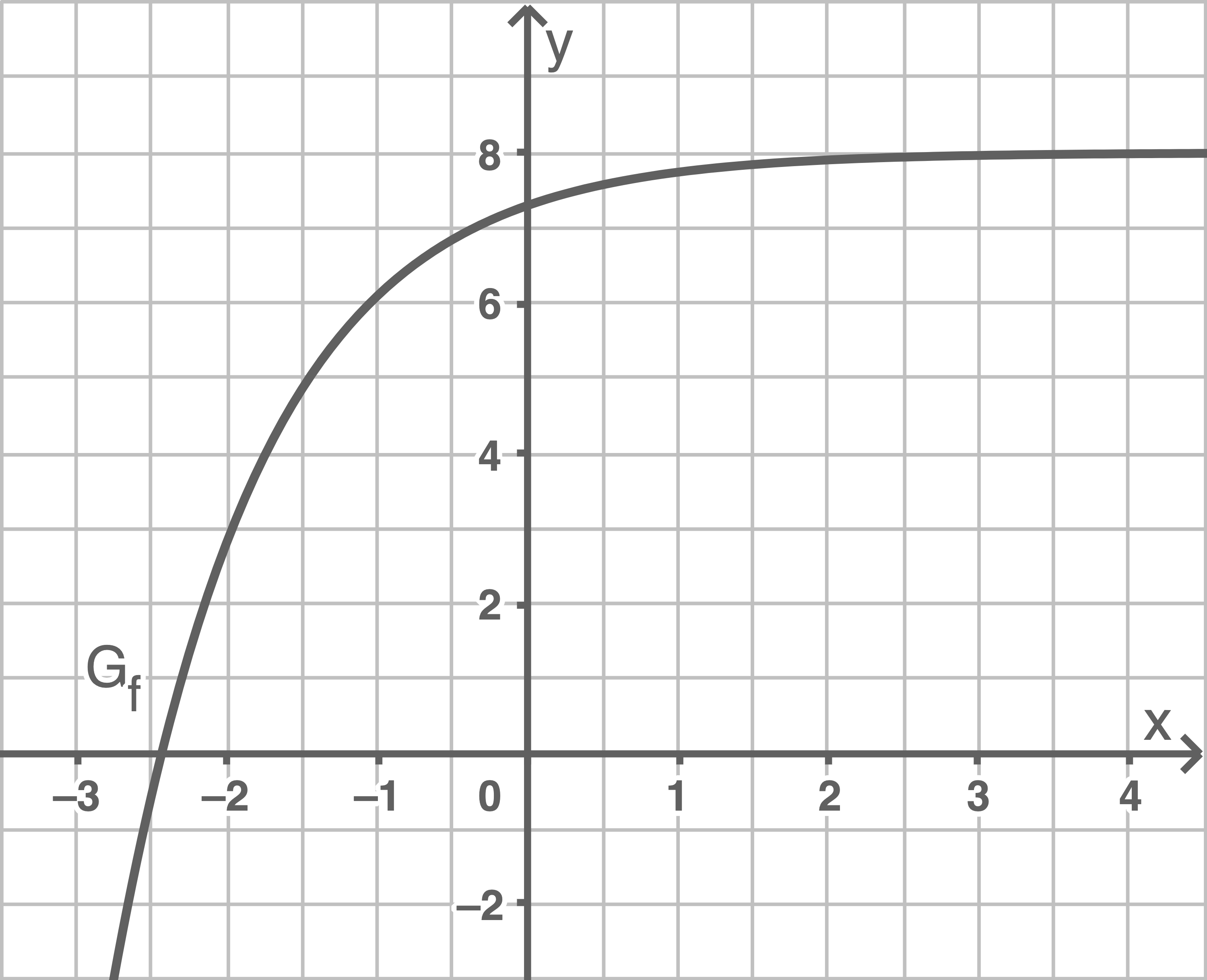
a)
Berechne die Koordinaten der Schnittpunkte mit den Koordinatenachsen und begründe, dass 
streng monoton wächst.
b)
Erkläre begründet, wie aus dem Graphen von 
hervorgeht.
c)
Deute den Term 
geometrisch und gib den Wert näherungsweise an.
d)
Gib die Gleichung der Tangente an im Punkt 
an.
e)
Überprüfe: „Es gibt ganzrationale Funktionen vierten Grades, deren Graph drei Wendepunkte besitzt.“
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Schnittpunkte mit der 
-Achse
![\(\begin{array}[t]{rll}
f(x)&=& 0 \\[5pt]
8-0,7\cdot \mathrm e^{-x}&=& 0\quad \scriptsize \mid\;-8 \mid\;:(-0,7) \\[5pt]
\mathrm e^{-x}&=& \dfrac{80}{7}\quad \scriptsize \mid\; \ln() \\[5pt]
-x&\approx & 2,44 \\[5pt]
x&\approx & -2,44
\end{array}\)](https://mathjax.schullv.de/cab0b45f91c781e79a82dfa369d229858e4178b9eec8e813cb6fc89c61fbd890?color=5a5a5a)
Die Koordinaten des Schnittpunktes mit der -Achse folgen mit 
Schnittpunkt mit der 
-Achse
Die Koordinaten des Schnittpunktes mit der -Achse folgen mit 
Monotonieuntersuchung
Eine Funktion ist streng monoton wachsend wenn für die Ableitung 
gilt.
Anwenden der Kettenregel:
Da 
ist auch für alle 
und somit ist streng monoton wachsend.
b)
- Spiegelung an der
- Spiegelung an der
- Stauchung in
- Verschiebung in
c)
d)
Die allgemeine Tangentengleichung lautet 
Die -Koordinate des Punktes 
ist 
und damit folgt:
Einsetzen in die allgemeine Tangentengleichung ergibt:
![\(\begin{array}[t]{rll}
y&=& f](https://mathjax.schullv.de/1dc2efbd05190796696038799f347ccce26acd77566fe73a961d38360818ab4f?color=5a5a5a)
e)
Die zweite Ableitung einer ganzrationalen Funktion vierten Grades ist eine ganzrationale Funktion zweiten Grades. Eine ganzrationale Funktion zweiten Grades kann höchstens zwei Nullstellen annehmen.
Die Nullstellen der zweiten Ableitungsfunktion entsprechen den Wendestellen der Funktion. Also kann eine ganzrationale Funktion vierten Grades höchstens zwei Wendestellen besitzen.
Die Aussage ist somit falsch.