Grundlagen
Einführung
Schwingungen und Wellen begegnen dir jeden Tag in deinem alltäglichen Leben. Die Geräusche, die du in deinem Leben wahrnimmst, bestehen alle aus
Wellen, welche sich im Raum ausbreiten. Außerdem sind die
Wasserwellen oder eine
La-Ola-Welle im Stadion typische Formen von
Wellen.
Frequenz
Die
Frequenz 
der Schwingung gibt die Anzahl der Schwingungen in einer Sekunde an. Die
Frequenz lässt sich mit der
Periodendauer 
berechnen. Die
Periodendauer ist die Zeit, die die
Schwingung benötigt, um genau einmal hin und her zu schwingen. Also falls das schwingende Objekt bei der
maximalen Auslenkung (Amplitude) beginnt, ist die
Periodendauer die Zeit, die benötigt wird, um zum
Ausgangspunkt zurückzukehren.
Die
Frequenz berechnet sich dann mit folgender Formel:
Einheit der
Frequenz:
Die
Einheit Hertz (Hz) bezeichnet hierbei die Anzahl der Schwingungen pro Sekunde.
Elongation (Auslenkung)
Die
Elongation 
gibt die
momentane Auslenkung des schwingenden Objekts zu einem bestimmten
Zeitpunkt 
an. Die
Elongation lässt sich in einem
--Diagramm während der Schwingung darstellen. Wenn wir davon ausgehen, dass zum Zeitpunkt
s das Objekt sich in der Ruhelage befindet und dass während der gesamten Schwingung keine
Reibung herrscht, dann sieht die
Elongation in Abhängigkeit der Zeit
folgendermaßen aus.
Amplitude
Die Amplitude 
bezeichnet den betragsmäßig größtmöglichen Wert der Zustandsgröße. Also gerade die maximale Auslenkung 
aus der Gleichgewichtslage einer Schwingung.
Die Ausbreitungsgeschwindigkeit
Die
Ausbreitungsgschwindigkeit 
, mit der sich eine
Welle ausbreitet, ist abhängig von der
Wellenlänge 
und der
Periodendauer . In der
Periodendauer in der ein Wasserteilchen genau einmal hoch und runter schwingt hat sich das
Wellental genau eine
Wellenlänge weiter bewegt. Da die
Ausbreitungsgeschwindigkeit konstant ist, lässt sie sich durch die Formel
berechnen. Wenn wir nun für den
Weg 
die
Wellenlänge 
und für die
Zeit die
Periodendauer einsetzen, erhalten wir folgende Formel.
Setzt man nun ein, dass die Frequenz
ist, erhält man folgende Formel für die
Ausbreitungsgeschwindigkeit .
Einheit der
Ausbreitungsgeschwindigkeit
Transversalwelle
Transversalwellen oder Querwellen sind physikalische Wellen, bei denen die Schwingung der Teilchen senkrecht zur Ausbreitungsrichtung erfolgt:
Ein typisches Beispiel zu den Transversalwellen sind die Wasserwellen.
Longitudinalwelle
Bei Longitudinalwellen oder Längswellen erfolgt die Schwingung parallel zur Ausbreitungsrichtung:
Insbesondere Druckschwankungen verursachen eine solche Longitudinalwelle. Du kannst sie dir folgendermaßen vorstellen:
Ein typisches Beispiel zu den Longitudinalwellen ist der Schall.
Bildnachweise [nach oben]
© SchulLV
© SchulLV
© SchulLV
Abb. 1: Elongation
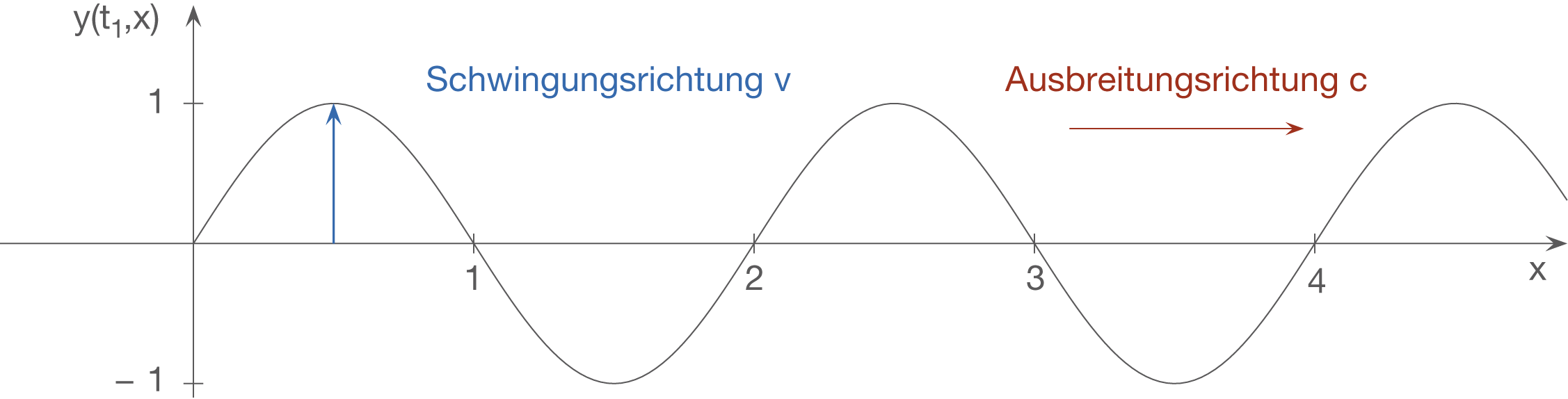Abb. 2: Transversalwellen
Abb. 3: Longitudinalwellen