Interferenz

Einführung

Abb. 1: Wellen können riesige Ausmaße annehmen
(hier zum Nachweis)

Hast du schon einmal etwas von Monsterwellen gehört? Wellen die so hoch sind, wie ein Mehrfamilienhaus?
Diese Wellen sind zwar selten, kommen allerdings dennoch vor. Auf Grund der enormen Kräfte und der Steilheit der Welle stellen sie selbst für große Schiffe eine ernstzunehmende Gefahr dar. Dabei sind diese ehemals als Seemannsgarn abgespeisten Wellen erst seit 1995 richtig anerkannt und werden derzeit noch intensiv erforscht. Bei der Entstehung dieser Monsterwellen spielen Interferenzerscheinungen eine große Rolle.

Abb. 2: Dank Interferenz kann man Musik in
Ruhe genießen (hier zum Nachweis)

Doch nicht nur Querwellen (Transversalwellen) können interferieren. Auch bei Longitudinalwellen, wie etwa beim Schall, macht man sich dieses Phänomen zu Nutze. Etwa bei dem Versuch der aktiven Lärmkompensation. Moderne Kopfhörer machen sich dieses Phänomen zu Nutze und können durch gezielte Signale in Form von Wellen Interferenzen erzeugen, die wiederum die Umgebungsgeräusche stark minimieren.

Interferenz

Das Interferieren von Wellen bezeichnet eine Überlagerung von zwei oder mehr Wellen. Dabei tritt das Prinzip der Superposition auf. Dieses Superpositionsprinzip besagt, dass wenn zwei Störungen oder Wellen aufeinander treffen, sie sich nicht gegenseitig stören, sondern sich ungestört durchdringen. Dabei addieren sich die jeweiligen Elongationen und Schnellen. Die Wellen laufen also sozusagen aufeinander auf, wobei es aussieht, als würde eine neue Welle entstehen. Dieses Überlagerungsphänomen nennt man Interferenz. Es tritt bei allen Arten von Wellen auf.

Interferenz gleichlaufender Wellen

Nach dem Superpositionsprinzip stören sich zwei in dieselbe Richtung laufende Wellen nicht, sondern überlagern sich zu einer neuen Welle. Dies kann bei folgendem Beispiel beobachtet werden: Es laufen eine rote und eine grüne Welle mit gleicher Amplitude aber unterschiedlicher Frequenz nach rechts. Dabei entsteht durch Überlagerung die blaue Welle aus der roten und der grünen.

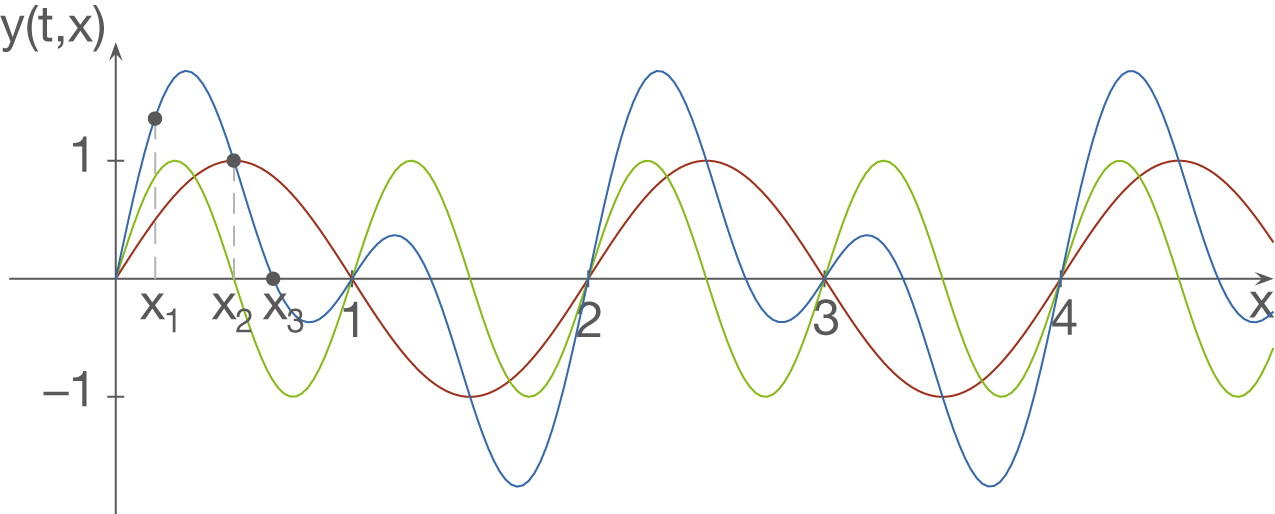
Alternativ kannst du dir die Überlagerung von Wellen auch im bereits bekannten Zeigermodell vorstellen. Hierbei ist der Zeiger der resultierenden Welle gerade die vektorielle Addition der Zeiger der beiden Einzelwellen. Aus der Definition des Zeigermodells ergibt sich entsprechend dieses resultierenden Zeigers dann gerade die momentane Auslenkung (grau gestrichelt) der aus der Überlagerung hervorgegangenen Welle. Für die ausgewählten Punkte aus dem obigen Beispiel, ergeben sich dann folgende Zeigermodelle:

Laufen darüber hinaus zwei Wellen in die gleiche Richtung und besitzen dieselbe Wellenlänge $\lambda$ , so unterscheiden sie sich voneinander durch die Phasendifferenz $\Delta\varphi$ bzw. den Gangunterschied $\delta$ . Die Phasendifferenz gibt an, wie sich die Phasen der beiden Wellen in einem bestimmten Punkt unterscheiden. Der Gangunterschied dagegen ist die räumliche Distanz zwischen zwei gleichen Schwingungszuständen auf verschiedenen Wellen. Die Phasendifferenz $\Delta \varphi$ kannst du dem Zeigermodell entnehmen:

Den Gangunterschied $\delta$ kannst du dir bildlich folgendermaßen vorstellen:

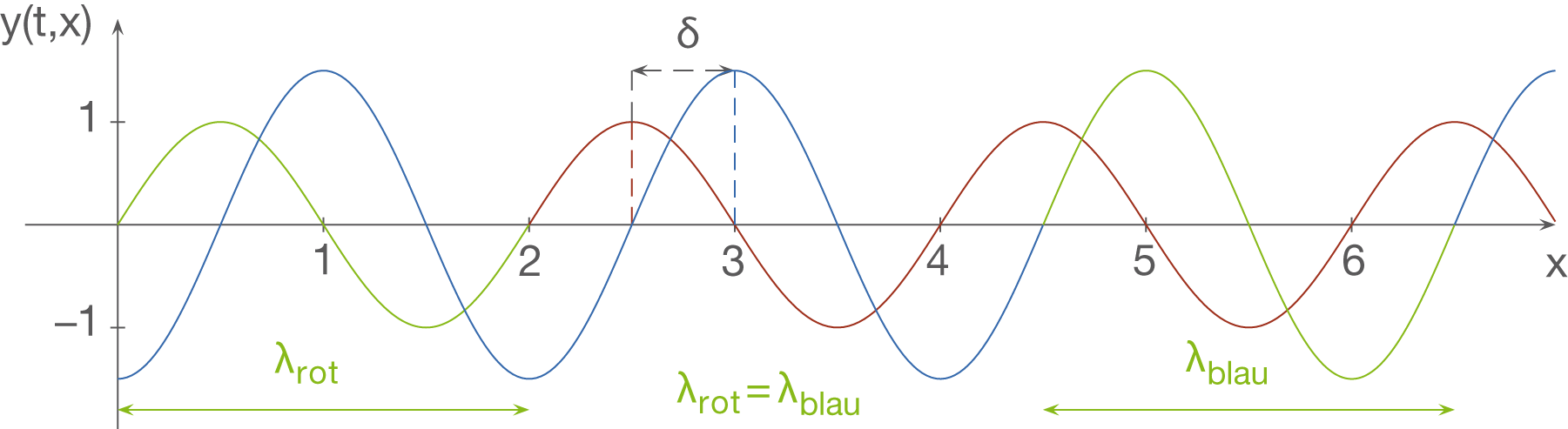
Laufen zwei Wellen auf dasselbe Ziel zu und haben unterschiedlich lange Wege zurückgelegt, so kommt es ebenfalls zu einem Gangunterschied $\delta$ : Hierbei kannst du erkennen, dass die roten Abschnitte gerade gleich lang sind. Der Gangunterschied ist in diesem Fall also gerade die Differenz der beiden verschiedenen Wege zum Ziel.

Dabei kann es zu zwei Sonderfällen kommen.

Konstruktive Interferenz

Konstruktive Interferenz tritt immer dann auf, wenn sich die Amplituden beider Einzelwellen addieren. Dies ist genau dann der Fall, wenn die Wellenberge der einen Welle genau auf die Wellenberge der anderen Wellen treffen.
Dies ist also der Fall bei einer Phasendifferenz von $\Delta \varphi=2 \cdot n \cdot \pi \quad$ $(n=0,1,2,...)$ .
Diese Phasenbeziehung entspricht dem Gangunterschied $\delta=n \cdot \lambda \quad$ $(n=0,1,2,...)$ .
Graphisch sieht das folgendermaßen aus:

Man spricht davon, dass die beiden Einzelwellen in Phase schwingen.

Destruktive Interferenz

Von destruktiver Interferenz spricht man, wenn sich die Amplituden subtrahieren und sich dabei eventuell sogar auslöschen.
Bei der destruktiven Interferenz treffen gerade die Wellenberge der einen Welle auf die Wellentäler der anderen Welle. Wenn dazu noch die Amplituden gleich groß sind, so kommt es zur Auslöschung. Von Auslöschung spricht man, da hierbei die Amplitude der resultierenden Welle an allen Stellen dauernd Null ist.

Bei diesem Fall liegt eine Phasendifferenz von $\Delta \varphi =(2n-1) \cdot \pi \quad$ $(n=1,2,3,...)$ vor.
Dies entspricht einem Gangunterschied von $\delta=(2n-1) \cdot \dfrac{\lambda}{2} \quad$ $(n=1,2,3,...)$ .

Bildlich kannst du dir das folgendermaßen vorstellen:

Bei gleichen Amplituden tritt der Fall der Auslöschung ein:

Man spricht davon, dass die beiden Einzelwellen gegenphasig schwingen.

Interferenz gegenläufiger Wellen

Laufen zwei Wellen aufeinander zu, so stören auch sie sich nach dem Superpositionsprinzip nicht, sondern durchdringen sich und laufen sozusagen aufeinander auf. Das Prinzip ist hier also das gleiche wie bei der Interferenz gleichlaufender Wellen. Der einzige Unterschied besteht darin, dass nach der Durchdringung keine fortschreitende Welle mehr zu erkennen ist, sondern sich eine stehende Welle ausbildet:

Die Sonderfälle der konstruktiven und destruktiven Interferenz treten hier, wie du erkennen kannst, abwechselnd auf. Näheres zur stehenden Welle findest du im PhysikLV-Skript Wellenformen.

Bildnachweise [nach oben]

[1]

http://commons.wikimedia.org/wiki/File: Wea00800_-_Flickr_-_NOAA_Photo_Library.jpg - Unknown CC-BY-SA

[2]

http://commons.wikimedia.org/wiki/ File:Headphones_1.jpg - PJ CC-BY-SA