Masse, Volumen, Dichte

Die Masse

Was wiegt deiner Meinung nach mehr: $1 \, \text{kg}$ Steine oder $1 \, \text{kg}$ Federn? Es ist beides gleich schwer, denn die Masse von beidem ist gleich. Masse $m$ ist eine unveränderliche Eigenschaft von Körpern. Sie ist überall gleich, egal wo du dich befindest. Die Masse wird in Kilogramm $[m]=1\,\text{kg}$ angegeben. Im Alltag wird auch die Angabe Gramm g häufig verwendet. In folgender Tabelle sind noch weitere wichtige Einheiten angegeben.

Einheit	in Kilogramm	in Gramm
$1$ Tonne	$1000$	$1000000$
$1$ Pfund	$0,5$	$500$
$1$ Zentner	$50$	$50000$

Die Masse ist an jedem Ort gleich, das Gewicht eines Körpers aber an jedem Ort verschieden. Würdest du dein Gewicht einmal auf der Erde und einmal auf dem Mond messen, könntest du einen enormen Unterschied feststellen. Auf dem Mond hättest du nur $\dfrac{1}{6}$ des Gewichtes, das du auf der Erde hast. Dies wird durch die Schwerkraft hervorgerufen. Du kannst darüber mehr lesen in dem Skript zu Schwerkraft.

Das Volumen

Du hast auf einer Milchpackung sicher schon einmal die Aufschrift $1 \, \text{l}$ gesehen oder auf eine Wasserflasche $0,3 \, \text{l}$ gelesen. Diese Angaben geben das Volumen $V$ an. Das Volumen beschreibt die räumliche Ausdehnung eines Körpers und wird im Alltag mit Liter $[V]=1\,\text{l}$ angegeben. Die Basiseinheit ist $1\,\text{m}^3$ .

$1\,\text{dm}^3 =$ $1\,\text{l} =$ $0,001\,\text{m}^3$

Das Volumen eines Quaders kannst du berechnen, indem du alle Seitenlängen miteinander multiplizierst:

Abb. 1: Volumen eines Quaders

$V=a\cdot b\cdot c$

Mit Gegenständen, bei denen die Seiten nicht einfach abzumessen sind, ist es schwieriger das Volumen zu bestimmen. Um z.B das Volumen eines unförmigen Steines zu bestimmen, musst du anders vorgehen, denn du kannst die Seitenlängen nicht einfach mit einem Lineal abmessen.

Versuch zur Bestimmung des Volumens:

Du brauchst einen Messbecher, der zur Hälfte mit Wasser gefüllt ist. Du kannst das Volumen an der Seite ablesen und notieren. Nun legst du den Körper in den Messbecher, dessen Volumen du bestimmen möchtest (z.B einen Stein). Es ist zu beobachten, dass die Wassersäule ansteigt: Der Stein verdrängt das Wasser und zwar genau so viel, wie er selbst Platz einnimmt. Das Volumen, das du danach am Messbecher ablesen kannst, ist also das Anfangsvolumen und zusätzlich das Volumen des Steines. Wenn du von dem Endvolumen das Anfangsvolumen abziehst, erhältst du das Volumen des Steins.

$V_{\text{End}}-V_{\text{Anfang}}= V_{\text{Stein}}$

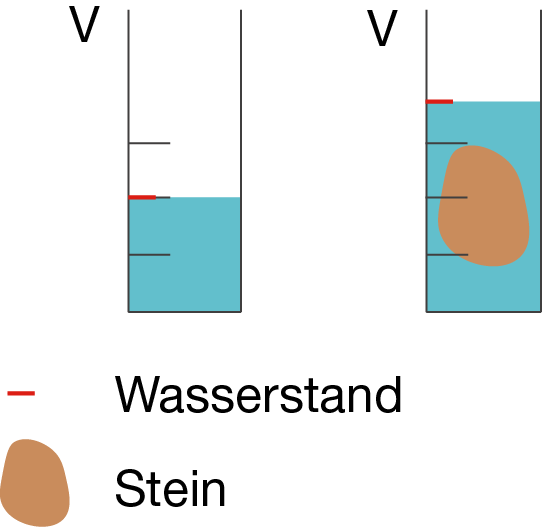Abb. 2: Bestimmung des Volumens eines Körpers

Die Dichte

Wenn du zwei gleich große Würfel aus unterschiedlichem Material in die Hand nimmst, bemerkst du, dass sie unterschiedlich schwer sind, obwohl ihr Volumen gleich ist. Sie haben eine unterschiedliche Dichte $\rho$ (sprich "rho"). Die Dichte ist eine Stoffeigenschaft, die für jedes Material spezifisch ist. Man kann sie berechnen aus dem Quotienten von Masse und Volumen.

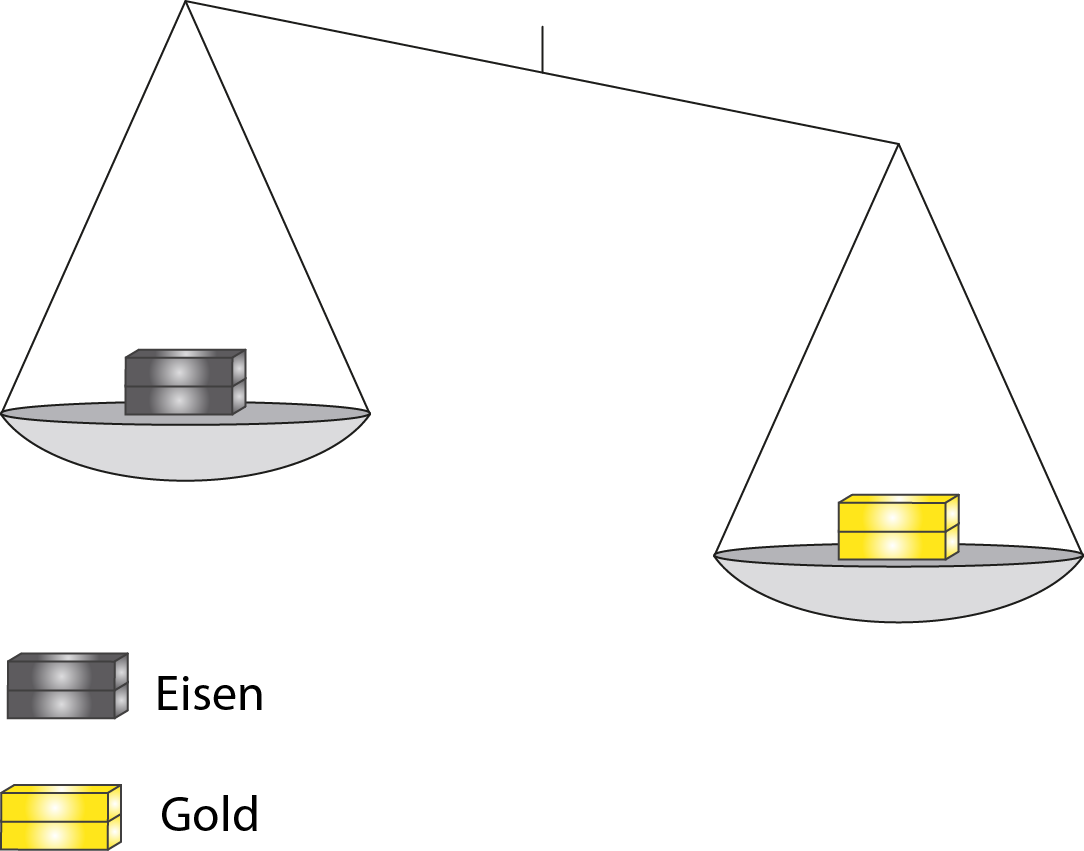Abb. 3: Dichte (Gold) > Dichte (Eisen)

$\rho=\dfrac{m}{V}$

Bildnachweise [nach oben]

[1]

[2]

[3]