Flaschenzug und Hebel

Denkst du, dass du eine Masse $m$ von $100 \, \text{kg}$ hochheben kannst? Mit reiner Muskelkraft wird das schwer. Es gibt aber Möglichkeiten, dies mit physikalischen Methoden zu schaffen. Der Flaschenzug und der Hebel wurden konstruiert, um das Anheben von Gewichten zu erleichtern. Früher, als es noch keine Motoren gab und alle Arbeiten von Hand erledigt werden mussten, brachten diese beiden Verfahren große Erleichterung.

Der Flaschenzug

Das Prinzip des Flaschenzugs besteht darin, die gesamte Kraft $F$ auf das Seil so umzuleiten, dass die Kraft mit der man zieht, geringer wird. Dieses Seil wird über Rollen geleitet. Die Rolle kann entweder fest sein oder lose. Wir gehen hier zur Vereinfachung davon aus, dass keine Reibung vorliegt und die Masse der Rolle zu vernachlässigen ist.

Die feste Rolle:

Die Masse m, die an dem Seil hängt, verursacht eine Kraft $F$ von ( $F= m \cdot g$ ). Um das Gewicht anzuheben, musst du genau mit dieser Kraft ziehen. Du kannst allerdings die Kraft in eine andere Richtung lenken, was das Ziehen angenehmer machen kann. Die Kraft mit der du ziehst, ist aber die gleiche.

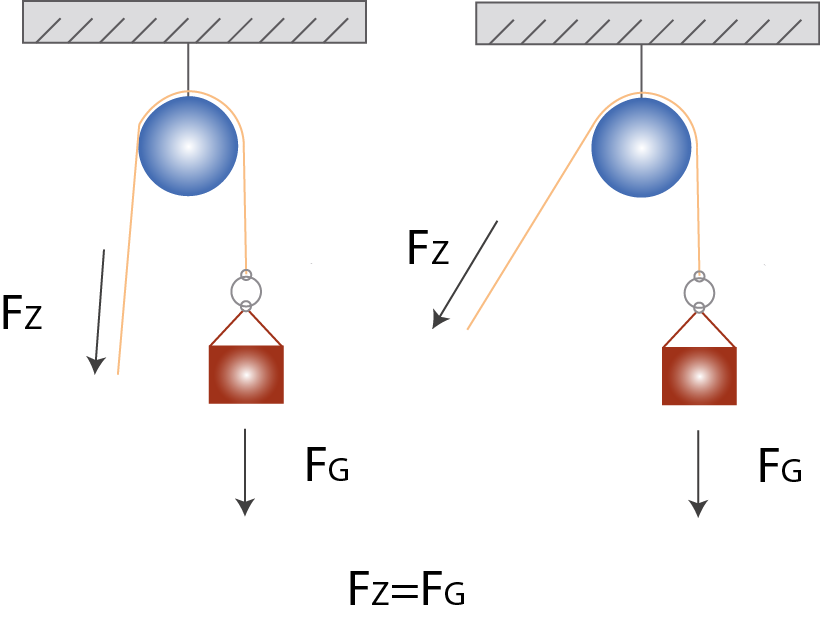Abb. 1: einfacher Flaschenzug: die Kraft kann umgelenkt werden

Die lose Rolle

Um die Zugkraft zu verringern, kann man die Kraft auf das Seil verteilen. Das Seil wird so um die Rolle gewunden, dass es wie zwei tragende Seile betrachtet werden kann, da es doppelt an der Rolle angreift. Diese Verbindungen zwischen den Rollen werden mit $n$ bezeichnet. Die Kraft mit der zu ziehen musst, ist bei $n=2$ nur noch halb so groß.

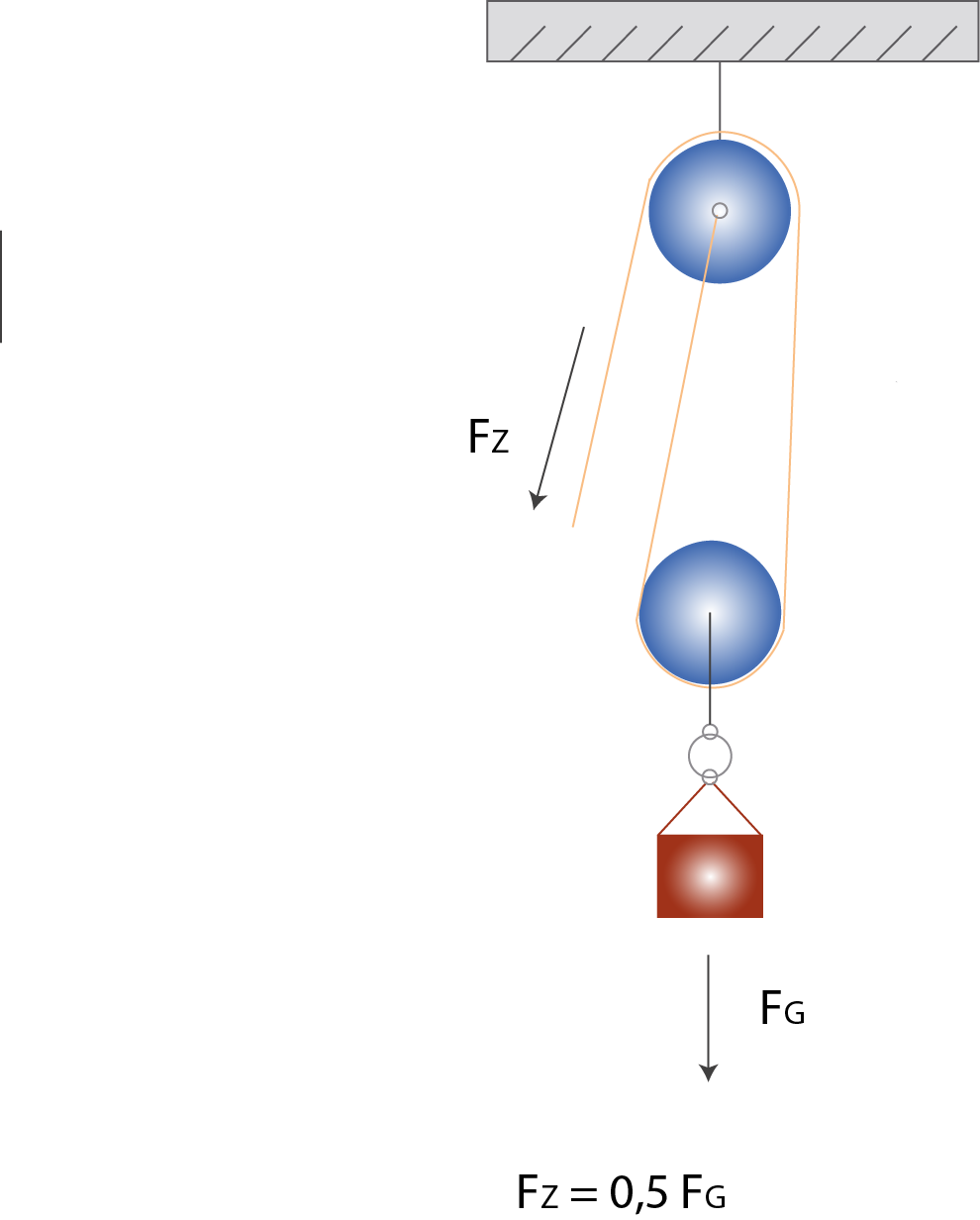Abb. 2: Flaschenzug mit zwei Rollen: die Kraft wird auf das Seil verteilt

Es gibt allerdings auch einen Nachteil. Durch das Umlenken der Kraft, verlängerst du die Strecke $s$ , die das Seil gezogen werden muss. Um das Gewicht um $10 \, \text{cm}$ zu heben, musst du das Seil $20 \, \text{cm}$ nach unten ziehen.

Die Berechnung der Zugkraft $F_z$ mit $n$ Verbindungen zwischen den Rollen, kann mit der Formel

$F_z=\frac{F_g}{n}$

berechnet werden. Der Flaschenzug verringert also die Kraft mit dem gezogen werden muss oder lenkt die Kraft in eine andere Richtung um. Beides kann eine große Erleichterung sein. Heute hat der Flaschenzug noch immer Anwendung, auch wenn er in vielen Situationen durch den Motor ersetzt wurde. Noch etwas häufiger im Alltag zu finden ist der Hebel.

Der Hebel

Der Hebel ist ebenfalls dafür gedacht, das Anheben von schweren Gegenständen einfacher zu machen.

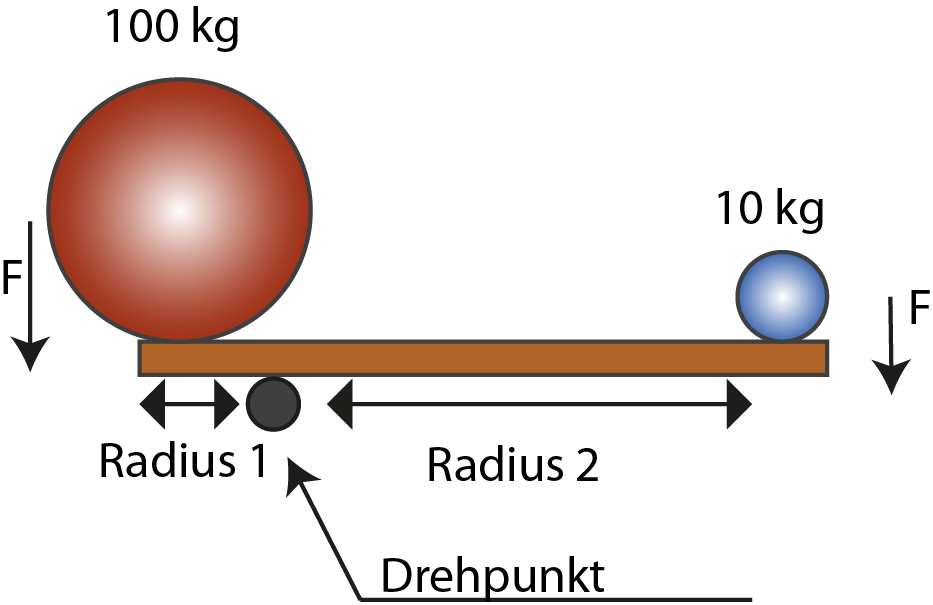Abb. 3: Wippe im Gleichgewicht

Es besteht der Zusammenhang:

$F_1 \cdot r_1 = F_2 \cdot r_2$

Das bedeutet, dass eine Kraft $F_1$ multipliziert mit dem Abstand zum Drehpunkt $r_1$ , auch Hebelarm genannt, gleich sein muss der Kraft auf der anderen Seite $F_2$ , multipliziert mit dem Abstand $r_2$ zum Drehpunkt. Es ist also Möglich eine Masse von $100 \, \text{kg}$ anzuheben, wenn der Hebelarm lang genug ist. Das Produkt aus Kraft und Hebelarm wird Drehmoment M genannt.

$M = F_1 \cdot r_1$

Es herrscht ein Gleichgewicht, wenn das Drehmoment der einen Seite, genauso groß ist, wie das Drehmoment der anderen Seite.

Die Wippe auf dem Spielplatz ist auch ein Hebelsystem. Der Drehpunkt ist genau in der Mitte und die Kräfte werden durch die Masse der Personen verursacht, die auf der Wippe sitzen. Das System ist nur im Gleichgewicht, wenn beide Personen die gleiche Masse haben und somit auch die gleiche Schwerkraft. Du kannst das Prinzip des Hebels an der Wippe sehr gut testen. Je weiter du dich nach außen setzt, desto mehr Kraft muss die Person auf der anderen Seite ausüben, um dich herunterzudrücken.

Hebel können aber auch einseitig sein. Es gibt dann einen Drehpunkt am Ende des Hebels. Ein Beispiel dafür, dass du sicher kennst, ist der Schubkarren oder der Nussknacker.

Denkst du nun, dass du $100 \, \text{kg}$ anheben könntest? Mit den hier genannten Hilfsmitteln, ist das sicher möglich.

Wie lange müsste ein Hebelarm sein, damit du eine Kugel mit $100 \, \text{kg}$ , die $10 \, \text{cm}$ vom Drehpunkt entfernt ist, anheben könntest. Wir gehen, davon aus, dass du eine Kraft von $200 \, \text{N}$ aufwendest.

geg:

$m_1= 100 \, \text{kg}$ ; $r_1= 10 \, \text{cm}$ = $0,1 \, \text{m}$ ; $F_2= 200\, \text{N}$ ; $g =9,81 \dfrac{\text{N}}{\text{kg}}$

$F_1 = 100\text{kg} \cdot 9,81 \dfrac{\text{N}}{\text{kg}}= 981\text{N}$

$\begin{array}[t]{rll} F_1 \cdot r_1 &=&F_2 \cdot r_2 &\quad \scriptsize \mid\;:F_2 \\[5pt] \frac{F_1 \cdot r_1 }{F_2}&=& r_2 &\quad \scriptsize \\ \\[5pt] \frac{981\,\text{N} \cdot 0,1\, \text{m}}{200\,\text{N}}&=& 0,49 \text{m} \end{array}$

Der Hebelarm, an dem du drückst, müsste also ca. $50$ $cm$ sein, damit du $100$ $kg$ anheben könntest.

Bildnachweise [nach oben]

[1]

[2]

[3]