Magnetische Flussdichte und Messmethoden

Einführung

Sind Hochspannungsleitungen gesundheitsgefährdend?

Hochspannungsleitungen sind nicht nur stumm Zeugen unserer postindustriellen Gesellschaft, sondern sie bringen den Strom über weite Distanzen hinweg zu uns nach Hause. Daher sind sie heutzutage nicht mehr wegzudenken. Dennoch gibt es immer wieder große Streitigkeiten um solche Stromtrassen und dies nicht nur auf Grund von ästhetischen Bedürfnissen. Als Argument gegen solche Hochspannungsleitungen wird häufig die Gesundheitsgefährdung genannt. Denn wie im PhysikLV-Skript „Einführung und Definitionen“ erwähnt sind stromdurchflossene Leitungen von einem kreisrunden Magnetfeld umgeben. Daher sind auch die Hochspannungsleitungen von Magnetfeldern umgeben, die wenn sie stark genug sind, elektrische Geräte stören oder sogar gesundheitsgefährdend sein können. Doch um so etwas zu überprüfen, muss zunächst einmal klar gemacht werden, wie die Stärke eines Magnetfeldes definiert ist. Dem PhysikLV-Skript „Elektrische Feldstärke“ kannst du entnehmen, dass die Stärke eines elektrischen Feldes definiert ist über die Kraft die auf eine Probeladung wirkt:

$E=\dfrac{F}{q}$

Eine ähnliche Definition für das Magnetfeld ist allerdings nicht möglich, da es keine magnetischen Monopole gibt. Daher wird die Stärke eines Magneten über die magnetische Flussdichte definiert, welche durch folgendes Experiment eingeführt werden soll: Ein Leiterrahmen mit der Länge $s$ wird in das Magnetfeld eines Permanentmagneten eingeführt, welches nach schräg hinten gerichtet ist. Der senkrecht zu den Feldlinien stehende Rahmen ist an einem Kraftmesser befestigt und wird von einem Strom $\boldsymbol{I}$ durchflossen:

Da der Leiterrahmen senkrecht zu den Magnetfeldlinien hängt, bewegen sich die Elektronen ebenfalls senkrecht zu den Feldlinien. Dadurch entsteht die Lorentzkraft $\boldsymbol{F_L}$ , welche auf die Elektronen des Leiterrahmens wirkt. Die Richtung der Lorentzkraft kannst du der unten stehenden Abbildung entnehmen und mit der „3-Finger-Regel“ nachvollziehen. Dabei zeigt der Zeigefinger deiner linken Hand immer in die Richtung der magnetischen Feldlinien, also in die Zeichenebene hinein, dein Daumen weist in die jeweilige Bewegungsrichtung der Elektronen und der Mittelfinger zeigt dir dann die Richtung der wirkenden Lorentzkraft an. Das Ergebnis ist, dass sich die nach außen gerichteten Kräfte kompensieren und somit die Lorentzkraft nur nach unten wirkt.

Der Zeigefinger der linken Hand weißt in die Zeichenebene, der Daumen nach rechts und der Mittelfinger in Richtung ${F_L}_1$ , also nach unten.

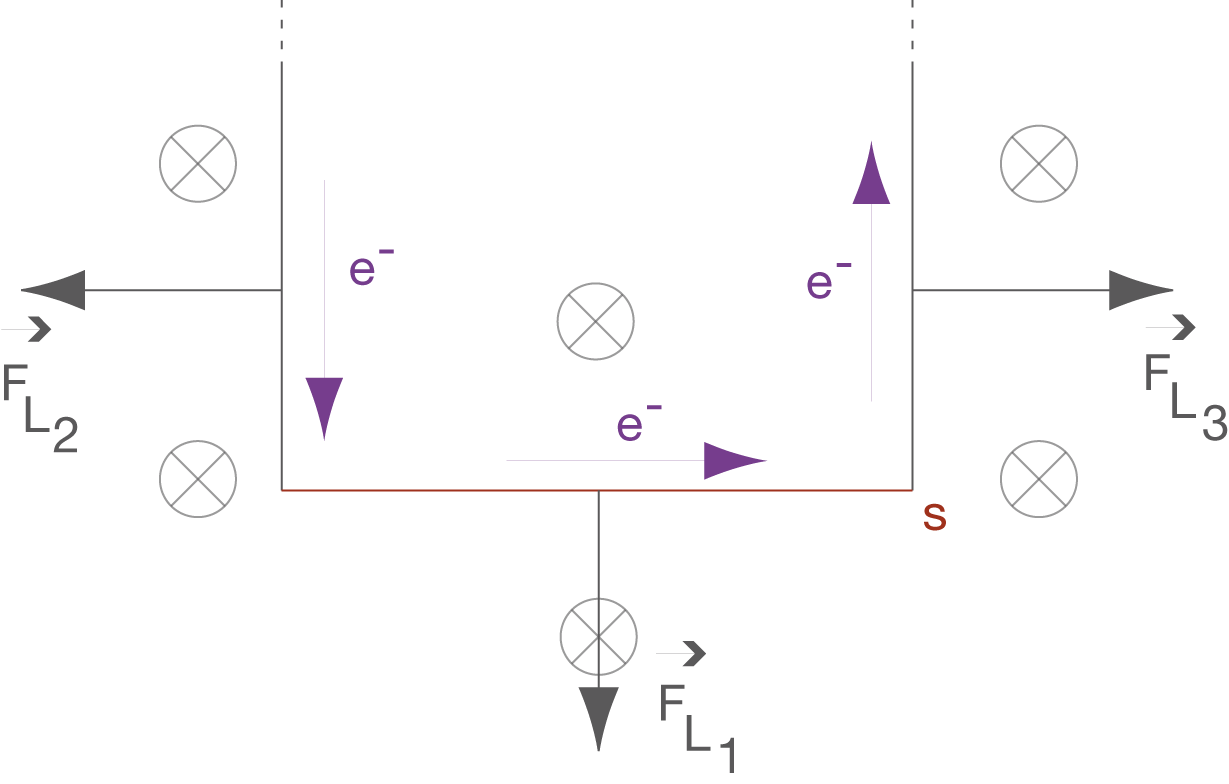
Die beiden nach außen wirkenden Kräfte kompensieren sich gerade.

Da die Lorentzkraft nur nach unten zieht ist ihr Betrag direkt am Kraftmesser ablesbar. Werden im unveränderten Versuchsaufbau andere Magnete benutzt, so fällt auf, dass die Lorentzkraft $F_L$ am Kraftmesser sich für die verschiedenen Magnete unterscheidet. Diese sind nämlich unterschiedlich „stark“. Die Stärke des magnetischen Feldes wird somit durch die magnetische Flussdichte dargestellt.

Magnetische Flussdichte

Aus obigem Versuch lässt sich damit die Definition der magnetischen Flussdichte mit dem Formelzeichen $\boldsymbol{B}$ herleiten.

Die magnetische Flussdichte $\boldsymbol{B}$ ist durch die Kraft $\boldsymbol{F_L}$ auf einen mit dem Strom $\boldsymbol{I}$ durchflossenen Leiter der Länge $\boldsymbol{s}$ , der senkrecht zu den magnetischen Feldlinien steht, definiert.

Die magnetische Flussdichte ist demnach ein Maß für die Stärke des magnetischen Feldes und wird wie die elektrische Feldstärke durch die Feldlinien sichtbar gemacht. Je dichter also die magnetischen Feldlinien sind, desto stärker ist das Magnetfeld. Außerdem besitzt die magnetische Flussdichte eine Richtung und wird deshalb als Vektor angegeben. Somit wird obige Definition folgendermaßen als physikalische Formel ausgedrückt:

$\overrightarrow{B}=\dfrac{\overrightarrow{F}}{I \cdot s}$

Die internationale SI-Einheit der magnetischen Flussdichte heißt Tesla und wurde nach dem großen Physiker und Erfinder Nikola Tesla benannt und wird entsprechend der Einheiten der obigen Gleichung folgendermaßen definiert:

$1\,\text{T} = \dfrac{1\,\text{N}}{1\,\text{A}\cdot\text{m}}$

Messmethoden

Nachfolgend werden zwei Messmethoden vorgestellt mit denen die magnetische Flussdichte und damit die Stärke eines Magnetfeldes gemessen werden kann.

Stromdurchflossener Leiterrahmen

Diese Art, die magnetische Flussdichte zu messen, wurde bereits eingangs vorgestellt. Hierbei wird ein Leiterrahmen an einem Kraftmesser aufgehängt und von einem Strom durchflossen. Senkrecht zu diesem Rahmen ist ein Magnetfeld gerichtet, das von einem Stabmagneten oder einer Spule aufgebaut wird. Strom und Magnetfeld sind dabei so gerichtet, dass eine Lorentzkraft entsteht die den Leiterrahmen mit der Kraft $F_L$ nach unten zieht. Diese Kraft kann am Kraftmesser abgelesen werden. Der Betrag der magnetischen Flussdichte wird schließlich nach ihrer Definition aus dieser abgelesenen Kraft $F_L$ , der Stromstärke $I$ und der Länge des Leiterrahmens $s$ folgendermaßen berechnet:

$B=\dfrac{F_L}{I \cdot s}$

Der beschriebene Versuchsaufbau und -ablauf sieht folgendermaßen aus:

Hallsonde

Die Hallsonde benutzt den sogenannten Halleffekt zur Messung von Magnetfeldern. Sie besteht aus einem Metallband oder noch häufiger aus Halbleiterplättchen. In folgender Messung wird die Hallsonde mit der Höhe $h$ senkrecht zum magnetischen Feld (von links nach rechts) von einem Strom (von vorne nach hinten) durchflossen. Die Elektronen im Stromkreis bewegen sich also entgegen der elektrischen Stromrichtung von hinten nach vorne. Das obere und untere Ende der Hallsonde ist mit einem Spannungsmessgerät verbunden, an dem die später erwähnte Hallspannung gemessen wird. Der Versuchsaufbau sieht demnach folgendermaßen aus:

Mithilfe der „3-Finger-Regel“ kannst du nachvollziehen, dass die Lorentzkraft nach unten wirkt und somit die Elektronen in der Hallsonde nach unten ablenkt. Am unteren Ende des Halbleiterplättchens entsteht somit schnell ein Elektronenüberschuss.

Die Ladungsdifferenz zwischen dem oberen und dem unteren Ende der Hallsonde lässt ein elektrisches Feld und eine Spannung, die sogenannte Hallspannung, entstehen. Dieses Feld ist von oben nach unten gerichtet und lenkt daher die negativ geladenen Elektronen nach oben ab. Die Hallspannung wächst solange an, bis sich ein Kräftegleichgewicht zwischen der elektrischen Kraft und der Lorentzkraft einstellt und die weiteren Elektronen ohne Ablenkung durch die Hallsonde fließen können.

Für die Lorentzkraft $\boldsymbol{F_L}$ gilt, wie im PhysikLV-Skript „Lorentzkraft“ hergeleitet, die folgende Formel:

$F_L= q \cdot v \cdot B$

Aus der Definition der elektrischen Feldstärke des gleichnamigen PhysikLV-Skripts kannst du entnehmen, dass für die elektrische Kraft $\boldsymbol{F_{el}}$ gilt:

$F_{el}= q \cdot E$

In homogenen elektrischen Feldern, wie wir sie in unserem vorliegenden Fall vorfinden, gilt zudem, dass die Feldstärke aus dem Quotient der Spannung $U$ und der Distanz der Ladungen, in unserem Fall $\boldsymbol{h}$ bezeichnet, berechnet werden kann. Somit ergibt sich beim Halleffekt als Gleichung für die elektrische Kraft $F_{el}$ :

$F_{el}= q \cdot \dfrac{U}{h}$

Wie bereits oben erwähnt herrscht während der Messung ein Kräftegleichgewicht zwischen der elektrischen Kraft und der Lorentzkraft. Daher folgt:

$\begin{array}{rcl} F_{el}&=&F_{L}& \\ \color{orange}{q} \cdot \dfrac{U}{h}&=&\color{orange}{q} \cdot v \cdot B \end{array}$

Für die sogenannte Hallspannung $U_H$ folgt somit:

$U_{H}= h \cdot v \cdot B$

Es folgt damit, dass die Hallspannung $\boldsymbol{U_H}$ proportional zur magnetischen Flussdichte $\boldsymbol{B}$ ist:

$U_{H} \sim B$

Diese Proportionalität nutzt man bei der Hallsonde aus, um die magnetische Flussdichte zu messen. Da die Geschwindigkeit der Elektronen meist nicht gegeben ist, kalibriert man die Hallsonde mit einem Magneten, dessen Flussdichte bekannt ist. Daraus wird ein Umrechnungsfaktor bestimmt, mit dem die magnetische Flussdichte eines unbekannten Magneten ermittelt werden kann.