Einführung

Bei der Kernspaltung oder auch Kernfission wird ein Atomkern in zwei oder mehrere kleinere Atomkerne gespalten. Bei der Kernfusion verschmelzen zwei Atomkerne zu einem Größeren. Die beiden Vorgänge können exotherm, also Energie freisetzend, sowie endotherm, Energie benötigend, ablaufen. Die exothermen Vorgänge nutzt man technisch zur Energiegewinnung.

Massendefekt

Als Massendefekt bezeichnet man das Phänomen, dass die Masse eines Atoms kleiner ist als die Summe der Teilchen, aus denen es aufgebaut ist. Jeder Atomkern besitzt einen spezifischen Massendefekt. Den höchsten Massendefekt weisen Kerne mit einer Nukleonenzahl von ca. auf. Der Massendefekt entsteht durch eine bessere Bindung der Nukleonen im Atomkern als im freien Zustand. Den Massendefekt kann man nach dieser Formel berechnen. Wobei die Anzahl der Protonen und die Anzahl der Neutronen im Kern angibt. ist die Neutronenmasse, ist die Protonenmasse und ist die Masse des Atomkerns. Der Massendefekt lässt sich mit Einsteins Formel zur Äquivalenz von Masse und Energie zu einer Energie umrechnen.

Kernspaltung

Vorgänge

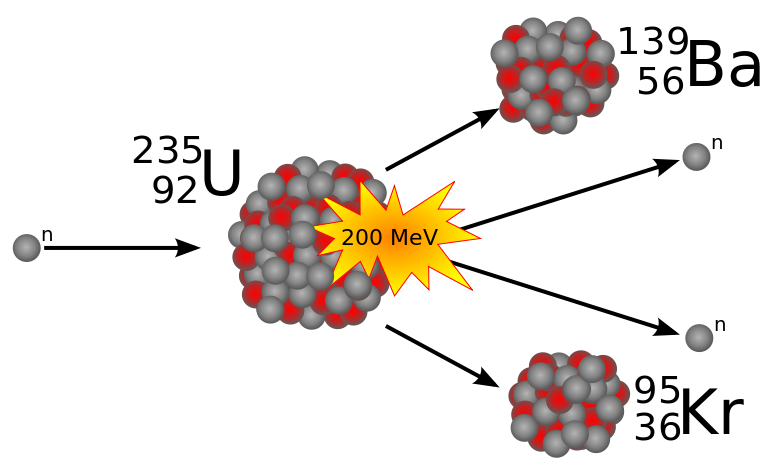
Bei der Kernspaltung stößt ein Neutron, oder ein anderes Teilchen mit genügend Energie, gegen einen Atomkern. Durch die Energie, die der Atomkern absorbiert, kann er sich spalten. Meistens teilt sich der Kern in zwei Teile, es kommt allerdings auch vor, dass er sich in drei oder mehr Teile spaltet. Die neu entstandenen Atomkerne können gleich groß sein, sind in der Regel allerdings ein größerer und ein kleinerer Kern. Zusätzlich zu den Kernen werden ein oder mehrere Neutronen freigesetzt, die sich aus dem Atomkern gelöst haben. Die Teile, in die sich der Atomkern aufteilt, werden Spaltprodukte genannt. Die entstandenden Spaltprodukte befinden sich idealerweise in einem energetisch besseren Zustand als das Ursprungsatom. Misst man die Masse der Spaltprodukte, so sind sie in Summe, aufgrund des Massendefekts, kleiner als die Masse des ursprünglichen Atomkerns und dem des stoßenden Neutrons. Die verlorene Masse geht über Einsteins Formel zur Äquivalenz von Masse und Energie in Bewegungsenergie der Spaltprodukte über. Bei der Spaltung von Uran-235 zu Barium-139 und Krypton-95 ist der Massendefekt der Spaltprodukte in etwa größer als der Massendefekt des gespaltenen Urans. Die freigewordenen Energie lässt sich berechnen.

Nutzen

Die Energie, die pro Kernspaltung frei wird, ist deutlich größer als die Energie, die bei einer chemischen Reaktion frei wird. Daher wird deutlich weniger Material benötigt um die gleiche Energie frei zusetzten. Um die selbe Energie, die bei der Spaltung von einem Gramm Uran-235 freigesetzt wird, durch die Verbrennung von Kohlenstoff zu erreichen, braucht man kg Kohlenstoff. Das heißt, die Energiemenge durch Kernspaltung von Uran ist mal größer als die Energiemenge der Verbrennung der selben Masse an Kohlenstoff. Der Vorgang der Kernspaltung wird in Kernreaktoren sowie bei der Atombombe genutzt. In Kernreaktoren läuft die Kernspaltung kontrolliert ab, die freigesetzte Wärme wird über Wärmemaschinen und Generatoren in elektrischen Strom gewandelt und genutzt. Bei der Atombombe läuft die Kernspaltung schlagartig ab, die frei werdende Energie wird in die Umwelt abgegeben.

Kernfusion

Die Kernfusion läuft entgegen der Kernspaltung ab. Bei der Kernfusion verschmelzen zwei leichte Atomkerne zu einem schwereren Atomkern. Dabei können auch freie Neutronen mit hoher Bewegungsenergie entstehen. Hat der entstehende Atomkern einen größeren Massendefekt als die Summe der Massendefekte der ursprünglichen Kerne, wird bei der Verschmelzung mehr Energie frei als benötigt wurde. Die freiwerdende Energie kommt daher, dass der Massendefekt des entstandenden Atomkerns höher ist als die Summe der Massendefekte der Atomkerne, die verschmelzen. Die Differenz kann mit Einsteins Formel zur Äquivalenz von Masse und Energie von Masse zu Energie umgerechnet werden.

Stellare Kernfusion

Bei allen Sternen im All, also auch unserer Sonne, ist die Kernfusion der Vorgang, der die Sterne zum Leuchten bringt. In der Sonne verschmelzen pro Sekunde Wasserstoff zu Helium. Der Masseverlust von pro Sekunde entspricht der Strahlungsleistung von . Bei einer Masse von kann die Sonne noch Milliarden Jahre so wie bisher weiter strahlen. Wenn der Wasserstoff in der Sonne knapp wird, wird sich die Sonne aufblähen und Heliumkerne verschmelzen zu schwereren Elementen.

Kernfusionsreaktor

Bereits seit den 1960er Jahren forscht man an Kernfusionsreaktoren, in denen wie in der Sonne Wasserstoffkerne zu Heliumkernen verschmolzen werden. Dazu soll Deuterium, also Wasserstoff mit zwei Nukleonen, und Tritium, also Wasserstoff mit drei Nukleonen, bei großer Hitze zu Helium verschmolzen werden. Der Vorgang stellt aktuell noch große Schwierigkeiten dar, da für die Fusion extreme Hitze benötigt wird. Erste Erfolge gibt es bei der Experimentieranlage Wendelstein 7-X in Greifswald. Dort wurde am 10. Dezember 2015 ein erstes Helium-Plasma erzeugt. Kernfusion hat gegenüber Kernspaltung den großen Vorteil, dass fast keine radioaktiv strahlenden Abfälle entstehen. Zudem können durch Kernfusion noch größere Energiemengen als bei der Kernspaltung freigesetzt werden. Die Fusion von einem Gramm Deuterium und Tritium zu Helium setzt die gleiche Energie wie die Verbrennung von über Tonnen Kohlenstoff frei.