Einführung
Eine sehr wichtige physikalische Größe ist der
Impuls. Den klassischen Impuls kann man sogar auf wichtige Vorgänge der
Quantenmechanik übertragen. Durch Berechnung des Impuls kann man beim Billard spielen voraussagen, wo eine Kugel landen wird.
Impuls
Der
Impuls 
ist ein Vektor. Das heißt, der Impuls hat eine
Richtung und einen
Betrag. Den Impuls eins Körpers bestimmt man, indem man die Masse

des Körpers mit seiner Geschwindigkeit

multipliziert:
Die Einheit des Impuls ergibt sich aus dem Produkt der Einheiten von Masse und Geschwindigkeit.
Drehimpuls
Der
Drehimpuls 
beschreibt den Impuls eines Körpers, der sich in einer
Kreisbahn um einen Punkt bewegt. Den Drehimpuls berechnet man aus dem Produkt aus dem Impuls

und dem Radius der Kreisbahn

. Genau genommen bildet er sich aus dem
Kreuzprodukt des Ortes

und dem Vektor

.
Quanten- mechanischer Impuls
Auch in der Quantenmechanik kann man Impulse berechnen.
Beispiel Photon
Ein Photon, also ein Lichtquant, bewegt sich mit Lichtgeschwindigkeit

. Der Betrag des Impulses des Photons ist demnach:

. Die Energie eines Photons berechnet man aus dem Produkt des Planckschen Wirkungsquantum

und der Frequenz

des Photons:

. Zudem kennst du die Einsteinsche Formel zur Äquivalenz von Masse und Energie

. Jetzt kannst du den Impuls eines Photons bestimmen:
Erhaltungsgröße
In einem geschlossenen System ist der Impuls erhalten. Das heißt, dass sich der Gesamtimpuls des Systems nicht ändert. Der Impuls eines einzelnen Körpers kann sich ändern. Der Impuls wird dann allerdings auf einen oder mehrere andere Körper übertragen. Auch der Drehimpuls ist erhalten, wenn keine Kraft von außen wirkt.
Beispiel Sitzkarussell
Die Erhaltung des Drehimpulses kannst du auf einem Sitzkarussell auf einem Spielplatz ausprobieren. Drehst du dich mit einer gleichmäßigen Geschwindigkeit und verlagerst dein Gewicht nach außen, so wirst du langsamer. Bewegst du dich in Richtung der Drehachse, dreht sich das Karussell schneller. Mit einem Blick auf die Formel für den Drehimpuls, wird dir klar warum. Es reicht dafür aus die Beträge zu betrachten. Der Drehimpuls ist erhalten:

Vergrößerst du den Radius

, muss die Geschwindigkeit

oder die Masse

kleiner werden, damit das Produkt konstant bleibt. Deine Masse ändert sich während der Fahrt nicht, daher muss deine Geschwindigkeit verringert werden.
 [Abb. 1]: Drehimpulserhaltung am Beispiel Karussell
[Abb. 1]: Drehimpulserhaltung am Beispiel Karussell
Kraftstoß
Veränderen sich die Impulse zweier Körper, weil sie sich stoßen, so wirkt immer eine Kraft zwischen diesen Körpern. Leitest du den Impuls nach der Zeit ab, so erhältst du die Kraft, die zwischen den Körpern wirkt.
Je schneller sich ein Impuls ändert, desto größer ist die Kraft, die wirkt.
Beispiel Autounfall
Bei einem Autounfall ändert sich der Impuls

innerhalb einer sehr kurzer Zeit

. Die Kraft, die auf den Körper wirkt, ist deshalb sehr groß:

.
Durch die Knautschzone des Autos wird der Aufprall verlangsamt, sodass der Zeitraum

größer wird. Die Impulsänderung

bleibt allerdings gleich. Dadurch wird die wirkendede Kraft kleiner:

.
Nehmen wir an, dass du einen Chrashtest-Dummy mit einer Masse von

hast, der im Auto mit

fährt. Einmal lässt du das Auto gegen eine harte Betonwand fahren. Dann wiederholst du den Test, lässt das Auto allerdings gegen eine nachgebende Spezialwand fahren. Die Impulse werden während der Tests aufgezeichnet und sind im nachfolgenden Diagramm dargegstellt.
Du kannst jetzt die wirkende Kraft berechnen:
Bei der schnellen Impulsänderung ist die Kraft

deutlich höher als bei dem langsamen Chrash

gegen die Spezialwand.
Genauso verringert ein Airbag die Kraft, die auf den Kopf bei einem Chrash wirkt, da die Impulsänderung verlangsamt wird.
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
 [Abb. 1]: Drehimpulserhaltung am Beispiel Karussell
[Abb. 1]: Drehimpulserhaltung am Beispiel Karussell
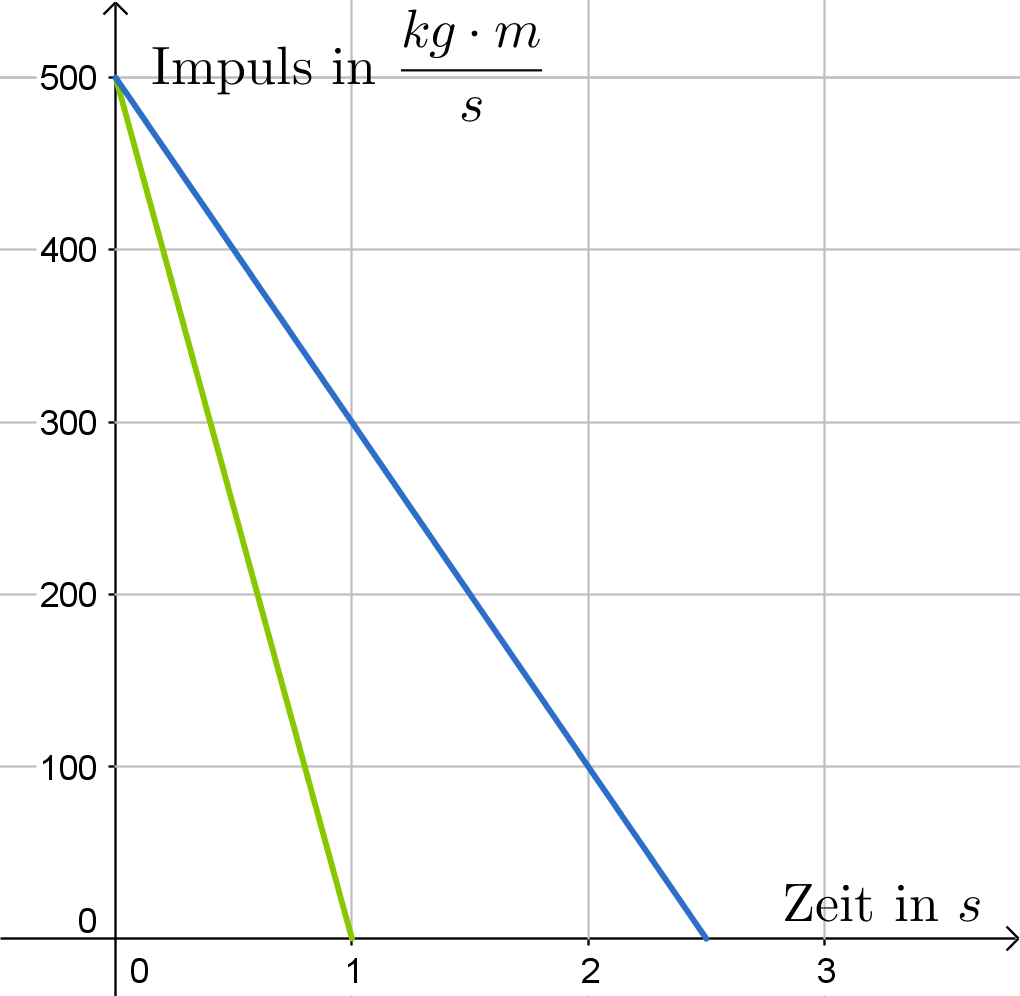 [Abb. 2]: Aufzeichnung des Impulses
[Abb. 2]: Aufzeichnung des Impulses