Dynamik

Einführung

Die Dynamik beschreibt die Bewegung von Körpern unter dem Einfluss von Kräften.
Der Begriff stammt von dem griechischen Wort dynamis (Kraft) ab.
Sie ist, ebenso wie die Kinematik, ein Teilgebiet der Mechanik. Die Kinematik beschreibt die Bewegung von Punkten und Körpern im Raum. Damit sich ein Körper bewegen kann, muss eine äußere Ursache vorhanden sein, also eine Kraft, die auf den Körper wirkt. Diese Kräfte können bewegliche Körper beschleunigen und verlangsamen oder unbewegliche Körper verformen. Mit diesen Kräften befasst sich die Dynamik.

Größen und ihre Einheiten

Zwei wichtige Größen in der Dynamik sind die Kraft und die Masse.

Abb. 1: Nicht nur die Kraft sondern
auch der Angriffspunkt ist beim Bowling wichtig

Kraft

Die Kraft $\boldsymbol{F}$ beschreibt eine äußere Einwirkung auf einen Körper.
Wenn zum Beispiel eine Bowlingkugel auf Pins trifft, wirkt zwischen den beiden Körpern eine Kraft: Die Kugel stößt die Kegel um und wird durch den Widerstand der Kegel geringfügig langsamer.
Die Einheit der Kraft ist Newton $\text{[N]}$ .

Es gilt:

$1\,\text{N} = 1\,\frac{\text{kg}\cdot{\text{m}}}{\text{s}^2}$

Kräfte werden durch Kraftvektoren dargestellt. Diese sind abhängig von Richtung, Betrag und Angriffspunkt:

Die Richtung wird dargestellt durch den Pfeil
Der Betrag wird durch die Länge des Pfeils dargestellt
Der Angriffspunkt ist der Punkt in dem die Kraft angreift

Abb. 2: Wirkung von Kräften

Masse

Jeder Körper besitzt eine Masse. Wenn du dich beispielsweise morgens auf die Waage stellst, ermittelst du deine Masse. Die Masse eines Körpers ist ortsunabhängig, das heißt, du wiegst überall im Universum gleich viel. Ihre Maßeinheit ist Kilogramm [kg]. Es gilt:

$1\,\text{kg}=1.000\,\text{g}$

Superpositionsprinzip

Superposition ist die Überlagerung von gleichen physikalischen Größen, zum Beispiel von Kräften, Schwingungen oder Wellen.
Das Superpositionsprinzip in der Mechanik besagt, dass mehrere Kräfte, die am gleichen Angriffspunkt eines Körpers angreifen, die gleiche Bewegung verursachen wie ihre Summe, also die Resultierende $\overrightarrow{F_{res}}$ der Einzelkräfte $\overrightarrow{F_i}$ .

$\overrightarrow{F_{res}} = \displaystyle\sum\limits_{i=1}^{n} \overrightarrow{F_i}$

Hier ein kleines Beispiel:

Jonas zieht um. Um den bereits vollgepackten Umzugskarton auf den Tisch zu stellen, schiebt er ihn mit dem Fuß nach vorne. Dabei wirkt sein Fuß eine Kraft $\overrightarrow{F_1}$ auf den Karton aus.

Nun hebt er den Karton mit einer Kraft $\overrightarrow{F_2}$ nach oben und stellt ihn mit der Kraft $\overrightarrow{F_3}$ auf den Tisch.

Nach dem Superpositionsprinzip würde Jonas das gleiche Ziel erreichen indem er die Kiste mit einer Kraft $\overrightarrow{F_{res}}$ vom Startpunkt bis zum Tisch stetig anhebt und gleichzeitig nach vorne trägt.

Die Resultierende Kraft wäre hier: $\overrightarrow{F_{res}} = \overrightarrow{F_1} + \overrightarrow{F_2} + \overrightarrow{F_3}$

Rechenbeispiel:

Jonas hebt die Umzugskiste wie im vorherigen Beispiel gezeigt auf den Tisch. Wie groß ist der Betrag der resultierenden Kraft?

Gegeben sind die Kräfte: $\overrightarrow{F_1} = \begin{pmatrix}50\,\text{N}\\ 0 \end{pmatrix}$ , $\overrightarrow{F_2} = \begin{pmatrix}0 \\ 100\,\text{N}\end{pmatrix}$ und $\overrightarrow{F_3} = \begin{pmatrix}10\,\text{N}\\ 0\end{pmatrix}$

Lösung:

$\begin{array}{rl} \overrightarrow{F_{res}}&=\begin{pmatrix}50\,\text{N} + 0 + 10\,\text{N}\\ 0 + 100\,\text{N} + 0\end{pmatrix} \\ &=\begin{pmatrix}60\,\text{N}\\ 100\,\text{N}\end{pmatrix} \\ \end{array}$

Der Betrag von $\overrightarrow{F_{res}}$ ist dann:

$\begin{array}{rl} F_{res}&=\sqrt{(60\,\text{N})^2 + (100\,\text{N})^2} \\ &=\sqrt{13600\,\text{N}^2} \\ &\approx116,2\,\text{N} \\ \end{array}$

Newtonsche Axiome

Abb. 3: Sir Isaac Newton

Isaac Newton, ein englischer Physiker und Mathematiker (Geboren 1643 in Woolsthorpe, verstorben 1727 in London), veröffentlichte 1687 sein Hauptwerk Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie). Darin legte er mit den drei Newtonschen Axiomen den Grundstein zur klassischen Mechanik.
Ein Axiom ist ein Grundsatz der ohne Beweis vorausgesetzt wird. Zum Beispiel: „Wasser ist nass.“

Auf der Grundlage dieser drei Axiome kann jede Form der Bewegung beschrieben werden.

1. Newtonsches Axiom

Das 1. Newtonsche Axiom wird auch Trägheitsgesetz genannt.

Der Bewegungszustand eines Körpers ändert sich nicht, solange keine äußere Kraft auf ihn einwirkt.

Stell dir vor, ein Fußball liegt auf einer Wiese. Solange keine äußere Kraft, zum Beispiel dein Fuß, auf ihn einwirkt, wird er sich auch nicht bewegen. Das heißt, seine Geschwindigkeit behält den Wert $0\dfrac{\text{m}}{\text{s}}$ .

2. Newtonsches Axiom

Das 2. Newtonsche Axiom beschreibt den Zusammenhang zischen Kraft, Masse und Beschleunigung.
Die Kraft ist definiert als Produkt aus Masse und Beschleunigung.

$\vec{F} = m\cdot \vec{a}$

Nochmal zurück zu unserem Fußball: Wenn du den Ball trittst, wirkt eine Kraft, hier durch deinen Fuß, auf den Ball. Je nachdem wie fest du schießt, variiert die Beschleunigung. Das heißt, der Ball bewegt sich schneller oder langsamer.
Nimm nun anstelle des Fußballs einen Medizinball: Die Kraft, die du aufwenden musst, damit sich der Medizinball genauso schnell bewegt wie der Fußball, ist viel größer, da der Medizinball eine wesentlich größere Masse hat als der Fußball.

Beispielaufgabe:

Abb. 4: Der entscheide Elfmeter
- Sieg oder Niederlage? (hier zum Nachweis)

Im Champions League Finale 2012 kommt es zum Elfmeterschießen. Ein Profi-Fußballer schießt den Ball, der eine Masse $m = 0,45\,\text{kg}$ hat. Physikalisch bedeutet das, der Fußballer mit seinem Fuß beschleunigt den Ball, sodass er mit einer Endgeschwindigkeit von $100,8\,\frac{\text{km}}{\text{h}}$ ins Tor fliegt. Der Ballkontakt dauert dabei $0,05\;\text{s}$ .
Wie viel Kraft wenden Sie dazu auf?
Wie viel größer wäre die Kraft, die aufgewendet werden muss, um die gleiche Geschwindigkeit zu erzielen, wenn anstelle des Fußballs ein Medizinball mit der Masse $m = 1\,\text{kg}$ am Elfmeterpunkt liegt?

Lösung:

Gesucht ist die Kraft, mit der Fuß- und Medizinball getreten werden. Um diese zu ermitteln, nutzen wir das 2. Newtonsche Gesetz: $\boldsymbol{F = m \cdot a}$ . Die Masse ist bereits gegeben, es fehlt nur noch die Beschleunigung $a$ . Im PhysikLV Skript Kinematik hast du gelernt wie diese berechnet wird.
Dazu müssen wir zuerst die Einheiten anpassen:

$\begin{array}{rl} v&=100,8\,\frac{\text{km}}{\text{h}}\\ &=\frac{100,8}{3,6}\,\frac{\text{m}}{\text{s}}\\ &=28\,\frac{\text{m}}{\text{s}}\\ \end{array}$

Die Beschleunigung ist definiert als $\boldsymbol{a = \frac{\Delta v}{\Delta t}}$ . Dazu verwendest du die Dauer des Ballkontaktes von $0,05\;\text{s}$ .

$\begin{array}{rl} a&=\frac{v}{t}\\ &=\frac{28\,\frac{\text{m}}{\text{s}}}{0,05\,\text{s}}\\ &={560\,\frac{\text{m}}{\text{s}^2}}\\ \end{array}$

Jetzt nehmen wir wieder das 2. Newtonsche Axiom $\boldsymbol{F = m \cdot a}$ zur Hand.

$\begin{array}{rl} F&=m \cdot a\\ &=0,45\,\text{kg} \cdot 560\,\frac{\text{m}}{\text{s}^2}\\ &=252\,\frac{\text{kg} \cdot \text{m}}{\text{s}^2}\\ &=252\,\text{N}\\ \end{array}$

Also bringt der Fußballspieler beim Elfmeterschießen eine Kraft von $252\,\text{N}$ auf.
Der einzige Unterschied zwischen dem Fußball und dem Medizinball ist die Masse. Alle anderen Größen bleiben gleich. Daher müssen wir in der Formel nur die Masse ändern:

$\begin{array}{rl} F&=m \cdot a\\ &=1,0\,\text{kg} \cdot 560\,\frac{\text{m}}{\text{s}^2}\\ &=560\,\frac{\text{kg} \cdot \text{m}}{\text{s}^2}\\ &=560\,\text{N}\\ \end{array}$

Die Kraft, die gebraucht wird, um einen Medizinball ins Tor zu befördern, ist ungefähr doppelt so groß wie die Kraft, die wir bei einem Fußball aufbringen müssen.

3. Newtonsches Axiom

Das 3. Newtonsche Axiom wird auch Wechselwirkungsgesetz genannt und ist bekannt als:

„Actio = Reactio“

Kräfte treten immer paarweise auf. Jede Kraft besitzt eine Gegenkraft die genau entgegengesetzt wirkt. Wenn beide Kräfte gleich groß sind, befindet sich das System in Ruhe. Eine Bewegung entsteht, sobald die Kräfte einen unterschiedlichen Betrag haben.
Ein Beispiel dafür ist das Rudern:

Abb. 5: Ohne Newton wäre das Rudern sehr schwierig

Actio: Die Sportler tauchen die Ruderblätter ins Wasser ein und ziehen sie mit Kraft nach vorne.

Reactio: Über die Ruder wirkt das Wasser (das wir als Widerstand gegen die Bewegung bemerken) eine Kraft auf das Boot aus, das sich dadurch nach hinten bewegt, denn Ruderboote fahren nun mal rückwärts.

Gravitationsgesetz

Einer Legende nach soll Isaac Newton eines Tages, als er unter einem Baum ruhte, ein Apfel auf den Kopf gefallen sein. Das brachte ihn auf eine Idee: Es muss eine Kraft geben, die den Apfel in Richtung Boden beschleunigt, die Gravitationskraft.
Die Gravitation die sich aus dem lateinischen Wort für die Schwere, gravitas, herleitet, wird auch Schwerkraft oder Massenanziehung genannt. Sie wirkt zwischen verschiedenen Massen. Diese Kraft sorgt unter anderem dafür, dass Planeten auf ihren Umlaufbahnen bleiben. Planeten bewegen sich. Durch die Gravitation, also die Anziehungskraft, der Sonne, kreisen sie um diese herum. Die Fliehkraft, die durch die Kreisbewegung der Himmelskörper um die Sonne zustande kommt, zieht, zum Beispiel die Erde, auf ihrer Umlaufbahn nach außen und sorgt dafür, dass sie nicht in die Sonne fliegt.
Newtons Erkenntnis, die zum Gravitationsgesetz führte, veröffentlichte er ebenfalls in seinem Werk Philosophiae Naturalis Principia Mathematica.

3. Keplersches Gesetz

Abb. 6: Johannes Keppler

Zur Herleitung des Gravitationsgesetzes von Newton brauchen wir das 3. Keplersche Gesetz.
Johannes Kepler, ein deutscher Mathematiker, Astronom und Naturphilosoph (Geboren 1571 in Weil der Stadt, verstorben 1630 in Regensburg), formulierte die drei Keplerschen Gesetze. Diese beschreiben die Planetenbewegungen.
Das 3. Keplersche Gesetz besagt, dass sich die Quadrate der Umlaufzeiten von zwei Planeten genauso zueinander verhalten, wie die dritten Potenzen der großen Halbachsen dieser Planeten.

$\boldsymbol{\frac{(T_1)^2}{(T_2)^2}=\frac{(a_{H1})^3}{(a_{H2})^3}}$

$T$ Umlaufzeit des Planeten
$a_H$ große Halbachse des Planeten

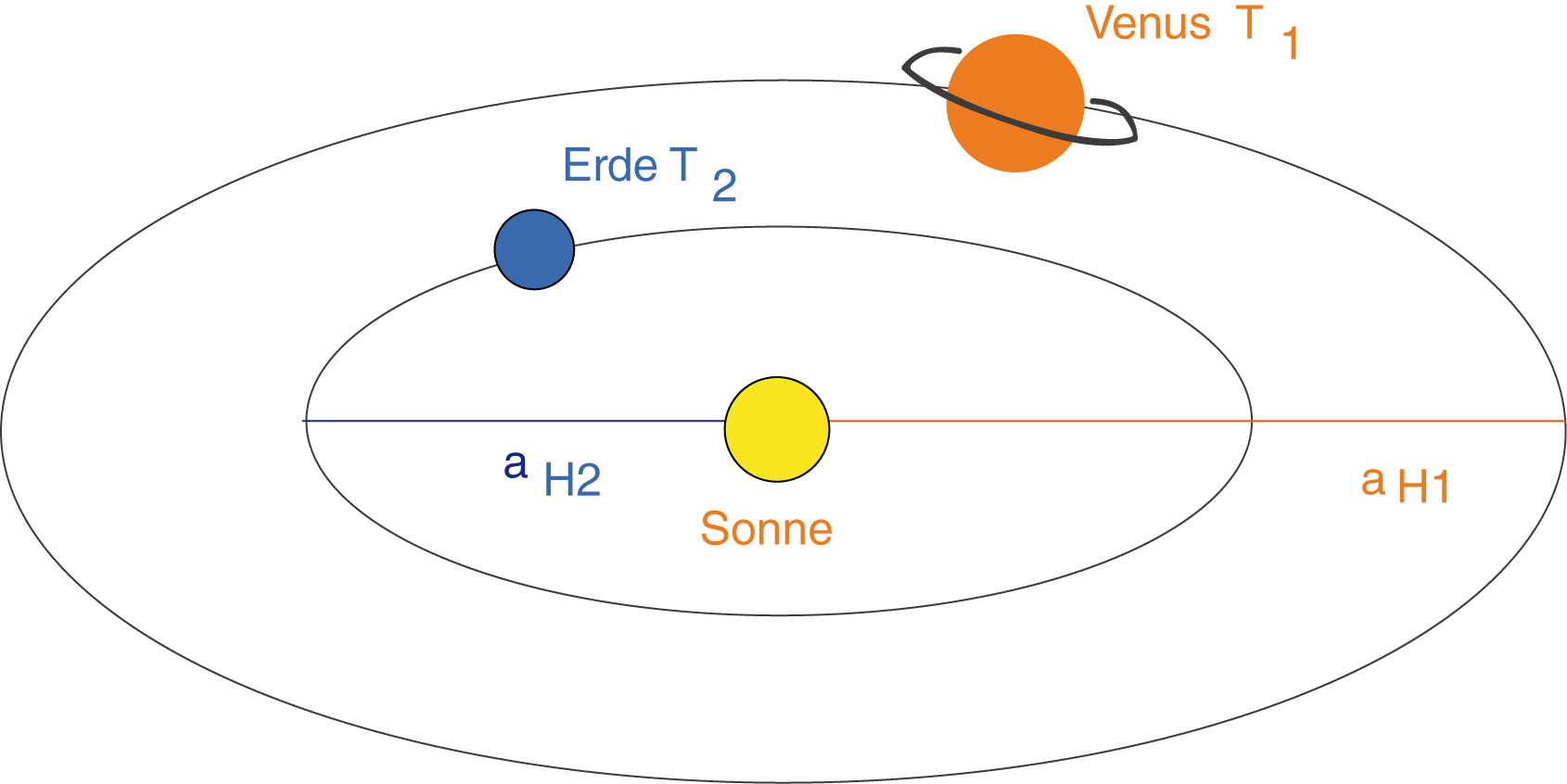Abb. 7: Die elliptische Bahn der Planeten

Planeten bewegen sich auf Ellipsenbahnen. Ellipsen haben zwei Durchmesser. Als große Halbachse wird die Hälfte des größeren Durchmessers bezeichnet. Die großen Halbachsen von Erde $a_{H2}$ und Venus $a_{H1}$ siehst du im Bild eingezeichnet. Das Verhältnis des Quadrates der Umlaufzeit zur dritten Potenz der großen Halbachse ist für jeden Planeten konstant:

$\boldsymbol{\frac{T^2}{a_H^3}= const.}$

Das bedeutet, desto weiter ein Planet von der Sonne entfernt ist, desto länger braucht er, um sie einmal zu umrunden.

Herleitung des Gravitationsgesetzes

Betrachtet man die Umlaufbahn des Mondes um die Erde, kann man vereinfacht annehmen, dass sich der Mond auf einer Kreisbahn bewegt.
Die Geschwindigkeit ist $\boldsymbol{v = \frac{\Delta s}{\Delta t}}$ . Der Kreisumfang berechnet sich mit der Formel $\boldsymbol{u = 2 \pi \cdot r}$ . Das ist der Weg, den der Mond zurücklegt, um die Erde einmal zu umkreisen. Die Zeit, die er dafür benötigt, haben wir oben schon als Umlaufzeit $T$ kennengelernt.
Also ist $\boldsymbol{v = \frac{2 \pi \cdot r}{T}}$ .
Im PhysikLV-Skript Rotation, wurde die Beschleunigung auf einer Kreisbahn definiert als $\boldsymbol{a = \frac{v^2}{r}}$ .
Im vorherigen Kapitel haben wir das zweite Newtonsche Gesetz kennengelernt: $\boldsymbol{F = m \cdot a}$ .
Jetzt können wir die ganzen Formeln zusammensetzen:

$\begin{array}{rl} F&=m \cdot a \\ &=m \cdot \frac{v^2}{r} \\ &=m \cdot \frac{(\frac{2 \pi \cdot r}{T})^2}{r} \\ &=m \cdot \frac{4 \pi^2 \cdot r^2}{T^2} \cdot \frac{1}{r} \\ &=m \cdot \frac{4 \pi^2 \cdot r}{T^2} \\ \end{array}$

Das 3. Keplersche Gesetz kann auch vereinfacht für eine Kreisbahn betrachtet werden. In diesem Fall gilt: $a_H \stackrel{!}{=} r$
Damit gilt:

$\begin{array}{cl} &const. = \frac{T^2}{r^3} \\ \Leftrightarrow &T^2 = const. \cdot r^3 \\ \end{array}$

Das können wir wiederum in $F$ einsetzen:

$\begin{array}{rl} F&=m \cdot a \\ &=m \cdot \frac{4 \pi^2 \cdot r}{const. \cdot r^3} \\ &=\frac{4 \pi^2}{const.} \cdot \frac{m}{r^2} \\ \end{array}$

Der Teil $\frac{4 \pi^2}{const.}$ besteht nur aus Konstanten, also können wir aus dem Rest der Formel folgendes schließen:

$F \sim m$
$F \sim \frac{1}{r^2}$

Das 3. Newtonsche Gesetz besagt, dass jede Kraft $F$ eine gleich große Gegenkraft besitzt. Da $F = m \cdot a$ gilt und im Falle einer Kreisbewegung $a$ konstant ist (also zeitunabhängig), gilt hier $F = m_1 \cdot a$ und $F = m_2 \cdot a$ . Daraus können wir folgern, dass $F \sim m_1$ und $F \sim m_2$ .
Wenn dies der Fall ist, gilt ebenfalls $F \sim m_1 \cdot m_2$ .

$\Rightarrow F \sim \frac{m_1 \cdot m_2}{r^2}$

Um nun das Proportionalitätszeichen durch ein Gleichheitszeichen ersetzen zu können, benötigen wir einen Proportionalitätsfaktor, der hier Gravitationskonstante genannt wird. Damit kommen wir zum Gravitationsgesetz:

$\boldsymbol{F = G \cdot \frac{m_1 \cdot m_2}{r^2}}$

Bildnachweise [nach oben]

[1]

Public Domain

[2]

[3]

Public Domain

[4]

wikimedia.org - Markus Unger CC-BY-SA

[5]

Public Domain

[6]

Public Domain

[7]