Interferenz und Beugung

Einführung

Abb. 1: Nordseebrandung.

Egal ob im Alltag oder im Urlaub, Wellen begegnen uns immer wieder - in Form von Wasser, Licht, Schall, ... Eine einfache Welle besteht aus einem Maximum und einem Minimum. Bei der Meereswelle nennt man dieses Maxi- und Minimum Wellenberg und Wellental. Unter Wellenlänge $\lambda$ versteht man die Länge einer Schwingung, also den kürzesten Abstand zwischen zwei gleichen Zuständen wie dem Maxi- oder Minimum. Wie viele dieser Schwingungen pro Sekunde stattfinden, gibt man mit der Frequenz $\nu$ an.

Allgemeines

Häufig kommt es vor, dass sich Wellen überlagern. Dieses Phänomen nennt man Interferenz. Dabei können sich die Auslenkungen zweier Wellen entweder verstärken oder auch auslöschen.

Abb. 2: Konstruktive und destruktive Interferenz.

Überlagern sich zwei Schwingungen, so gilt für die Amplitude, also für die maximale Auslenkung:

$A_{ges}=A_1+A_2$

Trifft das Maximum von Welle $1)$ auf das Maximum von Welle $2)$ oder das Minimum von Welle $1)$ auf das Minimum von Welle $2)$ , dann verstärken sich die beiden Wellen und es ergibt sich die Maximalauslenkung. Man spricht von konstruktiver Interferenz. Sind zwei Wellen mit gleicher Amplitude zueinander so verschoben, dass das Maximum der Welle $1)$ und das Minimum der Welle $2)$ aufeinander treffen, dann löschen sich die beiden Wellen gegenseitig komplett aus und man spricht man von destruktiver Interferenz.

Die Verschiebung der Wellen zueinander nennt man Gangunterschied $\Delta{s}$ .

Abb. 3: Interferenz in der Wasserwanne.

Das Bild, das bei der Überlagerung entsteht, nennt man Interferenzmuster. An diesen Mustern erkennt man die Stellen von konstruktiver und destruktiver Interferenz sehr gut: Überlagern sich zum Beispiel Lichtwellen, so erscheinen die Maxima der entstehenden Welle hell. Die Stellen, an denen sich die Wellen auslöschen (hier findet destruktive Interferenz statt), erscheinen dagegen dunkler. Dieses Interferenzmuster verwendet man, um den Wellencharakter z. B. von Licht nachzuweisen.

Schwebung

Bisher hatten die beiden Wellen sowohl die gleiche Amplitude als auch die gleiche Frequenz.
Überlagern sich zwei Wellen mit unterschiedlichen Frequenzen, so entsteht eine neue Welle mit der Frequenz $\nu_{schnell}$ .
Haben die beiden Wellen nahe beieinander liegende Frequenzen kommt es zur so genannten Schwebung. Darunter versteht man das Phänomen, dass sich die Amplitude der neuen stehenden Welle mit der Frequenz $\nu_{Schwebung}$ verändert.

Abb. 4: Schwebung entsteht bei der Überlagerung von zwei Wellen mit unterschiedlicher Frequenz.

Diese Frequenz berechnest du mit folgender Formel:

$\nu_{Schwebung}=\nu_2-\nu_1$

Die Frequenz der neuen Welle berechnet man mit

$\nu_{schnell}=\dfrac{\nu_1+\nu_2}{2}$

Brechung

Allgemeines

Abb. 5: Strohhalm im Wasserglas.

Das physikalische Phänomen der Brechung tritt am Phasenübergang zwischen verschiedenen Medien auf, in denen eine Welle unterschiedliche Phasengeschwindigkeiten besitzt, z. B. am Übergang zwischen Luft und Wasser. Dabei gehen zwei Wellen von der Grenzfläche aus: Die an der Grenzfläche reflektierte Welle und die gebrochene Welle, die sich im anderen Medium mit veränderter Geschwindigkeit bewegt.

Mit diesem Prinzip lässt sich auch die Entstehung von Regenbögen erklären:

Abb. 6: Entstehung von Regenbögen.

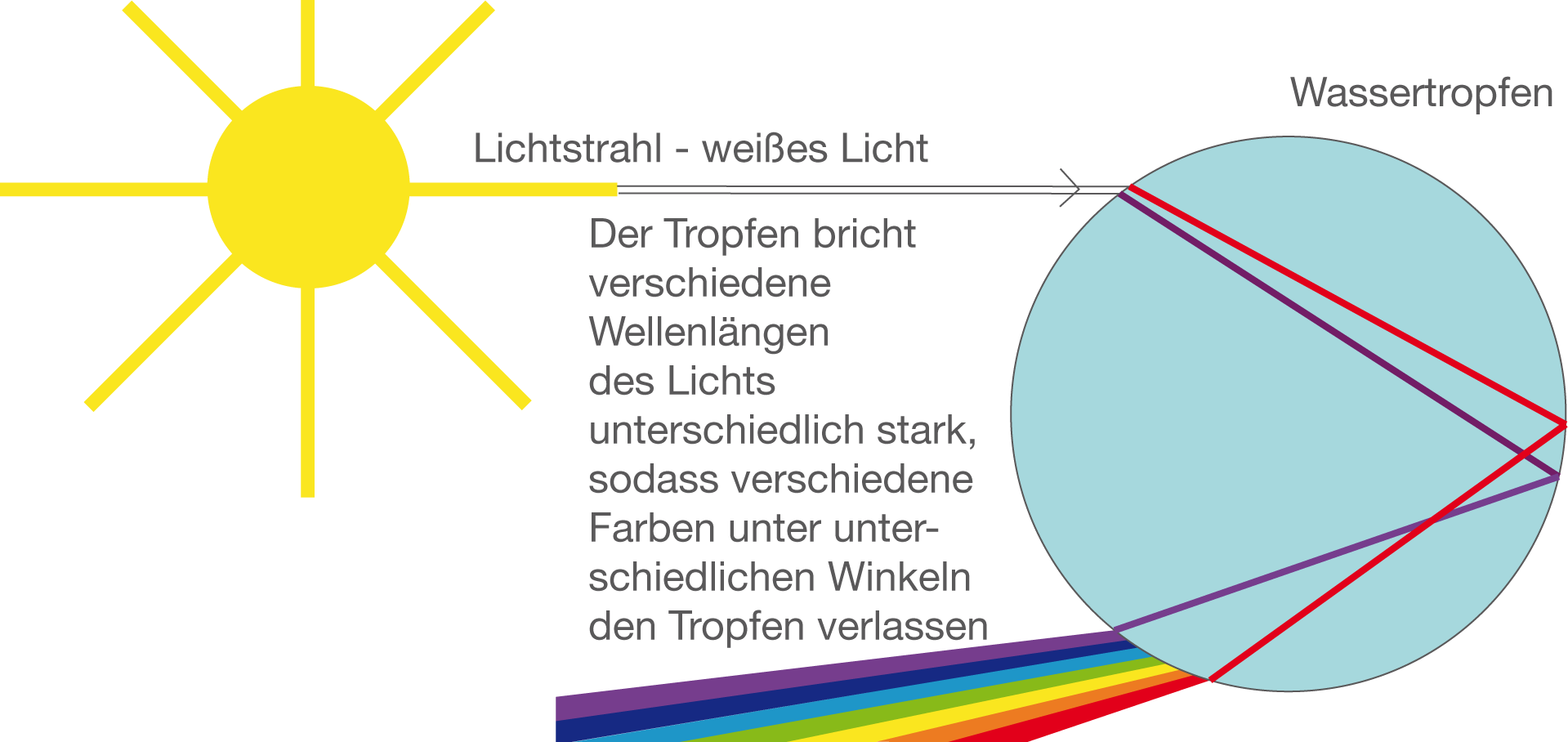
Sonnenstrahlen treffen auf die Oberfläche der Wassertropfen. Die verschiedenen Farben, die in weißem Licht enthalten sind, werden an der Oberfläche unter verschiedenen Winkeln reflektiert und treten unter unterschiedlichen Winkeln aus dem Tropfen aus.

Das Huygens‘sche Prinzip

Das Huygens‘sche Prinzip besagt, dass jeder Punkt einer Wellenfront sich als Ausgangspunkt einer Elementarwelle auffassen lässt. Desweiteren werden die Wellenfronten von Einhüllenden der Elementarwellen gebildet.
Außerdem gelangen Wellen in den Schattenraum eines Hindernisses (sie werden gebeugt), weil von jedem Randpunkt des Hindernisses Elementarwellen ausgehen. Darauf werden wir im Abschnitt Beugung wieder zurückkommen.

Schauen wir uns nun das Beispiel einer Wasserwelle an, die schräg von tiefem Wasser in flaches Wasser trifft. Dabei ändert sich die Ausbreitungsgeschwindigkeit.

Abb. 7: Wellen-Brechung; hier zum Bildnachweis.

Wenn die Wellenfront die Grenzlinie mit Geschwindigkeit $c_1$ erreicht, werden nacheinander viele Elementarwellen ausgelöst. Da die Welle schräg verläuft, hat sich die erste Elementarwelle bereits mit dem Radius $c_2 \cdot \Delta t$ im flachen Wasser ausgebreitet, wenn die letzte Elemtarwelle die Grenzlinie erreicht. $\Delta t$ ist dabei der zeitliche Abstand zwischen dem Eintreffen der beiden Elementarwellen an der Grenzlinie, $c_1$ die Ausbreitungsgeschwindigkeit im tiefen, $c_2$ die im flachen Wasser.

Es gilt dabei:

$c_2 \cdot \Delta t < c_1 \cdot \Delta t$

Die neue Wellenfront im flachen Wasser ist Einhüllende der während des Zeitraums $\Delta t$ zwischen erster und letzter Elementarwelle ausgegangenen Kreiswellen. Da die Ausbreitungsgeschwindigkeit im flachen Wasser langsamer als im tiefen ist ( $c_2 < c_1$ ), ändern die Wellenstrahlen ihre Richtung am Übergang, es tritt Brechung zum Lot hin ein. Die Tangente der ersten Kreiswelle, die die Grenzlinie am Übergang der letzten Elemtarwelle schneidet, beschreibt nach der Brechung die Wellenfront.

Das Brechungsgesetz

Das Brechungsgesetz besagt, dass bei der Brechung das Verhältnis von Sinus des Einfallswinkels zum Sinus des Ausfallswinkels gleich dem Vehältnis der Ausbreitungsgeschwindigkeiten vom ersten zum zweiten Medium ist. Formal sieht das wie folgt aus:

$\dfrac{sin(\alpha)}{sin(\beta)} = \dfrac{c_1}{c_2} = n$

Dabei ist $\alpha$ der Einfallswinkel und $\beta$ der Ausfallswinkel, beide gegen das Lot gemessen. n wird Brechungszahl gennant, $c_1$ und $c_2$ sind wie oben die Ausbreitungsgeschwindigkeiten in den verschiedenen Medien.

Beugung

Allgemeines

Unter Beugung versteht man die Ablenkung einer Welle an einem Hindernis, also wenn die Welle in den geometrischen Schattenraum hinter Hindernissen oder Öffnungen eindringt. Hierbei ist das Verhältnis der Größe des beugenden Elements (z. B. des Einzelspalts, siehe unten) zur Wellenlänge entscheidend. Ist die Wellenlänge von gleicher Größenordnung oder auch größer, tritt das Phänomen der Beugung besonders stark auf.

Beugung am Einzelspalt

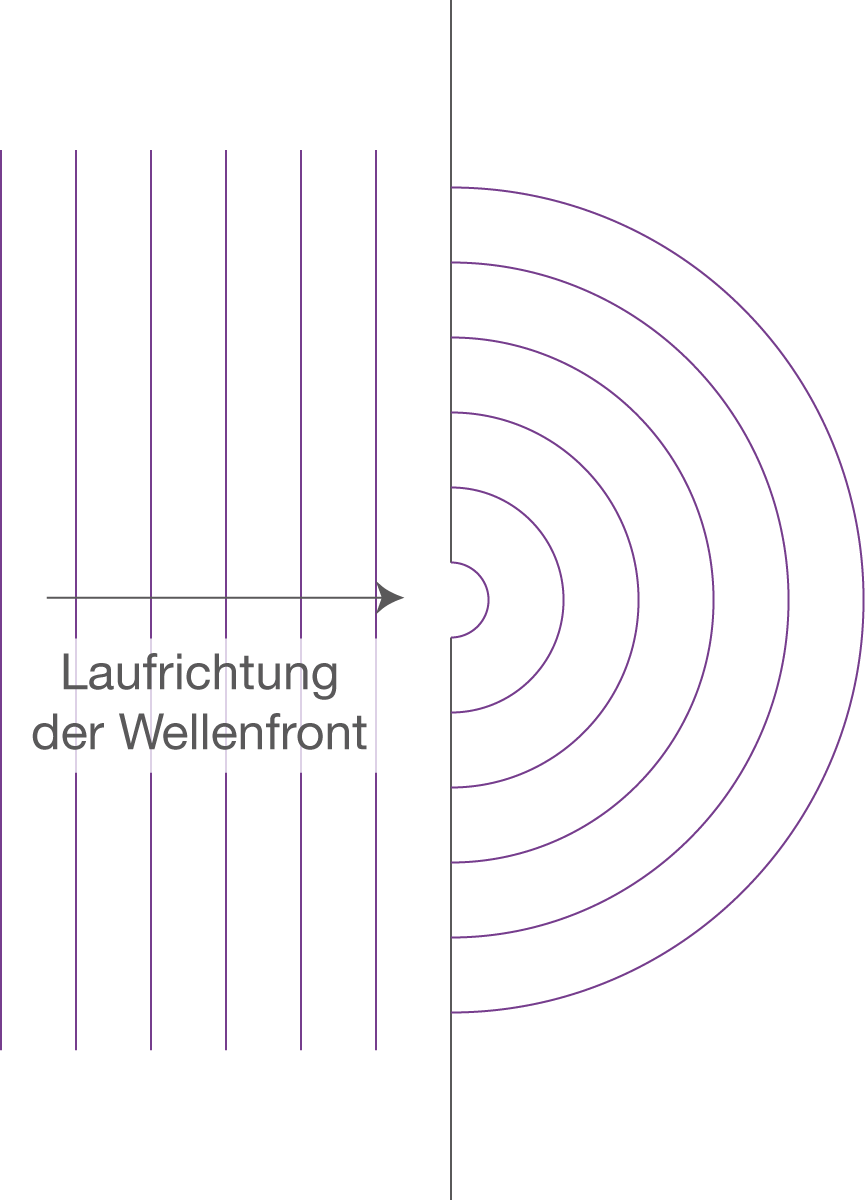
Abb. 8: Kugelförmige Elementarwelle.

Durch Beugung von Wellen an einem Spalt entstehen neue Wellen nach dem Huygens-Prinzip.
Wir benötigen nun, dass jeder Punkt an einer Wellenfront Ausgangspunkt einer neuen Elementarwelle ist:
Wie du in der nebenstehenden Abbildung erkennen kannst, trifft eine Wellenfront (links) auf eine Wand, in der sich ein einzelner Spalt befindet. Bis auf einen Punkt wird die komplette Front an der Mauer reflektiert. Nur der eine Punkt auf Höhe des Spalts kann weiterlaufen und erzeugt auf der anderen Seite eine neue kreisförmige Welle.

Beugung am Doppelspalt

Abb. 9: Kugelförmige Elementarwellen interferieren.

Hat man anstelle des einen Spalts zwei Spalte, so entsteht an beiden jeweils eine kugelförmige Elementarwelle. Hinter der Wand kommt es zur Interferenz dieser beiden Wellen.

Interferenzmuster

Trifft das Licht nach Passieren des einen oder der beiden Spalte oder eines Gitters auf eine Fläche - der Abstand zwischen Spalt und Schirm/Detektor ist viel größer als der Abstand zwischen den Spalten -, kann man beobachten, dass die Intensität an manchen Stellen stärker ist als an anderen. Teilweise ist es sogar komplett dunkel. Anhand dieser Bilder kann man auf das Spaltmuster schließen:

Abb. 10: Einzelspalt.

Das breite Hauptmaximum ist in diesem Schaubild sehr auffällig. Die weiteren Maxima sind dagegen kaum zu erkennen, da die Intensität nach außen hin sehr schnell abnimmt. Das sind eindeutige Charakteristika eines Einzelspaltes, demnach wird das Schaubild diesem zugeschrieben.

Abb. 11: Doppelspalt.

In diesem Schaubild sind die Hauptmaxima alle nahezu gleich breit. Zwischen ihnen befinden sich keine Nebenmaxima. Darüber hinaus nimmt die Intensität nach außen hin zwar ab, aber nicht so schnell wie im obigen Schaubild. Infolgedessen wird mehr Licht durchgelassen, was auf die höhere Spaltanzahl zurückzuführen ist. Es folgt hiermit: Dieses Schaubild ist dem Doppelspalt zuzuordnen.

Abb. 12: Mehrfachspalt.

Zwischen den Hauptmaxima lassen sich Nebenmaxima erkennen. Diese treten auf, wenn Licht durch mehr als zwei Spalte tritt. Die Intensitäten der Hauptmaxima nehmen nach außen hin deutlich stärker ab als dies im letzten Schaubild der Fall ist. Dieses Schaubild gehört zum Mehrfachspalt.

Abb. 13: Gitter.

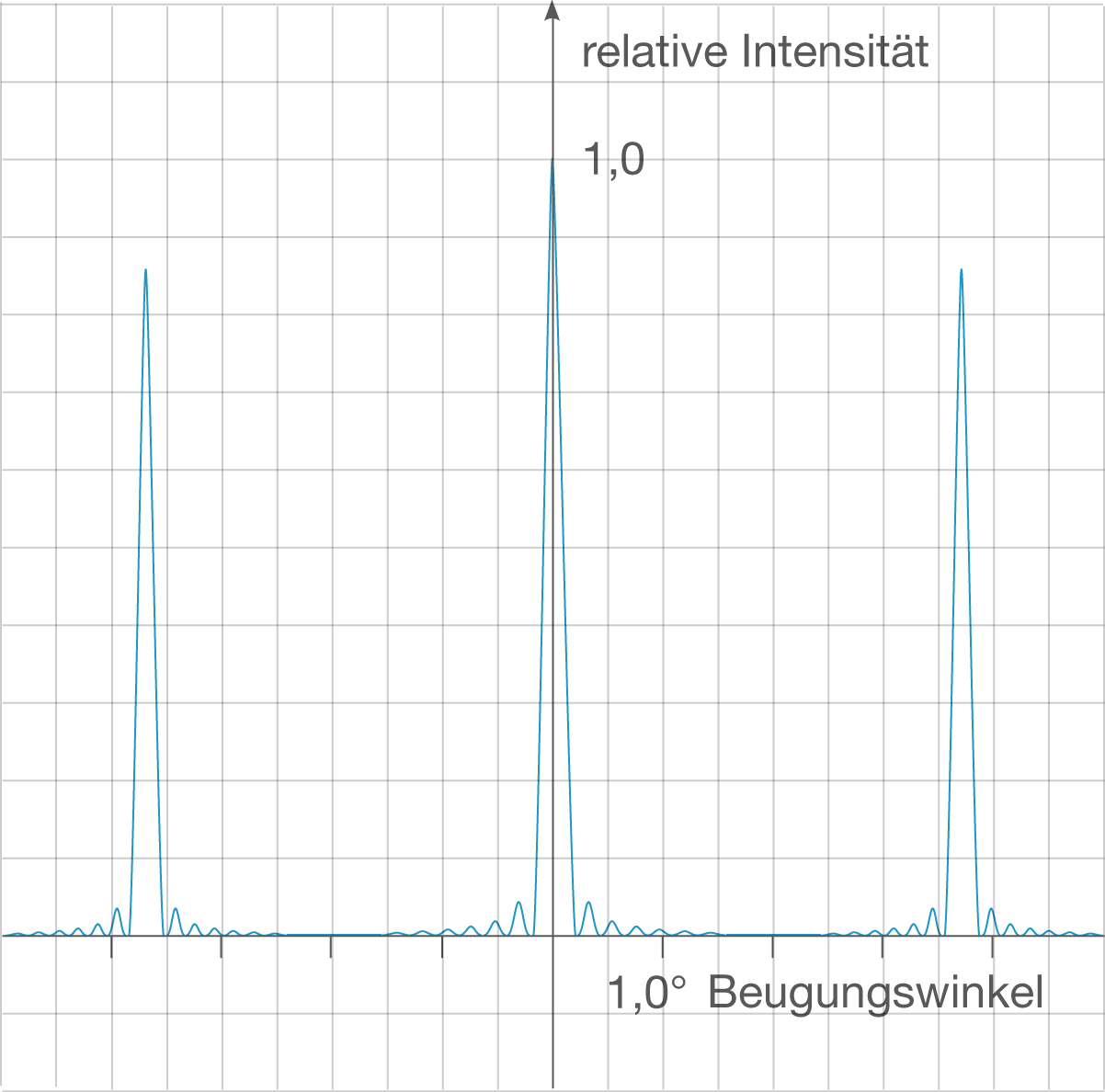
An diesem Schaubild ist auffällig, dass zwischen den Hauptmaxima eine große Anzahl Minima liegen und diese eine geringe Breite aufweisen. Dies hat zur Folge, dass sich ihre Lagen sehr genau ablesen lassen und sie schärfer werden. Darüber hinaus nimmt die Höhe und damit die Intensität dieser Hauptmaxima nach außen hin kaum ab. Auf Grund dieser Tatsachen ist dieses Schaubild einem Gitter zuzuordnen. Sehr viele enge Spalte, die in gleichen Abständen angeordnet sind, nennt man dabei Gitter.

Änderung der Lichtquelle

Erhöhst du etwa den Abstand zwischen dem Gitter und deiner Lichtquelle, so vergrößert sich der auf dem Gitter auftreffende Lichtkreis. Hierdurch werden mehr Spalte beleuchtet:

Abb. 14: Abstand beim Gitter.

Wichtig ist hierbei, dass du dir klar machst, dass wir dasselbe Gitter verwenden. Das bedeutet, dass lediglich die Anzahl der beleuchteten Spalte erhöht wird und eben nicht, dass die Spalte näher aneinander rücken. Der Spaltmittenabstand (auch Gitterkonstante $g$ genannt) verringert sich also nicht.

Da der Spaltmittenabstand nicht verändert wird, verbleiben die Maxima in derselben Lage. Der Abstand zwischen den Maxima wird also ebenfalls nicht verändert.

Hingegen treten aus mehr beleuchteten Spalten mehr Lichtwellen in den Raum hinter das Gitter ein, wo sie miteinander interferieren. Hierdurch nimmt zum einen die Helligkeit der Hauptmaxima zu, da mehr Strahlen mit dem Gangunterschied $\delta=k\cdot \lambda$ konstruktiv interferieren als bei kleinerer Spaltanzahl.

Das letzte Schaubild (Gitter) würde sich qualitativ folgendermaßen ändern:

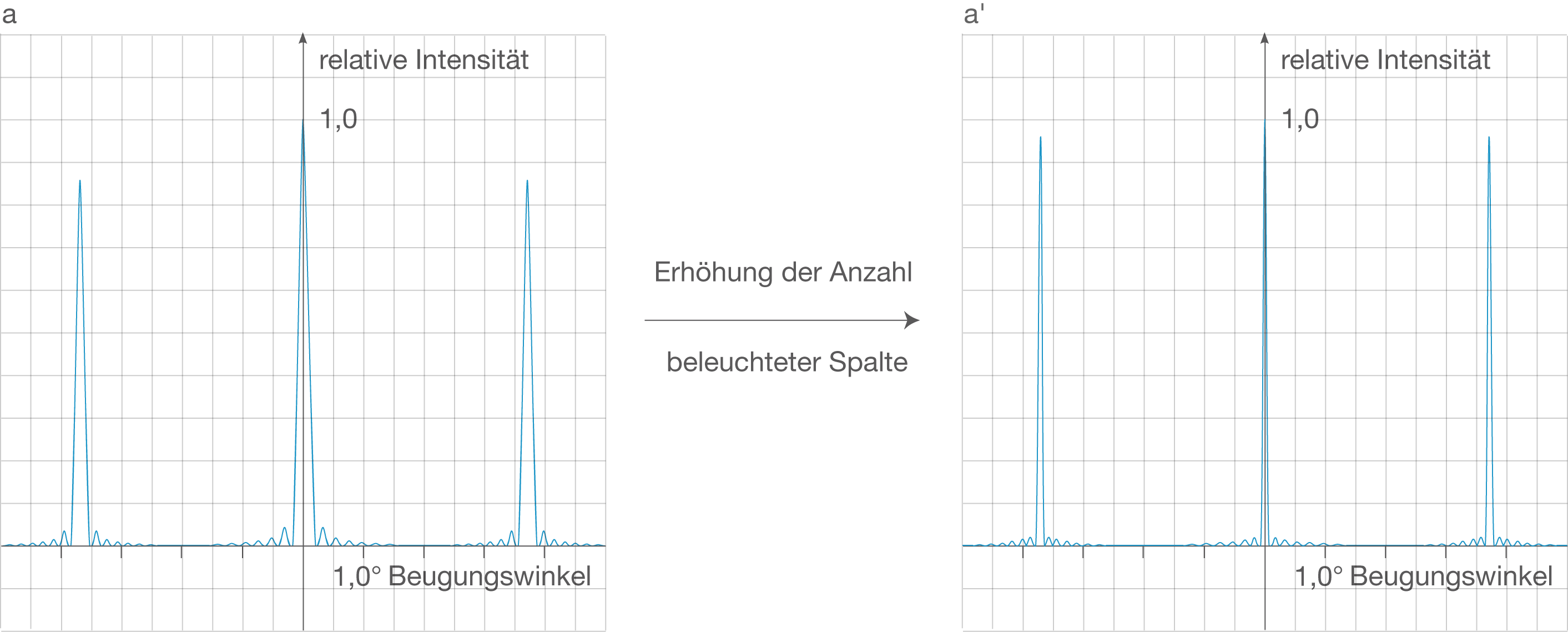
Abb. 15: Erhöhung beleuchteter Spalte.

Wenn die Anzahl der beleuchteten Spalte erhöht wird, verändert sich die registrierte Intensitätsverteilung des Gitters dahingehend, dass die Maxima heller und schärfer werden. Die Lage der Maxima ändert sich hingegen nicht.

Spaltbreite und -abstand berechnen

Abb. 16: Intensitätsverteilung eines Doppelspalts.

Für folgende Berechnungen verwenden wir das nebenstehende Schaubild (Intensitätsverteilung eines Doppelspalts).

Den Abstand der beiden Spalten berechnet sich über den Spaltmittenabstand $g$ mittels der Lage der Maxima.
Generell treten Maxima auf, wenn sich die Elementarwellen aus den Spaltmitten konstruktiv überlagern. Dies ist dann der Fall, wenn für den Gangunterschied $\delta$ der am Detektor zusammenlaufenden Wellen gilt:

$\delta=n \cdot \lambda$ , $\quad$ $n \in \mathbb{N}_0$

Der Faktor $n$ steht hierbei für die Ordnung des jeweiligen Maximums. Für das Maximum 2. Ordnung gilt daher: $n=2$ .

Dieser Gangunterschied lässt sich geometrisch wiederfinden, wenn man den Weg zweier Elementarwellen zu einem Punkt am Detektor als nahezu parallele Linien betrachtet:

Abb. 17: Gangunterschied.

Du kannst erkennen: Der Winkel, unter dem die Wellen auf dem Schirm eintreffen, lässt sich in einem rechtwinkligen Dreieck wiederfinden. Die Hypotenuse ist gleich dem gesuchten Spaltmittenabstand $g$ und eine der Katheten ist gerade der Gangunterschied $\delta$ .

Für den Winkel $\alpha$ , unter dem die Wellen auf dem Schirm auftreffen, gilt dann:

$\sin(\alpha)=\dfrac{\delta}{g}$

Nun wissen wir, dass für Maxima der Gangunterschied $\delta=n\cdot \lambda$ sein muss. Setze diese Bedingung in die gerade ermittelte Beziehung ein.
Es ergibt sich eine Gleichung, die alle Winkel $\alpha$ liefert, bei denen Maxima zu beobachten sind:

$\sin(\alpha)=\dfrac{n\cdot\lambda}{g}$

Dem obigen Diagramm kannst du nun die Lage eines Maximums entnehmen:

Das 1. Hauptmaximum, für das also $n=1$ gilt, tritt laut dem Diagramm bei einem Beugungswinkel von $\alpha_1=1,0^\circ$ auf.

Weiterhin fällt im Diagramm auf, dass das Maximum 3. Ordnung, welches unter dem Beugungswinkel $\alpha_3=3,0^\circ$ auftreten sollte, fehlt. Dies lässt sich damit erklären, dass dieses Doppelspaltmaximum mit einem Einzelspaltminimum eines der Spalte zusammenfällt.

Abb. 18.

Diese Tatsache ist darauf zurückzuführen, dass die einzelnen Spalte selbst jeweils als Zentren einer großen Zahl von Elementarwellen wirken. Sie interferieren im Bereich hinter dem Spalt. Die Wellen interferieren destruktiv, wenn der Gangunterschied von je zwei Wellen $n\cdot \frac{\lambda}{2}$ beträgt.

Stellen wir uns vor, dass genau 100 Elementarwellen dem Einzelspalt entspringen würden, so herrscht ein solcher Gangunterschied von $n \cdot \frac{\lambda}{2}$ gerade zwischen der 1. und der 51. Welle, der 2. und der 52. Welle usw.
Der Gangunterschied zwischen der 1. und der 100. Welle liegt damit exakt bei $n \cdot \lambda$ .

Abb. 19.

Die Skizze kann dir bei der Vorstellung behilflich sein:
In diesem Fall löschen sich die Wellen gegenseitig aus. Fehlt das Licht aus einem Spalt, kann in diesem Punkt folglich auch keine Doppelspaltinterferenz stattfinden. Das zu erwartende Maximum fehlt.

Mit der Tatsache, dass der Gangunterschied zwischen der 1. und der 100. Welle exakt bei $n \cdot \lambda$ liegt, folgt für die Breite $b$ der Einzelspalte die folgende Ablenkungsformel:

$\sin(\alpha)$	=	$\dfrac{\delta}{b}$
	=	$\dfrac{n \cdot \lambda}{b}$

Mit den hier vorgestellten Formel lassen sich durch Umformen der Abstand und die Breite der Spalten des Beugungsobjekts des Diagramms bestimmen.

Abstand der Spalte bestimmen

Laut Einleitung treten alle Maxima der Ordnung $n$ des Doppelspaltes unter folgenden Winkeln auf:

$\sin(\alpha)=\dfrac{n\cdot \lambda}{g}$

Das 1. Hauptmaximum, für das also $n=1$ gilt, tritt laut Diagramm bei einem Beugungswinkel von $\alpha_1=1,0^\circ$ auf. Nehmen wir für die Wellenlänge des Lichts, das auf die Spalte leuchtet, beispielsweise den Wert $\lambda=632\,\text{nm}$ an.

Setze diese Werte in die obige Ablenkungsformel ein und forme sie nach dem Spaltmittenabstand $g$ um. Dieser entspricht dem Abstand der beiden Spalte.

$$ \sin(\alpha) = \dfrac{n\cdot\lambda}{g} $$ $$ ... $$

Vollständigen Rechenweg
anzeigen

Breite der Spalte bestimmen

Wie bereits erwähnt, treten alle Einzelspaltminima der Ordnung $n$ unter folgenden Winkeln auf:

$\sin(\alpha)=\dfrac{n\cdot \lambda}{b}$

Das 1. Einzelspaltminimum, für das also $n=1$ gilt, trifft mit dem Doppelspaltmaximum 3. Ordnung zusammen. Laut Diagramm treten diese bei einem Beugungswinkel von $\alpha_3=3,0^\circ$ auf.

Setze diese Beobachtungen in die obige Ablenkungsformel ein und forme nach der Breite eines Einzelspalts $b$ um.

$$ sin(\alpha) = \dfrac{n\cdot\lambda}{b} $$ $$ ... $$

Vollständigen Rechenweg
anzeigen

Das Beugungsobjekt des Diagramms besitzt einen Spaltabstand von ungefähr $36\,\mu\text{m}$ und eine Spaltbreite von etwa $12\,\mu\text{m}$ .

Bildnachweise [nach oben]

[1]

Public Domain.

[2]

[3]

[4]

[5]

[6]

[7]

http://commons.wikimedia.org/wiki/File:Wellen-Brechung.png - Stefan-Xp, CC BY-SA.

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

$\sin(\alpha)$	$=$	$\dfrac{n\cdot\lambda}{g}$	$\mid\; \cdot{g}$ $\text{ und }$ $\sin(\alpha)$
$g$	$=$	$\dfrac{n\cdot\lambda}{\sin(\alpha)}$	$\mid\; n \text{ und } \alpha_1\,\text{einsetzen}$
	$=$	$\dfrac{1\cdot \lambda}{\sin(1^\circ)}$	$\mid\; \lambda\,\text{einsetzen}$
	$=$	$\dfrac{1\cdot 632\,\text{nm}}{\sin(1^\circ)}$
	$\approx$	$\dfrac{632 \cdot 10^{-9}\,\text{m}}{0.01745}$
	$\approx$	$3,6\cdot 10^{-5}\,\text{m}$
	$\approx$	$36\,\mu\text{m}$

$\sin(\alpha)$	$=$	$\dfrac{n\cdot\lambda}{b}$	$\mid\; \cdot{b}$ $\text{ und }$ $\sin(\alpha)$
$b$	$=$	$\dfrac{n\cdot\lambda}{\sin(\alpha)}$	$\mid\; n \text{ und } \alpha_3\,\text{einsetzen}$
	$=$	$\dfrac{1\cdot \lambda}{\sin(3^\circ)}$	$\mid\; \lambda\,\text{einsetzen}$
	$=$	$\dfrac{1\cdot 632\,\text{nm}}{\sin(3^\circ)}$
	$\approx$	$\dfrac{632 \cdot 10^{-9}\,\text{m}}{0.05234}$
	$\approx$	$1,2\cdot 10^{-5}\,\text{m}$
	$\approx$	$12\,\mu\text{m}$