Reelle Zahlen

Du kennst bereits

die natürlichen Zahlen $\mathbb{N}$ $= \{1, 2, 3, 4, ... \},$

die ganzen Zahlen $\mathbb{Z} = \{...,$ $-2, -1, 0, 1, 2, ... \}$ und
die rationalen Zahlen

$\mathbb{Q} = \left\{ \frac{p}{q} ~ \big \vert ~ p \in \mathbb{Z}, ~ q \in \mathbb{N} \right\}$

Vollständige Lösung anzeigen

$\mathbb{Q} = \left\{ \frac{p}{q} ~ \big \vert ~ p \in \mathbb{Z}, ~ q \in \mathbb{N} \right\} = \left\{ ..., \frac{-1}{3}, \frac{-2}{1}, \frac{-1}{2}, \frac{-1}{1}, 0, \frac{1}{1}, \frac{1}{2}, \frac{2}{1}, \frac{1}{3},... \right\}.$

Die natürlichen Zahlen sind dabei eine Teilmenge der ganzen Zahlen und die ganzen Zahlen sind eine Teilmenge der rationalen Zahlen, d.h. $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}.$

Nun gibt es Zahlen wie $\sqrt{3}, -\sqrt{5}, \pi$ oder $\mathrm e$ die keine rationalen Zahlen - somit auch keine ganzen oder natürlichen Zahlen - sind. Die Vereinigung dieser Zahlen und der rationalen Zahlen $\mathbb{Q}$ wird als reelle Zahlen $\mathbb{R}$ bezeichnet. Also ist jede Zahl, die du bist jetzt kennst, reell.

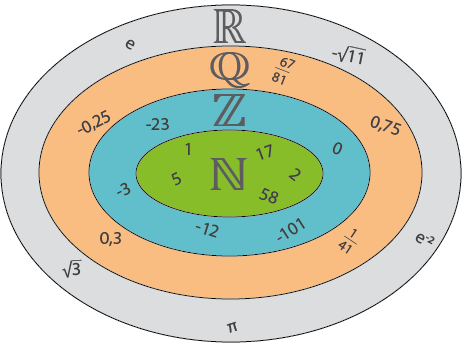Beispiele

$-8$ ist eine ganze Zahl, somit auch automatisch eine rationale und reelle, aber keine natürliche Zahl.

$5$ ist eine natürliche Zahl, somit auch automatisch eine ganze, rationale und reelle Zahl.

$\sqrt{2}$ ist eine reelle Zahl, aber weder rational noch ganz oder natürlich.