Winkelhalbierende
Die Winkelhalbierende  teilt einen Winkel
teilt einen Winkel  in der Mitte.
Die Winkelhalbierende
in der Mitte.
Die Winkelhalbierende  ist gleichzeitig eine Ortslinie, da alle Punkte, die denselben Abstand zu den beiden Schenkeln haben, auf ihr liegen.
ist gleichzeitig eine Ortslinie, da alle Punkte, die denselben Abstand zu den beiden Schenkeln haben, auf ihr liegen.

Konstruktion Winkelhalbierende
- Kreis um S
- A und B markieren
- Kreise um A und B
- Schnittpunkte beider Kreise
- Gerade durch Schnittpunkte ist

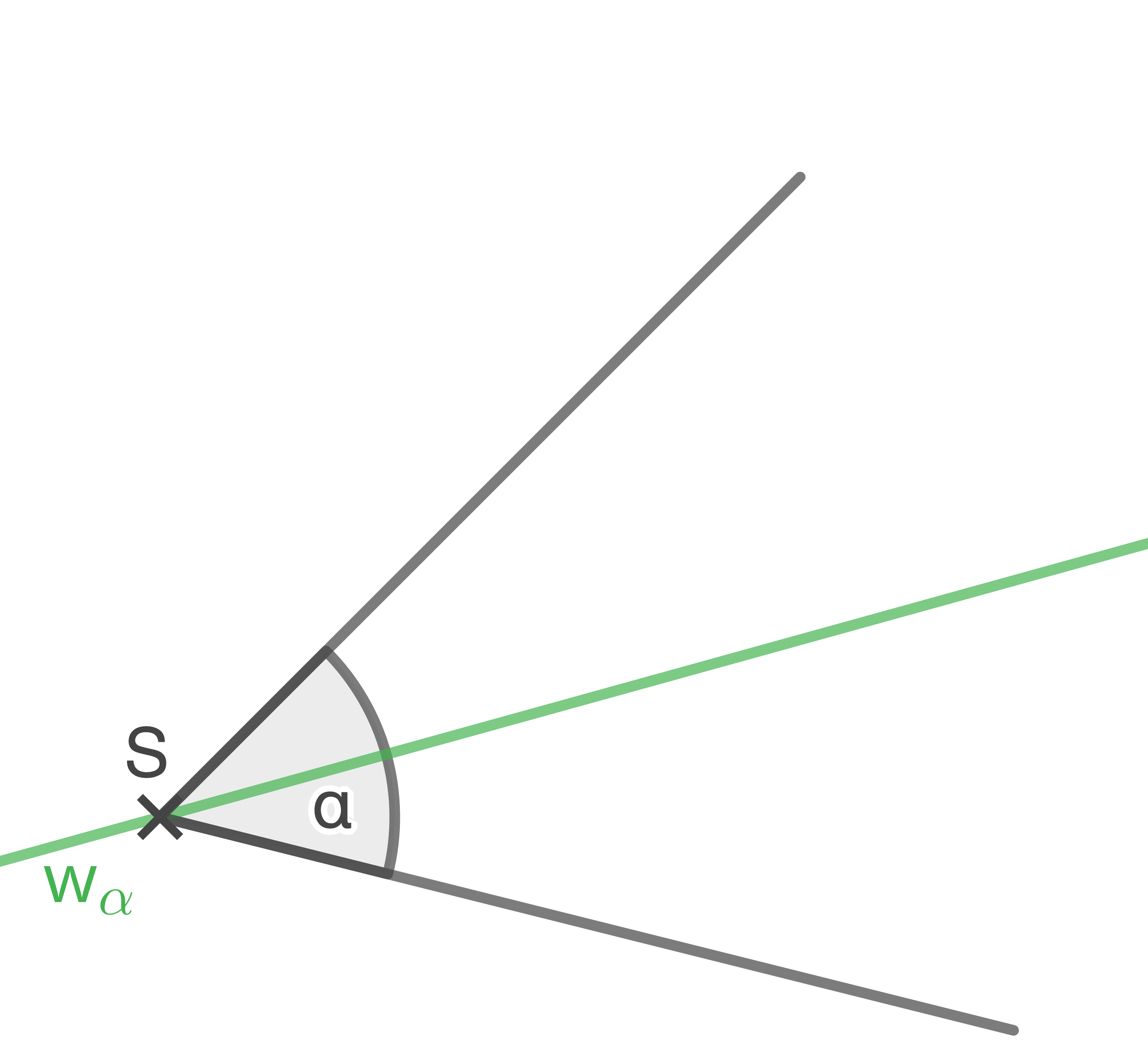
Eine Gerade, die einen Winkel  in der Mitte teilt, heißt Winkelhalbierende
in der Mitte teilt, heißt Winkelhalbierende 
Konstruktion der Winkelhalbierenden mit Zirkel und Lineal
- Zeichne einen Kreis um den Schnittpunkt S der Schenkel.
- Markiere die Schnittpunkte A und B des Kreises mit den Schenkeln.
- Konstruiere zwei Kreise mit jeweils demselben Radius um die Punkte A und B.
- Markiere die Schnittpunkte der beiden Kreise um A und B. Die Schnittpunkte dieser beiden Kreise liegen auf der Winkelhalbierenden.
- Konstruiere die Winkelhalbierende
, indem du eine Gerade durch die Schnittpunkte der beiden Kreise und den Punkt S zeichnest.
Ortslinie Winkelhalbierende

Alle Punkte, die den gleichen Abstand zu beiden Schenkeln haben, liegen auf der Winkelhalbierenden  Diese nennt man auch Ortslinie dieser Punkte.
Diese nennt man auch Ortslinie dieser Punkte.