Einführung in lineare Funktionen
Eine Funktion ordnet jedem  -Wert genau einen
-Wert genau einen  -Wert, auch Funktionswert genannt, zu. Eine lineare Funktion ist eine Funktion, deren Funktionsgleichung die folgende Form hat:
-Wert, auch Funktionswert genannt, zu. Eine lineare Funktion ist eine Funktion, deren Funktionsgleichung die folgende Form hat:
 von
von  nennt man Steigung oder Steigungswert. Der Wert
nennt man Steigung oder Steigungswert. Der Wert  gibt den y-Achsenabschnitt an, also den Funktionswert an der Stelle
gibt den y-Achsenabschnitt an, also den Funktionswert an der Stelle  Gilt für den y-Achsenabschnitt
Gilt für den y-Achsenabschnitt  so nennt man die lineare Funktion eine Ursprungsgerade.
so nennt man die lineare Funktion eine Ursprungsgerade.
 steht, was gleichbedeutend mit
steht, was gleichbedeutend mit  ist. Ausdrücke wie
ist. Ausdrücke wie 
 oder andere Potenzen sind also nicht erlaubt. Daher nennt man lineare Funktionen auch Funktionen ersten Grades. Bei Funktionen dieser Art ist die Ab- bzw. Zunahme immer gleichmäßig.
oder andere Potenzen sind also nicht erlaubt. Daher nennt man lineare Funktionen auch Funktionen ersten Grades. Bei Funktionen dieser Art ist die Ab- bzw. Zunahme immer gleichmäßig.
 gibt an, wie steil die Gerade ansteigt oder abfällt. Ist
gibt an, wie steil die Gerade ansteigt oder abfällt. Ist  negativ, so fällt die Gerade, ist
negativ, so fällt die Gerade, ist  positiv, so steigt sie.
positiv, so steigt sie.
Die Steigung einer linearen Funktion kann graphisch durch ein Steigungsdreieck bestimmt werden:
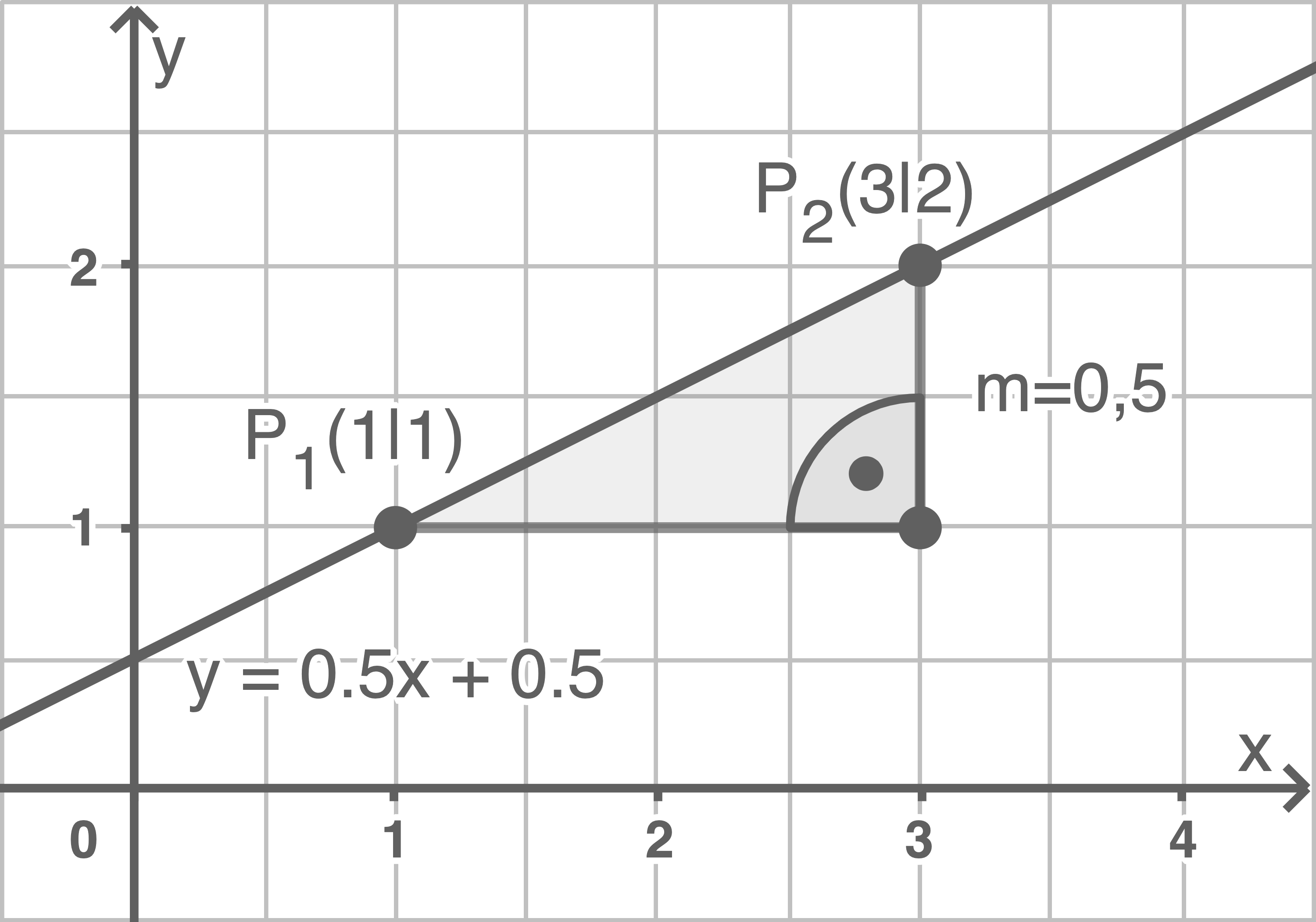 Die Abbildung zeigt den Graphen der linearen Funktion
Die Abbildung zeigt den Graphen der linearen Funktion  im Koordinatensystem. Um die Steigung ablesen zu können, werden zwei Punkte
im Koordinatensystem. Um die Steigung ablesen zu können, werden zwei Punkte  und
und  auf dem Graphen gewählt, die möglichst einfach abgelesen werden können. Dann wird das durch die beiden Punkte und die lineare Funktion eindeutig festgelegte rechtwinklige Dreieck eingezeichnet. Die Steigung kann nun mit folgender Formel für lineare Funktionen berechnet werden:
auf dem Graphen gewählt, die möglichst einfach abgelesen werden können. Dann wird das durch die beiden Punkte und die lineare Funktion eindeutig festgelegte rechtwinklige Dreieck eingezeichnet. Die Steigung kann nun mit folgender Formel für lineare Funktionen berechnet werden:
 In obigem Beispiel gilt für die Steigung
In obigem Beispiel gilt für die Steigung  Da der y-Achsenabschnitt
Da der y-Achsenabschnitt  direkt aus dem Schaubild entnommen werden kann, ergibt sich direkt die Funktionsgleichung
direkt aus dem Schaubild entnommen werden kann, ergibt sich direkt die Funktionsgleichung  Sind statt einem Schaubild nur zwei Punkte einer linearen Funkion bekannt, so kann die Steigung analog mit obiger Formel berechnet werden. Ist nicht nur die Steigung einer linearen Funktion, sondern ihre ganze Funktionsgleichung gesucht, so setzt man den berechneten Wert für die Steigung und die Koordinaten einer der beiden gegebenen Punkte in die Geradengleichung ein und stellt die so erhaltene Gleichung nach
Sind statt einem Schaubild nur zwei Punkte einer linearen Funkion bekannt, so kann die Steigung analog mit obiger Formel berechnet werden. Ist nicht nur die Steigung einer linearen Funktion, sondern ihre ganze Funktionsgleichung gesucht, so setzt man den berechneten Wert für die Steigung und die Koordinaten einer der beiden gegebenen Punkte in die Geradengleichung ein und stellt die so erhaltene Gleichung nach  um. In obigem Beispiel gilt also (für die Koordinaten von
um. In obigem Beispiel gilt also (für die Koordinaten von  ):
):
![\(\begin{array}[t]{rll}
2&=& 0,5\cdot 3+b \\[5pt]
2&=& 1,5+b \quad \scriptsize \mid\;-1,5 \\[5pt]
0,5&=&b
\end{array}\)](https://mathjax.schullv.de/216dd0874e3603193cab04b6b0c1247c9017a92b6489878f5d51947d259b0470?color=5a5a5a) Damit sind alle Parameter der Funktionsgleichung bekannt und es ergibt sich auch hier
Damit sind alle Parameter der Funktionsgleichung bekannt und es ergibt sich auch hier 
Aus der Funktionsgleichung kann sofort der y-Achsenabschnitt abgelesen werden. Mithilfe des Steigungsdreiecks kann ausgehend von diesem Punkt die Gerade eingezeichnet werden. Beispielsweise kann man eine Einheit in positive
abgelesen werden. Mithilfe des Steigungsdreiecks kann ausgehend von diesem Punkt die Gerade eingezeichnet werden. Beispielsweise kann man eine Einheit in positive  -Richtung gehen und anschließend den Wert der Steigung in
-Richtung gehen und anschließend den Wert der Steigung in  -Richtung gehen. Durch den so erhaltenen Punkt und den y-Achsenabschnitt wird nun die Gerade gezeichnet.
Alternativ kann mit der Funktionsgleichung eine Wertetabelle erstellt werden. Diese Wertetabelle besteht aus den
-Richtung gehen. Durch den so erhaltenen Punkt und den y-Achsenabschnitt wird nun die Gerade gezeichnet.
Alternativ kann mit der Funktionsgleichung eine Wertetabelle erstellt werden. Diese Wertetabelle besteht aus den  -Werten und dem jeweils zugehörigen Funktionswert, der durch Einsetzten des
-Werten und dem jeweils zugehörigen Funktionswert, der durch Einsetzten des  -Werts in die Funktionsgleichung ermittelt werden kann. Mithilfe der Wertetabelle können dann die Punkte der linearen Funktion in das Koordinatensystem eingetragen werden und daraus schließlich der Graph der linearen Funktion gezeichnet werden.
Beispiel:
-Werts in die Funktionsgleichung ermittelt werden kann. Mithilfe der Wertetabelle können dann die Punkte der linearen Funktion in das Koordinatensystem eingetragen werden und daraus schließlich der Graph der linearen Funktion gezeichnet werden.
Beispiel:  Wertetabelle:
Wertetabelle:

 aufgelöst. Um den zugehörigen Funktionswert zu ermitteln, wird der berechnete
aufgelöst. Um den zugehörigen Funktionswert zu ermitteln, wird der berechnete  -Wert in eine der beiden Geradengleichungen eingesetzt. Es existiert immer ein eindeutiger Schnittpunkt, wenn die beiden linearen Funktionen nicht parallel oder identisch sind. Sind die Geraden parallel, so haben die sie die gleiche Steigung und es existiert kein Schnittpunt. Sind die Geraden identsich, so existieren quasi undendlich viele Schnittpunkte.
Ist speziell der Schnittpunkt von linearen Funktionen mit einer der Koordinatenachsen gesucht, so kann man wie folgt vorgehen:
-Wert in eine der beiden Geradengleichungen eingesetzt. Es existiert immer ein eindeutiger Schnittpunkt, wenn die beiden linearen Funktionen nicht parallel oder identisch sind. Sind die Geraden parallel, so haben die sie die gleiche Steigung und es existiert kein Schnittpunt. Sind die Geraden identsich, so existieren quasi undendlich viele Schnittpunkte.
Ist speziell der Schnittpunkt von linearen Funktionen mit einer der Koordinatenachsen gesucht, so kann man wie folgt vorgehen:
Der Schnittpunkt mit der -Achse ist gerade die Nullstelle der linearen Funktion. Um diesen zu berechnen, muss die Funktionsgleichung der linearen Funktion gleich Null gesetzt werden. Anschließend wird nach
-Achse ist gerade die Nullstelle der linearen Funktion. Um diesen zu berechnen, muss die Funktionsgleichung der linearen Funktion gleich Null gesetzt werden. Anschließend wird nach  aufgelöst und der zugehörige Funktionswert berechnet.
aufgelöst und der zugehörige Funktionswert berechnet.
Der Schnittpunkt mit der -Achse ist durch den y-Achsenabschnitt
-Achse ist durch den y-Achsenabschnitt  gegeben.
gegeben.
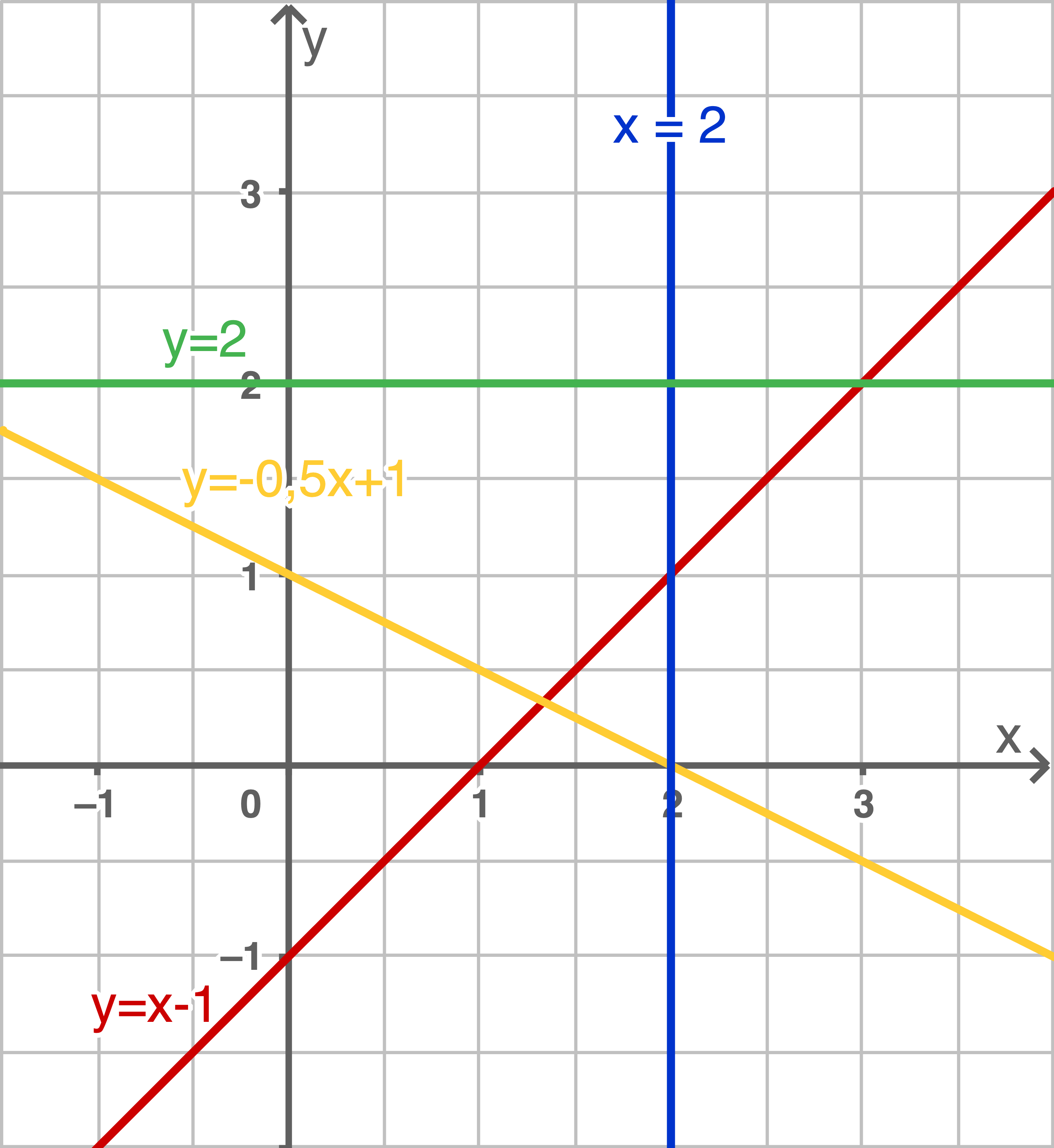

 Lösung 2
Lösung 2
 Lösung 3
Lösung 3
y = mx+b
Lineare Funktionen Erklärung
Was ist eine lineare Funktion? Der Graph einer linearen Funktion ist immer eine Gerade, also sozusagen eine „durchgehende Linie“. Die Funktionsgleichung einer linearen Funktion ist also eine Geradengleichung. Den KoeffizientenEigenschaften linearer Funktionen
Eine lineare Funktion hat immer höchstens Grad 1. Das bedeutet, dass in einer linearen Funktion immer nurSteigung einer linearen Funktion
Die SteigungDie Steigung einer linearen Funktion kann graphisch durch ein Steigungsdreieck bestimmt werden:

Steigungsdreieck
Lineare Funktionen zeichnen
Es gibt unterschiedliche Angaben, mit denen man lineare Funktionen zeichnen kann:- zwei Punkte gegeben
- Funktionsgleichung gegeben
Aus der Funktionsgleichung kann sofort der y-Achsenabschnitt
| x | y |
|---|---|
| -3 | 2 |
| -2 | |
| -1 | |
| 0 | 1 |
| 1 | |
| 2 | |
| 3 | 0 |

Lineare Funktion mit Wertetabelle
Schnittpunkt linearer Funktionen berechnen
Um den Schnittpunkt zweier linearer Funktionen zu berechnen, müssen ihre beiden Geradengleichungen gleichgesetzt werden. Die daraus resultierende lineare Gleichung wird anschließend nachDer Schnittpunkt mit der
Der Schnittpunkt mit der
Lineare Funktionen Übersicht
Die Steigung einer linearen Funktion kann unendlich viele Werte annehmen. Es gibt jedoch auch zwei Spezialfälle, wie eine lineare Funktion verlaufen kann.In diesem Fall verläuft die lineare Funktion waagrecht und hat die Steigung null.
In diesem Fall werden einer
-Koordinate alle
-Werte zugeordnet, die Gerade verläuft also senkrecht. Die Steigung ist dann sozusagen unendlich.

Verschiedene Steigungen linearer Funktionen
Lineare Funktionen Aufgaben mit Lösungen
Aufgabe 1
a)
Gib die Geradengleichung der linearen Funktion  an.
an.

Graph von y
b)
Berechne die Funktionsgleichung der linearen Funktion, die durch die Punkte  und
und  verläuft.
verläuft.
Aufgabe 2
a)
Zeichne den Graphen der linearen Funktion durch die Punkte  und
und 
b)
Zeichne den Graphen der linearen Funktion 
Aufgabe 3
a)
Berechne den Schnittpunkt der beiden linearen Funktionen  und
und 
b)
Berechne die Nullstelle der linearen Funktion 
Lösung 1
a)
Der Funktionswert der linearen Funktion an der Stelle  kann direkt aus dem Schaubild abgelesen werden. Für den y-Achsenabschnitt gilt also
kann direkt aus dem Schaubild abgelesen werden. Für den y-Achsenabschnitt gilt also  Die Steigung lässt sich mithilfe eines geeigneten Steigungsdreiecks berechnen. Wähle hierfür beispielsweise die beiden Punkte
Die Steigung lässt sich mithilfe eines geeigneten Steigungsdreiecks berechnen. Wähle hierfür beispielsweise die beiden Punkte  und
und  die beide auf dem Graphen von
die beide auf dem Graphen von  liegen. Mit der oben gegebenen Formel, mit der man für lineare Funktionen m berechnen kann, gilt:
liegen. Mit der oben gegebenen Formel, mit der man für lineare Funktionen m berechnen kann, gilt:
 Damit lautet die gesuchte Geradengleichung für die lineare Funktion
Damit lautet die gesuchte Geradengleichung für die lineare Funktion 
b)
Mit obiger Formel, mit der man für lineare Funktionen die Steigung berechnen kann, folgt  Der y-Achsenabschnitt lässt sich nun wie oben beschrieben wie folgt berechnen (für die Koordinaten von
Der y-Achsenabschnitt lässt sich nun wie oben beschrieben wie folgt berechnen (für die Koordinaten von  ):
):
![\(\begin{array}[t]{rll}
4&=& -1 \cdot 1+b \quad \scriptsize \mid\; +1 \\[5pt]
5&=& b
\end{array}\)](https://mathjax.schullv.de/fa36bfbbc93bfe57422581d77cbbab082fa0a0cbeda2fbf00597eb2b5acba23c?color=5a5a5a) Insgesamt ergibt sich also die Funktionsgleichung
Insgesamt ergibt sich also die Funktionsgleichung 

Skizze (nicht gefordert)
a)
Die beiden Punkte werden in das Koordinatensystem eingezeichnet und mit einer Gerade verbunden. Das Ergebnis sieht wie folgt aus:


b)
Für den y-Achsenabschnitt gilt  Von dem Punkt
Von dem Punkt  kann nun die Gerade mit der Steigung
kann nun die Gerade mit der Steigung  eingezeichnet werden, indem eine Einheit in postitve
eingezeichnet werden, indem eine Einheit in postitve  -Richtung und zwei Einheiten in positive
-Richtung und zwei Einheiten in positive  -Richtung gegangen wird. Durch den so erhaltenen Punkt und den y-Achsenabschnitt wird nun die Gerade gezeichnet.
Alternativ kann auch eine Wertetabelle angelegt werden, mithilfe derer Werte die Gerade gezeichnet werden kann.
-Richtung gegangen wird. Durch den so erhaltenen Punkt und den y-Achsenabschnitt wird nun die Gerade gezeichnet.
Alternativ kann auch eine Wertetabelle angelegt werden, mithilfe derer Werte die Gerade gezeichnet werden kann.
| x | y |
|---|---|
| -1 | -3 |
| 0 | -1 |
| 1 | 1 |
| 2 | 3 |

a)
Um den Schnittpunkt der beiden Funktionen zu berechnen, müssen zunächst die beiden Funktionsgleichungen gleichgesetzt werden.
![\(\begin{array}[t]{rll}
-2x+3&=& x-1\quad \scriptsize \mid\; +1\\[5pt]
-2x+4 &=& x\quad \scriptsize \mid\; +2x\\[5pt]
4 &=& 3x \quad \scriptsize \mid\;:3 \\[5pt]
\dfrac{4}{3}&=& x
\end{array}\)](https://mathjax.schullv.de/59a2c8b73ae96d35451a9d97d35b62ec72c139c6ce7f01c6f3e8bcdac6a4a796?color=5a5a5a) Der Schnittpunkt befindet sich also an der Stelle
Der Schnittpunkt befindet sich also an der Stelle  Um den
Um den  -Wert des Schnittpunktes zu ermitteln, wird der berechnete
-Wert des Schnittpunktes zu ermitteln, wird der berechnete  -Wert in eine der beiden Funktionsgleichungen eingesetzt.
-Wert in eine der beiden Funktionsgleichungen eingesetzt.
 Der Schnittpunkt hat also die Koordinaten
Der Schnittpunkt hat also die Koordinaten 
b)
Um bei einer linearen Funktion die Nullstelle zu berechnen, muss die Funktionsgleichung gleich Null gesetzt werden.
![\(\begin{array}[t]{rll}
-3x+5&=& 0 \quad \scriptsize \mid\;+3x \\[5pt]
5&=& 3x \quad \scriptsize \mid\;:3\\[5pt]
\dfrac{5}{3}&=& x
\end{array}\)](https://mathjax.schullv.de/b17834bcd5335d201ba3b4bbf6d8431bb0f8a4b0ec0e5c9c42a8cbad51146cc8?color=5a5a5a) Die Nullstelle befindet sich also an der Stelle
Die Nullstelle befindet sich also an der Stelle 
Bildnachweise [nach oben]
© 2016 - SchulLV.