Umkreis

Erklärung

Der Umkreis eines Dreiecks ist ein Kreis, der alle Ecken des Dreiecks enthält.

Für die Konstruktion eines Umkreises des Dreicks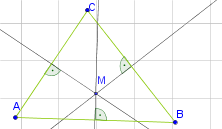 $ABC$ führt man folgende Schritte durch:

1. Schritt: Mittelsenkrechten aller Seiten einzeichnen

Dazu:

Bestimme die Mitte der Strecken $\;\overline{AB},\;\overline{BC},\;\overline{AC}$

Konstruiere die Mittelsenkrechten. Zeichne hierfür drei Geraden ein, die orthogonal zu der Seite sind und durch den jeweiligen Seitenmittelpunkt gehen.

Der Schnittpunkt der
Mittelsenkrechten ist $M$ .
Dabei gilt: $\boldsymbol{M}$ hat zu jeder Ecke den gleichen Abstand

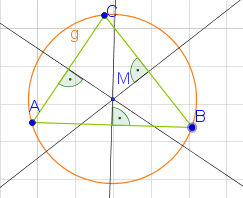
2. Schritt: Umkreis um das Dreieck $\boldsymbol{ABC}$ konstruieren

Da $M$ von allen Ecken gleich weit entfernt ist, liegen alle Ecken auf einem Kreis.

Zeichne nun einen Kreis mit Radius $\;\overline{MA}=\overline{MB}=\overline{MC}$ um den Mittelpunkt $M$ .

Damit ist der Umkreis des Dreiecks $\boldsymbol{ABC}$ ein Kreis mit Radius $\boldsymbol{\;\overline{MA}=\overline{MB}=\overline{MC}}$ und Mittelpunkt $\boldsymbol{M}$ .

Für den Radius des Umkreises des Dreiecks $ABC$ gilt:

$R=\dfrac{\mid AB \mid \cdot \mid BC \mid\cdot \mid AC\mid}{4A_{\text{Dreieck}}}$

$A_\text{Dreieck}$ ist dabei die Fläche des Dreiecks.