SchulLV Logo

Inkreis

Erklärung

Der Inkreis eines Dreiecks ist ein Kreis, der alle Seiten des Dreiecks berührt.
Für die Konstruktion eines Inkreises des Dreiecks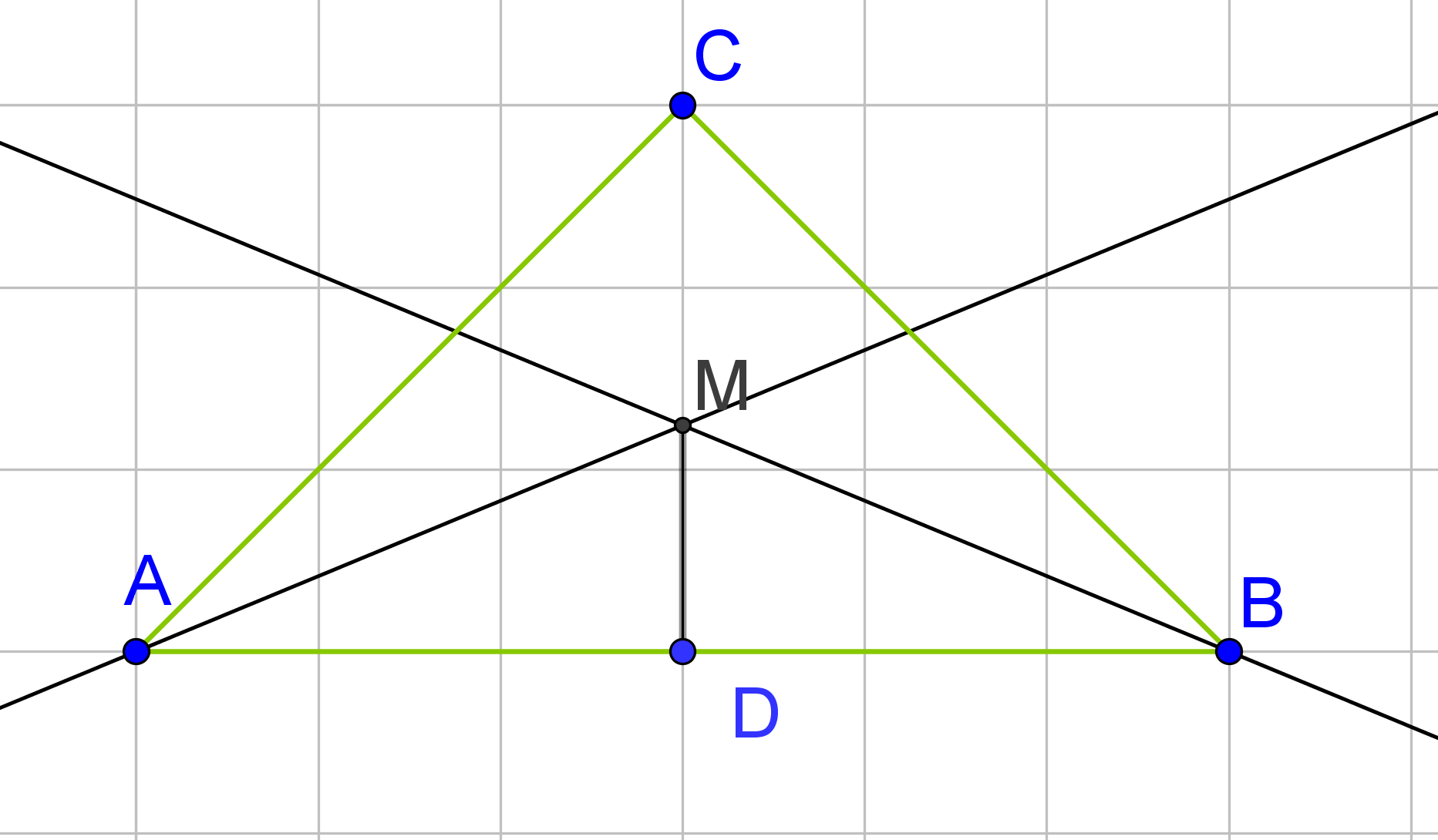 \(ABC\) führt man folgende Schritte durch:
1. Schritt: Winkelhalbierenden aller Seiten einzeichnen
Dazu:
  • Bestimme die Mitte der Winkel \( \angle CAB\;\) und \(\; \angle ABC \).
  • Konstruiere die Winkelhalbierenden. Zeichne dazu die Geraden ein, die die Winkel halbieren.
  • Den Schnittpunkt der
    Winkelhalbierenden bezeichne mit \(M\).
  • Lege durch \(M\) eine Halbgerade, die orthogonal zu der Seite \(\;\overline{AB}\;\) ist.
  • Den Schnittpunkt der Geraden mit der Seite \(\;\overline{AB}\;\) bezeichne mit \(D\).
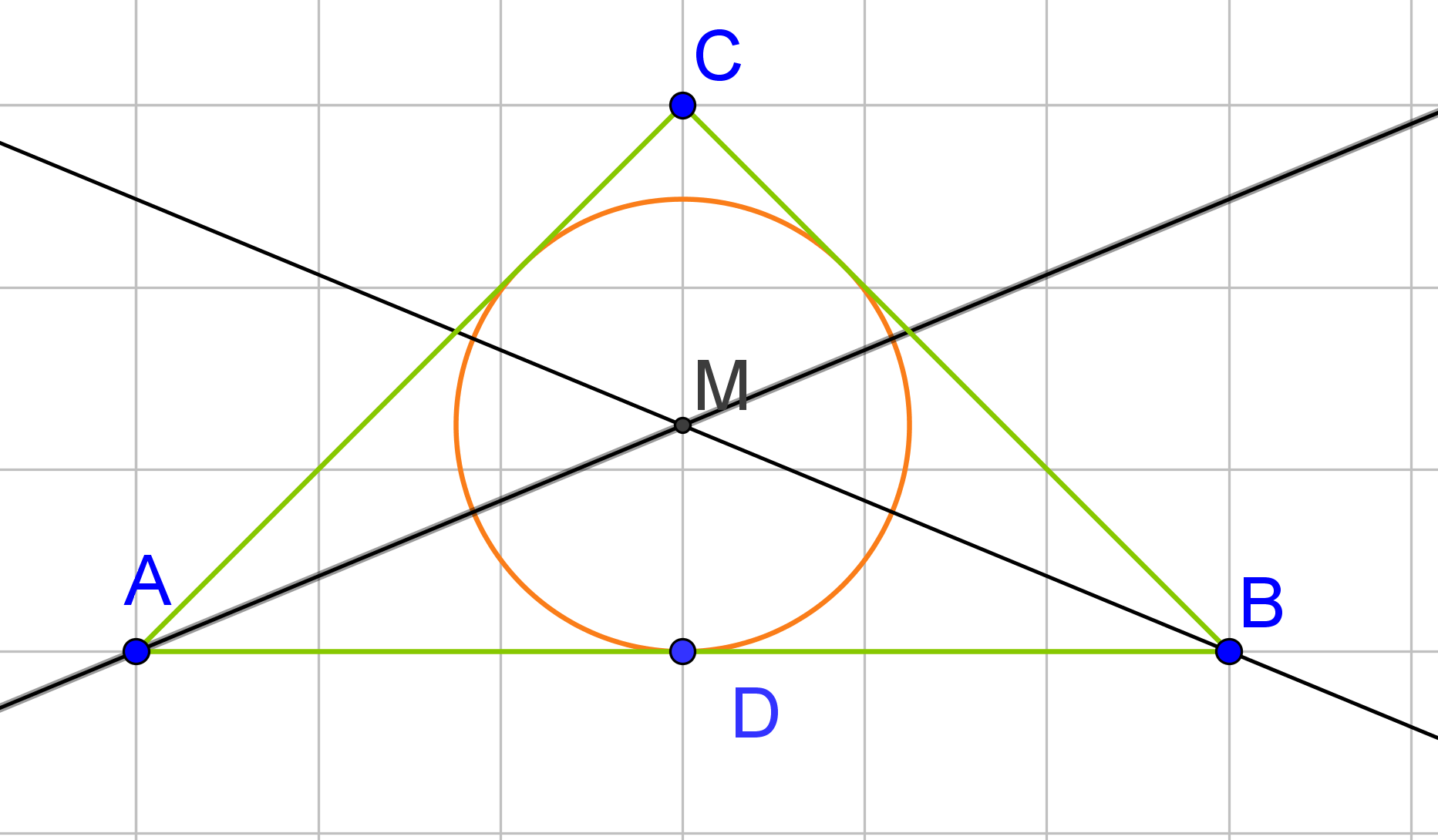
2. Schritt: Inkreis des Dreieck \(\boldsymbol{ABC}\) konstruieren
  • Miss den Abstand zwischen den Punkten \(M\) und \(D\) mit dem Zirkel.
  • Zeichne einen Kreis mit dem Radius \(\overline{MD}\) ein. Dieser ist der Inkreis des Dreiecks \(ABC\).
Zeichne einen Kreis mit dem Radius \(\overline{MD}\) um den Mittelpunkt \(M\).
Somit ist der Inkreis des Dreiecks \(\boldsymbol{ABC}\) ein Kreis mit Radius \(\boldsymbol{\;\overline{MD}}\) und Mittelpunkt \(\boldsymbol{M}\).
Für den Radius des Inkreises des Dreiecks \(ABC\) gilt:
\(r=\dfrac{2A}{u}\)
\(A\) entspricht dabei der Fläche des Dreieicks.