Verhalten von Teilchen im E- und B-Feld
Einführung
Gerade wenn es darum geht, sehr kleine Teilchen sichtbar zu machen oder unsichtbare Stoffe zu identifizieren sowie zu quantifizieren, kommt man an dem Verhalten von geladenen Teilchen in Feldern nicht herum. Die Anwendung der in diesem Skript vorgestellten Bewegungsformen sind sehr weitreichend und in vielen Bereichen nicht mehr wegzudenken. Die bekannteste Anwendung ist wohl noch immer in vielen Schulbüchern die Kathodenstrahlröhre, auch Braunsche Röhre genannt, die in früheren Röhrenbildschirmen verbaut war und dort für die Erzeugung des Elektronenstrahls und für die Entstehung des Bildes verantwortlich war.
 Abb. 1: Früherer Röhrenbilschirme machten sich das Verhalten
Abb. 1: Früherer Röhrenbilschirme machten sich das Verhaltenvon Elektronen im E-Feld zu Nutze (hier zum Nachweis)
In modernen TV-Geräten spielt diese Anwendung zwar keine Rolle mehr, doch findet man sie z.B. im Elektronenmikroskop noch heute. Hierbei werden Elektronen benutzt, um die Probe „auszuleuchten“. Die Fokussierung der Probe erfolgt, indem die negativ geladenen Elektronen des Elektronenstrahls durch elektrische Felder abgelenkt werden.
Auch in der klassischen Experimentalphysik und der Chemie findet sich ein breites Anwendungsfeld. Die analytische Chemie beispielsweise macht sich zunutze, dass Isotope, also geladene Atome, in Magnetfeldern und elektrischen Feldern beschleunigt und abgelenkt werden. In Massenspektrometern werden so chemische Substanzen und Verbindungen, selbst bei sehr geringer Menge, analysiert und quantifiziert. Somit kann z.B. das Paläoklima rekonstruiert werden oder eine Schwermetallbelastung aufgedeckt werden.
In der modernen Experimentalphysik ist die prominenteste Anwendung der Teilchenbeschleuniger. Ein solcher steht z.B. auf dem Gelände des CERN, der europäischen Organisation für Kernforschung, im schweizerischen Kanton Genf. Hier werden geladene Teilchen in einem riesigen Teilchenbeschleuniger beschleunigt und aufeinander geschossen, um die Zeit nach dem Urknall zu rekonstruieren und die moderne Theoretische Physik zu belegen. Hierbei wurde im Jahr 2013 höchstwahrscheinlich das Higgs-Boson, das im Jahre 1964 von verschiedenen Wissenschaftlern, u.a. Peter Higgs vorhergesagt wurde, nachgewiesen. Es ist ein Elementarteilchen und soll der Theorie zufolge aller Materie ihre Masse verleihen.
 Abb. 3: In den Anlagen des CERN werden die spannendsten Experimente der heutigen Wissenschaft durchgeführt.
Abb. 3: In den Anlagen des CERN werden die spannendsten Experimente der heutigen Wissenschaft durchgeführt.
Verhalten im E-Feld
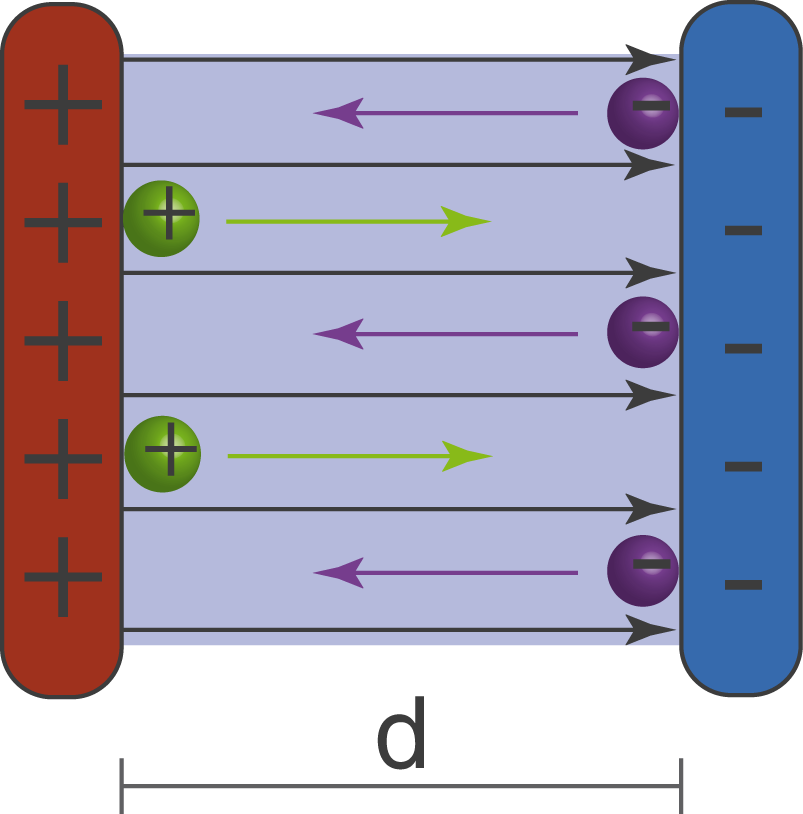
Bei einem solchen Teilchenbeschleuniger werden geladene Teilchen in einem homogenen elektrischen Feld beschleunigt. Negativ geladene Teilchen werden dabei zur Anode und positiv geladene Teilchen zur Kathode beschleunigt. Beachte dabei, dass die elektrischen Feldlinien in die Bewegungsrichtung eines positiv geladenen Teilchens zeigen.
Im Folgenden soll gezeigt werden, wie sich ein E-Feld auf ruhende und auf bewegte Ladungen auswirkt.
Ruhendes geladenes Teilchen
Ein ruhendes, geladenes Teilchen erfährt in einem E-Feld die elektrischen Kraft
mit und wird durch diese Kraft, laut dem 1. Newtonschen Gesetz
, beschleunigt. Diese Beschleunigung erfolgt in Richtung der von außen angelegten anders geladenen Ladungen.
mit .
Die zur Verrichtung der Arbeit nötige elektrische Energie entstammt dem elektrischen Feld, welches also die Arbeit am geladenen Teilchen verrichtet.
Diese elektrische Energie wird bei der Beschleunigung des Teilchens in kinetische Energie umgewandelt. Es gilt also demnach:
Aus dieser Energiebetrachtung lässt sich die Geschwindigkeit des geladenen Teilchens bestimmen, wobei
dessen Masse und
dessen Ladung darstellt.
Allgemein lässt sich das Bewegungsgesetz eines ruhenden, geladenen Teilchens im elektrischen Feld folgendermaßen beschreiben. Da das Teilchen zu Beginn ruht, besitzt es die Anfangsgeschwindigkeit . Es wird anschließend im elektrischen Feld mit einer konstanten Beschleunigung
beschleunigt. Für die gleichmäßig beschleunigte Bewegung gilt folglich mit
und
:
Somit folgt für die zu einem beliebigen Zeitpunkt zurückgelegte Strecke
:
Bewegtes geladenes Teilchen
Bewegen sich Teilchen bereits mit konstanter Geschwindigkeit durch ein elektrisches Feld, so kommt es entweder zur weiteren Beschleunigung, zur Abbremsung oder zu einer Ablenkung.
Bewegung parallel zum E-Feld
Beschleunigung oder Abbremsung tritt dann auf, wenn das Feld parallel zur Bewegungsrichtung der geladenen Teilchen gerichtet ist. Abbildung 5 zeigt dir einen solchen Fall.
- Das positiv geladene Teilchen bewegt sich auf die gleichnamige Metallplatte zu. Da sich gleichnamige Ladungen abstoßen, sorgt die elektrische Kraft
dafür, dass das Teilchen abgebremst wird.
- Das negativ geladene Teilchen bewegt sich auf die entgegengesetzt geladene Metallplatte zu und wird von dieser angezogen. Die elektrische Kraft
sorgt hierbei für eine Beschleunigung des Teilchens. Dieser Fall ist analog zum Fall des ruhenden, geladenen Teilchen, mit dem Unterschied, dass in diesem Fall das Teilchen zu Beginn eine konstante Geschwindigkeit
aufweist.
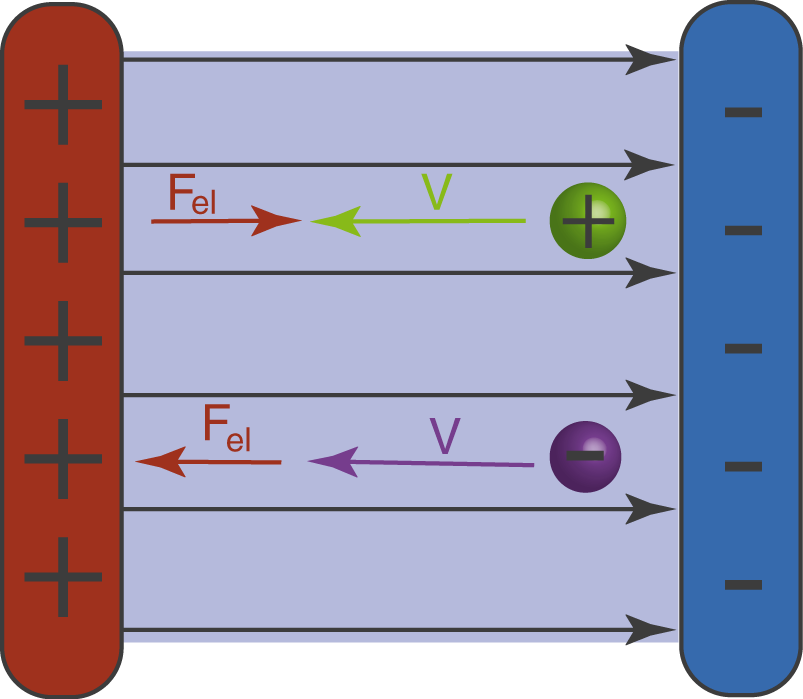 Abb. 5: Zwei unterschiedlich geladene Teilchen, die sich im E-Feld zur negativ geladenen Seite bewegen.
Abb. 5: Zwei unterschiedlich geladene Teilchen, die sich im E-Feld zur negativ geladenen Seite bewegen.
Wie oben beschrieben verrichtet das elektrische Feld Arbeit an den geladenen Teilchen. Dabei wird elektrische Energie in zusätzliche kinetische Energie umgewandelt und das Teilchen erhält als Energiezuwachs . Daher gilt für die gesamte kinetische Energie der Teilchen
bzw.
, dass diese die Summe aus der kinetischen Energie der Anfangsbewegung und der elektrischen Energie des Feldes ist:
Für diese gleichmäßig beschleunigte Bewegung mit Anfangsgeschwindigkeit ergibt sich folglich mit und
:
Da sich das Teilchen vor der Beschleunigung durch das elektrische Feld gleichförmig, also mit einer konstanten Geschwindigkeit , bewegt hat, legte es bis dahin die Strecke
zurück. Somit folgt für die zu einem beliebigen Zeitpunkt
zurückgelegte Strecke
:
Bewegung senkrecht zum E-Feld
Im Folgenden sollen sich geladene Teilchen gleichförmig, also mit konstanter Geschwindigkeit, in einem elektrischen Feld senkrecht zu den Feldlinien bewegen. Dabei wird das Teilchen in Richtung der entgegengesetzt geladenen Kondensatorplatten gleichmäßig beschleunigt. Da die elektrische Kraft senkrecht zur Bewegungsrichtung steht, wird die ursprüngliche gleichförmige Bewegung des Teilchens nicht von der neu entstehenden Bewegung gestört. Es gilt somit das Newtonsche Superpositionsprinzip und das Teilchen führt folgende Bewegungen durch:
- gleichförmige Bewegung parallel zu den Kondensatorplatten bzw. senkrecht zum E-Feld
- gleichmäßig beschleunigte Bewegung senkrecht zu den Kondensatorplatten bzw. parallel zum E-Feld
Diese zwei Teilbewegungen überlagern sich nach dem Superpositionsprinzip zur endgültigen Bewegungsrichtung des Teilchens. Diese Situation ist vergleichbar mit dem waagerechten Wurf. Da die Bewegungsrichtungen senkrecht zu den Kondensatorplatten, also in Abbildung 6 in -Richtung, beschleunigt wird, steigt dessen Geschwindigkeit in die selbe Richtung. Es steigt also
. Die gleichförmige Bewegung in
-Richtung hingegen ist gekennzeichnet durch eine konstante Geschwindigkeit
. Dies führt zu einer Parabelbahn des geladenen Teilchens, was in Abbildung 6 dargestellt wird.
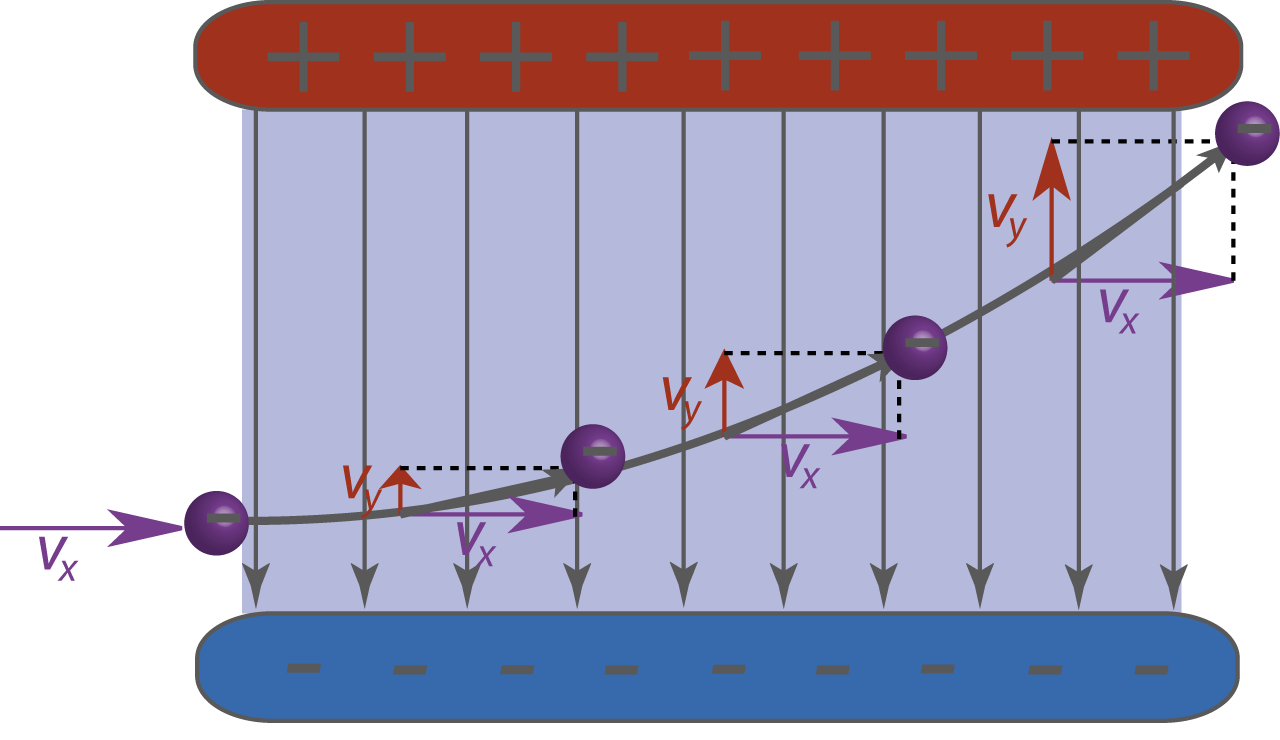 Abb. 6: Geladene Teilchen die sich senkrecht zum E-Feld bewegen, werden auf eine Parabelbahn abgelenkt.
Abb. 6: Geladene Teilchen die sich senkrecht zum E-Feld bewegen, werden auf eine Parabelbahn abgelenkt.
Braunsche Röhre
Dies findet Anwendung in der sogenannten Braunschen Röhre. Dies ist eine luftleere Röhre in der sich eine Elektronenkanone und Ablenkplatten befinden. Dabei werden Elektronen aus einer Heizspule ausgelöst und aus der Ruhe zur Anode hin beschleunigt. Hier gelten die Gesetze aus Ruhendes geladenes Teilchen.
 Abb. 7: Der Aufbau einer Braunschen Röhre.
Abb. 7: Der Aufbau einer Braunschen Röhre.
Legen wir eine Ablenkspannung an die Kondensatorplatten entsteht zwischen diesen ein elektrisches Feld mit der Feldstärke
. Die durch aus Feld entstehende elektrische Kraft
sorgt für eine Beschleunigung
der Elektronen in
-Richtung. Daher gilt:
Eliminieren wir aus den Zeit-Weg-Funktionen
die Zeit so erhalten wir als Bahngleichung der Elektronen eine Parabelgleichung:
Da der zurückgelegte Weg in -Richtung gerade der Länge
des Kondensators entspricht, ergibt sich für die Ablenkung
der Elektronen nach Durchlaufen des Kondensators:
Die Ablenkung vergrößert sich also, wenn
- die Ablenkspannung
erhöht wird
- die Länge
des Kondensators zunimmt
- die Dicke
des Kondensators kleiner wird
- die Ausgangsgeschwindigkeit
klein ist
Verhalten im B-Feld
Analog zum Verhalten von geladenen Teilchen im E-Feld unterscheiden wir im Folgenden das Verhalten von geladenen Teilchen, die sich senkrecht oder nicht senkrecht zum B-Feld bewegen.
Bewegung senkrecht zum B-Feld
Das Verhalten von Teilchen senkrecht zum Magnetfeld wollen wir mithilfe eines Fadenstrahlrohrs innerhalb eines Helmholtz-Spulenpaars verdeutlichen. Das von dem orangenen Helmholtz-Spulenpaar erzeugte magnetische Feld ist in die Zeichenebene hinein gerichtet. Dies kannst du an den Kreuzen in den grauen Kreisen der rechten Abbildung entnehmen. Senkrecht zu diesem Magnetfeld bewegen sich die Elektronen. Die linke Abbildung zeigt das Fadenstrahlrohr von vorne. Man sieht hier ebenfalls, dass die Feldlinien des Magnetfeldes durch die Glaskugel nach hinten weisen. Es fällt auf, dass das Magnetfeld in dem Bereich, wo sich die Elektronen befinden, als nahezu homogen aufgefasst werden kann.
 Abb. 8: Richtung der Feldlinien beim Betrachten des Fadenstrahlrohres von vorne.
Abb. 8: Richtung der Feldlinien beim Betrachten des Fadenstrahlrohres von vorne.
 Abb. 9: Die Elektronen werden vom Magnetfeld auf eine Kreisbahn gezwungen
Abb. 9: Die Elektronen werden vom Magnetfeld auf eine Kreisbahn gezwungen
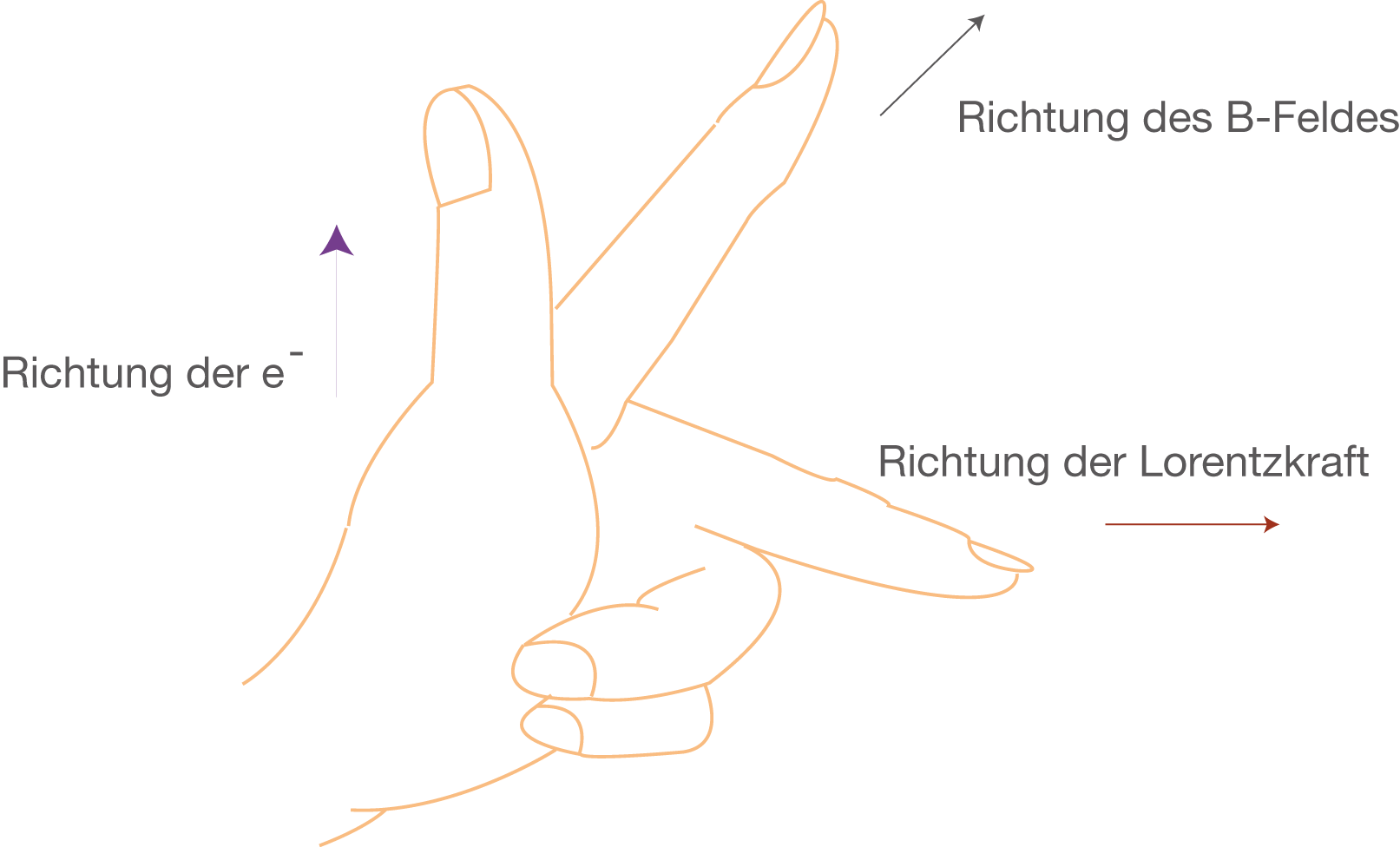 Abb. 10: Die Linke-Hand-Regel veranschaulicht die Richtung der Lorentzkraft.
Abb. 10: Die Linke-Hand-Regel veranschaulicht die Richtung der Lorentzkraft.
Durch den Verlauf der Glasröhre im rechten Bild werden die Elektronen nach unten abgelenkt und sollten eigentlich geradeaus weiter fliegen. Diese Flugbahn ist von den hellen Elektronen dargestellt. Durch das Anlegen des Magnetfeldes allerdings werden die Elektronen auf eine Kreisbahn mit dem Radius abgelenkt. Dies geschieht auf Grund der Lorentzkraft
. Bewegen sich die Elektronen nach unten und ist das Magnetfeld in die Zeichenebene hinein gerichtet, so sorgt die Lorentzkraft
dafür, dass diese nach rechts abgelenkt werden. Dies geht aus der Linken-Hand-Regel der Abbildung 9 hervor.
Da sich die Bewegung der Elektronen bei Punkt 1 nach unten (blau) und nach rechts (rot) überlagern, ergibt sich die kommende Bewegungsrichtung (grün) des Elektrons aus der Vektoraddition dieser zwei Pfeile. In Punkt 2 ist die Bewegungsrichtung der Elektronen nun die vormals grün markierte Richtung. Da sich diese Richtung allerdings erneut mit der Lorentzkraft überlagert, fliegt das Elektron nach rechts. Bei Position 3 wird die vorher grün markierte kommende Bewegungsrichtung des Elektrons nun blau dargestellt und es erfolgt wieder eine Ablenkung durch die Lorentzkraft
. Dieser Vorgang setzt sich in jedem Moment fort und führt dazu, dass sich das Elektron auf einer Kreisbahn (punktiert) verweilt.
 Abb. 11: Die Vektoraddition der Bewegungsrichtung der Elektronen (blau) und der Lorentzkraft (rot) ergibt die kommende Richtung (grün) der Elektronen
Abb. 11: Die Vektoraddition der Bewegungsrichtung der Elektronen (blau) und der Lorentzkraft (rot) ergibt die kommende Richtung (grün) der Elektronen
Die Lorentzkraft (rot) hält also geladene Teilchen auf einer Kreisbahn und ist immer nach innen gerichtet. Sie wirkt hier als Zentripetalkraft
. Da die Kraft immer senkrecht zur Bewegungsrichtung steht, bleibt die kinetische Energie
und damit auch die Geschwindigkeit
der Elektronen vom Betrag her unverändert.
Laut dem PhysikLV-Skript Rotationen ist die Formel für die Zentripetalkraft :
Laut dem gleichnamigen PhysikLV-Skript lautet eine Formel für die Lorentzkraft , die die magnetische Flussdichte
enthält, folgendermaßen:
Die Ladung enthält hierbei das Vorzeichen der Ladung. Liegt eine positive Ladung vor, so ist das Vorzeichen der Lorentzkraft gerade umgekehrt und das Teilchen wird in die andere Richtung auf eine Kreisbahn gelenkt.
Zur Bestimmung der Ablenkungsrichtung bzw. der Richtung der Lorentzkraft nutzt du die
- Linke-Hand-Regel für negative Ladungen.
- Rechte-Hand-Regel für positive Ladungen.
Da im vorliegenden Fall die Lorentzkraft der Zentripetalkraft
entspricht, gilt das Kräftegleichgewicht wie folgt:
Der Radius der Kreisbahn eines geladenen Teilchens im Magnetfeld berechnet sich durch folgende Formel:
Da die geladenen Teilchen eine Kreisbewegung mit konstanter Geschwindigkeit ausführen, gilt die Formel der gleichförmigen Bewegung. Die Strecke auf der Kreisbahn entspricht dem Umfang des Kreises, der mit der Formel
berechnet werden kann. Aus dieser Beziehung ergibt sich für die Umlaufdauer
auf der Kreisbahn für die Dauer einer ganzen Umrundung:
Wie du erkennen kannst, ist die Umlaufdauer der Kreisbahn unabhängig von der Geschwindigkeit:
Bewegung nicht senkrecht zum B-Feld
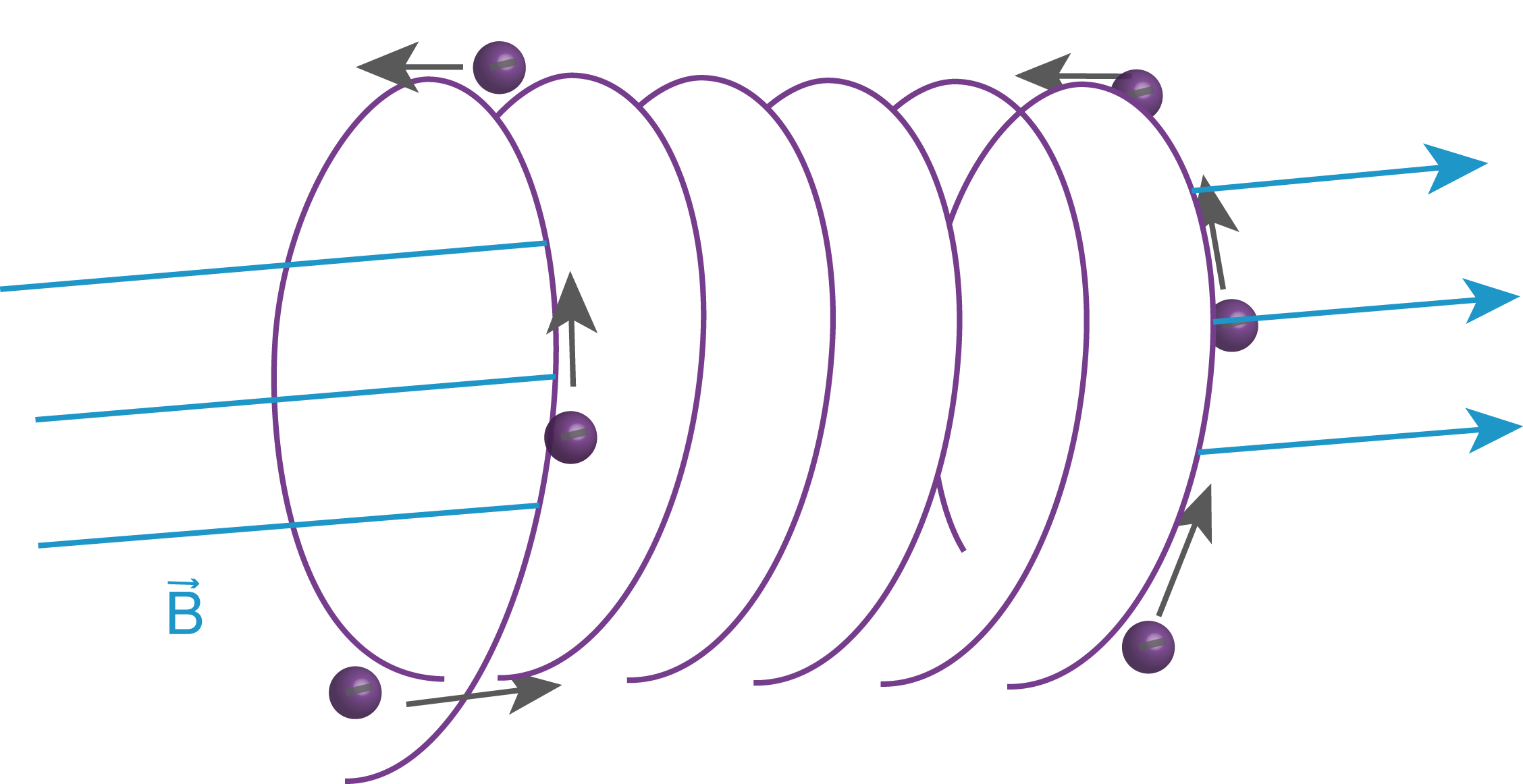 Abb. 12: Die Elektronen, die sich nicht senkrecht zu den magnetischen Feldlinien bewegen, fliegen sich auf einer Schraubenbahn.
Abb. 12: Die Elektronen, die sich nicht senkrecht zu den magnetischen Feldlinien bewegen, fliegen sich auf einer Schraubenbahn.
Bei Bewegungen von geladenen Teilchen die nicht senkrecht zum Magnetfeld stattfinden, lässt sich die Geschwindigkeit in zwei Teilkomponente aufteilen. Die Geschwindigkeitskomponente senkrecht zum B-Feld erzeugt wieder eine Kreisbahn um die magnetischen Feldlinien. Die Komponente parallel zum B-Feld zieht diese Kreisbahn in deren Fortpflanzungsrichtung auseinander. Es ergibt sich somit eine Schraubenbahn.