Aufladen und Entladen
Einführung
Kondensatoren werden ebenfalls in den PhysikLV-Skripten Einführung und Definition und Kondensatoren - Kapazität und Energiegehalt, behandelt. Auf Grund seiner Wichtigkeit ist dieses elektrische Bauteil aus dem Stromkreis nicht mehr wegzudenken. Seine Aufgabe ist es, Ladung und damit auch Energie zu speichern. Damit kann der Kondensator beim Entladen ein elektrisches Gerät auch ohne Anschluss an die Stromquelle mit Energie versorgen.
Im kommenden Versuch möchten wir vorher abschätzen, wie lange eine Glühbirne ohne Verbindung zur Stromquelle, mit der im Kondensator gespeicherten Energie, weiter brennen kann. Daher solltest du dir noch einmal einige Formeln und Zusammenhänge klar machen.
Im Versuch werden wir drei verschiedene Spannungen unterscheiden. Die Spannung , die an einem Plattenkondensator anliegt (siehe PhysikLV-Skript Kondensatoren - Kapazität und Energiegehalt), die Spannung
, die dafür sorgt, dass eine bestimmte Stromstärke durch den Stromkreis fließt (siehe PhysikLV-Skript Einführung und Definition) und die Spannung
, die von außen angelegt wird.
Laut der Maschenregel, einem physikalischen Gesetz, addieren sich alle Teilspannungen zu Null.
Es ergibt sich also eine Gleichung für die Gesamtspannung im Stromkreis:


Ebenfalls wichtig wird sein, dass du dir klar machst, was die Leistung bedeutet. Sie bezeichnet in der Mechanik die bezogene Energie eines Verbrauchers pro Zeiteinheit (siehe PhysikLV-Skript Einführung und Definition). Sie bezeichnet also den Quotienten aus der geleisteten Arbeit
und der zugehörigen Zeitspanne
.
Wird in der Elektrostatik eine elektrische Leistung umgesetzt, so kann diese auch als Produkt der Spannung mit der elektrischen Stromstärke
definiert werden:
Beim Entladen eines Kondensators wird die im Feld gespeicherte Energie dazu benutzt, die Arbeit zu verrichten.
Den Energiegehalt eines Kondensators, der dazu benutzt werden kann, den gleichen Betrag an Arbeit zu leisten, kannst du dem PhysikLV-Skript Kondensatoren - Kapazität und Energiegehalt entnehmen und wird folgendermaßen berechnet:
Versuch: Wie lange brennt die Glühbirne?
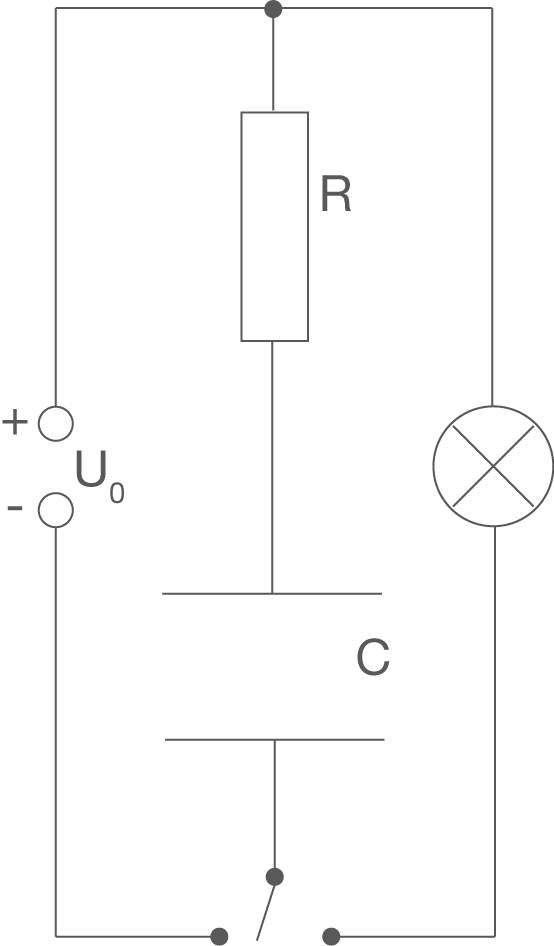
Im kommenden Versuch entladen wir einen Superkondensator () über eine Glühbirne und messen dabei, wie lange diese mit Hilfe der gespeicherten Energie im Kondensator, also ohne Verbindung zur Stromquelle, brennen kann. Dies möchten wir zunächst mit den oben eingeführten Formeln rechnerisch abschätzen und anschließend mit dem nebenstehenden Versuchsaufbau belegen.
Im Versuch wird ein Superkondensator mit einer Ladespannung von 4V aufgeladen. Bei einer Kapazität von 1F speichert der Kondensator damit als Energie
Dies hört sich nicht gerade viel an. Doch über die Formel der Leistung können wir berechnen wie lange die Glühbirne leuchten wird.
Die Lampe ist ausgelegt auf 3,8V und 70mA. Damit hat sie eine Leistungsaufnahme von:
Allgemein gilt für die Leistung . Stellen wir diese Formel nach der Zeitspanne
um, so können wir die Zeit berechnen, die die Glühlampe mit der im Feld des Superkondensators gespeicherten Energie leuchtet:
Laut unserer Berechnung sollte die Glühlampe also etwa 30s lang leuchten. Das ist schon eine beachtlich lange Zeit, für so ein unscheinbares Bauteil. Führen wir allerdings den Versuch nach obigem Versuchsaufbau durch, so stellen wir fest, dass in Realität die Glühbirne mit etwa 40s noch länger leuchtet. Wie kann das sein?
Die Antwort auf diese Frage ergibt sich bei der Beobachtung der Glühbirne. Je länger die Birne brennt, desto schwächer leuchtet sie. Der Grund hierfür hängt mit einer Eigenschaft des Kondensators zusammen, die beim Entladen zum Tragen kommt.
Entladen
Entlädt sich der Kondensator, so fließen dabei die Ladungen zur jeweils anders geladenen Elektrode über den ohmschen Widerstand ab. Dabei sinkt die nun zeitabhängige Ladung auf den Kondensatorplatten. Daraus resultiert, dass die Spannung
zwischen den Platten in Abhängigkeit von der Zeit ebenfalls sinkt.
Ergebnis: Die Leuchtstärke der Glühbirne lässt ebenfalls nach.
Laut Maschenregel addieren sich alle Teilspannungen zu Null.
Im geschlossenen Stromkreis gilt generell, dass die Ladespannung ist. Für die Gesamtspannung folgt dann:
Da die Ladung beim Entladen sinkt, geht die linke Seite der Gleichung gegen Null. Damit muss sich die Stromstärke
ebenfalls der Null annähern. Da die rechte Seite der Gleichung zusätzlich negativ ist, nähert sich der Graph der Funktion der Stromstärke der
-Achse von unten an. Sie nimmt also betragsmäßig ab und ist \textbf{nicht konstant}.
Es gilt also:
Die Stromstärke wiederum ist definiert als die Ladungsmenge
, die in einer gewissen Zeitspanne
durch den Stromkreis fließt:
Sie ist damit ein Maß für die durchschnittliche Änderungsrate der durch den Leiter bewegten Ladung. Diese Betrachtung entspricht gerade dem Differenzenquotienten:
Möchten wir aber wissen, wie viele Ladungen genau in einem bestimmten Moment den Leiterquerschnitt passieren, wählen wir hierzu die untersuchte Zeitspannen immer kleiner. Wir lassen also den Abstand zwischen und
immer geringer werden. Wird schließlich die Zeitspanne unendlich (infinitesimal) klein, so betrachten wir die Änderung der durch den Leiter bewegten Ladung an einem ganz bestimmten Zeitpunkt, anstatt gemittelt über eine Zeitspanne.
Laut der mathematischen Definition der Ableitung wird der Grenzwert dieses Differenzenquotienten für als Ableitung der Funktion
bezeichnet.
Die Stromstärke stellt also die Ableitung der Ladungsfunktion
dar.
Die Ableitung nach der Zeit wird in der Physik mit einem Punkt über der Ableitungsfunktion verdeutlicht. Daher gilt:
Setzen wir diese Tatsache in die Maschenregel ein, so erhalten wir eine Differentialgleichung, eine Gleichung, die sowohl die Funktion , sowie ihre zeitliche Ableitung
enthält:
Als Lösung dieser Gleichung kommt nur ein Typ Funktion in Frage, bei der die Ableitung gleich der Gleichung mal einen konstanten Faktor ist. Dies ist bei Exponentialfunktionen der Fall. Daher kann folgende Funktion als Lösung dieser Gleichung gelten:
Probe
Um diese nicht hergeleitete Lösung zu überprüfen, setzen wir sie in die Differentialgleichung ein.
Hierzu leiten wir erst einmal die Lösung ab:
Diese beiden Gleichungen setzen wir nun in die Differentialgleichung ein und überprüfen, ob diese die Gleichung lösen können.
Ergebnis: Die Funktion ist damit also wirklich eine Lösung der Differentialgleichung.
Durch das Sinken der Ladungsfunktion und der Spannungsfunktion
folgt wie oben beschrieben direkt, dass die Funktion
betragsmäßig abnehmen muss. Es verringert sich also damit auch
, die Steigung des Graphen der Funktion
.
Die Geschwindigkeit des Ladungstransportes ist also beim Start des Entladens am größten und nimmt dann exponentiell ab. Je länger die Entladung fortschreitet, desto weniger Ladungen werden zur anderen Elektrode übertragen und desto langsamer ist dieser Transport. Dadurch sinkt die Spannung und die Stromstärke
immer langsamer.
Aus diesen Zusammenhängen ergeben sich die folgenden Schaubilder. Alle Funktionen nähern sich exponentiell der Null an. und
von oben und
von unten.


Dem ersten Schaubild kannst du die anfängliche Ladungsmenge auf den Kondensatorplatten entnehmen. Ist zusätzlich bekannt, mit welcher Spannung
der Kondensator aufgeladen wurde, so kannst du die Kapazität des Kondensators bestimmen:
Da die Funktion der Stromstärke die Ableitungsfunktion
der Ladung darstellt, lässt sich aus dem Graphen der Ladungsfunktion
die Stromstärke
bestimmen, die zu Beginn der Entladung herrscht. Hierzu wird eine Tangente an die Funktion im Schnittpunkt mit der
-Achse gelegt. Die Ladungsmenge
, die in der Zeitspanne
näherungsweise die Elektroden verlässt, und
selbst lassen sich wie unten aufgezeigt dem Schaubild entnehmen. Der Zeitpunkt
ergibt sich aus dem Schnittpunkt der Tangente mit der
-Achse.
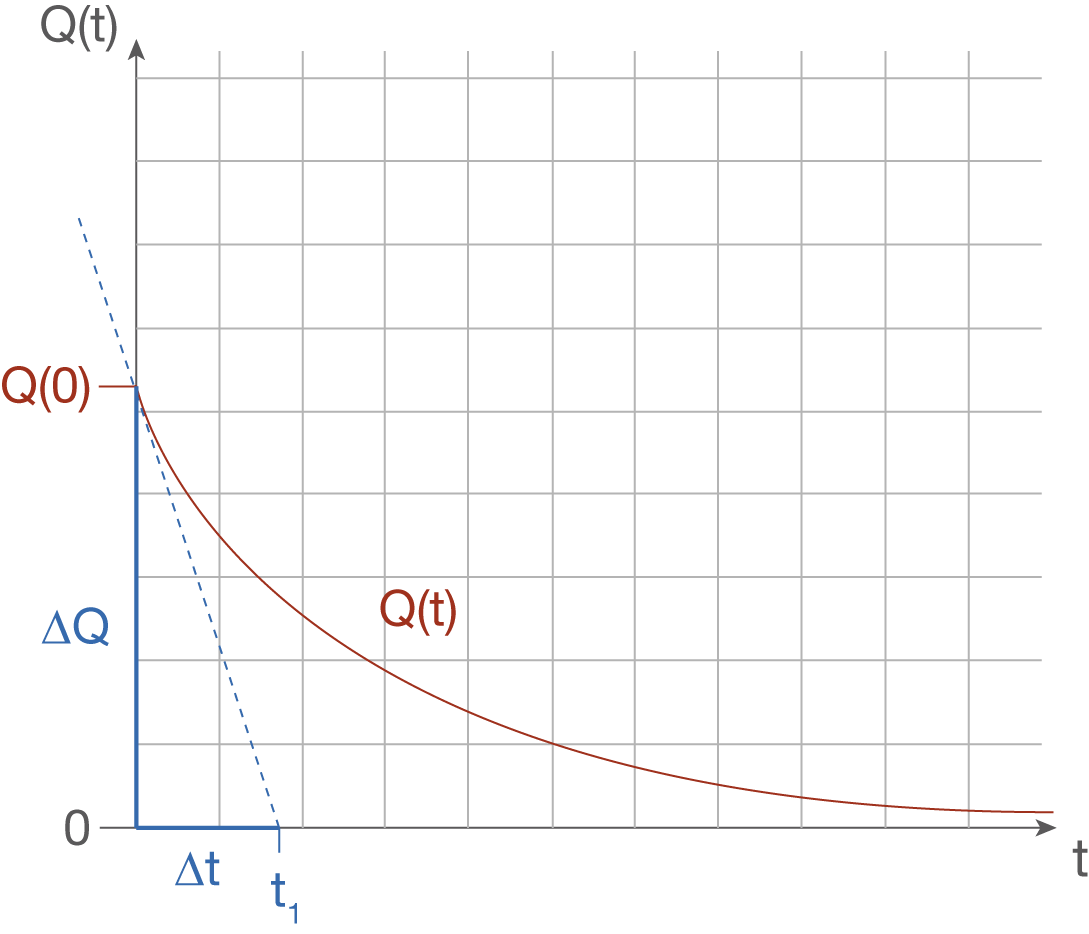
Als Stromstärke zu Beginn der Entladung ergibt sich dann:
Da die Stromstärke zu Beginn der Entladung immer ungleich Null ist, lässt sich aus der Maschenregel ebenfalls der elektrische Widerstand
berechnen:
Aus dem Q-t-Schaubild lässt sich ebenfalls die Halbwertszeit ablesen. Dies ist der Zeitpunkt, an dem genau die Hälfte der Ladungsmenge bereits von den Elektroden abgewandert ist. Die andere Hälfte ist noch gespeichert. Zu diesem Zeitpunkt ist damit ebenfalls die Spannung halbiert worden. Die Glühbirne leuchtet also nur noch halb so intensiv.
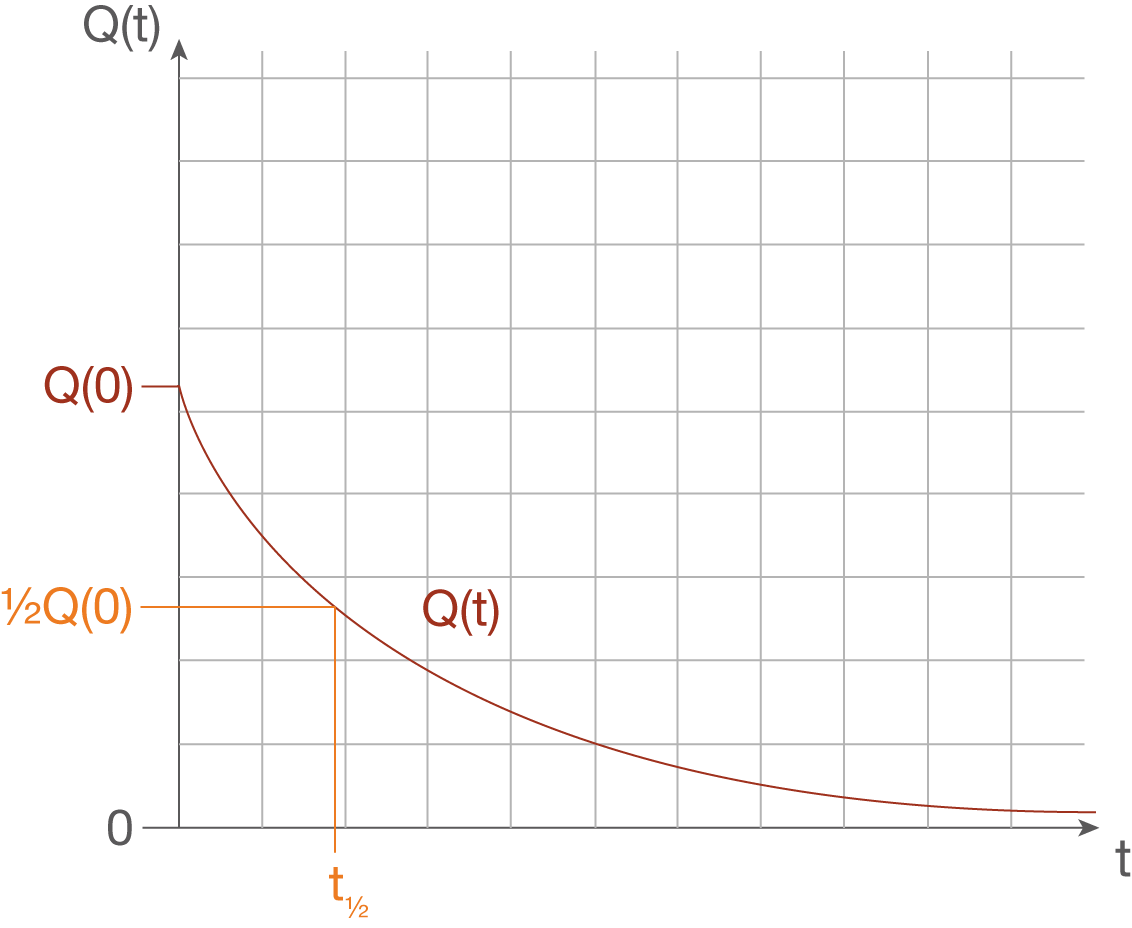
Berechnen lässt sich die Halbwertszeit folgendermaßen:
 Abb. 3: Nach der Halbwertszeit leuchtet die Glühbirne nur noch halb so intensiv.
Abb. 3: Nach der Halbwertszeit leuchtet die Glühbirne nur noch halb so intensiv.
Aufladen
Ist der Kondensator vollständig entladen, so befinden sich keine Ladungen mehr auf den Platten. Zum Aufladen legt man von außen eine Spannung an, die erneut Ladungen über den Ohmschen Widerstand auf die Kondensatorplatten treibt. Die Ladungsmenge
des Kondensators nimmt entsprechend zu. Daraus resultiert auch eine Zunahme der Spannung
zwischen den Elektroden.
Durch die Zunahme der Spannung zwischen den Elektrodenplatten verringert sich die Spannungsdifferenz zwischen dieser und der außen angelegten Spannung
. Da diese Spannungsdifferenz „der Motor“ des Aufladevorgangs ist, werden die Ladungen immer langsamer auf die Platten übertragen. Dadurch sinkt die Stromstärke
und die Spannung
nimmt immer langsamer zu.
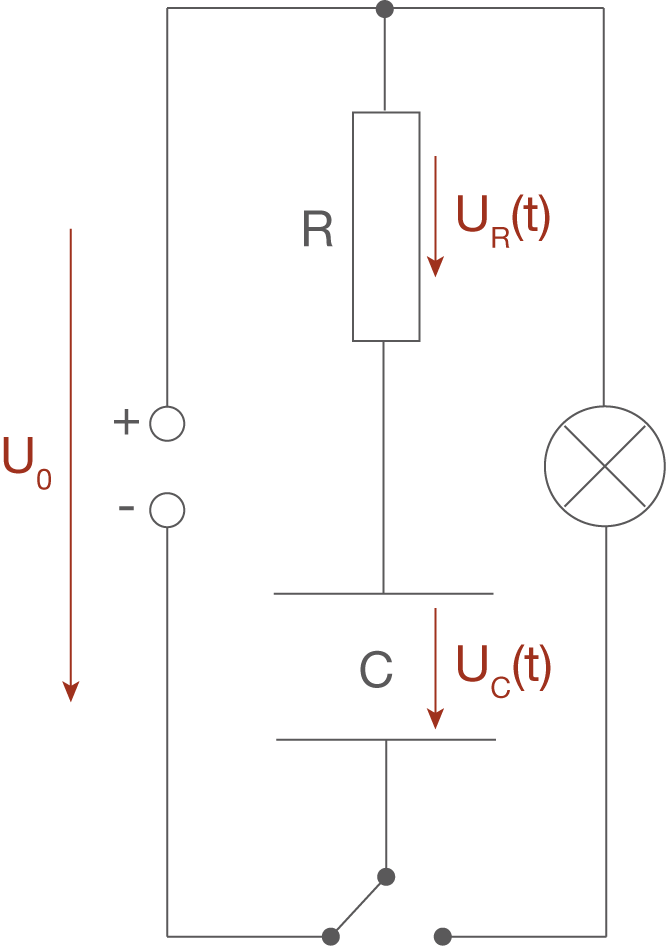 Abb. 2: Nach der Halbwertszeit leuchtet die Glühbirne nur noch halb so intensiv.
Abb. 2: Nach der Halbwertszeit leuchtet die Glühbirne nur noch halb so intensiv.
Verfolgst du in nebenstehendem Bild den Stromverlauf, so kannst du erkennen, dass die Spannung genau umgekehrt gerichtet ist wie die Spannungen
und
. Auf Grund der entgegengesetzten Richtung ist
in der unten stehenden Formel negativ.
Nach der ersten Umformung kannst du erkennen, dass sich diese angelegte Spannung auf die Spannung
am Widerstand und die Spannung
am Kondensator aufteilt.
Die Gleichung für die Gesamtspannung lautet also:
Diese Gleichung ist eine Differentialgleichung und enthält die Funktion , sowie ihre Ableitung
. Als Lösung dieser Gleichung kommt nur ein Typ Funktion in Frage, bei der die Ableitung gleich der Gleichung mal einen konstanten Faktor ist. Dies ist bei Exponentialfunktionen der Fall. Daher kann folgende Funktion als Lösung dieser Gleichung gelten:
Probe
Um diese nicht hergeleitete Lösung zu überprüfen, setzen wir sie in die Differentialgleichung ein.
leiten wir erst einmal die Lösung ab:
Diese beiden Gleichungen setzen wir nun in die Differentialgleichung ein und überprüfen, ob diese die Gleichung lösen können.
Ergebnis: Die Funktion ist damit also wirklich eine Lösung der Differentialgleichung.
Betrachte die Ableitungsfunktion der Ladungsmenge. Sie entspricht wie oben hergeleitet der Funktion der Stromstärke
. Für
gilt dann ebenfalls:
Da die Größen ,
und
immer positiv sind, ist der Exponent der Exponentialfunktion negativ. Deshalb nähert sich der Graph der Funktion der Stromstärke im Laufe des Aufladevorgangs der Null an.
Die Geschwindigkeit des Ladungstransportes ist also beim Start des Aufladens am größten und nimmt dann exponentiell ab.
Die Spannungs-, Ladungs- und Stromstärkefunktion sind Exponentialfunktionen. Die Graphen der Spannungs- und der Ladungsfunktion wachsen beschränkt, wohingegen sich der Graph der Stromstärkefunktion der Null annähert.


Solltest du in einer Aufgabe ein Schaubild erhalten, so kannst du diesem einiges entnehmen.
Aus dem Q-t-Schaubild kannst du den Grenzwert der Ableitungsfunktion ablesen. Dies ist also die Ladungsmenge, die sich nach dem Aufladen auf den Kondensatorplatten befindet. Ist zusätzlich noch die außen angelegte Spannung
gegen, so kannst du die Kapazität des Kondensators bestimmen. Hierfür benötigst du die Maschenregel.
Wichtig ist, dass du dir klar machst, dass am Ende des Aufladevorgangs kein Strom mehr fließt und daher der Grenzwert der Stromstärke Null ist.
Laut Maschenregel ergibt sich dann:
Aus dem Q-t-Schaubild lässt sich die Stromstärke zu Beginn des Aufladevorgangs, auf Grund der Tatsache, dass die Stromstärkefunktion als Ableitung
der Ladungsfunktion
definiert ist, mit Hilfe der Tangente an die Ladungsfunktion (im Schnittpunkt mit der
-Achse) näherungsweise bestimmen. Dieser Vorgang wird im folgenden Bild verdeutlicht.

Als Stromstärke zu Beginn des Aufladevorgangs ergibt sich dann:
Hast du die Stromstärke zu Beginn des Aufladevorgangs berechnet oder aus dem I-t-Schaubild abgelesen, kannst du mittels der Maschenregel den elektrischen Widerstand
bestimmen.
Wichtig ist, dass du dir klar machst, dass am Anfang des Aufladevorgangs die Ladung auf den Kondensatorplatten Null ist.

Nun haben wir die Fälle am Anfang und am Ende des Aufladevorgangs betrachtet. Misst man im nebenstehenden Stromkreis die aktuelle Stromstärke mit einem Amperemeter, so kann man näherungsweise die bereits auf die Kondensatorplatten geflossene Ladung bestimmen. Hierzu verwendet man das arithmetische Mittel
der Stromstärke im bereits verstrichenen Zeitraum:
Mit der Maschenregel lässt sich so für jeden Zeitpunkt die Kapazität des Kondensators berechnen:

