Stereoisomerie und optische Aktivität

Einführung

Dieses Skript behandelt die theoretischen und experimentellen Grundlagen der Enantiomerie, als Sonderfall der Stereoisomerie und der optischen Aktivität von Enantiomeren. Im Zusammenhang mit der Stereoisomerie steht der Begriff der Struktur von organischen Verbindungen in diesem Skript für uns im Vordergrund. Der Aufbau gliedert sich grob in zwei größere Blöcke:

Enantiomerie als Sonderfall der Stereoisomerie: Struktur und Geometrie von organischen Verbindungen.
Optische Aktivität

Wir beginnen mit dem Begriff der Enantiomerie als Sonderfall der Stereoisomerie und ordnen diesen in das Konzept der Isomerie ein. Anschließend wenden wir uns chiralen und achiralen Molekülen zu, welche wir auf Grundlage einfacher Symmetrieelemente unterscheiden können. Dafür werfen wir zum Abschluss der ersten Blocks einen Blick auf die für uns relevanten Symmetrien in organischen Molekülen.

Im nächsten Schritt gehen wir auf das Phänomen der optischen Aktivität ein. Wir klären zunächst den Begriff des linear polarisierten Lichts, um darauf aufbauend die optische Aktivität von Enantiomeren zu verstehen. Wir schließen dieses Skript mit dem Experiment in Form des Polarimeters ab. Dieses wird uns erlauben, die Polarisation von Licht direkt zu messen.

Anmerkung:

Der Begriff der Struktur ist ein zentrales Element der organischen Chemie, weshalb er im ChemieLV-Themengebiet Naturstoffe in vielen Fällen sehr wichtig wird. Deswegen spielt hier vor allem dein räumliches Vorstellungsvermögen, welches wir mit geeigneten Abbildung unterstützen werden, eine zentrale Rolle.

Eine spezielle Form der Isomerie: Stereoisomerie

Die Keil-Strich-Schreibweise

Wir beginnen mit Molekülen und deren Struktur. Da es sich bei Molekülen um dreidimensionale Objekte handelt, wollen wir eine geeignete Darstellung wählen: die Keil-Strich-Schreibweise (vgl. Abb.1).

Abb. 1: Keil-Strich-Schreibweise am Beispiel von Chlorethan und 1,2-Dibromethan

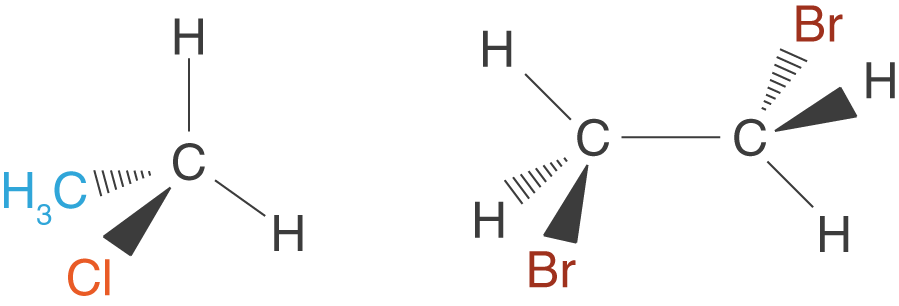
Beachte bei dieser Darstellung folgende drei Punkte, wobei es sich bei der Zeichenebene um das Blatt Papier handelt, das du vor die liegen hast:

Alle einfach gezeichneten Bindungen liegen in der Zeichenebene.
Alle fett gezeichneten Bindungen zeigen aus der Zeichenebene auf den Betrachter zu.
Alle gestrichelt gezeichneten Bindungen zeigen hinter die Zeichenebene, also vom Betrachter weg.

Mit diesem Wissen können wir uns nun den strukturellen Fragen zuwenden und den Begriff der Stereoisomerie klären.

Die Stereoisomerie: Enantiomere und Diastereomere

Wir beginnen damit, den Begriff der Stereoisomerie in den Kontext anderer Isomerietypen einzuordnen (vgl. Abb. 2). Unter Isomerie verstehen wir das Auftreten von Molekülen, die sich nicht in ihren atomaren Bestandteilen, sondern ihrer Struktur unterscheiden. Somit kennzeichnen sich Isomere durch gleiche Summenformeln und gleiche molare Massen.

Abb. 2: Übersicht Isomerie

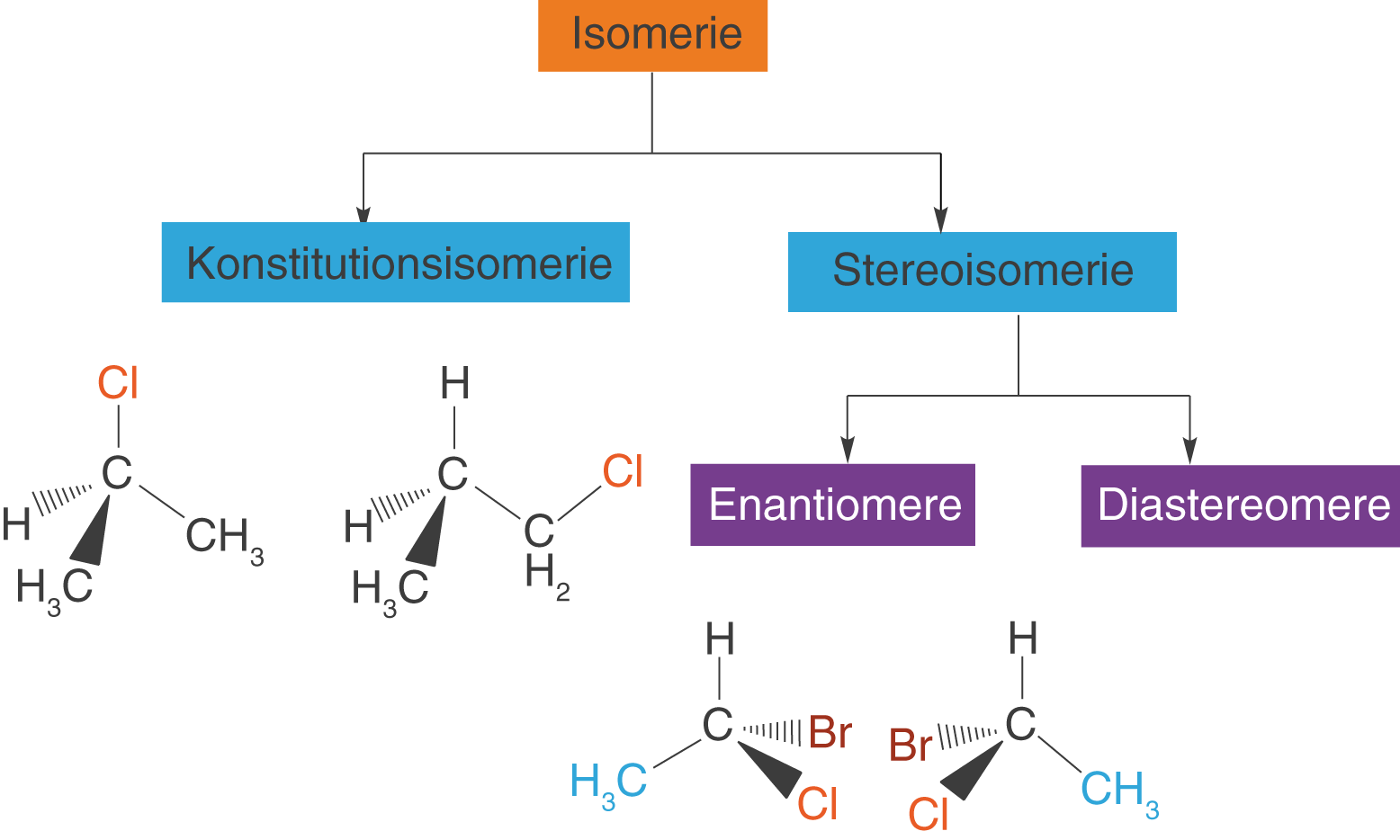
Wir interessieren uns nun weiterhin für die Stereoisomerie, folgen also dem rechten Pfad des in Abbildung 2 dargestellten Diagramms. Bei den Konstitutionsisomeren unterscheiden sich die Moleküle insbesondere in der Atomanordnung. Diese interessieren uns hier aber nicht.

Im Falle von Stereoisomeren sind die Atome im Molekül gleichartig angeordnet, unterscheiden sich jedoch in ihrer räumlichen Orientierung. Gleichartig angeordnet bedeutet, dass die Reihenfolge der aneinander gebundenen Atome in einem Molekül immer gleich ist. Diese Eigenschaft führt zur Bildung von zwei weiteren Gruppen: den Enantiomeren und den Diastereomeren. Insbesondere die Enantiomere werden uns im Zusammenhang mit dem Begriff der Chiralität beschäftigen (s.u.). An dieser Stelle nur so viel:

Zwei Enantiomere verhalten sich zueinander wie Bild und Spiegelbild.
Zwei Diastereomere verhalten sich nicht wie Bild und Spiegelbild zueinander.

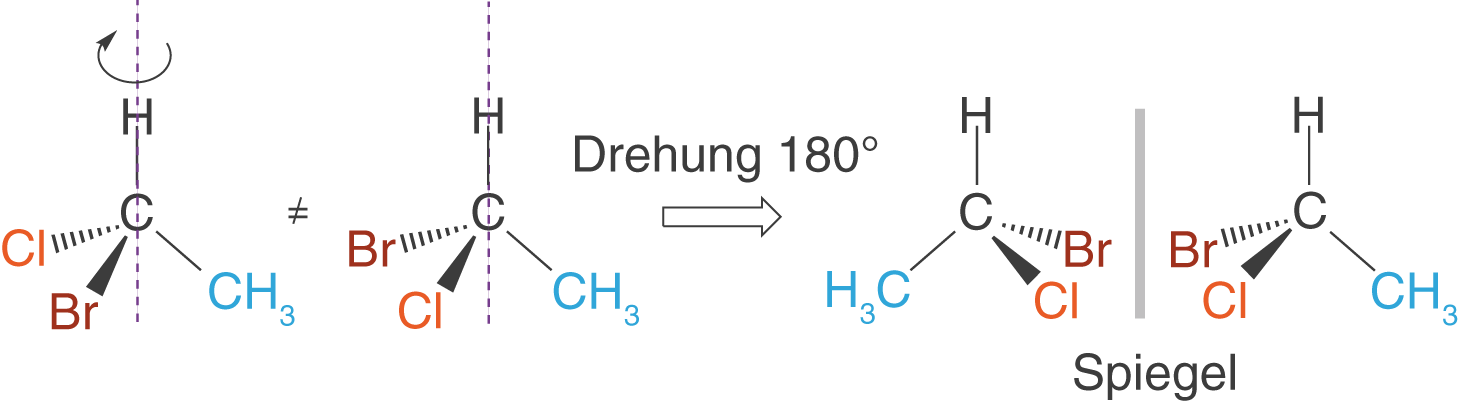
Wir wollen die Eigenschaft der Enantiomere an einem Beispiel veranschaulichen. Dazu nehmen wir das linke der beiden Enantiomere aus Abbildung 2 und drehen es schrittweise um die senkrechte Achse, bis es von der Stellung der Substituenten (Reste) dem auf der rechten Seite entsprechen würde:

Abb. 3: Drehung von 1,1-Bromchlorethan um die senkrechte Rotationsachse

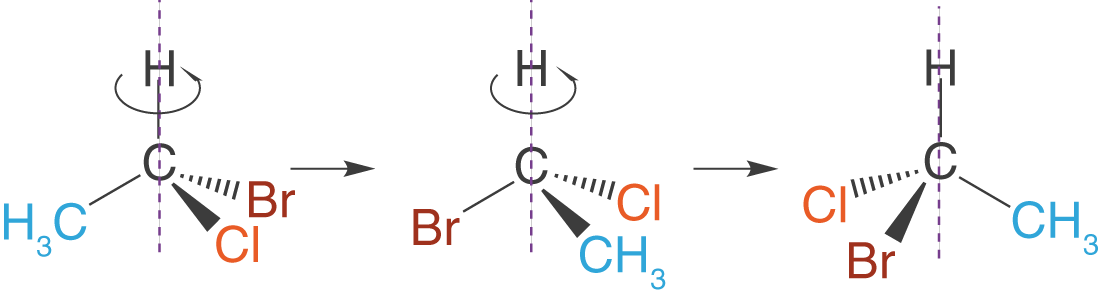
Nun vergleichen wir die beiden Enantiomere (vgl. Abb.4) und erkennen, dass sie nicht die gleiche Struktur aufweisen: Es sind Spiegelbilder, die durch Drehung nicht ineinander überführt werden können.

Abb. 5: Spiegelbildlichkeit von Enantiomeren

Ein prominentes Beispiel für diese Eigenschaft findest du auch im Alltag: deine Hände. Lege diese mit den Handflächen nach unten vor dir auf den Tisch. Du kannst sehen, dass die beiden sich wie Spiegelbilder zueinander verhalten, wenn du eine Spiegelebene in die Mitte legst (vgl. Abb.5).

Abb. 6: Spiegelbildlichkeit von Händen

Bewegst du nun eine der beiden Hände über die andere, dann bemerkst du, dass du die beiden nicht zur Deckung bringen kannst. Ganz genauso verhalten sich Enantiomere.

Chirale und achirale Moleküle

Wir wollen uns nun eingehender mit Enantiomeren und ihrer Molekülstruktur beschäftigen. Die Eigenschaft, die es uns erlaubt Enantiomere als solche zu bezeichnen, ist die Chiralität dieser Moleküle. Verbindungen, die zu den Enantiomeren gezählt werden, sind chiral. Chirale Moleküle können mit ihren Spiegelbildern nicht zur Deckung gebracht werden.
Es gibt zwei Kriterien für Chiralität:

Moleküle mit genau einem asymmetrischen C-Atom sind immer chiral.
Verbindungen, die keine Symmetrieebene bzw. kein Symmetriezentrum aufweisen, sind chiral.

Das asymmetrische Kohlenstoffatom und chirale Moleküle

Das asymmetrische Kohlenstoffatom (C-Atom) wird folgendermaßen definiert:

Ein Kohlenstoffatom mit vier unterschiedlichen Substituenten bezeichnet man als asymmetrisch.

Wir ziehen das Beispiel von oben heran.

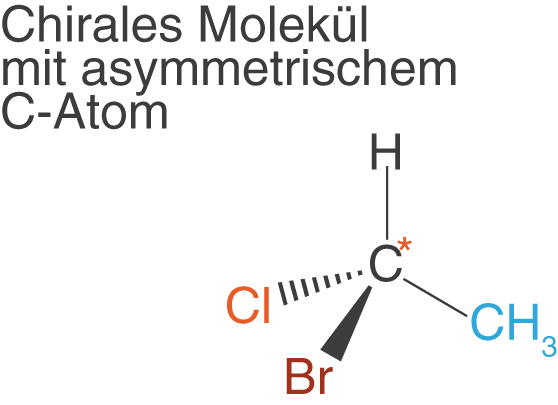
Das Kohlenstoffatom hat vier unterschiedliche Substituenten: H, Cl, Br und $\text{CH}_{3}$
Das asymmetrische C-Atom wird mit einem Stern (hier orange) gekennzeichnet.
Synonyme für asymmetrisches C-Atom sind Stereozentrum und Chiralitätszentrum.

Achtung:

An dieser Stelle ist es sehr wichtig die Definition der Chiralität auf Grundlage des asymmetrischen C-Atoms im Auge zu behalten. Nur Moleküle mit genau einem asymmetrischen C-Atom sind immer chiral! Bei Molekülen mit mehr als einem asymmetrischen C-Atom (Diastereomere) ist das nicht zwangsläufig der Fall.

Die zweite Definition der Chiralität, die wir durch das Fehlen von Symmetrieelementen wie Symmetrieebenen und Symmetriezentren gegeben haben, werden wir im Abschnitt 2.2 besprechen. Das liegt daran, dass wir uns zunächst die angesprochenen Symmetrieelemente anschauen wollen, bevor wir die Definition verstehen können.

Achirale Moleküle

Moleküle, die sich mit ihrem Spiegelbild zur Deckung bringen lassen, werden achiral genannt. Im folgenden sind einige Beispiele für achirale Moleküle im Vergleich zu einem Enantiomerenpaar dargestellt.

Abb. 6: Beispiele für chirale und achirale Moleküle auf Grundlage des asymmetrischen C-Atoms

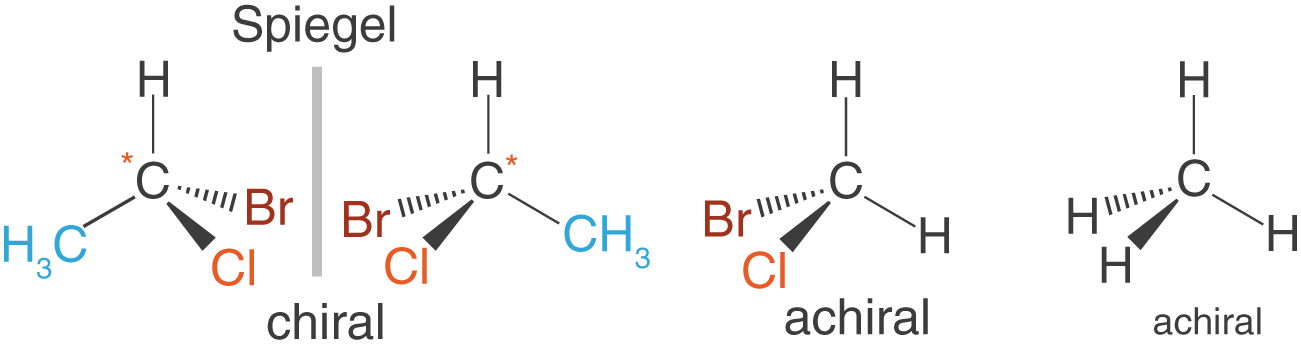
Das Enantiomerenpaar siehst du ganz links, wobei die asymmetrischen C-Atome wieder mit einem Stern gekennzeichnet sind (bedenke die vier unterschiedlichen Substituenten). An zweiter Stelle siehst du ein achirales Molekül, bei dem wir nun zwei Wasserstoffatome vorliegen haben, also nur drei und nicht vier unterschiedliche Substituenten. Rechts siehst du Methan, welches vier identische Substituenten aufweist und folglich auch achiral ist: wir können es mit seinem Spiegelbild durch Drehen zur Deckung bringen.

Das Racemat

Ein wichtiger Begriff, den wir hier zum Abschluss betrachten und später insbesondere im Zusammenhang mit der optischen Aktivität wieder aufgreifen, ist der des Racemat oder racemischen Gemischs. Dabei handelt es sich um ein Gemisch eines Enantiomerenpaares, bei welchem beide Enantiomere zu gleichen Teilen vorliegen.
Ein Racemat kann etwa bei der Chlorierung von Butan auftreten. Hierbei kann das elementare Chlor ( $\text{Cl}_{2}$ ) durch Wärmeenergie ( $\Delta E$ ) gespalten werden, damit die Reaktion ablaufen kann.

Abb. 7: Bildung eines Racemats bei der Chlorierung von Butan

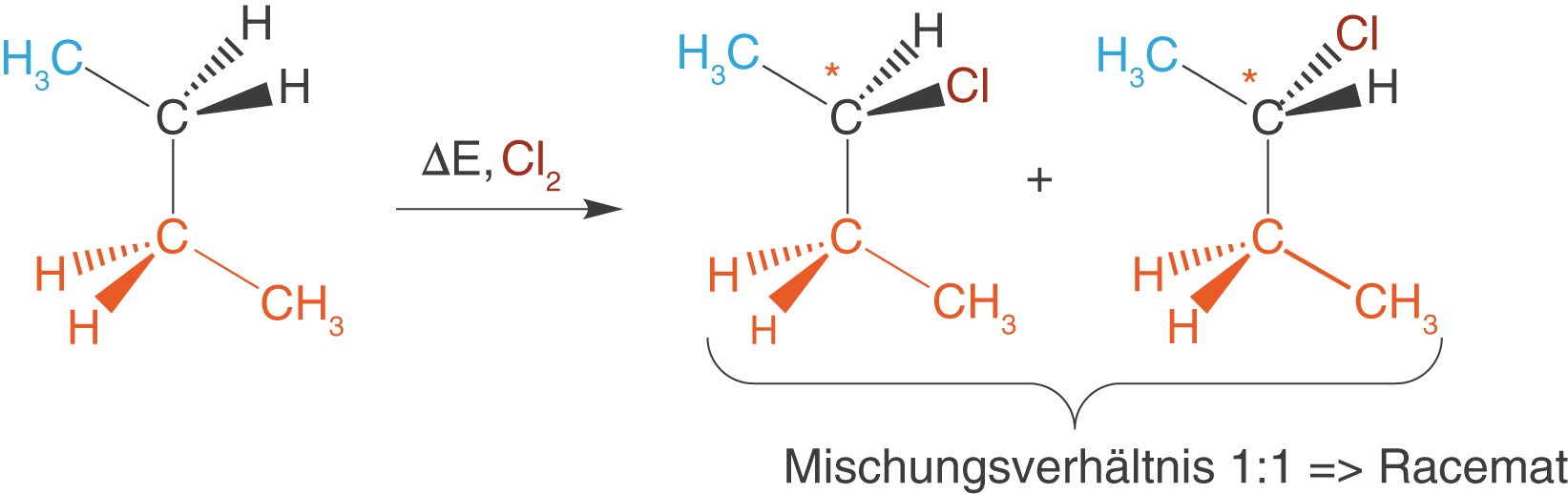
Bei dieser Reaktion ist keines der beiden schwarz eingefärbten H-Atome von Butan bevorzugt. Folglich können beide durch Chloratome ersetzt (substituiert) werden. Führt diese Reaktion zu einem Mischungsverhältnis der Produkte von 1:1, dann liegt ein Racemat vor. Hier liegen die beiden Produkte zu gleichen Teilen (1:1) vor. Auf dieses Thema werden wir im Zusammenhang mit dem Begriff der optischen Aktivität zurückkommen.

Symmetrien in organischen Molekülen

Anhand der Definition haben wir gesehen, dass wir die Chiralität von Molekülen auch über deren Symmetrieeigenschaften definieren können. Das Konzept der Symmetrie hört sich zunächst sehr abstrakt an, doch du bist damit bereits aus dem Alltag vertraut.

Symmetrien in der Natur

Wir betrachten zunächst Objekte aus der Natur und deren Symmetrieeigenschaften.

Abb. 8: Symmetrie in der Natur

Wir schauen uns nun die Symmetrien der dargestellten Objekte von links nach rechts an:

Die linke Flügelhälfte des Schmetterlings sieht genauso aus wie seine rechte; die Flügelhälften sind symmetrisch.
Die Samen der Tomate sind ebenfalls nahezu symmetrisch in das Fruchtfleisch eingebettet.
Der Baum ist unsymmetrisch gewachsen; das erkennst du bei der Betrachtung der Äste.

Uns geht es nun darum, solche Eigenschaften auch in organischen Molekülen zu finden. Du wirst relativ schnell merken, dass ein solches Vorhaben oft keinesfalls einfach ist.

Die Symmetrieebene in organischen Molekülen

Eine Symmetrie- oder Spiegelebene liegt so in einem Objekt, dass eine der anderen Seite entspricht. Beispielsweise weist der Schmetterling im ersten Bild eine senkrechte Symmetrieebene auf, die genau zwischen den beiden Flügelhälften verläuft.
Wenden wir uns nun den Symmetrieebenen in organischen Molekülen zu. Zur besseren Veranschaulichung werden die einzelnen Atome als farbige Kugeln dargestellt.

Abb. 9: Perspektivische Darstellung von Methan ( $\text{CH}_{4}$ ) und Dichlormethan ( $\text{CH}_{2}\text{Cl}_{2}$ )

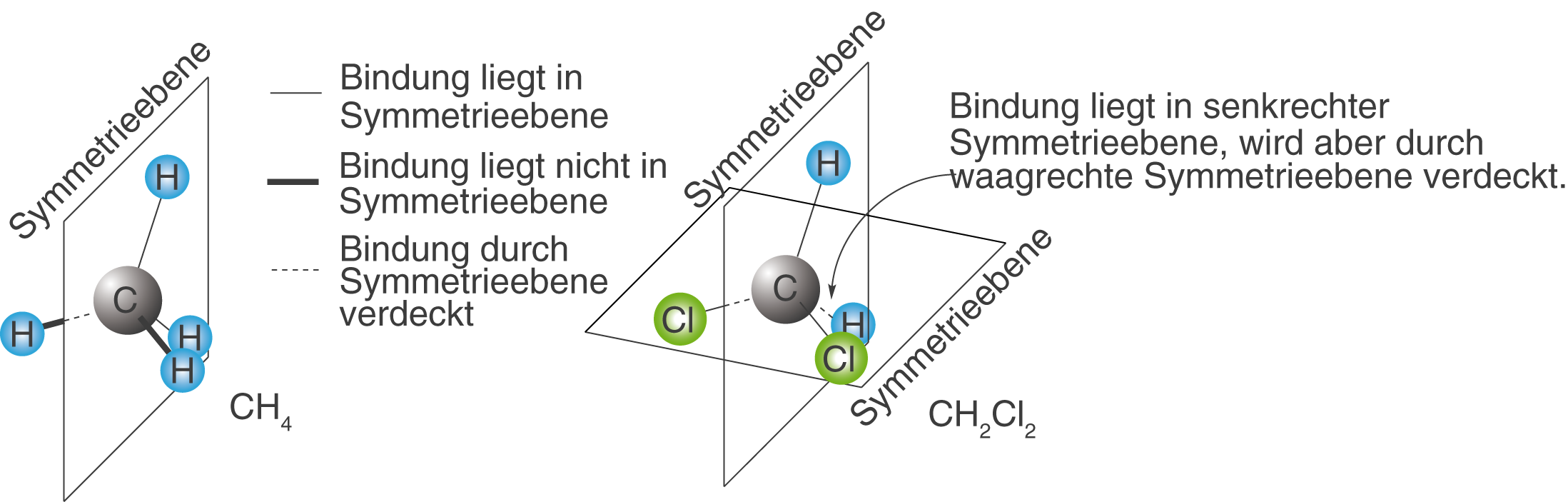
Links siehst du Methan mit einer eingezeichneten Symmetrieebene und rechts Dichlormethan mit zwei eingezeichneten Symmetrieebenen. Du siehst, dass Moleküle wie im zweiten Fall auch mehrere Symmetrieebenen aufweisen können.

Abb. 10: Drei unterschiedliche Substituenten führen zu einer Symmetrieebene)

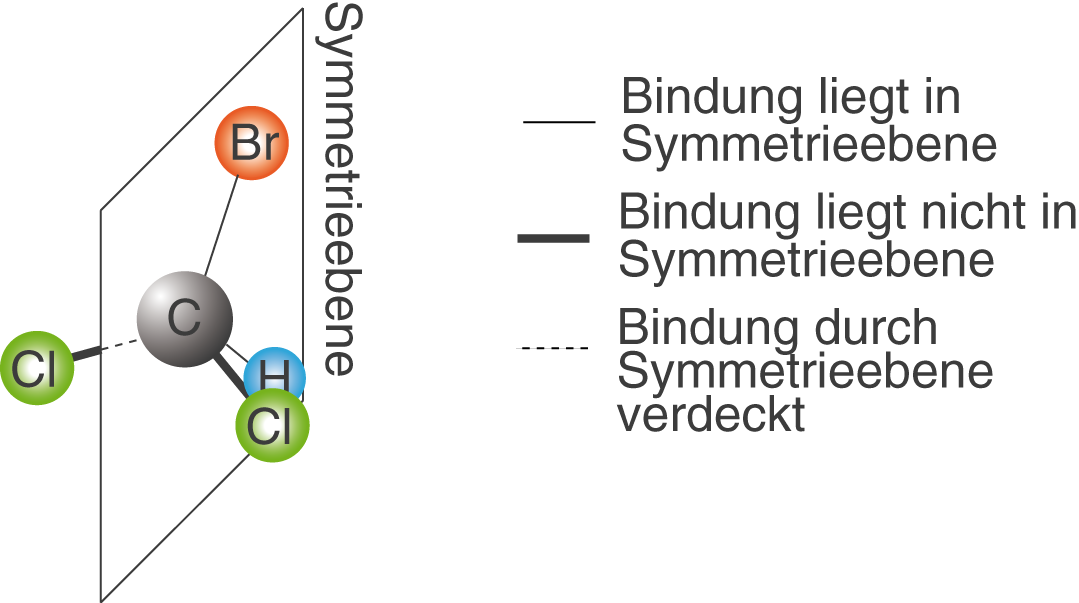
Beachte, dass die Orientierung der Ebene im Raum eine wichtige Rolle spielt. In Abbildung 10 haben wir eines der Wasserstoffatome durch ein Bromatom ersetzt. Das Ergebnis ist das Verschwinden der waagrechten Symmetrieebene.

Insbesondere beim letzten Molekül ist nicht gleich ersichtlich, dass hier überhaupt eine Symmetrieebene vorliegt. Denke immer daran, dass du diese auch „durch“ Atome „hindurchlegen“ kannst; du spaltest quasi die hier dargestellten Kugeln in der Mitte. Nach diesem Vorgehen erhältst du die Symmetrieebene in Abbildung 10.

Das Symmetriezentrum in organischen Molekülen

Neben der Symmetrieebene ist das Symmetriezentrum ein weiteres wichtiges Symmetrieelement. Ein anderer Begriff für das Symmetriezentrum lautet Inversionszentrum. Dabei handelt es sich um einen Punkt in einem Molekül, an welchem du mittels Punktspiegelung einzelne Elemente des Moleküls ineinander überführen kannst.

Abb. 11: Beispielhaftes Molekül mit Symmetriezentrum

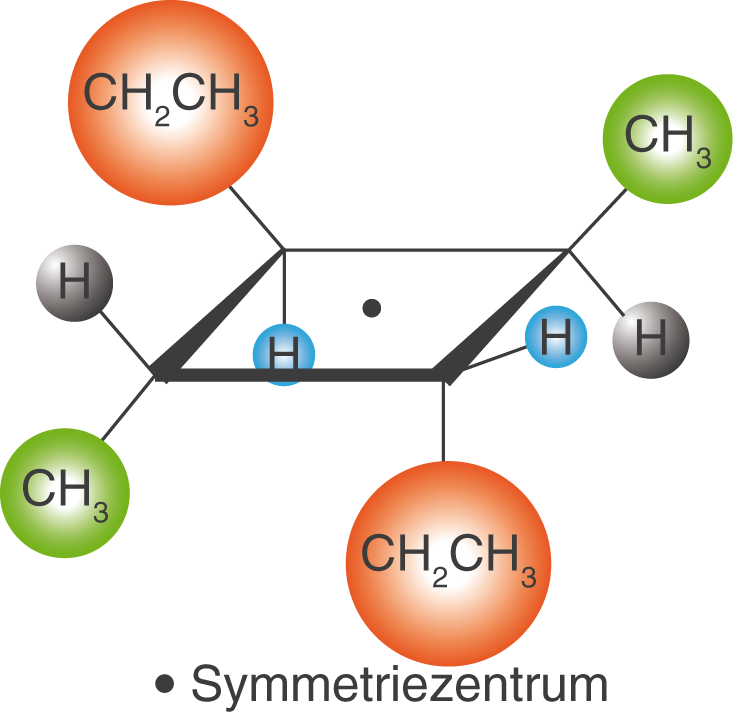
Du kannst durch alle dargestellten Substituenten eine Gerade ziehen, auf der jeweils zwei gleiche Substituenten und das Symmetriezentrum liegen.
Mit unserem Wissen um die beiden Symmetrieelemente Symmetrieebene und Symmetriezentrum können wir an dieser Stelle nun auch die zweite Definition für chirale Moleküle verstehen:

Moleküle, die weder eine Symmetrieebene noch ein Symmetriezentrum aufweisen, sind chiral.

Optische Aktivität

Bis hierhin haben wir die Eigenschaften der Enantiomere kennengelernt und wissen nun, wie wir die Chiralität von Molekülen aufgrund von Symmetrieelementen herausfinden können.
Problematisch wird es, wenn wir Enantiomere im Experiment unterscheiden wollen, da wir die Moleküle ja nicht sehen können. Das Knifflige an dieser Situation ist die große Ähnlichkeit der Moleküle eines Enantiomerenpaares. Viele physikalische Eigenschaften, wie das Gewicht, der Schmelz- und Siedepunkt sowie die Dichte, stimmen überein. Wir müssen folglich eine andere Eigenschaft zur Unterscheidung heranziehen: die optische Aktivität.

Optische Aktivität: Eigenschaft eines Enantiomers, die Schwingungsebene von linear polarisiertem Licht um einen gewissen Betrag in eine bestimme Richtung zu drehen.

In dieser Definition sind viele neue Begriffe enthalten. Wir wollen in diesem Kapitel folgendermaßen vorgehen:

Wir klären zunächst, was man unter der Schwingungsebene von Licht versteht.
Anschließend klären wir den Begriff des linear polarisierten Lichts.
Nun können wir die Eigenschaft der optischen Aktivität verstehen.
Abschließend betrachten wir eine experimentelle Methode in Form des Polarimeters, um die Polarisation von Licht zu messen.

Linear polarisiertes Licht

Linear polarisiertes Licht weist im Gegensatz zu unpolarisiertem Licht nur eine Schwingungsrichtung des elektrischen Felds auf.
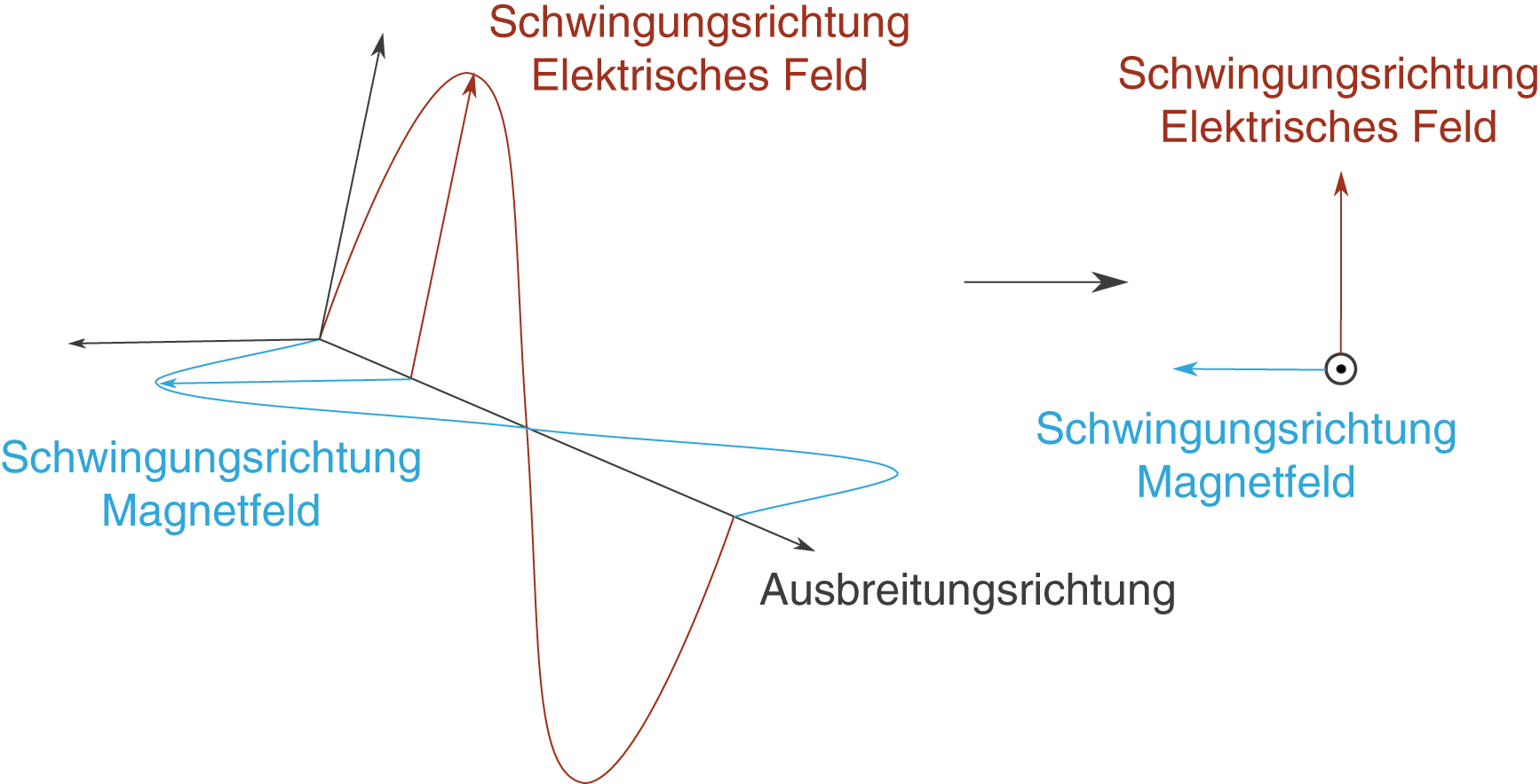
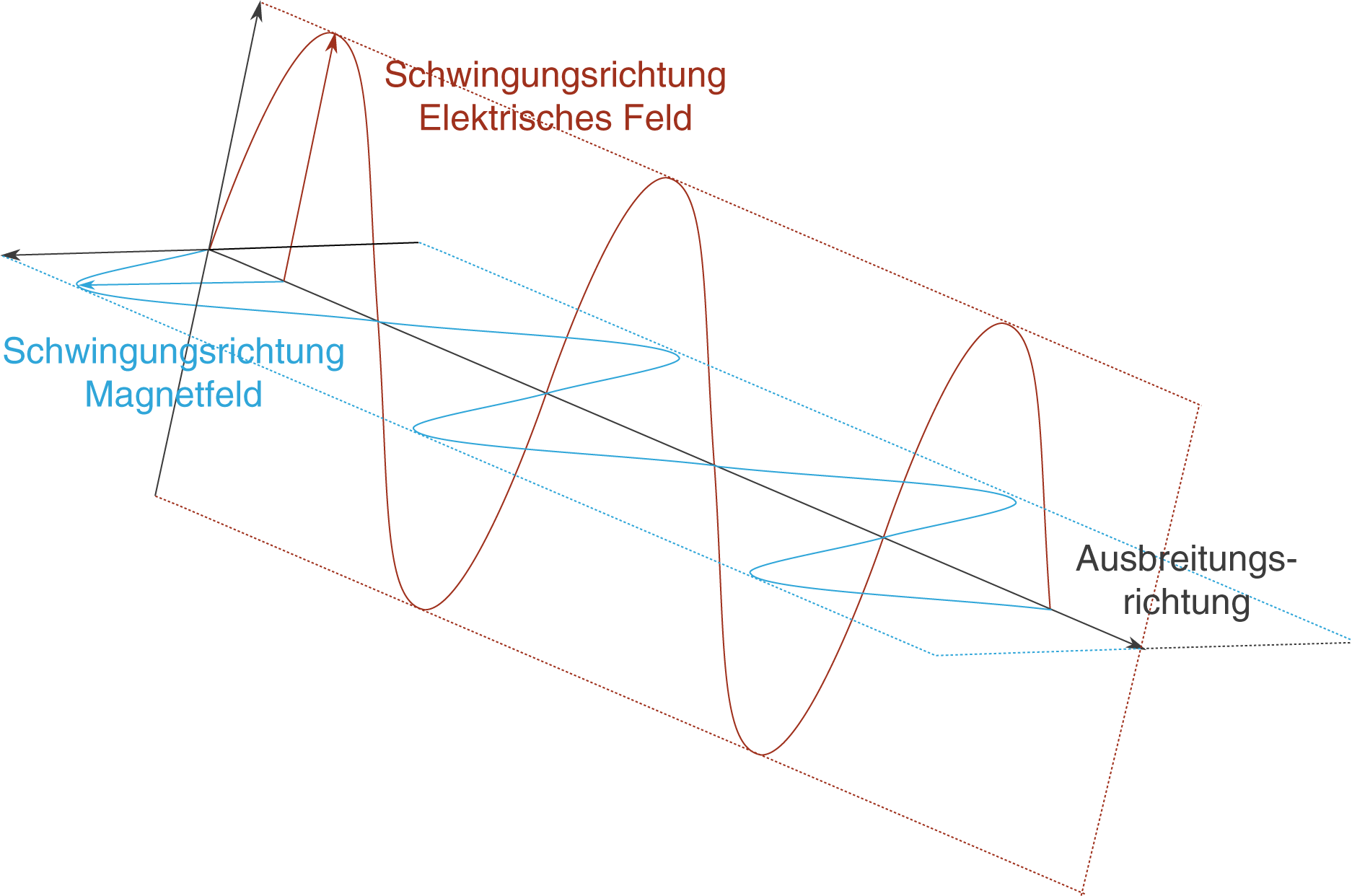
Licht ist eine elektromagnetische Welle. Dabei schwingt das elektrische Feld (roter Pfeil) senkrecht zur Ausbreitungsrichtung des Lichts. Der zweite Anteil einer elektromagnetischen Welle besteht aus einem Magnetfeld (blauer Pfeil), das sowohl senkrecht zur Ausbreitungsrichtung als auch senkrecht zum elektrischen Feld schwingt (vgl. Abb.12).

Abb. 12: Eine Schwingungsrichtung des elektrischen und des magnetischen Feldes bei Licht

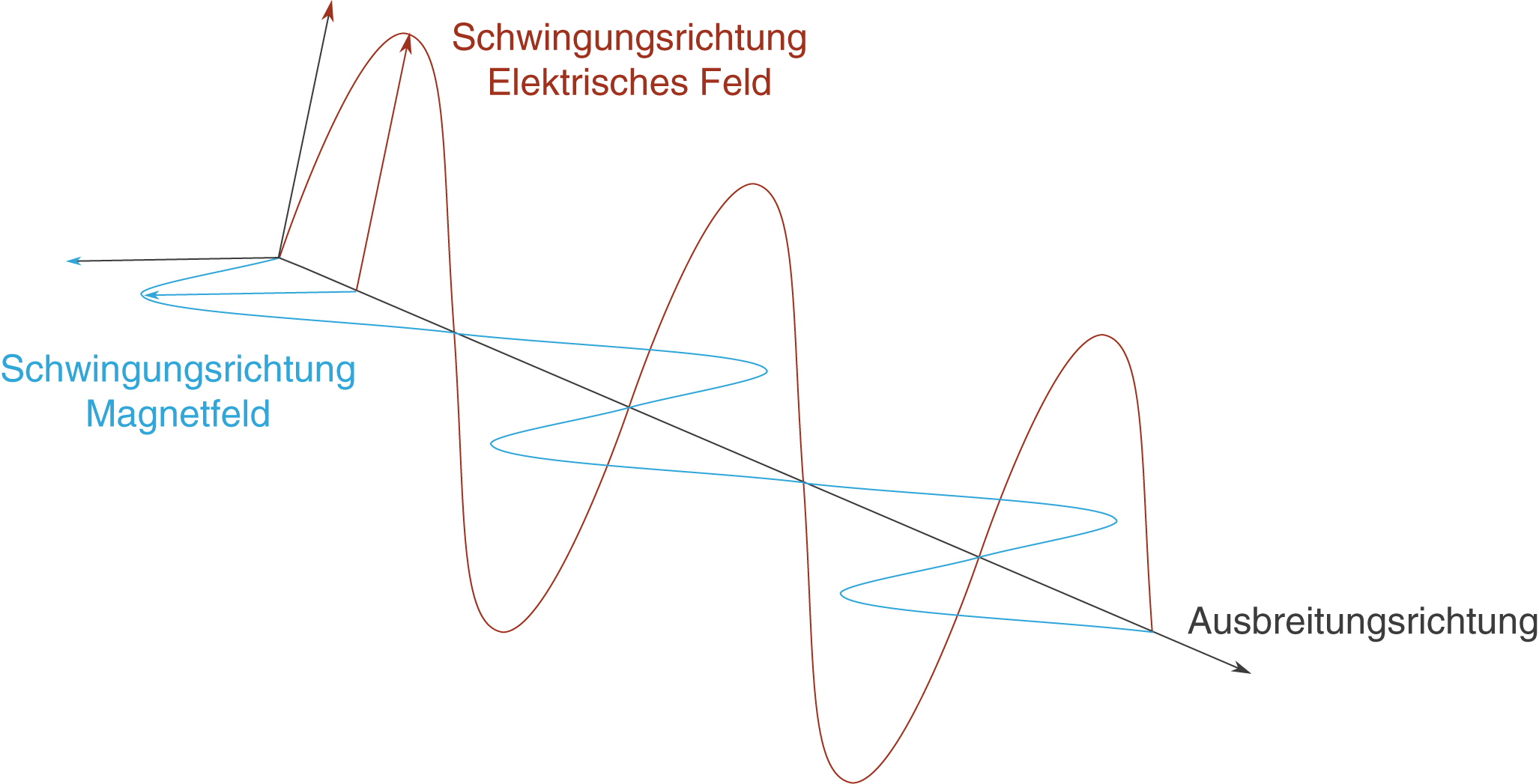
Um die Darstellung zu vereinfachen, schauen wir entgegen der Ausbreitungsrichtung auf die elektromagnetische Welle; diese kommt also gleichsam auf uns zu (vgl. Abb.13).

Abb. 13: Veränderte Ansicht der Schwingungsrichtung

Nehmen wir unpolarisiertes Licht, dann ist nicht nur eine solche Schwingungsebene vorhanden, wie hier gezeigt, sondern sehr viele. Das elektrische Feld schwingt in unpolarisiertem Licht also in allen möglichen Raumrichtungen. „Zwingen“ wir dieses Licht nun dazu, dass das elektrische Feld nur in einer bevorzugten Richtung schwingt, dann spricht man von linear polarisiertem Licht. Der Prozess, der dazu führt, wird Polarisierung genannt (vgl. Abb.14).

Abb. 14: Schematische Darstellung der Polarisierung von Licht

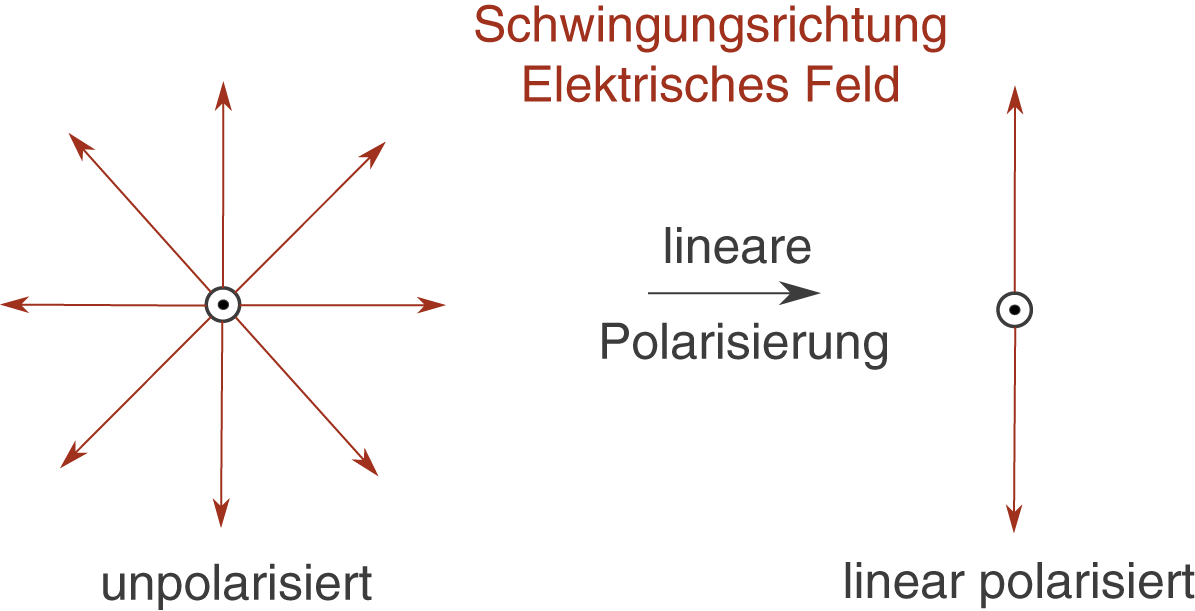
Wenn wir nun wieder die anfänglich gewählte Darstellung wählen, erhalten wir ein ganz ähnliches Bild (vgl. Abb.15). Das elektrische Feld (rot) von linear polarisiertem Licht schwingt nur in einer Ebene, die hier gestrichelt angedeutet ist.

Abb. 15: Linear polarisiertes Licht mit angedeuteter Schwingungsebene von elektrischem und magnetischem Feld

Im nächsten Schritt betrachten wir die Wechselwirkung von linear polarisiertem Licht mit Enantiomeren: die optische Aktivität.

Die optische Aktivität

Nun können wir die Definition der optischen Aktivität aufgreifen, die wir zu Beginn dieses Abschnitts gegeben haben. Bei der Wechselwirkung von linear polarisiertem Licht mit einem Enantiomer wird die Schwingungsebene des Lichts um einen gewissen Winkel gedreht.

Wird die Schwingungsebene des linear polarisierten Lichts durch die Wechselwirkung mit einem Enantiomer mit dem Uhrzeigersinn gedreht, dann bezeichnet man das Enantiomer als rechtsdrehend und kennzeichnet es laut Konvention als (+)-Enantiomer.
Nimmt man nun das andere Enantiomer und lässt es in Wechselwirkung mit linear polarisiertem Licht treten, dann wird die Schwingungsebene um den gleichen Betrag wie im ersten Fall gegen den Uhrzeigersinn gedreht. Hierbei handelt es sich dann um das linksdrehende Enantiomer, welches als (-)-Enantiomer bezeichnet wird.

Substanzen, die linear polarisiertes Licht drehen, werden als optisch aktiv bezeichnet - solche, die keine Drehung zur Folge haben, als optisch inaktiv.
Die Drehung des linear polarisierten Lichts können wir mithilfe eines Polarimeters messen. Diesen Messprozess wollen wir uns nun im Detail anschauen.

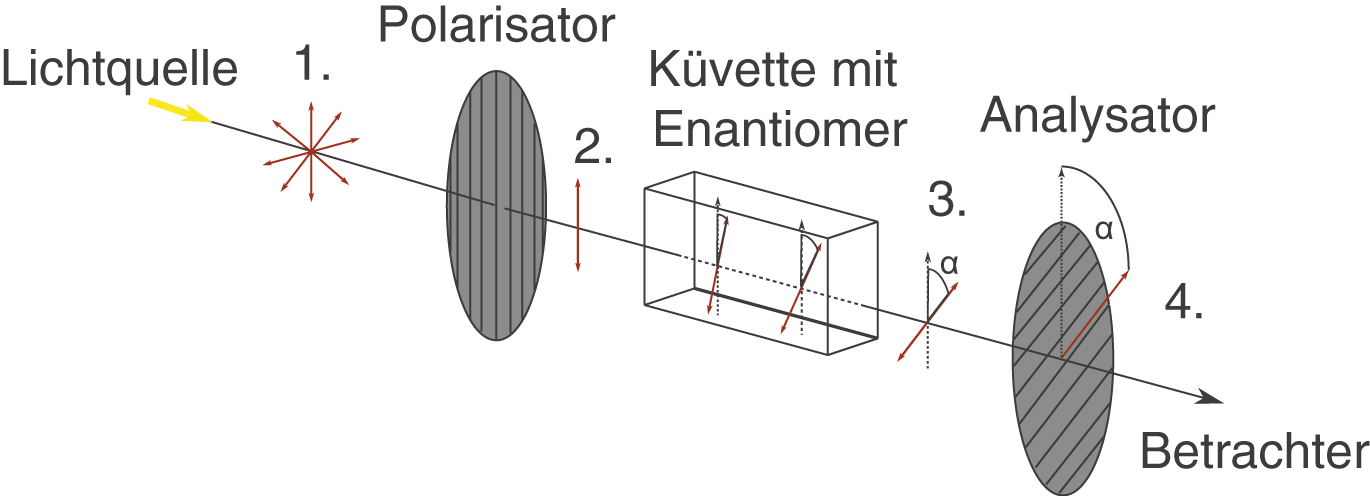
Messen der optischen Drehung - das Polarimeter

Wir schauen uns den Aufbau des Polarimeters an und betrachten dann schrittweise die einzelnen Bestandteile und ihren Beitrag zum Messprozess. Für die Darstellung des Lichts beschränken wir uns auf die vereinfachte Darstellung der Schwingungsrichtung des elektrischen Feldes und ignorieren das Magnetfeld.

Abb. 16: Aufbau eines Polarimeters

Ein Polarimeter besteht aus vier Komponenten:

einer Lichtquelle
einem Polarisator
einer Küvette (Messzelle) mit der optisch aktiven Substanz
einem Analysator

Wir wollen uns nun die Wirkungsweise des Polarimeters anhand der Schritte 1 - 4 klar machen.

Eine Lichtquelle (Lampe bspw.) emittiert Licht ohne bevorzugte Polarisationsrichtung; das elektrische Feld schwingt in alle Raumrichtungen. Dieses Licht breitet sich in Richtung des Betrachters aus.
Das Licht trifft auf den Polarisator. Diesen kannst du dir als eine Art „senkrechtes“ Gitter vorstellen, welches nur eine einzige Schwingungsrichtung des Lichts durchlässt. Alle anderen werden durch den Polarisator blockiert. Als Ergebnis erhalten wir an dieser Stelle das linear polarisierte Licht.
Das linear polarisierte Licht trifft auf eine Küvette (Messzelle), die eine optisch aktive Verbindung (ein Enantiomer) enthält. Hier treten das linear polarisierte Licht und die optisch aktive Verbindung in Wechselwirkung, was dazu führt, dass die Schwingungsrichtung des Lichts um einen gewissen Winkel $\alpha$ gegen die Senkrechte gedreht wird.
Der Analysator entspricht vom Aufbau her dem Polarisator. Im Experiment wird der Analysator solange gegen die Senkrechte gedreht, bis genau die Schwingungsebene des Lichts, die das Resultat der Wechselwirkung mit der optisch aktiven Substanz darstellt, das Gitter passieren kann. Der erhaltene Winkel entspricht dem Winkel $\alpha$ , gemessen in Grad $^{\circ}$ .

Das Polarimeter erlaubt die Messung des Winkels $\alpha$ , um den das linear polarisierte Licht durch die Wechselwirkung mit der optisch aktiven Substanz gegen die Senkrechte verdreht wird. Liegt hingegen keine optisch aktive Substanz vor, so kommt es auch zu keiner Drehung des linear polarisierten Lichts. Die Einstellung des Analysators erfolgt ganz praktisch durch Drehen, bis das Licht am hellsten erscheint.

Achtung:

Eine optisch inaktive Substanz führt nicht zur Drehung von linear polarisiertem Licht. Der Umkehrschluss, dass wenn keine Drehung vorliegt, auch eine optisch inaktive Substanz vorliegt, ist jedoch falsch! Wir werden sehen, dass im Fall von racemischen Gemischen ebenfalls keine Drehung gemessen werden kann, obwohl die Bestandteile optisch aktiv sind.

Die spezifische Drehung $\boldsymbol[\alpha]$

Um vergleichbare Ergebnisse zu erhalten und Missverständnisse zu vermeiden, wurde statt der beobachtbaren optischen Drehung $\boldsymbol{\alpha}$ die spezifische Drehung $\boldsymbol[\alpha]$ eingeführt. Diese Größe berechnet sich zu:

$[\alpha]=\dfrac{\alpha}{\beta\cdot l}$ mit $T=\text{const.}$ und $\lambda=\text{const.}$

Folgende Größen fließen hier ein:

die beobachtbare optischen Drehung $\alpha$
die Massenkonzentration $\beta$ der Analysesubstanz
die Länge $l$ der Küvette (Messzelle)
Die Temperatur $T$ wird während der Messung konstant gehalten.
Durch die Verwendung spezifischen Lichts ist die Wellenlänge $\lambda$ des verwendeten Lichts ebenfalls konstant.

Optische Rotation und Probenzusammensetzung

In Kapitel 2.1 haben wir den Begriff des Racemats eingeführt. Zur Wiederholung: Hierbei handelt es sich um das Gemisch eines Enantiomerenpaares, bei dem die beiden Enantiomere im Verhältnis von 1:1 vorliegen. Mit diesem Wissen können wir nun die Zusammensetzung von Gemischen ermitteln.

Optische Aktivität des Racemat

Ein Racemat stellt ein Gemisch zweier Enantiomere dar, welche im Verhältnis von 1:1 vorliegen.
Ein Enantiomerenpaar besteht aus zwei Enantiomeren, die linear polarisiertes Licht um den gleichen Betrag in die jeweils andere Drehrichtung drehen. Hierbei spielen die Begriffe des ( $+$ )- und ( $-$ )-Enantiomers eine Rolle.
Durch die gleichen Beträge und unterschiedliche Vorzeichen der Drehrichtung hat ein Racemat eine spezifische Drehung von $[\alpha]=0^{\circ}$ .

Optische Aktivität von Gemischen mit ungleichen Anteilen

Dominiert in einem Gemisch eines der beiden Enantiomere, schlägt sich das auf die mittlere optische Drehung nieder. Die Drehrichtung der anteilsmäßig häufigeren Verbindung dominiert. Sind die spezifischen Drehungen der beiden enthaltenen Enantiomere bekannt, dann kann folglich der Anteil der beiden berechnet werden.

Zusammenfassung

Moleküle, die sich wie Bild und Spiegelbild zueinander verhalten, werden Enantiomere genannt.
Enantiomere gehören zu den Stereoisomeren, also zu den Molekülen, bei denen sich die räumliche Orientierung der Atome voneinander unterscheidet.
Enantiomere sind chirale Verbindungen.
Chirale Verbindungen sind durch das Vorhandensein eines asymmetrischen C-Atoms bzw. durch das Fehlen von Symmetrieebenen und Symmetriezentren gekennzeichnet.
Ein Kohlenstoffatom mit vier unterschiedlichen Substituenten wird als asymmetrisches C-Atom bezeichnet.
Ein 1:1 Gemisch eines Enantiomerenpaares wird Racemat bzw. racemisches Gemisch genannt.
Die Eigenschaft der optischen Aktivität zeigt sich darin, dass optisch aktive Substanzen die Schwingungsebene von linear polarisiertem Licht um einen Winkel $\alpha$ drehen.
Das elektrische Feld von \textbf{linear polarisiertem Licht} schwingt in einer einzigen Ebene.
Die optische Drehung ((-) = links; (+) = rechts) kann mithilfe eines Polarimeters gemessen werden; hierbei wird die beobachtbare optische Drehung $\boldsymbol{\alpha}$ gemessen.
Um Missverständnisse zu vermeiden wird die beobachtbare optische Drehung $\boldsymbol{\alpha}$ auf die Länge der Küvette (Messzelle) und auf die Massenkonzentration der Enantiomerlösung bezogen; somit wird die spezifische Drehung $\boldsymbol{[\alpha]}$ definiert.
Die spezifische Drehung $\boldsymbol{[\alpha]}=\dfrac{\alpha}{\beta\cdot l}$ wird bei konstanter Temperatur $\boldsymbol{T}$ und mit konstanter Wellenlänge $\boldsymbol{\lambda}$ gemessen.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

Public Domain

[6]

[7]

[8]

Public Domain

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Public Domain