Definition

Als chemische Bindung bezeichnen wir das Phänomen, dass Atome in Form von Molekülen bzw. chemischen Verbindungen zusammenhält. Die chemische Bindung ist ein Überbegriff, der sich in drei Bindungstypen unterteilen lässt:

Die kovalente Bindung oder Elektronenbindung
Die Ionenbindung
Die metallische Bindung

Eine chemische Bindung ist in vielen Fällen nicht nur einem dieser drei Typen zuzuordnen, sondern weist Eigenschaften aller drei Bindungstypen auf. Die hier aufgeführten Bindungen, die wir in diesem Skript besprechen wollen, stellen somit die Idealfälle verschiedener Bindungstypen dar, die in ihrer „reinen“ ausgeprägten Form in der Realität vorrangig aber nicht existieren. Eine chemische Bindung ist im Allgemeinen sehr stabil und nicht einfach aufzubrechen. Im Gegensatz dazu stehen die zwischenmolekularen Kräfte. Diese wollen wir anhand von

Wasserstoffbrückenbindungen (H-Brücken)
Dipol-Dipol-Wechselwirkungen
Van-der-Waals-Kräfte (vdWK)

im zweiten Teil dieses Skriptes besprechen. Diese Kräfte und Wechselwirkungen sind bei Weitem nicht so stark wie eine chemische Bindung, spielen jedoch in vielen Fällen eine zentrale Rolle beim Aufbau und der Reaktivität von Molekülen.

Die chemische Bindung

Die kovalente Bindung - Elektronenbindung

Konzept der kovalenten Bindung

$\blacktriangleright \;$ Die Lewis-Schreibweise

Die kovalente Bindung, die auch als Elektronenbindung bekannt ist, wird im Allgemeinen durch die Lewis-Schreibweise oder auch Valenzstrichformel dargestellt. Diese geht auf den amerikanischen Chemiker Gilbert N. Lewis zurück. Hierbei gilt es folgende Regeln zu beachten:

Bindende Elektronenpaare werden als Strich zwischen den Bindungspartnern dargestellt.
Nicht-bindende oder freie Elektronenpaare werden ebenfalls durch einen Strich dargestellt.
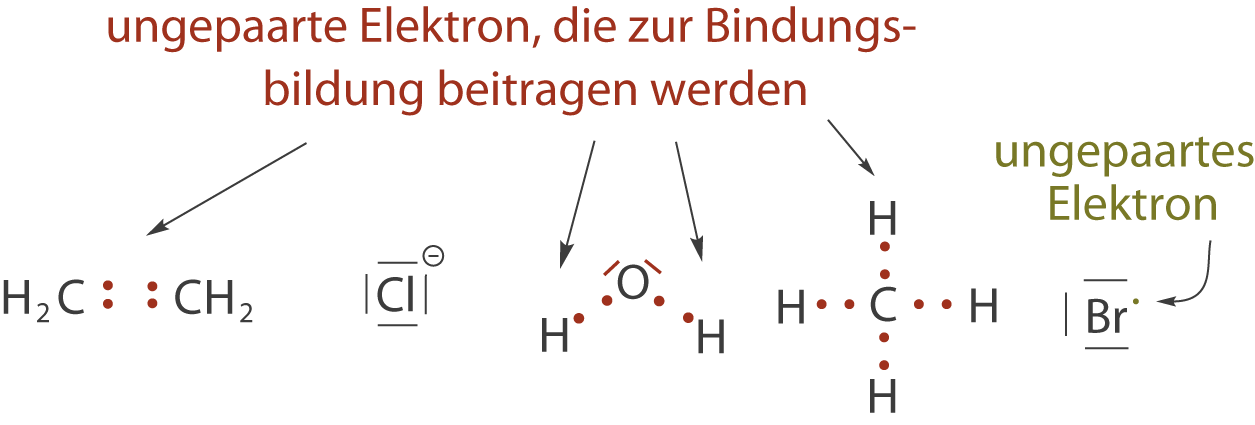
Ungepaarte Elektronen werden durch einen Punkt dargestellt.
Es werden nur die Valenzelektronen (Außenelektronen) der beteiligten Atome berücksichtigt, deshalb auch die Bezeichnung Valenzstrichformel.

Diese Regeln können wir anhand folgender Beispiele nachvollziehen. Wir betrachten zunächst die freien Elektronen der Bindungspartner (vgl. Abb. 1) und knüpfen im Anschluss die jeweiligen Bindungen (vgl. Abb. 2).

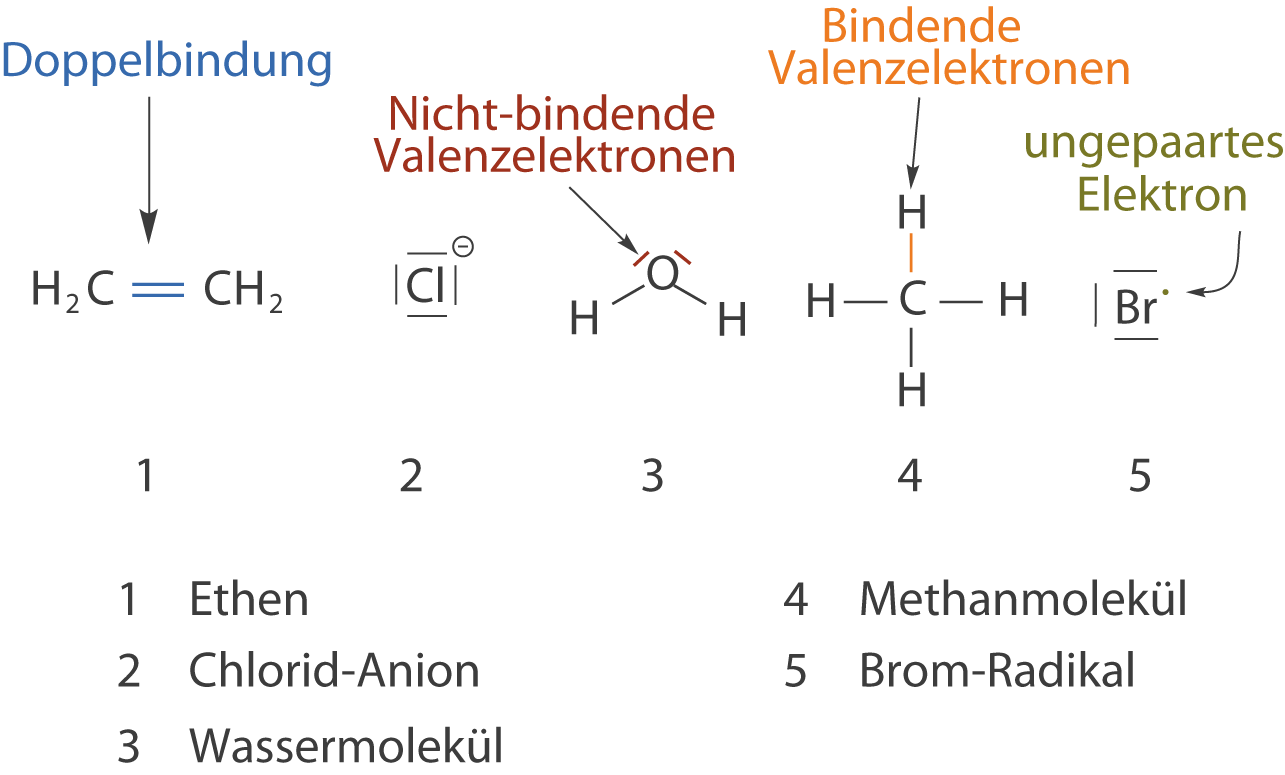
Abb. 1: Beispielatome, Ionen und Radikale mit ihren jeweiligen Valenzelektronen

Nun knüpfen wir die Bindungen und erhalten die jeweiligen Moleküle.

Abb. 2: Beispiele für Moleküle, Atome und Ionen in der Lewis-Schreibweise

Du kannst in Abbildung 2 sehen, dass wir Mehrfachbindungen, wie die Doppelbindung durch einen doppelten Strich darstellen. Eine Dreifachbindung ergibt sich demnach zu drei Strichen in der Valenzstrichformel. Im nächsten Schritt betrachten wir die Oktettregel, die uns in einfachen Fällen eine Möglichkeit an die Hand gibt mithilfe derer wir bewerten können, wieviele Bindungen ein Element ausbilden kann.

$\blacktriangleright \;$ Die Oktettregel

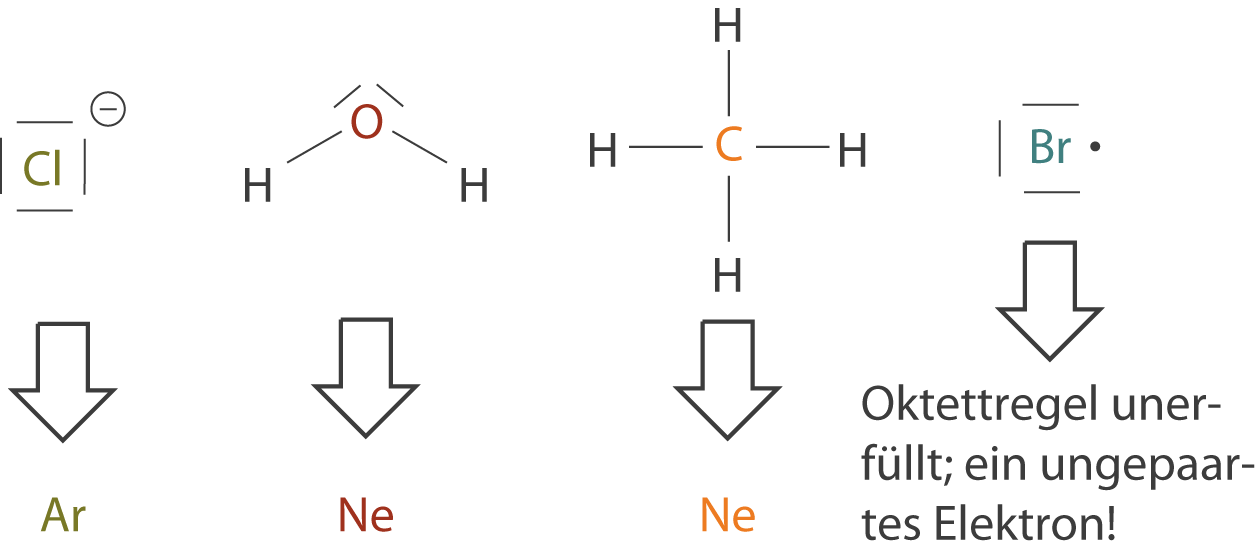
Schauen wir uns die Beispiele in Abbildung 1 und 2 genauer an, dann fällt auf, dass Sauerstoff und Kohlenstoff genau so viele Bindungen eingehen, dass sie in der Summe acht Valenzelektronen (Außenelektronen) aufweisen. Diesen Aspekt können wir mit der Oktettregel erklären, welche besagt, dass eine Elektronenkonfiguration von acht Valenzelektronen energetisch bevorzugt wird. Das bedeutet, dass Atome Elektronen entweder abgeben oder aufnehmen, um diese Oktettregel zu erfüllen. In diesem Zusammenhang spricht man auch davon, dass Elemente eine Edelgaskonfiguration bezüglich ihrer Valenzelektronen anstreben. Die Edelgase haben jeweils acht Valenzelektronen, mit Ausnahme von Helium, welches nur zwei Valenzelektronen aufweist, da es nicht mehr als diese beiden auf seiner äußersten Schale aufnehmen kann (vgl. Abb. 3).

Abb. 3: Beispiele zur Oktettregel und die beispielhaften Edelgaskonfigurationen

Beachte folgende Punkte:

Sauerstoff (O) und Kohlenstoff (C) gehen Bindungen mit dem Wasserstoff (H) ein, so dass die Oktettregel für sie erfüllt wird. Beide Elemente nehmen die Edelgaskonfiguration von Neon (Ne) ein.
Die Edelgaskonfiguration von Wasserstoff (H) entspricht der von Helium (He); hier sind nur zwei statt acht Valenzelektronen vorhanden.
Als Halogen muss ein Chloratom (Cl) nur ein Elektron aufnehmen, damit die Edelgaskonfiguration erfüllt ist. Wir erhalten das Chlorid-Anion, welches die Edelgaskonfiguration von Argon (Ar) hat.
Im Fall des Brom-Radikals ist die Oktettregel nicht erfüllt; ein Elektron bleibt ungepaart. Aus diesem Grund ist dieses Radikal auch sehr reaktiv, um schnellstmöglich an das fehlende Elektron zu kommen.

Wichtig:

Die Oktettregel ist nur für eine Auswahl an Elementen vernünftig anwendbar, z.B. für die Elemente der ersten und zweiten Periode. Im Fall von Schwefel versagt sie, was du am folgenden Beispiel sehen kannst: Schwefel bildet in Schwefelsäure sechs Bindungen aus, was effektiv zu zwölf und nicht zu acht Valenzelektronen führt.

$\blacktriangleright \;$ Die Grenzen der Lewis-Schreibweise: Mesomere Grenzformeln

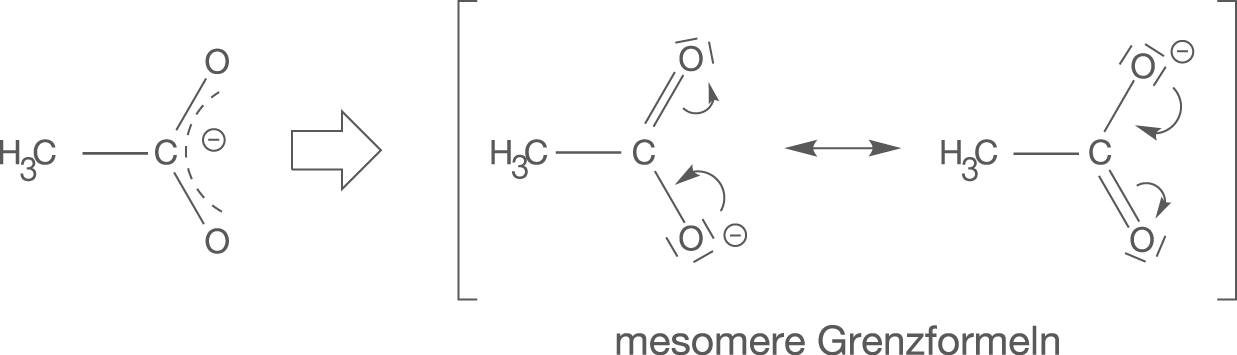
Die Lewis-Schreibweise oder Valenzstrichformel erlaubt es uns alle gebundenen und ungebundenen Elektronenpaare darzustellen, die eine feste Position innerhalb des betrachteten Moleküls, Ions etc. einnehmen. Wenn wir uns das Phänomen der Mesomerie anschauen, dann fällt auf worüber diese Darstellung keine Aussagen treffen kann (vgl. Abb. 4).

Abb. 4: Mesomerie am Beispiel des Acetat-Anions

Die Elektronen im Acetat-Anion sind realistisch gesehen ungefähr so verteilt, wie in der ersten Strukturformel dargestellt. Es existiert in dem Sinn überhaupt keine Doppelbindung und die negative Ladung ist zwischen den beiden Sauerstoffatomen verteilt. Verwenden wir hier die Valenzstrichformel, dann erhalten wir mesomere Grenzformeln. Diese stellen jeweils eine Grenzstruktur des Acetat-Ions dar, geben jedoch nicht die Realität wieder. Die negative Ladung sitzt weder am oberen noch am unteren O-Atom, sondern ist irgendwie dazwischen verteilt.

Was ist die kovalente Bindung?

Wir haben zwar bisher besprochen, wie wir kovalente Bindungen mithilfe der Valenzstrichformel darstellen können und wissen, dass kovalente Bindungen auch als Elektronenbindung bezeichnet werden können, dennoch wissen wir nicht, was eine kovalente Bindung tatsächlich ist.

Achtung:

Wir können die Frage nach den Eigenschaften einer kovalenten Bindung an dieser Stelle bzw. im Rahmen der Schul-Chemie nicht beantworten. Aus diesem Grund wollen wir die Informationen im Folgenden sehr knapp halten und einige Fragen und Tatsachen formulieren, die die außergewöhnlichen Eigenschaften der kovalenten Bindung aufzeigen. Es ist hier in keinem Fall notwendig Antworten bzw. Erklärungen zu finden. Wie bereits erwähnt, ist das im Rahmen des Schulwissens nicht möglich. Es ist viel wichtiger zu erkennen, dass eine kovalente Bindung sehr viel spannender und tiefgründiger ist, als ein einfacher Strich auf einem Blatt Papier.

Eine kovalente Bindung wird dadurch möglich, dass die Elektronen, die sich zwischen zwei Bindungspartnern befinden, ein Energiegewinn verzeichnen können. Salopp ausgedrückt könnte man auch sagen, dass sich die Elektronen an dieser Stelle „wohler fühlen“.
Im Folgenden findest du einige Fragen und Tatsachen, die wir hier zwar nicht beantworten bzw. erklären können, die dir aber einen Eindruck des außergewöhnlichen Wesens der kovalenten Bindung geben können.

Warum ist es für zwei Elektronen günstig im Fall einer kovalenten Bindung so nah beisammen zu sein, obwohl sie sich als Träger gleichnamiger Ladungen eigentlich abstoßen müssten?
Wieso ist die Position zwischen den Atomen für Elektronen überhaupt energetisch günstiger?
Das einfachste Molekül ist das $\boldsymbol{\text{H}_{2}^{+}}$ -Molekülkation, dessen Bindung nur durch ein Elektron zu Stande kommt!
Liegt ein Molekül mit einer Doppelbindung vor, dann befinden sich die Elektronen, die die zweite Bindung ausmachen nicht zwischen den gebundenen Atomen, sondern über und unter der Bindungsachse!

Die Ionenbindung

Konzept der Ionenbindung

$\blacktriangleright \;$ Ionen als Träger elektrischer Ladung

Ionen sind elektrisch geladene Atome oder Moleküle. Im Zusammenhang mit der Ionenbindung wollen wir uns auf die Bindung zwischen Metallen und Nicht-Metallen konzentrieren. Dementsprechend interessieren wir uns hier insbesondere für elektrisch geladene Atome.
Ionen können das Produkt von Oxidations- und Reduktionsprozessen sein, wie wir beispielhaft an der folgenden Reaktionsgleichung sehen können:

$2\,\text{Na}+\frac{1}{2}\;\text{O}_{2} \longrightarrow 2\,\text{Na}^{+}+\text{O}^{2-}$

Unter Konzept der kovalenten Bindung haben wir die Oktettregel kennen gelernt, die wir nun auf die an dieser Reaktion beteiligten Reaktanden anwenden können.

Als Alkalimetall (1. Hauptgruppe) besitzt Natrium (Na) ein Valenzelektron (Außenelektron). Dieses wird im Rahmen der Redox-Reaktion abgegeben, so dass die Elektronenkonfiguration des entstandenen $\text{Na}^{+}$ -Ions der von Neon (Ne) entspricht.
Sauerstoff (O) gehört zu den Chalkogenen (6. Hauptgruppe) besitzt also noch zwei „freie“ Plätze auf seiner Valenzschale, wo Elektronen aufgenommen werden können. Aus diesem Grund wird ein O-Atom zu einem $\text{O}^{2-}$ -Ion reduziert. Achtung: Normalerweise liegt Sauerstoff als $\text{O}_{2}$ vor.
Wir unterscheiden positiv geladenen Kationen und negativ geladenen Anionen.

$\blacktriangleright \;$ Elektrostatische Kräfte zwischen Ladungen

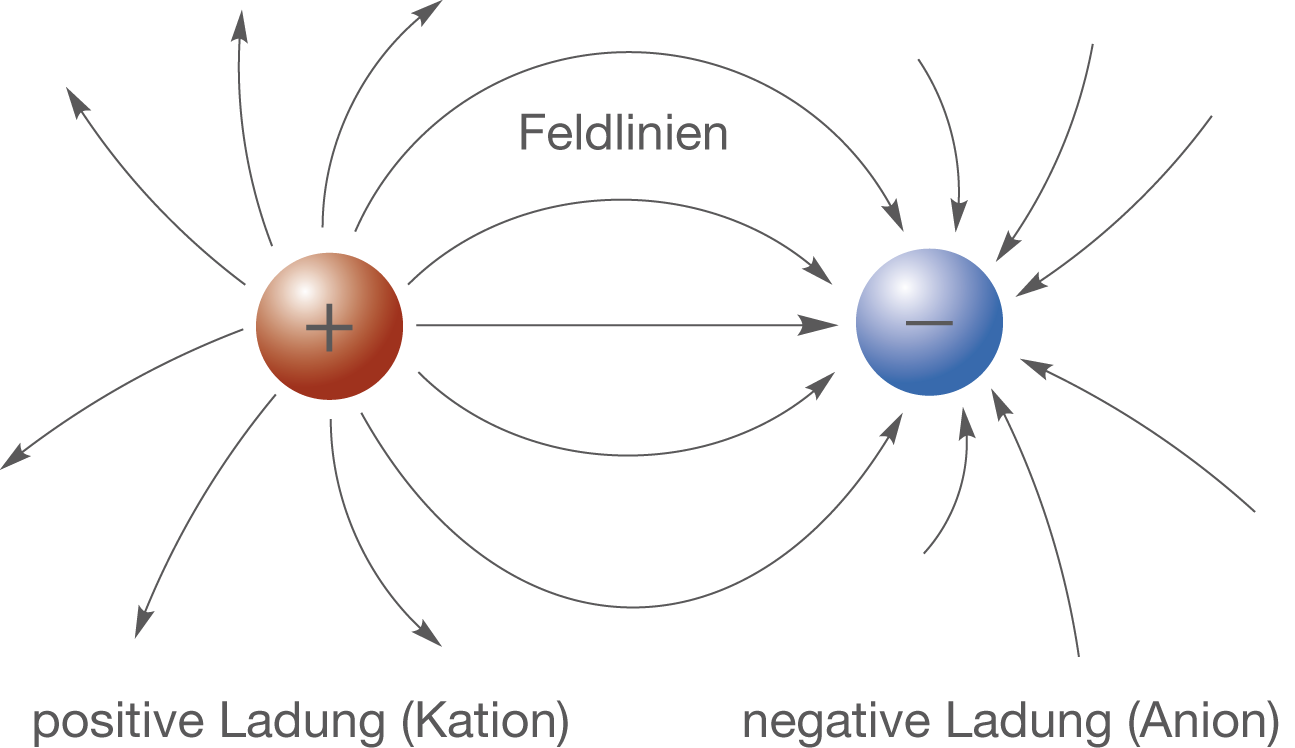
Wie wir gesehen haben, tragen Ionen elektrische Ladungen. Somit können wir die Gesetze der Elektrostatik für die Erklärung der Ionenbindung verwenden. Zwischen zwei Ladungen wirken elektrostatische Kräfte, die auf das elektrische Feld der Ladungen zurückgehen (vgl. Abb. 5).

Abb. 5: Elektrisches Feld zwischen einem Kation und einem Anion

Die elektrostatischen Kräfte zwischen diesen beiden Ladungen können wir mithilfe des Coulombschen Gesetzes beschreiben:

$F_{\text{c}}=\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{q_{1}\cdot q_{2}}{r^2}$

Hierbei ist $F_{\text{c}}$ die Coulombkraft, die zwischen den beiden Ladungen wirkt. $\frac{1}{4\pi\varepsilon_{0}}$ ist ein konstanter Vorfaktor, der uns an dieser Stelle nicht weiter interessieren soll. $q_{1}$ und $q_{2}$ sind die Ladungen unserer beiden Ionen und $r>0$ ist der Abstand zwischen den beiden Ionen. Wir wollen nun zwei Fälle unterscheiden, die für die Paarung der Ladungen im Fall unserer Ionen auftreten können.
Beachte: Wir gehen hier davon aus, dass jedes Ion nur einfach geladen ist, also jeweils genau eine Elementarladung $e$ trägt (vgl. ChemieLV-Skript Atommodelle und die Elektronenstruktur von Atomen). In der Formel entspricht $q_{1}=q_{2}=e$ .
Mithilfe der obigen Formel für die Coulombkraft $F_{\text{c}}$ können wir erklären, wann sich zwei Ladungen gegenseitig anziehen und wann sie sich abstoßen. Diese Begründung findest du im folgenden Kasten. Achte darauf, dass die Zahlenwerte hier gar nicht interessieren, sondern nur das Vorzeichen von $F_{\text{c}}$ . Wenn wir von gleichnamigen Ladungen sprechen, dann geht es um Ladungen $q$ mit dem gleichen Vorzeichen. Im Fall von ungleichnamigen Ladungen haben wir zwei Ladungen $q$ , die sich im Vorzeichen voneinander unterscheiden.

Gleichnamige Ladungen: $q_{1}=q_{2}$

Haben wir zwei gleichnamige Elementarladungen, dann erhalten wir mit $q_{1}=q_{2}=e$ :

$F_{\text{c}}=\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{e^2}{r^2}>0$

Laut Konvention bedeutet $F_{\text{c}}>0$ , dass es sich um eine abstoßende Kraft zwischen den beiden Ladungen handelt. Das entspricht unserer Erfahrung: gleichnamige Ladungen stoßen sich ab.

Ungleichnamige Ladungen: $q_{1}=-q_{2}$

Haben wir zwei ungleichnamige Elementarladungen, also bspw. ein Elektron und ein Proton, dann erhalten wir mit $q_{1}=-q_{2}\rightarrow e=-e$ :

$F_{\text{c}}=\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{e\cdot (-e)}{r^2}$ $=\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{-e^2}{r^2}<0$

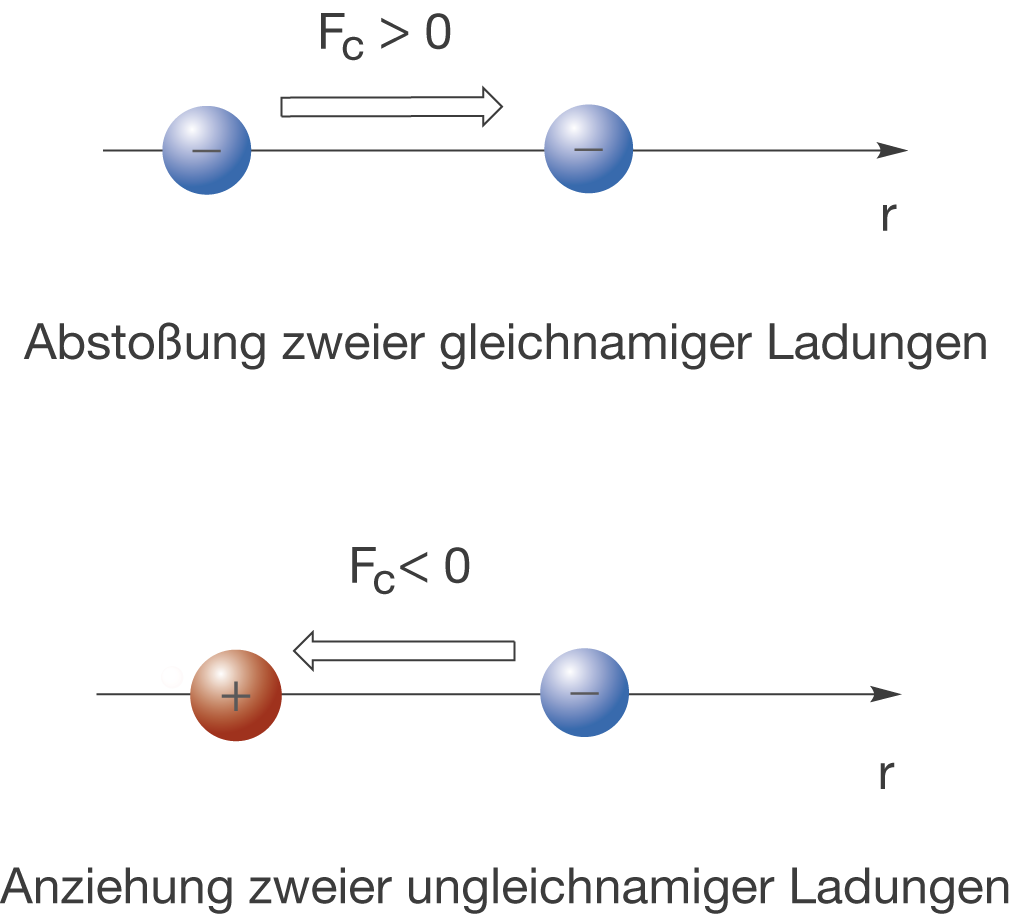
Hier bedeutet $F_{\text{c}}<0$ nun, dass es sich um eine anziehende Kraft zwischen den beiden Ladungen handelt. Das entspricht wiederum unserer Erfahrung: ungleichnamige Ladungen ziehen sich an.

Das gegenseitige Anziehen und Abstoßen elektrischer Ladungen ist in Abbildung 6 dargestellt. Dabei wird jeweils die Position des linken Ladungsträgers fest fixiert und wir schauen uns die Reaktion des rechten Ladungsträgers an.

Abb. 6: Abstoßende (ob.) und anziehende Kräfte (unt.) zwischen Ladungen

Im oberen Fall haben wir zwei gleichnamige Ladungen (gleiches Vorzeichen), was in einer abstoßenden Coulombkraft ( $F_{\text{c}}>0$ ) resultiert. Den gegensätzlichen Fall kannst du oben sehen: Zwischen einer positiven und einer negativen Ladung kommt es zur Anziehung, da $F_{\text{c}}<0$ (vgl. Kasten S. 5).

$\blacktriangleright \;$ Die Ionenbindung

Wir wollen uns nun mit dem bisher erarbeiteten Wissen der Ionenbindung zuwenden. Beispielhaft betrachten wir hier Natriumchlorid (NaCl), welches du als gewöhnliches Kochsalz aus der Küche kennst. Hieran können wir schon den ersten wichtigen Aspekt der Ionenbindung erkennen: diese liegt zwischen Metallen und Nicht-Metallen vor. Natrium (Na) ist in diesem Fall das Metall und Chlor (hier als Chlorid) das Nicht-Metall; Chlor zählt zu den Halogenen (7. Hauptgruppe).
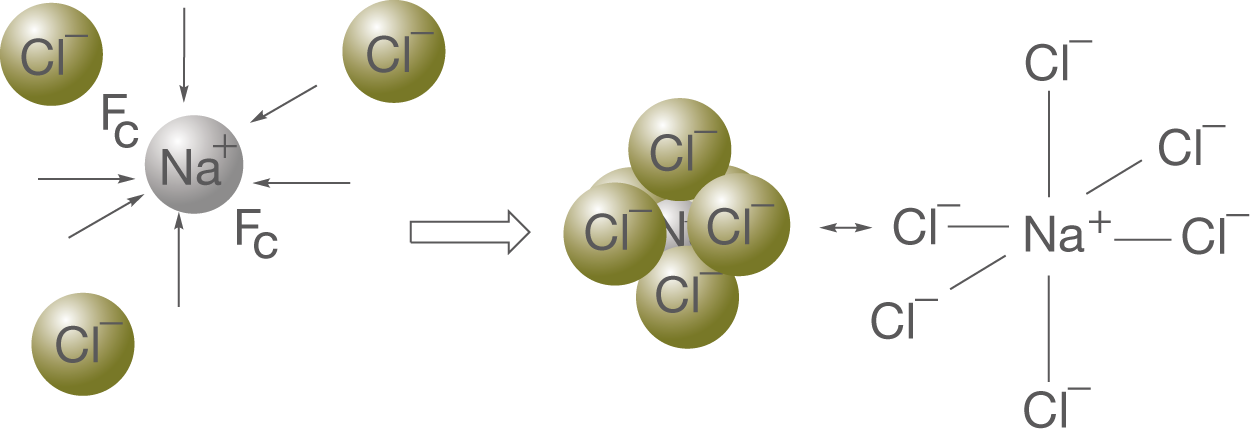
In Abbildung 6 haben wir gesehen, dass zwischen zwei ungleichnamigen Ladungen anziehende Coulombkräfte $F_{\text{c}}$ wirken. Wichtig ist nun, dass diese Kräfte in alle Raumrichtungen gleich stark ausgeprägt sind. Nehmen wir nun beispielhaft ein $\text{Na}^{+}$ -Kation und $\text{Cl}^{-}$ -Anionen, dann werden sich die Anionen so um das Kation anordnen, dass ihr Abstand so gering wie möglich ist. Anhand von Abbildung 7 können wir nun die Grundlagen der Ionenbindung und einige wichtige Begriffe erklären.

Abb. 7: Ionenbindung auf der Grundlagen elektrostatischer Wechselwirkungen von Kation und Anionen

Koordinationszahl: Die Koordinationszahl KZ gibt an, wieviele Ionen um ein Zentralion zu finden sind. In unserem Beispiel ist die Koordinationszahl von Natrium $\text{KZ}=6$ , da es von sechs Chlorid-Anionen koordiniert wird.
Die Koordination des Kations erfolgt so, dass die negativen Anionen gleichzeitig auch den größten Abstand zueinander haben (vgl. Abb. 7). Bedenke: Hierbei handelt es sich um den Einfluss der abstoßenden Coulombkräfte zweier gleichnamiger Ladungen.
Die Größe, die die Fähigkeit zur Ausbildung einer Ionenbindung beschreibt, ist die Elektronegativität (vgl. ChemieLV-Skript Periodensystem der Elemente - Gruppen und Tendenzen). Je größer die Differenz der beiden Elektronegativitätswerte, desto höher ist der ionische Charakter der Bindung.

Eigenschaften der Ionenbindung

$\blacktriangleright \;$ Das Kristallgitter

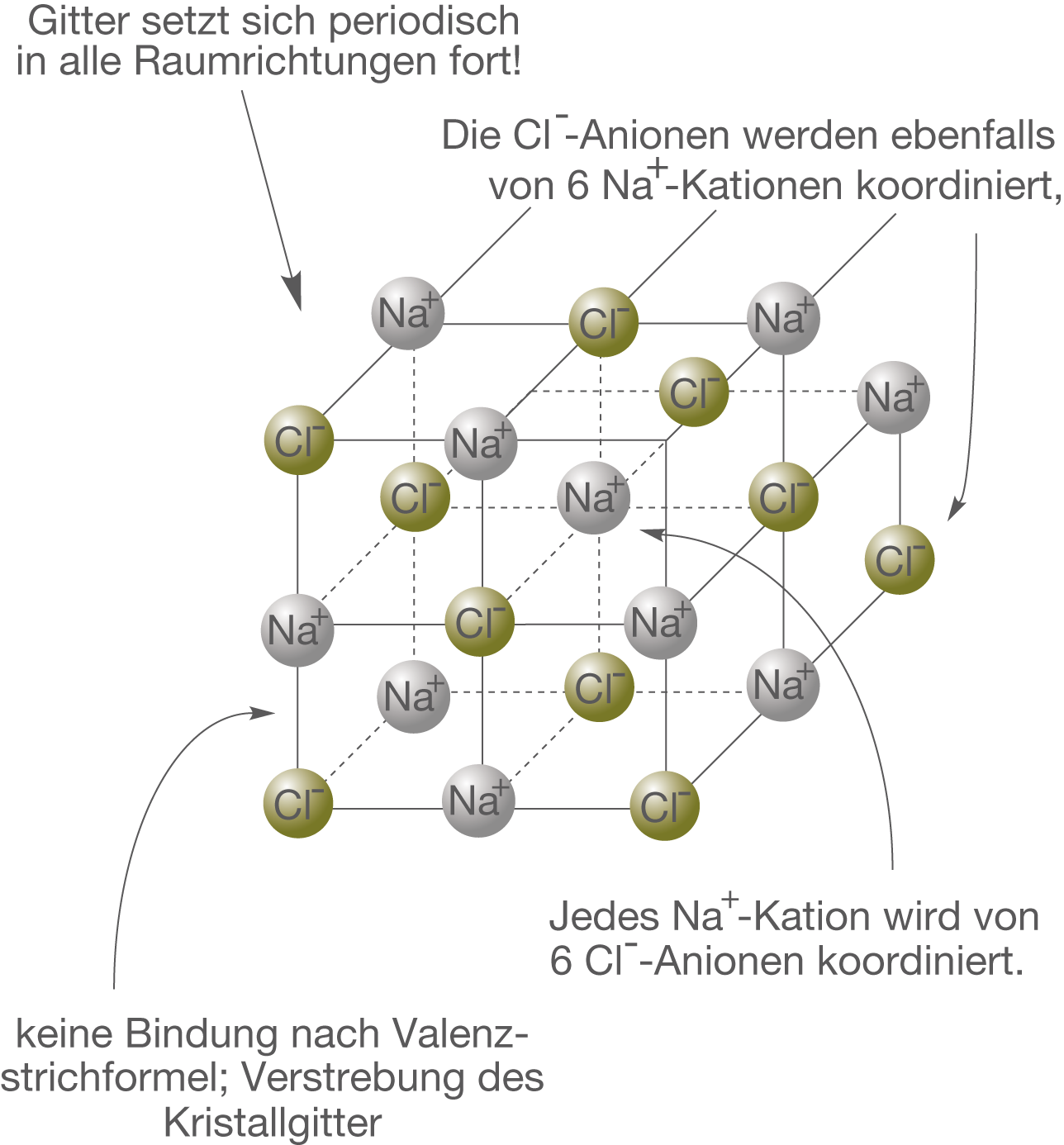
Wir haben gesehen, dass im Fall des NaCl das $\text{Na}^{+}$ -Kation von sechs $\text{Cl}^{-}$ -Anionen koordiniert ist. Diese Struktur setzt sich nun periodisch in alle Raumrichtungen fort und bildet somit das Kristallgitter (vgl. Abb. 8).

Abb. 8: Ionen bilden Kristallgitter aus

Periodisch bedeutet hier, dass auf jedes $\text{Na}^{+}$ -Kation ein $\text{Cl}^{-}$ -Anion folgt. Diese Eigenschaft ist charakteristisch für Stoffe, die aus Ionen aufgebaut sind. Solche nennen wir im allgemeinen Salze. Das Beispiel NaCl stellt einen der einfachsten Strukturtypen eines Kristallgitters da. Es existiert eine Vielzahl verschiedener Kristallgitter, die auf die beteiligten Ionen und deren Eigenschaften zurückgehen.
Im Bezug auf die Notation von bspw. NaCl in einer Reaktionsgleichung ist der folgende Aspekt sehr wichtig: Es gibt kein NaCl-Molekül! Wir haben gesehen, dass

die elektrostatischen Kräfte in alle Raumrichtungen gleich stark wirken, was hier dazu führte, dass sich sechs $\text{Cl}^{-}$ -Anionen um ein $\text{Na}^{+}$ -Kation anlagern.
sich das daraus entstehende Kristallgitter in alle Raumrichtungen fortsetzt.

Die Summenformel NaCl sagt uns etwas über das Verhältnis der Ionen im Salz und stellt kein Molekül dar, welches aus zwei Ionen bestehen würde. Letzteres ist schon aufgrund der elektrostatischen Wechselwirkungen nicht möglich, wie wir oben unter Punkt eins sehen konnten.

$\blacktriangleright \;$ Salze sind Festkörper

Salze werden durch elektrostatische Wechselwirkungen zwischen den beteiligten Ionen zusammengehalten. Diese Ionenbindung ist eine starke Bindung, sodass wir es in diesem Fall mit Festkörpern zu tun haben.
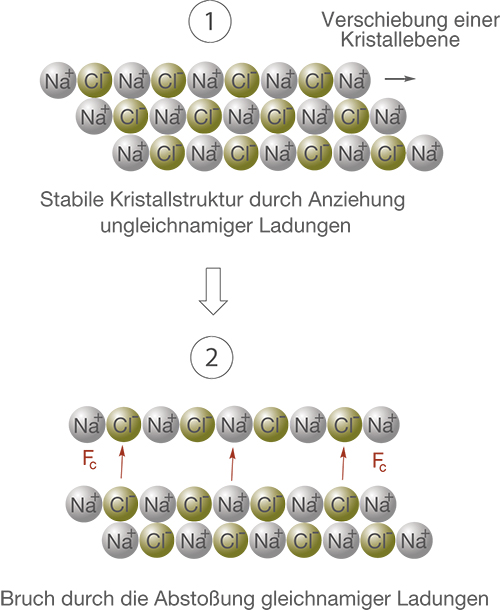
Anhand der Struktur des Kristallgitters und den Eigenschaften der Ionenbindung können wir uns hier nun erklären, warum ein Salz ein sprödes Material ist, dass sich nicht verformen lässt sondern leicht bricht (vgl. Abb. 9).

Abb. 9: Sprödes Verhalten von Salzen

Wir sehen in Abbildung 9 das Kristallgitter von NaCl aus Abbildung 8 von der Seite.

Hier sind die $\text{Na}^{+}$ -Kationen perfekt von den $\text{Cl}^{-}$ -Anionen koordiniert: Das Salz ist stabil. Üben wir nun eine Kraft auf den Salzkristall aus, beispielsweise indem wir mit einem Hammer draufschlagen, dann kann sich eine Kristallebene verschieben.
Nach der Verschiebung ist die optimale Koordination der $\text{Na}^{+}$ -Kationen nicht mehr gegeben. Nun liegen gleichnamig geladene Ionen übereinander. Dies führt zu abstoßenden Coulombkräften $F_{\text{c}}$ zwischen den gleichnamig geladenen Ionen, was die Zerstörung der Kristallstruktur zur Folge hat.

Die metallische Bindung

Konzept der metallischen Bindung

$\blacktriangleright \;$ Atomare Struktur von Metallen

Metalle findest du vor allem in den ersten beiden Hauptgruppen des Periodensystems der Elemente (PSE), in Form der Alkali- und Erdalkalimetalle sowie in den Nebengruppen. Uns interessiert an dieser Stelle kein spezifisches Metall, sondern wir wollen uns die Eigenschaften anschauen, die jedem Metall zu eigen sind und ein solches überhaupt erst zu einem Metall machen.
Die Struktur von Metallen ist vergleichbar mit der von Salzen: Der Aufbau basiert auf Ionen und diese sind in einem Kristallgitter angeordnet. Die Kristallgitter unterscheiden sich aber nicht so stark wie im Fall der Salze. Bei den Metallen geht es insbesondere darum, dass die näherungsweise kugelförmigen Kationen so dicht wie möglich aneinander gepackt vorliegen (vgl. Abb. 10). Hierbei handelt es sich schon um eine Besonderheit von Metallen: Sie sind aus Kationen aufgebaut und enthalten keine Anionen.

Abb. 10: Kationen liegen im Metall in sogenannten dichtesten Packungen vor

Wie in Abbildung 10 dargestellt könnte ein beispielhaftes Kristallgitter eines Metalls aussehen, wenn wir von der Seite darauf schauen (vgl. hierzu das Beispiel des Salzes in Abb. 9).

$\blacktriangleright \;$ Das Elektronengas-Modell

Die metallische Bindung können wir auf Grundlage des Elektronengas-Modells beschreiben. Dazu beginnen wir mit zwei allgemeinen Eigenschaften von Metallen, die uns letztendlich zu dieser Modellvorstellung führen werden.

Metallatome haben im Allgemeinen eine relativ geringe 1. Ionisierungsenergie, d.h. sie geben relativ leicht ein Elektron ab; sie werden relativ leicht ionisiert.
Metall als Festkörper sind elektrisch Leitfähig.

Wir wollen diese beiden Erkenntnisse nun kombinieren, um das Elektronengas-Modell plausibel darzustellen.
Nach Punkt eins wissen wir, dass Metallatome relativ leicht ionisiert werden können. Dies führt dazu, dass wir freie Elektronen erhalten.
Aus der Physik wissen wir, dass ein elektrischer Strom als Ladung pro Zeit beschrieben wird, also eine Größe darstellt, die uns angibt wieviele Elektronen pro Zeiteinheit fließen. Wie du aus dem Alltag bestimmt weist, leiten Metalle Strom vergleichsweise gut. Demnach müssen hier freie Ladungsträger vorhanden sein, die fließen können: Elektronen. Wenn wir nun die relativ geringe Ionisierungsenergie von Punkt eins beachten, dann wird plausibel, dass wir dadurch eben genau diese freien Ladungsträger erhalten, die für die gute elektrische Leitfähigkeit verantwortlich sind.
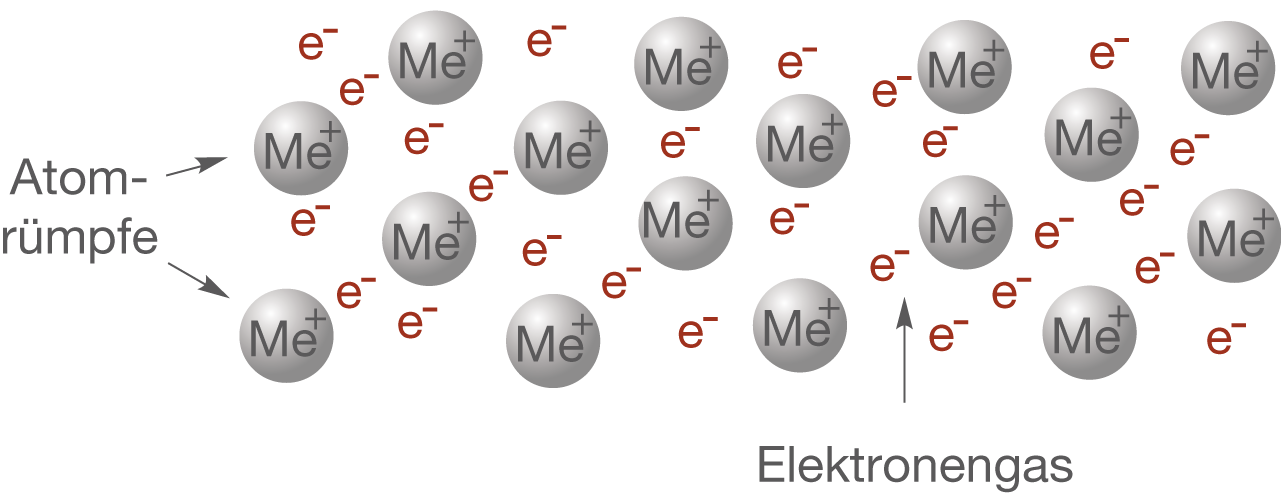
In Abbildung 11 siehst du eine beispielhafte Darstellung der Elektronengas-Modells an welchem wir die gerade erarbeiteten Tatsachen erklärend zusammenfassen können.

Abb. 11: Elektronengas-Modell

Jedes Metallatom liegt als Kation vor und trägt Valenzelektronen zum Elektronen-Gas bei. Das Elektronen-Gas beschreibt die freien Elektronen im Metall, die sich ungehindert bewegen können und nicht an ihre jeweiligen Atome gebunden sind. Die ionisierten Metallkationen werden als Atomrümpfe bezeichnet. Die Ladungen innerhalb eines Metalls neutralisieren sich nach außen hin, weil genau gleich viele positive wie negative Ladungen vorhanden sind.

Eigenschaften von Metallen

$\blacktriangleright \;$ Leitfähigkeit

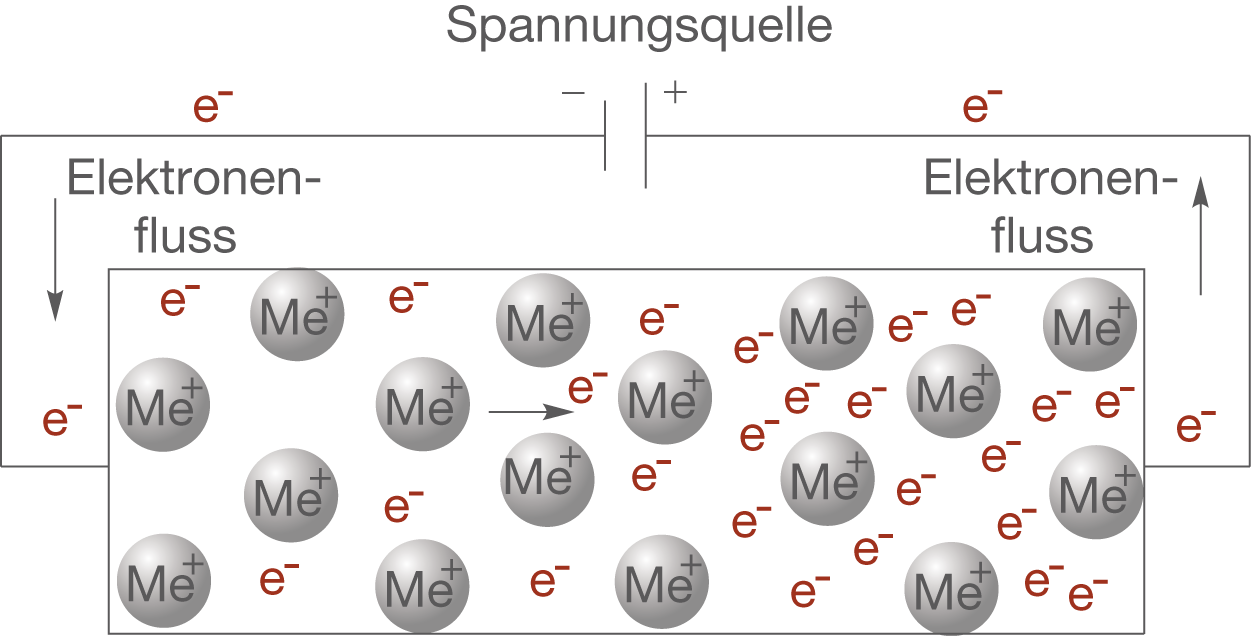
Die Leitfähigkeit von Metallen unterscheidet sich von Metall zu Metall und ist beispielsweise im Fall von Kupfer sehr stark ausgeprägt. Anhand von Abbildung 12 können wir erkennen, was passiert, wenn wir eine Spannung an ein Metallblock anlegen.

Abb. 12: Leitfähigkeit von Metallen

Durch das Anlegen einer Spannung $U$ bewegen sich Elektronen im Metall: Es fließt ein Strom.

$\blacktriangleright \;$ Verformbarkeit

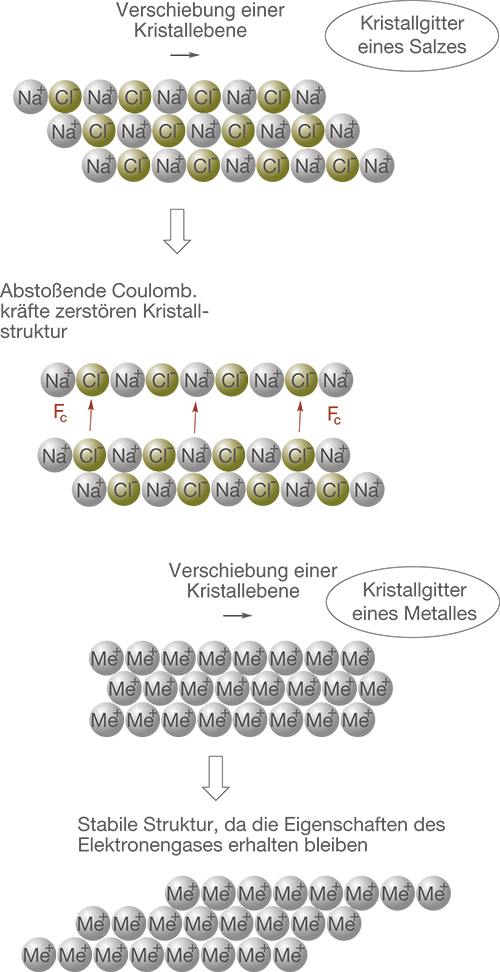
Die Verformbarkeit von Metallen wollen wir uns vergleichend zu den Salzen anschauen. So können wir schön sehen, warum es sich Fall von Salzen um spröde und im Fall von Metallen um relativ flexible Materialien handelt. Wir stellen das Kristallgitter eines Metalls und das eines Salzes gegenüber (vgl. Abb. 13).

Abb. 13: Die Kristallgitter eines Metalls (ob.) und eines Salzes (unt.)

Die Struktur des Salzes wird unter Krafteinwirkung zerstört, da sich gleichnamige Ladungen abstoßen. Die Verformung des Metalls führt nicht dazu, dass abstoßende Kräfte wirksam werden. Somit bleibt die Stabilität erhalten.

Zwischenmolekulare Kräfte und Wechselwirkungen

Dipol-Dipol-Wechselwirkungen

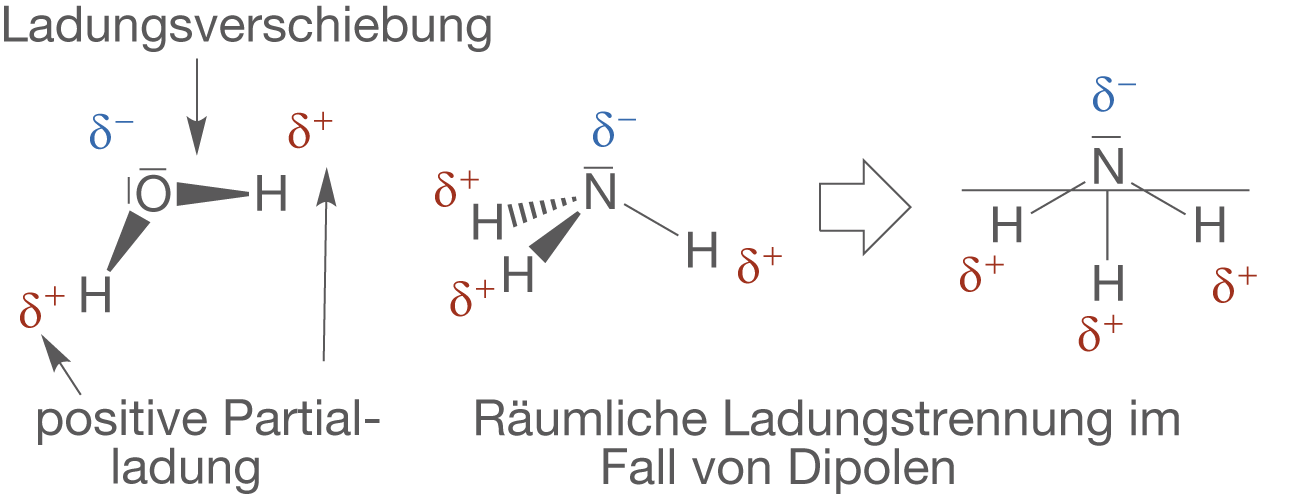
Wenn wir uns Verbindungen anschauen, die aus unterschiedlichen Atomen zusammengesetzt sind, dann fällt uns vor dem Hintergrund der Elektronegativität auf, dass die Elektronen der Bindung sich näher an einem der Bindungspartner befinden. Unter Elektronegativität verstehen wir die Eigenschaft von Elementen Elektronen an sich zu ziehen. Je größer die Elektronegativität, desto stärker zieht ein Element Elektronen zu sich. Das Ergebnis sind polare Atombindungen (vgl. Abb. 14).

Abb. 14: Polare Atombindungen, Dipole die räumliche Trennung von Partialladungen $\delta^{+}/\;\delta^{-}$

Du kannst dir merken, dass du bei einem Dipol-Molekül die Partialladungen immer so räumliche Trennen kannst, dass ein Teil des Moleküls ganz klar negativ und der andere Teil ganz klar positiv geladen ist. In Abbildung 14 ist diese Tatsache am Beispiel von Ammoniak ( $\text{NH}_{3}$ ) dargestellt.
Des Weiteren können wir an den Dipolen erkennen, was es bedeutet, dass die chemische Bindung nur selten in Form eines Typs vorkommt. Obwohl wir hier kovalente Bindungen zwischen den Bindungspartnern vorliegen haben, erhalten wir durch die Polarisierung eine effektiv Ladungsverschiebung. Diese führt zu einem teilweise ionischen Charakter polarisierter Bindungen.
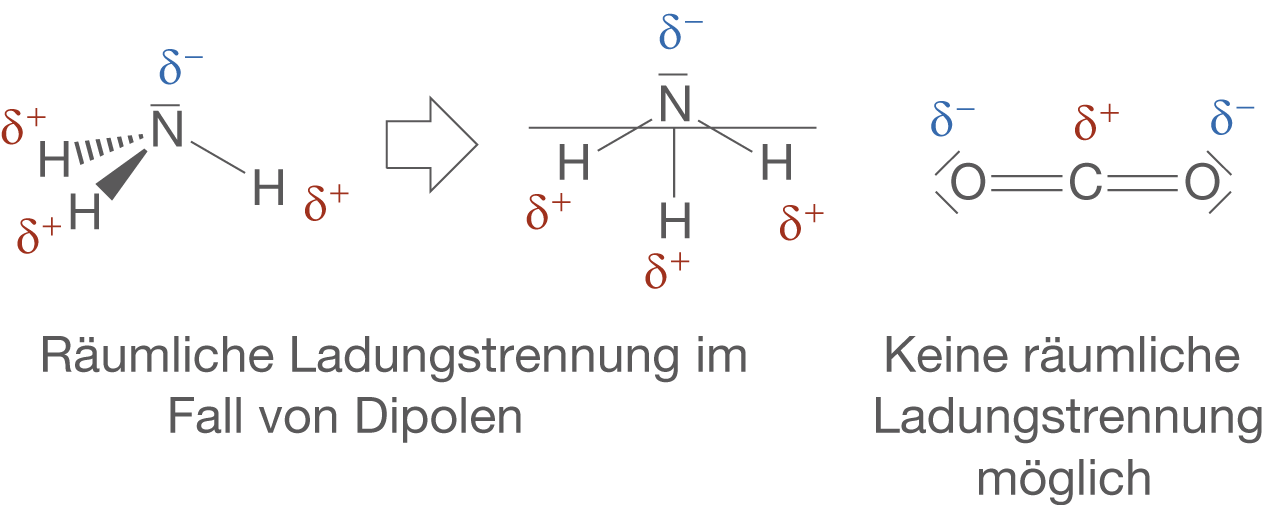
Die räumliche Ladungstrennung ist im Fall von Dipolen besonders wichtig, da der Ladungsschwerpunkt des Moleküls hier nicht zusammenfällt. Der Ladungsschwerpunkt eines Moleküls fällt genau dann zusammen, wenn du keine räumliche Ladungstrennung einzeichnen kannst. Wir wollen uns anhand der folgenden Abbildung 15 klar machen, was das bedeutet.

Abb. 15: Unterschied zwischen Dipolen und Molekülen ohne räumlicher Ladungstrennung

Solche Dipol-Moleküle treten nun mit anderen Dipolen in Wechselwirkung - die Dipol-Dipol-Wechselwirkung, die wiederum auf die elektrostatischen Wechselwirkungen zurückgeht, die wir zu Beginn von Konzept der Ionenbindung besprochen haben. Nehmen wir Wasser als Beispiel, dann führt diese Wechselwirkung dazu, dass sich die $\text{H}_{2}\text{O}$ -Moleküle in einem Wassertropfen auf Grundlage der Dipol-Dipol-Wechselwirkung gegenseitig beeinflussen und damit bspw. zu der relativ hohen Siedetemperatur von Wasser beitragen.

Wasserstoffbrückenbindungen

$\blacktriangleright \;$ Grundlagen

Wasserstoffbrückenbindungen oder kurz auch H-Brücken gehen auf stark polarisierte H-Atome zurück. Hierbei kommen vor allem H-Atome in Frage, die an

Sauerstoffatomen (O-Atome) gebunden sind, bspw. im Fall von Carbonsäuren oder Wasser.
Stickstoffatomen (N-Atomen) gebunden sind, bspw. im Fall von Ammoniak oder Peptidgruppen.
Fluor- oder Chloratomen gebunden sind, wie bspw. im Fall von Salzsäure.

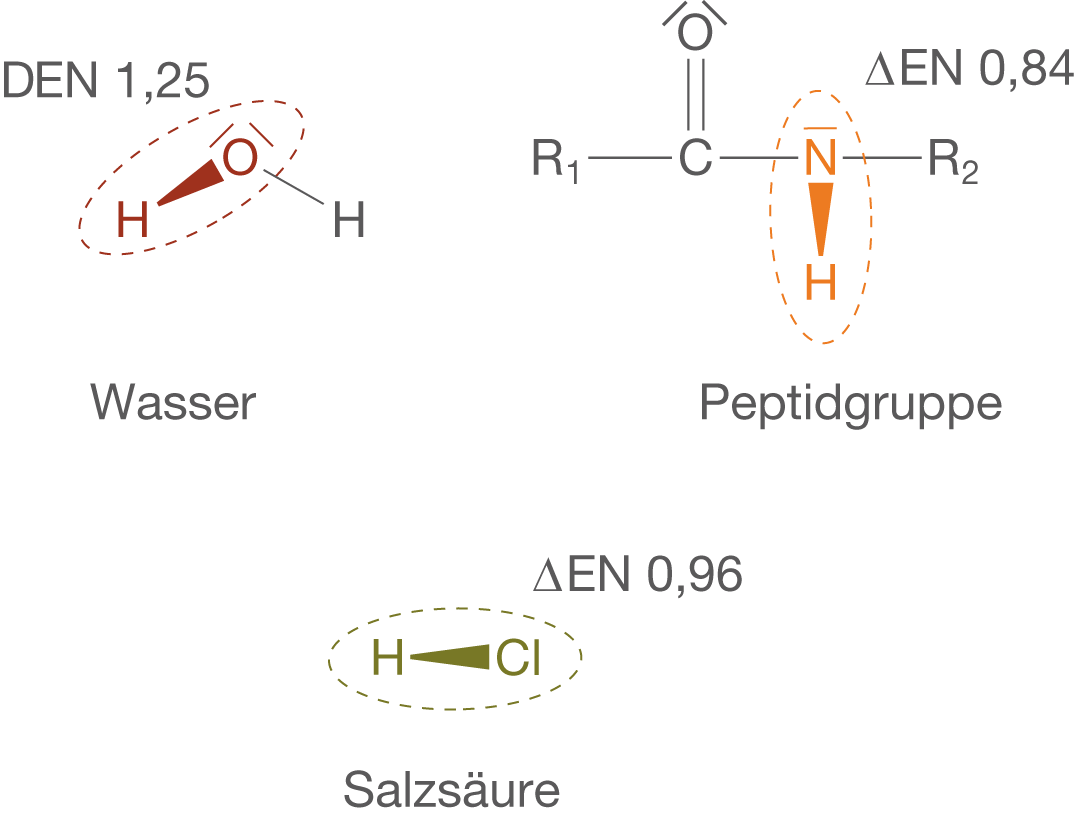
Diese Polarisierung kommt durch große Unterschiede in der Elektronegativität der beiden Bindungspartnern zu Stande, wie wir bereits bei den Dipol-Dipol-Wechselwirkungen sehen könnten. In Abbildung 16 siehst du beispielhaft einige der angesprochenen Verbindungen, die jeweiligen Elektronegativitäten sowie die Elektronenverteilung der betroffenen Bindung.

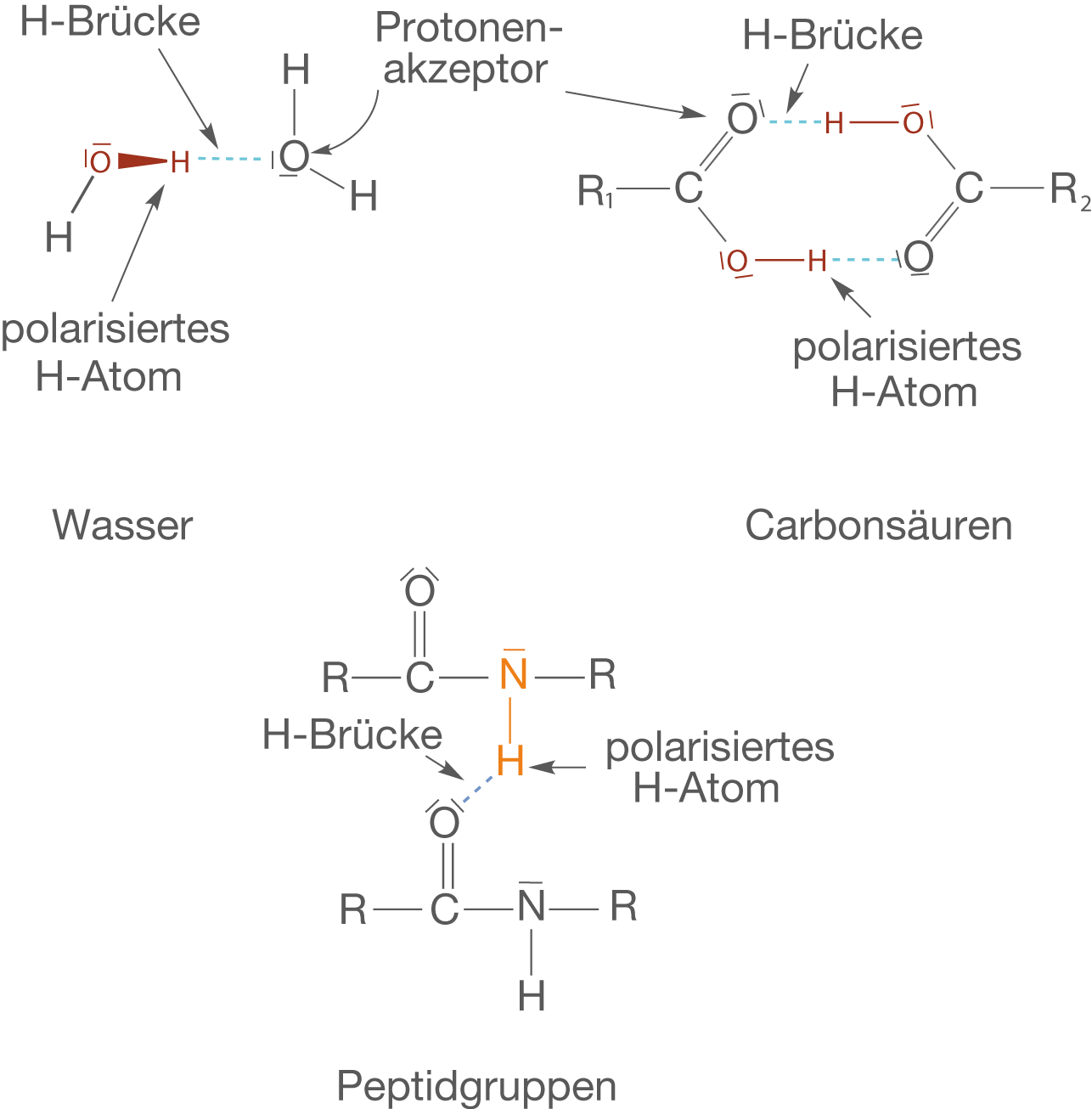
Abb. 16: Polarisierung des H-Atoms durch relativ große Unterschiede in der Elektronegativität

Treten nun Protonenakzeptoren mit einem freien Elektronenpaar auf, wie beispielsweise Sauerstoff oder Stickstoff, dann treten diese freie Elektronen mit den stark polarisierten H-Atomen in Wechselwirkung: Es bilden sich Wasserstoffbrückenbindungen aus.

$\blacktriangleright \;$ Wichtige Fälle des Auftretens von H-Brücken

Es gibt eine Menge sehr relevanter Beispiele, die für H-Brücken in Frage kommen. Wir beschränken uns hier auf Wasser, Carbonsäuren und Peptidgruppen (vgl. Abb. 17).

Abb. 17: Wasserstoffbrückenbindungen am Beispiel von Wasser, einer Carbonsäure und der Peptidgruppe

Ein sehr prominentes Beispiel, dass wir hier nicht unerwähnt lassen wollen sind die Wasserstoffbrückenbindungen zwischen den Nucleobasen der DNA. Hier sind diese zwischenmolekularen Wechselwirkungen dafür verantwortlich, dass die Doppelhelixstruktur zusammengehalten wird (vgl. ChemieLV-Skript DNA-Träger der Erbinformation).

Van-der-Waals-Kräfte

$\blacktriangleright \;$ Grundlagen

An dritter Stelle stehen die van-der-Waals-Kräfte (vdW-Kräfte), die schwächsten zwischenmolekularen Wechselwirkungen. Wie im Fall der Dipol-Dipol-Wechselwirkungen sind auch die vdW-Kräfte elektrostatischer Natur, gehen also auf die Wechselwirkung von Ladungen zurück.
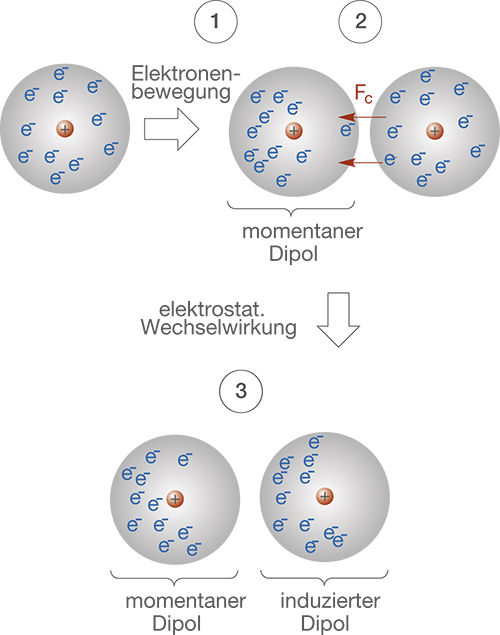
Der große Unterschied liegt jedoch darin begründet, dass die vdW-Kräfte gleichsam von der Elektronenverteilung innerhalb eines Moleküls abhängen. Dazu rufen wir uns ins Gedächtnis, dass Elektronen nicht fest lokalisiert sind, sondern sich im Rahmen ihrer Aufenthaltsbereiche (Orbitale) bewegen. Das bedeutet, dass es zu einer Situation kommen kann, in welcher in einem Bereich mehr Elektronen vorhanden sind, was einer effektiven Ladungstrennung entspricht. In diesem Zusammenhang spricht man auch von einem momentanen Dipol, da sich die Ladungstrennung durch die Bewegung der Elektronen schnell wieder auflösen kann. Haben wir jedoch den Fall eines momentanen Dipols, dann wirkt sich dessen Ladungsverteilung auf nahegelegen Moleküle aus: gleichnamige Ladungen stoßen sich ab und ungleichnamige Ladungen ziehen sich an. Wir erhalten induzierte Dipole (vgl. Abb. 18).

Abb. 18: van-der-Waals-Kräfte, momentane und induzierte Dipole

Zufällige Elektronenbewegung führen zu einer spontanen Ladungstrennung: Es entsteht ein momentaner Dipol. Dieser existiert nur für einen kurzen Zeitraum, da sich die Elektronen weiterbewegen.
Die ungleiche Ladungsverteilung führt zu elektrostatischen Wechselwirkungen mit anderen Molekülen, die sich in nächster Nähe befinden.
Auf Grundlage der elektrostatischen Wechselwirkungen wird in anderen Molekülen eine Elektronenverschiebung herbeigeführt (induziert): Es entsteht ein induzierter Dipol.

$\blacktriangleright \;$ Auftreten von van-der-Waals-Kräften

Die van-der-Waals-Kräfte sind im Fall aller Moleküle vertreten, haben aber je nachdem einen schwankenden Einfluss. Sind beispielsweise auch H-Brücken vorhanden, so dominieren diese. Van-der-Waals-Kräfte besitzen nur eine sehr kurze Reichweite, weswegen sie insbesondere die nächsten Nachbarn beeinflussen. Sie werden dann relevant, wenn sehr große, unpolare Moleküle vorliegen. Dies ist beispielsweise bei biologischen und künstlichen Makromolekülen wie Cellulose und Polyethylen der Fall. Des Weiteren spielen auch aromatische Verbindungen eine große Rolle, da hier ebenfalls sehr viele Elektronen vorliegen, die die van-der-Waals-Kräfte stärken. Hast du beispielsweise einen Kunststoff, der aromatische Reste in seiner Polymerstruktur aufweist, dann ist dieser widerstandsfähiger als ein vergleichbarer Kunststoff ohne aromatische Reste.

Zusammenfassung

Als chemische Bindung bezeichnen wir das Phänomen, welches dazu führt, dass Atome in Form von Molekülen bzw. chemischen Verbindungen zusammengehalten werden.
Es gibt drei Bindungstypen: kovalente, ionische und metallische Bindungen.
Die kovalente Bindung basiert auf einem Energiegewinn der Bindungselektronen.
Die Lewis-Schreibweise oder Valenzstrichformel erlaubt die Darstellung von kovalenten Bindungen.
Im Fall der Mesomerie und polarisierter Moleküle versagt die Darstellung der Valenzstrichformel.
Die Oktettregel besagt, dass Atome bestrebt sind ihrer äußerste Schale mit acht Elektronen aufzufüllen, um die Edelgaskonfiguration zu erreichen. Die Regel ist vor allem auf Elemente der ersten Periode anwendbar.
Die Ionenbindung basiert auf elektrostatischen Wechselwirkungen ungleichnamiger Ladungen. Die Ladungsträger nennt man Ionen: positive Kationen und negative Anionen.
Ionische Verbindungen sind Festkörper mit einem Kristallgitter.
Die metallische Bindung wird durch das Elektronengas-Modell beschrieben. Hierbei sind die positiven Atomrümpfe von freien Elektronen umgeben, die für die charakteristischen Eigenschaften des Metalls verantwortlich sind.
Charakteristische Eigenschaften von Metallen sind bspw. eine gute Leitfähigkeit und Verformbarkeit.
Zwischenmolekulare Kräfte können in Wasserstoffbrückenbindungen, Dipol-Dipol-Wechselwirkungen und van-der-Waals Kräfte unterschieden werden.
Dipole bilden sich aus, wenn die Elektronen aufgrund von Elektronegativitätsunterschieden unregelmäßig in Molekülen verteilt sind. Dipol-Dipol-Wechselwirkungen sind elektrostatische Wechselwirkungen auf Grundlage dieser Ladungsverschiebung.
Wasserstoffbrückenbindungen bilden sich zwischen stark polarisierten H-Atomen und einem Protonenakzeptor aus. Sie zählen zu den stabilsten zwischenmolekularen Wechselwirkungen.
Van-der-Waals Kräfte gehen auf die Elektronenbewegung zurück. Es können sich spontan räumliche Ladungstrennungen ergeben, die momentane Dipole genannt werden.
Momentane Dipole sorgen dafür, dass in naheliegenden Molekülen ebenfalls ein Dipol induziert wird. Induzierte Dipole entstehen.
Van-der-Waals Kräfte sind insbesondere im Fall großer, unpolarer Makromoleküle relevant, wie bspw. bei Kunststoffen.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]